High-accuracy Ising machine using Kerr-nonlinear parametric oscillators with local four-body interactions

Abstract

A two-dimensional array of Kerr-nonlinear parametric oscillators (KPOs) with local four-body interactions is a promising candidate for realizing an Ising machine with all-to-all spin couplings, based on adiabatic quantum computation in the Lechner–Hauke–Zoller (LHZ) scheme. However, its performance has been evaluated only for a symmetric network of three KPOs, and thus it has been unclear whether such an Ising machine works in general cases with asymmetric networks. By numerically simulating an asymmetric network of more KPOs in the LHZ scheme, we find that the asymmetry in the four-body interactions causes inhomogeneity in photon numbers and hence degrades the performance. We then propose a method for reducing the inhomogeneity, where the discrepancies of the photon numbers are corrected by tuning the detunings of KPOs depending on their positions, without monitoring their states during adiabatic time evolution. Our simulation results show that the performance can be dramatically improved by this method. The proposed method, which is based on the understanding of the asymmetry, is expected to be useful for general networks of KPOs in the LHZ scheme and thus for their large-scale implementation.

Introduction

Hardware devices for solving the Ising problem¹ have attracted attention because this problem can represent various combinatorial optimization problems². Such Ising machines are thus expected to be applied to real-world problems, such as integrated circuit design³, computational biology^4,5, and financial portfolio management⁶. The Ising machines have been developed in several implementations, including quantum annealing^7,8 or adiabatic quantum computation^9,10,11 with superconducting circuits¹² and coherent Ising machines with laser pulses^13,14,15. In these devices, quantum effects such as quantum tunneling and quantum fluctuations are expected to be exploited for solving the Ising problem. Classical Ising machines have also been implemented with digital circuits based on simulated annealing^16,17,18 and simulated bifurcation^19,20,21,22.

Another adiabatic quantum computation for the Ising problem has been proposed using Kerr-nonlinear parametric oscillators (KPOs)^23,24. A KPO is a parametrically driven oscillator with Kerr nonlinearity and exhibits a bifurcation²⁵. The bifurcation allows KPOs to represent binary Ising spins. Furthermore, a KPO can generate nonclassical states such as a quantum superposition of coherent states, known as a Schrödinger cat state, via a quantum adiabatic bifurcation^23,24. This Ising machine has been referred to as a quantum bifurcation machine (QbM)^24,26. As driven states in KPOs are used, QbMs can contrast with quantum annealers operated in thermal equilibrium^12,27.

Utilizing these features of KPOs, applications other than Ising machines have also been proposed such as gate-based universal quantum computation^28,29,30, Boltzmann sampling²⁶, studies of quantum phase transitions^31,32, and on-demand generation of traveling cat states³³. KPOs can be implemented by superconducting circuits like Josephson parametric oscillators^34,35,36 and have recently been realized experimentally^37,38,39.

To solve a wider class of real-world problems, QbMs for the Ising problem with all-to-all spin couplings are necessary. For this purpose, however, the original QbM²³ literally requires all-to-all two-body interactions among the KPOs, and its scalable implementation has not been known. Thus alternative architectures of QbMs for all-to-all spin couplings have been proposed^40,41,42,43. The architecture in ref. ⁴¹ is based on the Lechner–Hauke–Zoller (LHZ) scheme^{44,45,46,47,48,49}, where the all-to-all spin couplings can be realized by a two-dimensional array of KPOs with local four-body interactions. Four KPOs connected by a four-body interaction constitute a plaquette, and the plaquettes form the whole array. This architecture is a promising candidate for large-scale implementation of the LHZ scheme, because in the case of QbM, the four-body interaction is realized by four-wave mixing in a single Josephson junction⁴¹. This simple four-body interaction can be an advantage over quantum annealers in the LHZ scheme with flux qubits⁵⁰ or transmon qubits⁵¹, where a four-body interaction may need complicated circuits with multiple ancilla qubits.

In the previous numerical studies, however, to our knowledge the number of KPOs in the LHZ scheme has been limited up to three (In numerical simulations of four KPOs in ref. ⁴¹, three KPOs are evolved in time via bifurcations, while another one is fixed in a coherent state.). The three KPOs are in one plaquette and are symmetric⁴¹. Such a symmetry is broken in general cases with multiple plaquettes. Thus whether this architecture works for large-scale implementations has not been revealed.

To examine this crucial issue, here we investigate adiabatic quantum computation using a KPO network in the LHZ scheme (LHZ-QbM) with a larger number of KPOs. This LHZ-QbM consists of multiple plaquettes and becomes asymmetric. We first find that mean photon numbers in the KPOs become inhomogeneous, i.e., unequal, owing to the asymmetry in the LHZ scheme, and this inhomogeneity degrades accuracy in solving the Ising problem. We then propose a method to reduce the inhomogeneity by scheduling the detunings of KPOs without monitoring their quantum states during adiabatic time evolution. Finally, we numerically demonstrate that this method can improve the solution accuracy dramatically. This method is applicable to arbitrary numbers of KPOs in the LHZ-QbM and therefore to its large-scale implementation.

Results

LHZ-QbM

We first briefly explain the Ising problem and the LHZ scheme and then introduce an LHZ-QbM. In the Ising problem¹, a dimensionless Ising energy, ${E}_{{\rm{Ising}}}=-\mathop{\sum }\nolimits_{i = 1}^{N}\ {\sum }_{j < i}\ {J}_{ij}{s}_{i}{s}_{j}$, is minimized with respect to N Ising spins $\left\{{s}_{i}=\pm1\right\}$, where $\left\{{J}_{ij}\right\}$ represents two-body interactions.

In the LHZ scheme⁴⁴, the product of two Ising spins s_is_j is mapped to a variable ${\tilde{s}}_{k}=\pm 1$, which we call an LHZ spin. This mapping reduces the two-body interaction J_ij to a local external field J_k, while increasing the number of the spins to L = N(N − 1)/2. The additional degrees of freedom are removed by four-body constraints on neighboring LHZ spins: ${\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}=1$, where a four-body constraint corresponds to a plaquette, as shown in Fig. 1. The lower edge of the lattice is terminated by ancillary LHZ spins fixed to 1.

Fig. 1: A network of Kerr-nonlinear parametric oscillators in the Lechner–Hauke–Zoller scheme for the four-spin Ising problem.

Here N = 4 and L = 6. KPOs 1–6 correspond to LHZ spins ${\tilde{s}}_{k}=\pm 1$, while the ancillary LHZ spins (Fixed) fixed to 1 are implemented by classical driving. A four-body constraint is imposed on four LHZ spins connected by a square (in green), which constitute a plaquette. The number of the four-body interactions (squares in green) connected to the kth KPO, z_k, are z₁ = z₃ = z₆ = 1, z₄ = z₅ = 2, and z₂ = 3 (see the main text).

To satisfy the constraints, terms proportional to ${\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}$ are added to the Ising energy, resulting in the LHZ energy, ${E}_{{\rm{LHZ}}}=-\mathop{\sum }\nolimits_{k = 1}^{L}\ {J}_{k}{\tilde{s}}_{k}-C\ {\sum }_{\langle k,l,m,n\rangle }\ {\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}$, to be minimized. Here the summation in the second term is over all the constraints. The second term means four-body interactions with their strength C. With sufficiently large C, the four-body constraints are satisfied by $\left\{{\tilde{s}}_{k}\right\}$ minimizing E_LHZ (Supplementary Note 1).

We search for the solution of the Ising problem by embedding the LHZ energy into a network of L KPOs described by a Hamiltonian,

$$H={H}_{{\rm{KPO}}}+{H}_{{\rm{LHZ}}},$$

(1)

$${H}_{{\rm{KPO}}}=\ \hbar \mathop{\sum }\limits_{k = 1}^{L}\ \left[\frac{K}{2}{a}_{k}^{\dagger 2}{a}_{k}^{2}-\frac{p}{2}\ \left({a}_{k}^{\dagger 2}+{a}_{k}^{2}\right)+{{{\Delta }}}_{k}{a}_{k}^{\dagger }{a}_{k}\right],$$

(2)

$${H}_{{\rm{LHZ}}}=-\hbar \xi \ \left(A\ \mathop{\sum }\limits_{k = 1}^{L}\ {J}_{k}{a}_{k}^{\dagger }+C\ \mathop{\sum }\limits_{\langle k,l,m,n\rangle }\ {a}_{k}^{\dagger }{a}_{l}^{\dagger }{a}_{m}{a}_{n}+{\rm{h.c.}}\right),$$

(3)

where a_k and ${a}_{k}^{\dagger }$ are, respectively, the annihilation and creation operators for the kth KPO; h.c. represents Hermitian conjugate; and $\hbar$, K, p, and Δ_k are the reduced Planck constant, the Kerr coefficient, the pump amplitude, and the detuning frequency for the kth KPO, respectively. This expression is obtained in a frame rotating at half the pump frequency, ω_p/2, of the parametric drive and in the rotating-wave approximation^23,25,41. In this work, we assume that Δ_k can be controlled individually.

H_LHZ corresponds to the LHZ energy. In Eq. (3), we introduce parameters, ξ and A, to scale H_LHZ and the term including $\left\{{J}_{k}\right\}$, respectively, where ξ has the dimension of frequency and A is dimensionless. H_LHZ is small compared with H_KPO, ξ ≪ K, for accurate embedding^23,41. A is chosen to reproduce E_LHZ (“Methods”). The first and second terms in H_LHZ physically mean local external drives at ω_p/2^26,28,41 and four-body interactions, respectively. Since the ancillary LHZ spins on the lower edge of the lattice are fixed to 1, as mentioned above, the corresponding KPOs can be replaced by classical driving⁴¹. Thus their annihilation and creation operators in H_LHZ are replaced by classical driving amplitudes denoted by β (Supplementary Note 2).

A solution of the Ising problem is found from the ground state of the LHZ-QbM after adiabatic time evolution via bifurcations^23,24,41. The sign of a quadrature amplitude ${x}_{k}=\ \left({a}_{k}+{a}_{k}^{\dagger }\right)/2$ provides the LHZ spin ${\tilde{s}}_{k}$^23,41, and the LHZ spins are transformed to Ising spins, giving the solution to the Ising problem. (x_k can be readout by using homodyne detection⁴¹.) Since the LHZ spins represent the relative signs of pairs of the Ising spins, a configuration $\left\{{\tilde{s}}_{k}\right\}$ corresponds to both $\left\{{s}_{i}\right\}$ and $\left\{-{s}_{i}\right\}$ simultaneously, which give an identical Ising energy. Thus in mapping the LHZ spins to the Ising spins, we can fix one of the Ising spins, e.g., s₁ = 1. The probabilities for the LHZ spins, hence for the Ising spins, can be evaluated from the wave function of the ground state.

In simulating a larger number of KPOs than before, we found that computational costs can be larger for the computation of the probabilities for the spins than that of time evolution. These large costs come from the continuous degrees of freedom of the KPOs, which are finally projected to the binary variables. We succeeded in calculating these probabilities within a reasonable computational time by noting that the Ising spins can be determined from only (N − 1) KPOs⁴⁴ and thus tracing out the others (“Methods”). For instance, only the KPOs 1, 2, and 3 are readout in the case where N = 4, as shown in Fig. 1.

Before showing simulation results, we evaluate the ground state by an analytical method, in which we find inhomogeneity in the KPOs. Since this inhomogeneity will degrade the accuracy of the solutions, we propose a method to correct the inhomogeneity.

Inhomogeneous photon numbers in the LHZ-QbM

We examine the mean photon numbers in the ground state of H in Eq. (1) by using a variational method. Here we assume a small ξ satisfying ξ/K ≪ 1. Although the terms yielded by the four-body interactions in Eq. (3) seem intractable, these terms are simplified when the four-body constraints hold (see “Methods”). As a result, the mean photon number in the kth KPO can be approximated by

$$\left\langle {a}_{k}^{\dagger }{a}_{k}\right\rangle \simeq \frac{p-{{{\Delta }}}_{k}}{K}+\frac{\xi }{{\alpha }_{0}K}\ \left(A{J}_{k}{\tilde{s}}_{k}+{\alpha }_{0}^{3}C{z}_{k}\right),$$

(4)

$${\alpha }_{0}=\ {\left(\frac{p-\bar{{{\Delta }}}}{K}\right)}^{1/2},$$

(5)

where $\bar{{{\Delta }}}$ is the average of Δ_k over the KPOs and z_k is the number of the four-body interactions connected to the kth KPO. The first term $\left(p-{{{\Delta }}}_{k}\right)/K$ is the mean photon number without H_LHZ, and the second term indicates inhomogeneity induced by H_LHZ. [See “Methods” for the detailed derivation of Eq. (4).]

In Eq. (4), the terms proportional to ${J}_{k}{\tilde{s}}_{k}$ and Cz_k are caused by the local external drives and the four-body interactions, respectively. Because the term proportional to Cz_k typically becomes dominant under the condition for satisfying the four-body constraints, we focus on this term and drop the term proportional to ${J}_{k}{\tilde{s}}_{k}$ in the following. In general, z_k takes the values of 1, 2, 3, and 4 as can be seen from Fig. 1. Hence, the variation in the mean photon number due to the four-body interactions can become smaller for KPOs near to the edge of the network while larger around its center.

This photon-number inhomogeneity due to the four-body interactions causes a wrong implementation of $\left\{{J}_{k}\right\}$ and degrades solution accuracy (see “Methods”). The solution accuracy is thus expected to be improved by reducing the photon-number inhomogeneity. (Amplitude inhomogeneity has been studied in systems such as coherent Ising machines^52,53.) In this work, we propose a method to reduce the inhomogeneity without measurement.

Correcting the inhomogeneous photon numbers

To cancel the term proportional to C in Eq. (4), we choose Δ_k as

$${{{\Delta }}}_{k}={{\Delta }}+{\alpha }^{2}\xi C{z}_{k},$$

(6)

$$\alpha ={\left(\frac{p-{{\Delta }}}{K}\right)}^{1/2},$$

(7)

when p − Δ > 0 and otherwise Δ_k = Δ, where Δ is a common detuning frequency. As a result, we obtain approximately homogeneous mean photon numbers (“Methods”):

$$\left\langle {a}_{k}^{\dagger }{a}_{k}\right\rangle \simeq {\alpha }^{2},$$

(8)

where the term proportional to ${J}_{k}{\tilde{s}}_{k}$ has been dropped, as mentioned above.

The correction by Eq. (6) is possible without knowing the solutions to the Ising problems, because the term proportional to C in Eq. (4) is independent of $\left\{{J}_{k}\right\}$ and $\left\{{\tilde{s}}_{k}\right\}$. The parameters are therefore scheduled in advance, and no measurement of the states is necessary during the time evolution.

In the following, we simulate the time evolution of the LHZ-QbM shown in Fig. 1 by numerically solving the Schrödinger equation with H in Eq. (1) (see “Methods” for details). Here we assume a closed system without dissipation. Although the time evolution in the presence of the dissipation can be simulated by a master equation, computational costs for such simulations are much higher than for the closed system. We thus leave such simulations for future work.

We choose N = 4, hence L = 6, because this network is the smallest among those where the KPO network is asymmetric, that is, the KPOs are unequal with respect to the four-body interactions. We first apply this LHZ-QbM to the Ising problem with uniform interactions to check the photon-number inhomogeneity and the validity of our proposed method and then with random interactions to demonstrate the usefulness of this method.

Simulation results for uniform antiferromagnetic interactions

Here we solve the Ising problem with uniform all-to-all connected antiferromagnetic interactions¹⁴, which is expressed by the same negative J for all $\left\{{J}_{k}\right\}$. In this work, we normalize the {J_k} such that

$$\mathop{\sum }\limits_{k = 1}^{L}\left|{J}_{k}\right|=1.$$

(9)

(This normalization does not change the Ising problem.) Thus, in the present case, J_k = − 1/L.

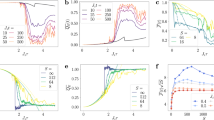
Figure 2a shows the mean photon number in each KPO after time evolution, where we compare the results for uniform Δ (without the correction) and modified Δ_k in Eq. (6) (with the correction). For uniform Δ, the mean photon numbers increase depending on z_k (z₁ = z₃ = z₆ = 1, z₄ = z₅ = 2, and z₂ = 3 as can be seen from Fig. 1), which are consistent with Eq. (4). Since $\left\{{J}_{k}\right\}$ is uniform, this inhomogeneity originates from the four-body interactions.

Fig. 2: Results for the four-spin Ising problem with uniform antiferromagnetic interactions.

a Mean photon number in each KPO for C = 0.3 and ξ/K = 0.3 (see “Methods” for other parameter settings). Here C = 0.3 is chosen because this satisfies the condition, C > 1/6, for satisfying the four-body constraints (Supplementary Note 1). b Probabilities for the configurations of the Ising spins, $\left\{{s}_{i}\right\}$. Only the configurations with s₁ = 1 are shown for the reason mentioned in the main text.

For modified Δ_k, on the other hand, all the mean photon numbers are nearly equal to 3, which coincides with the value predicted by Eq. (8). This result shows that the photon numbers can be made almost homogeneous by using Δ_k in Eq. (6) as expected.

Figure 2b shows the probabilities for the Ising spin configurations. Although the probabilities are finite only for the three degenerate ground states, namely, two spins in 1 and the others −1, the probabilities for these three configurations are not equal. In particular, uniform Δ results in the much higher probability for { + + − − } than the other configurations. The reason for this can be explained as follows. The configuration { + + − − } is mapped to the LHZ spins of ${\tilde{s}}_{1}={\tilde{s}}_{3}=1$ and the others in −1. While the negative J_k favors ${\tilde{s}}_{k}=-1$, the four-body constraints lead to ${\tilde{s}}_{1}={\tilde{s}}_{3}=1$. Here J₁ and J₃ become effectively small because of the relatively small mean photon numbers in KPOs 1 and 3 (“Methods”), as shown in Fig. 2a, which is caused by the four-body interactions. Thus the probability for this configuration becomes particularly high compared to the others.

When Δ_k in Eq. (6) are used, the probabilities are similar for two of the ground states, { + − − + } and { + + − − }, as shown in Fig. 2b. Thus the bias to one ground state { + + − − } observed for uniform Δ are suppressed by reducing the inhomogeneity in the photon numbers.

Simulation results for random interactions

Finally, we evaluate the performance of the LHZ-QbM for the Ising problem with all-to-all connected random interactions, generating $\left\{{J}_{ij}\right\}$ uniformly from {−1, −0.99, −0.98, ..., 1} for 100 instances^23,24,26 and normalizing them such that Eq. (9) holds. The performance is measured by a success probability P_s and a residual energy ${E}_{{\rm{res}}}$. The success probability is defined as a probability for obtaining $\left\{{s}_{i}\right\}$ minimizing E_Ising. The residual energy is given by the expectation value of E_Ising subtracted by the minimum E_Ising^23,24,54. A lower residual energy indicates higher accuracy and takes its minimum of 0 when the success probability is 1. The values of (C, ξ/K) are set to (0.3, 0.3) and (0.4, 0.6), respectively, without and with the correction, to maximize the success probabilities averaged over the instances (see Supplementary Note 3).

Figure 3a, b show the two-dimensional plots of P_s without and with the correction, and the corresponding plot of ${E}_{{\rm{res}}}$, respectively. Instances improved by the correction correspond to the points above the dashed line in Fig. 3a and those below the dashed line in Fig. 3b. As indicated by arrows in Fig. 3a, without the correction, the success probabilities for some instances are nearly 0. These success probabilities are increased to at least >0.3 by the correction. Furthermore, for most instances, the success probabilities are raised closely to 1 by the correction. With the nonzero success probability, repeated use of this LHZ-QbM gives a correct solution with probability rapidly approaching 1. Figure 3b shows that the residual energies are also substantially lowered by the correction, which means that obtained solutions become more accurate. Although two points are below the dashed line in Fig. 3a, their residual energies are improved by the correction and hence we can obtain better approximate solutions using the proposed method.

Fig. 3: Results for 100 random instances of the four-spin Ising problem.

a Two-dimensional plot of success probabilities without and with the correction, ${P}_{{\rm{s}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}$ and ${P}_{{\rm{s}}}^{{\rm{with}}\ {\rm{corr}}}$, where we set (C, ξ/K) = (0.3, 0.3) and (0.4, 0.6), respectively (see “Methods” for other parameter settings). b Corresponding results for residual energies ${E}_{{\rm{res}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}$ and ${E}_{{\rm{res}}}^{{\rm{with}}\ {\rm{corr}}}$. c Distributions of improvement rates defined as ${P}_{{\rm{f}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}/{P}_{{\rm{f}}}^{{\rm{with}}\ {\rm{corr}}}$ and ${E}_{{\rm{res}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}/{E}_{{\rm{res}}}^{{\rm{with}}\ {\rm{corr}}}$.

In Fig. 3c, we show improvement rates of a failure probability P_f = 1 − P_s and ${E}_{{\rm{res}}}$ in each instance, where an improvement rate is defined as the ratio of the value without the correction to that with it. Figure 3c shows that both P_f and ${E}_{{\rm{res}}}$ are improved by one or two orders of magnitude in many instances, with the factors of up to ${P}_{{\rm{f}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}/{P}_{{\rm{f}}}^{{\rm{with}}\ {\rm{corr}}}=364$ and ${E}_{{\rm{res}}}^{{\rm{w}}/{\rm{o}}\ {\rm{corr}}}/{E}_{{\rm{res}}}^{{\rm{with}}\ {\rm{corr}}}=185$, indicating dramatic improvements by the proposed correction.

Discussion

In this work, we have shown that photon-number inhomogeneity due to four-body interactions in the LHZ-QbM degrades its performance. This crucial issue on the LHZ-QbM has not been revealed because only a symmetric KPO network with one plaquette and three KPOs has been studied before. We have found this issue by simulating an asymmetric KPO network with six KPOs. Note that this issue arises even in the absence of dissipation. So we have focused on a closed system without dissipation. (The effect of dissipation is another important issue but needs much more computational costs. It is thus left for future work.)

We have then proposed a method to suppress the photon-number inhomogeneity by controlling detunings and demonstrated that the performance of the LHZ-QbM is dramatically improved by the proposed method. This method does not need to refer to the states of the KPOs during adiabatic time evolution, offering a simple operation. Also, this method can be used regardless of the number of KPOs in an LHZ-QbM, thus allowing its large-scale implementation. Because our method is based on the qualitative understanding of the asymmetry, this method is expected to be useful for general LHZ-QbMs. However, we leave evaluation of larger numbers of KPOs as a future work.

While we have modified only the detunings in the present work, similar corrections are possible by setting Kerr coefficients or pump amplitudes. In implementations with superconducting circuits, these three parameters can be controlled experimentally through parameters characterizing these circuits^24,41.

In the present study, we have assumed sufficiently small H_LHZ compared to H_KPO, and based on this assumption, we have determined the detunings to correct the inhomogeneity. Nevertheless from the simulation results, we have found that the optimal value, ξ/K = 0.6, is rather large (see Supplementary Note 3). This large optimal ξ/K may be because the time evolution becomes more adiabatic, that is, the larger H_LHZ widens gaps between the energy levels of ground states and excited states, and prevents transitions between these states during the time evolution¹¹. These results imply further possible improvement by increasing ξ/K together with more elaborate control of detunings than the present analytic ones.

Methods

Simulation of the LHZ-QbM

Each KPO is initialized to a vacuum, and the parameters in H given by Eq. (1) are set such that the vacuum is its ground state. For the initial parameters p/K = A = β = 0 and Δ/K > 0, the vacuum is the ground state if ξC/K ≤ 1 (Here β is the classical driving amplitude for the ancillary LHZ spins at “Fixed” in Fig. 1. See Supplementary Note 2.). This condition for the ground state is valid within an estimation by a variational method^23,26 (Supplementary Note 4).

Time evolution is then started, and the parameters are slowly varied to induce bifurcations. During the evolution, the state is expected to remain in the ground state. Figure 4 shows the parameters as functions of time^23,26,28, where the time interval for the evolution is T = 500/K. We use this long T so that the time evolution becomes adiabatic. p/K is increased to let the KPOs bifurcate. The rather small value of p/K ≤ 3 is used in order to reduce the size of the photon number basis necessary for representing the states of the KPOs, hence to reduce computational costs for the simulation. Δ/K is decreased during the time evolution so that the states are approximated better by coherent states as below. Because larger Δ/K is expected to open a larger energy gap between the ground (vacuum) and excited states for small p/K, we initially increase p/K more rapidly. To reproduce E_LHZ, A and β at t ≃ T are chosen such that A ≃ α³ (see below) and β ≃ α, where α is given by Eq. (7).

Fig. 4: Time dependence of parameters.

See Supplementary Note 5 for explicit forms of the functions.

The other parameters, K, ξ, and C, are set to be constant in time^24,41. The values of C and ξ/K are chosen depending on the instances (the uniform or random interactions) of the Ising problem (see Supplementary Notes 1 and 3) and whether the correction is used. In this study, positive K has been assumed^23,24 (For negative K, the same results can be obtained by changing the signs of p, Δ, and ξ^23,24. Negative K has been used in ref. ⁴¹.).

We have set parameters as above to obtain the present results. There may be room for further optimization of the parameters, but it is beyond the scope of this work.

After the bifurcations, the ground state approximately becomes an L-mode coherent state $\left|{\alpha }_{1}\right\rangle \cdots \ \left|{\alpha }_{L}\right\rangle$^23,24,41, where the coherent state $\left|{\alpha }_{k}\right\rangle$ satisfies ${a}_{k}\ \left|{\alpha }_{k}\right\rangle ={\alpha }_{k}\ \left|{\alpha }_{k}\right\rangle$⁵⁵. The signs of $\left\{{\alpha }_{k}\right\}$ are expected to give the LHZ spins minimizing E_LHZ⁴¹.

The time evolution is simulated by numerically solving the Schrödinger equation, where H and the state $\left|\psi \right\rangle$ are represented in the photon number basis with the largest photon number 12 truncating the Hilbert space^23,26.

After the time evolution, the probabilities for the LHZ spins are evaluated as follows. As the LHZ spin ${\tilde{s}}_{k}$ is given by the sign of the quadrature amplitude x_k, the probabilities for obtaining ${\tilde{s}}_{k}=\pm 1$ are equal to the probabilities for x_k ≷ 0, respectively. These probabilities can be formulated using eigenstates of x_k as^23,26,55

$$P\ \left({\tilde{s}}_{1},\cdots \ ,{\tilde{s}}_{L}\right)={\rm{Tr}}\ \left[\ \left|\psi \right\rangle \ \left\langle \psi \right|\ \mathop{\prod }\limits_{k = 1}^{L}{M}_{k}\ \left({\tilde{s}}_{k}\right)\right],$$

(10)

$${M}_{k}\ \left(\pm1\right)=\ {\int}_{{x}_{k}>rless 0}\ {\rm{d}}{x}_{k}\ \left|{x}_{k}\right\rangle \ \left\langle {x}_{k}\right|.$$

(11)

However, we found that their calculation becomes the largest in the simulation for large L. Then, noting that (N − 1) LHZ spins can determine the Ising spins⁴⁴, we trace out the other KPOs in Eq. (10) removing their corresponding ${M}_{k}\ \left({\tilde{s}}_{k}\right)$ and obtain the probabilities within reasonable computational costs.

Photon-number inhomogeneity in the LHZ-QbM

We evaluate the ground state using a variational method and assuming the bifurcations, small H_LHZ, and the four-body constraints. We employ $\left|{\alpha }_{1}\right\rangle \cdots \ \left|{\alpha }_{L}\right\rangle$ as a trial wave function^23,26 and minimize the expectation value 〈H〉 with respect to $\left\{{\alpha }_{k},{\alpha }_{k}^{* }\right\}$, where ${\alpha }_{k}^{* }$ is the complex conjugate of α_k. The following nonlinear equations are then yielded

$$K{\alpha }_{k}^{* }{\alpha }_{k}^{2}-p{\alpha }_{k}^{* }+{{{\Delta }}}_{k}{\alpha }_{k}-\xi \ \left(A{J}_{k}+C\ \mathop{\sum }\limits_{\langle l,m,n\rangle }\ {\alpha }_{l}^{* }{\alpha }_{m}{\alpha }_{n}\right)=0.$$

(12)

By assuming sufficiently small ξ, Eq. (12) is approximately solved within the first order in ξ as

$${\alpha }_{k}\simeq {\alpha }_{0k}{\tilde{s}}_{k}+\ \frac{\xi }{2{\alpha }_{0}^{2}K}\ \left(A{J}_{k}+{\alpha }_{0}^{3}C\ \mathop{\sum }\limits_{\langle l,m,n\rangle }\ {\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}\ \right),$$

(13)

where ${\alpha }_{0k}=\ {\left[\left(p-{{{\Delta }}}_{k}\right)/K\right]}^{1/2}$, and ${\alpha }_{0k}{\tilde{s}}_{k}$ is the solution of Eq. (12) for ξ = 0 after the bifurcation p − Δ_k > 0. Here α₀ is given by Eq. (5), and ${{{\Delta }}}_{k}-\bar{{{\Delta }}}$ has been assumed to be the first order in ξ, as in Eq. (6).

The term proportional to C in Eq. (13) can be simplified under the four-body constraints ${\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}=1$ as follows. Since ${\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}={\tilde{s}}_{k}$ holds, the summation in Eq. (13) reduces to the number of connected four-body interactions z_k, resulting in

$${\alpha }_{k}\simeq {\alpha }_{0k}{\tilde{s}}_{k}+\ \frac{\xi }{2{\alpha }_{0}^{2}K}\ \left(A{J}_{k}+{\alpha }_{0}^{3}C{\tilde{s}}_{k}{z}_{k}\right).$$

(14)

The condition for this expression to be accurate is clarified as $\xi /K\ll 2/\ \left(\ \left|{J}_{k}\right|+C{z}_{k}\right)\ \sim \ 1$.

As the L-mode coherent state $\left|{\alpha }_{1}\right\rangle \cdots \ \left|{\alpha }_{L}\right\rangle$ has been assumed, the mean photon number becomes $\langle {a}_{k}^{\dagger }{a}_{k}\rangle ={\left|{\alpha }_{k}\right|}^{2}$. Equation (14) then gives

$$\left\langle {a}_{k}^{\dagger }{a}_{k}\right\rangle \simeq {\alpha }_{0k}^{2}+\ \frac{\xi }{{\alpha }_{0}K}\ \left(A{J}_{k}{\tilde{s}}_{k}+{\alpha }_{0}^{3}C{z}_{k}\right),$$

(15)

where the term proportional to (ξ/K)² has been dropped. Hence, Eq. (4) is obtained.

When $\left|{\alpha }_{k}\right|$ is inhomogeneous owing to H_LHZ, the accuracy in implementing $\left\{{J}_{k}\right\}$ is lowered as follows. By using ${\alpha }_{k}=\left|{\alpha }_{k}\right|{\tilde{s}}_{k}$, the expectation value of H_LHZ is written as

$$\left\langle {H}_{{\rm{LHZ}}}\right\rangle \simeq \ -2\hbar \xi \left(A\mathop{\sum }\limits_{k = 1}^{L}\ {J}_{k}\ \left|{\alpha }_{k}\right|\ {\tilde{s}}_{k}\ +C\ \mathop{\sum }\limits_{\langle k,l,m,n\rangle }\ \left|{\alpha }_{k}{\alpha }_{l}{\alpha }_{m}{\alpha }_{n}\right|\ {\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}\ \right).$$

(16)

Because $\left\langle {H}_{{\rm{LHZ}}}\right\rangle$ is minimized with respect to $\left\{{\tilde{s}}_{k}\right\}$ in the ground state, Eq. (16) indicates that the resulting $\left\{{\tilde{s}}_{k}\right\}$ corresponds to a solution to a problem given by $\left\{{J}_{k}\left|{\alpha }_{k}\right|\right\}$, which is different from the original problem $\left\{{J}_{k}\right\}$. Thus the inhomogeneous mean photon numbers cause wrong embedding of the Ising problem.

For homogeneous $\left|{\alpha }_{k}\right|=\alpha$, $\left\langle {H}_{{\rm{LHZ}}}\right\rangle$ becomes

$$\left\langle {H}_{{\rm{LHZ}}}\right\rangle \simeq \ -2\hbar \alpha \xi \ \left(\ A\ \mathop{\sum }\limits_{k = 1}^{L}\ {J}_{k}\ {\tilde{s}}_{k}\ +{\alpha }^{3}C\ \mathop{\sum }\limits_{\langle k,l,m,n\rangle }\ {\tilde{s}}_{k}{\tilde{s}}_{l}{\tilde{s}}_{m}{\tilde{s}}_{n}\ \right).$$

(17)

Then, by choosing A = α³ with α in Eq. (7) as mentioned above, $\left\langle {H}_{{\rm{LHZ}}}\right\rangle$ is proportional to E_LHZ, and we can obtain $\left\{{\tilde{s}}_{k}\right\}$ that minimizes E_LHZ.

Correcting the inhomogeneity

The correction with Δ_k in Eq. (6) reduces the inhomogeneity as follows. Equation (6) leads to $\bar{{{\Delta }}}={{\Delta }}+{\alpha }^{2}\xi C\bar{z}$, where α is given in Eq. (7) and $\bar{z}$ is the average of z_k. Then ${\alpha }_{0}=\ {\left[\left(p-\bar{{{\Delta }}}\right)/K\right]}^{1/2}$ is determined. By substituting Eq. (6) and α₀ into Eq. (4) and dropping the term proportional to ${J}_{k}{\tilde{s}}_{k}$ for the reason mentioned in “Results,” the mean photon numbers become

$$\left\langle {a}_{k}^{\dagger }{a}_{k}\right\rangle \simeq {\alpha }^{2},$$

(18)

giving Eq. (8). Here second-order terms in ξ/K have been neglected.