Introduction

Two-level systems (TLSs) have attracted substantial interest in recent years1,2 as they are among the most important sources of loss limiting the performance of superconducting quantum circuits3,4,5,6,7,8. Considerable efforts have been invested in attempting to understand their properties in order to mitigate this problem9,10, and the dramatic improvements in the coherence of superconducting devices over the last decade are due mainly to design and process developments that reduce TLS loss. TLSs couple both to electromagnetic fields4,5,11 and to strain12,13,14 and recent approaches to investigating their behaviour typically involve measuring the lifetimes and resonance frequencies of superconducting resonators and qubits6,7,8,15. Much of the standard theory of TLSs, however, was developed prior to the emergence of superconducting qubits, in experimental and theoretical research on their ultrasonic properties16,17. In the present work we combine these approaches to probe TLSs in an acoustic resonator operating in the quantum regime where \(\hbar\)ω ≪ kBT.

From experiments applying strain to superconducting qubit devices, there is an evidence that the same individual TLSs couple to both strain and electric field12,18,19. Most TLSs inducing loss in superconducting devices are weakly coupled, and relaxation by phonon emission is generally understood to limit their lifetime2,20. The strain associated with applied acoustic fields therefore should probe the same ensemble as circuit electric fields.

Two-tone spectroscopy of TLSs has been performed using the fundamental and harmonic modes of a superconducting coplanar waveguide resonator21, as well as more recently with the two normal modes of a system of coupled resonators22. The large mode spacing of coplanar waveguide resonators limit these experiments to a small number of frequency points. In contrast, the short wavelength of sound compared to electromagnetic radiation gives rise to a spectrum with multiple closely spaced modes with small differences in spatial distribution. This allows for two-tone spectroscopy where the pump-probe detuning is variable with a resolution corresponding to the mode spacing. By varying this detuning, it is possible to probe the shape of the spectral hole burnt in the TLS ensemble by the pump as a function of both frequency and power.

Surface acoustic wave (SAW) devices have been used in a number of quantum acoustic experiments, coupling mechanical modes to superconducting qubits23. Exotic regimes of atom-field interaction have been demonstrated24, as well as the controlled generation of quantum states of SAW25. TLSs have also been demonstrated to induce significant loss in SAW resonators at cryogenic temperatures26. Here, we exploit this effect as well as the narrow free spectral range of a SAW resonator to perform pump-probe spectroscopy of the TLS ensemble.

Results

Single mode loss saturation

While the microscopic nature of TLSs is still not well understood, the phenomenological standard tunnelling model (STM)2,27,28 describes successfully many of the low-temperature properties of amorphous solids. The STM models a TLS as a particle in a double-well potential, where two minima of similar energy are separated by a tunnel barrier. Electric and strain fields deform the potential, inducing tunnelling between the two states. For the loss saturation of a single mode of frequency fr, the standard theory derived from the STM gives2,11

$$\frac{1}{{Q}_{{\rm{int}}}(n)}=\frac{1}{{Q}_{{\rm{TLS}}}(0)}\frac{\tanh \frac{\hslash {\omega }_{r}}{2{k}_{\rm{B}}T}}{\sqrt{1+{\left(\frac{n}{{n}_{C}}\right)}^{\beta }}}+\frac{1}{{Q}_{{\rm{res}}}},$$
(1)

where Qint is the internal Q-factor, QTLS the Q-factor corresponding to TLS loss and n (nC) is the average (critical) phonon number in the resonator. Residual internal loss not due to TLS is represented by \({Q}_{{\rm{res}}}\). The shape of the saturation curve is characterised by the phenomenological parameter β, where the scaling β = 1 is expected from the standard theory, while values β < 1 are commonly found in superconducting resonators. Since the temperature is low we use the approximation \(\tanh \left[\hslash {\omega }_{r}/(2{k}_{\rm{B}}T)\right]=1\) for the purpose of fitting.

Figure 1 shows the resonator spectrum measured with a vector network analyzer. The internal Q-factor is extracted from fits to the data and plotted as a function of probe power is in Fig. 1c. We observe an order-of-magnitude change with power, indicating that SAW propagation losses at low temperature are limited by the TLS loss. Fitting to Eq. (1), we find good agreement with theory and obtain β = 1.05, close to β = 1 as predicted by the STM.

Fig. 1: Resonator characterisation.
figure 1

a Magnitude of the reflection coefficient of the SAW resonator measured at high power (n ≈ 4 ⋅ 105). The dashed outline indicates the pump mode at 2.399 GHz. b Example of fit to the pump mode resonance at low power (n < 1). c Internal Q-factor as a function of phonon number in the pump mode for the pump mode (red dots) as well as three probe modes below the pump. The pump-probe detunings are indicated and fits are shown as solid lines. The single mode loss saturation is fitted with Eq. (1). The loss saturation in the detuned probe modes is fitted with Eq. (3).

Full size image

Two-tone spectroscopy

We now turn to the two-tone spectroscopy scheme. In this setup, a drive tone is applied at a mode in the centre of the stopband (ωr/2π = 2.399 GHz). As the power in the pump mode is swept, we measure the change in Q-factor and resonance frequency of all other modes using a weak probe signal. This yields the loss and frequency shift as a function of phonon number in the pump mode n as well as pump-probe detuning Δ = ωprobe − ωpump. Due to the frequency dependence of the IDT response, all the modes have slightly different external quality factors. For this reason, the pump is fixed to a single mode to avoid the pump power adjustments necessary to get the same average phonon number in different modes. Based on the STM, expressions for the probe mode response were derived in ref. 22, and give for the frequency shift

$$\frac{{{\Delta }}{\omega }_{r}}{{\omega }_{r}\tanh \frac{\hslash {\omega }_{r}}{2{k}_{\rm{B}}T}}=-\frac{3\sqrt{2}\tan \delta }{8}\frac{{{\Delta }}}{{{\Omega }}}\frac{\sqrt{1+\frac{{{{\Omega }}}^{2}}{2{{{\Delta }}}^{2}}}-1}{\sqrt{1+\frac{{{{\Omega }}}^{2}}{2{{{\Delta }}}^{2}}}+1}.$$
(2)

The effective Rabi frequency Ω of the pump may be expressed as ħΩ = 2γεpump, where γ is the average elastic dipole moment coupling the TLS to the strain field of amplitude εpump. This implies the drive strength depends on the average phonon number in the resonator as \({{\Omega }}\propto {\epsilon}_{{\rm{pump}}}\propto \sqrt{n}\). Here, \(\tan \delta\) is the dielectric loss tangent due to TLS. The frequency shift moves probe modes closer to the pump mode and for a given Δ it is maximised by a finite n = nmax. This can be understood from the dispersive interaction, where each off-resonant ground state TLS contributes a shift \({{\Delta }}{\omega }_{r,i}={g}_{i}^{2}/({\omega }_{r}-{\omega }_{i})\). Saturating TLSs disables this interaction. For pump phonon numbers n > nmax, TLSs on both sides of the probe mode get saturated, and the frequency shift starts to diminish. For n < nmax TLSs are saturated predominantly on one side of the probe mode.

The same model also yields the loss in two-tone spectroscopy. The change in probe mode loss is symmetric around the pump and given by22

$$\delta \left(\frac{1}{{Q}_{{\rm{TLS}}}}\right)\frac{{Q}_{{\rm{TLS}}}}{\tanh \frac{\hslash {\omega }_{r}}{2{k}_{\rm{B}}T}}=-1-{\left(\frac{{{\Delta }}}{{{\Omega }}}\right)}^{2}\left[6+3X\mathrm{ln}\,\left(1+{\left(\frac{{{\Omega }}}{{{\Delta }}}\right)}^{2}\left(1-X\right)\right)\right],$$
(3)

where

$$X=\sqrt{1+2{\left(\frac{{{\Delta }}}{{{\Omega }}}\right)}^{2}}.$$
(4)

The internal Q-factor as a function of pump power of modes detuned from the pump by 2, 4 and 8 times the FSR, respectively, is shown in Fig. 1c along with fits to Eq. (3). Comparing to the single mode loss, we note that saturation in detuned probe modes occurs at higher pump powers. In the single mode measurement, TLS losses are reduced by more than 90% at pump phonon numbers of n = ns ≈ 105. At this power, still only TLSs near-resonant with the pump mode are saturated, with little impact on the loss in other modes. As the pump power is increased further, TLSs are saturated across a wider frequency span, reducing losses in nearby modes. This is illustrated in Fig 2a.

Fig. 2: Two-tone spectroscopy of the TLS ensemble.
figure 2

a Illustration of TLS saturation due to the pump. Near-resonant TLSs in the ground state can be excited by the SAW field and the induce loss. Saturated TLSs do not contribute to the loss. At the single mode saturation phonon number ns, TLS loss is mitigated in the pump mode, while losses in other modes are only marginally affected. As the strength of the pump tone is increased, the spectrum of the saturated TLSs becomes wider, reducing loss substantially in nearby modes. In two-tone spectroscopy, a drive tone is applied at the pump mode and response in the other modes are measured as a function of detuning Δ and the number of pump phonons n. The TLS loss 1/QTLS is shown in b with fits to Eq. (3) (solid lines). The colour scale indicates the pump phonon number. Applying a detuned pump also induces a frequency shift in the probe mode, plotted in c with fits to Eq. (3) (solid lines) and a 5 kHz offset between traces. In d we plot the TLS loss as a function of detuning and pump phonon number, with the fit shown in e. The corresponding plots for the frequency shift are shown in f, g. The frequency resolution in Δ in the measurement is given by the free spectral range of the resonator.

Full size image

The full probe response as a function of detuning and pump power is shown in Fig. 2. The loss due to TLS is plotted in Fig. 2a and a fit to Eq. (3) is shown in Fig. 2c. For pump phonon numbers n > ns, the losses in the pumped mode are completely saturated and no additional effects of increased pump power can be resolved. The shape of the spectral hole, however, depends strongly on power in the entire range accessible in this experiment. The spectral hole due to the pump continues to widen as the pump power is increased even though pump mode losses are completely saturated. Conversely, holes in the absorption spectrum burnt using pump phonon numbers below ns are not well resolved by the free spectral range of the resonator. Figure 2b shows the measured frequency shifts, and the fit to Eq. (2) is plotted in Fig. 2d. We observe that unlike the loss saturation, the frequency shift is not monotonic in power for a given detuning Δ. This is consistent with our model of the dispersive interaction between off-resonant TLSs and the SAW modes.

Strength of SAW–TLS interaction

In the single mode measurements, we observe a scaling of the effective Rabi frequency with phonon number that is consistent with the STM. We extract β = 1.05 which is in good agreement with \({{\Omega }}\propto \sqrt{n}\). However, in the two-tone experiment the behaviour is different. The scaling of the extracted effective Rabi frequency characterising the coupling of the modes to the TLS bath does not correspond to the expected \({{\Omega }}\propto \sqrt{n}\). Instead, we find Ω ∝ nk with k ≈ 0.3, with a slight divergence between the values obtained from the frequency shift and loss. The Rabi frequency Ω as a function of pump strength is shown separately for the loss and frequency shift fits in Fig. 3. A mechanism that has been suggested to cause slower scaling than square root in the loss saturation with power is based on TLS–TLS interactions that cause TLSs to fluctuate in frequency in and out of resonance with the probe mode9,29,30. There are two main differences between the single mode and two-tone experiments. In addition to the pump being off-resonant in the two-tone case, the power is also substantially higher (n > ns). It is not clear why TLS–TLS interactions should play a larger role in the two-tone experiment. One reason could be that the effect of TLSs drifting in frequency between the pump and probe frequencies is more important in this case.

Fig. 3: Effective Rabi frequency of the pump extracted from fits as function of number of pump phonons.
figure 3

Data shown in black derives from fits to the probe loss in two-tone spectroscopy (Fig. 3b). The frequency shift (Fig. 3c) yields smaller values for the pump strength at high phonon numbers, shown here in red. Solid lines show fits to extract the scaling. The blue line shows the k = 0.5 slope predicted by the STM, corresponding to \({{\Omega }}\propto \sqrt{n}\).

Full size image

A simpler model for the two-tone spectroscopy was derived in ref. 31. Under the assumption of uniform coupling strength of TLSs to the resonant modes, the spectral hole has a Lorentzian lineshape. In Supplementary Note 1, we repeat the analysis of our two-tone spectroscopy data using this model and obtain a scaling for the Rabi frequency of Ω ∝ n0.3 (Supplementary Figs. 1–3). That a similar scaling is obtained with different models suggests the disparate scaling between on- and off-resonant pumping is a real effect, although it does not explain its physical mechanism.

If we instead fit Eqs. (2) and (3) with the power as independent variable, assuming \({{\Omega }}={{{\Omega }}}_{0}\sqrt{n}\) for each probe mode, we can extract an average single phonon Rabi frequency Ω0/2π = 25 kHz. This is of the same order as what is found in ref. 22. In order to obtain an estimate for the intrinsic TLS linewidth, we rewrite the denominator of the single mode power dependence given by Eq. (1) in terms of the effective Rabi frequency and loss rates as

$$n/{n}_{\rm{C}}={{{\Omega }}}^{2}{T}_{1}{T}_{2}$$
(5)

where T1 and T2 are the TLS excited state lifetime and coherence time, respectively. This implies that at above the critical phonon number nC, the effective Rabi frequency exceeds the effective loss rate \({{\Omega }}\,> \,1/\sqrt{{T}_{1}{T}_{2}}\). Still assuming the \({{\Omega }}={{{\Omega }}}_{0}\sqrt{n}\) behaviour for the drive strength, and that T2 = 2T1, we can extract an approximate characteristic TLS coherence time T2 ≈ 2 μs. While obtaining this value relies on many assumptions, it appears consistent with the width of the spectral holes observed in the two-tone spectroscopy.

Discussion

Our measurements have revealed the shape of the spectral hole burnt in a TLS ensemble by a strong pump. We have shown that the response in acoustic susceptibility due to pumping is qualitatively well captured by theory based on the STM22, but find a deviation in the scaling of the extracted Rabi frequency with pump power. From our measurements we extract estimations of the average single phonon Rabi frequency and linewidth of the TLS distribution.

Our results suggest using acoustic pumping to mitigate TLS loss in superconducting qubits. While improvements in design and fabrication methods have led to a rapid increase in coherence in recent years, active means of TLS saturation32 are hard to develop due to the incompatibility of resonant microwave pump fields with device functionality. This limitation does not necessarily apply to the acoustic pumping scheme demonstrated here. For a spectral hole due to an applied SAW drive, it is straightforward to reach a linewidth of several tens of MHz, which allows for pumping at sufficient detuning to prevent spurious excitations due to crosstalk, but still within range of the spectral hole. While high-coherence superconducting devices are not compatible with piezoelectric substrates33, the generation of high-frequency SAW on non-piezoelectric substrates, including silicon, is well established34,35,36. Combining SAW and superconducting qubits could then be done by fabricating IDTs on local piezoelectric thin films, while the qubits are placed directly on the non-piezoelectric substrate. Acoustic resonators also have a lower intrinsic sensitivity to temperature than superconducting devices, which should make them well suited for studying the temperature dependence of TLS-induced noise and dissipation across a wide temperature range.

Methods

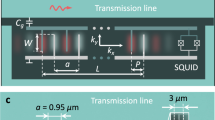
Our device, shown schematically in Fig. 4, consists of two Bragg mirrors with 800 fingers each, separated by a distance d = 1440 μm. An interdigital transducer (IDT) at the centre of the cavity provides an input and output port. The mirrors and IDT are fabricated from aluminium on a piezoelectric GaAs substrate. The IDT has 50 periods of 1.2 μm and a split-finger design to suppress mechanical reflections37. The mirrors provide a stopband of ~40 MHz centred around 2.40 GHz. As the IDT is spatially centered with respect to the mirrors, only even modes can be excited, giving an effective free spectral range of FSR = vSAW/L = 1.97 MHz, supporting 20 modes within the stopband. Due to the finite penetration depth (~15 μm) of the field into the reflectors, the effective cavity length L is greater than the mirror edge separation d. To probe the resonator we measure the reflection off the IDT via a circulator. In two-tone spectroscopy the pump tone is also applied at the same port. The measurements presented here are performed at the 10 mK base temperature of a dilution refrigerator.

Fig. 4: Device layout.
figure 4

Microscope image showing the IDT and right hand Bragg mirror and schematic illustration of the SAW resonator. The IDT and mirrors are fabricated in aluminium on a GaAs substrate with gold ground planes. Inset shows part of the Bragg mirror. The IDT with 50 periods provides a coupling port and is centered with respect to the Bragg mirrors. The mirrors have N = 800 fingers each that are shorted together. As the length of the resonator is more than 1000 wavelengths, the spatial distributions of the different modes are nearly identical. The resonator is measured in reflection using a microwave circulator.

Full size image