Introduction

Recent progress in experimental techniques for the fabrication, control and measurement of quantum coherent systems has allowed the routine creation of moderate-to-large arrays of controllable quantum units (e.g., superconducting qubits, trapped atoms and ions) expected to have revolutionary applications, e.g., in sensing, quantum communication and quantum computing1,2,3,4. They also allow the investigation of fundamental physics, such as the measurement problem5,6,7, the link between the chaotic behavior in classical systems and the corresponding dynamics in their quantum counterparts8,9,10,11,12 and the relative roles of entanglement and thermalization13,14,15,16,17.

The deployment of modern quantum technologies generally requires both the improvement of unit quantum elements (e.g., increasing their decoherence times) and the scaling up of quantum structures18.

It is known that large systems comprising many functional elements tend to demonstrate emergent phenomena in their dynamics, which cannot be observed in smaller systems19,20. Examples include dynamical phases in driven Bose–Einstein condensates21, synchronization in micromechanical oscillator arrays22, and coherent THz emission from layered high-temperature superconductors23,24,25. Nevertheless, the emergent phenomena are commonly neglected when designing and investigating large-scale coherent structures. This is possibly due to the absence of a convenient theoretical framework for studying these novel systems. One important open question to be tackled is how the dynamics scales with the increase of the system size (e.g., number of qubits) and what role in its change is played by emergent phenomena.

We address these questions by studying theoretically the far-from-equilibrium dynamics of a driven chain of interacting two-level quantum systems with dissipation and dephasing (Fig. 1a). We find that even a short chain comprising between two and four elements can demonstrate chaotic behavior. Remarkably, in systems with five or more elements a phenomenon known as hyperchaos emerges, a dynamical regime characterized by two or more positive Lyapunov exponents. Hyperchaos has features that resemble thermalization even though the system is far from equilibrium. We show that, in contrast to thermalization, the deterministic origin of hyperchaos allows it to be controlled either by tuning of the system parameters or by applying an external driving force. Our results give new insights into the dynamics of large artificial quantum coherent structures, which will be important for the design and control of quantum systems, such as Rydberg molecules, quantum information processors, simulators, and detectors.

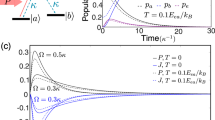
Fig. 1: Schematic representation of interacting qubits and the largest Lyapunov exponent dependence on model parameters for the case of two qubits.
figure 1

a Schematic representation of a circular chain of six interacting quantum units (e.g., Rydberg atoms or qubits), labeled by integer indexes and coupled via nearest neighbor interactions. b Atomic-level configuration reflected in the model [Eqs. (1)–(3)]. Coherent laser excitation from the ground state \(\left|g\right\rangle\) to an excited (“Rydberg”) state \(\left|e\right\rangle\) with a Rabi frequency ΩR and detuning δω, incoherent spontaneous decay γ, and the Rydberg interaction when an excited qubit shifts the transition frequency of a neighboring qubit by V. c Dependence of the largest Lyapunov exponent Λ1 on Δ and Ω calculated for c = 5 for the system of 2 coupled qubits. The color scale intensity indicates the value of Λ1.

Full size image

Results

Mathematical model

Here we investigate the dynamics of a one-dimensional (1D) chain of N qubits driven by an external electromagnetic field in the presence of decoherence. The system under consideration is equivalent to a system of Rydberg atoms, by rescaling and reidentification of parameters26,27,28,29,30,31. Along with superconducting structures, Rydberg systems provide a controllable testbed for studying fundamental quantum dynamics32,33,34 and for developing new quantum chemistry35,36,37. In particular, arrays of Rydberg atoms can be controlled experimentally with very high precision38,39,40. Each atom has a ground state \(\left|g\right\rangle\) and an electronically excited high-energy Rydberg state \(\left|e\right\rangle\) (Fig. 1b). Rydberg states have large polarizability ~n7 (where n is the principal quantum number), which generates strong and long-range interactions between atoms41.

To model an electromagnetically driven array of qubits (Rydberg atoms), we use the Hamiltonian

$$\begin{array}{l}H=\mathop{\sum }\limits_{j = 1}^{N}\left[-{\delta }_{\omega }\left|e\right\rangle {\left\langle e\right|}_{j}+\frac{{\Omega }_{R}}{2}\left(\left|e\right\rangle {\left\langle g\right|}_{j}+\left|g\right\rangle {\left\langle e\right|}_{j}\right)\right]\\ +\mathop{\sum }\limits_{j\,{<}\,k}{V}_{i,j}\left|e\right\rangle {\left\langle e\right|}_{j}\otimes \left|e\right\rangle {\left\langle e\right|}_{k},\end{array}$$
(1)

where δω = ωl − ω0 is the detuning between the laser and transition frequencies, ΩR is the Rabi frequency (tuned by the laser field amplitude), and Vi,j characterizes the interaction between ith and jth qubits.

The dynamics are described by the Liouville–von Neumann equation for the density matrix ρ,

$$\dot{\rho }=-i\left[H,\rho \right]+{\mathcal{L}}\left[\rho \right],$$
(2)

where relaxation and dephasing processes are taken into account through the appropriate Lindblad operator

$${\mathcal{L}}[\rho ]=\gamma \mathop{\sum }\limits_{j}\left[\left|g\right\rangle {\left\langle e\right|}_{j}\rho \left|e\right\rangle {\left\langle g\right|}_{j}-\frac{1}{2}\{\left|e\right\rangle {\left\langle e\right|}_{j},\rho \}\right],$$
(3)

with γ to be the decay rate from the excited state to the ground state. Rydberg atom interactions can range over a few tens of micrometers, larger than the physical size of the system (The same is true for superconducting qubits interacting through a resonator field mode.). Therefore, to simplify the analysis, we can initially assume that interactions are identical for any pair of qubits, Vi,j = V (see Fig. 1a, b). For a system of N qubits, ρ has the dimensionality of its Hilbert space, 2N.

This problem can be greatly simplified by substituting a fully factorized density matrix approximation, ρ ≈ ∏j ⊗ ρj, in Eq. (2). Here ρj is the (one-particle) density matrix of the jth qubit. This approximation is justified for a partially quantum coherent system, for which it has been shown accurately to describe experimental measurements on qubits, up to the corrections due to two-point correlations38,42,43,44,45. In such a case, the quantum coherence between spatially separated elements is disrupted, e.g., by local ambient noise46.

Rewriting the factorized density matrix ρ in terms of the population inversion of the jth qubit, \({w}_{j}={({\rho }_{j})}_{11}-{({\rho }_{j})}_{00}\), and its coherence, \({q}_{j}={({\rho }_{j})}_{10}={({\rho }_{j})}_{01}^{* }\), yields:

$$\begin{array}{l}{\dot{w}}_{j}=-2\Omega \Im {q}_{j}-({w}_{j}+1);\\ {\dot{q}}_{j}=i\left[\Delta -c\mathop{\sum }\limits_{k\ne j}({w}_{k}+1)\right]{q}_{j}-\frac{1}{2}{q}_{j}+i\frac{\Omega }{2}{w}_{j}.\end{array}$$
(4)

In Eq. (4), the dimensionless time τ = γt (i.e. \(\dot{x}\equiv dx/d\tau ={\gamma }^{-1}dx/dt\)), Ω = ΩR/γ, Δ = δω/γ, and c = Va/γ, where a is the lattice constant. In more detail, the derivation of Eq. (4) is discussed in Section A in Supplementary Information.

Emergence of chaos and hyperchaos

Here we study the dynamical regimes of chains of interacting qubits. To characterize the complexity (randomness) of the emergent chaos and hyperchaos, we calculate the full spectrum of the Lyapunov exponents47.

First we analyze two coupled qubits (N = 2). Previously, it has been shown that interplay between the energy pumping and dissipation can eventually trigger self-sustained state population oscillations in this system and even lead to the emergence of bistability, when homogeneous and antiferromagnetic states coexist27. Our investigation reveals another interesting phenomenon associated with deterministic chaos, which emerges via a cascade of period-doubling bifurcations for a periodic oscillations47. In Fig. 1c, we show a color map illustrating the dependence of the largest Lyapunov exponent Λ1 on Δ and Ω. A transition from yellow to black reflects the change from smaller to larger values of Λ1. The diagram clearly demonstrates the presence of chaotic dynamics, for which Λ1 > 0, in considerable areas of the parameter plane shaded by black color. This shows that the discovered chaos is a robust phenomenon existing in our system over wide parameter ranges. Notably, for certain parameter values it coexists with the antiferromagnetic steady state. The detailed descriptions of the bifurcation transitions and analysis of the Lyapunov exponents that characterize the stability of long-term dynamics are presented in Section B in Supplementary Information.

For N = 3 and 4, the same type of chaotic dynamics exists in the system. However, surprisingly, for N ≥ 5 a new type of chaotic dynamics appears, whose stability is characterized by more than one positive Lyapunov exponent. This type of chaos is known as hyperchaos48. A map of different dynamical regimes in the (Δ, Ω) parameter plane is shown in Fig. 2a for N = 5 and c = 5. This diagram was built by calculating the spectrum of Lyapunov exponents for the various limit sets that exist in the (Δ, Ω)-plane. When all the Lyapunov exponents are negative, there is a stable equilibrium state (white in the diagram). If the largest Lyapunov exponent equals 0, the oscillations are periodic (cyan). If the largest two Lyapunov exponents are both 0, the dynamics are quasiperiodic (red). However, when one or two Lyapunov exponents are positive, there is chaos (green) or hyperchaos (black), respectively.

Fig. 2: Hyperchaos in a ring of five qubits.
figure 2

a Map showing areas of (Δ, Ω) space corresponding to different regimes of long-term behavior for a ring of five qubits. Black denotes areas of hyperchaos with two positive Lyapunov exponents, green is a region of chaos with one positive Lyapunov exponent, cyan is a periodic regime, red areas correspond to quasiperiodic behavior, and white is a steady-state regime. b Variation of the four largest Lyapunov exponents with Δ; blue dots correspond to Δ increasing from 1 to 9, red dots to Δ decreasing down to 1. c A zoom of the region of b within the black rectangle. d Single-parametric bifurcation diagram corresponding to c, in which the vertical positions of each point correspond to the local maxima of w1(t). For all figures Ω = 2.5.

Full size image

Figure 2b illustrates the bifurcation transitions between the different dynamical regimes when Ω = 2.5 and Δ changes along the yellow dashed line in Fig. 2a. The blue curves represent the evolution of the four largest Lyapunov exponents Λ1 > Λ2 > Λ3 > Λ4. A number of distinctive phases emerge as we increase Δ from 1 to 9. The stable equilibrium state, which exists for small Δ, switches to a periodic solution as a result of an Andronov–Hopf bifurcation at Δ ≈ 1.7, where Λ1 becomes zero. At Δ ≈ 3.55, the periodic oscillations lose their stability via a Neimark–Sacker bifurcation, resulting in the onset of quasiperiodic oscillations (Λ1 = Λ2 = 0). Increasing Δ further leads to chaotic dynamics.

To better illustrate the transition to the chaotic regime, in Fig. 2c we present a zoom of the region of Fig. 2b framed by the black rectangle. The corresponding bifurcation diagram, shown in Fig. 2d, is constructed by plotting the points corresponding to the local maxima w1,max in the time evolution of w1(t), calculated for given Δ. For a particular value of Δ, periodic solutions are represented by one or few single dots on the graph, while the complex sets of many points for a specific Δ reflect quasiperiodic or chaotic dynamics. As Δ increases, the quasiperiodic oscillations where Λ1 = Λ2 = 0 (Fig. 2c) are replaced (at Δ ≈ 3.732) by complex periodic oscillations due to saddle–node bifurcation. These periodic oscillations are characterized by Λ1 = 0 and Λ2,3 < 0 (Fig. 2c) and represented in Fig. 2d by few isolated dots for a fixed Δ. For Δ ≳ 3.744, the periodic solutions undergo a cascade of period-doubling bifurcations giving rise to chaos with one positive Lyapunov exponent at Δ ≈ 3.75 (Fig. 2c). The period-doubling bifurcations do not affect the spectrum of Lyapunov exponents of the stable solution, since the latter remains periodic. However, each period-doubling causes additional Lyapunov exponent to approach zero (Fig. 2c), which manifests itself via doubling of the number of dots in Fig. 2d. Thus, for N = 5, the bifurcation mechanism leading to the onset of chaos stays the same as for the case of N = 2. Further investigation shows that this mechanism is also present at larger N.

Increasing Δ makes the chaotic oscillations more complicated and leads to the gradual development of hyperchaos, which emerges at Δ ≈ 4.4 (see Fig. 2b). This transition is linked to further instability of already unstable periodic orbits, which form the skeleton of the chaotic attractor. Accumulation of the corresponding bifurcations causes the second Lyapunov exponent to become positive.

We find that period-doubling is the most common but not the only route to chaos exhibited by the system. Figure 2a reveals some direct transitions from the red region where the dynamics is quasiperiodic to the green region where the dynamics are chaotic. This behavior can indicate the mechanism of torus destruction for the transition to chaos47,49. However, we did not specifically investigate the effect of this particular mechanism on the development of hyperchaos.

The dynamics of N = 5 coupled qubits in different dynamical regimes is exemplified in Fig. 3. Typical periodic solution is presented in Fig. 3a. Here n = 1, …, 5 denotes the qubit number in the chain, t is time, and the color scale indicates the value of wn. All qubits oscillate with the same frequency but with different phases. However, the phase shift is constant for each pair of qubits, meaning that they are synchronized. The latter is also indicated by the clearly periodic pattern in Fig. 3a. The quasiperiodic regime when Δ = 3.73 is shown in Fig. 3b. Now the phase shifts between oscillations of different qubits are no longer constant, and the periodic pattern of the spatio-temporal dynamics is lost, reflecting the loss of synchronization.

Fig. 3: Time evolution of wn for 5 qubits.
figure 3

a Periodic [Δ = 3.74], b quasiperiodic [Δ = 3.73], c chaotic [Δ = 4.05], and d hyperchaotic [Δ = 4.95] oscillations; n labels an qubit in the chain.

Full size image

Chaotic oscillations for Δ = 4.05 are illustrated in Fig. 3c. Here the qubit chain demonstrates erratic behavior, which is in marked contrast to the ordered dynamics presented in Fig. 3a, b. Figure 3d shows typical hyperchaotic oscillations calculated for Δ ≈ 4.95. In this regime, the oscillations in the chain become even more complicated than the chaotic behavior in Fig. 3c and now demonstrate no specific time scales in wn(t). The hyperchaotic behavior persists up to Δ ≈ 8.0, after which it rapidly switches to chaotic and then periodic solutions. For Δ > 8.53, all oscillations disappear, and all long-term solutions in the system correspond to stable equilibrium.

In order to further examine the presence of the multistability in the dynamics of the chain, we return to the evolution of the Lyapunov exponents as Δ changes from 9 down to 1. Values of Λ1,2,3,4 for this case are shown red in Fig. 2b. The plot shows that the stable homogeneous steady state (Λ1 = Λ2 = Λ3 = Λ4 < 0) exists down to Δ ≈ 5.491, where it suddenly changes to hyperchaotic oscillations. Thus, within the interval of Δ between 5.491 and 9.0, the homogeneous fixed point co-exists with different inhomogeneous regimes, including other types of equilibria, periodic and quasiperiodic oscillations, chaos, and hyperchaos (blue graphs in Fig. 2b). Multistability therefore appears to be a generic phenomenon, existing in chains of different size.

Analysis of chains with N > 5 reveals that hyperchaos is not only preserved in the system but also becomes more complicated as more Lyapunov exponents become positive. The results of our analysis are summarized in Fig. 4, where the number of positive Lyapunov exponents, M, is shown as a function of the number of qubits in the chain. The graph shows an almost linear growth, at a rate suggesting that adding two or three qubits leads to the appearance of an additional positive Lyapunov exponent. This phenomenon originates from a weak correlation between the oscillations in distant qubits. As a result, the addition of a subsystem, comprising two or more qubits, is able to demonstrate chaotic dynamics and adds one more positive value to the spectrum of the Lyapunov exponents. Since, for a given coupling, the smallest chaotic subsystem comprises two qubits, their inclusion produces one more positive Lyapunov exponent. The number of Lyapunov exponents grows roughly proportionally to the number N of qubits rather than with the dimensionality 2N of the Hilbert space of the system. This indicates the possibility of a reduced description of its dynamics. In such a case, the transitions between qualitatively different, distinct dynamical regimes are controlled by a relatively small number of independent dimensionless parameters.

Fig. 4: Number of positive Lyapunov exponents M vs. number of qubits N in the ring chain.
figure 4

Δ = 5, Ω = 2.5, c = 5.

Full size image

For large N, multiple positive Lyapunov exponents make the oscillations very complicated, demonstrating broadband continuous spectra, which are similar to random fluctuations in solids50. In addition, we found out that these hyperchaotic phenomena are preserved for non-identical qubits and open chains, as well as in chains with more complex qubit-coupling topology than those discussed above. The spatial correlations, the spectra of the chain oscillations calculated for different numbers of qubits, and Lyapunov analysis of chains with non-identical qubits and more complex topology are discussed in Sections C and D in Supplementary Information.

To study the significance of the system’s dimensionality, we analyze two-dimensional L × L lattices of L2 interacting qubits (Fig. 5a). As for 1D rings, these square lattices exhibit chaotic (for 2 × 2 lattices) and hyperchaotic behavior (for 3 × 3 and larger lattices). Figure 5c illustrates the Lyapunov exponents spectrum for a 3 × 3 square lattice. We observe two areas (2.7 < Δ < 3.8 and Δ ≈ 5.8) of chaos, one small area of hyperchaos with two positive Lyapunov exponents (Δ ≈ 4.2), and two areas of hyperchaos with three positive exponents (4.4 < Δ < 5.3 and 6.05 < Δ < 7.6). Therefore, for a lattice of 9 qubits, we observe a complicated behavior with three positive Lyapunov exponents, which is similar behavior to that we observe for a ring of 9 qubits. We investigate lattices with several values of L of nodes and find almost linear growth of the number of positive Lyapunov exponents with increasing the number of qubits in the lattice (see Fig. 5b). We can conclude that emergence of hyperchaos does not depend on the dimensionality of the system.

Fig. 5: 2D L × L lattices of L2 interacting qubits.
figure 5

a Schematic representation of a square lattice of nine interacting quantum units (e.g., Rydberg atoms or qubits), labeled by integer indexes and coupled via nearest neighbor interactions. b Number of positive Lyapunov exponents M vs. lattice size L in the L × L lattice calculated for Δ = 5, Ω = 2.0, c = 5. c Variation of the eight largest Lyapunov exponents with Δ for a square lattice of 9 qubits, Ω = 2.0.

Full size image

Chaos control via a coherent driving field

This dynamical complexity has a deterministic origin, which could be controlled (suppressed or enhanced) by an applied external field. Previously, it was demonstrated that a periodic perturbation can suppress hyperchaos with two positive Lyapunov exponents51,52. Here we apply a periodic modulation to the laser field amplitude, which modulates the Rabi frequency:

$$\Omega ={\Omega }_{m}[1+M\sin (2\pi ft)],$$
(5)

where Ωm is the amplitude of the Rabi frequency, while M and f are the modulation index and the frequency of modulation, respectively. We consider the case when N = 15, a large but practically feasible number of qubits such that the system shows hyperchaos, characterized by four positive Lyapunov exponents and a broadband spectrum. Figure 6 presents the 11 largest conditional Lyapunov exponents (Fig. 6a) and the corresponding bifurcation diagram (Fig. 6b) calculated for Ωm = 2.5, c = 5, Δ = 5.0, M = 0.684, and f changing from 0 to 2.0.

Fig. 6: Chaos control.
figure 6

a Conditional Lyapunov exponents spectrum and b bifurcation diagram for a ring of 15 qubits by means of an external parametric effect for Ωm = 2.5, c = 5, Δ = 5.0, M = 0.684.

Full size image

Due to the periodic modulation, chaos is suppressed in certain parameter regions. For f between 0.7 and 0.8, we find complex periodic oscillations characterized by the largest Lyapunov exponent <0 (see Fig. 6a) and multiple branches in the bifurcation diagram (Fig. 6b). Within the interval f ∈ (0.9, 1.1), we find period-one oscillations (one maxima per period) and Lyapunov exponents ≪0, corresponding to highly stable regular oscillations in this regime. In addition, the same controlling signal is able to significantly increase the complexity of hyperchaotic oscillations and a corresponding increase in the value of the largest Lyapunov exponent. For example, when f ≈ 0.3 the largest Lyapunov exponent becomes almost three time larger than in the case without the application of the signal (f = 0). Otherwise the number of positive Lyapunov exponents can be increased by 1 (f = 1.2) or 2 (f = 1.4). Our results demonstrate that periodic modulation of laser field amplitude can be used as an efficient method to control very complex hyperchaos in qubit arrays.

Discussion

We have shown that the interplay between dissipation and energy pumping in quantum systems comprising chains of qubits can produce highly nontrivial emergent phenomena associated with the onset of complex chaotic and hyperchaotic oscillations even in the absence of multi-particle entanglement. The complexity of the hyperchaos increases with the number of elements in the chain. The number of positive Lyapunov exponents grows linearly with the number of qubits, that is, as only log of the dimensionality of the Hilbert space. This indicates the possibility of a reduced description of the quantum system by a small (in comparison to the dimensionality of the Hilbert space) number of dimensionless parameters. This observation is consistent with the fact that the manifold of all quantum states that can be generated by arbitrary time-dependent local Hamiltonians in a polynomial time occupies an exponentially small volume in the Hilbert space of the system53.

Our results demonstrate a mechanism for randomizing the evolution of coupled qubits, which arises due to dynamical phenomena far from equilibrium and is thus unrelated to thermalization processes despite the superficial similarity. The model we have used is generic and can be applied and implemented directly in, e.g., chains of qubits or electromagnetically driven superconducting qubits. Our results will be important for the development of large quantum systems, where multi-point entanglement is neither required nor supported42,43,54. In particular, they suggest a controllable way of switching between different dynamical regimes via regular to chaos transitions either by tuning the parameters of the system or by applying a controlling signal via modulation of laser field amplitude, as another approach towards controlling quantum state dynamics55. Our results are of interest for the development of quantum random number generators56 and quantum chaotic cryptography57,58. A natural extension of this research will consider the effect of interqubit entanglement on the complexity revealed here and whether it can be utilized for controlling this far-from-equilibrium behavior.

Another interesting task will be to study how quantum signatures of classical chaos such as the growth rate of out-of-time-ordered correlators59 behave in the presence of hyperchaos. Preliminary results on the integration of the original quantum model (Eq. (2)), briefly discussed in Section E in Supplementary Information, indicate that the complexity of chain dynamics depends highly non-trivially on the parameters of the Hamiltonian (Eq. (1)). However, a detailed analysis of the dynamical regimes and their characteristics in the presence of entanglement, and especially of the question about the universality of these regimes and parameters that control them, requires extensive further research, which we hope this paper will stimulate.

Methods

Lyapunov exponents calculation

The Lyapunov exponents were calculated for the stable limit sets, which correspond to the solutions of the model equations as time t → ∞. Since we apply the periodic modulation (Eq. (5)) to the system (Eq. (4)), the Lyapunov exponents we calculate in this case are called conditional and missing one zero exponent, unlike the common Lyapunov exponents spectrum60. To determine them, we implement 3N perturbations vectors, where N is the number of units in the system, and use periodic Gram–Schmidt orthonormalization of the Lyapunov vectors to avoid a misalignment of all the vectors along the direction of maximal expansion61,62.

Bifurcation diagrams

In order to construct a bifurcation diagram, we plot the points corresponding to the local maxima w1,max in the time evolution of w1(t), calculated for given Δ and Ω.