Introduction

Quantum sensing devices are among the most promising quantum technologies. Their implementation relies on the use of quantum probes to attain enhanced performances in the estimation of one or more parameters compared to classical ones. Quantum metrology aims at identifying the best strategy able to provide this quantum advantage1,2,3,4,5,6,7,8. This is achieved by carefully tailoring the probe state, the interaction, and the measurement, in order to extract the information on the relevant parameter, and by the optimal choice of the estimator through data post-processing9. When performing a single-parameter estimation with a given measurement, the optimal strategy is unequivocally identified through the saturation of the Cramér-Rao bound (CRB), which establishes the maximum achievable precision on the measured parameter10. The CRB is asymptotically saturated with the number of resources employed to probe the system during the measurement. Conversely, the realization of quantum sensors, able to perform estimations in realistic scenarios, poses two constraints to sensing devices: the resources to be used for probing are limited, and systems can show high complexity, often involving more than one parameter. Having a limited number of resources demands for their optimization. This can be obtained by accurately tailoring the estimation protocols, from the probe preparation to the measurement strategies. In this way, one aims at attaining the saturation of the achievable bounds employing the smallest number of resources possible. Such problem has been explored with several theoretical analysis. A possible approach towards the protocol optimization is that of exploiting adaptive strategies. These have been successfully employed in single-parameter estimation8,11,12,13,14,15,16,17,18,19,20. In this regard, machine learning (ML) approaches have provided a significant speed up in the saturation of the ultimate bounds8,18,19,21,22,23.

On the other hand, measuring multiple parameters at once might be necessary in complex systems characterized by a set of parameters, where a time or spatial dependency can prevent the successful realization of subsequent single-parameter estimations. The parameters considered can span from multiple phases24,25,26, to phase and phase diffusion in frequency-resolved phase measurements27,28,29, and phase and loss in absorbing systems30,31. In other instances where a system depends solely on one parameter, a multiparameter approach could still be favorable as other parameters can be interrogated as a control to monitor the quality of the sensor itself32,33,34. In general, the saturable bounds for quantum multiparameter strategies are not as defined as in the single-parameter case, and trade-offs in the achievable precision for each of the parameters have to be sought35,36,37,38,39. Different theoretical works have studied a non-asymptotic Bayesian approach in quantum multiparameter estimation40,41,42,43,44, thus providing bounds and protocols to generally address limited-data quantum metrology.

In this context, it becomes of paramount importance to identify both a suitable estimation scenario and a corresponding platform for an experimental investigation of adaptive multiparameter estimation protocols. A notable scenario to investigate is multiphase estimation24,25,26,45,46,47,48,49,50,51,52,53,54. Not only such scenario provides a benchmark for multiparameter quantum metrology, but it has a plethora of practical applications in quantum imaging35,37. A fundamental step is to find a suitable experimental platform to realize multiphase estimation. A viable solution is provided by integrated photonics, which enables the implementation of complex circuits with reconfiguration capabilities55,56,57,58,59,60 with applications ranging from quantum simulation, to computation, and communication. This platform represents a promising system for optical quantum metrology, since interferometers with several embedded phases can be employed as a benchmark platform to study multiparameter estimation problems. In this direction, first results on multiphase estimation with quantum input probes have been recently reported24, using a three-arm interferometer fabricated by femtosecond laser writing61,62. Here, we report on multiphase estimation experiments performed with an integrated platform using different adaptive protocols. We identify the strategy providing better performances in terms of optimal estimation and computational resources. In particular, we have experimentally tested the proposed approach by feeding with single-photon states an integrated three-mode interferometer realized by the femtosecond laser writing technique. The employed technique is a Bayesian learning protocol, which exploits advantages of Monte carlo approach, such as its independence of integration space dimensions63. This solution seems to be ideal for adaptive multiparameter problems, where complex optimizations could involve multiple integrations. Here we employ experimentally an adaptive strategy optimized in the limited data regime for multiphase estimation. Using this algorithm, we demonstrate that the convergence to the CRB can be experimentally achieved after only few photons. Importantly, such convergence is achieved for both the simultaneously estimated phases. Our results improve research for identifying optimal learning strategy and finding experimental platforms suitable to test multiparameter estimation problems also in the limited data regime.

Results

Bayesian multiparameter estimation

In multiparameter estimation, the aim is to measure simultaneously an unknown set of parameters x = (x1, …, xn) by reaching the maximum precision allowed by the amount of resources employed in the process. In general, the set of parameters is encoded within the evolution of a system, either described through a unitary operator Ux or a more general map \({{\mathcal{L}}}_{{\boldsymbol{\mathrm{x}}}}\). The value of the unknown parameters x can be estimated by preparing a suitable probe state ρ and sending it to evolve throughout the system. Information on the unknown parameters can be retrieved by measuring the output state ρx with a set of measurement operators {\(\Pi\)d}, where d = 1, …, m represents the set of possible outcomes. Such process is then repeated N times to improve precision in the estimation process. After N probes have been prepared and measured, the obtained sequence of measurement outcomes d = (d1, …, dN) has to be converted in a set of parameters estimates \(\hat{{{{\mathbf{x}}}}}\) through a suitably chosen function \(\hat{{{{\mathbf{x}}}}}=\hat{{{{\mathbf{x}}}}}({d}_{1},\ldots ,{d}_{N})\). A possible choice of estimator is provided by Bayesian protocols10,64,65,66. This class of estimators is based on encoding the initial knowledge on the parameters in a probability function p(x), called prior distribution, which is updated according to the Bayes rule at each step of the estimation protocol. The posterior distribution after N probes reads \(p({{{\mathbf{x}}}}| {{{\mathbf{d}}}})={{\mathcal{N}}}^{-1}p({{{\mathbf{d}}}}| {{{\mathbf{x}}}})p({{{\mathbf{x}}}})\), where p(d∣x) is the likelihood function of the system expressing the conditional probability of obtaining the measurement sequence d for given values of the parameters x, and \({\mathcal{N}}\) is a normalization constant. Then, the mean of the posterior distribution can be exploited as the estimate of the unknown parameters \({\hat{x}}_{i}=\int {x}_{i}p({{{\mathbf{x}}}}| {{{\mathbf{d}}}}){\prod }_{i}d{x}_{i}\). Bayesian protocols present several important properties. In particular, it can be shown that such approach is asymptotically unbiased, meaning that the estimated values converge to the true values when N is large enough. This is related to the quadratic loss \(L({{{\mathbf{x}}}},\hat{{{{\mathbf{x}}}}};\tilde{{{{\mathbf{w}}}}})={\sum }_{i}{\tilde{w}}_{i}{({x}_{i}-{\hat{x}}_{i})}^{2}\), whose average value over all measurement sequences d is commonly employed as a figure of merit to quantify the convergence of the estimation process. The average of posterior distribution is the optimal estimator for minimizing this figure of merit8,65,67. The coefficients \({\tilde{w}}_{i}\) can be chosen to reflect different weights between the parameters, while for equally relevant parameters they can be set as \({\tilde{w}}_{i}=1\). Hereafter, we will consider this latter scenario and thus define the quadratic loss as \(L({{{\mathbf{x}}}},\hat{{{{\mathbf{x}}}}})={\sum }_{i}{({x}_{i}-{\hat{x}}_{i})}^{2}\). Furthermore, in a Bayesian framework the posterior distribution also provides a confidence region for the parameters estimates, which is represented by the covariance matrix \({\rm{Cov}}(\hat{{{{\mathbf{x}}}}})\) of p(x∣d). This latter figure of merit is obtained for each single estimation experiment composed of a sequence of N probes, and has no counterpart in frequentist approaches67. In general, Bayesian bounds for both the quadratic loss and the covariance matrix depend on the amount of a priori knowledge p(x) available17,44,67,68. Asymptotically for large values of N, corresponding to the regime where the amount of information acquired in the estimation process far exceeds the a priori knowledge, the covariance matrix satisfies the Cramér-Rao inequality \({\rm{Cov}}({{{\mathbf{x}}}})\ge {{\mathcal{F}}}^{-1}/N\), where \({\mathcal{F}}\) is the Fisher information matrix69 and thus \({{\mathcal{F}}}^{-1}\) corresponds to its inverse. Such quantity also provides an asymptotic bound for the quadratic loss as \(L({{{\mathbf{x}}}},\hat{{{{\mathbf{x}}}}})\ge {\rm{Tr}}[{{\mathcal{F}}}^{-1}]/N\).

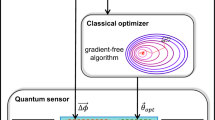
Adaptive protocols can be employed when, besides the set of unknown parameters x, the user has access to an additional set of control parameters c = (c1, …, cl) that can be changed throughout the estimation process. More specifically, after each of the N probes is sent and measured, the acquired knowledge is employed to change the values of c for the next probe to maximize the extraction of information in the subsequent measurement. Within a Bayesian framework, such knowledge is encoded in the posterior distribution. Hence, after each step of the estimation protocol, the user can decide the values of the control parameters c starting from p(x∣{c}, d) (see Fig. 1a). Considering the presence of these tunable control parameters during the estimation process, the likelihood after N probes reads \(p({{{\mathbf{d}}}}| {{{\mathbf{x}}}},\{{{{\mathbf{c}}}}\})=\mathop{\prod }\nolimits_{i = 1}^{N}p({d}_{i}| {{{\mathbf{x}}}},{{{{\mathbf{c}}}}}_{i})\), where di is the measurement result of the probe i after application of control values ci. Therefore, the Bayes rule for updating posterior distribution becomes p(x∣{c}, d) ∝ p(d∣x, {c})p(x), where p(x) does not depend on {c}, as control phases have no role in the prior knowledge. Adaptive protocols represent a relevant tool in phase estimation process. Indeed, the adoption of adaptive strategies becomes a crucial requirement even in the single-parameter case to optimize the algorithm performances11,12,13,16,18,19,21,22,63,70,71, with the aim of achieving the ultimate bounds provided by the Cramér-Rao inequality for small values of N18. Furthermore, in more complex systems characterized by a phase-dependent Fisher information matrix, adaptive strategies become crucial to reach equal performances for all values of the unknown parameter(s)34. Indeed, in several scenarios the quantum Cramér-Rao bound, namely the ultimate precision for a given probe, is parameter-independent. However, construction of the optimal measurement for its saturation requires in general significant a-priori knowledge on the parameter(s) since it can be defined in a local estimation framework25,26. Thus, in a scenario where limited or no a-priori knowledge on the parameter is available, and limited resources can be employed, adaptive protocols represent a powerful tool.

Fig. 1: Schemes of adaptive estimation.
figure 1

a General layout of an adaptive multiparameter estimation protocol. A sequence of probes ρ are sent to estimate the parameters x. At each step the results of the measurement Πd and the current knowledge on x are employed to optimize the control parameters c. b Multiarm interferometer for multiphase estimation. An m-mode interferometer embeds n = m − 1 unknown phase shifts ϕ, while additional controlled phases Φ can be employed for adaptive protocols.

Full size image

Adaptive protocols for multiarm interferometers

Given the general scenario described in the previous section, it is crucial to identify and test experimentally protocols to saturate the ultimate bounds with a very limited number of probes. In this context, multiarm interferometers represent a benchmark platform to perform simultaneous estimation of multiple phases. The platform is schematically shown in Fig. 1b, and represents the m-mode generalization of a Mach–Zehnder interferometer in the multimode regime24,50,72,73. More specifically, it is composed by a sequence of a first multiport splitter, employed to prepare the probe state, a series of phase shifts between all the optical modes, and a second multiport splitter, which defines the output measurement. Both multiport splitters can be in principle designed according to appropriate decompositions74,75 to implement any linear unitary transformation. The internal phase shifts can be divided in two layers. The first one ϕ = (ϕ1, …, ϕn) corresponds to the unknown parameters to be measured, while the second one Φ = (Φ1, …, Φn) takes the role of the control parameters for adaptive estimation; we note that in our implementation the number of controls is l = n. Here, n = m − 1 is the number of independent parameters, since one of the phases is considered as the reference mode. Both the unknown parameters and the control ones contribute to the overall phase differences Δϕ = (Δϕ1, …, Δϕn) within the interferometer.

We study different adaptive protocols for Bayesian learning of the unknown phases of this platform injected by a single-photon state, by focusing both theoretically and experimentally on the three-mode scenario (m = 3) with two independent parameters (n = 2). More specifically, we choose both for state preparation and state measurement transformation a balanced tritter described by unitary matrix U with ∣Ui,j∣2 = 1/3, ∀ (i, j)76. Injecting a single-photon on input port 1 corresponds to generating a sequence of probe states of the form \(\left|{\psi }_{{\rm{in}}}\right\rangle ={3}^{-1/2}(\left|1,0,0\right\rangle +\left|0,1,0\right\rangle +\left|0,0,1\right\rangle )\), which represents a single-photon state exiting in the balanced superposition of the three modes. The Fisher information matrix in this scenario shows a phase-dependent profile \({\mathcal{F}}(\Delta {\phi }_{1},\Delta {\phi }_{2})\), meaning that without adaptive strategies the asymptotic precision will be different depending on the actual phase values. In particular, by looking at the inverse of \({\mathcal{F}}\), we obtain \(\mathop{\min }\nolimits_{\Delta {\phi }_{1},\Delta {\phi }_{2}}{\rm{Tr}}({{\mathcal{F}}}^{-1})\simeq 3.866\), which is obtained for six different phase pairs \((\tilde{\Delta {\phi }_{1}},\tilde{\Delta {\phi }_{2}})\). For those pairs, minimum asymptotic quadratic loss is achieved. Note that, by using the results of refs. 25,26,54, an optimal measurement can be in principle constructed saturating the quantum Cramér-Rao bound. For instance, for small values of the unknown phases a measurement including the projector over the initial state can be employed, thus requiring a-priori knowledge on the parameters or adoption of a large number of probes.

Bayesian protocols require in general expensive computational resources, due to the need of evaluating complex integrals to determine the normalization constant \({\mathcal{N}}\), as well as the estimated values and their corresponding covariance matrices. A possible solution is to perform a discretization of the parameters space, thus converting integrals to sums. In this case, the bin size has to be chosen depending on the minimum error expected at the end of the estimation process. However, such solution becomes quickly unmanageable when the number of parameter increases, since such a discretization has to be performed in a n-dimensional space. A different solution has been explored in ref. 63 for Bayesian learning problems by using a Sequential Monte Carlo (SMC) approach. Indeed, Monte Carlo methods seems to be a natural solution, due to their capability of reaching convergence independently from the integration space dimension. The SMC method approximates the infinite dimensional support ϕ with a finite number M of elements ϕi, called particles, with associated probability weights wi. The error in the approximation can be arbitrarily reduced by increasing the number of particles, leading to a trade-off between computational time and accuracy of the approximation. In the context of Bayesian analysis, any distribution \(\tilde{p}({{\boldsymbol{\phi} }})\) in the particles approximation is expressed as \(\tilde{p}({\boldsymbol{\phi} })\approx \mathop{\sum }\nolimits_{i = 1}^{M}{w}_{i}\delta ({\boldsymbol{\phi} }-{{\boldsymbol{\phi} }}_{i})\).

We now consider the case of an initial prior knowledge p(ϕ) corresponding to a uniform distribution. In the particles scenario, this prior information is approximated by a set of M randomly drawn pair of phases ϕi with equal weights wi = 1/M to satisfy the normalization condition \((\mathop{\sum }\nolimits_{i = 1}^{M}{w}_{i}=1)\). During the experiment, the information about the unknown phases ϕ is updated according to the Bayes rule after each measurement outcome d. In the particle approximation, having fixed control phases, this corresponds to updating the particle weights as wi → wi p(d∣ϕi, Φ), while keeping the particles {ϕi} unchanged. The estimation of ϕ is then provided by the expectation value of the posterior distribution \(\hat{{\boldsymbol{\phi} }}=\mathop{\int}\nolimits_{\,}^{\,}d{\boldsymbol{\phi} }\ {\boldsymbol{\phi} }\ p({\boldsymbol{\phi} }| d,{\mathbf{\Phi }})\approx \mathop{\sum }\nolimits_{i = 1}^{M}{w}_{i}{{\boldsymbol{\phi} }}_{i}\). As discussed in ref. 63, the particle approximation needs some additional steps to avoid the introduction of further errors throughout the estimation process. In particular, after a few iterations the non-zero weights will be mostly concentrated on a small subset of {ϕi}, reducing the validity of the approximation. To avoid such effect, it is possible to employ resampling techniques77. More specifically, when the particle weights become too concentrated according to a given threshold condition, a new set of particles \(\{{{\boldsymbol{\phi} }}_{i}^{\prime}\}\) is generated by adding a small random perturbation to the original particles (see Supplementary Note 1A for more details). The weights are then reset to \({w}_{i}^{\prime}=1/M\), and the estimation process restarts. Within this framework, we now have to define the adaptive rule to determine the value of the control parameters at each step depending on the actual knowledge. More specifically, at each step of the estimation process one has to decide the control parameters c (here, the additional phases Φ) for the next probe. To this end, we consider different strategies.

A first approach (i) is based on choosing the control phases according to \(\hat{{\boldsymbol{\phi} }}+{\mathbf{\Phi }}\simeq {\delta \boldsymbol{\phi} }\), where \({\delta \boldsymbol{\phi} }=\mathop{\arg \min }\nolimits_{\Delta {\phi_1},\Delta {\phi_2}}{\rm{Tr}}({{\mathcal{F}}}^{-1})\). This strategy looks to set the interferometer phases Δϕ to those values, leading to a minimum bound for \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) according to the Cramér-Rao inequality. While this approach is tailored to work in the asymptotic regime of large N, its performances are not guaranteed to be optimal for small N. An upside of this approach is that setting the control parameters does not require complex optimization steps, since an analytic rule can be easily defined.

In order to devise a strategy working in the small N regime, one can consider a second strategy (ii) which is specifically tailored to work for all values of N. To this end, we adapted the protocol described in ref. 63 to the multiparameter scenario implemented by our system. By this approach, the choice of the control phases is performed to optimize a given figure of merit, known as utility function (\({\mathcal{U}}\)). Canonical choices for \({\mathcal{U}}\) are information gain or quadratic loss. In our case, we choose \({\mathcal{U}}(\hat{{\boldsymbol{\phi}}})={\rm{Tr}}[{\rm{Cov}}(\hat{{\boldsymbol{\phi} }})]\), calculated over the posterior distribution. Note that this approach is general and different utility functions can be chosen, based on the specific estimation scenario. For instance, if the parameter of interest is the correlation between the phases, the utility function should involve the off-diagonal terms of the covariance matrix. Hence, at each step the minimization algorithm finds the best control phases Φ that, averaged over all possible measurement outcomes, leads to a minimum value for the sum of the parameters confidence intervals. This is thoroughly discussed in Supplementary Note 1B. Given that this method relies on numerical optimization steps, it is more expensive in terms of computational resources than the previous strategy based on the Fisher information matrix. Conversely, it provides the advantage of searching the optimal control phases for all values of N, thus covering the limited data regime where asymptotic approaches may not be the proper choice.

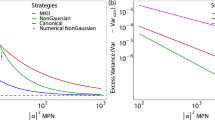
We have then performed numerical simulations to characterize the performances of the two algorithms. More specifically, we have sampled Nph = 100 random pairs of phases (ϕ1, ϕ2) in the interval [0, 2π] × [0, 2π]. For each pair, we simulated \({N}_{\exp }=100\) estimation processes where N = 100 single-photon probes are sent in the interferometer. The results are shown in Fig. 2. We first tested the performances of both algorithms (i) and (ii). We observe that, concerning strategy (i), the protocol fails to approach the Cramér-Rao bound even for N ~100. This is related to the non-injectivity of the likelihood function. In this way, a given probability can be associated with different possible pairs of phases. Approach (i) seeks for setting the phase differences Δϕ to a fixed point, and it is not able to resolve such ambiguity issue. Better results are obtained by applying at each step a random (but known) set of control phases (iii), which shows better convergence while not reaching the Cramér-Rao bound. However, the application of this strategy is capable of resolving the ambiguity. One can then consider a modified version (i’) of the asymptotic protocol (i), where the first K control phases are drawn from a uniform distribution, while for N > K the strategy works as (i). Numerical evidence shows that the best choice for this parameter is K ~ 20. We observe that, with this modified strategy, the Cramér-Rao bound is approached for N ~ 50. Better results are obtained with the optimized strategy (ii), in particular in the small N regime. For N > 60, we observe that both strategies (i’) and (ii) provide similar performances since the experiment progressively approaches a large N scenario where the Fisher information matrix defines the system sensitivity. Finally, in Supplementary Note 2 we perform some numerical simulations to show the superior performance of the optimized adaptive protocol with respect to non-adaptive strategies, that are not capable of resolving unambigously the estimation process in the full [0, 2π] × [0, 2π] interval (see Supplementary Figs. 1 and 2). In this work we experimentally implement the optimal strategy to guarantee a faster convergence of the estimation process.

Fig. 2: Numerical simulations of Bayesian adaptive protocols.
figure 2

For Nph = 100 pair of phases, we simulated the performance of the different strategies described in the main text, by averaging for each phase over \({N}_{\exp }=100\) different runs and by performing spline interpolation on the obtained curves. Top: quadratic loss \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) (solid lines). Bottom: utility function \({\mathcal{U}}(\hat{{\boldsymbol{\phi} }})={\rm{Tr}}[{\rm{Cov}}(\hat{{\boldsymbol{\phi} }})]\) (dashed lines), corresponding to the sum of the parameters confidence intervals. Inset: (top) ratio R between the performances of each protocol, compared with the optimized strategy (ii). R is computed both for \(L({\boldsymbol{\phi }},\hat{{\boldsymbol{\phi }}})\) (solid lines) and \({\mathcal{U}}(\hat{{\boldsymbol{\phi }}})\) (dashed lines), referring the same colors of the main panels. (bottom) two-dimensional map of uniform-distributed couples of phases drawn for the simulations. Green lines: approach (i) based on the Fisher information matrix. Red lines: approach (i'), which includes first N = 20 events with random control parameters, while for N > 20 works as (i). Blue lines: optimized approach (ii). Gray lines: benchmark approach with random control parameters (iii). Dotted black lines: Cramer-Rao bound for the asymptotic regime.

Full size image

Integrated circuit for multiphase estimation

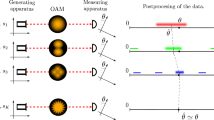
The platform employed in this experiment is an integrated three-arm interferometer. This system has been employed in ref. 24 for the simultaneous estimation of two relative phase shifts ϕ = (ϕ1, ϕ2) between the arms of a three-mode interferometer (Fig. 3). We first discuss the circuit layout and parameters, while we subsequently describe the working condition used for the multiphase estimation experiments reported below.

Fig. 3: Experimental platform.
figure 3

A type-II parametric down conversion source (PDC) generates photon pairs, which are spectrally selected via interference filters (IF) and coupled to single-mode fibers (SMF). One of the photons is directly measured by detector DT acting as trigger for the experiment. The other photon, after polarization compensation (PC), can be injected in any of the three input ports of the interferometer via a single-mode fiber array (SMFA). After evolution, photons are collected via a multimode fiber array (MMFA) and measured through detectors Di, with i = 1, 2, 3. Coincidences between DT and any of Di are recorded via a time-to-digital converter. The results of the measurement are processed and employed to apply the adaptive protocols. The layout of the integrated circuit (shown in the bottom panel) includes eight resistors to modulate the input transformation (RA), the output one (RB), and the internal phases (Ri, with i = 1, …, 6) as described in the main text.

Full size image

The platform is a three-arm interferometer realized in a glass chip through femtosecond laser writing61,62. The interferometer, optimized for operation at λ = 785 nm, is implemented by two cascaded tritters (three-mode beam splitters) A and B interspersed with phase shifters. Each tritter is decomposed in a 2-D planar configuration74 consisting of three balanced directional couplers and one phase shifter \({\phi }_{{\rm{T}}}^{{\rm{A}}}\) (\({\phi }_{{\rm{T}}}^{{\rm{B}}}\)) for tritter A (B). These phase shifters, as well as those placed between the two tritters, can be tuned by means of the thermo-optic effect, using microresistors that are patterned in a thin gold layer covering the chip surface. When an electrical current is applied to the resistor, an optical path change on the waveguide is induced by the dissipated heat78. In particular, let us consider the dissipated power \({P}_{i}={R}_{i}\ {I}_{{R}_{i}}^{2}\) on resistor Ri subjected to a current \({I}_{{R}_{i}}\), where we also include that the value of the resistor depends on the current due to its temperature change. The two induced relative phase shifts Δϕ = (Δϕ1, Δϕ2) between the arms of the interferometer with respect to the reference mode, have the following general dependence on the dissipated powers:

$$\Delta {\phi }_{j}={\phi }_{j0}+\mathop{\sum }\limits_{i=1}^{6}\left({\alpha }_{ji}{P}_{i}+\mathop{\sum }\limits_{k=i}^{6}{\alpha }_{jik}^{{\rm{NL}}}{P}_{i}{P}_{k}\right),$$
(1)

where j = 1, 2, and ϕj0 stands for the static phases of the interferometer. Parameters αji and \({\alpha }_{j,i = k}^{{\rm{NL}}}\) are the linear and quadratic response coefficients relative to the dissipated power Pi, respectively, while \({\alpha }_{j,i\ne k}^{{\rm{NL}}}\) represent the nonlinear coefficients associated with the product of the two powers Pi and Pk to include cross-talk effects. In our device 8 independent resistors are present (Fig. 3). Resistors RA and RB are exploited to tune tritter phases \({\phi }_{{\rm{T}}}^{{\rm{A}}}\) and \({\phi }_{{\rm{T}}}^{{\rm{B}}}\), respectively. Conversely, resistors R1, R4 along mode 1, R2, R5 along mode 2 and R3, R6 along mode 3, are employed to tune the internal relative phase shifts of the interferometer, according to (1). The operations of tritters A and B are described through the unitary evolutions UA and UB, respectively, while the action of each phase shifter along mode i is described through a unitary matrix PSi (i = 1, 2, 3). The overall evolution Utot of the interferometer is given by \({U}^{{\rm{tot}}}={U}_{{\rm{B}}}(\mathop{\prod }\nolimits_{i = 1}^{3}{{\rm{PS}}}_{i}){U}_{{\rm{A}}}\).

In order to characterize the relevant parameters necessary to fully describe the evolution of the interferometer, we measure the output probabilities when single photons are injected along input 1, tuning the current applied on each resistor. The probabilities have been theoretically modeled by modifying the ideal expression with additional terms, taking into account non-ideal visibilities and dark counts of the detectors. In this way, we performed an overall fit of all the measured probabilities to determine the 58 chip parameters (see Supplementary Note 3 and Supplementary Fig. 3) and finely reconstruct the likelihood probability p(d∣Δϕ) of our system.

According to the scheme of Fig. 1b, the unknown phases to be estimated are the pairs (ϕ1, ϕ2), relative to the chosen reference arm ϕref. The eight resistors allow us to finely tune and control all the relevant phase shifts of the interferometer. The tritters phases can be tuned and are chosen in order to maximize the sensitivity of the interferometer. Using single-photon probes, the optimal configuration for our interferometer employs mode 1 as input and mode 2 as reference. In this case, the trace of the inverse of Fisher Information matrix, minimized over all possible internal phases, is \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]=4.2\) (see Supplementary Note 4). This value represents the (phase-dependent) Cramér-Rao bound of our device, where the aim of the protocol is to saturate such bound for all phase pairs by using limited probes. In absence of adaptive strategies, such precision cannot be reached for all phase pairs, thus rendering the sensitivity of the sensor phase-dependent. The aim of our strategy is thus also to reach the bound \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]=4.2\) for all values of the parameters. The unknown phases ϕ = (ϕ1, ϕ2) are tuned by means of resistors R4, R5, and R6, according to (1), while the control phases Φ = (Φ1, Φ2) are tuned by resistors R1 and R2 (see “Methods”).

Experimental adaptive multiphase estimation

We perform the experiment by continuously adapting the present tunable circuit following the optimized Bayesian-SMC method [strategy (ii)]. This allows us to achieve the best attainable estimate with a limited number of resources. The probes are heralded single photons at 785 nm generated by a degenerate type-II SPDC process inside a BBO crystal, pumped by a pulsed 392.5 nm laser. A photon from each pair is sent through the circuit, entering in input 1, and acts as probe, while the other photon acts as the trigger for the heralding process (see Fig. 3). An event is then recorded as the coincidence between the trigger detector and one of the three outputs of the circuit. The interaction of the probe with the chip operator encodes information about ϕ onto its state. Finally, the result of the measurement is collected and used to identify the optimal settings for the next experimental step.

The phases ϕ to be estimated can be chosen by setting the currents flowing in three resistors R4, R5, R6 (see “Methods”). In order to test the protocol over different estimation experiments, we have identified Nph = 15 pair of phases uniformly distributed (Fig. 4). Resistors R1, R2 are used to tune the control phases necessary for the adaptive strategy. After the first event, where currents \({I}_{{R}_{1}},{I}_{{R}_{2}}\) are chosen at random, we implement strategy (ii): optimal control phases Φ are calculated by minimizing the expected posterior variance. The nearest available control currents \({I}_{{R}_{1}},{I}_{{R}_{2}}\), limited by the precision of our power supply (Keithley 2230) and by maximum dissipation power (<1 W, see “Methods”), are calculated and effective control phases are applied to the device. The calculation of the prior distribution for each step is made through the particle approximation. A uniform grid of M = 2000 pairs of phases (Fig. 5a) is assumed as initial set for the prior distribution. This choice is performed to avoid any possible harmful periodicity during the estimation process. Examples of prior information evolution during an experiment are reported in Fig. 5b–d. In Fig. 5c the resampling step is shown, where particles with zero weight of the previous step (Fig. 5b) are rearranged in more significant locations (see Supplementary Note 1A for more details). Each pair is estimated \({N}_{\exp }=100\) times, adopting N = 100 resources (photons) as for the numerical simulations discussed above. Individual experiments are reported in details in Supplementary Note 5 and Supplementary Fig. 4. Algorithm performances are shown in Fig. 6. A first evaluation consists in averaging the experimental quadratic loss for each pair of phases over all \({N}_{\exp }\) independent runs. As a result, the overall quadratic loss \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) saturates the CRB with a limited number of resources, in agreement with the numerical simulations described above. Furthermore, saturation occurs both for off- and diagonal matrix elements of the CRB. In particular, the latter show that the CRB is reached with similar performances in the estimation of both phases. This result is a fundamental feature for multiparameter metrology tasks when both parameters are treated equally. We observe from Fig. 6c that our algorithm reaches the CRB also when looking at the correlations between the parameters. This means that the employed estimation approach does not add additional sources of undesired correlations in the estimation process, which is relevant given the addressed multiparameter scenario. In our case the resulting difference in estimation of the two parameters is <10%, when compared to the sensitivity bound. Furthermore, a heuristic estimation of the convergence time to saturate the CRB can be calculated by studying the difference \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})-{\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]/N\). A characteristic time can be computed by using \(a+b\exp (-N/{\tau }_{N})\) as fit function, with \(a,b,{\tau }_{N}\in \mathbb{R}\) the fitting parameters. The value obtained for τN is \({\tau }_{N}^{{\rm{fit}}}=5.6\), which underlines the good performance of the adaptive adopted technique in using small number of probes. Note that the number of probes necessary to achieve the bound is generally scheme-dependent, as it can be seen studying different multiparameter scenarios44. Another significant property of Bayesian approach is the ability to provide the statistical error in each step of the estimation process, calculated as the variance of the posterior distribution. Final estimated pairs fall on average within the error from true set values of phases (Fig. 4).

Fig. 4: Final distribution of the estimated phases.
figure 4

Experimental simultaneous estimations of Nph = 15 different uniform-distributed pairs of phases. The estimation process uses an amount of N = 100 resources and Bayesian adaptive approach. Dark orange regions represent the error in the estimation obtained from the covariance matrix. Each estimated pair (red dot) is distant from true set value (blue dot) within the error (orange area), thus confirming the good performance of the algorithm.

Full size image
Fig. 5: Example of experiment.
figure 5

A typical estimation of two phases (red dots) is reported. a A uniform grid is generated as initial support for the prior distribution. b–d Evolution of the posterior distribution during experiment for three subsequent moments. In particular, the distribution before and after the resampling are shown respectively in b and c, where particles are rearranged in order to eliminate zero weight cases. The new posterior weights are uniform, while particles are distributed closer to the estimated phases. In a–d, particle colors represent the corresponding weight. e Study of standard deviation in estimation of the single phases (blue dashed lines) and their sum (red dashed lines). The saturation of their CRB (solid lines) occur for small N. f Experimental estimated pair of phases as function of the number N of adopted probes (dots). Dashed lines indicates true set values of the phases.

Full size image
Fig. 6: Experimental results.
figure 6

Simultaneous estimations of Nph = 15 different pairs of phases using Bayesian adaptive protocol. Quadratic loss is averaged for each phase over \({N}_{\exp }=100\) independent runs. a Comparison between overall quadratic loss \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) (red dots) and \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]/N\) (red solid line). The performances are in agreement with the numerical simulations. Red shaded regions represents the one-standard deviation interval where \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) can be found. b Analysis of diagonal elements of CRB by comparing quadratic loss relative to the single phase of the estimated pair \(L({\phi }_{i},\hat{{\phi }_{i}})\) (with i = 1, 2) (blue triangles) and \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]/(2N)\) (blue solid line). The algorithm shows symmetric optimal performances for estimation of both parameters, by using the same amount of resources. This feature is highlighted by the inset panel, where the ratio \(\Delta L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) between the difference of the two estimations and the bound value is reported. c, Analysis of phase correlations by comparing off-diagonal terms of \({{\mathcal{F}}}_{\exp }^{-1}\) (see Supplementary Note 4) and \({[{({{\mathcal{F}}}_{\exp })}^{-1}]}_{12}/N\) (green solid line). d Estimation of convergence time (τN) to CRB. The value can be estimated by fitting the distance between the averaged \(L({\boldsymbol{\phi} },\hat{{\boldsymbol{\phi} }})\) and CRB, after N > 2. The adopted fit function is \(a+b\exp (-N/{\tau }_{N})\), with \(a,b,{\tau }_{N}\in {\mathbb{R}}\) the fitting parameters, leading to τN = 5.6. The choice of this function is performed to provide a reasonable estimation of τN, as the number of probes necessary to approach the CRB.

Full size image

All these experimental results demonstrate the quality of Bayesian-SMC strategy, confirming it as largely suitable for multiparameter estimation problems. While the convergence to CRB in limited data regime has been accurately studied by theoretical works in both single-17,68,79 and multi-43,44 parameter estimation, the obtained results show the robustness of the employed Bayesian approach when applied to a realistic sensor, where calibration of the system has to be performed before it can be employed for phase estimation experiments. Indeed, we have shown the capability of saturating the Cramér-Rao bound by using limited probes when the calibration procedure is performed with finite size data. Note that such result is non-trivial, and shows that the actual modeling of the sensor permits to reach a high degree of control of the device, even when a larger number of phases is simultaneously tuned. Implementation of this strategy has been enabled only by the high reconfigurability of our employed integrated device, which highlights the fundamental role of an appropriate platform for metrology tasks, which involve more than one parameter. These features characterize our proof-of-principle experiment, defining it as a necessary step towards the realization of adaptive multiparameter algorithms for technological applications.

Discussion

Multiparameter estimation is a fundamental problem for the realization of realistic quantum sensors in several scenarios8,35,37. In this task, there are still several open problems and a comprehensive framework has yet to be defined. For instance no general strategies are available for the construction of optimal probes and measurements in different multiparameter scenarios.

While a general framework for Bayesian quantum multiparameter estimation exists (see ref. 41 for a complete review), there are several remaining open questions. In particular, the operational application of optimal strategies, measurements and probes preparation, is a field that needs to be largely explored, even if some theoretical results are available also in the limited data regime44. Furthermore, further progresses are still required on the technological platforms towards reaching unconditional violation of the standard quantum limit80 in complex sensors. Hence, it is crucial to identify an experimental platform versatile enough to address different possible approaches. Multiphase estimation provides an ideal scenario with different practical applications. Furthermore, it represents a testbed for different multiparameter estimation protocols. Applying these to real world scenario requires a further step, that is, the optimization of the available resources, so as to attain the minimum reachable uncertainties after a sufficiently small number of measurements. This can be achieved by implementing adaptive strategies. In the limited data scenario, theoretical works have shown the number of required resources to saturate the lower bounds44,68, but the multiparameter experimental counterpart still lacks its investigation.

Here, we have reported the experimental implementation of a multiphase Bayesian adaptive protocol on an integrated platform, optimized to operate in the limited data regime. We have reviewed different adaptive strategies and selected the one optimizing the cost function given by the trace of the covariance matrix. This has been employed to perform several simultaneous estimations of uniformly distributed pairs of phases. As we have shown, the achievable bounds are attained for both unknown phases after a limited number of N ~ 40 probes. Our experiment permits to underline the suitability of such an integrated circuit for performing multiparameter estimation tasks, as well as to exploit the capabilities of the proposed Bayesian adaptive strategy.

This work provides a versatile approach for future perspectives in multiparameter quantum metrology. In particular, these techniques can be directly generalized for multi-photon quantum probes, which would provide insight on the achievable quantum accuracy limit. Indeed, the framework behind this approach is general, and thus different probe states can be employed by suitable choice of the system likelihood function. At the same time, the algorithm here described can be applied to more complex integrated platforms, which enable optimized extraction of information. The realized platform can be exploited also for the realization of different optimal multiphase Bayesian protocols, such as that proposed in ref. 44. In that paper, given an arbitrary state, prior knowledge and number of repetitions of the experiment, explicit recipes for the optimal measurements are provided in the case where the estimators commute. Further perspectives include the study of different multiparameter scenarios, as well as practical applications to quantum sensing of delicate samples81 and quantum error correcting algorithms82,83,84.

Methods

Tuning of circuit parameters for adaptive two-phase estimation

We discuss in more details how we exploit the phases in our interferometer. The pair (ϕ1, ϕ2) represents the unknown phases relative to a reference arm with phase ϕref (Fig. 1b). All the relevant phases of the circuit can be finely tuned by means of eight resistors.

The first step performed aimed at finding the optimal choice for the tritter phases \({\phi }_{{\rm{T}}}^{{\rm{A}}}\), \({\phi }_{{\rm{T}}}^{{\rm{B}}}\) to maximize the sensitivity of the interferometer. To achieve this goal, we first evaluate the Fisher information matrix \({{\mathcal{F}}}_{\exp }\) associated with the device from the experimentally estimated parameters, Then, we numerically minimize \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]\) over all possible values of \({\phi }_{{\rm{T}}}^{{\rm{A}}}\), \({\phi }_{{\rm{T}}}^{{\rm{B}}}\) and internal phases Δϕ, in the allowed range of dissipated powers (the upper threshold being ~1 W, to avoid possible damages to the resistors). We identify such minimum for all combinations of possible inputs and reference arms. The best scenario for our interferometer corresponds to use mode 2 as reference mode and arm 1 as input mode for single photons, with the following values of phases: \({\phi }_{{\rm{T}}}^{{\rm{A}}}=1.49\) rad, \({\phi }_{{\rm{T}}}^{{\rm{B}}}=0.72\) rad, Δϕ1 = − 3.07 rad and Δϕ2 = 0.34 rad. In this working point, the trace of the inverse of Fisher Information matrix is \({\rm{Tr}}[{({{\mathcal{F}}}_{\exp })}^{-1}]=4.2\). We now have to assign each resistor Ri (i = 1, …, 6) to tune both the unknown phase shifts ϕ = (ϕ1, ϕ2), and the control phases Φ = (Φ1, Φ2) for the adaptive algorithms. More specifically, we choose to employ resistors R4, R5, and R6 to tune ϕ. Conversely, the control phases Φ are those modified by dissipating power in R1 and R2. Hence, considering (1) as Δϕ = ϕ + Φ, we find the following expressions:

$${\phi }_{j}={\phi }_{j0}+\mathop{\sum }\limits_{i=4}^{6}\left({\alpha }_{ji}{P}_{i}+\mathop{\sum }\limits_{k=i}^{6}{\alpha }_{jik}^{{\rm{NL}}}{P}_{i}{P}_{k}\right)$$
(2)
$${\Phi_j}={\sum \limits_{i=1}^{2}}\left({\alpha }_{ji}{P}_{i}+ {\sum \limits_{k=i}^{2}}{\alpha }_{jik}^{{\rm{NL}}}{P}_{i}{P}_{k}\right),$$
(3)

with j = 1, 2. In setting all phases of the device (Eqs. (2) and (3)) the effective number of applicable phases is finite, due to the upper damage threshold of global power (<1 W) and to the limited precision of the power supply (Keithley 2230). In particular, the generated control phases are distributed uniformly and quite densely over all the interval [0, 2π] × [0, 2π], sufficient to guarantee the correct functionality of the tested algorithms. Note that, in principle, only four resistors would be sufficient to tune independently the 4 phase shifts (two unknown and two controls). However, we employed five resistors in order to obtain large tunability of the device within limits of the damage threshold of each resistor.