A network-ready random-access qubits memory

Abstract

Photonic qubits memories are essential ingredients of numerous quantum networking protocols. The ideal situation features quantum computing nodes that are efficiently connected to quantum communication channels via quantum interfaces. The nodes contain a set of long-lived matter qubits, the channels support the propagation of light qubits, and the interface couples light and matter qubits. Toward this vision, we here demonstrate a random-access multi-qubit write-read memory for photons using two rubidium atoms coupled to the same mode of an optical cavity, a setup that is known to feature quantum computing capabilities. We test the memory with more than ten independent photonic qubits, observe no noticeable cross-talk, and find no need for re-initialization even after ten write-read attempts. The combined write-read efficiency is 26% and the coherence time approaches 1 ms. With these features, the node constitutes a promising building block for a quantum repeater and ultimately a quantum internet.

Introduction

Quantum networks enable faithful communication by exchanging photonic qubits that cannot be cloned¹. Networks conceived to generate an encryption key that is shared by two essentially classical parties, Alice and Bob, have already been demonstrated numerous times^2,3. Future genuine quantum-mechanical and multi-functional networks, however, will likely rely on multi-purpose nodes that can receive, store, send, and also process qubits^4,5. To accomplish these tasks, such nodes require at least two processable qubits^6,7,8,9.

For example, an elementary quantum repeater for long-distance entanglement distribution requires a chain of nodes, each with two memory qubits that are pairwise entangled with memory qubits in the neighboring nodes. This entanglement is typically established via photonic channels, which necessitate a corresponding qubit interface. In addition, such repeater nodes require single- and two-qubit gates to also realize efficient entanglement swaps and complete Bell-state measurements. These properties, in essence, represent the celebrated five quantum computation plus two quantum communication criteria that were put forward by DiVincenzo¹⁰. It needs to be emphasized that the criteria call for two contradictory physical capabilities¹¹: memories need isolated qubits, while processors necessitate coupled qubits.

In order to realize these nodes, the qubits can either be distributed over an ensemble of (real or artificial) atoms or be localized in single (real or artificial) atoms. Important achievements for ensemble-based nodes include static-access (temporal) multiplexing where qubits are received and retrieved in a fixed order (e.g., first-in-first-out)^12,13,14,15. This limitation can be resolved with spatial (dynamic-access) multiplexing instead of temporal multiplexing. In fact, a random-access quantum memory (RAQM) with an architecture resembling that of a classical random-access memory has been developed recently^16,17. This device can in principle receive and send an almost arbitrarily large number of qubits, limited only by the ratio of qubit coherence time to qubit access time. In the reported realization, this number was about three. However, no scalable information processing capability on and between the atomic qubits in all these ensemble nodes has been realized so far¹⁸.

Against this backdrop, it is still an open challenge to find a route toward multi-qubit memories that feature random qubit access, both for writing and reading, and controlled qubit processability. Individual real atoms are ideal to achieve this goal. They have already demonstrated, in complementary settings, their potential as faithful photonic qubit memories as well as qubit processors. The memory facet has been achieved by strongly coupling the atom to an optical cavity, which enables the efficient interconversion between stationary (matter) and flying (photonic) qubits¹⁹. Due to the high level of isolation from the environment and control of all degrees of freedom, these memories can feature long coherence times suitable for qubit storage²⁰. The processor facet has been demonstrated numerous times with qubits in atomic registers^{21,22,23,24,25} but without a connection to photonic qubits, or with a connection to photonic qubits^26,27,28, but in this case without multiplexed write-read capabilities.

Here we integrate the two facets by realizing an intracavity register with two individually addressable atomic memories that can independently write, store, and retrieve photonic qubits. We demonstrate the atom-selective absorption and emission of these qubits by implementing several different random-access quantum-memory protocols with up to eleven photonic qubits that are subsequently stored in the node without the need for re-initialization. In addition to these new capabilities, the capacity of one qubit per single atom also sets a new benchmark on scalability for constant resources²⁹.

Results

Apparatus

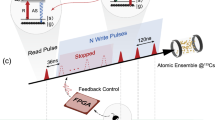
Figure 1a shows a sketch of the experimental setup. The system consists of two ⁸⁷Rb atoms trapped close to the center of a high-finesse optical cavity with parameters (g, κ, γ)/2π = (4.9, 2.7, 3.0) MHz. Here, g denotes the single-qubit light-matter coupling constant at the center of the optical cavity for the $\left|F=1,{m}_{{\rm{F}}}=0\right\rangle \leftrightarrow \left|F^{\prime} =1,{m}_{{\rm{F}}}=\pm \!1\right\rangle$ atomic transition at a wavelength of 780 nm, and κ and γ are the cavity field and atomic dipole decay rates, respectively²⁰.

Fig. 1: Illustrative view of the experimental setup and key elements toward the high-fidelity memory.

a Two atoms are trapped close to the waist of the cavity mode, symmetrically around the cavity axis. Via a high-NA objective, the atoms are imaged on an EMCCD camera. The same objective is used for addressing the individual atoms with a control laser beam by means of an acousto-optical deflector (AOD). b Possible cross-talk between the atoms due to their coupling to the same cavity mode. The state of an incoming photon should be mapped onto the addressed atom (A) via a stimulated Raman adiabatic passage (STIRAP) consisting of the cavity field g and the classical control field Ω. However, the unaddressed atom (B) offers a side-channel via off-resonant scattering of the photon. This leads to the storage of a random quantum state and thus a reduced fidelity. The lower part of the figure shows experimental data and a theory curve for how this effect can be minimized by increasing the single-photon detuning Δ. The error bars correspond to one standard deviation of the statistical uncertainties. c Cross-illumination of the addressing control field. The control intensity as a function of the addressing axis is shown, including a Gaussian fit yielding a full width at half maximum (FWHM) of the addressing beam of 2 μm. As a reference, white and gray regions indicate the trapping potential pattern, in which the typical spatial extent of the atomic wavefunction is about 50 nm. For small cross-illumination, only atomic configurations are used where the inter-atomic distance is at least three times the FWHM. The beam is elliptical (ratio 1:3) so that the atom positioning is less stringent in the direction of the long axis, illustrated by the ellipse in the second plot. The spacing of the atom leads to a reduced atom-cavity coupling g and thus to a reduced STIRAP efficiency (lower part). The blue-shaded rectangles highlight the trapping regions used for this work.

The two atoms are trapped in a two-dimensional optical lattice consisting of a red-detuned standing wave applied perpendicular to the cavity axis and a blue-detuned standing wave along the cavity axis. The two atoms are spaced symmetrically around the cavity center and therefore couple equally strong to the cavity mode. The two cavity mirrors have asymmetric transmission coefficients so that photons predominately leave the cavity via the high-transmission mirror. Outside the vacuum chamber, a high-numerical-aperture objective is used for imaging and laser-addressing of either atom³⁰.

Both atoms are initialized by optical pumping to the $\left|F=1,{m}_{{\rm{F}}}=0\right\rangle$ ground state. Using a stimulated Raman adiabatic passage (STIRAP) technique³¹, a single incoming photonic qubit is absorbed via the application of a classical control pulse. The information encoded in the photon polarization (in the basis of right and left circular polarization, σ⁺ and σ⁻, respectively) is coherently mapped to the two atomic states $\left|F=2,{m}_{{\rm{F}}}=1\right\rangle$ and $\left|F=2,{m}_{{\rm{F}}}=-1\right\rangle$, respectively. Thus, circular polarizations are mapped to atomic energy eigenstates whereas elliptical and especially linear polarizations are mapped to superpositions of atomic states. In order to reduce the impact of magnetic-field fluctuations, a small magnetic guiding field of about 44 mG is applied along the cavity axis. Consequently, the phase of the atomic superposition oscillates at twice the Larmor frequency, 30 kHz, during qubit storage, i.e., after write-in and before read-out. This oscillation is deterministic and could be compensated by a suitable setting of an optical wave plate. Finally, the stored photonic qubit is retrieved by vacuum STIRAP, the time-reversed process that is used for qubit storage. See Supplementary Notes 1 for more details on the timing of the experimental sequence.

Analysis and cross-talk elimination

The main challenge for the realization of a high-fidelity multi-qubit quantum memory lies in avoiding cross-talk between the individual qubit memories. This means, first, that only the illuminated atom must couple to the incoming or the outgoing photonic qubit and, second, that cross-illumination of the atoms from the STIRAP control laser must be eliminated. The first issue arises from the fact that both atoms are identically coupled to the same cavity field. Ideally, an incoming photon gets stored only in the addressed atom via the described STIRAP process (Fig. 1b). However, as all initialized atoms couple to the cavity, the incoming photon can interact with any atom including the unaddressed one. Scattering from this atom can transfer the atom into a random state and in this way scramble the fragile information encoded in the photon (Supplementary Notes 2). A way out of this dilemma is that the STIRAP efficiency can be made constant over a large range of negative single-photon detunings Δ,³¹ and that the incoherent scattering rate scales like Δ⁻². Quantitatively, we optimize the memory fidelity by increasing the detuning to Δ/2π = −100MHz with respect to $\left|F^{\prime} =1\right\rangle$ (Fig. 1b). At this point, the maximum incoherent scattering probability per input photon is only (0.15 ± 0.01)%, in contrast to a coherent storage efficiency of (38 ± 3)%.

For the second issue, cross-illumination is minimized by applying the STIRAP control field via an optical addressing system: After identifying the positions of the individual atoms via an electron-multiplying charge-coupled device (EMCCD) camera, the center of mass of the two atoms is shifted to the center of the cavity along one dimension (Fig. 1c). Note that the positions of the atoms are initially unknown. Then, a frequency-switchable radio frequency (RF) source is adaptively programmed so that each individual frequency drives the same acousto-optical deflector (AOD) in order to steer the beam onto one atom or the other (Fig. 1c). The pulse sequence on the atoms can be chosen randomly, with the only limitation being a delay time of 40 μs for switching between the atoms. This access time is mainly due to the sound-propagation time through the AOD, which could be reduced with, e.g., an electro-optical deflection system to about 2 μs. Altogether, this allows atom-number independent and thus scalable random access to the atoms. Practically, in order to reduce cross-illumination, we only use atom configurations where the interatomic distance is at least three times the full width at half maximum (FWHM) of the addressing beam along this direction, i.e., d_at−at ≥ 6 μm. For further details on the specific optical and electrical setup and on how the FWHM was measured at the atom’s position, see Supplementary Notes 3.

A side effect of this separation is a small reduction of g at the positions of the atoms. This results in a slightly reduced average memory efficiency of (26 ± 3)% for the combined storage and retrieval process (Fig. 1c). Nevertheless, the atom-to-photon state-transfer probability that is relevant, e.g., for atom-photon entanglement still exceeds 60% in our system. This is to the best of our knowledge larger than in any other multi-qubit memory that has been demonstrated so far.

Random-access memory with up to 11 qubits

We probe the memory coherence and efficiency by storing weak coherent pulses (mean photon number $\bar{n}=1$) of different polarizations and performing a polarization tomography on the retrieved single photon. In order to test for cross-talk between the atoms, we probe atom A and atom B with identical and orthogonal polarizations. Table 1 summarizes the measured fidelities of the two polarization configurations for both atoms in two different access patterns. Here, A_W, B_W and A_R, B_R stand for writing and reading, respectively, of one of the atoms, A or B. In both access patterns shown in the table, the storage of a photon in atom B occurs when the qubit already stored in atom A has rephased to its initial state. This timing is chosen to test for a maximum cross-talk that would manifest when the two input polarization change from identical to orthogonal.

Table 1 Fidelities in percent of qubit memory implementations for four different input polarization combinations and two random-access possibilities.

For the sequence A_WB_WA_RB_R, the minimum storage time for both qubits is 100 μs, given by the Larmor frequency and the delay time of the addressing system. The storage time for the data presented in Table 1 is 133 μs. For both atoms we achieve high fidelities for eigen- and superposition states as input, with no notable difference compared to the single-atom case²⁰.

In the A_WB_WB_RA_R case, the read order of atoms A and B is swapped while all pulse timings are preserved. This results in storage times of 83 and 183 μs for atom B and A, respectively. For atom B, this leads to a similar performance. In contrast, atom A shows a reduced fidelity for linear polarization inputs, independent of the polarization of atom B. We attribute this effect to magnetic-noise-induced decoherence, which becomes relevant at this timescale as shown further below.

Regardless of the memory sequence, the observed fidelities are similar and largely independent of whether the input qubits are identical or orthogonal. This indicates a vanishing cross-talk and therefore demonstrates the high degree of isolation of the two atoms. We remark that in a possible application where the whole sequence is retried until both memories successfully emitted a photon, the fidelity, as defined in Table 1, increases on average by 0.6% (not shown).

One of the most important properties of a quantum memory is the storage time that we test using the A_WB_WA_RB_R sequence. To this end, we vary the storage time between writing (A_WB_W) and reading (A_RB_R) of both atoms. The results for atom A and atom B are depicted in Fig. 2. Both atoms exhibit a coherence time of more than 800 μs for linear polarizations and no measurable decay of the fidelity for circular polarization. As in the single-atom case, the coherence time is limited by magnetic-field fluctuations on the few mG levels. In addition, the coherence time is reduced by spatially sampling the locally varying magnetic field. Indeed, the margin on the atom positions is chosen in a way to have a reasonable data rate (see Supplementary Notes 4 for further details). It is worth noting, that we expect no degradation of the coherence time for an even larger number of atoms as both atoms sample already a reasonably large region of the cavity mode.

Fig. 2: Coherence time for both atoms.

Time evolution of the fidelity for the storage of circular (orange) and linear (blue) polarizations for atom A and atom B. The sinusoidal fits to the 20 μs slices are fit with a Gaussian decay (green) giving a coherence time of more than 800 μs for both atoms. The error bars represent the 95% confidence intervals of the statistical uncertainties.

An extended case of the scenario A_WB_WB_RA_R is presented in Fig. 3. Here, atom B is used multiple times during the storage of atom A. This tests the cross-talk for systems where many qubits are stored and retrieved serially on a single atom as shown here and also for future implementations where the number of atoms is scaled up even further. In addition, it demonstrates that each atom can be used multiple times without re-initialization, allowing for higher repetition rates and potentially eliminating the need for atom-selective initialization. In orange and blue, Fig. 3b shows the achieved fidelity and efficiency, respectively, for the reused atom B as a function of the number of trials. Efficiency and fidelity decay by 0.29 and 0.44 pp per trial as predicted by theory (see Supplementary Notes 5). Figure 3b also shows the efficiency and fidelity of atom A after the ten memory trials on atom B. Although only about 20% of the trials resulted in a successful memory event, in every trial the cavity is populated and the classical control field is applied, potentially leading to cross-talk as discussed above. Nevertheless, as the achieved fidelity is in good agreement with the expectation from the coherence-time measurement (the green guide to the eye), any cross-talk can be neglected even after ten trials.

Fig. 3: Extended A_WB_WB_RA_R scenario.

a After initializing both atoms, a qubit is written on atom A. During its storage time, different qubits are stored and retrieved on atom B. After 10 attempts (successful or not) on atom B, atom A′s qubit is retrieved again. b Fidelity and efficiency for qubits retrieved from atom A (green, black) and B (orange, blue), respectively. Black circumferences denote linear input polarizations. The green guide to the eye is taken from Fig. 2 to illustrate the decay in fidelity of atom A due to residual magnetic-field fluctuations. Linear fits to efficiency and fidelity give a decay per intermediate write-read process of 0.29 pp and 0.44 pp, respectively. The error bars represent the 95% confidence intervals of the statistical uncertainties.

Discussion

We have demonstrated an efficient network-ready random-access multi-qubit memory using two individually addressable single atoms. We have identified and solved multiple challenges such as qubit cross-talk, which arise when making the most important step from one to several atoms in the same high-finesse optical cavity. Given a lower bound on the store-and-retrieve efficiency of 20% and a cavity mode waist of 30 μm, up to 5 atoms can be accommodated. We estimate that this number can be easily increased to more than 20 atoms while still using the same trapping geometry, e.g. by using a tighter focus of the addressing beam while still using the same objective. As all of those atoms would still be coupled to the same cavity mode, cavity-mediated multi-qubit gates^28,32 enable computation on all of them. For future implementations, deterministic and thus zero-tolerance atom positioning, as can be achieved in optical tweezer arrays^33,34, would further increase capacity, data rate, and fidelity. Also, it would allow for Zeeman selective coherent driving addressed onto single atoms, resulting in more than 100 ms coherence time²⁰. In combination with atom-photon entanglement and atom-atom gates^19,28, the extension to multiple individually addressable atoms renders the cavity platform a promising candidate for future quantum networks with quantum repeaters⁷ and distributed quantum computers⁹.