Introduction

Much of quantitative science deals with measuring a certain parameter, say ϕ, of a physical process precisely. Typically, this involves subjecting suitably engineered probe states to the physical process, and using measurement readout to recover an estimate of ϕ. The central limit theorem states that repeated applications of this procedure can improve our estimate, such that the resulting standard error scales as \(1/\sqrt{N}\) in the number of particles N. Remarkably, quantum technologies allow us to surpass this standard limit. By using suitably entangled probes, we can reach the Heisenberg limit—suppressing Δϕ, such that it scales as 1/N1,2,3. This quadratic scaling advantage can drastically reduce the resources required for precision measurement, and continues to catalyze rapid developments in the field of quantum metrology4,5,6,7,8,9,10,11,12,13,14,15.

While quantum metrology is well understood at the theoretical level, its physical application to large-scale quantum systems faces significant challenges16,17,18,19,20,21,22,23. Consider the iconic task of estimating the phase ϕ of some unitary process \({U}_{\phi }={e}^{-{\rm{i}}{\mathcal{H}}\phi }\). In this setting, the theory tells us how to determine the optimal quantum probe ρ for any possible Hamiltonian \({\mathcal{H}}\). However, when \({\mathcal{H}}\) acts on a many-body system, this optimal probe is typically a complex, entangled many-body state. Engineering this probe is often nontrivial, especially in the advent of limited access to the physical operations used to synthesize such probes16. Meanwhile, many realistic means of initializing such probes involve applying a sequence of controls, whose operational effects are not fully characterized21,24,25,26. These issues are further exacerbated by the exponentially growing size of the Hilbert space—making direct implementation of complex metrological schemes extremely challenging.

Here, we propose a closed-loop learning protocol that circumvents these issues. The resulting protocol has the following desirable features: (a) It does not require us to analytically solve for the optimal probe, nor possess prior knowledge of how this probe can be synthesized from available physical controls. These aspects are optimized through the learning process. (b) It does not require us to know the precise effects of these physical controls, nor implement tomography on the resulting quantum probes. (c) It does not require any computation involving matrix representations of \({\mathcal{H}}\), avoiding the curse of dimensionality. These features combined allow a versatile procedure for finding improved metrology protocols, ideal for complex many-body settings. We demonstrate a proof-of-principle experiment using nuclear magnetic resonance (NMR), illustrating the viability of this approach with present-day quantum technology.

Results

Framework of closed-loop learning-assisted quantum metrology

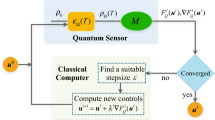
Here, we consider estimating the phase ϕ of a general N-body unitary process \({U}_{\phi }={e}^{-{\rm{i}}{\mathcal{H}}\phi }\). Each metrology protocol begins with a probe initialized in some easily prepared state ρ0 on N probes—typically a product state where each probe is initialized in some default state \(\left|0\right\rangle\). The goal then is to implement a control—a sequence of physical operations that we apply to the N-probe system, transforming ρ0 to some candidate entangled state ρC. By acting Uϕ on each probe, we end up with ρϕ, which encodes information regarding ϕ (see Fig. 1a). The efficacy of each candidate probe ρC is typically quantified by the quantum Fisher information FQ2. The rationale is that after repeating this process through ν independent runs, the standard error to which we can estimate ϕ is bounded below by \(1/\sqrt{\nu {F}_{{\rm{Q}}}}\). This lower bound is tight, and can always be saturated using an ideal measurement scheme.

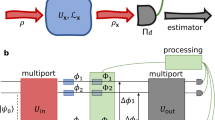
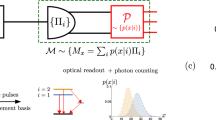
Fig. 1: Schematic diagram of closed-loop learning-assisted practical quantum metrology.
figure 1

a General procedure of quantum metrology, including probe state preparation (applying controls to the initial probe state to generate a candidate probe ρC), encoding some parameter ϕ by application of Uϕ to ρC, and measurement readout. b A candidate control sequence C is evaluated for efficacy through quantum information processing. This involves using C to prepare copies of the candidate probe state ρC, half of which are transformed into ρavg. The purities of ρC and ρavg are then measured, and their difference—the purity loss—is used as a proxy for efficacy. c Illustrates implementation of this process in experiment. The parameter encoding with fluctuations in the dotted box are switched off to determine the purity of ρC, and on to determine the purity of ρavg. Their difference is fed into a classical computer running a Nelder–Mead algorithm that generates candidate control sequences for subsequent iterations. In our experiment, this process is automated, such that control fields are tuned automatically at each iteration.

Full size image

The particular benefit of quantum metrology is that use of suitably entangled ρC enables one to reduced uncertainty of ϕ much more quickly than conventional strategies. One iconic case, for example, is when Uϕ corresponds to applying an identical unitary process \({e}^{-{\rm{i}}{\mathcal{H}}\phi }\) to each individual probe. In such scenarios, use of non-entangled ρC results in FQ that scales linearly with N, such that sensing ϕ to some desired Δ requires N > O(1/Δ2) probes. In contrast, if ρC is appropriately entangled, FQ scales as N2, enabling the Heisenberg limit scaling of N > O(1/Δ). The goal of quantum metrology can thus be split into two distinct tasks:

  1. 1.

    Determine the control sequence C that synthesizes some near-optimal state ρC whose corresponding quantum Fisher information FQ(ρC) is made as large as possible.

  2. 2.

    Use the control sequence to synthesize ρC, which can then be injected as input to Uϕ for purposes of estimating ϕ.

Here, our primary focus is the first task, with an understanding that our resulting control sequences can be used to synthesize the appropriate states to perform metrology. This is highly nontrivial for general \({\mathcal{H}}\). Notably, the dimensions of \({\mathcal{H}}\) grow exponentially with N, making analytical methods for finding the optimal ρC computationally intractable. Meanwhile, C is described by an ordered list of readily accessible elementary operations (e.g., pulse sequences). Inferring how these can be chained together to generate a given ρC is generally highly nontrivial, especially when the exact physical effect of each elementary operation on the probe state is not known. Typical means of optimizing FQ(ρC) are further hampered by difficulty in evaluating the efficacy of a candidate control sequence C. Given ρϕ, evaluation of the corresponding efficacy FQ(ρC) involves an optimization over all possible measurement bases—a task whose complexity also scales exponentially with system size.

In our protocol, we first tackle the difficulty in evaluating efficacy by using relations between quantum Fisher information and purity loss. Let ρavg = ∫Pxρϕ + x dx, where Px is some probability distribution with mean 0 and standard deviation Δx. Meanwhile, setting \(\Delta \gamma (\Delta x)={\rm{Tr}}({\rho }_{C}^{2})-{\rm{Tr}}({\rho }_{{\rm{avg}}}^{2})\). Then, recent results27 established that in the limit where Δx ≪ 1, the quantum Fisher information FQ(ρC) with respect to ϕ satisfies

$${F}_{{\rm{Q}}}({\rho }_{C})\ge 2\frac{\Delta \gamma (\Delta x)}{{\left(\Delta x\right)}^{2}}:={F}_{{\rm{Q}}}^{{\rm{L}}}.$$
(1)

Physically, ρavg represents the resulting ensemble state when the aforementioned metrology procedure is applied to a unitary Uϕ, such that ϕ undergoes stochastic fluctuations of magnitude Δx. Thus, Δγ(Δx) captures the purity loss of the resultant state induced by these fluctuations. Equation (1) then states that the efficacy of a metrology protocol is bounded below by the rate in which its output state loses purity when subject to stochastic noise in the parameter we are trying to sense. Therefore, we can effectively use \({F}_{{\rm{Q}}}^{{\rm{L}}}\) as a proxy for the efficacy of a probe.

The advantage is that purity loss is far more amendable to direct measurement than quantum Fisher information28. To evaluate the efficacy of a candidate C, we apply two pairs of the control sequence in parallel to obtain two copies of ρC. The rate of purity loss of the resulting outputs when subject to stochastic noise on ϕ can then be experimentally measured by application of suitable controlled-SWAP gates—coherently swapping output pairs controlled on an ancillary quantum mechanical degree of freedom (see Fig. 1c). We refer to this quantum algorithm as the quantum efficacy estimator, which can now be coupled with a suitable closed-loop learning algorithm for automated discovery of increasingly effective control sequences for sensing ϕ (see Fig. 1b).

In practice, we can use many different learning algorithms, ranging from simple direct search algorithms29 to more complex evolutionary algorithms30. Here, we found the Nelder–Mead algorithm31 to be particularly effective for our experiments. The entire learning process can then be summarized as follows: we begin by initializing a population of n + 1 control sequences at random, and make use of the quantum efficacy estimator to sort them in the order of decreasing efficacy, denoted \({{\mathcal{C}}}^{(g)}=\{{C}_{0}^{(g)},{C}_{1}^{(g)},\ldots,{C}_{n+1}^{(g)}\}\), with g = 0 indicating the 0th iteration. Meanwhile n is generally chosen to scale linearly with the number of actions (controls) we can apply in each particular time-step (e.g., if we have access to local rotations along x- and y-axis on N qubits, then n scales linearly with N). Once the initial population is set, the Nelder–Mead algorithm then stipulates a systematic method to generate a new candidate control through geometric considerations—which replaces the worst performer \({C}_{n+1}^{(g)}\) to form the population in the next iteration, which is then again sorted by decreasing efficacy to obtain \({{\mathcal{C}}}^{(g+1)}\). The exact mechanics of this algorithms involve mapping each control sequence into a vertex in some suitable convex space, the details of which are found in “Methods.” At each iteration g, the control sequence with maximum purity loss is denoted as C(g). The procedure is then continued until some designated stopping condition, such as when the purity loss of C(g) becomes sufficiently stable over multiple rounds, or when a set number of iterations are reached. Once the stopping condition is hit, the C(g) with maximum efficacy is delivered as the recommended control sequence.

This optimization process scales as a polynomial with respect to the number of free parameters that specifies a candidate control sequence. This latter condition is typically true for realistic settings, where (1) we are typically limited to one and two-body interactions, such that the number of possible control sequences we have at any particular point in time scales at most scales quadratically with N, (2) we are reasonably restricted to the reachable states within polynomial resource, such that the amount of time it takes to synthesize them does not scale exponentially with N. The protocol also has a number of other key advantages. First, at no stage does it require tomography of candidate probe states, either before or after the action of Uϕ. Second, it does not require complete mathematical knowledge of how the control sequences act on the Hilbert space. Finally, the algorithm automatically accounts for potentially physical anomalies, such as drift Hamiltonians when optimizing the control sequences of synthesizing the probe state. Each of these tasks would typically require a classical computer an exponential amount of time to address. Thus, the learning procedure inherits all the advantages of closed-loop learning—easily adaptable to diverse physical architectures32,33,34.

Example of sensing with spin chains

We illustrate these advantages numerically for a scenario with spin chains featuring unavoidable spin–spin interactions. Consider the case where we have access to N-qubit spin chains, and we wish to use them to estimate the strength of some external magnetic field in the z-axis. This problem aligns with estimating the phase ϕ of an N-qubit unitary \({U}_{\phi }={e}^{-{\rm{i}}\phi \mathop{\sum }\nolimits_{i = 1}^{N}{I}_{z}^{i}}\), where \({I}_{z}^{i}\) represents the angular momentum operator of the ith spin. If non-entangled qubits are used, the achieved Fisher information will scale as N. In contrast, the use of appropriately entangled probes can lead a quantum Fisher information FQ that scales as N2, enabling us to achieve the Heisenberg limit. While theory would enable us to work out the optimal probe, the catch here is that our control on the spin system is limited. First, the chain evolves naturally according to nearest-neighbor Ising coupling \({{\mathcal{H}}}_{S}=2\pi J\mathop{\sum }\nolimits_{i = 2}^{N}{I}_{z}^{i-1}{I}_{z}^{i}\) (J is the coupling strength). Second, our control of the system is limited to a sequence of local Ix and Iy interactions, whose strength we can adjust M times. What is then the optimal way to adjust our control fields? The question is nontrivial.

To apply our algorithm, we first formally describe C. Here, each time we adjust the control field, we have M(2N + 1) free parameters. (1) 2M parameters \({B}_{x}^{i}[m]\) and \({B}_{y}^{i}[m]\) describing the strength of the spin angular momentum operators \({I}_{x}^{i}\) and \({I}_{y}^{i}\) for the ith qubit for each i = 1, 2, …, N and m = 1, 2, …, M, (2) M parameters Δt[m] describing the amount of time we should wait before adjusting the fields again. As such, each control sequence is described by M(2N + 1) parameters, \(C=({B}_{x}^{i}[m],{B}_{y}^{i}[m],\Delta t[m])\), where m = 1, 2, . . . , M; i = 1, 2, . . . , N. Application of this control sequence would then correspond to enacting the unitary UC = UM…U2U1, where \({U}_{m}={e}^{-{\rm{i}}\Delta t[m]2\pi \{J\mathop{\sum }\nolimits_{i = 2}^{N}{I}_{z}^{i-1}{I}_{z}^{i}+\mathop{\sum }\nolimits_{i = 1}^{N}({B}_{x}^{i}[m]{I}_{x}^{i}+{B}_{y}^{i}[m]{I}_{y}^{i})\}}\). The goal is to find some near-optimal sequence, such that from some easily prepared initial probe \(\left|{\Psi }_{{\rm{i}}}\right\rangle\) the resulting probe state \(\left|{\Psi }_{{\rm{f}}}\right\rangle ={U}_{C}\left|{\Psi }_{{\rm{i}}}\right\rangle\) is near optimal for estimating ϕ.

For sufficiently low N (of up 7), it is feasible to simulate our algorithm classically. In Fig. 2a, b, we plot the maximum \({F}_{{\rm{Q}}}^{{\rm{L}}}\) and FQ with respect to the particle number for two possible choices of Δx. Observe that the purity loss becomes a better proxy for quantum Fisher information when Δx is reduced, in agreement with Eq. (1). Indeed, at (Δx)2 = 0.001, the relationship is almost exact. As such, our learning protocols produce results within 1% of the Heisenberg limit when using (Δx)2 = 0.001.

Fig. 2: Numerical simulations of the closed-loop learning algorithm when sensing with spin chains.
figure 2

a, b each illustrate the performance of our closed-loop learning algorithms for the respective cases where (Δx)2 = 0.01 and (Δx)2 = 0.001. In both graphs, the horizontal axis denotes iteration number g. The solid lines represent optimal quantum Fisher information achieved at each iteration, while the dashed lines represent the bound stipulated by purity loss (i.e., \({F}_{{\rm{Q}}}^{{\rm{L}}}\)). We see that both begin at low values at g = 0 as expected for random probes, and improve markedly during the learning process. c, d illustrate that the efficacy of the discovered probes approaches the Heisenberg limit, indicating their near optimality. Meanwhile, setting Δx to be smaller seemed to be marginally more advantageous, likely owing to the closer agreement between purity loss and quantum Fisher information in this regime. In e, we show a table of the fidelity between the quantum probe states generated and the closest theoretically optimal probe.

Full size image

To further verify the effectiveness of our algorithm, we compare the results of our algorithm with that of the theoretical optimal. In this specific case, theory indicates that the N-party entangled NOON states \(\left|{\Psi }_{{\rm{t}}}\right\rangle =({\left|0\right\rangle }^{\otimes N}+{e}^{{\rm{i}}\theta }{\left|1\right\rangle }^{\otimes N})/\sqrt{2}\) are the optimal probes—saturating the Heisenberg limit35. Executing our closed-loop learning algorithm, we note that the learned optimal probe state \(\left|{\Psi }_{{\rm{f}}}\right\rangle\) closely approximates these NOON states. In Fig. 2c, we list the fidelity 〈Ψt∣Ψf〉 between \(\left|{\Psi }_{{\rm{f}}}\right\rangle\) and theoretical optimal \(\left|{\Psi }_{{\rm{t}}}\right\rangle\). For small qubit numbers, the agreement is complete (fidelity = 1). While limitations in computational resources (in evaluating FQ for example) do slowly degrade the fidelity as we increase particle number, there is still a match of over 0.95 when N = 7.

The algorithm, itself, however, is not designed to run purely on classical computers. Indeed, the computational costs to do so scale exponentially with N. Tracking the dynamics of controls, and resulting purity loss becomes quickly intractable. However, when the algorithm is executed on a quantum processor, such information does not need to be tracked. In particular, we do not need to know the mathematical descriptions of the controls, nor the strength of the internal spin–spin interactions.

Proof-of-principle experiment

Our proof-of-principle experiment was conducted on a Bruker Avance III 400 MHz spectrometer using the sample diethyl-fluoromalonate at room temperature. This three-qubit NMR processor consists of three spins 13C, 1H, and 19F. Label these as qubits 1, 2, and 3. This process enables us to engineer controlled-SWAP gates that coherently swaps between qubits 2 and 3, controlled on qubit 1 (see “Methods” and Supplementary Note 3). Thus provided, we can initialize both qubits 2 and 3 in a designated state ρ; we can also experimentally measure the purity \({\rm{Tr}}({\rho }^{2})\)28. This processor is thus capable of realizing the quantum efficacy estimator for single qubit probes.

We illustrate the use of this device to estimate ϕ, encoded within the single qubit unitary \({U}_{\phi }={e}^{-{\rm{i}}{I}_{z}\phi }\). Here, the probe state is a single spin, which we can rotate along x and y directions. Assume M total pulse segments, each candidate control sequence is now described by 2M free parameters, C = (Bx[1], By[1], Bx[2], By[2], …Bx[M], By[M]). The resulting propagator could be expressed as UC = UM…U2U1 with

$${U}_{m}=\exp \{-{\rm{i}}({B}_{x}[m]{I}_{x}+{B}_{y}[m]{I}_{y})\Delta t\}.$$
(2)

Note that we have omitted the Δt[m], which was present in numerical simulation for the general N case, as the lack of a drift Hamiltonian makes this unnecessary. Our goal is then to find a control sequence C such that \({U}_{C}\left|0\right\rangle\) has maximal quantum Fisher information with respect to ϕ.

We implement our closed-loop learning algorithm with a population of n = 7, and M = 3 pulse segments. Each pulse sequence was set to T = Mτ = 30 μs. The key difference here from numerics is that the efficacy is now evaluated directly using our NMR processor. For a particular candidate control sequence C, we first initialize each of qubits 2 and 3 of our processor into the state \(\left|0\right\rangle\). The control sequence C is then applied to both qubits, setting them each to some resulting candidate probe state ρC. Application of the controlled-SWAP circuit then enables estimation of \({\gamma }_{C}={\rm{Tr}}({\rho }_{{C}}^{2})\) (see Fig. 1c).

Determination of \({\gamma }_{{\rm{avg}}}={\rm{Tr}}({\rho }_{{\rm{avg}}}^{2})\) requires us to simulate the effects of applying Uϕ + X, where X is Gaussian distribution with standard deviation Δx. This is a little more complex in the NMR regime, but can be done using a variation of stratified sampling (see “Methods”). Once done, we can then directly evaluate the efficacy estimator Δγ = γC − γavg (see Fig. 1b). Thus, our NMR processor is able to function as an effective quantum efficacy estimator.

This gives us all the tools in place for a quantum-assisted closed-loop learning algorithm. To begin, we generated a random selection of seven control sequences, denoted as \({{\mathcal{C}}}^{(0)}\). By evaluating their efficacy using the NMR processor, and feeding results into the Nelder–Mead algorithm, we can systematically produce subsequent populations \({{\mathcal{C}}}^{(1)}\), \({{\mathcal{C}}}^{(2)}\), …. We emphasize that the entire procedure was fully automated, such that this procedure can proceed ad infinitum without intervention till stopping conditions are met.

In our experiment, we set the stopping condition as g = 25. Figure 3b plots the resulting purity loss of various control sequences in \({{\mathcal{C}}}^{(g)}\) for each iteration g. Meanwhile, Fig. 3c shows the sliced control sequences along x and y directions for the maximum purity loss in the 1st, 10th, 20th, and 25th iteration. We see these control sequences quickly converge, and the resulting purity loss becomes almost maximal within 10 iterations.

Fig. 3: Closed-loop learning on the NMR computer.
figure 3

In the experimental implementation, each control sequence consisted of three pulses of duration T = 30 μs, with a stopping criterion of 25 iterations and a population size per iteration of 7. Each candidate probe state in iteration g is specified by \({\rho }_{C}^{(g)}=\left|\psi \right\rangle \langle \psi | \,{\rm{with}}\,| \psi \rangle =\cos (\delta /2)\left|0\right\rangle +\sin (\delta /2){e}^{{\rm{i}}\varphi }\left|1\right\rangle\). In a, we plot the candidate probes discovered during iterations 1, 10, 20, and 25, as overhead projections on the Bloch sphere. Here \((\varphi,\sin \delta )\) are effectively mapped to polar coordinates—such that \(\sin \delta\) becomes the magnitude (displacement of the point from the center), and φ is the angle relative to the x-axis. The points in each plot are color coded according to their efficacy. The plots then directly depict the convergence of the sequentially discovered candidate probes to the optimal probe (demarcated by δ = π/2). b plots the purity loss of these probe state (round circles with values given by axis on the left), together with the blue line indicating the bound stipulated by maximal purity loss out of all candidates in each iteration (solid blue line). The red line plots (with values given by axis on the right) the quantum Fisher information achievable by the associated probe state, should it be used to sense ϕ. These results illustrate that the learning algorithm converges quickly to near-optimal values by the tenth iteration. Meanwhile, c plots the associated control fields in the x and y directions (orange and pink bars) used to general the optimal probe of iterations 1, 10, 20, and 25.

Full size image

To verify that optimizing purity loss indeed optimizes the efficacy of the probe, we experimentally extracted the best candidate probe state, \({\rho }_{C}^{(g)}\), in each iteration from a full three-qubit state tomography36 (see Supplementary Note 3). The corresponding quantum Fisher information \({F}_{{\rm{Q}}}^{(g)}\) are obtained in Fig. 3b, illustrating the increments in efficacy of the probes closely follow that of increments in purity loss. Moreover, the final quantum Fisher information obtained is 0.9967 ± 0.0014 (statistical results over the last eight iterations), which is very close to the theoretical maximum of 1. Finally, Fig. 3a illustrates candidate probes at various iterations, illustrating how our controls quickly converge on engineering probe states that are maximal coherent with respect the computational basis—the requirement for a probe to be optimal for estimating ϕ.

Discussion

Here, we proposed a quantum-enhanced machine learning protocol for synthesizing effective probes for the purposes of quantum metrology. The protocol enables an automated method to discover what control sequences one should apply to many-body quantum system—in order to steer into a state ideally suited for probing the phase ϕ of some unitary process \({e}^{-{\rm{i}}{\mathcal{H}}\phi }\). We experimentally realized a proof-of-principle experiment using a three-qubit NMR processor, where the device was able to discover control sequences that prepare probe states whose sensitivity to a desired ϕ (as measured by quantum Fisher information) is within 1% of theoretical optimal values. Our numerics indicate that this methodology can remain effective when engineering probes involving a large number of entangled qubits—even when these qubits possess uncontrollable spin–spin interactions.

There are a number of open questions. The first is the issue of noise. One of the benefits of our approach is that it automatically accounts for noise during the control process, and naturally finds the optimal control sequence that accounts for such noise. However, the evaluation of purity loss does require the addition of an extra controlled-SWAP gate, and extra noise introduced at this stage can potentially skew the results. Fortunately, our analysis (see “Methods”) demonstrates that the protocol is highly resistant to one dominant source of noise in NMR—dephasing, such that any amount of dephasing noise can be corrected for by repeating our purity estimation protocol by some fixed number that does not scale with the size of the system. Sensitivity to other noise sources needs further investigation, and will likely require full tomographical data of the experimentally realized controlled-SWAP gate to correct.

As with all learning algorithms for solving intractable problems, there are of course caveats. The main one is that our algorithm will not always efficiently find the optimal probe. Like all optimization processes, the Nelder–Mead algorithm can be potentially trapped in local optima. Thus, one particular important line of future study would be the performance landscape of purity loss. In instances where this landscape is not ideal, our techniques can support multiple pathways for modification. Nelder–Mead, for example, could be replaced with genetic algorithms, neural networks, or other means of machine learning37,38,39. Meanwhile, there may exist other indicators of efficacy that outperform purity loss in certain settings. Thus, our closed-loop architecture could be modified to incorporate many possible alternative means of quantum-aided probe design.

Meanwhile, there will always be an ultimate limit to such learning algorithms. The reason is that there is a polynomial equivalence between time-complexity in optimal control and quantum gate complexity40,41. Coupled with knowledge that most quantum circuits cannot be efficiently decomposed into fundamental gates, this means that the optimal probes can easily lie outside the set of states that can be synthesized through a control sequence with free parameters that grow as a polynomial of N. In such instances, an ideal solution simply does not exist. However, such situations may in fact represent scenarios where such learning protocols are most useful—for its optimization represents all control sequences that can be implemented in some bounded amount of time. As such, the solution presented could be a good approximation for the best quantum probe we can synthesize with limited computation power.

Methods

Purity measurement in NMR

To establish the purity of \({\rho }_{{\rm{avg}}}^{(g)}\), we made use of stratified sampling. Let xk be drawn by the stratified sampling method from the discretized Gaussian distribution with K samples and a variance of (Δx)2 = 1.0721.

In our experiments, we divided the Gaussian distribution into K = 9 stratas, such that xk ∈ {−1.7046, −0.9757, −0.5922, −0.2832, 0, 0.2832, 0.5922, 0.9757, 1.7046}, (Δx)2 = 1.0721. Let \({\rho }_{{x}_{j}}={U}_{\phi ({x}_{j})}{\rho }_{C}^{(g)}{U}_{\phi ({x}_{j})}^{\dagger }\) with \({U}_{\phi ({x}_{j})}={e}^{-{\rm{i}}(\phi +{x}_{j}){I}_{z}}\). The purity of the ensemble-averaged state, namely \({\rho }_{{\rm{avg}}}^{(g)}\), can then be estimated as follows:

$$\begin{array}{rcl}{\rm{Tr}}[{({\rho }_{{\rm{avg}}}^{(g)})}^{2}]&\approx &{\rm{Tr}}\left[\left(\frac{1}{K}\mathop{\sum }\limits_{j=1}^{K}{\rho }_{{x}_{j}}\right)\left(\frac{1}{K}\mathop{\sum }\limits_{k=1}^{K}{\rho }_{{x}_{k}}\right)\right]\\ &=&\frac{1}{{K}^{2}}\mathop{\sum }\limits_{j,k=1}^{K}{\rm{Tr}}({\rho }_{{x}_{j}}{\rho }_{{x}_{k}})\\ &=&\frac{1}{{K}^{2}}\mathop{\sum }\limits_{j=k}^{K}{\rm{Tr}}({\rho }_{{x}_{j}}^{2})+\frac{2}{{K}^{2}}\mathop{\sum }\limits_{j<k}^{K}{\rm{Tr}}({\rho }_{{x}_{j}}{\rho }_{{x}_{k}}).\end{array}$$
(3)

Hence, estimation of the purity \({\rm{Tr}}[{({\rho }_{{\rm{avg}}}^{(g)})}^{2}]\) was achieved by measuring the purity of each term of \({\rm{Tr}}({\rho }_{{x}_{j}}{\rho }_{{x}_{k}})\) using the scheme of Fig. 1c, where qubit 2 and 3, respectively, were prepared in \({\rho }_{{x}_{j}}\) and \({\rho }_{{x}_{k}}\).

The Nelder–Mead algorithm

The Nelder–Mead algorithm functions by performing a series of geometric transformations on a simplex iteratively to get closer to the optimal control sequence. The simplex is a geometric shape consisting of n + 1 vertices, and each vertex represents a candidate control sequence Ci with i = 1, 2, . . . , n + 1. Here, n should be the product of the directions of the control sequence and and its sliced numbers. Note that n is closely related to the number of vertices. Based on the following defined performance function (relate to the efficacy estimator) with respect to each candidate control, namely \(f({C}_{i})=1-\Delta \gamma ({\rho }_{{C}_{i}})\), this algorithm attempts to replace the worst vertex by a new better one according to the geometric transformations reflection, expansion, contraction, and shrinkage. Concretely, we describe the procedure of the Nelder–Mead algorithm used in this study.

Step 1: Randomly generate an initial simplex with vertices \(\left\{{C}_{1},{C}_{2},\ldots\!,{C}_{n+1}\right\}\) and calculate their performance functions \({f}_{i}=f({C}_{i})=1-\Delta \gamma ({\rho }_{{C}_{i}})\). The amplitude of Ci in each slice is set in the range [−1000, 1000].

Step 2: Sort the vertices so that f(C1) ≤ f(C2) ≤ ⋯ ≤ f(Cn + 1), calculate the centroid of the best n points by \(\bar{C}=\mathop{\sum }\nolimits_{i = 1}^{n}{C}_{i}\).

Step 3: Calculate the reflected point, \({C}_{{\rm{r}}}=\bar{C}+\alpha ({C}_{n+1}-{C}_{n})\), evaluate the performance function fr = f(Cr), where the reflection factor is set as α = 1.

Step 4: Replace the worst vertex Cn + 1 and its corresponding performance function fn + 1 by the generated better one according to one of the following conditions:

  1. (1)

    if f1 ≤ fr < fn, let Cn + 1 = Cr, fn + 1 = fr;

  2. (2)

    if fr < f1. Calculate the expanded point \({C}_{{\rm{e}}}=\bar{C}+\gamma * \alpha ({C}_{n+1}-{C}_{n})\), evaluate its performance fe = f(Ce), where the expansion factor is set as γ = 2. (2a) if fe < fr, let Cn + 1 = Ce, fn + 1 = fe; (2b) if fe > fr, let Cn +1 = Cr, fn + 1 = fr;

  3. (3)

    if fr ≥ fn, (3a) if fn ≤ fr < fn + 1, calculate the outside contracted point, \({C}_{{\rm{c}}}=\bar{C}+\beta * \alpha ({C}_{n+1}-{C}_{n})\), evaluate the function value fc = f(Cc), where the contraction factor is set as β = 0.5. Let Cn + 1 = Cc, fn + 1 = fc when fc ≤ fr, or shrink the simplex Ci = C1 + (1 − δ)Ci, fi = f(Ci), i = 2, 3, … , n + 1 when fc > fr, where δ is the shrinkage factor and set as 0.5. (3b) if fr ≥ fn + 1, calculate the inside contracted point, \({C}_{{\rm{c}}}=\bar{C}-\beta * \alpha ({C}_{n+1}-{C}_{n})\), evaluate the function value fc = f(Cc), where the contraction factor is set as β = 0.5. Let Cn + 1 = Cc, fn + 1 = fc when fc ≤ fr, or shrink the simplex Ci = C1 + (1 − δ)Ci, fi = f(Ci), i = 2, 3, … , n + 1 when fc > fr, where δ is the shrinkage factor and set as 0.5.

Step 5: Check the stopping conditions, if not satisfied, change the iteration number with g = g + 1 and continue at Step 2.

Effects of decoherence

Here, we analyze the effect of decoherence in algorithm. This is because our process for benchmarking the efficacy of a control sequence makes use of the same quantum device that will be used to during the actual metrological process. Specifically, each iteration of the learning algorithm can be casted as the following procedures:

  1. (A)

    Synthesize two copies of candidate probe states ρC corresponding to a candidate control sequence C.

  2. (B)

    Synthesize two copies of the state ρavg, by first preparing a second pair of copies of the candidate probe state ρC, and then applying the physical encoding process of parameter ϕ subject to stochastic fluctuations separately to each copy.

  3. (C)

    Estimate the purity loss due to stochastic fluctuations by experimentally measuring the purity of the resulting states from step (A) to step (B).

We can now consider the impact of docoherence in each of these three steps. The first thing to note is that decoherence in steps (A) and (B), respectively, represent the intrinsic decoherence of our probe preparation device and that of the physical process it is trying to sense. As such, their inclusion in our learning process is actually desired. That is, as the device that is used to estimate the efficacy of the probes is the device that will eventually be used for metrology, we naturally want all decoherence within this device to be accounted for while benchmarking the efficacy of candidate control sequences. A similar argument also holds for decoherence when applying the physical process, as this decoherence will also exist during sensing.

Given these considerations, the only undesired decoherence is that which occurs during estimation of purity loss (step (C)). This procedure is done via the SWAP test, summarized as follows:

  1. (i)

    Take two copies of ρC, and one ancillary qubit initialized in state \(\left|+\right\rangle =(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}\).

  2. (ii)

    Apply a controlled-SWAP gate to swap the pair of ρC, add a Hadmard gate to the ancillary qubit, and measure the expectation value 〈Iz〉 of ancillary control qubit in the Iz basis (see Fig. 1c), to estimate \({\rm{Tr}}({\rho }_{C}^{2})\).

  3. (iii)

    Repeat the above procedure for ρavg to estimate \({\rm{Tr}}({\rho }_{{\rm{avg}}}^{2})\).

  4. (iv)

    The difference \(\Delta \gamma ={\rm{Tr}}({\rho }_{C}^{2})-{\rm{Tr}}({\rho }_{{\rm{avg}}}^{2})\) is then used to estimate the efficacy of the control sequence C.

Noise and decoherence during this procedure can affect the accuracy in which we estimate purity loss. In general, its effect is likely nontrivial, and tomography will be needed to work out what noise introduces to 〈Iz〉 so that this error can be corrected for.

In the case of NMR, the dominant source arises from dephasing. This dephasing noise can be described by a non-unitary channel \({\varepsilon }^{i}(\rho )=(1-p)\rho +4p{I}_{z}^{i}\rho {I}_{z}^{i}\) that acts on each qubit seperately, where \({I}_{z}^{i}\) denotes the angular momentum operator acting on the ith qubit and p is the strength of the dephasing. Following an error analysis similar to that of other NMR experiments that employ controlled gates42, we see that this noise does not change the relative order of our purity loss estimates. That is, provided there is a sufficient number of repetitions, our conclusion of which control sequence has greater purity loss between two candidates will not change under dephasing.

In particular, let \({\langle {I}_{z}\rangle }_{p}\) denote the expectation value of Iz under dephasing strength p, then our measured purity has expectation value \({\langle {I}_{z}\rangle }_{p}={(1-p)}^{2}\langle {I}_{z}\rangle\) with variance bounded above by 1. To correctly compare two probe states whose purity loss differs by at most δ requires each purity measurement to have a variance <δ2/4 (as differences in purity loss involve four additive purity measurements). This is guaranteed provided we repeat our measurement process of order \(\frac{4}{\delta {(1-p)}^{2}}\) times—a overhead of 1/(1 − p)2 compared to the case where there is no decoherence. Notably, this overhead does not scale with N, and thus the protocol remains efficient. In our experiment, p is ~0.025, thus we are able to discern rank control sequences whose purity loss differ by >0.045.