Quantum inverse iteration algorithm for programmable quantum simulators

Abstract

We propose a quantum inverse iteration algorithm, which can be used to estimate ground state properties of a programmable quantum device. The method relies on the inverse power iteration technique, where the sequential application of the Hamiltonian inverse to an initial state prepares the approximate ground state. To apply the inverse Hamiltonian operation, we write it as a sum of unitary evolution operators using the Fourier approximation approach. This allows to reformulate the protocol as separate measurements for the overlap of initial and propagated wavefunction. The algorithm thus crucially depends on the ability to run Hamiltonian dynamics with an available quantum device, and can be used for analog quantum simulators. We benchmark the performance using paradigmatic examples of quantum chemistry, corresponding to molecular hydrogen and beryllium hydride. Finally, we show its use for studying the ground state properties of relevant material science models, which can be simulated with existing devices, considering an example of the Bose-Hubbard atomic simulator.

Introduction

Quantum computing offers drastic speed up for certain computational problems, and has evolved as a unique direction in the theoretical information science.¹ However, the field of experimental quantum computing is yet at its infancy. The typical size of quantum chips for the reliable gate based quantum computation ranges from one to several tens of physical qubits, with the main limits posed by decoherence. Despite the imperfections, the algorithms of ever-increasing complexity were implemented on different platforms, with circuit depth exceeding a thousand gates,^2,3 ultimately allowing for quantum supremacy demonstration.⁴

At the same time, the vox populi of quantum engineers says that while experimental setups are developed and mastered rapidly, the theorists in the field lag behind. Whereas by now textbook examples of quantum algorithms with exponential and quadratic speed up for factoring and search serve as a great motivation,¹ the estimates of gate counts are daunting, making them distant goals for the future fault-tolerant quantum computers.⁵ Recent developments in this fast evolving field call for new short depth algorithms which can solve useful problems in the era of noisy intermediate scale quantum (NISQ) devices,⁶ and in future lead to quantum advantage.

One of the most promising directions for quantum computation is the field of quantum chemistry and materials.^5,7 Targeting the access to ground state properties of molecules and strongly correlated matter, it can offer huge gain for various technological applications, for instance helping to find a catalyst for the nitrogen fixation.⁸ To date, different quantum theoretical protocols were developed, and several proof-of-principle experiments on various platforms were performed in the simplest cases. Examples include simulation of molecular hydrogen with the linear optical setup,⁹ superconducting circuits,^10,11,12,13 and trapped ions.¹⁴ Finally, the variational simulation for larger molecules (LiH and BeH₂) were reported recently.¹¹ From the material science perspective, the use of cold atom quantum simulators has shown great promise, where simulations of Fermi-Hubbard lattice dynamics,¹⁵ large scale quantum Rydberg chain¹⁶ and Ising model,¹⁷ and two-dimensional many-body localization¹⁸ have been performed. However, in the latter cases the analog approach to simulation is taken, given an access to unitary dynamics, while precluding the study of ground state properties.

To access the ground state properties of quantum chemical Hamiltonian, several routines can be used (see refs ^19,20 for the review). First option corresponds to the quantum phase estimation algorithm (PEA),²¹ which exploits unitary dynamics of the system controlled by register qubits. Although this algorithm is efficient, giving logarithmic error and polynomial gate scaling, its implementation requires substantial circuit depth for currently available circuits.¹⁰ Moreover, the controlled type of operations require the digitization of the circuit, thus complicating the use of analog quantum simulators for PEA. Another approach is adiabatic quantum computing, which was already applied to quantum chemistry problems.²² However, the required adiabaticity of dynamics typically results in the effectively long circuit depth. Finally, an alternative route to quantum chemistry and materials is offered by hybrid-classical variational approaches, which were proposed recently.²³ They rely on term-by-term energy measurement for the prepared trial quantum state (ansatz) with consequent classical optimization, and are referred to as Variational Quantum Eigensolvers (VQE).^19,20,24 VQE can use a chemically inspired ansatz,²⁴ Hamiltonian variational ansatz,²⁵ or rely on the variational imaginary time evolution.²⁶ The search for a simple and efficient ansatz represents an important ongoing research direction.^27,28 In this case the depth of the quantum circuit is greatly reduced, though at the expense of increased number of measurements, being favorable strategy for NISQ devices. For VQE the number of variational parameters scales as O[(3N)^k], where N is a number of qubits and k represents an approximation order.²⁴ While for quantum chemistry applications k = 2 suffices to give useful results, these approaches are yet to be tested for larger system sizes, where the multi-variable optimization may raise problems for the genuine ground state estimation.²⁹

In the following, we propose the quantum inverse iteration algorithm for the estimation of the ground state energy (GSE) of a quantum system. It is inspired by the classical inverse power iteration algorithm for finding the dominant eigenstate of the matrix, where the computationally demanding part of matrix inversion and multiplication is performed by a quantum circuit. Previously, a direct iteration approach was considered as a general purpose quantum algorithm,³⁰ aiming for large scale fault-tolerant implementation. Here, we present the protocol of the hybrid quantum-classical nature. It relies on performing quantum evolution for different propagation times and classical post-processing of the measured observables. The approach is applied to quantum chemistry examples (H₂ and BeH₂ molecules), showing favourable scaling with system parameters. Finally, when applied to the Bose-Hubbard quantum simulator, it allows to study its ground state properties, showing promise as a protocol for analog quantum simulators and near-term quantum devices.

Results

We start by considering a generic interacting system, which can be described by the second quantized Hamiltonian. It can be written as sum of two-body and four-body parts

$$\hat{{\mathcal{H}}}=\sum _{ij}{v}_{ij}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}+\sum _{ijkl}{V}_{ijkl}{\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}^{\dagger }{\hat{a}}_{k}{\hat{a}}_{l},$$

(1)

where ${\hat{a}}_{i}^{\dagger }$ (${\hat{a}}_{i}$) can correspond to fermionic or bosonic creation (annihilation) operators, and cover broad range of models. In the fermionic case, Hamiltonian (1) can describe the full configuration interaction problems in quantum chemistry, with operator ${\hat{a}}_{j}$ corresponding to molecular orbital j. Using the existing mappings between fermionic and spin-1/2 systems, one can rewrite Eq. (1) in the form of a local Hamiltonian $\hat{{\mathcal{H}}}$ for interacting qubits, which involves strings of Pauli operators. The task is then to find the lowest eigenvalue of large matrix $\hat{{\mathcal{H}}}$, corresponding to GSE.

Inverse iteration

We propose the procedure which can be seen as a quantum version of the inverse power iteration algorithm for finding the dominant eigenvalue of the matrix, represented by the inverse of Hamiltonian matrix ${\hat{{\mathcal{H}}}}^{-1}$, which is treated as a dimensionless matrix in this section. Given that $\hat{{\mathcal{H}}}$ is invertible, the order of eigenvalues is reversed and, with the appropriate shift of the diagonal to make eigenvalues positive, the power iteration allows to find GSE. Namely, starting with an initial state $|{\psi}_{0}\rangle$, which has nonzero overlap with the sought ground state $|{\psi}_{gs}\rangle$, by repetitive application of the inverted matrix one can prepare (unnormalized) state, $\left|{\widetilde{\psi }}_{k}\right\rangle ={({\hat{{\mathcal{H}}}}^{-1})}^{k}\left|{\psi }_{0}\right\rangle$, such that ${\left|\left\langle {\psi }_{{\rm{gs}}}| {\psi }_{k}\right\rangle \right|}^{2}\,<\,\epsilon$ for sufficiently large number of iterations k ≥ K,³¹ where $\left|{\psi }_{k}\right\rangle =\left|{\widetilde{\psi }}_{k}\right\rangle /\parallel \left|{\widetilde{\psi }}_{k}\right\rangle \parallel$ (Fig. 1). We note that generally this method has favorable logarithmic complexity in the iteration depth, being K = log[ϵ sin⁻²(θ₀)∕(λ₁ − λ_n)]∕[2 log(λ₂∕λ₁)], where λ₁, λ₂, and λ_n correspond to dominant, sub-dominant, and smallest eigenvalue of ${\hat{{\mathcal{H}}}}^{-1}$. Here sin²θ₀ parametrizes the overlap between $|{\psi}_{0}\rangle$ and $|{\psi}_{gs}\rangle$, marking that convergence of the procedure depends on the initial guess, and generally can be made nonzero taking $|{\psi}_{0}\rangle$ as a random state. While classical power iteration methods generally have good convergence in the number of iterations, the main caveat comes from the complexity scaling with the system size N. The requirement for K matrix multiplications leads to O[K2^2N] operations (for dense matrices), yielding exponential scaling. Even worse situation is for the inverse matrix algorithm, where an overhead comes from the ${\hat{{\mathcal{H}}}}^{-1}$ calculation, requiring extra O[2^N] operations.

Fig. 1: Flowchart of the quantum inverse iteration algorithm.

First, the initial product state is prepared and the inverse Hamiltonian operation is represented as a sum unitary evolution operators. Next, the iterated wavefunction can be formally obtained by applying the inverse. Finally, physical quantities (e.g., energy) are estimated as expectation values of corresponding operator, and recast as a sum of wavefunction overlaps.

Fourier approximation

In the following we show that we can exploit the iterative procedure with logarithmic iteration depth in ϵ, while providing exponential speed up for the inverse Hamiltonian multiplication process. The latter comes from the approximation theory,³² observing that the inverse can be represented as an integral ${x}^{-1}={\int }_{0}^{+\infty }\mathrm{exp}(-xy)dy$, which by applying the trapezoidal rule can be written as a sparse sum of exponents. For quantum systems a similar idea was proposed in ref., ³³ where Fourier approximation of the Hamiltonian inverse was presented as a double integral of the unitary propagator. This was further used to design an efficient solver for the quantum linear equation system problem.^33,34 Here we extend the Fourier approximation to the k-th power of the inverse (k ≥ 1), which formally reads

$${\hat{{\mathcal{H}}}}^{-k}=\frac{i{{\mathcal{N}}}_{k}}{\sqrt{2\pi }} \int\nolimits_{0}^{{+\infty}}{\mathrm{d}}y \int\nolimits_{-\infty }^{{+\infty }}{\mathrm{d}}z (z {y}^{k-1}) {\mathrm{exp}}(-{z}^{2}/2){\mathrm{exp}}(-iyz\hat{{\mathcal{H}}}),$$

(2)

and ${\mathcal{N}}_{k}$ is a normalization factor. The integral can be then discretized as

$${\hat{{\mathcal{H}}}}^{-k}\approx \frac{i{{\mathcal{N}}}_{k}}{\sqrt{2\pi }}\sum _{{j}_{y}=0}^{{M}_{y}-1}{\Delta }_{y}{({j}_{y}{\Delta }_{y})}^{k-1}\sum _{{j}_{z}=-{M}_{z}}^{{M}_{z}}{\Delta }_{z}({j}_{z}{\Delta }_{z}){\mathrm{exp}}[-{j}_{z}^{2}{\Delta }_{z}^{2}/2]{\mathrm{exp}}[-i({j}_{y}{\Delta }_{y})({j}_{z}{\Delta }_{z})\hat{{\mathcal{H}}}],$$

(3)

where Δ_y,z correspond to the discretization steps for integration variables, and M_y,z represent cutoffs for integration. Notably, once applied to the physical Hamiltonian inverse, the discretization variable Δ_z remains dimensionless, while Δ_y has the units of inverse energy, serving akin to discrete time variable. The success of approximation (3) depends on the condition number of the Hermitian matrix $\hat{{\mathcal{H}}}$, given by the ratio of its largest to smallest eigenvalue, $\kappa ={\lambda }_{n}^{\hat{{\mathcal{H}}}}/{\lambda }_{1}^{\hat{{\mathcal{H}}}}$. Finally, Eq. (3) can be conveniently redefined as

$${\hat{{\mathcal{H}}}}^{-k}=\sum _{\ell =1}^{{L}_{k}}{c}_{k,\ell }{\mathrm{exp}}(-i{\phi }_{k,\ell }\hat{{\mathcal{H}}})\equiv {\hat{{\mathcal{H}}}}_{{\rm{a}}}^{-k},$$

(4)

where we have rewritten the double summation in Eq. (3) using the superindex ℓ(j_y, j_z), ϕ_k,ℓ = (j_yΔ_y)(j_zΔ_z) is a phase of evolution for parameters chosen to discretize k-th inverse, and L_k = M_y(2M_z + 1). Here c_k,ℓ represent purely imaginary coefficients for the series, and ∣c_k,ℓ∣ define corresponding weights. The required size and number of discretization steps Δ_y,z and M_y,z depends on ϵ and κ (see Methods, section A, for the details). Importantly, they set the maximal evolution phase ϕ_max = (M_yΔ_y)(M_zΔ_z), which serves as an equivalent of the total gate count for analog quantum simulation.

As we need to prepare the approximate ground state by applying generally nonunitary operator ${\hat{{\mathcal{H}}}}^{-K}$ to the initial state $|{\psi}_{0}\rangle$, we shall either introduce an ancillary register to perform it, or properly account for the normalization of the resulting wavefunction. The former option is an excellent strategy for the future fault-tolerant devices, and has beneficial scaling (Methods, Section A). It has deep connection to linear composition of unitaries (LCU) methods and duality quantum computing.³⁵ The latter is more suitable for programmable quantum simulators. In the following we present the strategy, which can be applied to estimate the ground state properties by sequential evaluation of terms in the series. Similarly to VQE approaches, this relies on performing large number of measurements, and thus adds an extra complexity as compared to the generic implementation of the inverse operator. At the same time, term-by-term readout offers better resilience to errors where even imperfect procedure can yield reasonable GSE estimate for quantum simulators.

Sequential energy estimation

Our final goal is to estimate system observables, provided that the approximate ground state is prepared. For any operator $\hat{{\mathcal{A}}}$ it can be retrieved from the measurement $A=\langle {\psi }_{{\rm{gs}}}| \hat{{\mathcal{A}}}| {\psi }_{{\rm{gs}}}\rangle /\langle {\psi }_{{\rm{gs}}}| {\psi }_{{\rm{gs}}}\rangle$, where the normalization is accounted for explicitly. In particular, we are interested in calculating the ground state energy λ_gs ≈ λ_k, choosing the operator $\hat{{\mathcal{A}}}$ as $\hat{{\mathcal{H}}}$. This amounts to measurement of Hamiltonian expectation value for $\left|{\psi }_{k}\right\rangle ={\hat{{\mathcal{H}}}}^{-k}\left|{\psi }_{0}\right\rangle$ in the form

$${\lambda }_{k}=\frac{\langle {\psi }_{k}| \hat{{\mathcal{H}}}| {\psi }_{k}\rangle }{\langle {\psi }_{k}| {\psi }_{k}\rangle }.$$

(5)

We proceed by considering each propagated wavefunction separately, such that λ_k can be related to wavefunction overlaps (see flowchart in Fig. 1). This is motivated by the Hamiltonian averaging procedure³⁶ used in VQE to reduce the circuit depth at the expense of larger number of sequential measurements. Using Fourier expansion of the inverse Hamiltonian (4), the estimated energy reads

$${\lambda }_{k}^{{\rm{(a)}}}=\frac{\sum _{\ell,\ell ^{\prime} }\langle {\psi }_{k,\ell ^{\prime} }| \hat{{\mathcal{H}}}| {\psi }_{k,\ell }\rangle }{\sum _{\ell,\ell ^{\prime} }\langle {\psi }_{k,\ell ^{\prime} }| {\psi }_{k,\ell }\rangle }=\frac{\sum _{\ell,\ell ^{\prime} }{c}_{k,\ell ^{\prime} }^{* }{c}_{k,\ell }\langle {\psi }_{0}| {e}^{-i({\phi }_{k,\ell }-{\phi }_{k,\ell ^{\prime} })\hat{{\mathcal{H}}}}\hat{{\mathcal{H}}}| {\psi }_{0}\rangle }{\sum _{\ell,\ell ^{\prime} }{c}_{k,\ell ^{\prime} }^{* }{c}_{k,\ell }\langle {\psi }_{0}| {e}^{-i({\phi }_{k,\ell }-{\phi }_{k,\ell ^{\prime} })\hat{{\mathcal{H}}}}| {\psi }_{0}\rangle }.$$

(6)

Note that expression (6) now includes overlaps between initial and evolved wavefunction for the fixed phase, which shall be calculated separately for the numerator (“energy”) and denominator (“norm”). Finally, we note that the wavefunction overlap can be inferred using different approaches. One option corresponds to using the SWAP test,^37,38 which represents a common quantum measurement strategy and requires system doubling. It can be conveniently realized in some near-term setups, being successfully demonstrated for cold atom lattices by many-body interferometry of two copies of a quantum state.³⁹ The overlap measurement schemes continue to improve.⁴⁰ Additionally, in the Methods, section B, we describe an alternative approach, which does not require extra qubits and relies on the measurements of observables, once the reference state for the system is chosen.

In the previous section we described the general algorithm and discussed its key properties, namely the scaling and sequential operation. To show its use for the ground state estimation and characterize the required resources for realistic problems, we apply it to quantum chemistry.

Applications: molecular hydrogen

We start with by now the standard example of molecular hydrogen, H₂. As a test task we consider the spinful case. This allows to examine the protocol for a system of higher complexity (N = 4), comparable to lithium hydrate four-qubit simulation considered in ref. ¹¹ The details of mapping of quantum chemical structure into qubits are presented in Methods, section C. In the following we work with four-qubit molecular hydrogen Hamiltonian ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$, with all eigenenergies shifted to positive values. Starting from the Hartree-Fock (HF) energy λ₀, the task is to estimate GSE λ_gs, using the protocol described in the preceding section. This shall be done within the chemical precision ϵ, which is equal to ϵ = 0.0016 Hartree, and thus defines the relevant cutoff for the iteration procedure.

We start by benchmarking the inverse power procedure in its general form, and define how many iteration steps one needs to come close to the ground state. For this, we first perform the inverse Hamiltonian iteration in the ideal setting, assuming that an exact inverse is known. Then, we compare it to the quantum inverse iteration, which uses the Fourier approximation (4). GSE is estimated using the measurement of propagated and initial wavefunction overlaps. To quantify the performance two characteristics are employed. The first, and the most natural one, corresponds to the difference between estimated energy value λ_k and true GSE λ_gs, being Δλ∕J ≡ (λ_k − λ_gs)∕J. It allows to observe the convergence and provides an indication of how well the procedure works for a given system. The second quantity corresponds to the trace distance between an idealized inverse iteration matrix ${\hat{{\mathcal{H}}}}^{-k}$ and its approximation ${\hat{{\mathcal{H}}}}_{a}^{-k}$, defined as a half of trace norm for the difference of two matrices. It reveals the actual success of mimicking the ideal inverse in full generality. At the same time, this is the quantity which cannot be straightforwardly observed in the experiment, and only serves for the analysis.

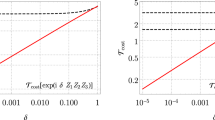
The results of the inverse power iteration for molecular hydrogen Hamiltonian ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$ are shown in Fig. 2a as a function of iteration step k. The ideal version of inverse iteration is plotted in red and reveals exponential convergence to GSE. The chemical precision is achieved already at the second iteration step, as depicted by the blue shaded area starting at Δλ = 1.6 × 10⁻³J. The idealized case is then compared to the quantum inverse iteration procedure with combined measurement of wavefunction overlaps as stated in Eq. (6). Here, we assumed that the genuine unitary evolution with Hamiltonian ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$ is run in the analog simulation fashion. The case of digital evolution with associated Trotterization technique and its benchmarking is considered in the Supplemental Material, where we also present the circuit scheme for digital evolution. The approximation was performed using equal number of steps M_z = M_y = 30, and the discretization values Δ_z = Δ_yJ were adjusted to match the maximal propagation phases of ϕ_max∕2π = J(M_yΔ_y)(M_zΔ_z)∕2π = {0.3, 0.35, 0.6, 0.95, 1.35} (here, the propagation phase is taken to be dimensionless by absorbing energy unit prefactor J from the Hamiltonian). The corresponding curves show the improvement of the quantum power iteration estimation for increasing number of iteration steps. The convergence rate also depends on the maximal phase of the propagation. For small phases (top curves in Fig. 2a), the initial estimator does not give successful convergence, but comes closer to GSE for large k. As the propagation phase grows, the approximation ${\lambda }_{k}^{{\rm{(a)}}}$ starts to resemble the idealized iteration procedure. However, this only happens up to a certain value of k past which the approximate energy grows, thus deviating from the ideal solution. From the point of view of process fidelity, the trace distance ${\rm{Tr}}[{\hat{{\mathcal{H}}}}^{-k},{\hat{{\mathcal{H}}}}_{{\rm{a}}}^{-k}]$ between ideal and approximate inverse operators increases monotonically with k (Fig. 2b). The increase of ϕ_max allows to reduce ${\rm{Tr}}[{\hat{{\mathcal{H}}}}^{-k},{\hat{{\mathcal{H}}}}_{{\rm{a}}}^{-k}]$ at each k.

Fig. 2: Molecular hydrogen (H–H) example for benchmarking the quantum inverse power iteration (N = 4 qubits).

a Energy difference between the exact ground state and quantum inverse iteration estimate, shown as a function of the iteration step k for different maximal phases of Fourier approximation (log scale). Solid red line shows the result for the ideal inverse iteration. Blue shaded area corresponds to the chemically precise estimate (same in c, e). b Trace distance ${\rm{Tr}}[{\hat{{\mathcal{H}}}}^{-k},{\hat{{\mathcal{H}}}}_{{\rm{a}}}^{-k}]$ between the ideal and approximate inverse operators shown as a function of iteration step number for different phases. c Energy difference Δλ vs maximal propagation phase at different k (log scale). d Trace distance ${\rm{Tr}}[{\hat{{\mathcal{H}}}}^{-k},{\hat{{\mathcal{H}}}}_{{\rm{a}}}^{-k}]$ vs phase for k = 2, 4, 7. e, f Energy difference (e) and trace distance (f) plotted for the fixed maximal phase of ϕ_max∕2π = 0.92, but different arrangement of the approximation grid defined by the skew parameter Δ_yJ∕Δ_z. Several iteration steps k = 2, 4, 7 are depicted.

The performance of the quantum inverse iteration procedure is further analyzed in Fig. 2c, d where energy distance to ground state and trace distance are shown as a function ϕ_max for several fixed iteration steps (k = 2, 4, 7). Calculations were performed accounting for two different ways of arranging the phase. First, the approximation grid was fixed setting M_y = M_z = 30 while changing Δ_z = Δ_yJ (solid curves in Fig. 2c, d). In the second case the fixed step size Δ_z = Δ_yJ = 0.05 was combined with the increment of M_z,y (dashed curves in Fig. 2c, d). For both energy distance (Fig. 2c) and trace distance (Fig. 2d) we observe no difference between two approximation procedures, but clear indication of the importance of maximal propagation phase (time). For Δλ one sees a non-monotonic dependence on ϕ_max, which starts with a decrease of the energy difference for increasing maximal phase (ϕ_max∕2π < 0.4). At larger phases the dependence experiences pronounced dips (note the log scale), which are more visible for many iterations. Overall the difference remains well-within chemical precision and experiences saturation. When the trace distance is considered, one sees that success of the approximation monotonically improves with ϕ_max. At the same time, for fixed approximation parameters {M_z,y, Δ_z,y} it is more difficult to represent inverse iteration operator faithfully, in-line with scaling analysis discussed in Methods. Finally, the comparison of results in Fig. 2c, d allows to suggest that nonmonotonicity in the spectroscopic signatures can come from the particular structure of the Hamiltonian and the initial state, where certain phases might be preferable (i.e., not all elements of the Hamiltonian matrix contribute equally to the inverse iteration procedure).

To decide on the optimal way to approximate the inverse, we consider different discretization steps for y and z auxiliary variables, characterized by the skewness parameter Δ_yJ∕Δ_z. The calculation is done for M_z = M_y = 30 with the maximal phase fixed to ϕ_max∕2π = 0.92. The results are shown in Fig. 2e, f as a function of skew. The energy difference parameter shows that for approximating the inverse for small iteration numbers (k = 2 curve in Fig. 2e) larger skew factors are preferable, with z variable requiring finer approximation. However, for increased iteration number the optimum flows to Δ_yJ∕Δ_z ~ 1 values, suggesting close-to-equal spacing can work well for varied k. Examining the trace distance, we see that in unbiased setting the skew ratio of Δ_yJ∕Δ_z ~ 2 is preferable.

Finally, the very important issue to address is an influence of noise on the operation of quantum inverse iteration protocol. For this we have performed the analysis including relevant dephasing processes, which influence the estimate for overlaps (see details in the Supplemental Material). Although noise makes the estimation of energies at large iteration step k less reliable, it is possible to estimate the energy within chemical precision using simple noise mitigation techniques.

Applications: beryllium hydride

To test the scalability of the approach, we consider a molecule of bigger size, which requires larger Hilbert space simulation. For this, we choose to simulate beryllium hydride (BeH₂) in the full spinful version using N = 8 qubits (see Methods, section D, for the details).

We proceed in the same manner as for H₂ molecule, and quantify the operation of the quantum inverse iteration procedure for BeH₂. The approximation parameters were chosen as Δ_yJ = Δ_z = 0.05, with the number of discretization points M_y,z adjusted accordingly to maintain maximal propagation phase. The results of the simulation are shown in Fig. 3. The first plot (Fig. 3a) shows that ideal iteration works well for the beryllium hydride, with chemically precise GSE obtained already at k = 1 iteration step. The Fourier approximation for the inverse at small phases does not reach required accuracy, while for the increased iteration step number and ϕ_max∕2π > 1 chemically accurate ground state estimate can be attained. Figure 3b shows this behavior as a function of phase for several representative k’s, and yields the same conclusion. The increase of the required propagation phase is attributed to the increased condition number for BeH₂ Hamiltonian matrix, being 39.2 as compared to 3.38 for H₂.

Fig. 3: Beryllium hydride (H–Be–H) ground state energy estimation (N = 8 qubits).

a Energy difference for true GSE and quantum inverse iteration shown for different iteration steps k and maximal propagation phases ϕ_max (log scale). The red line corresponds to an ideal iteration procedure. b Same energy difference shown as a function of maximal phase at k = 2, 4, 7. In both panels the blue shaded area corresponds to the chemically precise estimate.

Applications: Bose-Hubbard simulator

Finally, to provide an example where quantum inverse iteration algorithm can be largely beneficial, we consider the bosonic version of the Hubbard model (see sketch in Fig. 4a). The corresponding system Hamiltonian reads

$${\hat{{\mathcal{H}}}}_{{\rm{B-H}}}=-J\sum\limits_{\langle i,j\rangle }({\hat{a}}_{i}^{\dagger }{\hat{a}}_{j}+h.c.)+\frac{U}{2}{\sum\limits_{i}}{\hat{n}}_{i}({\hat{n}}_{i}-1)-\mu \sum\limits_{i}{\hat{n}}_{i},$$

(7)

where ${\hat{a}}_{i}^{\dagger }$ (${\hat{a}}_{i}$) corresponds to the bosonic creation (annihilation) operator at lattice site i. Here, ${\hat{n}}_{i}={\hat{a}}_{i}^{\dagger }{\hat{a}}_{i}$ corresponds to the number operator. The first term in the Hamiltonian (7) describes the tunneling of bosons with rate J, which leads to their delocalization at the lattice. For simplicity we consider a one-dimensional lattice, and that tunneling happens only between neighbouring sites 〈i, j〉. The second term in Eq. (7) denotes the contact interaction between bosons with strength U. The last term corresponds to the chemical potential μ. Importantly, the Bose-Hubbard model corresponds to the paradigmatic example of hard material science problem,⁴¹ and received considerable attention from both theoretical^42,43 and experimental perspective.⁴⁴ In particular, the model was shown to be easily solvable in the so-called Mott insulating regime where U ≫ J and ground state corresponds to the product state of one atom per site, $|{\psi}_{Mott}\rangle$ = ∏_i$|1\rangle$_i. However, going into the superfluid regime, where J becomes comparable to U, the ground state is entangled, and it is generally difficult to study the low energy properties of this system.

Fig. 4: Bose-Hubbard ground state energy estimation for a chain of five atoms.

a Sketch of the system, which depicts coherent tunneling processes with the rate J and the nonlinear interaction of strength U. Correlations are measured for a set of distances r = [0, 1, 2]. b Energy difference for the true GSE and quantum inverse iteration estimate are shown for different iteration steps k (log scale). Several tunneling values are chosen, J∕U = 0.01, 0.05, 0.1, 0.2, capturing the transition between insulating and superfluid behaviour. c–e Correlation functions of the form $\langle {\hat{a}}_{c+r}^{\dagger }{\hat{a}}_{c}\rangle$ are calculated for the approximate ground state at increasing iteration step k, and for several values of J∕U (log scale). Correlations for true ground state are shown in blue (large dots and top curves).

We show that quantum inverse iteration algorithm can be applied to study the ground state properties of the Bose-Hubbard Hamiltonian in the wide range of parameters. For this, we consider an initial state corresponding to the Mott state, $|{\psi}_{0}\rangle\;=\;|{\psi}_{Mott}\rangle$, and perform the iteration as detailed in the “Protocol” subsection of Results. The numerical results for the energy deviation are shown in Fig. 4b, where Δλ∕U ≡ ∣λ_k − λ_gs∣∕U is plotted as a function of iteration step k. We consider N = 5 lattice with μ∕U = 0.5, different values of tunneling rate J, and similarly to H₂ and BeH₂ examples the energies were adjusted by trivial overall shift E₀ to ensure positive eigenvalues. The Fourier approximation is performed using M_y = M_z = 40 and Δ_z = Δ_yU = 0.075. While for relatively small tunneling J = 0.01U the product state is a good ground state approximation, thus giving small energy deviation (lowest curve in Fig. 4b), for larger J ~ 0.1U the system enters a superfluid phase (critical value for μ = 0.5U approximately corresponds to J_crit∕U ≈ 0.13⁴²). Despite the qualitatively different initial state, the algorithm allows to distill correct energy properties even for large J.

Going beyond the ground state energy estimation, quantum inverse iteration can be also used to measure the correlations in the ground state of the model. We considered the correlation function of the form $\langle {\psi }_{k}| {\hat{a}}_{c+r}^{\dagger }{\hat{a}}_{c}| {\psi }_{k}\rangle$, where $|{\psi}_{k}\rangle$ corresponds to the propagated state, and overall procedure is similar to the one described in Eq. (6). We fix c = 3 to be the central site in the lattice, and look for intra and intersite correlations with r = 0, 1, 2. The results are shown in Fig. 4c, d, e where in the Mott insulator regime correlations fall-off rapidly (Fig. 4c), while in the superfluid case the quantum inverse iteration method allows to restore genuine correlations (blue dots and curve) at increased k (Fig. 4e).

Importantly, the described Bose-Hubbard simulation can be performed experimentally using available controllable devices.^39,44 First, it allows to run unitary dynamics for sufficiently long times and large particle numbers. Second, the many-body interference technique enables the convenient measurement of the wavefunction overlap, where part of the system is evolved and later is interfered with the initial copy.³⁹ We note that our approach also bears similarities with recently introduced Quantum Virtual Cooling.⁴⁵ This study demonstrated the reduction of the temperature in half, while the inverse iteration offers the access to close-to-zero temperature. Finally, the intriguing possibility is an application of quantum inverse iteration to 2D models¹⁸ and Fermi-Hubbard model,¹⁵ which shall be possible with improved interference techniques.⁴⁵

Discussion

We have presented the algorithm for the ground state energy (GSE) estimation of a quantum Hamiltonian. It is based on the iterative application of the Hamiltonian inverse to the initial state, and can be represented as a sum of unitary evolution operators. Targeting near-term quantum simulators, we described the protocol as a separate estimation of GSE contributions from the wavefunction overlap measurements. Then, the results from the quantum dynamical simulation are post-processed classically, and provide energy estimate for each iteration step.

The algorithm was applied to several quantum chemistry examples, being molecular hydrogen and beryllium hydride. Using the four-qubit H₂ simulator, we benchmarked the performance of iteration and inverse approximation, showing that the most valuable resource for GSE estimation is a maximal available time for unitary evolution. Both digital and noisy operation was considered, and found to be sufficient for a GSE calculation with chemical accuracy.

As an outlook, we highlight that the approach can be beneficial for analog quantum simulators such as cold atoms lattices,¹⁸ Rydberg atom simulators,¹⁶ trapped ions,¹⁷ and superconducting devices.⁴⁶ For instance, the analog-type fermionic quantum chemistry simulator⁴⁷ would be much valued for the task. Future applications also include material science problems, with the main target being Fermi-Hubbard model.¹⁵ For instance, we note that recently proposed approach of Quantum Virtual Cooling,⁴⁵ which was experimentally applied to Bose-Hubbard model, has similar iterative structure and requires interferometric measurements. This poses the question of connection between the measurement-based cooling scheme and the dynamic protocol described in the current study. Finally, we note growing interest to protocols, which exploit wavefunction overlap measurements.^48,49 This can be seen as an emergence of hybrid algorithms, which mimic nonunitary operation, and together can form the base for dynamical quantum computing.

Methods

Scaling and fault-tolerant implementation

In this section we consider the scaling for the quantum inverse iteration algorithm. For k = 1 it was shown in ref. ⁵⁰ that the inverse Hamiltonian can be approximated up to an error ϵ setting the discretization steps to Δ_y = Θ (ϵ∕log(κ∕ϵ)), Δ_z = Θ (1∕κ log(κ∕ϵ)), and summing up to M_y = Θ (log(κ∕ϵ)κ∕ϵ), M_z = Θ (κ log(κ∕ϵ)) (κ is a condition number). The maximal evolution phase then scales as ϕ_max = (M_yΔ_y)(M_zΔ_z) = O(κ log(κ∕ϵ)), and is an equivalent of the total gate count for analog quantum simulation. Generalizing the result to k-th inverse iteration, the upper limit on the maximal required phase shall be multiplied by K, where truncation of the inverse iteration introduces an additional error. In the study we considered particular examples, and quantified the validity of Fourier approximation as a function of {M_y, Δ_y, M_z, Δ_z} parameters.

Considering the fault-tolerant implementation, the approximate ground state can be prepared by applying generally nonunitary operator ${\hat{{\mathcal{H}}}}^{-K}$ to the initial state $|{\psi}_{0}\rangle$ using an ancillary qubit register. One possible option here is the amplitude amplification approach,⁵¹ which addresses the task of implementing the sum of unitary operators, of the same type as the one in Eq. (4). Moreover, since we also require simulation of Hamiltonian dynamics for $exp(-i{\phi }_{k,\ell }\hat{{\mathcal{H}}})$, which may be not accessible in analog-type simulation, the subsequent use of Hamiltonian simulation⁵² or qubitization⁵³ methods would lead to favourable resource scaling. The algorithm will require O(log(L)log(cϕ_max∕ϵ)∕log[log(cϕ_max∕ϵ)]) auxiliary qubits (c ≡ ∑_ℓ∣c_ℓ∣, L = M_y(2M_z + 1)) and same order of controlled unitaries. This scaling can be compared to the iterative modification of the quantum phase estimation procedure (IPEA), based on a small fixed register⁵⁴ or a single auxiliary qubit.⁵⁵ The latest represents conceptually the closest algorithm to the one described in the paper, and thus will serve as benchmark. The complexity of IPEA was discussed in ref., ⁵⁵ showing the requirement of O[log(ϵ)log(log(ϵ)∕ϵ)] phase iterations to approach an error of ϵ = 2^−m (energy is rescaled such that $\parallel \hat{H}\parallel\,<\,2\pi$, and m is the number of relevant bits of precision, typically limited to <20 for quantum chemistry applications). Each k-th IPEA step then requires implementation of the c-U^k operation, defined as implementation of ${({e}^{-i\hat{H}})}^{k}$, controlled on the register qubit. This leads to O[N⁴ log(ϵ)log(log(ϵ)∕ϵ)] gate count, comparable to the inverse iteration procedure described above.

Given the favorable scaling, the cost of the general purpose quantum inverse iteration algorithm can be small for future large scale quantum devices. However, generally there is no simple procedure to perform c-U operation, and it requires decomposition into a set of universal gates or multi-layer SWAP technique.⁵⁶ This enlarges the actual circuit depth (while being polynomial), and precludes the implementation of $U=exp(-i\phi \hat{H})$ in analog fashion. Therefore, we target programmable devices with possible analog-type implementation and use sequential estimation strategy described in the main text.

Overlap measurement

To measure the overlap between the evolved and initial wavefunction, we propose to exploit a single eigenstate $|{\psi}_{R}\rangle$ of the system as a reference, and measure the overlap with respect to its energy λ_R (usually set to zero). This nicely fits the task of GSE estimation for the fermionic Hamiltonian, as its Hilbert space includes a vacuum state with no fermions present (unless space reduction procedure was performed). Similar technique was used for extracting spectroscopic signatures of photon localization.⁵⁷ The main steps for the measurement are as follows. The task is formulated as finding 〈ψ₀∣ψ₀(t)〉, where $|{\psi}_{0}\rangle$ is the initial state (typically corresponding to the Hartree-Fock solution). The state $\left|{\psi }_{j}(t)\right\rangle =\hat{{\mathcal{U}}}(t)\left|{\psi }_{j}\right\rangle$ is a time-propagated state with some unitary $\hat{{\mathcal{U}}}$ defined by the expansion. The HF state can be prepared from the reference $|{\psi}_{R}\rangle$ (vacuum or other product state) using the product of local operators, and we note that these states are orthogonal. Then, the overlap probability is measured as an expectation value of the operator ${\hat{M}}_{0}=\left|{\psi }_{0}\right\rangle \left\langle {\psi }_{0}\right|$ for time-evolved wavefunction, which reads

$${\rm{Tr}}\{{\hat{M}}_{0}\left|{\psi }_{0}(t)\right\rangle \left\langle {\psi }_{0}(t)\right|\}=| \langle {\psi }_{0}| {\psi }_{0}(t)\rangle {| }^{2}=:| {{\mathcal{O}}}_{0,t}{| }^{2}.$$

(8)

Next, the superposition of the vacuum and initial state shall be prepared as $\left|{\psi }_{+}\right\rangle =(\left|{\psi }_{{\rm{R}}}\right\rangle +\left|{\psi }_{0}\right\rangle )/\sqrt{2}$ and evolved to $|{\psi}_{+}(t)\rangle$. Its overlap probability is measured as an expectation value of ${\hat{M}}_{+}=\left|{\psi }_{+}\right\rangle \left\langle {\psi }_{+}\right|$ operator. This can be written as

$$\begin{array}{ll}&{\rm{Tr}}\{{\hat{M}}_{+}\left|{\psi }_{+}(t)\right\rangle \left\langle {\psi }_{+}(t)\right|\}=| \langle {\psi }_{+}| {\psi }_{+}(t)\rangle {| }^{2}\\ &=\displaystyle\frac{1}{4}\left(1+| {{\mathcal{O}}}_{0,t}{| }^{2}+2{\rm{Re}}\{{{\mathcal{O}}}_{0,t}{e}^{-i{\lambda }_{{\rm{R}}}t}\}\right)=:| {{\mathcal{O}}}_{+,t}{| }^{2},\end{array}$$

(9)

and provides an information about real and imaginary parts of ${{\mathcal{O}}}_{0,t}$. The same procedure is performed for measuring an expectation value of the operator ${\hat{M}}_{i}=\left|{\psi }_{i}\right\rangle \left\langle {\psi }_{i}\right|$, where $\left|{\psi }_{i}\right\rangle =(\left|{\psi }_{{\rm{R}}}\right\rangle +i\left|{\psi }_{0}\right\rangle )/\sqrt{2}$. An additional information is gained with

$$\begin{array}{ll}&{\rm{Tr}}\{{\hat{M}}_{i}| {\psi }_{+}(t)\rangle \langle {\psi }_{+}(t)| \}=| \langle {\psi }_{i}| {\psi }_{+}(t)\rangle {| }^{2}\\ &=\displaystyle\frac{1}{4}\left(1+| {{\mathcal{O}}}_{0,t}{| }^{2}-2{\rm{Im}}\{{{\mathcal{O}}}_{0,t}{e}^{-i{\lambda }_{{\rm{R}}}t}\}\right)=:| {{\mathcal{O}}}_{i,t}{| }^{2},\end{array}$$

(10)

and both real and imaginary part of ${{\mathcal{O}}}_{0,t}$ can be found for the known reference λ_R from the system of Eqs. (8)–(10) as

$$\begin{array}{ll}{\rm{Re}}\{{{\mathcal{O}}}_{0,t}\}=\left[\right.2| {{\mathcal{O}}}_{+,t}{| }^{2}-(| {{\mathcal{O}}}_{0,t}{| }^{2}+1)/2\left]\right.{\mathrm{cos}}({\lambda }_{{\rm{R}}}t)\\-\left[\right.2| {{\mathcal{O}}}_{i,t}{| }^{2}-(| {{\mathcal{O}}}_{0,t}{| }^{2}+1)/2\left]\right.{\mathrm{sin}}({\lambda }_{{\rm{R}}}t),\end{array}$$

(11)

$$\begin{array}{ll}{\rm{Im}}\{{{\mathcal{O}}}_{0,t}\}=-\left[\right.2| {{\mathcal{O}}}_{i,t}{| }^{2}-(| {{\mathcal{O}}}_{0,t}{| }^{2}+1)/2\left]\right.{\mathrm{cos}}({\lambda }_{{\rm{R}}}t)\\-\left[\right.2| {{\mathcal{O}}}_{+,t}{| }^{2}-(| {{\mathcal{O}}}_{0,t}{| }^{2}+1)/2\left]\right.{\mathrm{sin}}({\lambda }_{{\rm{R}}}t).\end{array}$$

(12)

Note that we are mostly interested in the real part of the sought overlap ${\rm{Re}}\{\langle {\psi }_{0}| \psi (t)\rangle \}$, as both the “norm” and “energy” terms of λ_k are real, and imaginary parts of the overlap cancel out. This can be also shown formally if an exact form of expansion (3) is considered. The numerator of Eq. (6) can written term-by-term such that terms with equal ${j}_{z}=j^{\prime}_z$ are considered, accompanied by associated exponents ${e}^{i\delta \phi \hat{{\mathcal{H}}}}$ and ${e}^{-i\delta \phi \hat{{\mathcal{H}}}}$. Similarly, the terms with ${j}_{z}=-j^{\prime}_z$ can be grouped. Combined this leads to ${\lambda }_{k}\propto \langle {\psi }_{0}| {\mathrm{cos}}(\delta \phi \hat{{\mathcal{H}}})| {\psi }_{0}\rangle$ dependence, while odd imaginary terms have vanished. Thus, it is also possible to deduce the real part indirectly as

$$| {\rm{Re}}\{{{\mathcal{O}}}_{0,t}\}| =\sqrt{| {{\mathcal{O}}}_{0,t}{| }^{2}-{\rm{Im}}{\{{{\mathcal{O}}}_{0,t}\}}^{2}},$$

(13)

and its sign can be inferred from the measurement in Eq. (11). We note that in principle these are two related ways to estimate the real part of the overlap, corresponding to Eqs. (11) and (13). While being equivalent in the noiseless case, the effects of decoherence make two approaches distinct (see Supplemental Material for the details). For the practical purposes we thus refer to the overlap estimate in (11) as direct estimation approach and refer to (13) as the indirect estimation.

Physically, the measurement procedure resembles the Bell-type measurement, where in the simple case of two-qubits a single CNOT operation and the Hadamard gate are required. For the larger system the measurement is generalized to GHZ-type, and consequently requires increasing number of two qubit operators, which depends on how much an initial HF state is different from the reference state.

Finally, we note that direct measurement is possible in atomic setups, where many-body interferometry is applied to two copies. This can be used in the analog circuits where system size doubling plays lesser role, and can compensate the absence of fully addressable individual gate operation.

Molecular hydrogen Hamiltonian

The fermionic Hamiltonian ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$ is first written in the form of Eq. (1) (main text), where coefficients v_ij and V_ijkl are calculated by conventional quantum chemistry methods. Here, we exploited the OpenFermion package for Python,⁵⁸ which allows to extract the interfermionic interactions for four Gaussian orbitals fit via STO-3G method and perform the fermions-to-qubits transformation. For the small N = 4 system we have chosen to use the Jordan-Wigner transformation, although other options may be used as the system size increases. Specifically, we consider the bond length for H₂ to be 0.7414 (measured in Ångström) and consider full excitation space. For concreteness, we provide the full form for the Hamiltonian, being

$$\begin{array}{ll}&{\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}={\xi }_{0}+{\xi }_{1}({Z}_{0}+{Z}_{1})-{\xi }_{2}({Z}_{2}+{Z}_{3})+{\xi }_{3}{Z}_{0}{Z}_{1}\\ &+{\xi }_{4}({Z}_{0}{Z}_{2}+{Z}_{1}{Z}_{3})+{\xi }_{5}({Z}_{0}{Z}_{3}+{Z}_{1}{Z}_{2})+{\xi }_{6}{Z}_{2}{Z}_{3}\\ &-{\xi }_{7}({X}_{0}{X}_{1}{Y}_{2}{Y}_{3}-{X}_{0}{Y}_{1}{Y}_{2}{X}_{3}-{Y}_{0}{X}_{1}{X}_{2}{Y}_{3}+{Y}_{0}{Y}_{1}{X}_{2}{X}_{3}),\end{array}$$

(14)

where X_j, Y_j, Z_j denote Pauli matrices for qubit j. The coefficients read ξ₀∕J = −0.098864, ξ₁∕J = 0.171198, ξ₂∕J = 0.222786, ξ₃∕J = 0.168622, ξ₄∕J = 0.120545, ξ₅∕J = 0.165867, ξ₆∕J = 0.174348, ξ₇∕J = 0.045322. The energy scale J for the actual H₂ Hamiltonian corresponds to Hartree units, while for the quantum simulator J corresponds to the effective qubit coupling. Throughout the text, we measure energy in units of J, and the time is measured in J⁻¹ units. The digital implementation for the unitary evolution with Hamiltonian (14) is presented in the Supplemental Material. The Hartree-Fock (HF) solution for the problem is given by the approximate ground state ψ₀ = (↓, ↓, ↑, ↑)^T, and associated HF energy is −1.116684J. As required by the Fourier approximation approach, the reference energy is then shifted towards positive values by adding constant term equal to E₀∕J = 2, and we refer to the shifted Hamiltonian as ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$ in the main text. Its HF energy is λ₀ = 0.883316J after the shift. The task is then to estimate the ground state energy λ_gs of the Hamiltonian ${\hat{{\mathcal{H}}}}_{{{\rm{H}}}_{2}}$, achieved by preparation of approximate ground state $|{\psi}_{k}\rangle$. This shall be done within the chemical precision ϵ, which is equal to ϵ = 0.0016 Hartree, and thus defines the relevant cutoff for the iteration procedure.

Beryllium hydride Hamiltonian

The molecular data structure of beryllium hydride (BeH₂) was generated using Psi4 quantum chemistry package⁵⁹ considering equal Be−H distances equal to 1.33 Ångström. While generically described by six spin orbitals, we set lowest and second excited orbital to be occupied, and set multiplicity of unity, such that the ground state energy lies close to the full configurational space solution (STO-3G basis). The fermionic Hamiltonian is then obtained using OpenFermion package, and as in the case of H₂ the Jordan-Wigner transformation was used to rewrite it in the qubit form.⁵⁹ The problem then can be solved using N = 8 qubits. The GSE from the exact diagonalization of original BeH₂ Hamiltonian reads −1.806750 Hartree, and analogously to the molecular hydrogen the Hamiltonian matrix is shifted by constant energy term of 2 Hartree. The product state corresponding to Hartree-Fock solution reads ψ₀ = (↓, ↓, ↑, ↑, ↑, ↑, ↑, ↑)^T, with associated energy for the shifted Hamiltonian being λ₀∕J = 0.203323.