Abstract
Quantum key distribution (QKD) based on entangled photon pairs holds the potential for repeater-based quantum networks connecting clients over long distance. We demonstrate long-distance entanglement distribution by means of polarisation-entangled photon pairs through two successive deployed 96 km-long telecommunications fibres in the same submarine cable. One photon of each pair was detected directly after the source, while the other travelled the fibre cable in both directions for a total distance of 192 km and attenuation of 48 dB. The observed two-photon Bell state exhibited a fidelity 85 ± 2% and was stable over several hours. We employed neither active stabilisation of the quantum state nor chromatic dispersion compensation for the fibre.
Similar content being viewed by others
Introduction
The maturity of quantum communication and the information theoretic security it provides have already found multiple applications in metropolitan fibre networks1 including some elections.2 Studying quantum communication over long-distance links marks the next step in the advancement of this technology. Notably, entanglement provides the potential for being able to generate a secure key, over longer distance than decoy based quantum cryptography.3,4 Entanglement also facilitates device independent quantum key distribution (QKD), where a secure key can be generated even if the devices used are provided by an adversary.5,6 Measurement-device independent QKD7,8 (MDI QKD) avoids side-channels in the detectors and promises a similar scaling of the key rates with increased loss as entanglement-based QKD. Although its implementation has its own challenges, MDI QKD has been demonstrated over 404 km of optical fibre.9 Further, the distribution of entanglement allows entanglement purification, which is a fundamental part of the implementation of quantum repeaters. Since even an ideal quantum repeater would be susceptible to loss, it is of paramount importance to demonstrate entanglement distribution over the longest distance possible. This will enable applications such as QKD and distributed quantum computation over distances beyond the metropolitan length scale. Thus in the long run, we believe that entanglement distribution will play a key role in future quantum communication techniques.
Using a satellite, a distance record has been achieved both for QKD with a trusted node10 as well as for entanglement-based QKD, establishing a secure key between a satellite and a ground station bridging a distance range of 530–1000 km.11
The same satellite has also been used to demonstrate the longest distance quantum entanglement has ever been deployed over,12 bridging a geographical distance of 1200 km while yielding coincident counts at a rate of 1.1 s−1 over a total loss in the dual link of 64–82 dB. If the distance were to be bridged by a fibre-optic cable connecting the two end-points directly, the attenuation would be at least 170 dB, assuming world-record low-loss fibres having a loss of 0.142 dB/km.13 Nevertheless, for links of moderate length, fibre-optic connections are often the more suitable solution, in terms of the amount of key generated per year.
The distribution of entanglement through fibre-optic cables has been predominantly focused on time-bin entanglement,14,15,16,17,18 where the entangled degree of freedom between the two photons is temporal, i.e., related to the order in which the photons arrive, as opposed to their polarisation. The former has been demonstrated over two 150 km arms,17 while the latter has been demonstrated over a single arm consisting of a 100 km fibre spool.19 The longest distribution of polarisation entanglement over deployed fibre so far is 96 km.20
Polarisation entanglement/encoding, in particular, provides a conceptually higher key generation rate. The largest concern is its susceptibility to environmental influences like movement or temperature changes along the link. Fluctuations in the polarisation state transmitted through the fibre cable result in an increased quantum bit error rate (QBER) and therefore a reduction of the key rate. Our results suggest, that polarisation encoding can be used to its full advantage, even on a deployed long-distance fibre link.
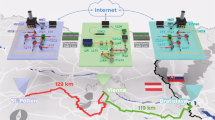
In this paper we demonstrate entanglement distribution, using the polarisation degree of freedom, through a total of 192 km of deployed optical fibre that is part of the active classical telecommunications network linking the Mediterranean islands of Malta and Sicily. The fibres we used are dark fibres carrying no classical signals, deployed in a bundle containing other optical fibres carrying classical signals.
Although polarisation entanglement has been demonstrated in a laboratory setting over 100 km of spooled fibre,19 and the longest deployed fibre link was 96 km long,20 it is possible to extend this range significantly. In the present work, one photon from each entangled pair was detected right at the source in Malta, whilst the second was sent through the submarine cable to Sicily and back to Malta via a second dark fibre, where it was eventually detected. This is equivalent to a prepare-and-measure scheme. Our demonstration is carried out at the same location as in ref. 20 The experiment was conducted without the use of either compensation of chromatic dispersion, or any active stabilisation techniques. We conclude that polarisation entanglement is robust enough to be used in current commercial scenarios and provides an attractive alternative to time-bin entanglement over long fibre links.
Results
Experimental setup
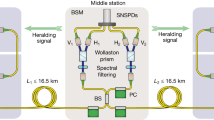
An illustration of our experimental setup is depicted in Fig. 1. The photon source creates pairs of frequency anti-correlated photons by type-0 spontaneous parametric down-conversion. The Sagnac scheme is used to produce the polarisation-entangled quantum state
We used a fibre optic cable which links the Mediterranean islands of Malta and Sicily. A continuous-wave laser at 775 nm produces, via spontaneous parametric down-conversion, photon pairs which are entangled in polarisation due to the Sagnac geometry. Signal and idler photons are separated by frequency into two different fibres; one photon is detected immediately in Malta in a polarisation analysis module consisting of a half-wave plate in front of a PBS and one superconducting nanowire single-photon detector (SNSPD), and the other detected by a second detector in the same cryostat after transmission through the 192 km submarine fibre loop and a polarisation analysis module. (\(\lambda /4\), \(\lambda /2\): wave-plates; PBS, polarising beam-splitter; YVO\({}_{4}\), yttrium orthovanadate plate; DM, dichroic mirror; PPLN, MgO-doped periodically poled lithium niobate crystal (MgO:ppLN); WDM1: 0.6 nm band-pass filter (centre wavelength 1551.72 nm); WDM2: 0.6 nm band-pass filter (centre wavelength 1548.51 nm); PC, fibre polarisation controllers; LPF, 780 nm long-pass filter; SNSPD, superconducting nanowire single photon detectors; TTM, time-tagging module; FSB, free-space beam. Mirrors and fibre couplers not labelled, lenses omitted.) Image taken from NASA Worldview [https://earthdata.nasa.gov/worldview] which is free to use under public domain.
Spectral filtering using wavelength-division multiplexers separates the photons into two frequency channels—ITU Grid channels 32 (1551.72 nm) and 36 (1548.51 nm)—with the spacing between adjacent channels being 100 GHz and with each channel having a full-width at half maximum (FWHM) of 0.6 nm (similar to that described in the ref. 20).
One photon from each pair was sent to a polarisation analysis and detection module located in Malta close to the source. Its entangled partner photon was sent to Sicily via a submarine telecommunications optical fibre cable and looped back to Malta. The submarine cable, 96 km long each way, introduced a one-way attenuation of 24 dB and consisted of a bundle of several non-zero dispersion shifted fibres (Corning LEAF21) which comply with the specifications of the International Telecommunication Union (ITU-T G.655). The cable contained some fibres carrying classical data in the C-band around 1550 nm at optical powers in the order of milliwatts, as well as two dark fibres that were used as the quantum channel. In Sicily the two fibre ends were patched together in an underground utility vault on the outskirts of the town of Pozzallo (Italy), resulting in a looped quantum channel 192 km in length, over which the total attenuation was measured at 48 dB. Although the fibres were located inside the same cable, no cross-talk from the classical signals was observed in the quantum channel at our wavelengths. Upon its return to Malta, the photon was detected in close proximity to the source.
Identification of photon pairs
Pairs of photons were identified using timing cross-correlations, an example of which is shown in Fig. 2. The large effective jitter of the system was a primary source of error. In an independent measurement without a long fibre, this peak is 250 ps wide, mainly due to timing uncertainties in the time-tagging unit and the jitter of the detection system. Improved electronics could more than halve this. Chromatic dispersion accounted for a further 760 ps,21 taking into account the shape of the spectrum. This effect can also be mitigated, for example by using narrow band chirped fibre Bragg grating filters.23 Further, separate laboratory experiments have shown that the synchronisation scheme employed using the time taggers introduced a further 500 ps of timing uncertainty when measuring a temporal delay of about 1 ms. This effect could also be compensated by locking the internal clock of the time tagging unit to a more stable external clock. The above techniques should enable us to significantly increase the link distance and key rate.
The cross-correlation function between the time tags from the two detectors shows a peak at a relative delay of \(0.945\) ms, which corresponds exactly to the total loop distance of (192,820.538 \(\pm\) 0.004) m, assuming that the latency of the two detectors is identical. The full-width at half-maximum is \(1\) ns. The three main factors that contribute to the peak width are the chromatic dispersion of the fibre link of \(760\) ps for our signal spectrum, the timing jitter of the detectors and of the time-tagging units — \({\sim}{250}\) ps and the clock accuracy estimated from a separate measurement (using a 1 ms delay in the lab) of about 500 ps. The data shown here was measured over \(100\) s, while the rate of coincident clicks was \(3.8\pm 0.2\) s−1. The orange graph is a fit to a measurement using the same detectors without the long fibre link. It has been normalised to the same height as the measured counts from the link experiment. The FWHM is here \(250\) ps in this case.
The number of coincident pairs of photons was calculated by integrating the correlation function over a region of \(823\) ps, equivalent to \(10\) time-bins of the time tagging unit. The local count rates were \(2.1\,\times\,1{0}^{6}\) s−1 in the first detector and \(55\) s−1 \(\pm\) \(2\) s−1 in the detector after the link, with \(20\) s−1 of these being dark counts. The average rate of coincidence counts for the \(100\) s-long measurements was \(4.3\,\pm\,0.3\) s−1 for the measurements that were supposed to be correlated, horizontal-horizontal (H-H), vertical-vertical (V-V), diagonal-antidiagonal (D-A) and antidiagonal-diagonal (A-D). During the remaining combinations, where no correlation was expected, the average observed coincidence rate was \(0.3\,\pm\,0.2\) s−1.
Measurements of the fidelity of the quantum state
To quantify the quality of the entangled state after transmission through both fibres used in the submarine cable, we performed a series of two-photon correlation measurements. The polarisation-analysis modules were used to measure the coincidence visibility in the H–V or D–A bases, with four measurements required for each basis setting. The fidelity of the two-photon state with respect to Bell state (Eq. (1)) is lower-bounded by the arithmetic mean of the two visibilities.24,25 The highest fidelity measured was \(88\,\pm\,2\)%. Locally, the fidelity was characterised to be \(98\,\pm\,0.2\)%. This apparent deterioration of the quantum state is attributed mainly to the rather large coincidence window of 823 ps (which was a compromise between the optimum pair rate and least error rate) as well as the high local count rate of \(2.1\,\times\,1{0}^{6}\) s−1. This, together with the dark counts, increases the accidental coincidence count rate and deteriorates the detected quantum state. At the given count rate and local visibility, the best fidelity that can be achieved with this current system and coincidence window is approximately \(93.5\)%, since accidental coincidence clicks deteriorate the quality of the measured quantum state. The discrepancy of roughly \(5\)% between this value and our measured results is attributed to the imperfect fibre birefringence compensation and other systematic effects such as offsets in the calibration of the polarisation analysis modules. Previous studies concerning polarisation-mode-dispersion suggest that a deterioration in fidelity by only a few tenths of a percent26,27 is expected for situations such as ours, where about \(0.6\) ps of polarisation-mode-dispersion is expected;21 however, this is clearly not the dominant effect in our case.
Stability of the fidelity
In order to measure the stability of our setup, including the submarine fibre link, we performed a long-duration measurement of the visibility over a period of about \(6.5\) h. Throughout this period, the visibilities in the H–V and D–A bases were measured alternately. Imperfect compensation of the quantum channel and other systematic issues mean that the visibilities of the two bases were quite different. In the H–V basis, the visibility ranged from \(74\,\pm\,2\)% to \(86\,\pm\,2\)%, which corresponds to a maximum polarisation rotation on the Poincare sphere of \(1{2}^{\circ }\). The visibility in the D–A basis was slightly more stable, as it ranged from \(87\pm 2\) to \(94\,\pm\,2\)%, corresponding to a maximum polarisation rotation of \({9}^{\circ }\). Nevertheless, our results show that the lower bound to the fidelity hardly changes over the course of the 6 h. The measured average fidelity was \(85\,\pm\,2\)%, well above \(1/\sqrt{2}\approx 70.7\)%, which is the minimum fidelity required to violate a CHSH inequality and therefore certify entanglement, for the duration of the experiment. For entanglement-based QKD protocols, a fidelity of \(81\)% is required to yield a positive secret key rate.28 This more stringent bound is also surpassed in our data.
Estimation of the secure key rate
As shown in Fig. 3a, the measured QBER stays below 9% with the exception of one measurement and therefore facilitates the generation of a secure key. Since only two detectors were available to us, without a fast basis choice, in total eight measurements were needed to estimate the fidelity. We use these results to estimate the sifted key rate. A setup which chooses a random basis with 50% probability would measure all these measurement combinations in the same time interval, together with another eight combinations, in which both users measure in a different basis. Therefore, the fast switching QKD setup would be able to analyse sixteen combinations of polarisation during the time in which a two-detector setup, like ours, can measure only one combination. However, the rate of coincident photons in each basis combination would only be one quarter of the rate of the two-detector setup, since the setups will only measure both in the D–A and both in the H–V for one quarter of the time, respectively. Therefore, the sifted key \({R}_{{\mathrm{s}}}\) which would have been observed in a fast-switching QKD setup is estimated to be one fourth of the sum of coincident clicks of our eight measurements. In Fig. 3b, the red points correspond to an estimate of the secure key rate, based on the observed count rate and fidelity3 in the asymptotic temporal limit, therefore ignoring finite size effects. For this, an error correction efficiency of 1.15 was assumed.29
A measurement over 6.5 h demonstrates excellent passive stability of the system. a QBER, estimated from the visibility measurements. The QBER shown were calculated from eight different combinations of measurement bases each integrated over 100 s (The third and fourth data points correspond to a measurement duration of \(84\) s and \(80\) s long, respectively). b The red points correspond to the estimated secure key rate, based on the observed count rate and fidelity in the asymptotic time limit. c Position of the coincidence peak, as observed from histograms similar to Fig. 2 over an interval of several hours during which no compensation of the fibre birefringence was carried out. The error bars correspond to one standard deviation as derived from the fitting parameters.
Length changes of the fibre
Another observable that we have access to is the relative delay between the two photons, corresponding to the length of the optical link. We used this data, shown in Fig. 3c, to assess the stability of the net optical length of the fibre by tracking the evolution of the temporal position of the coincidence peaks, which were determined via Gaussian fits similar to the one shown in Fig. 2. The error bars have been obtained from the covariance matrix of the corresponding Gaussian fits. The maximum change of the coincidence delay, \(124\) ps, between hours \(2.28\) and \(6.28\) can be explained by a net change in the average temperature of the fibre, which we consider a proxy for the temperature of the seabed. We estimated the temperature change to be about \(22\) mK using a thermal expansion coefficient of optical fibres of \(\frac{{\rm{d}}L}{{\rm{d}}T}=5.6\times 1{0}^{-7}\ {{\rm{K}}}^{-1}\) and the change of refractive index per kelvin of \(\frac{{\rm{d}}n}{{\rm{d}}T}=8.45\times 1{0}^{-6}\ \,{{\rm{K}}}^{-1}\).30 This agrees roughly with the findings of ref. 31 where the environmentally induced phase noise in submarine fibre cables was investigated in this region. This temperature change corresponds to a length change of approximately \(2.4\) mm, which does not have any significant effect on the transmitted fidelity since slow length changes do not exert sufficient strain to cause significant birefringence. When compared to refs, 32,33 our results show that this submarine environment is very favourable for polarisation-based quantum communication in optical fibres, demonstrating even greater stability than in laboratories with conventional climate control, which often only regulates the temperature with the accuracy of \(1\) or 2 K.
Discussion
We have demonstrated the distribution of polarisation-entanglement over a total length of \(192\) km using a dark fibre that is deployed in a submarine cable in close proximity with fibres actively carrying classical communication signals. Our demonstration does not involve any active stabilisation, in spite of which we observe remarkable passive stability for the polarisation state over several hours. The stability of the polarisation state depends on the environmental conditions of the deployed fibre and has been investigated for buried33,34 or aerial33,35 fibres, which often exhibit faster changes. For a technical implementation of a QKD system, the polarisation state of the fibre cable would have to be automatically aligned, which in the case of the submarine fibre used for the present experiment requires only very slow live adjustments or interruptions of the measurement for alignment, whenever necessary. For aerial fibres, the stability would require much faster compensation systems which constantly optimise the QBER of the QKD system.
Our work extends the length over which polarisation entanglement distribution is proven to be possible using entangled photon pairs and heralds the use of polarisation entangled photons and submarine telecommunication optical fibre links as building blocks for a quantum internet.
Methods
The polarisation-entangled photon-pair source
Our source was based on type-0 spontaneous parametric down-conversion in a \(4\) cm-long magnesium oxide doped periodically poled temperature stabilised lithium niobate (MgO:ppLN) bulk crystal with a poling period of \(19.2\) µm. The type-0 process converts, with low probability, one linearly-polarised pump photon at \(775.075\) nm from a CW laser to two daughter photons, commonly referred to as the signal (s) and idler (i) photons, in the C-band, having the same polarisation as the pump photon. The MgO:ppLN crystal was bidirectionally pumped inside a Sagnac-type setup22 including a half-wave plate, thus creating a polarisation-entangled state (Eq. (1)).
Alignment of the polarisation state of the quantum channel
The birefringence of the quantum channel was compensated for in both the H–V and the D–A bases by sending laser light at \(1551.72\) nm through the quantum channel from the point in the setup corresponding to where the SNSPD system lies in the figure, and analysing it with a polarimeter in the region labled “FSB” in Fig. 1. With the manual polarisation controllers, the fibre was aligned such that the polarisation state of the light, as defined by the polarising beam splitter and half-wave plate in front of the detector also arrives at FSB. Following this, the laser was disconnected again and the SNSPD was connected in its stead, allowing quantum measurements to be performed in the configuration depicted in Fig. 1.
The detection system
The photons were detected using two separate fibre-coupled superconducting nanowire single-photon detectors (SNSPD) in the same commercial croystat (Single Quantum Eos) operating at \(2.9\) K. A current driver (Single Quantum Atlas) was used to read out the signals, which were digitised by a time tagging device. Since the efficiency of the detectors is dependent on the photon polarisation, we used a manual fibre polarisation controller to optimise the detection efficiency. Detector “A” exhibited a dark-count rate of \(900\) s−1 at an efficiency of \(60\)%, whereas detector “B” was operated at an efficiency of \(12\)% to reduce the dark-count rate to \(20\) clicks per second.
Data availability
The data that support the findings of this study are available from the corresponding authors on request.
References
Wonfor, A. et al. in Broadband Access Communication Technologies XII, Vol. 10559 (eds Dingel, B. B. et al.) 6 (SPIE, 2018). https://spiedigitallibrary.org/conference-proceedings-of-spie/10559/2290544/Field-trial-of-a-QKD-and-high-speed-classical-data/10.1117/12.2290544.full.
Optics.org. Cryptography secures Swiss elections historical archive. http://optics.org/article/31646 (2007). Accessed: 22 May 2019.
Ma, X., Fung, C.-H. F. & Lo, H.-K. Quantum key distribution with entangled photon sources. Phys. Rev. A 76, 012307 (2007).
Scheidl, T. et al. Feasibility of 300 km quantum key distribution with entangled states. New J. Phys. 11, 085002 (2010).
Masanes, L., Pironio, S. & Acín, A. Secure device-independent quantum key distribution with causally independent measurement devices. Nat. Commun. 2, 238 (2011).
Branciard, C., Cavalcanti, E. G., Walborn, S. P., Scarani, V. & Wiseman, H. M. One-sided device-independent quantum key distribution: security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501 (2016).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Yin, J. et al. Satellite-to-ground entanglement-based quantum key distribution. Phys. Rev. Lett. 119, 200501 (2017).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Tamura, Y. et al. in Optical Fiber Communication Conference, Th5D–1 (Optical Society of America, 2017).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Violation of bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81, 3563–3566 (1998).
Marcikic, I. et al. Time-bin entangled qubits for quantum communication created by femtosecond pulses. Phys. Rev. A 66, 062308 (2002).
Honjo, T. et al. Long-distance distribution of time-bin entangled photon pairs over 100 km using frequency up-conversion detectors. Opt. Express 15, 13957 (2007).
Inagaki, T., Matsuda, N., Tadanaga, O., Asobe, M. & Takesue, H. Entanglement distribution over 300 km of fiber. Opt. Express 21, 23241 (2013).
Aktas, D. et al. Entanglement distribution over 150 km in wavelength division multiplexed channels for quantum cryptography. Laser Photon. Rev. 10, 451–457 (2016).
Hübel, H. et al. High-fidelity transmission of polarization encoded qubits from an entangled source over 100 km of fiber. Opt. Express 15, 7853 (2008).
Wengerowsky, S. et al. Entanglement distribution over a 96-km-long submarine optical fiber. Proc. Natl Acad. Sci. (2019). https://www.pnas.org/content/early/2019/03/13/1818752116.full.pdf.
Corning. Corning Leaf data sheet. https://www.corning.com/media/worldwide/coc/documents/Fiber/LEAF%20optical%20fiber.pdf (2014). Accessed 28 Nov 2018.
Kim, T., Fiorentino, M. & Wong, F. N. Phase-stable source of polarization-entangled photons using a polarization sagnac interferometer. CLEO/QELS 2006 73, 12316 (2006).
Hill, K. O. et al. Chirped in-fiber bragg gratings for compensation of optical-fiber dispersion. Opt. Lett. 19, 1314–1316 (1994).
Blinov, B. B., Moehring, D. L., Duan, L.-M. & Monroe, C. Observation of entanglement between a single trapped atom and a single photon. Nature 428, 153–157 (2004).
Chang, X.-Y. et al. Experimental realization of an entanglement access network and secure multi-party computation. Sci. Rep. 6, 29453 (2016).
Antonelli, C., Shtaif, M. & Brodsky, M. Sudden death of entanglement induced by polarization mode dispersion. Phys. Rev. Lett. 106, 80404 (2011).
Brodsky, M., George, E. C., Antonelli, C. & Shtaif, M. Loss of polarization entanglement in a fiber-optic system with polarization mode dispersion in one optical path. Opt. Lett. 36, 43 (2011).
Hongyang, M. & Bingquan, C. Quantum network based on multiparty quantum secret sharing. In Proceedings—SNPD 2007: Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing, Vol. 2 (ed. Feng, W.), 347–351 (IEEE, 2007).
Elkouss, D., Leverrier, A., Alléaume, R. & Boutros, J.J. Efficient reconciliation protocol for discrete-variable quantum key distribution. In 2009 IEEE International Symposium on Information Theory, 1879–1883 (IEEE, 2009).
Leviton, D.B. & Frey, B.J. in Optomechanical Technologies for Astronomy, Vol. 6273, 62732K (International Society for Optics and Photonics, 2006).
Clivati, C. et al. Optical frequency transfer over submarine fiber links. Optica 5, 893–901 (2018).
Waddy, D. S., Chen, L. & Bao, X. Polarization effects in aerial fibers. Opt. Fiber Technol. 11, 1–19 (2005).
Ding, Y.-Y. et al. Polarization variations in installed fibers and their influence on quantum key distribution systems. Opt. Express 25, 27923 (2017).
Rubenok, A., Slater, J. A., Chan, P., Lucio-Martinez, I. & Tittel, W. Real-world two-photon interference and proof-of-principle quantum key distribution immune to detector attacks. Phys. Rev. Lett. 111, 130501 (2013).
Yoshino, K.-i, Ochi, T., Fujiwara, M., Sasaki, M. & Tajima, A. Maintenance-free operation of wdm quantum key distribution system through a field fiber over 30 days. Opt. Express 21, 31395–31401 (2013).
Acknowledgements
We are deeply indebted to Simon Montanaro, Roderick Cassar, and Charles Peresso at Melita Ltd. for providing assistance and access to their network. We thank Jesse Slim for programming a user interface for our motorised rotation stages, Lukas Bulla, Matthias Fink, Aron Szabo, Leah Paula Vella, and Ryan Vella for helpful discussions and technical assistance. We gratefully acknowledge financial support from the Austrian Research Promotion Agency (FFG) Agentur für Luft- und Raumfahrt (FFG-ALR contract 844360 and FFG/ASAP:6238191 / 854022), the European Space Agency (ESA contract 4000112591/14/NL/US), the Austrian Science Fund (FWF) through (P24621-N27) and the START project (Y879-N27), as well as from the Austrian Academy of Sciences, the European Research Council under the grant agreement No. 307687 (NaQuOp), the Swedish Research Council (grants 638-2013-7152 and 2016-04527), the Linneaus Centre in Advanced Optics and Photonics (Adopt), the University of Malta Research, Innovation & Development Trust (RIDT). We acknowledge the use of imagery from the NASA Worldview application (https://worldview.earthdata.nasa.gov/), part of the NASA Earth Observing System Data and Information System (EOSDIS).
Author information
Authors and Affiliations
Contributions
The experiment was conducted by S.W. and S.K.J. The setup was designed by F.S., S.W. and S.K.J. J.R.Z., S.M.D., R.vdM., J.W.N.L., V.Z. and M.A.M.V. helped with the detection of the single photons. A.M., D.C. and M.I. helped to conduct the experiment. A.X. analysed the data, helped to conduct the experiment, and oversaw the work in Malta. L.B. and T.S. helped to analyse the data. A.Z. and R.U. contributed to the experimental design and source as well as supervising the project. The paper was written by S.W., F.S., S.K.J. and A.X. All authors discussed the results and contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wengerowsky, S., Joshi, S.K., Steinlechner, F. et al. Passively stable distribution of polarisation entanglement over 192 km of deployed optical fibre. npj Quantum Inf 6, 5 (2020). https://doi.org/10.1038/s41534-019-0238-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0238-8
This article is cited by
-
Distributed quantum sensing of multiple phases with fewer photons
Nature Communications (2024)
-
Second-Order Correlation Measurement for Single-Photon Metrology
MAPAN (2023)
-
Experimental implementation of secure anonymous protocols on an eight-user quantum key distribution network
npj Quantum Information (2022)
-
Continuous entanglement distribution over a transnational 248 km fiber link
Nature Communications (2022)
-
Strategies for achieving high key rates in satellite-based QKD
npj Quantum Information (2021)