Scalable repeater architectures for multi-party states

Abstract

The vision to develop quantum networks entails multi-user applications, which require the generation of long-distance multi-party entangled states. The current rapid experimental progress in building prototype-networks calls for new design concepts to guide future developments. Here we describe an experimentally feasible scheme implementing a two-dimensional repeater network for robust distribution of three-party entangled states of GHZ type in the presence of excitation losses and detector dark counts — the main sources of errors in real-world hardware. Our approach is based on atomic or solid state ensembles and employs built-in error filtering mechanisms peculiar to intrinsically two-dimensional networks. This allows us to overcome the performance limitation of conventional one-dimensional ensemble-based networks distributing multi-party entangled states and provides an efficient design for future experiments with a clear perspective in terms of scalability.

Introduction

The development of quantum networks holds the promise to realize quantum technologies such as secure communication schemes,¹ distributed quantum computing,² and metrological applications.^3,4,5,6 This prospect resulted in intense efforts to build prototype-networks with few nodes. The creation of long-range bipartite entangled states has been demonstrated^{7,8,9,10,11,12,13,14,15,16,17} and multi-party entangled states shared between several remote parties can be realized in the near-future. The ability to distribute such multi-party entangled states over long-distances¹⁸ will be an essential prerequisite for future quantum networks^{19,20,21,22,23,24} consisting of large two-dimensional (2D) structures that allow for multi-user applications. This need and the current experimental possibilities raise the question which type of architecture can be used to distribute long-range multi-party entanglement in a practical and scalable fashion. We address this problem from an implementation-oriented point of view and propose a networking scheme that allows for a robust and efficient realization with current and near-future experimental means.

Future quantum networks will require different types of multi-party entangled states suitable for different tasks. We concentrate on distributing three-party GHZ states,²⁵ e.g. $\left(\left|001\right\rangle +\left|110\right\rangle \right)/\sqrt{2}$, between remote parties, that can be used for clock synchronization,³ quantum secret sharing,^26,27 quantum secret voting,²⁸ or for fundamental tests of nature.²⁹ A key challenge for distributing quantum states over long-distances is the fact that losses and decoherence scale exponentially in the distance.^30,31 To solve this problem, quantum repeaters^32,33,34 have been introduced, which however are inherently one-dimensional (1D) schemes aiming at generating a bipartite entangled state connecting two remote parties. Therefore, an intrinsically 2D network can be preferable for a multipartite entanglement distribution as it was shown³⁵ to have a higher error threshold than a 1D counterpart under assumptions of a generic noise model and full Bell state analysis (or a universal gate set) availability.

In this work, we propose an implementation-oriented 2D repeater scheme that, in contrast to,³⁵ (i) can be realized using a constrained set of quantum operations available in atomic or solid state ensembles and (ii) has a mechanism to mitigate an excitation loss error and detector dark counts — major imperfections for this type of system. The resulting robust architecture is custom-tailored to implementations based on atomic or solid state ensembles, as these systems are promising for realizing long-lived quantum memories.^36,37 While atomic ensembles allow a limited set of operations for processing quantum information, record coherence lifetimes ($2{T}_{{\rm{coh}}}$) up to 6 h have been observed in rare-earth doped crystals.³⁸ This makes them particularly promising for entanglement distribution over continental distances using repeater schemes which inevitably requires memory times corresponding to the duration needed for classical communication between remote nodes.

Our scheme is inspired by the seminal DLCZ proposal for generating Bell pairs between two nodes,³⁹ and requires optical cavities with good cooperativities, linear optical elements, and photodetectors. GHZ states are first generated over moderate distances and then merged to form GHZ states connecting increasingly remote parties [see inset in Fig. 1a and Fig. 2a]. Similar to the DLCZ proposal, our protocol does not require a universal gate set or a full Bell-state analysis. However, unlike the DLCZ scheme, the new protocol suppresses the propagation of so-called vacuum and multi-excitation errors. These errors are resulted from excitation loss or detection of a dark count during the generation of the elementary state or merging operation and lead to the preparation of a state containing more/fewer excitations than expected. In the DLCZ scheme, the vacuum and multi-excitation errors freely propagate decreasing fidelity dramatically with the increase of nesting level and therefore making the scheme not scalable (Sangouard et al.³⁴ and Sec. A1 of Supplemental Material). In comparison, our 2D scheme results in a truly scalable architecture. As shown in Fig. 1 and explained below, this feature allows our repeater scheme to cover longer distances than networks based on combining conventional (one-dimensional) quantum links.

Fig. 1: Generation of long-distance GHZ states.

a Generation with the 2D scheme shown in inset and Fig. 2 and b with the 1D benchmark (see inset and text). Both panels display the fidelity $F$ versus the memory excitation lifetime ${T}_{{\rm{coh}}}$ and the covered distance $L$ for the parameters specified in Methods section. Red dash-dotted lines indicate the threshold beyond which entanglement distillation is impossible (see Supplemental Material, Sec. D). Dashed lines separate network structures with a different optimal number of nesting levels (indicated with roman numbers).

Fig. 2: 2D repeater scheme.

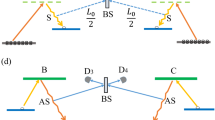
a Merging of GHZ states of three elementary segments spanning the length ${L}_{0}$ into a GHZ state of a segment covering the length $2{L}_{0}$, which are further merged to a segment of the length $4{L}_{0}$. Blue circles represent ensembles, and triangles depict network segments. The merging is realized by three swapping operations (see text) that are shown as gray ellipses. b Generation of the GHZ states at the elementary level. At nodes A and C, a $\Lambda$-type level structure is used allowing for standard DLCZ-type write-in and read-out operations.³⁹ Node B employs an ensemble with a double-$\Lambda$ configuration placed in a cavity (see Supplemental Material, Sec. G).

Results

Scheme

We propose a nested structure of quantum network³⁵ consisting of segments in three-party entangled states of increasing size as shown in Fig. 2a. The scheme requires the ability to generate GHZ states of elementary segments spanning a length ${L}_{0}$, and generalized entanglement swapping procedure to merge the GHZ states doubling the covered distance. We detail the generation and swapping operations separately in the next two paragraphs.

The generation of GHZ states at the elementary level is illustrated in Fig. 2b. We consider two types of ensembles: (i) ensembles with a $\Lambda$-level scheme at nodes A and C, allowing for the efficient storage and read-out of photons^39,40,41 and (ii) ensembles with a double-$\Lambda$ configuration placed in a cavity at node B. Information is encoded in the absence or presence of a collective spin excitation in the ensembles, i.e. in the logical states $\left|0\right\rangle =\left|{g}_{1}{g}_{2}...{g}_{N}\right\rangle$ and $\left|1\right\rangle =\frac{1}{\sqrt{N}}{\sum }_{i=1}^{N}\left|{g}_{1}{g}_{2}...{s}_{i}...{g}_{N}\right\rangle$, where $N$ is the number of emitters per ensemble and $\left|g\right\rangle$, $\left|s\right\rangle$ denote ground state levels of the emitters [see Fig. 2b]. Ensembles A and C are driven by weak coherent laser pulses resulting in entangled states of the ensembles and the corresponding forward-scattered photons,³⁹$\left|{0}_{A(C)}{0}_{a(c)}\right\rangle +{\epsilon }_{a(c)}\left|{1}_{A(C)}{1}_{a(c)}\right\rangle +{\mathcal{O}}({\epsilon }_{a(c)}^{2})$, ${\epsilon }_{a(c)}\ll 1$ (the role of the parameter $\epsilon$ is explained in Sec. B of Supplemental Material, our analysis includes also higher order terms). The capital and lowercase subscripts refer to the states of the ensemble and the corresponding emitted light field. Node B performs the gate operation $\left|{1}_{a}{0}_{B}{0}_{b}\right\rangle \to \left|{0}_{a}{1}_{B}{1}_{b}\right\rangle$, $\left|{0}_{a}{0}_{B}{0}_{b}\right\rangle \to \left|{0}_{a}{0}_{B}{0}_{b}\right\rangle$. The working mechanism and imperfections are detailed in Supplemental Material, Sec. G. The light fields emitted from nodes B and C are synchronously directed to a swapping station equipped with a 50/50 beamsplitter and two single-photon detectors, as illustrated in Fig. 2b. Conditioning on detecting a single photon allows for a probabilistic projection onto the state $\left|{\Psi }_{{\rm{GHZ}}}\right\rangle =\left(\left|{0}_{A}{0}_{B}{1}_{C}\right\rangle +\left|{1}_{A}{1}_{B}{0}_{C}\right\rangle \right)/\sqrt{2}$. The path length fluctuation in fibers AB and CB can be solved by phase stabilization, similar to 1D repeater schemes.³⁴ For example, it can be achieved by exciting memories in A and C in a Sagnac interferometer configuration,^42,43 such that the excitation laser pulses for the two memories and the emitted photons travel the same path in a counter-propagating fashion.

For merging three GHZ states, the states of ensembles at adjacent nodes are projected onto the one-excitation subspace. This operation is realized by reading out the atomic excitations^39,40,41 and directing the emitted light fields to the swapping station described above [see also inset of Fig. 2a], where success is heralded by the detection of a single photon (see Sec. A of Supplemental Material for details), otherwise the resulting state is discarded.

Error filtering

Apart from the major challenge to mitigate photon transmission losses, experimental limitations at the individual nodes have to be taken into account. The most important local error sources are the read-out inefficiency $v$ and imperfect photon detectors (with a detection inefficiency $f$ and a dark count probability $d$ during a photon pulse detection). Moreover, quantum states stored in the ensembles are degraded over time. Due to the encoding used here, the relevant physical mechanism — dephasing of individual emitters — leads to an effective decay of the stored collective excitations (Supplemental Material, Sec. F). In the considered ensemble-based setting, the main imperfections are therefore errors of loss type and detector dark counts.

The proposed 2D repeater protocol is designed to prevent the propagation of this kind of errors by employing an intrinsic redundancy of the native 2D network to filter out the errors in the merging process at each nesting level. The filtering mechanism, illustrated in Fig. 3, works as follows. At each nesting level one has to perform three merging operations to complete the entanglement generation between the three outermost nodes (X, Y, Z in Fig. 3). The third merging operation is redundant and it shows, if unsuccessful, that there is a lack or an excess of excitations in the generated state. This indicates an occurrence of either the loss type error or the multi-excitation error at previous stages of the protocol. In our protocol, the errors have, therefore, to conspire within one nesting level to pass undetected. In contrast, in the 1D benchmark scheme the errors can conspire within all levels of the bipartite state preparation to pass filtration in the last generation step. As a result, the 2D architecture exhibits a slower rate of error probabilities growth with the increase of the network nesting level (see Supplemental Material, Sec. A).

Fig. 3: Error filtering mechanism of the 2D repeater scheme.

Solid (red dashed) lines represent quantum (classical) correlations of the states of the nodes shown with circles. The states of the nodes of the same (different) colors are correlated (anti-correlated). Merging operations are shown with gray ellipses, the corresponding success probabilities (neglecting merging imperfections) are indicated nearby. a The no errors case: two successful probabilistic mergings of the three constituent GHZ states are followed by the third deterministic merging producing a perfect GHZ state $\left(\left|{0}_{X}{0}_{Y}{1}_{Z}\right\rangle +\left|{1}_{X}{1}_{Y}{0}_{Z}\right\rangle \right)/\sqrt{2}$. b One loss type error or one multi-excitation error leading to preparation of a network segment in a wrong state (red triangle) can be deterministically filtered out.

However, the filtering is a passive operation, therefore, it is important to start the entanglement distribution with initial states of high fidelity. As detailed in Sec. A and B of Supplemental Material, the protocol for generating entanglement at the elementary level and the relative orientation of GHZ states in the scheme is chosen such that the involved measurements allow for (i) identifying imperfect merging operations for ideal input states and (ii) filtering out imperfect states for ideal merging operations. The initial states of high fidelity at the elementary level and the subsequent error filtering at each nesting level result in the scheme robust against the vacuum and multi-excitation errors.

Key features

In the following, we highlight some of the main properties of our scheme and summarize the effect of limited memory coherence times in the presence of experimental imperfections. Figure 1a shows the fidelity of the generated state $\rho$ with respect to the target state $\left|{\Psi }_{{\rm{GHZ}}}\right\rangle$, $F=\sqrt{\left\langle {\Psi }_{{\rm{GHZ}}}\right|\rho \left|{\Psi }_{{\rm{GHZ}}}\right\rangle }$, for the proposed architecture. In Fig. 1b, for comparison, we introduce a fidelity benchmark representing the performance of a 1D scheme based on long-distance bipartite entanglement distribution. The 1D benchmark uses conventional ensemble-based repeater scheme which creates three long-distance Bell pairs to be subsequently merged to generate the desired target state. The benchmark estimates an upper bound of the fidelity as ideal local GHZ states [shown with double lined triangles in the inset in Fig. 1b] are used for the final merging. In contrast to the 2D approach, which relies on multi-party entanglement at all network levels, the 1D scheme exploits the distribution of long-distance Bell pairs and involves the error filtering mechanism only in the end (Methods section).

The most striking feature of Fig. 1 is the fact that the 2D protocol can distribute GHZ states over increasingly large distances by increasing the memory coherence time (or alternatively, by using so-called multiplexing approaches^{44,45,46,47,48} in which several quantum memories or memory modes are used in parallel to compensate for limited coherence times). An increase of ${T}_{{\rm{coh}}}$ significantly extends the distance that can be covered, since our protocol profits from using higher nesting levels for larger distances. This property makes the scheme practical and scalable. This is not the case for the 1D benchmark based on a regular DLCZ scheme, which is hampered by fundamental difficulties associated with the creation of long-range bipartite links (see Supplemental Material, Sec. A3 and Sec. C for details). Therefore, the 1D strategy reaches its performance limit at much shorter distances than the 2D scheme as can be seen in Fig. 1b in comparison with Fig. 1a.

To further characterize the potential of our approach, we analyze the case of infinite memory coherence time. Figure 4 shows the fidelity achievable by a network for which the number of nesting levels is optimal for a given distance in the presence of typical experimental imperfections for ${T}_{{\rm{coh}}}\to \infty$. A network with more nesting levels divides the target distance into shorter segments what reduces the probability to lose photons during transmission at the cost of additional errors generated by the repeater scheme itself. For each target distance, there is an ideal number of nesting levels beyond which the addition of a repeater station becomes undesirable. The comparison of the 2D approach (black line) with the 1D benchmark (green line) for generating three-party GHZ states shows that the latter suffers from severe limitations in the achievable fidelities for large distances even for perfect quantum memories. This is the result of the faster errors accumulation with the growing network size in 1D scheme which lacks the filtering mechanism of the native 2D protocol, as discussed in the previous section.

Fig. 4: Fidelity ${\boldsymbol F}$ for the proposed 2D scheme and the 1D benchmark (see text) in the limit of infinite memory coherence time, as a function of the covered distance ${\boldsymbol L}$.

This plot corresponds to a cut of Fig. 1 at ${T}_{{\rm{coh}}}\to \infty$. The gray area illustrates that for large distances, certain target fidelities can only be reached by the 2D scheme (the desired target fidelity depends on the application, in this example ${F}_{{\rm{target}}}=0.8$). Roman numbers indicate the optimal number of nesting levels for the network. Transitions between the optimal numbers of levels are shown by circles. Red dots indicate the distance beyond which entanglement distillation is impossible.

Here we emphasize that although the 1D benchmark uses fewer resources (memory cells) than our 2D scheme (see Supplemental Material Sec. A2) its performance is saturated at much shorter distances and can not be improved by a simple increase of resources invested into multiplexing. The presented 2D architecture allows us to convert the extra resources into longer entanglement distribution distances with higher target fidelities. Moreover, the additional memory cells improve coverage of intrinsically 2D networks by allowing the multi-party entanglement generation between arbitrary nodes of the network (see Supplemental Material Sec. A1), while 1D based schemes entangle only the outermost ensembles.

A detailed analysis of the 2D protocol performance, including an assessment of the achievable rates, is provided in Supplemental Material (Sec. A3 and Sec. C). In the following, we discuss means to further improve the performance by temporal filtering.

Temporal filtering protocol

Limited coherence times of quantum memories are generally an important restricting factor for quantum repeaters. To mitigate their effect, we introduce a temporal filtering mechanism by defining a time window $\tau$, after which quantum states are discarded. During the probabilistic generation and merging procedure shown in Fig. 2, ensembles storing excitations longer than $\tau$ are reset to their ground state, such that the entanglement generation process involving these nodes starts anew. As a result, the influence of decoherence is decreased at the expense of a reduced rate. The time $\tau$ can be changed dynamically by the control software without changing the hardware in a quantum network. Due to this added flexibility, different types of applications — requiring either high fidelities or high rates — can be accommodated. The corresponding tradeoff has been calculated semi-analytically (as described below) and is shown in Fig. 5.

Fig. 5: Temporal filtering for a 2D network with nesting level I, i.e. 9 ensembles [see Fig. 2b] for the parameters specified in Methods section.

The fidelity $F$ is shown versus the entanglement generation time $T$ for a target distance $L=50$ km and different memory times ${T}_{{\rm{coh}}}=\{1{0}^{-2},1{0}^{-1},1\}$s. Black solid (dashed green) lines represent results with (without) temporal filtering. The gray solid line indicates the fidelity in the limit of infinite quantum memory times.

Diagrammatic technique

We used a numerical Monte Carlo algorithm and developed a new semi-analytical technique to analyze the performance of our scheme in the presence of realistic imperfections. The Monte Carlo method is very flexible and simulates the full repeater protocol step by step.^49,50 The strength of this exact simulation is also its weakness — the runtime is proportional to the entanglement generation time in the quantum network, growing quickly with the network’s scale.

The analytical method overcomes this difficulty while still incorporating all relevant error sources, including finite memory coherence times. It takes time delays due to classical communication into account and can be used to analyze a large class of repeater schemes, including 1D protocols. The main idea is to determine the density matrix distribution $\varrho (t)$ for the ensemble of states generated by the network at time $t$. More precisely, we obtain the Laplace image of this distribution, $\tilde{\varrho }(s)$, which fully describes the statistics of the network and allows one to infer the average generated state $\rho \equiv {\int }_{0}^{\infty }\varrho (t){\mathrm{d}}t=\tilde{\varrho }(s){| }_{s=0}$, corresponding generation time $T\equiv {\int }_{0}^{\infty }t\ {\rm{Tr}}\varrho (t){\mathrm{d}}t=-\frac{d}{ds}{\rm{Tr}}\tilde{\varrho }(s){| }_{s=0}$, and other relevant statistical quantities.

We assume that the probability ${p}_{1}$ to generate an entangled state of an elementary segment is small for each time step $\Delta t$, such that the continuous probability density $p(t)\equiv \nu {e}^{-\nu t}$ with the rate $\nu \equiv {p}_{1}/\Delta t$ can be introduced. As an example, we consider a linear network consisting of two links, where the density matrix distribution for generating the ${\alpha }^{{\rm{th}}}$ link in a state ${\rho }_{\alpha }$ before the ${\beta }^{{\rm{th}}}$ link has been generated at time $t$ in a state ${\rho }_{\beta }$ is given by ${\varrho }_{\alpha \beta }(t)={p}_{\beta }(t){\int }_{0}^{t}{\mathrm{d}}{t}^{\prime}\ {p}_{\alpha }$(${t}^{\prime}$)${e}^{(t-t^\prime){\mathcal{L}}_{\alpha}}{\rho}_{1}\otimes{\rho}_{2}$ with $\alpha \beta \in \{12,21\}$. Here we sum over all intermediate times $t^{\prime}$ of the ${\alpha }^{{\rm{th}}}$ link creation. The degradation of the link during the waiting time $t-{t}^{\prime}$ due to finite memory life times is taken into account using the superoperator ${{\mathcal{L}}}_{\alpha }$. The corresponding Laplace image of the distribution is given by ${\tilde{\varrho }}_{\alpha\beta}(s)={\nu}_{\alpha}{\nu}_{\beta}/[({s}^{\prime}+{\nu}_{\alpha })({s}^{\prime}-{{\mathcal{L}}}_{\alpha })]\cdot {\rho }_{1}\otimes{\rho}_{2}{|}_{{s}^{\prime}=s+{\nu }_{\beta}}$.

The probability to generate and successfully merge states of two segments during the time window $[t,t+dt)$ is given by ${\rm{Tr}}\ {\mathcal{M}}{\varrho }_{\alpha \beta }(t)dt$, with ${\mathcal{M}}$ the merging superoperator. The summation over all possible combinations of unsuccessful mergings leading to the generation of an entangled state results in a sum of multiple convolutions in the time domain. In the Laplace domain, the sum converges to

$$\tilde{\varrho }\left(s\right)=\frac{{\sum }_{\alpha \beta }{\mathcal{M}}{\tilde{\varrho }}_{\alpha \beta }(s)}{1-{\sum }_{\alpha \beta }{\rm{Tr}}\left({\mathcal{I}}-{\mathcal{M}}\right){\tilde{\varrho }}_{\alpha \beta }(s)}\ ,$$

(1)

with ${\sum }_{\alpha \beta }$ the sum over all possible orders in which links are generated and ${\mathcal{I}}$ the unit superoperator. The Laplace image (1) is used to find the average density matrix $\rho ^{\prime}$ and generation time $T^{\prime}$ for the given nesting level of the network, as described above. To address the next network level, we apply the approximation that the segments are generated time-independently in the state $\rho ^{\prime}$ with the rate $\nu ^{\prime} =1/T^{\prime}$. In a recursive procedure, the state $\rho$ and generation time $T$ of an arbitrary network level can be found. As detailed in Sec. E of Supplemental Material, we introduce diagrams to conveniently deal with probabilistic processes in networks of arbitrary complexity.

Discussion

We proposed a scalable 2D architecture for generating long-distance multi-party entanglement and provided a full performance analysis with emphasis on the effect of finite memory lifetimes. Covering increasingly longer distances as shown in Fig. 1 can be achieved either using memories with long coherence times or using multiplexing approaches,^{44,45,46,47,48} in which several memory-modes are used in parallel. The presented scheme provides a flexible structure for creating GHZ states between arbitrary nodes of the 2D network, not only between the outermost ensembles. The logical topology of the network [shown in Fig. 2a] is thereby not identical to the topology of the required fiber links, which can easily be adjusted to accommodate urban constraints. We are here primarily interested in metropolitan distances and applications requiring only moderate bit-rates. Important examples include secret voting and the protection of classified information that requires several parties for decryption.^26,27

The presented scheme can be modified to work without cavities at the expense of using a larger number of ensembles (see Supplemental Material, Sec. H). This modification uses polarization-type qubits^34,39 and two-click conditioning,⁵¹ enhancing its resistance with respect to fiber-length fluctuations. It will be interesting to develop similarly robust schemes for other platforms such as trapped ions,^8,52 in which a universal gate set can be implemented. In this case, more complicated 2D repeater protocols involving quantum error correction³³ instead of error filtering could be envisaged.

Methods

Parameters of the simulated network

The results of simulations presented in Figs 1, 4, and 5 are obtained with the following parameters of the network: detection inefficiency $f=0.05$, read-out inefficiencies $v=0.05$, fiber attenuation length $L_{\rm{att}}=22$ km, gate efficiency (see text) $\eta =0.6$, signal length $l=1{0}^{-4}$s, and dark count probability in the signal measurement operation $d=10\,{\rm{Hz}}\times 1{0}^{-4}{\rm{s}}=0.001$.

One-dimensional benchmark scheme

Here we present an alternative, one-dimensional (1D), repeater approach for distribution of multi-partite GHZ state, which provides us with the fidelity benchmark used in the present work. This 1D benchmark scheme is based on the generation of long-range bipartite quantum states that are created using regular DLCZ quantum repeaters. A comparison of various nesting levels structures for the 1D benchmark scheme and the propose 2D scheme is presented in Fig. 6a.

Fig. 6: One-dimensional benchmark scheme.

a Comparison of the 2D scheme and the 1D benchmark scheme at different nesting levels. Dots represent quantum memories. Dots connected by lines represent elementary segments of the networks. Triangles with double lines indicate ideal GHZ states. b The last step of generating $\left|{\Psi }_{{\rm{GHZ}}}\right\rangle$ in the 1D benchmark scheme. The pictorial representation of states is explained in Fig. 3. The three distant parties X, Y, and Z hold perfect tripartite GHZ states, represented by triangles. The final filtering step described in the text is depicted in two stages, shown by arrows. Gray dashed lines and circles indicate the actual successive merging pattern, during which the long-range quantum links are first merged with the local GHZ states and then with each other.

While two links are enough to distribute entanglement between three parties, we equip the 1D scheme with the third link, which is used to implement error filtering procedure in the final step, similar to the original DLCZ protocol, as explained below. To ensure the robustness of the benchmark we assume that the distant parties X, Y, and Z of the 1D scheme have access to ideal GHZ states that can be generated on demand. This provides an upper bound on the performance of 1D schemes of DLCZ type for distribution of tripartite GHZ states. Therefore, the corresponding fidelity of the 1D scheme serves as a benchmark for our 2D scheme.

Figure 6b shows the final merging step of the 1D scheme acting as an error filtering operation. In this step, five swapping operations are followed by the last one, which is deterministic in the ideal case. A failure of the last swapping operation indicates an erroneous state. More details about the 1D benchmark scheme are presented in Sec. A of Supplemental Material.

Note added

Recently we have become aware of Santra et al.⁵³ discussing a similar temporal filtering technique