Abstract
Future-proofing current fibre networks with quantum key distribution (QKD) is an attractive approach to combat the ever growing breaches of data theft. To succeed, this approach must offer broadband transport of quantum keys, efficient quantum key delivery and seamless user interaction, all within the existing fibre network. However, quantum networks to date either require dark fibres and/or offer bit rates inadequate for serving a large number of users. Here we report a city wide high-speed metropolitan QKD network—the Cambridge quantum network—operating on fibres already populated with high-bandwidth data traffic. We implement a robust key delivery layer to demonstrate essential network operation, as well as enabling encryption of 100 Gigabit per second (Gbps) simultaneous data traffic with rapidly refreshed quantum keys. Network resilience against link disruption is supported by high-QKD link rates and network link redundancy. We reveal that such a metropolitan network can support tens of thousands of users with key rates in excess of 1 kilobit per second (kbps) per user. Our result hence demonstrates a clear path for implementing quantum security in metropolitan fibre networks.
Similar content being viewed by others
Introduction
Reliably securing current network infrastructure has never been a more pressing issue. Accounts of breaches in personal and corporate data are frequently reported and the fall-out can be extremely damaging and costly to the parties involved.1,2 Strengthening the security of networks that transport sensitive data is therefore of paramount importance to mitigating the threat of data theft. Securing network data channels through the use of quantum cryptography3,4 is a robust method of safeguarding data communications—the security of which derives from the laws of quantum mechanics. However, this security comes at a price: quantum states must in general be used to transport information and these carriers are extremely fragile. Consequently previous approaches at building quantum networks have allocated additional dark fibres for quantum communication, distinct from the fibres carrying conventional data traffic.5,6,7,8,9
The simplest configuration of a quantum network consists of three geographically separated nodes, which are linked by quantum channels.10 This differs from simple point-to-point links consisting of only two nodes. It is also understood that a quantum network also includes all the functional layers required in a real network such as key delivery and application layers. Ideally the approach to building quantum networks should not adopt dedicated resources. Rather for quantum networks to become a mainstay in commercial networks, it must be implemented as an upgrade to existing network infrastructures.
Progress has been made starting with point-to-point quantum key distribution (QKD) experiments multiplexing classical data onto a single fibre in the laboratory11,12,13,14,15,16,17,18,19 evolving to moderate speed point-to-point QKD link multiplexing demonstrations in the field with secure bit rates in the range of tens of kbps20 or a factor of ten greater.21 At the same time the classical data intensities have been increased to as much as +20 dBm in a very impressive multiplexed point-to-point QKD field trial.20 Multiplexed quantum networks have been demonstrated both in the laboratory22,23 and the field24,25,26,27,28 but secure bit rates are low; generally on the order of 1 kbps. Furthermore, although these quantum networks employ quantum and classical traffic multiplexing, it is unclear whether these networks can coexist with high ≥100 Gbps third-party data bandwidths. Finally, support for classical data quantum encryption has been limited to low-bandwidth applications such as telephone one-time-pad encryption.28 There is therefore an urgent need for demonstrating the feasibility of concomitant high-speed Mbps quantum encryption in single fibre real-world quantum networks. Table 1 gives a comparison of some of the state-of-the-art quantum links and networks.
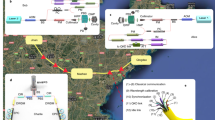
Metropolitan networks inhabit a critical region in the overall three layer network model.29 They bridge the gap between the access network and the core or backbone network and for legacy reasons are mostly based on fibre ring topologies.30 Meshing of such a ring permits all nodes to communicate, as well as link redundancy in the event of partial network failure. To preserve these important features in a quantum network, QKD has to offer high bit rates, as explained below. Consider for example the ring network with N = 5 nodes A–E in Fig. 1(a). All nodes are logically interconnected by arranging the intermediate nodes to act as relays. An example relay is shown between node A and node C via the relay node B. In this way, although the network is still physically a ring, it is topologically fully meshed. Of course to adequately support the network with a minimum bandwidth per logical link, B, the QKD links themselves must supply a minimum key rate, R. As the number of nodes in the ring, N, grows, the minimum bandwidth (or bit rate) per logical link decreases quadratically (see Methods) as
For only N = 10 nodes and a QKD link key rate of R = 1.5 kbps found in a typical network field trial,9 the bandwidth (or bit rate) per logical link drops to B < 100 bps. In all, 100 bps can be considered a practical lower limit for most user applications.16 On the other hand, QKD link key rates of R = 2.5 Mbps or greater can support individual logical links with practical rates of 100 kbps or greater. Even in a large city, which may feature a metropolitan ring the user bandwidth is still a serviceable, 1 kbps.
Metropolitan network topologies. a A five node ring topology, which is logically fully meshed. Five QKD links are connected in a ring (salmon lines) supporting ten logical network connections (grey dashed lines) between all nodes. The QKD links are assumed to have similar secure bit rates R. To realise the fully meshed network, nodes act as intermediary key relays as well as end points. An example relay is shown between node A and node C via the relay node B. The salmon arrows represent the QKD links A–B /B–C and the grey arrow represents the logical link that utilises the QKD links A–B/ B–C. b The bandwidth per logical link as a function of the number of nodes in a fully meshed ring network for R = 1.5 kbps (orange), and 2.5 Mbps (wine) using Eq. (1) in the main text. c A three node ring network in the Cambridge metropolitan area. Three nodes denoted CAPE, TREL, and ENGI are connected in a triangular arrangement using underground single mode optical fibres. Map credits: Imagery ©2017 Google, Infoterra Ltd + Bluesky, Getmapping plc, The GeoInformation Group, Map data ©2017 Google United Kingdom. d Cambridge quantum network with up to 3n users attached to metro nodes via quantum access networks (QANs). e The total number of users, 3n that can be supported as a function of bandwidth per user link for the topology depicted in d for QKD link speeds of 1.5 kbps (orange line) and 2.5 Mbps (wine line)
The example above described a ring network built with point-to-point QKD links. An alternative approach using point-to-point QKD for building quantum networks could be Measurement Device Independent QKD (MDI-QKD). This offers a linear improvement in the scaling in the number of links versus the number of nodes, as well as a relaxation in the security of the single photon detectors.31 However, the rates are typically low: of the order of tens of bps for a recent three node quantum network field trial.32 We remark there is promise of MDI-QKD becoming a practical reality with recent laboratory experiments33 and also on asymmetric MDI-QKD displaying kbps secure bit rates.34
In the context of wavelength multiplexing quantum signals with classical signals, continuous variable (CV) QKD16,17 can be utilised instead of its discrete variable (DV) QKD counterpart. CV-QKD has an intrinsically high tolerance to noise from Raman scattering, due to homodyne detection acting like a filter and thus can endure high-classical laser launch powers.35 Nevertheless, DV-QKD has been proven to operate in the presence of up to +5 dBm launch powers18 and up to +20 dBm when the quantum channel is moved to O-band.20 Furthermore, the full security of the DV-QKD protocol adopted in this paper has been well established for a number of years, even in the finite-size scenario.36
In this work, we present a three node high-speed quantum metropolitan ring network based in the city of Cambridge, UK. The Cambridge quantum network is depicted in Fig. 1(c) and forms a portion of a wider UK quantum network stretching from Cambridge to Bristol via London, which is part of the UK Quantum Communications Hub. It is composed of three underground fibres connecting sites in the north-east of the city (TREL, premises of Toshiba Research Europe Limited) with the south (ENGI, Department of Engineering, University of Cambridge) and the west (CAPE, Centre for Advanced Photonics and Electronics). Fibre distances (losses) are 10.6 km (3.9 dB) [CAPE – TREL], 9.8 km (4.2 dB) [TREL – ENGI] and 5.0 km (~2.5 dB) [ENGI – CAPE]. The average fibre loss coefficient across all three links was 0.43 dB/km, which is very similar to a dark fibre three-link quantum network previously demonstrated.9 To satisfy the requirements of a practical level of bandwidth for users explored above, the building blocks of this network are state of the art single fibre QKD systems with secure bit rates exceeding 3 Mbps over short distances. A similar design has been successfully demonstrated in the laboratory,37 but never in the field or in a quantum network. We remark that an extremely high speed, 10 Mbps, QKD system has been recently reported, but it utilised a dark fibre for the quantum channel.38 A network key delivery layer39 is used to serve keys to applications in the Cambridge quantum network, as well as performing key relaying functions.40 We demonstrate a 200 Gbps encrypted link operating over the same fibre as QKD, which simultaneously consumes QKD keys for high-speed Advanced Encryption Standard (AES) encryption. Uninterrupted application key consumption is observed when keys are re-routed via different network paths.
Results
We first built, installed and evaluated the quantum layer in the network, Fig. 2(a). Three single fibre GHz clocked QKD systems were constructed. These systems run an efficient version of the phase encoded DV-QKD BB84 protocol with decoy states41 and finite sample sizes.42 The quantum channels of all systems operate on the International Telecommunication Union Dense Wavelength Division Multiplexing (DWDM) 100 GHz C-band grid43 at wavelengths around 1550 nm and are multiplexed with the classical QKD reconciliation channels using standard wavelength spacing. A portion of the DWDM C-band spanning sixteen 100 GHz channels (1528 nm–1540 nm) is reserved for multiplexing in application traffic; an example of which is discussed below. The QKD systems are fully autonomous, featuring automatic initialisation and automatic feedback for photon temporal, polarisation, and phase drift.44 Room temperature operation of the single photon detectors in the QKD systems’ receivers improves system reliability due to the absence of detector cooling.45 All these attributes are essential for ease of network deployment and maintenance.
Cambridge quantum metro network— quantum layer. a Layout of the quantum layer which uses three, high-speed GHz clocked QKD systems connecting three geographically separated nodes as depicted in Fig. 1(c). Each QKD link produces a set of QKD keys identified by the link colour; b Quantum layer QBER, secure bit rate and total key material distilled for all three links over 580 days of operation. Blue data: CAPE-TREL, Red data: TREL-ENGI, Green data ENGI-CAPE. The blue arrow shows the duration of the 200G traffic being injected over the CAPE-TREL link
Figure 2(b) shows the performance of the quantum layer over a period of 580 days or ~1.6 years. All three links exhibited secure bit rates of >2 Mbps during this period, including outages. These outages were due to a number of factors including uninterruptable power supply (UPS) failure as well as power supply outages, which lasted longer than the UPS batteries could support. We also executed several software and hardware updates, which interrupted network operation. Normally, the outages would range from a few hours to a few days (if it had happened over a weekend for example). The probability of power supply related outages could be reduced by using UPSs with longer battery lifetimes.
The CAPE-TREL link achieved an average secure bit rate of 2.58 Mbps with a corresponding 129 Terabit (Tbit) of key material distilled. The TREL-ENGI link displayed a slightly lower average secure bit rate, including outages of 2.40 Mbps and a resultant total of 120 Tbit of key material created over the 580-day period. The final link, CAPE-ENGI resulted in the lowest amount of key material distilled in the network (111 Tbit) with a concomitant average secure bit rate of 2.22 Mbps. As the losses of all three links in the network were very similar, the average secure bit rates for all three links are much alike.
These long-term results from the Cambridge metro network quantum layer can be favourably compared with the closest long-term network demonstration; namely the SwissQuantum network.9 This network was composed of three metropolitan length links and ran over ~2 years but with comparatively low secure bit rates of kbps despite employing dark fibres for the quantum traffic. In the SwissQuantum network the total secure bits distilled was around 0.13 Tbits for the best performing link. Instead the Cambridge quantum network’s best performing link produced 129 Tbits of key material, so approximately three orders of magnitude larger. The aggregate secure key material of all three links was 360 Tbits. This constitutes the highest amount of key material ever distilled in a quantum network by a significant margin.
Having demonstrated the quantum layer, we move up a layer into the network key delivery layer. We note network key management for QKD has been developed by Peev et al.,6 Sasaki et al.,8 and Stucki et al.9 However, for this study we adopt a recent design by Tanizawa et al.,39,40 which features significant benefits over other network key management architectures, in particular high speed, Mbps operation compatible with our network bandwidth. Figure 3(a) shows the basic idea of the network key delivery layer. Each node is assumed to be trusted and can generate a buffer of “global keys”, which are shared with peer nodes using one-time-pad (OTP) tunnels encrypted by QKD keys. In this way, the global keys are quantum secure and can be used by applications through a dedicated application interface (API) based on representational state transfer (REST).39 As an example application we used two pairs of ADVA 100G classical encryption line cards installed in two ADVA FSP3000 shelves, Fig. 4(a), which operate over the CAPE-TREL link. Owing to the bi-directional nature of the line cards, each card has an AES encryptor for one direction and an AES decryptor for the opposite direction. Each pair of line cards requests global keys from their local node approximately every 4 s, i.e.: the QKD link supplies global keys on average every 2 s (since there are two pairs of line cards). The global keys replace the regular AES key used to normally encrypt the 100G data traffic. We point out that the key refresh rate of 1 global key every 4 s corresponds to a (global) bit rate of ~100 bps. The current key exchange frequency is not limited by the AES hardware, but rather due to the speed of the REST API that hands over each key individually from the QKD device to the AES engine. A speed-up could be achieved, e.g., by transferring multiple keys and by optimising the runtime of the protocol. Note a standard C-band transmission system design allows for a fully loaded system to work by collecting QKD keys in parallel without any further changes.
Cambridge quantum metro network—network key delivery layer. a Layout of the network key delivery layer depicting the one-time-pad (OTP) tunnels securing global keys by consuming quantum keys from the quantum layer, as described in Fig. 2(a). b Network key relay results: An application, which is a 100G encrypted link between TREL-CAPE, consumes global keys from the TREL-CAPE global keystore (orange line). When the keystore is depleted to a level of 800 keys, the keystore is replenished to 1000 keys by OTP quantum encryption, as shown by the TREL-CAPE OTP traffic activity in bytes(blue line, section (i)). Initiating a link outage for the TREL-CAPE link causes the TREL-ENGI and ENGI-CAPE links to automatically route OTP traffic (green/red lines) thus maintaining network operation, section (ii). Note the green line has been offset for clarity. Restoring the original TREL-CAPE link causes the OTP traffic to be automatically directed back along the TREL-CAPE link, section (iii)
Cambridge quantum metro network—application layer. a Layout of the application layer depicting two 100G links which share the same forward fibre as the TREL-CAPE QKD link. Encryptor images credit: Dynes et al.37 b 100G pre-FEC error probability (grey line), QKD link QBER (red symbols) as a function of optical receiver power and simulated QBER (red line). QBER error bars are one standard deviation. See Methods for more details on the simulation. The dotted line shows the upper limit on the 100G pre-FEC error rate for error free operation after error correction. c 100G pre-FEC error probability over 24 h corresponding to a receiver power of approximately −12 dBm
Now we describe the network key delivery layer in action. For clarity we restrict the results reported here to a single 24 h period, Fig. 3(b), although we emphasise the network key delivery layer has been successfully tested in the network over many months. A zoomed 3 h section of the overall 24 h period is also shown in Fig. 3(b). When the network key delivery layer is initialised three sets of 1000 global keys are distributed throughout the network. This consumes ~180 kbytes of QKD keys as evidenced by the initial increase in OTP traffic for all three links. Shortly after, the 100G application starts consuming global keys, which gradually reduces the global keystore on the CAPE-TREL link. When the global keys consumed reaches a threshold of 800 keys the network key delivery layer reacts and refreshes the global key stores to their starting value. This consumes further QKD keys from the CAPE-TREL link (Fig. 3(b), section (i), blue line) and results in OTP traffic activity. A step-like behaviour in the OTP traffic for the CAPE-TREL link is observed, each step corresponding to refreshment of the global key stores. Note the other two links do not show any OTP traffic activity since the key stores for those links are unaffected.
An important aspect of the network key delivery layer is resilience to network outages,40 which we validate now. Imagine there is a problem with the CAPE-TREL link, for example perhaps the QKD link has failed for some reason due to an assailant attacking this link. Automatically the network layer can react and relay keys the opposite way around the Cambridge quantum network, i.e.: via TREL-ENGI-CAPE. We simulated this by disconnecting the CAPE-TREL OTP link as evident by the increasing one-time-pad tunnel activity on the TREL-ENGI and ENGI-CAPE links, Fig. 3(b), section (ii) (red/green lines). Note the original CAPE-TREL (blue link’s) OTP activity has stopped since that link is no longer used. This demonstrates resilience of the network —applications can still keep making successful key requests; even if one of the QKD links in the network goes down. If the original CAPE-TREL QKD link becomes available again Fig. 3(b), section (iii), then the network can react to this. In this case it will then start using the CAPE-TREL OTP link to distribute the global keys while the TREL-ENGI and CAPE-ENGI OTP activity goes quiet again.
Finally, we discuss the application layer, Fig. 4(a). As already pointed out, we have installed two 100G encryptors at both CAPE and TREL as an example application. This traffic was added to the network approximately halfway through the 1.6-year field trial (see blue arrow in Fig. 2(b)).The forward directed 100G traffic from these encryptors are wavelength multiplexed onto the same fibre as the QKD traffic thus removing the need for a second dedicated fibre for QKD. This significantly reduces deployment costs as a dedicated fibre is not required and QKD can integrate seamlessly into conventional optical networks.
A potential downside of this approach is that the launch powers of the classical data traffic must be tailored to avoid deleterious Raman scattering into the quantum channel around 1550 nm14 thereby circumventing increases in the Quantum Bit Error Rate (QBER) due to this effect. However, as we show now, relatively high-classical data traffic optical receiver powers can be achieved with minimal degradation of the QKD link. Figure 4(b) shows the error rate before forward error correction (pre-FEC error rate) as a function of the measured receiver power of a 100G line card. Note a C-band EDFA is placed before the 100G optical receiver, see Methods. Also shown is the measured and simulated QBER of the QKD link over the same fibre. As the optical receiver power increases, the QBER increases marginally from 2.4% to 2.7% at the highest receiver power of +4.7 dBm; thus the QKD link is barely affected. At these receiver powers, the 100G pre-FEC error rate saturates at ∼10−6. We choose to operate the 100G encryptors using an optical receiver power of ~ −12dBm, corresponding to a pre-FEC error rate ∼2 × 10−4, Fig. 4(c). This corresponds to a 5 dB margin in the optical receiver power below the upper limit on the 100G pre-FEC error rate for error free operation (after error correction). Such a margin was used to account for equipment temperature effects and aging.46 Note optical communication systems should operate with a post-FEC error rate of at least 10−12 but preferably 10−15.47 With our 100G optical transport system, a post-FEC error rate of 10−15 is guaranteed with BERs below 1.9 × 10−2 (dotted line in Fig. 4b).
We also checked the full network support in a configuration where 200 Gbps data traffic was sent around the full ring of the Cambridge metro network. In this case both pairs of 100G line card encryptors were placed at CAPE. The forward directed traffic was directed CAPE-TREL-ENGI-CAPE over all three quantum links. No performance degradation in the quantum layer was observed over a 1 week operation period.
Discussion
The Cambridge quantum network is a fully functional quantum network operating over lit fibre with Mbps quantum key generation rates. These high key rates are compatible with metropolitan architecture with tens of nodes. For OTP encryption users can access much higher bandwidths than previously reported—around three orders of magnitude improvement, Fig. 1(b). For AES encryption users can expect 100 Gbps data bandwidths with ~1 Hz AES quantum key refresh rates— operating in the same fibre as QKD. The quantum key rates reported here are sufficient to support thousands of users, which is sufficient for most major cities. For example, in the overall three layer network model,29 we might expect each node in the Cambridge quantum network to support a number of quantum access networks (QAN)48,49 serving the area in the city surrounding the node, Fig. 1(d). QANs have been proven to work with aggregate bandwidths up to hundreds of kbps50 and, therefore, several of these at each metro node would be highly suitable for this metropolitan network. Consider a situation where each QAN user communicates with just one other QAN user via the Cambridge quantum network. The bandwidth per user on average then scales (see Methods) as
where n is the total number of users per node. For a practical bandwidth (or bit rate) per user (which can support AES key exchange) of >100 bps, it can be seen from Fig. 1(e) that the Cambridge quantum metro network, which displays QKD link speeds of 2.5 Mbps can support around 100,000 users, which is comparable to the population of Cambridge. Figure 1(e) shows that larger populations in bigger cities, such as London, can also be supported, albeit with lower data bandwidths. Hence our results show that our quantum network design can work in the vast majority of metropolitan environments.
Methods
Quantum layer
Each QKD system consists of a 2U rack mountable unit. To maximise the secure bit rate they run an efficient version42 of the BB84 protocol with two decoy states.41 The intensities of the signal states was 0.4 photons per pulse, 0.1 photons per pulse for the strong decoy states and ~10−4 photons per pulse for the weak decoy states. These values were selected based on a simulation of the QKD protocol, which would yield the highest secure bit rate. Error correction is performed using a multithreaded version of the Cascade protocol.51 Finite key size effects are minimised by using large sifted block sizes of 100 Mbit. The choice of a 100 Mbits for the sifted block size is given by examining the trade-off between efficiency and speed of the privacy amplification algorithm. In all, 100 Mbits gives a secure bit rate, which is >85% the asymptotic bit rate (in particular see Fig. 2 in Lucamarini et al.42), so reasonably efficient. At the same time the speed of the algorithm for this block size is fast enough that it does not provide a bottleneck to the QKD throughput. Privacy amplification is implemented with a number theoretic transform38 method in software using the C programming language. The number theoretic transform used52 is attractive since it gives an exact result with no round off error. The security parameter for privacy amplification was chosen to be 10−10. This is a typical value used in QKD42 and represents a very conservative key failure probability of 1 key every 30,000 years (for a secure bit rate of 1 Mbps and a block size of 100 Mbits). Note this point-to-point security parameter should be reduced by N(N–1)/2 depending on the number of logical links in the network. For example if N = 100, the security parameter should be reduced for the point-to-point links from 10−10 to of the order of 10−14. This ensures a 10−10 security parameter for the entire network. Reducing the security parameter in this way decreases the secure bit rate of the point-to-point QKD links by around a few percent. Thus, it has a close to negligible effect on network performance. Phase encoding is achieved by utilising polarisation maintaining fibre-based asymmetric Mach–Zehnder interferometers. Active feedback to maintain system alignment is implemented with separate proportional/integral/derivative (PID) control systems for phase, polarisation and temporal synchronisation. Single photon avalanche photodiodes (APDs) operating in self-differencing mode are used in the QKD receiver for quantum channel signal recovery. Room temperature operation enables high detection efficiencies of around 30%, as well as low afterpulsing (~3%).45
QKD classical channels are wavelength multiplexed onto the same fibre as the quantum channel and comprise synchronisation and reconciliation channels. The total launch powers of these channels are around −12 dBm. Note the reconciliation channels include a standard bi-directional 1G Ethernet link that ran continuously for the 1.6-year field trial. The launch power dependent spontaneous Raman scattering powers can be obtained from Eqs. (2), (3) in Eraerds et al.14 and then can be converted into detector noise counts.
We simulated the effect on the QBER on varying the launch power of the 100G traffic by using Eq. (4) in Patel et al.15 This considers contributions from single photon detector dark counts, afterpulsing, as well as noise counts from spontaneous Raman scattering.
Network key delivery Layer
The key delivery module, located at each node, comprises four distinct sub-modules: quantum key collection and buffering, OTP key relay, global key management and application interface (API). We use an efficient software implementation of the key delivery module to cope with the high-quantum key rates. The QKD systems push quantum keys when they are generated to the key delivery modules using a secured link. These keys are buffered locally in the key delivery module. Global keys are generated locally using a random number generator and are routed to peer nodes via OTP encryption of quantum keys using IP address-based tunnels and buffered using the global key management sub-module. For key relaying via intermediate nodes, the intermediate node determines the following node by routing table lookup.40 The global key management sub-module also keeps track of the number of global keys stored and calls upon the OTP key relay sub-module to top-up the global keys as and when required. Users connect to the key delivery module to request global keys for their applications in a client-server manner using a REST-style API. This encompasses a Hyper Text Transfer Protocol Secure (HTTPS) protocol and JavaScript Object Notation (JSON) data format, which is simple, lightweight, and widely used. Users are authenticated by a certificate-based authentication scheme. The HTTPS and JSON protocols are only used inside the trusted node between the key management and application devices (e.g., the 100G encryption system) in the Cambridge quantum network. None of these protocols are used outside trusted nodes.
Application layer
Two ADVA FSP3000 network communication chassis each containing two CFP 100G encryption line cards were installed at CAPE and TREL sites. The two CFP line cards employ dual polarisation quadrature phase shift keying with coherent reception and soft decision FEC for data transmission and were configured to emit at the DWDM wavelengths of 1530.33 nm and 1531.90 nm. The forward directed traffic from these cards was multiplexed together using a 48 channel DWDM multiplexer with nominal loss of 5 dB before being sent over the same fibre as the QKD link. The backward directed traffic was sent over a second fibre. For quantum encryption, we modified the line card firmware to accept external keys from the network control unit (NCU) of each FSP3000 (in place of AES keys exchanged by public key cryptography). The NCU of each FSP3000 was configured to connect with the global key delivery module and request keys via the global key delivery module API.
Bandwidth per logical link derivations
Here, we empirically derive Eq. (1), (2).
For Eq. (1), consider a ring network of N = 3 nodes. To connect each node logically, i.e., with a single link connecting each node to each other, the total number of logical links matches the number of physical links, i.e.: 3. For a fully meshed ring network of N = 4 the total number of logical links is 6, whereas the number of physical links is 4. Now consider a ring network of N = 5 nodes, as in Fig. 1(a). The network is fully meshed so the number of logical links is 10 whereas the number of physical links is 5. Therefore, for an arbitrary number of nodes, in a fully meshed network the number of logical links scales with the number of nodes as: \(N\left( {N - 1} \right)/2\).
Now for simplicity, we assume each of the physical links in the network has the same QKD link secure bit rate, R. For three nodes N = 3, labelled A, B and C, the two nodes A and B can distil keys in two ways: (1) directly from A to B, with rate R; (2) through the third node C, again with rate R. Therefore, logical link AB can distil a key at an effective rate of 2R by concatenating the rates AB and ACB while at the same time the other logical links AC and BC have zero secure bit rates (since they act as key relays). So to find the minimum average secure bit rate per logical link we then divide this rate by the number of logical links 3, arriving at \(B \ge 2R/3\).
For four nodes N = 4, labelled A, B, C and D, the two nodes A and B can again distil keys in two ways (1) directly from A to B, with rate R; (2) through the third and fourth nodes C and D, again with rate R. Therefore, logical link AB can distil a key at an effective rate of 2R by concatenating the rates AB and ADCB while at the same time the other logical links AD, DC and CB have zero secure bit rates. To find the minimum average secure bit rate per logical link we then divide this rate by the number of logical links 6, arriving at \(B \ge \frac{{2R}}{6} = R/3\).
The argument above is provable for any number of nodes N thus arriving at the formula in Eq. (1), namely: \(B \ge 4R/\left[ {N\left( {N - 1} \right)} \right]\).
For Eq. (2), we consider only the case of three nodes connected in a triangle as for the Cambridge quantum network, Fig. 1(d). For simplicity we assume each of the three links in the network has the same QKD link secure bit rate, R. We also assume the same number of users n are connected to each of the three nodes. Therefore, there are a total of 3n users in the network. Consider the case where there are just n = 4 users per node. If each user communicates to exactly one other user via the Cambridge quantum network, then on average two users will communicate across one QKD link with secure bit rate R. Then the bandwidth (or bit rate) per user link scales as \(B\sim R/2\) since ½ the total QKD link secure bit rate will be shared between two users. Now consider the case where there are n = 6 users per node. Again if each user communicates with exactly one other user via the Cambridge quantum network, then on average three users will communicate across one QKD link with secure bit rate R. Then the bandwidth (or bit rate) per user link scales as \(B\sim R/3\) since 1/3 of the total QKD link secure bit rate will be shared between three users. It will be seen the general rule for n users (per node) is that the bandwidth (or bit rate) per user link scales as \(B\sim 2R/n\).
Trusted node architecture
Trusted node architectures in QKD are well established approaches to building large scale networks and extending the reach of QKD. For example in China, the QKD link between Bejing and Shanghai is based on a trusted node architecture.53 Almost all QKD networks up to the current day have been based on trusted node;6,8,9 however, the opportunities to build secure QKD networks based on untrusted relays appears to be opening up with ground to satellite QKD links54 as well as practical MDI-QKD34 and the recent inception of twin-field QKD,55 a more efficient form of MDI-QKD, which has also been experimentally demonstrated.56,57,58 We acknowledge that while no node can be perfectly secure, in terms of “real-life security” many network nodes in commercial environments are extremely well secured typically requiring high-level authorisation to access. Furthermore, network equipment is placed inside network nodes in lockable rack cabinets.
Data availability
Additional data related to this publication is available at https://doi.org/10.17863/CAM.44524. Further data that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
References
Symantec. Internet Security Threat Report (Symantec, 2018).
Ziegeldorf, J. H., Morchon, O. G. & Wehrle, K. Privacy in the internet of things: threats and challenges. Security Commun. Networks 7, 2728–2742 (2014).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. Int. Conf. Computers, Syst. Signal Process. 1, 175–179 (1984).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Elliott, C., Colvin, A., Pearson, D., Pikalo, J. S. & Yeh, H. Current status of the DARPA quantum network. quantum information and computation III. Proc. SPIE 5815, 138–149 (2005).
Peev, M. et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 11, 75001 (2009).
Mirza, A. & Petruccione, F. Realizing long-term quantum cryptography. J. Opt. Soc. Am. B 27, A185 (2010).
Sasaki, M. et al. Field test of quantum key distribution in the Tokyo QKD network. Opt. Express 19, 10387–10409 (2011).
Stucki, D. et al. Long-term performance of the SwissQuantum quantum key distribution network in a field environment. New J. Phys. 13, 123001 (2011).
Shields, A. J. & Yuan, Z. L. Key to the quantum industry. Phys. World 20, 24–29 (2007).
Townsend, P. D. Simultaneous quantum cryptographic key distribution and conventional data transmission over installe. Electron. Lett. Electron. Lett. 33, 188–190 (1997).
Chapuran, T. E. et al. Optical networking for quantum key distribution and quantum communications. New J. Phys. 11, 105001 (2009).
Choi, I. P., Young, R. J. & Townsend, P. D. Quantum Key distribution on a 10Gb/s WDM-PON. Opt. Express 18, 9600–9612 (2010).
Eraerds, P., Walenta, N., Legré, M., Gisin, N. & Zbinden, H. Quantum key distribution and 1 Gbps data encryption over a single fibre. New J. Phys. 12, 63027 (2010).
Patel, K. A. et al. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2, 041010 (2012).
Kumar, R., Qin, H. & Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 17, 43027 (2015).
Huang, D. et al. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 23, 17511–17519 (2015).
Patel, K. A. et al. Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks. Appl. Phys. Lett. 104, 51123 (2014).
Wang, L.-J. et al. Long-distance copropagation of quantum key distribution and terabit classical optical data channels. Phys. Rev. A 95, 413 (2017).
Mao, Y. et al. Integrating quantum key distribution with classical communications in backbone fiber network. Opt. Express 26, 6010 (2018).
Choi, I. et al. Field trial of a quantum secured 10 Gb/s DWDM transmission system over a single installed fiber. Opt. Express 22, 23121–23128 (2014).
Ciurana, A. et al. Quantum metropolitan optical network based on wavelength division multiplexing. Opt. Express 22, 1576–1593 (2014).
Wang, L.-J. et al. Experimental multiplexing of quantum key distribution with classical optical communication. Appl. Phys. Lett. 106, 81108 (2015).
Chen, T.-Y. et al. Field test of a practical secure communication network with decoy-state quantum cryptography. Opt. Express 17, 6540 (2009).
Chen, W. et al. Field experiment on a “Star Type” metropolitan quantum key distribution network. IEEE Photon. Technol. Lett. 21, 575–577 (2009).
Wang, S. et al. Field test of the wavelength-saving quantum key distribution network. Opt. Lett. 35, 2454 (2010).
Chen, T.-Y. et al. Metropolitan all-pass and inter-city quantum communication network. Opt. Express 18, 27217–27225 (2010).
Wang, S. et al. Field and long-term demonstration of a wide area quantum key distribution network. Opt. Express 22, 21739–21756 (2014).
Ashwin, G. & Tony, A. Dwdm Network Designs and Engineering Solutions (Cisco Press, 2002).
Bianco, A., Bonald, T., Cuda, D. & Indre, R.-M. Cost, power consumption and performance evaluation of metro networks. J. Opt. Commun. Netw. 5, 81 (2013).
Roberts, G. L. et al. Experimental measurement-device-independent quantum digital signatures. Nat. Commun. 8, 1098 (2017).
Tang, Y.-L. et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 6, 83 (2016).
Comandar, L. C. et al. Quantum key distribution without detector vulnerabilities using optically seeded lasers. Nat. Photon 10, 312–315 (2016).
Liu, H. et al. Experimental demonstration of high-rate measurement-device-independent quantum key distribution over asymmetric channels. Phys. Rev. Lett. 122, 160501 (2019).
Eriksson, T. A. et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2, 167 (2019).
Fröhlich, B. et al. Long-distance quantum key distribution secure against coherent attacks. Optica 4, 163 (2017).
Dynes, J. F. et al. Ultra-high bandwidth quantum secured data transmission. Sci. Rep. 6, 35149 (2016).
Yuan, Z. et al. 10-Mb/s quantum key distribution. J. Lightwave Technol. 36, 3427–3433 (2018).
Tanizawa, Y., Takahashi, R. & Dixon, A. R. An approach to integrate quantum key distribution technology into standard secure communication applications. The Ninth International Conference on Ubiquitous and Future Networks. (July 4 (Tue.)–July 7 (Fri.), 2017, Milan, Italy, 2017).
Tanizawa, Y., Takahashi, R. & Dixon, A. R. A routing method designed for a quantum key distribution network. The Eighth International Conference on Ubiquitous and Future Networks. (July 5 (Tue.)–July 8 (Fri.), Technische Universität (TU) Wien, Vienna, Austria, 2016).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Lucamarini, M. et al. Efficient decoy-state quantum key distribution with quantified security. Opt. Express 21, 24550 (2013).
International Telecommunication Union (ITU-T). Spectral grids for WDM applications: DWDM frequency grid: Recommendation: G.694.1. (International Telecommunication Union (ITU-T), 2012).
Dixon, A. R. et al. High speed prototype quantum key distribution system and long term field trial. Opt. Express 23, 7583–7592 (2015).
Comandar, L. C. et al. Room temperature single-photon detectors for high bit rate quantum key distribution. Appl. Phys. Lett. 104, 21101 (2014).
Cvijetic, M. & Djordjevic, I. Advanced Optical Communication Systems and Networks (Artech House, 2013).
Tzimpragos, G. et al. A survey on FEC codes for 100 G and beyond optical networks. IEEE Commun. Surv. Tutor. 18, 209–221 (2016).
Townsend, P. D. Quantum cryptography on multiuser optical fibre networks. Nature 385, 47–49 (1997).
Fröhlich, B. et al. A quantum access network. Nature 501, 69–72 (2013).
Fröhlich, B. et al. Quantum secured gigabit optical access networks. Sci. Rep. 5, 18121 (2015).
Brassard, G. & Salvail, L. In Advances in Cryptology—EUROCRYPT ’93 (ed. Helleseth, T.) 410–423 (Springer Berlin Heidelberg, Berlin, Heidelberg, 1994)
Agarwal, R. C. & Burrus, C. S. Number theoretic transforms to implement fast digital convolution. Proc. IEEE 63, 550–560 (1975).
Zhang, Q., Xu, F., Chen, Y.-A., Peng, C.-Z. & Pan, J.-W. Large scale quantum key distribution: challenges and solutions Invited. Opt. express 26, 24260–24273 (2018).
Yin, J. et al. Satellite-to-ground entanglement-based quantum key distribution. Phys. Rev. Lett. 119, 200501 (2017).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 13, 334–338 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 123, 100505 (2019).
Acknowledgements
This work has been partially funded by the UK EPSRC Quantum Technology Hub for Quantum Communications Technologies project EP/M013472/1. A.W., R.V.P. and I.H.W. acknowledge support from the UK EPSRC Quantum Technology Hub for Quantum Communications Technologies project EP/M013472/1.
Author information
Authors and Affiliations
Contributions
J.F.D., W.W.-S.T., A.W.S., M.L. & A.P. designed and implemented the quantum layer. R.T., Y.T., A.D. & J.F.D designed and implemented the network key delivery layer. J.F.D., A.W., & J.C. designed and implemented the application layer. All layers were installed, tested and debugged in the field by J.F.D., A.W. & A.W.S. Z.L.Y., J-P.E., H.G., I.H.W., R.V.P. & A.J.S. guided the work. J.F.D. analysed the experimental results and wrote the manuscript with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dynes, J.F., Wonfor, A., Tam, W.W.S. et al. Cambridge quantum network. npj Quantum Inf 5, 101 (2019). https://doi.org/10.1038/s41534-019-0221-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0221-4
This article is cited by
-
Verifying the security of a continuous variable quantum communication protocol via quantum metrology
npj Quantum Information (2024)
-
Improved security bounds against the Trojan-horse attack in decoy-state quantum key distribution
Quantum Information Processing (2024)
-
Twin-field quantum key distribution without optical frequency dissemination
Nature Communications (2023)
-
Recent progress in quantum photonic chips for quantum communication and internet
Light: Science & Applications (2023)
-
Advances in device-independent quantum key distribution
npj Quantum Information (2023)