Introduction

Envisioned quantum networks1 consist of distributed matter-based quantum nodes, for the storage, manipulation and application of quantum information, which are interconnected with photonic links to establish entanglement between the nodes. While the most ambitious form of a quantum network is a collection of remote quantum computers, far simpler networks with a handful of qubits at each node could already enable powerful applications in quantum enhanced distributed sensing, timekeeping, cryptography and multiparty protocols.2

Entanglement has been achieved between two atoms in traps a few 10 m apart,3 between two ions in traps a few metres apart4 and recently between two nitrogen-vacancy centres 1.3 km apart.5

In these experiments, photon-matter entanglement is first generated, then detection of one or two photons heralds remote matter-matter entanglement (entanglement is ‘swapped’ from matter-light to matter-matter). A current goal is to significantly scale up the distance over which quantum matter can be entangled to a 100 km or more, which are practical internode spacings to enable large-scale quantum networks.

Some key challenges to entangling matter over such distances are now described. First, the aforementioned matter systems emit photons at wavelengths that are strongly absorbed in optical waveguides (such as optical fibre), limiting the internode distance to a few kilometres. For example, in the present work 854 nm photons are collected from a trapped atomic ion. While the ~3 dB per km losses suffered by 854 nm photons through state-of-the-art optical fibre allows for few kilometre internode distances, transmission over 50 km of fibre would be 10−15. Single-photon quantum frequency conversion to the telecom C band (1550 nm) would offer a powerful solution: this wavelength suffers the minimum fibre transmission losses (~0.18 dB per km, yielding 10% transmission over 50 km) and is therefore an ideal choice for a standard interfacing wavelength for quantum networking. Photons from solid-state memories,6 cold gas memories,7,8 quantum dots and nitrogen-vacancy centres9 have been converted to telecom wavelengths. Frequency conversion of photons from ions has very recently been performed, including to the telecom C band (without entanglement),10 to the telecom O band with entanglement over 80 m11 and directly to an atomic Rubidium line at 780 nm.12 The use of photon conversion to extend the distance over which light-matter and matter-matter entanglement can be distributed has not previously been achieved.

A second challenge to long distance matter entanglement is to preserve entanglement when such long photonic channels are involved. Uncontrolled decoherence processes that act on the photon as it travels along its path, and those that act on the quantum matter during the photon travel time, can easily destroy entanglement. For example, the entanglement-carrying photon signal, which attenuates exponentially with distance in any lossy waveguide, can be overwhelmed by added photon noise from the photon frequency conversion process or dark counts of the photon detectors. The inter-node photon travel time also imposes a minimum coherence time for matter, which for e.g. 50 km of optical fibre is already significant at 250 μs (and 500 μs to allow for the classical signal of a successful herald to return). Moreover, quantum networking applications require distributed entanglement of a quality above certain thresholds, for which the required matter coherence times and photon signal to noise ratio are far more challenging.

A third challenge comes again from the photon travel time. The shortest time required to entangle remote matter (or indeed light) in two places is the light travel time between them. The 500 μs wait time over 50 km of optical fibre yields a maximum attempt rate of only 2 kHz: one must wait 500 μs to learn if an individual attempt to distribute remote entanglement has been successful. To achieve practical entanglement distribution rates in the face of such a restriction, one can work on achieving a high probability for individual attempts to succeed and (or) to run many attempts in parallel (as discussed later).

In this work, entanglement between a trapped-ion qubit and a photon that has travelled over 50 km of optical fibre is achieved. The quality of the entanglement is sufficiently high to allow for a clear violation of a Bell inequality—as required for some of the most challenging device-independent quantum network applications.13 Furthermore, when modestly optimised, the achieved rate is expected to allow for entanglement distribution between 100 km-spaced trapped ions at rates over 1 Hz. The paper is organised as follows. First, there is a short motivation for quantum networking trapped ions. Second, a brief overview of the experimental methods is given, with much detail left for the Supplementary Material. Third, the tomographically reconstructed entangled state, of the ion qubit and photon polarisation qubit after 50 km, is presented and the achieved fidelity, efficiency and rate are analysed. Fourth, the ion qubit is shown to provide a quantum information storage time (coherence time) of more than 20 ms, allowing for future entanglement distribution over thousands of kilometers. Finally, the prospects for 100 km ion–ion entanglement are presented as well as a path to significantly increase the rate via multi-mode and hybrid quantum networking.

Trapped ions are particularly powerful systems to enable quantum networking and the envisioned applications. For example, a complete set of tools for deterministic universal manipulation of quantum information encoded into registers of trapped ions is readily available and of a quality near fault tolerant thresholds,14,15,16 as required for arbitrary distance quantum networking via the quantum repeater approach.17,18 Key quantum networking functionalities have been demonstrated between ions over a few meters, including remote state teleportation19 and multi-ion protocols.20 Trapped ions are also some of the most sensitive measurement probes yet developed. For example, many ion species, including the one used in this work, contain optical atomic clock transitions and therefore entangling them over distance enables the ideas presented in21,22 to be explored.

Results

Our network node consists of a 40Ca+ ion in a radio-frequency linear Paul trap with an optical cavity that enhances photon collection on the 854 nm electronic dipole transition (Fig. 1). A Raman laser pulse at 393 nm triggers emission, by the ion, of a photon into the cavity via a bichromatic cavity-mediated Raman transition (CMRT).23 Two indistinguishable processes are driven in the CMRT, each leading to the generation of a cavity photon and resulting in entanglement between photon polarisation and the electronic qubit state of the ion of the form \(1/\sqrt 2 (D_{J = 5/2,m_j = - 5/2},V + D_{J = 5/2,m_j = - 3/2},H)\), with horizontal (H) and vertical (V) photon polarisation and two metastable Zeeman states of the ion \((D_{J, m_j})\), see Supplementary Fig. 3. The total measured probability of obtaining an on-demand free-space photon out of the ion vacuum chamber (entangled with the ion) is Pout = 0.5 ± 0.1 (Secction II, Supplementary material of this paper), enabled by the novel low-loss cavity in our setup.

Fig. 1
figure 1

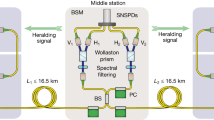
Simplified experiment schematic. From left to right: a single atomic ion (red sphere) in the centre of a radio-frequency linear Paul trap (gold electrodes) and a vacuum anti-node of an optical cavity. A Raman laser pulse triggers emission of an 854 nm photon into the cavity, which exits to the right. The photon, polarisation-entangled with two electronic qubit states of the ion (two Zeeman states of the DJ = 5/2 manifold, not shown), is then wavelength-converted to 1550 nm using difference frequency generation involving ridge-waveguide-integrated periodically-poled lithium niobate (PPLN) chips and a strong (~1 W) pump laser at 1902 nm.26 The photon then passes through a 50 km single-mode fibre spool, is filtered with a 250 MHz bandwidth etalon (SF) to reduce noise from the conversion stage,26 and is polarisation-analysed using waveplates, a polarising beam splitter (PBS) and a solid-state single photon counting module (SPCM, InGaAs ID230 from IDQuantique). The electronic state of the ion is measured (not shown), conditional on the detection of a photon. Additional photon conversion filters are not shown.26 For further details see, Supplementary material of this paper section I

Full size image

The CMRT yields an entangled state with a frequency-degenerate photon qubit (the two polarisation components have the same frequency to within the cavity linewidth23), providing a significant benefit for long distance networking: the phase of the light-matter entangled state does not depend on the time at which the photon detection event occurs at a given distance from the ion. Photon detection time fluctuates due to the intrinsic finite temporal extent of the photon wavepacket and in the case of optical path length changes, which could be significant over tens of kilometres of deployed optical fibre. Our photons are generated over several tens of microseconds, with a corresponding bandwidth of tens of kilohertz. This unusually narrow bandwidth allows for strong frequency filtering, which we exploit in the photon conversion process and could have further benefits in future deployed networks, e.g to enable co-propagating classical and quantum light. Furthermore, the corresponding photon coherence-length is potentially thousands of metres, allowing for essentially path-length-insensitive entanglement swapping between remote ions via Hong-Ou-Mandel interference.4,24,25

Single-mode fibre-coupled photons from the ion are injected into a polarisation-preserving photon conversion system (previously characterised using classical light26). In summary, a χ(2) optical nonlinearity is used to realise difference frequency generation, whereby the energy of the 854 nm photon is reduced by that of a pump-laser photon at 1902 nm, yielding 1550 nm. Two commercially available free-space and crossed PPLN ridge waveguide crystals are used, one to convert each polarisation, in a self-stable polarisation interferometer. The total fibre-coupled device conversion efficiency here is 25 ± 0.02%, for an added white noise of 40 photons per second, within the filtering bandwidth of 250 MHz centred at 1550 nm. As discussed in,26 the 854 nm line in 40Ca+ is almost unique amongst trapped-ion transitions in its potential for low-noise, highly-efficient single-step frequency conversion to the telecom C band.

Following conversion, the telecom photon is injected into a 50.47 km ‘SMF28’ single-mode fibre spool with 0.181 dB per km loss (10.4 ± 0.5% measured total transmission probability). The spool is not actively stabilised. Polarisation dynamics in an unspooled fibre could be actively controlled using methods developed in the field of quantum cryptography (e.g.,27). Finally, free-space projective polarisation analysis is performed and the photon is detected using a telecom solid-state photon detector with an efficiency of 0.10 ± 0.01 and free-running dark count rate of 2 counts per second (cps). Measurement of the ion-qubit state is performed conditional on the detection of a 50 km photon within a 30 μs time window: the Zeeman ion qubit is mapped into the established 40Ca+ optical quadrupole clock qubit28 via laser pulses at 729 nm, followed by standard fluorescence state detection (see Methods).

Quantum state tomography is performed to reconstruct the two-qubit (ion qubit and photon polarisation qubit) state, Supplementary material of this paper section III. The 247 μs photon travel time through the fibre limits the maximum attempt rate for generating a photon from the ion to 4 kHz (2 kHz if the fibre was stretched out away from our ion to force an additional delay for the classical signal ‘photon click’ to return). Here, until photon detection occurs, photon generation is (Raman laser pulses are) performed every 453 μs, yielding an attempt rate of 2.2 kHz. For the complete experimental sequence see Methods. All error bars on quantities derived from the tomographically-reconstructed states (density matrices) are based on simulated uncertainties due to finite measurement statistics (see Supplementary Material section III).

A strongly entangled ion–photon state is observed (Fig. 2) over 50 km, quantified by a concurrence29 C = 0.75 ± 0.05 and state fidelity Fm = 0.86 ± 0.03 with a maximally entangled state (C = 1). Simulating a CHSH Bell inequality test30 on our tomographic data yields a value of 2.304 ± 0.125, thereby exceeding the classical bound (of 2) by 2.4 standard deviations. Using a shorter detection window (first 2/3 of the full photon wavepacket) increases the signal to noise ratio and yields Fm = 0.90 ± 0.03 and CHSH Bell inequality violation by 4.8 standard deviations at the expense of an efficiency decrease of only 10%. The quality of our light-matter entangled state therefore surpasses this stringent threshold for its subsequent application.

Fig. 2
figure 2

Observation of ion-photon entanglement over 50 km of optical fibre. (i) 2D red bar chart: histogram of photon detection times (photon wavepacket in dashed box), following the generation of an 854 nm photon with a 30 μs Raman laser pulse (R) ≈ 250 μs earlier, repeated at 2.2 kHz. Ion–photon state tomography is performed for photon detection events recorded in the dashed box (total contained probability P = 5.3 × 10−4). (ii) 3D bar chart: absolute value of experimentally-reconstructed density matrix of the telecom photonic polarisation qubit (H and V are Horizontal and Vertical, respectively) and ion-qubit state (\(0 = D_{J = 5/2,m_j = - 3/2}\), \(1 = D_{J = 5/2,m_j = - 5/2}\))

Full size image

For a detailed analysis of the sources of infidelity in the entangled state see, Supplementary material of this paper section IV; here now is a short summary. In a second experiment, the telecom entangled state is reconstructed right after the conversion stage (without the 50 km spool), yielding Fm = 0.92 ± 0.02. The drop in fidelity when adding the 50 km spool can, to within statistical uncertainty, be entirely explained by our telecom photon detector dark counts (2 cps). In a third experiment, the 854 nm entangled state is reconstructed right out of the vacuum chamber (without conversion), yielding Fm = 0.967 ± 0.006. The observed drop in fidelity through the conversion stage alone is dominated by a drop in photon signal to noise signal. Here the noise consists of comparable rates of telecom detector dark counts and conversion noise (caused by Anti-Stokes Raman scattering of the pump laser26) and the signal is reduced by the finite conversion setup efficiency and the lower telecom detector’s efficiency compared to the 854 nm one. The infidelity in the 854 nm photon-ion entangled state is consistent with that achieved in.23

The total probability that a Raman pulse led to the detection of a photon after 50 km was P = 5.3 × 10−4, which given an attempt rate of 2.2 kHz yielded a click rate of ≈1 cps. Photon loss mechanisms in our experiment are discussed in, Supplementary material of this paper section II. In summary, the 50 km fibre transmission (0.1) and our current telecom detector efficiency (0.1) limit the maximum click probability to P = 0.01. The majority of other losses are in passive optical elements, and could largely be eliminated by e.g. more careful attention to coupling into optical fibres and photon conversion waveguides. In combination with state-of-the-art telecom detectors (e.g. Scontel recently supplied us superconducting nanowire detectors providing 0.8 cps dark count rate and 77% efficiency according to the company’s calibration), a total 50 km efficiency of P ≈ 0.01 would be expected and a corresponding click rate of ≈20 cps.

One of the functions played by matter in a quantum network is as a memory to store established entanglement, while entanglement is being made or processed in other parts of the network. Decoherence processes in the matter qubit will limit the distance over which it is possible to distribute quantum entanglement (the distance a photon could possibly travel in the ‘coherence time’ of the matter qubit). In our 50 km experiment, the ion qubit is already stored for the 250 μs photon travel time through the 50 km fibre, with no statistically significant reduction in the ion–photon entanglement quality (this was achieved by installing a mu-metal shield around the ion-trap vacuum chamber to attenuate ambient magnetic field fluctuations).

Additional tomographic measurements are performed to see for how long ion–photon entanglement could be stored in our ion-trap network node before decoherence in the ion-qubit would destroy it. Specifically, state tomography is performed for increasing delays introduced between measurements of the telecom photon polarisation state (0 km fibre travel distance) and measurements of the state of the ion-qubit. This is equivalent to introducing an additional storage time for the ion-qubit. The results show that strong entanglement is still present after 20 ms wait time (Fm = 0.77 ± 0.04, C = 0.57 ± 0.08), the longest wait time employed. This already opens up the possibility of distributing entanglement over several thousands of kilometers and the time to perform hundreds of single and multi-qubit ion quantum logic gates.31

A dominant source of decoherence of our ion-qubit are uncontrolled fluctuating energy-level shifts due to intensity fluctuations of the 806 nm laser field used to lock the cavity around the ion. Further attention to minimising the absolute size of these fluctuations should lead to entanglement storage times of more than ≈100 ms and therefore the possibility to distribute entanglement to the other side of the earth. Beyond this, the ion-qubit could be transferred to hyperfine clock transitions within different co-trapped ion species that offer coherence times of many seconds and longer.32

Discussion

The rates for future 100 km-spaced photon-detection heralded ion–ion entanglement using our methods are now discussed (see Fig. 3). A modestly optimised version of our experimental system in this work is now considered (see dashed box in Fig. 3), that achieves an on-demand detected 50 km photon click probability of P = 0.01 and operates at an attempt rate of R = 2 kHz (the two-way light travel time). By duplicating our optimised system (Fig. 3), and following a two-photon click heralding scheme,24 the probability of heralding a 100 km-spaced ion–ion entangled state would be \(H_2 = \frac{1}{2}P^2 = 5 \times 10^{ - 5}\), at an average click rate of H2 × R = 0.1 cps (comparable with the first rates achieved over a few meters33 of 0.03 cps. Following instead a one-photon click heralding scheme,24 the probability of heralding a 100 km-spaced ion–ion entangled state would be H1 = 2P × 0.1 = 0.002, at an average click rate of H1 × R = 4 cps, where 0.1 is the reduced photon generation probability at each node (as required for this scheme). The factor 40 improvement (H1/H2) of the one-photon scheme over the two-photon scheme comes at the expense of the need to interferometrically stabilise the optical path length across the 100 km network.

Fig. 3
figure 3

Path to 100 km matter-matter entanglement. This work: quantum frequency conversion (QFC) converts a photon, emitted on-demand from and entangled with an ion qubit (A1) in node A, to the telecom C band at 1550 nm. The photon then travels through 50 km of optical fibre before detection (D1 or D2). Future work: duplicating the system, interfering the two photonic channels on a beamsplitter (BS). Single or two photon detection heralds the projection of ions A1 and B1 into an entangled state.24 Deterministic intra-node quantum logic and measurement between e.g. B1 and B2 and A1 and A2 can swap the entanglement over larger distances (quantum repeater). Additional qubits in nodes are available for entanglement purification. Nodes could as well contain solid-state memories,35 NV centres9 or neutral atoms.7,8

Full size image

An approach to significantly increase the remote entanglement heralding rate is multi-mode quantum networking, where many photons are sent, each entangled with different matter qubits. In this way, of running many such processes in parallel, the probability of at least one successful heralding event occurring can be made arbitrarily high. In our setup, for example, multiple ions can be trapped and it may be possible to produce a train of photons, each entangled with a different ion. In this case, a higher rate of photon production can be employed, as the time between photons in the train is not limited by the light travel time. Furthermore, multi-mode networking could be realised using inhomogenously broadened ensemble based solid-state quantum memories.34 Such memories could be quantum-networked with ions via a photon conversion interface35 to form a powerful hybrid system for long distance quantum networking.

The 50 km photon in our experiments is entangled with the 729 nm optical-qubit clock transition in 40Ca+, over which a fractional frequency uncertainty of 1 × 10−15 has been achieved (comparable with the Cs standard).36 Furthermore, 40Ca+ can be co-trapped with Al+,37 which contains a clock transition for which a fractional systematic frequency uncertainty at the 1 × 10−18 level was recently achieved.38,39 Transfer of the remote 40Ca+ entanglement to a co-trapped Al+ ion could be done via quantum logic techniques.39,40 As such, our work provides a direct path to realise entangled networks of state-of-the-art atomic clocks over large distances.21 Entangling clocks provides a way to perform more sensitive measurements of their average ticking frequencies21 and to overcome current limits to their synchronisation.22

Methods

Trapped ion node

We use a 3D radio-frequency linear Paul trap with a DC endcap to ion separation of 2.5 mm and ion to blade distance of 0.8 mm. The trap electrodes are made of titanium, coated with gold and are mounted on Sapphire holders. The trap drive frequency is 23.4 MHz. The radial secular frequencies are ωx ≈ ωy = 2π × 2.0 MHz, split by approximately 10 kHz and the axial frequency is ωz = 2π × 0.927 MHz. Atoms are loaded from a resistively heated atomic oven and ionised via a two photon process involving 375 and 422 nm laser light.

The optical cavity around the ion is near-concentric with a length l = 19.9057 ± 0.0003 mm and radii of curvature ROC = 9.9841 ± 0.0007 mm, determined from simultaneous measurements of the free spectral range (FSR) and higher-order TEM mode spacing (assuming identical mirror geometries).41 From this we calculate an expected cavity waist of ω0 = 12.31 ± 0.07 μm and a maximum ion-cavity coupling rate of gmax = 2π × 1.53 ± 0.01 MHz. The finesse of the cavity (at 854 nm) is \({\cal{F}} = \frac{{2\pi }}{{\cal{L}}} = 54000 \pm 1000\), with the total cavity losses \({\cal{L}} = T_1 + T_2 + L_{1 + 2} = 116 \pm 2\) ppm, determined from measurements of the cavity ringdown time. This gives the cavity linewidth 2κ = 2π × 140 ± 3 kHz, κ being the half-width at half maximum. Taking into account the spontaneous scattering rate of the P3/2 state of the ion (γ = 2π × 11.45 MHz, half-width) the expected cooperativity is \(C = \frac{{g_{{\mathrm{max}}}^2}}{{2\kappa \gamma }} = 1.47 \pm 0.03\).

The transmission T1,2 of our cavity mirrors was measured to be T1 = 2.2 ± 0.3 ppm, T2 = 97 ± 4 ppm, that yields expected probability of extracting a photon from the cavity of \(P_{{\mathrm{out}}}^{{\mathrm{max}}} = T_2/(T_1 + T_2 + L_{1 + 2}) = 0.83 \pm 0.03\) (polishing of the mirror substrates done by Perkins Precision Development, Boulder (Colorado), coating done by Advanced Thin Films).

The optical cavity axis is close to perpendicular to the principle ion trap axis (~5° difference). A magnetic field of 4.22 G is applied perpendicular to the cavity axis and at an angle of 45° to the principal ion trap axis (Supplementary Fig. 1). The Raman photon generation beam is circularly polarised and parallel to the magnetic field (to maximise the coupling on the relevant dipole transition \(S_{J = 1/2,m_j = - 1/2} \leftrightarrow P_{J = 3/2,m_j = - 3/2}\), see Supplementary Fig. 3).

Pulse sequence for 50 km experiment

First, a 30 μs ‘initialisation’ laser pulse at 393 nm is applied, measured by a photodiode in transmission of the ion-trap chamber, which allows for intensity stabilisation of the subsequent 393 nm photon generation Raman pulse via a sample and hold system. The initialisation pulse is followed by a 1500 μs Doppler cooling pulse. Next, a loop starts in which single photons are generated (see Supplementary Fig. 2). This loop consists of an additional Doppler cooling pulse (50 μs), optical pumping to the \(S = S_{J = 1/2,m_j = - 1/2}\) state via circularly polarised 397 nm ‘sigma’ laser light (60 μs), and a 393 nm photon generation Raman pulse (30 μs). This is followed by a wait time for the photon to travel through the 50 km fibre and a subsequent photon detection window. This sequence loops until a photon is detected.

In the case of a photon detection (detector ‘click’), the state of the ion is measured. To perform an ion state measurement, the \(D\prime = D_{J = 5/2,m_j = - 5/2}\) electron population is first mapped to the \(S = S_{J = 1/2,m_j = - 1/2}\) state via a 729 nm π pulse (Supplementary Figs. 2 and 3). That is, the D-manifold qubit is mapped into an optical qubit (with logical states \(S = S_{J = 1/2,m_j = - 1/2}\) and \(D = D_{J = 5/2,m_j = - 3/2}\)). In order to measure which of these states the electron is in, the standard electron shelving technique is used. We perform this measurement for a ‘detection time’ (397 nm photon collection time) of 1500 μs, which is sufficient to distinguish bright (scattering) and dark (non-scattering) ions with an error of less than 1%. The aforementioned process implements a projective measurement into the eigenstates of the σz basis (Pauli spin-1/2 operator).

To perform measurements in other bases e.g σx (σy), as required for full quantum state tomography, an additional π/2 pulse on the \(S_{m_j = - 1/2}\) to \(D_{m_j = - 3/2}\) with a 0 (π/2) phase is applied after the π pulse and before the 397 nm pulse, to rotate the ion-qubit measurement basis. The scheme of the experimental sequence is given in Supplementary Fig. 2.

State characterisation

To reconstruct the ion–photon state, a full state tomography of the two-qubit system is performed. On the photon polarisation qubit side, the state is projected to one of 6 states (horizontal, vertical, diagonal, anti-diagonal, right circular and left circular) by waveplates and a polariser. This is equivalent to performing projective measurements in three bases described by the Pauli spin-1/2 operators. For example, horizontal and vertical are the eigenstates of the Pauli σz operator. On the ion qubit side, measurement is performed in the three Pauli bases as described in the previous section. From these measurements’ outcomes probabilities we reconstruct the 2-qubit state density matrix by linear search with subsequent Maximum Likelihood method.42 The values of fidelity, concurrence and other measures presented in the Results section are calculated using reconstructed density matrices for each of the experiments. The error bars for all quantities provided in the Results section represent one standard deviation of distribution of these quantities over randomised set of data following the Monte-Carlo approach, for more details see Supplementary material of this paper section III.