Abstract
Heisenberg’s original uncertainty relation is related to measurement effect, which is different from the preparation uncertainty relation. However, it has been shown that Heisenberg’s error disturbance uncertainty relation is not valid in some cases. We experimentally test the error-tradeoff uncertainty relation by using a continuous-variable Gaussian Einstein–Podolsky–Rosen (EPR)-entangled state. Based on the quantum correlation between the two entangled optical beams, the errors on amplitude and phase quadratures of one EPR optical beam coming from joint measurement are estimated, respectively, which are used to verify the error–tradeoff relation. Especially, the error–tradeoff relation for error-free measurement of one observable is verified in our experiment. We also verify the error–tradeoff relations for nonzero errors and mixed state by introducing loss on one EPR beam. Our experimental results demonstrate that Heisenberg’s error–tradeoff relation is violated in some cases for a continuous-variable system, while the Ozawa’s and Branciard’s relations are valid.
Similar content being viewed by others
Introduction
As one of the cornerstones of quantum mechanics, uncertainty relation describes the measurement limitation on two incompatible observables.1 It should be emphasized that the uncertainty relation actually states an intrinsic property of a quantum system, rather than a statement about the observational success of current technology. Uncertainty relation has deep connection with many special characters in quantum mechanics, such as quantum metrology,2,3 Bell non-locality and entanglement,4,5,6 which cannot occur in classical world. With rapid progress in quantum technology, such as quantum communication and quantum computation,7,8 it is important for us to know the fundamental limitations in the achievable accuracy of quantum measurement.
Note that there are two different types of uncertainty relations, one is the preparation uncertainty relation, which studies the minimal dispersion of two quantum observables before measurement.9,10 The Robertson uncertainty relation,10 reads as σ(x)σ(p) ≥ ℏ/2, is a typical example in this sense, where σ(x) and σ(p) are the standard deviations of position and momentum of a particle. For such uncertainty relation, the measurements of x and p are performed on an ensemble of identically prepared quantum systems. While in the original spirit of Heisenberg’s idea,1 the Heisenberg’s uncertainty principle should be based on the observer’s effect, which means that measurement of a certain system cannot be made without affecting the system. So this leads to the second type of uncertainty relation: measurement uncertainty relation, which studies to what extent the accuracy of position measurement of a particle is related to the disturbance of the particle’s momentum, so called the error–disturbance uncertainty relation.11,12 It is also called the error–tradeoff relation in the approximate joint measurements of two incompatible observables.13,14
Heisenberg’s error–tradeoff uncertainty relation for joint measurement is generally expressed as
where CAB = |〈[A, B]〉|/2, [A, B] = AB−BA, ε(A) and ε(B) represent the errors on observables A and B in the measurement of a quantum state, respectively. This uncertainty relation interprets the physical content of the non-commutativity as the limitation to our ability of observation by quantifying the amount of unavoidable disturbance caused by measurement. However, it has been shown that this relation is not valid in some cases.15 For this reason, Ozawa and Hall proposed new measurement uncertainty relations which have been theoretically proven to be universally valid for any incompatible observables, respectively.11,13,16 After that, Branciard proposed a new uncertainty relation, which is universally valid and tighter than the Ozawa’s relation.14 There are also other types of measurement uncertainty relations generalizing Heisenberg’s original idea, which can be found in refs 17,18,19,20,21,22. Experimental tests of the measurement uncertainty relations have been demonstrated in photonic,23,24,25,26,27,28 spin-1/2,29,30,31,32 and ion trap systems.33 All of these experiments are limited in discrete-variable systems. Up to now, experimental test of the measurement uncertainty relation based on continuous-variable system has not been reported.
Here, we present the experimental test of the error–tradeoff relation for two incompatible variables, amplitude and phase quadratures of an optical mode, using a continuous-variable Gaussian Einstein–Podolsky–Rosen (EPR) entangled state. Based on quantum correlations of the EPR entangled beams, the error–tradeoff relation with zero error (error-free) of one observable is verified directly by performing joint measurement on two EPR beams. In this case, Heisenberg’s error–tradeoff relation with continuous variables is violated, while Ozawa’s and Branciard’s relations are valid. We also test the error–tradeoff relations for nonzero errors and mixed state by introducing loss on signal mode. Our experimental test of the continuous-variable error–tradeoff relations makes the test of the measurement uncertainty relation more complete.
Results
Theoretical framework
The idea that EPR entangled state violates Heisenberg’s uncertainty relation for joint measurement was first appeared in ref. 34. This idea was addressed as “Schrödinger’s clever modification of the EPR argument” and argued that this does not cause the violation of Heisenberg’s uncertainty relation for “state preparation”, but causes, according to Schrödinger, “hypermaximal” knowledge of the state of one particle.35 This scenario that was naturally interpreted as the violation of Heisenberg’s uncertainty relation for “joint measurement” has been rigorously formulated later in ref. 12
A Gaussian EPR entangled state is used in the experimental test of error–tradeoff uncertainty relations with continuous variables. The amplitude and phase quadratures of an optical mode \(\hat a\) are defined as \(\hat x = (\hat a + \hat a^\dagger )/2\) and \(\hat p = (\hat a - \hat a^\dagger )/2i\), respectively.6 The variances of amplitude and phase quadratures of two EPR modes are \(\sigma (\hat x_1)^2 = \sigma (\hat x_2)^2 = \sigma (\hat p_1)^2 = \sigma (\hat p_2)^2 = (V_{\mathrm {S}} + V_{\mathrm {A}})/2\), where \(V_{\mathrm {S}} = e^{ - 2r}/4\) and VA are the variances of squeezed and anti-squeezed quadratures of a squeezed state, respectively, and r \(\left( {0 \le r \;<\; \infty } \right)\) is the squeezing parameter [see the “Methods” section for details]. \(V_{\mathrm {A}} = e^{2r}/4\) only if the squeezed state is pure. If the squeezed state is not pure, we have \(V_{\mathrm {A}} \;>\; e^{2r}/4\). The quantum correlation between two EPR modes are \(\sigma (\hat p_2 - \hat p_1)^2 = \sigma (\hat x_2 + \hat x_1)^2 = e^{ - 2r}/2 = 2V_{\mathrm {S}}\). It is obvious that perfect quantum correlation is obtained in the case of infinite squeezing parameter \(\left( {r \to \infty } \right)\).
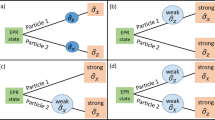
One mode of a Gaussian EPR entangled state is used as signal mode ρ and two incompatible observables are taken as \(A = \hat x_1\) and \(B = \hat p_1\), respectively (Fig. 1a). Another mode of EPR-entangled state with amplitude and phase quadratures \(\hat x_2\) and \(\hat p_2\) is used as the meter mode ρM. In the joint measurement apparatus, two compatible observables C and D, which belong to two EPR modes, respectively, are jointly measured simultaneously by two homodyne detectors to approximate observables A and B, respectively. The quality of the approximations are characterized by defining the root-mean-square (rms) errors ε(A) = 〈(C−A)2〉1/2 and ε(B) = 〈(D−B)2〉1/2. Ozawa’s error–tradeoff relation is expressed by11,12,13
where σ(A) and σ(B) are the standard deviations of observables A and B, and the parameter CAB = 1/4 denote that A and B cannot be jointly measured on ρ simultaneously in our experiment. It is obvious that this relation involves not only the errors, but also the standard deviations of each observable. This relation holds for every measurement and every input state as long as all the relevant terms are finite.12 The Branciard’s error–tradeoff relation is given by14
which is also a universally valid relation and the bound is tighter than Ozawa’s uncertainty relation. In the experiment, we test Heisenberg’s, Ozawa’s and Branciard’s error-tradeoff relations in three cases, i.e., error-free measurement of one observable, nonzero error and mixed state cases.
a Schematic of the test principle for error–tradeoff relation by joint measurement on a continuous-variable entangled state. A quantum state ρ is measured in a joint measurement apparatus M, where two compatible observables C and D are measured simultaneously to approximate two incompatible observables A and B, respectively. The right inset describes the joint measurement apparatus for the error-free measurement of observable A. b Schematic of experimental setup. A Gaussian EPR entangled state is produced by a nondegenerate optical parametric amplifier (NOPA) operating in the state of deamplification. The two modes of EPR state are used as the signal mode ρ and the meter mode ρM which are detected by the homodyne detectors HD1 and HD2, respectively. The lossy channel is simulated by a half-wave plate (HWP) and a polarization beam splitter (PBS). LO local oscillator
Experimental implementation and results
At first, we consider a situation that the observable A is measured accurately (error-free measurement of observable A), i.e., the optimal estimation C = A. The measured phase quadrature \(D = \hat p_2\) is used to approximate the observable B. Because the amplitude quadrature \(\hat x_1\) of ρ and the phase quadrature \(\hat p_2\) of ρM are compatible, they can be measured simultaneously. The errors for approximating A and B are expressed as \(\varepsilon (A) = \sqrt {\langle (C - A)^2\rangle } = 0\), and \(\varepsilon (B) = \sqrt {\langle (D - B)^2\rangle } = \sqrt {\sigma (\hat p_2 - \hat p_1)^2} = \sqrt {2V_{\mathrm {S}}} ,\) respectively. Since ε(A) = 0 and ε(B) < ∞, we have
It is obvious that Heisenberg’s relation in Eq. (1) is violated. The violation of Heisenberg’s uncertainty relation for ‘joint measurement’ of EPR-entangled state of ε(A) = 0 has been theoretically discussed in ref. 12.
The Ozawa’s and Branciard’s relations are the same for the case of ε(A) = 0, which are
The amplitude quadrature \(\hat x_1\) of the signal mode is measured by a homodyne detector HD1 in the time domain, as shown in Fig. 1b, and the standard deviation of \(\hat x_1\),
is obtained. To evaluate the error ε(B), we experimentally measure the observables B and D, i.e. the phase quadratures \(\hat p_1\) and \(\hat p_2\), by two homodyne detectors (HD1 and HD2) simultaneously. The details of experiment can be found in the “Methods” section.
In our experiment, the achievable lower bound is limited by the quantum correlation of the EPR entangled state. In order to demonstrate this property, we change the quantum correlation of signal mode and meter mode by changing the relative phase difference θ between the two modes of EPR entangled state. Thus, the error
is measured in experiment, where \(\hat p_2(\theta ) = {\mathrm{cos}}\,\theta \hat p_2 + {\mathrm{sin}}\,\theta \hat x_2\). The left-hand sides (LHS) of Ozswa’s and Branciard’s relations can be obtained by substituting Eqs. (6) and (7) into Eq. (5).
When the relative phase difference θ = 0° and θ = 360°, the minimum error is obtained [Fig. 2a] and the LHS of the relation reaches its minimum value [Fig. 2b], which is determined by the present squeezing level. When θ = 180°, the maximum error is obtained. The error increases when the relative phase difference θ varies from 0° to 180°, which simulates the results of the decreasing of quantum correlation (squeezing) of the EPR-entangled state. The results confirm that the Ozawa’s and Branciard’s relations are the same and valid for the error-free measurement of observable A.
Results of the uncertainty relation in the case of error-free measurement of observable A. a The error ε(B) as a function of the relative phase difference between the two modes of EPR entangled state. b The LHS of the Ozawa’s and Branciard’s relations as functions of the relative phase difference. The right-hand side of the relations CAB is indicated by the red line. The solid curves and data points are the theoretical calculated results and experimental results, respectively. The error bars are obtained by root-mean-square of repeated measurements for 10 times. The experimentally measured results are in good agreement with the theoretical calculations
Then, we test the error–tradeoff relation with nonzero errors. When both errors are not equal to zero, Ozawa’s and Branciard’s relations are different. In the experiment, we apply a linear operation on the signal mode, which is done by transmitting the signal mode through a lossy channel, as shown in the inset of Fig. 1b. In the lossy channel, the signal mode and a vacuum mode are coupled via a beam splitter with transmission efficiency T. In this case, the amplitude and phase quadratures of the signal mode are changed to \(\hat x_1^\prime = \sqrt T \hat x_1 + \sqrt {1 - T}\hat x_{\mathrm {v}}\) and \(\hat p_1^\prime = \sqrt T \hat p_1 + \sqrt {1 - T} \hat p_{\mathrm {v}}\), respectively, after transmitted over the lossy channel, where \(\hat x_{\mathrm {v}}\) and \(\hat p_{\mathrm {v}}\) represent the amplitude and phase quadratures of vacuum. The variances of the amplitude and phase quadratures of the vacuum and the transmitted mode \(\rho \prime\) are \(\sigma (\hat x_{\mathrm {v}})^2 = \sigma (\hat p_{\mathrm {v}})^2 = 1/4\), \(\sigma (\hat x_1^\prime )^2 = T\sigma (\hat x_1)^2 + (1 - T)\sigma (\hat x_{\mathrm {v}})^2\), and \(\sigma (\hat p_1^\prime )^2 = T\sigma (\hat p_1)^2 + (1 - T)\sigma (\hat p_{\mathrm {v}})^2\), respectively. By choosing \(C = \hat x_1^\prime\) and \(D = \hat p_2\), which are compatible, the errors for the two incompatible observables \(A = \hat x_1\) and \(B = \hat p_1\) are
and
respectively. In this case, the standard deviations of A and B are
respectively.
In the experiment, since the signal mode is transmitted through a lossy channel, we record the corresponding transmission efficiency T and measure \(\hat x_1^\prime\) in time domain by homodyne detector HD1. We also measure the variance of \(\hat x_{\mathrm {v}}\) and \(\hat p_{\mathrm {v}}\) by blocking the signal mode of homodyne detector HD1. Based on the transformation relation of the lossy channel, \(\sigma (\hat x_1^\prime )^2 = T\sigma (\hat x_1)^2 + (1 - T)\sigma (\hat x_{\mathrm {v}})^2\), the variance of \(\hat x_1\) can be derived. So the error \(\varepsilon (A)\) is obtained based on the information of transmission efficiency T, \(\sigma \left( {\hat x_1^\prime } \right)^2\) and \(\sigma (\hat x_{\mathrm {v}})^2\). We measure the phase quadratures \(\hat p_1^\prime\) and \(\hat p_2\) by two homodyne detectors simultaneously. According to the relation \(\hat p_1^\prime = \sqrt T \hat p_1 + \sqrt {1 - T} \hat p_{\mathrm {v}}\), the information of \(\hat p_1\) is obtained, and then the error of observable B and the variance of the phase quadrature \(\hat p_1\) are obtained experimentally.
In this case, the LHS of the error–tradeoff relations are obtained by substituting Eqs. (8–10) into Heisenberg’s, Ozawa’s and Branciard’s Eqs. (1–3). The error ε(A) increases with the decreasing of channel efficiency, while the error ε(B) is not affected by the channel efficiency according to Eq. (9) (Fig. 3a). Heisenberg’s relation in Eq. (1) is violated when the transmission efficiency is higher than 0.3. While the Ozawa’s and Branciard’s relations are always valid (Fig. 3b). By comparing the LHS of Ozawa’s and Branciard’s relations, we confirm that Branciard’s relation is tighter than Ozawa’s relation.
Results of the uncertainty relations in the case of nonzero errors. a The errors ε(A) (red curve) and ε(B) (blue curve) as functions of the transmission efficiency. b The LHS of the relations as functions of the transmission efficiency. Blue curve: the Heisenberg’s relation in Eq. (1). Yellow curve: the Ozawa’s relation in Eq. (2). Black curve: the Branciard’s relation in Eq. (3). The right-hand side of the relations CAB is indicated by the red line
Finally, we demonstrate the error–tradeoff relation for the mixed state, i.e., the state ρ transmitted over a lossy channel. Here, observables \(C = A = \hat x_1^\prime\), \(B = \hat p_1^\prime\), and \(D = \hat p_2\) are chosen, and thus errors for the mixed state are ε(A) = 0 and
respectively. And the standard deviation of A is
In this case, Heisenberg’s error–tradeoff relation is violated, Ozawa’s and Branciard’s relations are the same as given by Eq. (5).
In the experiment, when \(\hat p_2\) and \(\hat p_1^\prime\) are recorded in time domain simultaneously, the error ε(B) is obtained. We also measure \(\hat x_1^\prime\) in time domain to obtain \(\sigma \left( {\hat x_1^\prime } \right)\). By substituting Eqs. (11) and (12) into Eq. (5), the LHS of Ozawa’s and Branciard’s relations are obtained. In this case, the error ε(B) and the LHS of the relations increase along with the decreasing of transmission efficiency as shown in Fig. 4a, b, respectively. The error and LHS of the relations get the minimum value when the transmission efficiency is unit.
The predicted lower bounds for Heisenberg’s [Eq. (1)], Ozawa’s [Eq. (2)], and Brinciard’s [Eq. (3)] error–tradeoff relations are compared in the plane (ε(A), ε(B)), as shown in Fig. 5. For the Heisenberg’s relation (bounded by the blue dashed curve), one of the error must be infinite when the other goes to zero. While in our experiment, for the case of error ε(A) = 0, the finite error ε(B) is observed (red circles), which violates the Heisenberg’s error–tradeoff relation, yet satisfies the Ozawa’s and Branciard’s error–tradeoff relations. For the case of nonzero errors, only one of the observed values satisfies the Heisenberg’s error–tradeoff relation (the data with 0.2 transmission efficiency), the other values violate Heisenberg’s error–tradeoff relation, yet satisfy Ozawa’s and Branciard’s relations.
Lower bounds of the error–tradeoff relations. Blue dashed curve: the Heisenberg’s bound. Yellow dotted curve: the Ozawa’s bound. Gray solid curve: the Branciard’s bound. Red circles: experimental data for error free measurement of observable A as shown in Fig. 2. Black diamonds: experimental data for nonzero errors condition as shown in Fig. 3
Discussion
It is important to show that the error–tradeoff relation can be saturated, i.e., the lower bound of error–tradeoff relation can be reached. In our experiment, the LHS of Ozawa’s and Branciard’s error–tradeoff relations depend on the squeezing parameter of the Gaussian EPR entangled state. With the increasing of squeezing parameter, the lower bound of the error–tradeoff relations can be approached. The lower bound of the error–tradeoff relations can be reached only in the case of infinite squeezing of the EPR entangled state.
There are some objections in the definition of the rms error in error–disturbance relation.17 They show that for some special cases, the error vanishes for some inaccurate measurements, in which the meter does not commute with the measured observable. Ozawa proposed an improved definition for the rms error, which is state-dependent, operationally definable, and perfectly characterizes accurate measurements.36 But in our experiment, for the observables A and C are always commute, the objections discussed in ref. 17 do not apply to the cases considered in our experiment.
We experimentally test the Heisenberg’s, Ozawa’s, and Branciard’s error–tradeoff relations for continuous-variable observables, i.e., amplitude and phase quadratures of an optical mode. Especially, we investigate the error–tradeoff relation in the case of zero error by using Gaussian EPR entangled state. We test the error–tradeoff relation for three different cases, which are zero error of one observable, nonezero errors and mixed state, respectively. The results demonstrate that the Heisenberg’s error–tradeoff relation is violated in some cases while the Ozawa’s and the Brinciard’s error–tradeoff relations are valid. Our work is useful not only in understanding fundamentals of physical measurement but also in developing of continuous variable quantum information technology.
Methods
The Gaussian EPR entangled state
In our experiment, the Gaussian EPR entangled state is produced by a nondegenerate optical parametric amplifier (NOPA) operating in the state of deamplification. The amplitude and phase quadratures of two EPR modes are expressed as37
where \(\hat x_{1(2)}(0)\) and \(\hat p_{1(2)}(0)\) are the amplitude and phase quadratures of vacuum state, and \(\sigma (\hat x_{1(2)}(0))^2 = \sigma (\hat p_{1(2)}(0))^2 = 1/4\). From Eq. (13), we obtain that the variances of amplitude and phase quadratures of two EPR modes are \(\sigma (\hat x_1)^2 = \sigma (\hat x_2)^2 = \sigma (\hat p_1)^2 = \sigma (\hat p_2)^2 = (e^{2r} + e^{ - 2r})/8\). The quantum correlated noise between two EPR modes are \(\sigma (\hat p_2 - \hat p_1)^2 = \sigma (\hat x_2 + \hat x_1)^2 = e^{ - 2r}/2\), and the anti-correlated noise are \(\sigma (\hat p_2 + \hat p_1)^2 = \sigma (\hat x_2 - \hat x_1)^2 = e^{2r}/2\).
Because of imperfect factors in the experiment, for example loss, the obtained EPR entangled state may not be pure. In this case, the variances of the Gaussian EPR entangled state can be described by two parameters VS and VA, which are the variances of squeezed and anti-squeezed quadratures of a squeezed state, respectively. When the state is pure, we have VS = e−2r/4 and VA = e2r/4. When the state is not pure, we have VA > e2r/4. Thus, the variances of amplitude and phase quadratures of two EPR modes are \(\sigma (\hat x_1)^2 = \sigma (\hat x_2)^2 = \sigma (\hat p_1)^2 = \sigma (\hat p_2)^2 = (V_{\mathrm {A}} + V_{\mathrm {S}})/2\) and the quantum correlated noise between two EPR modes are \(\sigma (\hat p_2 - \hat p_1)^2 = \sigma (\hat x_2 + \hat x_1)^2 = 2V_{\mathrm {S}}\) in our experiment.
Details of experiment
In the experiment, an EPR entangled state with VS = 0.129 (corresponding to −2.9 dB squeezing) and VA = 0.619 (corresponding to 3.9 dB antisqueezing) is prepared by a NOPA, which consists of an a-cut type-II KTP crystal and a concave mirror as shown in Fig. 1b.38 The front face of the KTP crystal is used as the input coupler, and the concave mirror with 50 mm curvature serves as the output coupler. The front face of the KTP crystal has the 42% transmission at 540 nm and high reflectivity at 1080 nm. The end face of the KTP crystal is antireflection coated for both 540 and 1080 nm. The AC output signals from HD1 and HD2 are mixed with a local reference signal of 3 MHz, and then filtered by low-pass filters with bandwidth of 30 kHz and amplified 1000 times (Low noise preamplifier, SRS, SR560), respectively. And then the two outputs of the preamplifiers are recorded by a digital storage oscilloscope simultaneously. A sample size of 5 × 105 data points is used for all quadrature measurements with sampling rate of 500K/s. The mode-matching efficiency between signal and local oscillator is 99% and the quantum efficiency of photodiodes are 99.6%.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172–198 (1927).
Genoni, M. G. et al. Optimal estimation of joint parameters in phase space. Phys. Rev. A 87, 012107 (2013).
Sebastian, S. et al. Quantum-dense metrology. Nat. Photon. 7, 626–629 (2013).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Publisher’s Note: Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000).
Furusawa, A. & van Loock, P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing (Wiley-VCH Verlag Press, Weinheim, 2011).
Kennard, E. H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44, 326–352 (1927).
Robertson, H. P. The uncertainty principle. Phys. Rev. 34, 163–164 (1929).
Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurements. Phys. Rev. A 67, 042105 (2003).
Ozawa, M. Physical content of Heisenbergs uncertainty relation: limitation and reformulation. Phys. Lett. A 318, 21–29 (2003).
Ozawa, M. Uncertainty relations for joint measurements of noncommuting observables. Phys. Lett. A 320, 367–374 (2004).
Branciard, C. Error-tradeoff and error-disturbance relations for incompatible quantum measurements. Proc. Natl Acad. Sci. USA 110, 6742–6747 (2013).
Ballentine, L. E. The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381 (1970).
Hall, M. J. W. Prior information: how to circumvent the standard joint-measurement uncertainty relation. Phys. Rev. A 69, 052113 (2004).
Busch, P., Lahti, P. & Werner, R. F. Colloquium: quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys. 86, 1261–1281 (2014).
Dressel, J. & Nori, F. Certainty in Heisenberg’s uncertainty principle: revisiting definitions for estimation errors and disturbance. Phys. Rev. A 89, 022106 (2014).
Baek, K., Farrow, T. & Son, W. Optimized entropic uncertainty relation for successive measurement. Phys. Rev. A 89, 032108 (2014).
Buscemi, F., Hall, M. J. W., Ozawa, M. & Wilde, M. M. Noise and disturbance in quantum measurements: an information-theoretic approach. Phys. Rev. Lett. 112, 050401 (2014).
Lu, X. M., Yu, S., Fujikawa, K. & Oh, C. H. Improved error-tradeoff and error-disturbance relations in terms of measurement error components. Phys. Rev. A 90, 042113 (2014).
Barchielli, A., Gregoratti, M. & Toigo, A. Measurement uncertainty relations for position and momentum: relative entropy formulation. Entropy 19, 301 (2017).
Ringbauer, M. et al. Experimental joint quantum measurements with minimum uncertainty. Phys. Rev. Lett. 112, 020401 (2014).
Kaneda, F., Baek, S. Y., Ozawa, M. & Edamatsu, K. Experimental test of error-disturbance uncertainty relations by weak measurement. Phys. Rev. Lett. 112, 020402 (2014).
Rozema, L. A. et al. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 109, 100404 (2012).
Lund, A. P. & Wiseman, H. M. Measuring measurement–disturbance relationships with weak values. New J. Phys. 12, 093011 (2010).
Baek, S. Y., Kaneda, F., Ozawa, M. & Edamatsu, K. Experimental violation and reformulation of the Heisenberg’s error-disturbance uncertainty relation. Sci. Rep. 3, 2221 (2013).
Weston, M. M., Hall, M. J. W., Palsson, M. S., Wiseman, H. M. & Pryde, G. J. Experimental test of universal complementarity relations. Phys. Rev. Lett. 110, 220402 (2013).
Erhart, J. et al. Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements. Nat. Phys. 8, 185–189 (2012).
Sulyok, G. et al. Experimental test of entropic noise-disturbance uncertainty relationsfor spin-1/2 measurements. Phys. Rev. Lett. 115, 030401 (2015).
Demirel, B., Sponar, S., Sulyok, G., Ozawa, M. & Hasegawa, Y. Experimental test of residual error-disturbance uncertainty relations for mixed spin-1/2 states. Phys. Rev. Lett. 117, 140402 (2016).
Ma, W. C. et al. Experimental test of Heisenberg’s measurement uncertainty relation based on statistical distances. Phys. Rev. Lett. 116, 160405 (2016).
Zhou, F. et al. Verifying Heisenberg’s error-disturbance relation using a single trapped ion. Sci. Adv. 2, e1600578 (2016).
Schrödinger, E. Die gegenwa rtige Situation in der Quantenmechanik. Naturwissenschaften 23, 807 (1935).
Halvorson, H. & Clifton, R. Maximal beable subalgebras of quantum mechanical observables. Int. J. Theor. Phys. 38, 2441 (1999).
Ozawa, M. Soundness and completeness of quantum root-mean-square errors. npj Quantum Inf. 5, 1–8 (2019).
Reid, M. D. Demonstration of the Einstein–Podolsky–Rosen paradox using nondegenerate parametric amplification. Phys. Rev. A 40, 913 (1989).
Su, X. et al. Gate sequence for continuous variable one-way quantum computation. Nat. Commun. 4, 2828 (2013).
Acknowledgements
This research was supported by the NSFC (Grant nos. 11834010 and 61601270), the program of Youth Sanjin Scholar, the Applied Basic Research Program of Shanxi Province (Grant no. 201601D202006), National Key R&D Program of China (Grant no. 2016YFA0301402), and the Fund for Shanxi “1331 Project” Key Subjects Construction.
Author information
Authors and Affiliations
Contributions
Y.L., H.K., and X.S. designed the experiment and carried out the experiment; Z.M. and X.S. conceived the original idea; Y.L. and X.S. analyzed the data; D.H., M.W., and Z.Q. participated in part of the experiment and discussion of the results. Y.L., Z.M., X.S., and K.P. prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Y., Ma, Z., Kang, H. et al. Experimental test of error-tradeoff uncertainty relation using a continuous-variable entangled state. npj Quantum Inf 5, 68 (2019). https://doi.org/10.1038/s41534-019-0183-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0183-6
This article is cited by
-
Strong majorization uncertainty relations and experimental verifications
npj Quantum Information (2023)