A new class of efficient randomized benchmarking protocols

Abstract

Randomized benchmarking is a technique for estimating the average fidelity of a set of quantum gates. However, if this gateset is not the multi-qubit Clifford group, robustly extracting the average fidelity is difficult. Here, we propose a new method based on representation theory that has little experimental overhead and robustly extracts the average fidelity for a broad class of gatesets. We apply our method to a multi-qubit gateset that includes the T-gate, and propose a new interleaved benchmarking protocol that extracts the average fidelity of a two-qubit Clifford gate using only single-qubit Clifford gates as reference.

Introduction

Randomized benchmarking^{1,2,3,4,5,6,7} is arguably the most prominent experimental technique for assessing the quality of quantum operations in experimental quantum computing devices.^{4,8,9,10,11,12,13} Key to the wide adoption of randomized benchmarking are its scalability with respect to the number of qubits and its insensitivity to errors in state preparation and measurement. It has also recently been shown to be insensitive to variations in the error associated to different implemented gates.^14,15,16

The randomized benchmarking protocol is defined with respect to a gateset G, a discrete collection of quantum gates. Usually, this gateset is a group, such as the Clifford group.² The goal of randomized benchmarking is to estimate the average fidelity¹⁷ of this gateset.

Randomized benchmarking is performed by randomly sampling a sequence of gates of a fixed length m from the gateset G. This sequence is applied to an initial state ρ, followed by a global inversion gate such that in the absence of noise the system is returned to the starting state. Then the overlap between the output state and the initial state is estimated by measuring a two-component POVM {Q, 1 − Q}. This is repeated for many sequences of the same length m and the outputs are averaged, yielding a single average survival probability p_m. Repeating this procedure for various sequence lengths m yields a list of probabilities {p_m}_m.

Usually G is chosen to be the Clifford group. It can then be shown (under the assumption of gate-independent CPTP noise)² that the data {p_m}_m can be fitted to a single exponential decay of the form

$$p_m \approx _{{\mathrm{fit}}}A + Bf^m$$

(1)

where A, B depend on state preparation and measurement, and the quality parameter f only depends on how well the gates in the gateset G are implemented. This parameter f can then be straightforwardly related to the average fidelity F_avg.² The fitting relation Eq. (1) holds intuitively because averaging over all elements of the Clifford group effectively depolarizes the noise affecting the input state ρ. This effective depolarizing noise then accretes exponentially with sequence length m.

However it is possible, and desirable, to perform randomized benchmarking on gatesets that are not the Clifford group, and a wide array of proposals for randomized benchmarking using non-Clifford gatesets appear in the literature.^{18,19,20,21,22,23,24} The most prominent use case is benchmarking a gateset G that includes the vital T-gate^18,19,22 which, together with the Clifford group, forms a universal set of gates for quantum computing.¹⁷ Another use case is simultaneous randomized benchmarking,²³ which extracts information about crosstalk and unwanted coupling between neighboring qubits by performing randomized benchmarking on the gateset consisting of single qubit Clifford gates on all qubits. In these cases, and in other examples of randomized benchmarking with non-Clifford gatesets,^20,22,23 the fitting relation Eq. (1) does not hold and must instead be generalized to

$$p_m \approx _{{\mathrm{fit}}}\mathop {\sum}\limits_{\lambda \in R_{\mathrm{G}}} {A_\lambda } f_\lambda ^m,$$

(2)

where R_G is an index set that only depends on the chosen gateset, the f_λ are general ‘quality parameters’ that only depend on the gates being implemented and the A_λ prefactors depend only on SPAM (when the noise affecting the gates is trace preserving there will be a λ ∈ R_G -corresponding to the trivial subrepresentation- such that f_λ = 1, yielding the constant offset seen in Eq. (1)). The above holds because averaging over sequences of elements of these non-Clifford groups averaging does not fully depolarize the noise. Rather the system state space will split into several ‘sectors’ labeled by λ, with a different depolarization rate, set by f_λ, affecting each sector. The interpretation of the parameters f_λ varies depending on the gateset G. In the case of simultaneous randomized benchmarking²³ they can be interpreted as a measure of crosstalk and unwanted coupling between neighboring qubits. For other gatesets an interpretation is not always available. However, as was pointed out for specific gatesets in ref. ^18,19,20,22 and for general finite groups in ref., ²¹ the parameters f_λ can always be jointly related (see Eq. (5)) to the average fidelity F_avg of the gateset G. This means that in theory randomized benchmarking can extract the average fidelity of a gateset even when it is not the Clifford group.

However in practice the multi-parameter fitting problem given by Eq. (2) is difficult to perform, with poor confidence intervals around the parameters f_λ unless impractically large amounts of data are gathered. More fundamentally it is, even in the limit of infinite data, impossible to associate the estimates from the fitting procedure to the correct decay channel in Eq. (2) and thus to the correct f_λ, making it impossible to reliably reconstruct the average fidelity of the gateset.

In the current literature on non-Clifford randomized benchmarking, with the notable exception of ref., ²² this issue is sidestepped by performing randomized benchmarking several times using different input states ρ_λ that are carefully tuned to maximize one of the prefactors A_λ while minimizing the others. This is unsatisfactory for several reasons: (1) the accuracy of the fit now depends on the preparation of ρ_λ, undoing one of the main advantages of randomized benchmarking over other methods such as direct fidelity estimation,²⁵ and (2) it is, for more general gatesets, not always clear how to find such a maximizing state ρ_λ. These problems aren’t necessarily prohibitive for small numbers of qubits and/or exponential decays (see for instance²⁶) but they do limit the practical applicability of current non-Clifford randomized benchmarking protocols on many qubits and more generally restrict which groups can practically be benchmarked.

Here, we propose an adaptation of the randomized benchmarking procedure, which we call character randomized benchmarking, which solves the above problems and allows reliable and efficient extraction of average fidelities for gatesets that are not the Clifford group. We begin by discussing the general method, before applying it to specific examples. Finally, we discuss using character randomized benchmarking in practice and argue the new method does not impose significant experimental overhead. Previous adaptations of randomized benchmarking, as discussed in^8,27,28 and in particular²² (where the idea of projecting out exponential decays was first proposed for a single qubit protocol), can be regarded as special cases of our method.

Results

In this section, we present the main result of this paper: the character randomized benchmarking protocol, which leverages techniques from character theory²⁹ to isolate the exponential decay channels in Eq. (2). One can then fit these exponential decays one at a time, obtaining the quality parameters f_λ. We emphasize that the data generated by character randomized benchmarking can always be fitted to a single exponential, even if the gateset being benchmarked is not the Clifford group. Moreover, our method retains its validity in the presence of leakage, which also causes deviations from single exponential behavior for standard randomized benchmarking¹⁴ (even when the gateset is the Clifford group).

For the rest of the paper, we will use the Pauli Transfer Matrix (PTM) representation of quantum channels (This representation is also sometimes called the Liouville representation or affine representation of quantum channels^30,31). Key to this representation is the realization that the set of normalized non-identity Pauli matrices σ_q on q qubits, together with the normalized identity σ₀ := 2^−q/21 forms an orthonormal basis (with respect to the trace inner product) of the Hilbert space of Hermitian matrices of dimension 2^q. Density matrices ρ and POVM elements Q can then be seen as vectors and co-vectors expressed in the basis $\{ \sigma _0\} \cup {\boldsymbol{\sigma }}_{\mathbf{q}}$, denoted |ρ〉〉 and 〈〈Q| respectively. Quantum channels ${\cal{E}}$³² are then matrices (we will denote a channel and its PTM representation by the same letter) and we have ${\cal{E}}|\rho \rangle \rangle = |{\cal{E}}(\rho )\rangle \rangle$. Composition of channels ${\cal{E}},{\cal{F}}$corresponds to multiplication of their PTM representations, that is $|{\cal{E}} \circ {\cal{F}}(\rho )\rangle \rangle = {\cal{E}}{\cal{F}}|\rho \rangle \rangle$. Moreover, we can write expectation values as bra-ket inner products, i.e. $\langle \langle Q|{\cal{E}}|\rho \rangle \rangle = {\mathrm{Tr}}(Q{\cal{E}}(\rho ))$. The action of a unitary G on a matrix ρ is denoted ${\cal{G}}$, i.e. ${\cal{G}}|\rho \rangle \rangle = |G\rho G^\dagger \rangle \rangle$ and we denote its noisy implementation by $\tilde {\cal{G}}$. For a more expansive review of the PTM representation, see Section I.2 in the Supplementary Methods.

We will, for ease of presentation, also assume gate-independent noise. This means we assume the existence of a CPTP map ${\cal{E}}$ such that $\tilde {\cal{G}} = {\cal{E}}{\cal{G}}$ for all G ∈ G. We however emphasize that our protocol remains functional even in the presence of gate-dependent noise. We provide a formal proof of this, generalizing the modern treatment of standard randomized benchmarking with gate-dependent noise,¹⁴ in the Methods section.

Standard randomized benchmarking

Let’s first briefly recall the ideas behind standard randomized benchmarking. Subject to the assumption of gate-independent noise, the average survival probability p_m of the standard randomized benchmarking procedure over a gateset G (with input state ρ and measurement POVM {Q, 1 − Q}) with sequence length m can be written as: ref. ²

$$p_m = \langle \langle Q|\left( {\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\cal{G}}^\dagger {\cal{E}}{\cal{G}}} \right)^m|\rho \rangle \rangle .$$

(3)

where ${\Bbb E}_{G \in {\mathrm{G}}}$ denotes the uniform average over G. The key insight to randomized benchmarking is that ${\cal{G}}$ is a representation (for a review of representation theory see section I.1 in the Supplementary Methods) of G ∈ G. This representation will not be irreducible but will rather decompose into irreducible subrepresentations, that is ${\cal{G}} = \oplus _{\lambda \in R_{\mathrm{G}}}\phi _\lambda (G)$ where R_G is an index set and ϕ_λ are irreducible representations of G which we will assume to all be mutually inequivalent. Using Schur’s lemma, a fundamental result in representation theory, we can write Eq. (3) as

$$p_m = \mathop {\sum}\limits_\lambda {\langle \langle Q|{\cal{P}}_\lambda |\rho \rangle \rangle f_\lambda ^m}$$

(4)

where ${\cal{P}}_\lambda$ is the orthogonal projector onto the support of ϕ_λ (note that this is a superoperator) and $f_\lambda : = {\mathrm{Tr}}({\cal{P}}_\lambda {\cal{E}})/{\mathrm{Tr}}({\cal{P}}_\lambda )$ is the quality parameter associated to the representation ϕ_λ (note that the trace is taken over superoperators). This reproduces Eq. (2). A formal proof of Eq. (4) can be found in the Supplementary Methods and in ref. ²¹ The average fidelity of the gateset G can then be related to the parameters f_λ as

$$F_{{\mathrm{avg}}} = \frac{{2^{ - q}\mathop {\sum}\nolimits_{\lambda \in R_{\mathrm{G}}} {{\mathrm{Tr}}} ({\cal{P}}_\lambda )f_\lambda }}{{2^q + 1}}.$$

(5)

Note again that R_G includes the trivial subrepresentation carried by |1〉〉, so when ${\cal{E}}$ is a CPTP map there is a λ ∈ R_G for which f_λ = 1. See Lemma’s 4 and 5 in the Supplementary Methods for a proof of Eq. (5)

Character randomized benchmarking

Now we present our new method called character randomized benchmarking. For this we make use of concepts from the character theory of representations.²⁹ Associated to any representation $\hat \phi$ of a group ${\hat{\mathrm G}}$ is a character function $\chi _{\hat \phi }:{\hat{\mathrm G}} \to {\Bbb R}$, from the group to the real numbers (Generally the character function is a map to the complex numbers, but in our case it is enough to only consider real representations). Associated to this character function is the following projection formula:²⁹

$$\mathop {{\Bbb E}}\limits_{\hat G \in {\hat{\mathrm G}}} \chi _{\hat \phi }(\hat G)\hat {\cal{G}} = \frac{1}{{|\hat \phi |}}{\cal{P}}_{\hat \phi },$$

(6)

where ${\cal{P}}_{\hat \phi }$ is the projector onto the support of all subrepresentations of $\hat {\cal{G}}$ equivalent to $\hat \phi$ and $|\hat \phi |$ is the dimension of the representation $\hat \phi$. We will leverage this formula to adapt the randomized benchmarking procedure in a way that singles out a particular exponential decay $f_\lambda ^m$ in Eq. (2).

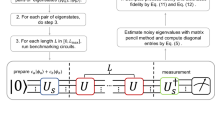
We begin by choosing a group G. We will call this group the ‘benchmarking group’ going forward and it is for this group/gateset that we will estimate the average fidelity. In general we will have that ${\cal{G}} = \oplus _{\lambda \in R_{\mathrm{G}}}\phi _\lambda (G)$ where R_G is an index set and ϕ_λ are irreducible representations of G which we will assume to all be mutually inequivalent (It is straightforward to extend character randomized benchmarking to also cover the presence of equivalent irreducible subrepresentation. However do not make this extension explicit here in the interest of simplicity). Now fix a λ′ ∈ R_G. f_λ′ is the quality parameter associated to a specific subrepresentation ϕ_λ′ of ${\cal{G}}$. Next consider a group ${\hat{\mathrm G}} \subset {\mathrm{G}}$ such that the PTM representation $\hat {\cal{G}}$ has a subrepresentation $\hat \phi$, with character function $\chi _{\hat \phi }$, that has support inside the representation ϕ_λ′ of G, i.e. ${\cal{P}}_{\hat \phi } \subset {\cal{P}}_{\lambda \prime }$ where ${\cal{P}}_{\lambda \prime }$ is again the projector onto the support of ϕ_λ′. We will call this group ${\hat{\mathrm G}}$ the character group. Note that such a pair ${\hat{\mathrm G}},\hat \phi$ always exists; we can always choose ${\hat{\mathrm G}} = {\mathrm{G}}$ and $\hat \phi = \phi _{\lambda \prime }$. However other natural choices often exist, as we shall see when discussing examples of character randomized benchmarking. The idea behind the character randomized benchmarking protocol, described in Fig. 1, is now to effectively construct Eq. (6) by introducing the application of an extra gate $\hat G$ drawn at random from the character group ${\hat{\mathrm G}}$ into the standard randomized benchmarking protocol. In practice this gate will not be actively applied but must be compiled into the gate sequence following it, thus not resulting in extra noise (this holds even in the case of gate-dependent noise, see Methods).

Fig. 1

The character randomized benchmarking protocol. Note the inclusion of the gate $\hat G$ and the average over the character function $\chi _{\hat \phi }$, which form the key ideas behind character randomized benchmarking. Note also that this extra gate $\hat G$ is compiled into the sequence of gates (G₁, …, G_m) and thus does not result in extra noise

This extra gate $\hat G \in {\hat{\mathrm G}}$ is not included when computing the global inverse $G_{{\mathrm{inv}}} = (G_1 \ldots G_m)^\dagger$. The average over the elements of ${\hat{\mathrm G}}$ is also weighted by the character function $\chi _{\hat \phi }$ associated to the representation $\hat \phi$ of ${\hat{\mathrm G}}$. Similar to eq. (3) we can rewrite the uniform average over all $\vec G \in {\mathrm{G}}^{ \times m}$ and $\hat G \in {\hat{\mathrm G}}$ as

$$k_m^{\lambda^{\prime} } = |\hat \phi |\langle \langle Q|\left[ {\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\cal{G}}^\dagger {\cal{E}}{\cal{G}}} \right]^m\mathop {{\Bbb E}}\limits_{\hat G \in {\hat{\mathrm G}}} \chi _{\hat \phi }(\hat G)\hat {\cal{G}}|\rho \rangle \rangle .$$

Using the character projection formula (Eq. (6)), the linearity of quantum mechanics, and the standard randomized benchmarking representation theory formula (Eq. (4)) we can write this as

$$k_m^{\lambda^{\prime} } = \mathop {\sum}\limits_{\lambda \in R_{\mathrm{G}}} {\langle \langle Q|{\cal{P}}_\lambda {\cal{P}}_{\hat \phi }|\rho \rangle \rangle f_\lambda ^m = \langle \langle Q|{\cal{P}}_{\hat \phi }|\rho \rangle \rangle f_{\lambda^{\prime} }^m}$$

(7)

since we have chosen ${\hat{\mathrm G}}$ and $\hat \phi$ such that ${\cal{P}}_{\hat \phi } \subset {\cal{P}}_{\lambda \prime }$. This means the character randomized benchmarking protocol isolates the exponential decay associated to the quality parameter f_λ′ independent of state preparation and measurement. We can now extract f_λ′ by fitting the data-points $k_m^{\lambda^{\prime} }$ to a single exponential of the form $Af_{\lambda \prime }^m$. Note that this remains true even if ${\cal{E}}$ is not trace-preserving, i.e. the implemented gates experience leakage. Repeating this procedure for all λ′ ∈ R_G (choosing representations $\hat \phi$ of ${\hat{\mathrm G}}$ such that ${\cal{P}}_{\hat \phi } \subset {\cal{P}}_{\lambda \prime }$) we can reliably estimate all quality parameters f_λ associated with randomized benchmarking over the group G. Once we have estimated all these parameters we can use Eq. (5) to obtain the average fidelity of the gateset G.

Discussion

We will now discuss several examples of randomized benchmarking experiments where the character randomized benchmarking approach is beneficial. The first example, benchmarking T-gates, is taken from the literature¹⁸ while the second one, performing interleaved benchmarking on a 2-qubit gate using only single qubit gates a reference, is a new protocol. We have also implemented this last protocol to characterize a CPHASE gate between spin qubits in Si/SiGe quantum dots, see ref. ³³

Benchmarking T-gates

The most common universal gateset considered in the literature is the Clifford + T gateset.¹⁷ The average fidelity of the Clifford gates can be extracted using standard randomized benchmarking over the Clifford group, but to extract the average fidelity of the T gate a different approach is needed. Moreover one would like to characterize this gate in the context of larger circuits, meaning that we must find a family of multi-qubit groups that contains the T gate. One choice is to perform randomized benchmarking over the group T_q generated by the CNOT gate between all pairs of qubits (in both directions), Pauli X on all qubits and T gates on all qubits (another choice would be to use dihedral randomized benchmarking²² but this is limited to single qubit systems, or to use the interleaved approach proposed in ref. ²⁴). This group is an example of a CNOT-dihedral group and its use for randomized benchmarking was investigated in.¹⁸ There it was derived that the PTM representation of the group T_q decomposes into 3 irreducible subrepresentations ϕ₁, ϕ₂, ϕ₃ with associated quality parameters f₁, f₂, f₃ and projectors

$${\cal{P}}_1 = |\sigma _0\rangle \rangle \langle \langle \sigma _0|,\quad {\cal{P}}_2 = \mathop {\sum}\limits_{\sigma \in {\cal{Z}}_q} {|\sigma \rangle \rangle \langle \langle \sigma |} ,\quad {\cal{P}}_3 = \mathop {\sum}\limits_{\sigma \in \sigma _q/{\cal{Z}}_q} {|\sigma \rangle \rangle \langle \langle \sigma |} ,$$

where σ₀ is the normalized identity, σ_q is the set of normalized Pauli matrices and ${\cal{Z}}_q$ is the subset of the normalized Pauli matrices composed only of tensor products of Z and 1. Noting that f₁ = 1 if the implemented gates $\tilde {\cal{G}}$ are CPTP we must estimate f₂ and f₃ in order to estimate the average fidelity of T_q. Using standard randomized benchmarking this would thus lead to a two-decay, four-parameter fitting problem, but using character randomized benchmarking we can fit f₂ and f₃ separately. Let’s say we want to estimate f₂, associated to ϕ₂, using character randomized benchmarking. In order to perform character randomized benchmarking we must first choose a character group ${\hat{\mathrm G}}$. A good choice for ${\hat{\mathrm G}}$ is in this case the Pauli group P_q. Note that P_q ⊂ T_q since T⁴ = Z the Pauli Z matrix.

Having chosen ${\hat{\mathrm G}} = {\mathrm{P}}_q$ we must also choose an irreducible subrepresentation $\hat \phi$ of the PTM representation of the Pauli group P_q such that ${\cal{P}}_{\hat \phi }{\cal{P}}_2 = {\cal{P}}_{\hat \phi }$. As explained in detail in section V.I in the Supplementary Methods the PTM representation of the Pauli group has 2^q irreducible inequivalent subrepresentations of dimension one. These representations ϕ_σ are each associated to an element $\sigma \in \{ \sigma _0\} \cup {\boldsymbol{\sigma }}_{\mathbf{q}}$ of the Pauli basis. Concretely we have that the projector onto the support of ϕ_σ is given by ${\cal{P}}_\sigma = |\sigma \rangle \rangle \langle \langle \sigma |$. This means that, to satisfy ${\cal{P}}_{\hat \phi }{\cal{P}}_2 = {\cal{P}}_{\hat \phi }$ we have to choose $\hat \phi = \phi _\sigma$ with $\sigma \in {\cal{Z}}_q$. One could for example choose σ proportional to Z^⊗q. The character associated to the representation ϕ_σ is χ_σ(P) = (−1)^〈P,σ〉 where 〈P, σ〉 = 1 if and only if P and σ anti-commute and zero otherwise (we provided a proof of this fact in section V.1 of the Supplementary Methods). Hence the character randomized benchmarking experiment with benchmarking group T_q, character group P_q and subrepresentation $\hat \phi = \phi _\sigma$ produces data that can be described by

$$k_m^2 = \langle \langle Q|\sigma \rangle \rangle \langle \langle \sigma |\rho \rangle \rangle f_2^m,$$

(8)

allowing us to reliably extract the parameter f₂. We can perform a similar experiment to extract f₃, but we must instead choose $\sigma \in {\boldsymbol{\sigma }}_q\backslash {\cal{Z}}$. A good choice would for instance be σ proportional to X^⊗q.

Having extracted f₂ and f₃ we can then use Eq. (5) to obtain the average fidelity of the gateset T_q as:¹⁸

$$F_{{\mathrm{avg}}} = \frac{{2^q - 1}}{{2^q}}\left( {1 - \frac{{f_2 + 2^qf_3}}{{2^q + 1}}} \right)$$

(9)

Finally we would like to note that in order to get good signal one must choose ρ and Q appropriately. The correct choice is suggested by Eq. (7). For instance, if when estimating f₂ as above we choose σ proportional to Z^⊗q we must then choose $Q = \frac{1}{2}(1 + Z^{ \otimes 2})$ and $\rho = \frac{1}{d}(1 + Z^{ \otimes 2})$. This corresponds to the even parity eigenspace (in the computational basis).

2-for-1 interleaved benchmarking

The next example is a new protocol, which we call 2-for-1 interleaved randomized benchmarking. It is a way to perform interleaved randomized benchmarking³⁴ of a 2-qubit Clifford gate C using only single qubit Clifford gates as reference gates. The advantages of this are (1) lower experimental requirements and (2) a higher reference gate fidelity relative to the interleaved gate fidelity allows for a tighter estimate of the average fidelity of the interleaved gate (assuming single qubit gates have higher fidelity than two qubit gates). This latter point is related to an oft overlooked drawback of interleaved randomized benchmarking, namely that it does not yield a direct estimate of the average fidelity F(C) of the interleaved gate C but only gives upper and lower bounds on this fidelity. These upper and lower bounds moreover depend^34,35 on the fidelity of the reference gates and can be quite loose if the fidelity of the reference gates is low. To illustrate the advantages of this protocol we have performed a simulation comparing it to standard interleaved randomized benchmarking (details can be found in section V.2 in the Supplementary Methods). Following recent single qubit randomized benchmarking and Bell state tomography results in spin qubits in Si/SiGe quantum dots^36,37,38 we assumed single qubit gates to have a fidelity of $F_{{\mathrm{avg}}}^{(1)} = 0.987$ and two-qubit gates to have a fidelity of F_avg(C) = 0.898. Using standard interleaved randomized benchmarking³⁴ we can guarantee (using the optimal bounds of ref. ³⁵) that the fidelity of the interleaved gate is lower bounded by $F_{{\mathrm{avg}}}^{{\mathrm{int}}} \approx 0.62$ while using 2-for-1 interleaved randomized benchmarking we can guarantee that the fidelity of interleaved gate is lower bounded by F_avg(C) ≈ 0.79, a significant improvement that is moreover obtained by a protocol requiring less experimental resources. On top of this the 2-for-1 randomized benchmarking protocol provides strictly more information than simply the average fidelity, we can also extract a measure of correlation between the two qubits, as per.²³ In another paper³³ we have used this protocol to characterize a CPHASE gate between spin qubits in Si/SiGe quantum dots.

An interleaved benchmarking experiment consists of two stages, a reference experiment and an interleaved experiment. The reference experiment for 2-for-1 interleaved randomized benchmarking consists of character randomized benchmarking using 2 copies of the single-qubit Clifford group ${\mathrm{G}} = {\mathrm{C}}_1^{ \otimes 2}$ as the benchmarking group (this is also the group considered in simultaneous randomized benchmarking²³). The PTM representation of ${\mathrm{C}}_1^{ \otimes 2}$ decomposes into four irreducible subrepresentations and thus the fitting problem of a randomized benchmarking experiment over this group involves 4 quality parameters f_w indexed by w = (w₁, w₂) ∈ {0, 1}^×2. The projectors onto the associated irreducible representations ϕ_w are

$${\cal{P}}_w = \mathop {\sum}\limits_{\sigma \in \sigma _w} {|\sigma \rangle \rangle \langle \langle \sigma |}$$

(10)

where σ_w is the set of normalized 2-qubit Pauli matrices that have non-identity Pauli matrices at the i’th tensor factor if and only if w_i = 1. To perform character randomized benchmarking we choose as character group ${\hat{\mathrm G}} = {\mathrm{P}}_2$ the 2-qubit Pauli group. For each w ∈ {0, 1}^×2 we can isolate the parameter f_w by correctly choosing a subrepresentation ϕ_σ of the PTM representation of P₂. Recalling that ${\cal{P}}_\sigma = |\sigma \rangle \rangle \langle \langle \sigma |$ we can choose $\hat \phi = \phi _\sigma$ for $\sigma = (Z_1^w \otimes Z_2^w)/2$ to isolate the parameter f_w for w = (w₁, w₂) ∈ {0, 1}^×2. We give the character functions associated to these representation in section V.2 of the Supplementary Methods. Once we have obtained all quality parameters f_w we can compute the average reference fidelity F_ref using Eq. (5).

The interleaved experiment similarly consists of a character randomized benchmarking experiment using ${\mathrm{G}} = {\mathrm{C}}_1^{ \otimes 2}$ but for every sequence $\vec G = (G_1, \ldots ,G_m)$ we apply the sequence (G₁, C, G₂, …, C, G_m) instead, where C is a 2-qubit interleaving gate (from the 2-qubit Clifford group). Note that we must then also invert this sequence (with C) to the identity.³⁴ Similarly choosing ${\hat{\mathrm G}} = {\mathrm{P}}_2$ we can again isolate the parameters f_w and from these compute the ‘interleaved fidelity’ F_int. Using the method detailed in ref. ³⁵ we can then calculate upper and lower bounds on the average fidelity F_avg(C) of the gate C from the reference fidelity F_ref and the interleaved fidelity F_int. Note that it is not trivial that the interleaved experiment yields data that can be described by a single exponential decay, we will discuss this in greater detail in the methods section.

Finally we would like to note that the character benchmarking protocol can be used in many more scenarios than the ones outlined here. Character randomized benchmarking is versatile enough that when we want to perform randomized benchmarking we can consider first what group is formed by the native gates in our device and then use character benchmarking to extract gate fidelities from this group directly, as opposed to carefully compiling the Clifford group out of the native gates which would be required for standard randomized benchmarking. This advantage is especially pronounced when the native two-qubit gates are not part of the Clifford group, which is the case for e.g. the $\sqrt {{\mathrm{SWAP}}}$ gate.^39,40

Methods

In this section will discuss three things: (1) The statistical behavior and scalability of character randomized benchmarking, (2) the robustness of character randomized benchmarking against gate-dependent noise, and (3) the behavior of interleaved character randomized benchmarking, and in particular 2-for-1 interleaved benchmarking.

First we will consider whether the character randomized benchmarking protocol is efficiently scalable with respect to the number of qubits (like standard randomized benchmarking) and whether the character randomized benchmarking protocol remains practical when only a finite amount of data can be gathered (this last point is a sizable line of research for standard randomized benchmarking^6,28,30,41).

Scalability of character randomized benchmarking

The resource cost (the number of experimental runs that must be performed to obtain an estimate of the average fidelity) of character randomized benchmarking can be split into two contributions: (1) The number of quality parameters f_λ associated that must be estimated (this is essentially set by |R_G|, the number of irreducible subrepresentations of the PTM representation of the benchmarking group G), and (2) the cost of estimating a single average $k_m^{\lambda \prime }$ for a fixed λ′ ∈ R_G and sequence length m.

The first contribution implies that for scalable character randomized benchmarking with (a uniform family of) groups G_q (w.r.t. the number of qubits q) the number of quality parameters (set by |R_G|) must grow polynomially with q. This means that not all families of benchmarking groups are can be characterized by character randomized benchmarking in a scalable manner.

The second contribution, as can be seen in Fig. 1, further splits up into three components: (2a) the magnitude of $|\hat \phi |$, (2b) the number of random sequences $\vec G$ needed to estimate $k_m^{\lambda \prime }$ (given access to $k_m^{\lambda \prime }(\vec G)$) and (2c) the number of samples needed to estimate $k_m^{\lambda \prime }(\vec G)$ for a fixed sequence. We will now argue that the resource cost of all three components are essentially set by the magnitude of $|\hat \phi |$. Thus if $|\hat \phi |$ grows polynomially with the number of qubits then the entire resource cost does so as well. Hence a sufficient condition for scalable character randomized benchmarking is that one chooses a family of benchmarking groups where |R_G| grows polynomially in q and character groups such that for the relevant subrepresentations $|\hat \phi |$ the dimension grows polynomially in q.

We begin by arguing (2c):The character-weighted average over the group ${\hat{\mathrm G}}$ for a single sequence $\vec G$: $k_m^{\lambda \prime }(\vec G)$, involves an average over $|{\hat{\mathrm G}}|$ elements (which will generally scale exponentially in q), but can be efficiently estimated by not estimating each character-weighted expectation value $k_m^{\lambda \prime }(\vec G,\hat G)$ individually but rather estimate $k_m^{\lambda \prime }(\vec G)$ directly by the following procedure

• 1. Sample $\hat G \in {\hat{\mathrm G}}$ uniformly at random

• 2. Prepare the state ${\cal{G}}_{{\mathrm{inv}}}{\cal{G}}_m \cdots {\cal{G}}_1\hat {\cal{G}}|\rho \rangle \rangle$ and measure it once obtaining a result $b(\hat G) \in \{ 0,1\}$

• 3. Compute $x(\hat G): = \chi _{\hat \phi }(\hat G)|\hat \phi |b(\hat G) \in \{ 0,\chi _{\hat \phi }(\hat G)|\hat \phi |\}$

• 4. Repeat sufficiently many times and compute the empirical average of $x(\hat G)$

Through the above procedure we are directly sampling from a bounded probability distribution with mean $k_m^{\lambda \prime }(\vec G)$ that takes values in the interval $[ - \chi _{\hat \phi }^ \ast ,\chi _{\hat \phi }^ \ast ]$ where $\chi _{\hat \phi }^ \ast$ is the largest absolute value of the character function $\chi _{\hat \phi }$. Since the maximal absolute value of the character function is bounded by the dimension of the associated representation,²⁹ this procedure will be efficient as long as $|\hat \phi |$ is not too big.

For the examples given in the discussion section (with the character group being the Pauli group) the maximal character value is 1. Using standard statistical techniques⁴² we can give e.g. a 99% confidence interval of size 0.02 around $k_m^{\lambda \prime }(\vec G)$ by repeating the above procedure 1769 times, which is within an order of magnitude of current experimental practice for confidence intervals around regular expectation values and moreover independent of the number of qubits q. See section VI in the Supplementary Methods for more details on this.

We now consider (2b): From the considerations above we know that $k_m^{\lambda \prime }(\vec G)$ is the mean of a set of random variables and thus itself a random variable, taking possible values in the interval $[ - \chi _{\hat \phi }^ \ast ,\chi _{\hat \phi }^ \ast ]$. Hence by the same reasoning as above we see that $k_m^{\lambda \prime }$, as the mean of a distribution (induced by the uniform distribution of sequences $\vec G$) confided to the interval $[ - \chi _{\hat \phi }^ \ast ,\chi _{\hat \phi }^ \ast ]$ can be estimated using an amount of resources polynomially bounded in $|\hat \phi |$. We would like to note however that this estimate is probably overly pessimistic in light of recent results for standard randomized benchmarking on the Clifford group^28,30 where it was shown that the average $k_m^{\lambda \prime }$ over sequences $\vec G \in {\mathrm{G}}^{ \times m}$ can be estimated with high precision and high confidence using only a few hundred sequences. These results depend on the representation theoretic structure of the Clifford group but we suspect that it is possible to generalize these results at least partially to other families of benchmarking groups. Moreover any such result can be straightforwardly adapted to also hold for character randomized benchmarking. Actually making such estimates for other families groups is however an open problem, both for standard and character randomized benchmarking.

To summarize, the scalability of character randomized benchmarking depends on the properties of the families of benchmarking and character groups chosen. One should choose the benchmarking groups such that the number of exponential decays does not grow too rapidly with the number of qubits, and one should choose the character group such that the dimension of the representation being projected on does not grow too rapidly with the number of qubits.

Gate-dependent noise

Thus far we have developed the theory of character randomized benchmarking under the assumption of gate-independent noise. This is is not a very realistic assumption. Here we will generalize our framework to include gate-dependent noise. In particular we will deal with the so called ‘non-Markovian’ noise model. This noise model is formally specified by the existence of a function ${\mathrm{\Phi }}:{\mathrm{G}} \to {\cal{S}}_{2^q}$ which assigns to each element G of the group G a quantum channel ${\mathrm{\Phi }}(G) = {\cal{E}}_G$. Note that this model is not the most general, it does not take into account the possibility of time dependent effects or memory effects during the experiment. It is however much more general and realistic than the gate-independent noise model. In this section we will prove two things:

• 1. A character randomized benchmarking experiment always yields data that can be fitted to a single exponential decay up to a small and exponentially decreasing corrective term.

• 2. The decay rates yielded by a character randomized benchmarking experiment can be related to the average fidelity (to the identity) of the noise in between gates, averaged over all gates.

Both of these statements, and their proofs, are straightforward generalizations of the work of Wallman¹⁴ which dealt with standard randomized benchmarking. We will see that his conclusion, that randomized benchmarking measures the average fidelity of noise in between quantum gates up to a small correction, generalizes to the character benchmarking case. We begin with a technical theorem, which generalizes [¹⁴, Theorem 2] to twirls over arbitrary groups (with multiplicity-free PTM representations).

Theorem 1

Let G be a group such that its PTM representation ${\cal{G}} = \oplus _{\lambda \in R_{\mathrm{G}}}\phi _\lambda (G)$ is multiplicity-free. Denote for all λ by f_λ the largest eigenvalue of the operator ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))$ where $\tilde {\cal{G}}$ is the CPTP implementation of G ∈ G. There exist Hermicity-preserving linear superoperators ${\cal{L}},{\cal{R}}$ such that

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} (\tilde {\cal{G}}{\cal{L}}{\cal{G}}^\dagger ) = {\cal{L}}{\cal{D}}_{\mathrm{G}},$$

(11)

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} ({\cal{G}}^\dagger {\cal{R}}\tilde {\cal{G}}) = {\cal{D}}_{\mathrm{G}}{\cal{R}},$$

(12)

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} ({\cal{G}}{\cal{R}}{\cal{L}}{\cal{G}}^\dagger ) = {\cal{D}}_{\mathrm{G}},$$

(13)

where ${\cal{D}}_{\mathrm{G}}$ is defined as

$${\cal{D}}_{\mathrm{G}} = \mathop {\sum}\limits_\lambda {f_\lambda } {\cal{P}}_\lambda ,$$

(14)

with ${\cal{P}}_\lambda$ the projector onto the representation ϕ_λ for all λ ∈ R_G.

Proof. Using the definition of ${\cal{G}}$ and ${\cal{D}}_{\mathrm{G}}$ we can rewrite Eq. (11) as

$$\mathop {\sum}\limits_\lambda {\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} } (\tilde {\cal{G}}({\cal{L}}{\cal{P}}_\lambda )\phi _\lambda (G)^\dagger ) = \mathop {\sum}\limits_\lambda {f_\lambda } {\cal{L}}{\cal{P}}_\lambda .$$

(15)

This means that, without loss of generality, we can take ${\cal{L}}$ to be of the form

$${\cal{L}} = \mathop {\sum}\limits_\lambda {{\cal{L}}_\lambda } ,\quad {\cal{L}}_\lambda {\cal{P}}_{\lambda^{\prime} } = \delta _{\lambda \lambda^{\prime} }{\cal{L}}_\lambda ,\quad \forall \lambda^{\prime} .$$

(16)

Similarly we can take ${\cal{R}}$ to be

$${\cal{R}} = \mathop {\sum}\limits_\lambda {{\cal{R}}_\lambda } ,\quad {\cal{P}}_{\lambda^{\prime} }{\cal{R}}_\lambda = \delta _{\lambda \lambda^{\prime} }{\cal{R}}_\lambda ,\quad \forall \lambda^{\prime} .$$

(17)

This means Eqs. (11) and (12) decompose into independent pairs of equations for each λ:

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} (\tilde {\cal{G}}{\cal{L}}_\lambda \phi _\lambda (G)^\dagger ) = f_\lambda {\cal{L}}_\lambda$$

(18)

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} (\phi _\lambda (G)^\dagger {\cal{R}}\tilde {\cal{G}}) = f_\lambda {\cal{R}}_\lambda .$$

(19)

Next we use the vectorization operator ${\mathrm{vec}}:{\mathrm{M}}_{2^{2q}} \to {\Bbb R}^{2^{4q}}$ mapping the PTM representations of superoperators to vectors of length ${\Bbb R}^{2^{4q}}$. This operator has the property that for all $A,B,C \in {\mathrm{M}}_{2^{2q}}$ we have

$${\mathrm{vec}}(ABC) = A \otimes C^T{\mathrm{vec}}(B)$$

(20)

where C^T is the transpose of C. Applying this to the equations Eqs. (18) and (19) and noting that ${\cal{G}}^\dagger = {\cal{G}}^T$ since ${\cal{G}}$ is a real matrix we get the eigenvalue problems equivalent to Eqs. (18) and (19),

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} (\tilde {\cal{G}} \otimes \phi _\lambda (G)){\mathrm{vec}}({\cal{L}}_\lambda ) = f_\lambda {\mathrm{vec}}({\cal{L}}_\lambda )$$

(21)

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} (\tilde {\cal{G}} \otimes \phi _\lambda (G))^T{\mathrm{vec}}({\cal{R}}_\lambda ) = f_\lambda {\mathrm{vec}}({\cal{R}}_\lambda ).$$

(22)

Since we have defined f_λ to be the largest eigenvalue of ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))$ (and equivalently of ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))^T$) we can choose ${\mathrm{vec}}({\cal{L}})$ and ${\mathrm{vec}}({\cal{R}})$ to be the left and right eigenvectors respectively of ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))$ associated to f_λ. Inverting the vectorization we obtain solutions to the equations Eqs. (18) and (19) and hence also Eqs. (11) and (12). To see that this solution also satisfies Eq. (13) we note first that ${\Bbb E}_{G \in {\mathrm{G}}}({\cal{G}}{\cal{R}}_\lambda {\cal{L}}_\lambda {\cal{G}}^\dagger )$ is proportional to P_λ for any ${\cal{R}}_\lambda ,{\cal{L}}_\lambda$ satisfying Eqs. (16) and (17) (by Schur’s lemma). Since the eigenvectors of ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))$ are only defined up to a constant we can for every λ choose proportionality constants such that ${\Bbb E}_{G \in {\mathrm{G}}}({\cal{G}}{\cal{R}}_\lambda {\cal{L}}_\lambda {\cal{G}}^\dagger ) = f_\lambda P_\lambda$ and thus that Eq. (13) is satisfied.

Next we prove that if we perform a character randomized benchmarking experiment with benchmarking group G, character group $\hat G$ and subrepresentations $\hat \phi \subset \phi _{\lambda^{\prime} }$ for some λ′ ∈ R_G, the observed data can always be fitted (up to an exponentially small correction) to a single exponential decay. The decay rate of f_λ′ associated to this experiment will be the largest eigenvalue of the operator ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _{\lambda^{\prime} }(G))$ mentioned in the theorem above. Later we will give an operational interpretation of this number. We begin by defining, for all G ∈ G a superoperator Δ_G which captures the ‘gate-dependence’ of the noise implementation of ${\cal{G}}$,

$${\mathrm{\Delta }}_G: = \tilde {\cal{G}} - {\cal{L}}{\cal{G}}{\cal{R}},$$

(23)

where ${\cal{R}},{\cal{L}}$ are defined as in Theorem 1. Using this expansion we have the following theorem, which generalizes [¹⁴, Theorem 4] to character randomized benchmarking over arbitrary finite groups with multiplicity-free PTM representation.

Theorem 2

Let G be a group such that its PTM representation ${\cal{G}} = \oplus _{\lambda \in R_{\mathrm{G}}}\phi _\lambda (G)$ is multiplicity-free. Consider the outcome of a character randomized benchmarking experiment with benchmarking group G, character group $\hat G$, subrepresentations $\hat \phi \subset \phi _{\lambda \prime }$ for some λ′ ∈ R_G, and set of sequence lengths ${\Bbb M}$. That is, consider the real number

$$k_m^{\lambda^{\prime} } = \mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} \mathop {{\Bbb E}}\limits_{\hat G \in {\hat{\mathrm G}}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_m \cdots \widetilde {{\cal{G}}_1\widehat {\cal{G}}}|\rho \rangle \rangle$$

(24)

for some input state ρ and output POVM {Q, 1 − Q} and $m \in {\Bbb M}$. This probability can be fitted to an exponential of the form

$$k_m^{\lambda^{\prime} } = _{{\mathrm{fit}}}Af_{\lambda^{\prime} }^m + \varepsilon _m,$$

(25)

where A is a fitting parameter, f_λ is the largest eigenvalue of the operator ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _\lambda (G))$ and $\varepsilon _m \le \delta _1\delta _2^m$ with

$$\delta _1 = |\hat \phi |\mathop {{{\mathrm{max}}}}\limits_{\hat G \in {\hat{\mathrm G}}} |\chi _{\hat \phi }(\hat G)|\mathop {{{\mathrm{max}}}}\limits_{G \in {\mathrm{G}}} \left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit ,$$

(26)

$$\delta _2 = {\Bbb E}_{G \in {\mathrm{G}}}\left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit ,$$

(27)

where $\left\| \cdot \right\|_\diamondsuit$ is the diamond norm on superoperators.⁴³

Proof. We begin by expanding $\widetilde {{\cal{G}}_{1}\widehat {\cal{G}}} = {\cal{L}}{\cal{G}}_{1}\hat {\cal{G}}{\cal{R}} + {\mathrm{\Delta }}_{G_{1}\hat {G}}$. This gives us

$$k_{m}^{\lambda^{\prime} } = - \mathop {\Bbb E}\limits_{\begin{array}{c} \hat{G} \in {\hat{\mathrm G}} \\ G_{1}, \ldots ,G_{m} \in {\mathrm{G}} \end{array}} \chi _{\hat {\phi} }(\hat {G})|\hat {\phi} |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots {\cal{L}}{\cal{G}}_{1}\hat {\cal{G}}{\cal{R}}|\rho \rangle \rangle$$

(28)

$$+ \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_m \cdots {\mathrm{\Delta }}_{G_{1}\hat {G}}|\rho \rangle \rangle .$$

(29)

We now analyze the first term in Eq. (28). Using the character projection formula, the fact that ${\cal{G}}_1 = ({\cal{G}}_{inv}{\cal{G}}_m \ldots {\cal{G}}_2)^\dagger$ and Eq. (11) from Theorem 1 we get

$$\mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} \hat G \in {\hat{\mathrm G}} \\ G_{1}, \ldots ,G_{m} \in {\mathrm{G}} \end{array}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots {\cal{L}}{\cal{G}}_{1}\hat {\cal{G}}{\cal{R}}|\rho \rangle \rangle$$

$$= \mathop {{\Bbb E}}\limits_{G_{1}, \ldots ,G_{m} \in {\mathrm{G}}} \langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{2}{\cal{L}}{\cal{G}}_{2}^\dagger \ldots {\cal{G}}_{{\mathrm{inv}}}^\dagger {\cal{P}}_{\hat \phi }{\cal{R}}|\rho \rangle \rangle$$

(30)

$$=\mathop {\Bbb E}\limits_{G_{3}, \ldots ,G_m \in {\mathrm{G}}} \langle \langle Q|\tilde {\cal{G}}_{\mathrm{inv}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_3{\cal{L}}{\cal{D}}_{\mathrm{G}}{\cal{G}}_3^\dagger \ldots {\cal{G}}_{{\mathrm{inv}}}^\dagger {\cal{P}}_{\hat \phi }{\cal{R}}|\rho \rangle \rangle$$

(31)

$$= \langle \langle Q|{\cal{L}}{\cal{D}}_{\mathrm{G}}^m{\cal{P}}_{\hat \phi }{\cal{R}}|\rho \rangle \rangle$$

(32)

$$= f_{\lambda^{\prime} }^m\langle \langle Q|{\cal{L}}{\cal{P}}_{\hat \phi }{\cal{R}}|\rho \rangle \rangle$$

(33)

where we used that ${\cal{D}}_{\mathrm{G}}$ commutes with ${\cal{G}}$ for all G ∈ G and the fact that ${\cal{D}}_{\mathrm{G}}{\cal{P}}_{\hat \phi } = f_{\lambda^{\prime}}{\cal{P}}_{\hat \phi }$. Next we consider the second term in Eq. (28). For this we first need to prove a technical statement. We make the following calculation for all j ≥ 2 and $\hat G \in {\hat{\mathrm G}}$:

$$\mathop {{\Bbb E}}\limits_{G_{1}, \ldots ,G_{m} \in {\mathrm{G}}} \tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{j + 1}{\cal{L}}{\cal{G}}_{j}{\cal{R}}{\mathrm{\Delta }}_{G_{j - 1}} \ldots {\mathrm{\Delta }}_{G_{1}\hat{G}}$$

(34)

$$= \mathop {\Bbb E}\limits_{G_{1}, \ldots ,G_{m} \in {\mathrm{G}}} \tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{j + 1}{\cal{L}}{\cal{G}}_{j + 1}^\dagger \ldots {\cal{G}}_{m}^\dagger$$

$$\times {\cal{G}}_{{\mathrm{inv}}}{\cal{G}}_{1}^\dagger \ldots {\cal{G}}_{j - 1}^\dagger {\cal{R}}{\mathrm{\Delta }}_{G_{j - 1}} \ldots {\mathrm{\Delta }}_{G_{1}\hat{G}}$$

(35)

$$= \mathop {{\Bbb E}}\limits_{G_{1}, \ldots ,G_{m} \in {\mathrm{G}}} \tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{j + 1}{\cal{L}}{\cal{G}}_{j + 1}^\dagger \ldots {\cal{G}}_{m}^\dagger$$

$$\times {\cal{G}}_{{\mathrm{inv}}}{\cal{G}}_{1}^\dagger \ldots {\cal{G}}_{j - 1}^\dagger {\cal{R}}(\tilde {\cal{G}}_{j - 1} - {\cal{L}}{\cal{G}}_{j - 1}{\cal{R}})$$

$$\times {\mathrm{\Delta }}_{G_{j - 2}} \ldots {\mathrm{\Delta }}_{G_{1}\hat {G}}$$

(36)

$$= \mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {G_{1}, \ldots ,G_{j - 1},} \\ {G_{j + 1}, \ldots G_{m} \in {\mathrm{G}}} \end{array}} \tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{j + 1}{\cal{L}}{\cal{G}}_{j + 1}^\dagger \ldots {\cal{G}}_{m}^\dagger$$

$$\times {\cal{G}}_{{\mathrm{inv}}}{\cal{G}}_1^\dagger \ldots {\cal{G}}_{j - 2}^\dagger ({\cal{D}}_{\mathrm{G}} - {\cal{D}}{\mathrm{G}}){\cal{R}}{\mathrm{\Delta }}_{G_{j - 2}} \ldots {\mathrm{\Delta }}_{G_{1}\hat{G}}$$

(37)

$$= 0$$

(38)

where we used the definition of ${\mathrm{\Delta }}_{G_{j - 1}}$, the fact that $G_{j - 1} = (G_m \ldots G_{j + 1})^\dagger G_{{\mathrm{inv}}}(G_1 \ldots G_{j - 1})^\dagger$ and Eqs. (12) and (13). We can apply this calculation to the second term of Eq. (28) to get

$$\mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat {G}\in{\hat{\mathrm G}}} \\ {G_{1}, \ldots,G_{m} \in {\mathrm{G}}} \end{array}} \chi _{\hat{\phi} }(\hat {G})|\hat {\phi} |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_2{\mathrm{\Delta }}_{G_{1}\hat{G}}|\rho \rangle \rangle$$

(39)

$$=\mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_m \cdots ({\cal{L}}{\cal{G}}_2{\cal{R}} + {\mathrm{\Delta }}_{G_2})$$

$$\times {\mathrm{\Delta }}_{G_1\hat G}|\rho \rangle \rangle$$

(40)

$$=\mathop {{\Bbb E}}\limits_{\begin{array}{c} \hat {G} \in {\hat{\mathrm G}} \\ G_1, \ldots ,G_m \in {\mathrm{G}} \end{array}} \chi _{\hat {\phi} }(\hat {G})|\hat {\phi} |\langle \langle Q|\tilde {\cal{G}}_{{\mathrm{inv}}}\tilde {\cal{G}}_{m} \cdots \tilde {\cal{G}}_{3}{\mathrm{\Delta }}_{G_{2}}{\mathrm{\Delta }}_{G_{1}\hat {G}}|\rho \rangle \rangle$$

(41)

$$= \mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|{\mathrm{\Delta }}_{G_{{\mathrm{inv}}}}{\mathrm{\Delta }}_{G_m} \ldots {\mathrm{\Delta }}_{G_1\hat G}|\rho \rangle \rangle$$

(42)

Hence we can write

$$k_m^\lambda = f_{\lambda \prime }^m\langle \langle Q|{\cal{L}}{\cal{P}}_\phi {\cal{R}}|\rho \rangle \rangle + \varepsilon _m$$

(43)

with

$$\varepsilon _m = \mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|{\mathrm{\Delta }}_{G_{{\mathrm{inv}}}}{\mathrm{\Delta }}_{G_m} \ldots {\mathrm{\Delta }}_{G_1\hat G}|\rho \rangle \rangle .$$

(44)

We can upper bound ε_m by

$$\mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} \chi _{\hat \phi }(\hat G)|\hat \phi |\langle \langle Q|{\mathrm{\Delta }}_{G_{{\mathrm{inv}}}}{\mathrm{\Delta }}_{G_m} \ldots {\mathrm{\Delta }}_{G_1\hat G}|\rho \rangle \rangle$$

(45)

$$\le \mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} |\chi _{\hat \phi }(\hat G)||\hat \phi |\left\| {{\mathrm{\Delta }}_{G_{{\mathrm{inv}}}}} \right\|_\diamondsuit \left\| {{\mathrm{\Delta }}_{G_m}} \right\|_\diamondsuit \ldots \left\| {{\mathrm{\Delta }}_{G_1\hat G}} \right\|_\diamondsuit$$

(46)

$$\le \mathop {{{\mathrm{max}}}}\limits_{\hat G \in {\hat{\mathrm G}}} |\chi _{\hat \phi }(\hat G)||\hat \phi |\mathop {{{\mathrm{max}}}}\limits_{G \in {\mathrm{G}}} \left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit \left( {{\Bbb E}_{G \in {\mathrm{G}}}\left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit } \right)^m.$$

(47)

Setting

$$\delta _1 = |\hat \phi |\left( {\mathop {{{\mathrm{max}}}}\limits_{\hat G \in {\hat{\mathrm G}}} |\chi _{\hat \phi }(\hat G)|} \right)\left( {\mathop {{{\mathrm{max}}}}\limits_{G \in {\mathrm{G}}} \left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit } \right)$$

(48)

$$\delta _2 = \mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} \left\| {{\mathrm{\Delta }}_G} \right\|_\diamondsuit$$

(49)

we complete the proof.

In¹⁴ it was shown that δ₂ is small for realistic gate-dependent noise. This implies that for large enough m the outcome of a character randomized benchmarking experiment can be described by a single exponential decay (up to a small, exponentially decreasing factor). The rate of decay f_λ′ can be related to the largest eigenvalue of the operator ${\Bbb E}_{G \in {\mathrm{G}}}(\tilde {\cal{G}} \otimes \phi _{\lambda^{\prime} }(G))$. We can interpret this rate of decay following Wallman¹⁴ by setting w.l.o.g. $\tilde {\cal{G}} = {\cal{L}}_G{\cal{G}}{\cal{R}}$ where ${\cal{R}}$ is defined as in Theorem 1 and is invertible (we can always render ${\cal{R}}$ invertible by an arbitrary small perturbation). Now consider from $\tilde {\cal{G}} = {\cal{L}}_G{\cal{G}}{\cal{R}}$ and the invertibility of ${\cal{R}}$:

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\mathrm{Tr}}({\cal{G}}^\dagger {\cal{R}}\tilde {\cal{G}}{\cal{R}}^{ - 1}) = \mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\mathrm{Tr}}({\cal{G}}^\dagger {\cal{R}}{\cal{L}}_G{\cal{G}}{\cal{R}}{\cal{R}}^{ - 1})$$

(50)

$$= \mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\mathrm{Tr}}({\cal{R}}{\cal{L}}_G)$$

(51)

and moreover from Eq. (12):

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} {\mathrm{Tr}}({\cal{G}}^\dagger {\cal{R}}\tilde {\cal{G}}{\cal{R}}^{ - 1}) = \mathop {\sum}\limits_{\lambda \in R_{\mathrm{G}}} {f_\lambda } {\mathrm{Tr}}({\cal{P}}_\lambda ).$$

(52)

From this we can consider the average fidelity of noise between gates (the map $({\cal{R}}{\cal{L}}_G)$ averaged over all gates:

$$\mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} F_{{\mathrm{avg}}}({\cal{R}}{\cal{L}}_G) = \mathop {{\Bbb E}}\limits_{G \in {\mathrm{G}}} \frac{{2^{ - q}{\mathrm{Tr}}({\cal{R}}{\cal{L}}_G) + 1}}{{2^q + 1}}$$

(53)

$$= \frac{{2^{ - q}\mathop {\sum}\nolimits_{\lambda \in R_{\mathrm{G}}} {f_\lambda } {\mathrm{Tr}}({\cal{P}}_\lambda ) + 1}}{{2^q + 1}}.$$

(54)

Hence can interpret the quality parameters given by character randomized benchmarking as characterizing the average noise in between gates, extending the conclusion reached in¹⁴ for standard randomized benchmarking to character randomized benchmarking. In ref. ¹⁶ an alternative interpretation of the decay rate of randomized benchmarking in the presence of gate dependent noise is given in terms of Fourier transforms of matrix valued group functions. One could recast the above analysis for character randomized benchmarking in this language as well but we do not pursue this further here.

Interleaved character randomized benchmarking

In the main text we proposed 2-for-1 interleaved randomized benchmarking, a form of character interleaved randomized benchmarking. More generally we can consider performing interleaved character randomized benchmarking with a benchmarking group G, a character group ${\hat{\mathrm G}}$, and an interleaving gate C. However it is not obvious that the interleaved character randomized benchmarking procedure (for arbitrary G and C) always yields data that can be fitted to a single exponential such that the average fidelity can be extracted. Here we will justify this behavior subject to an assumption on the relation between the interleaving gate C and the benchmarking group G which we expect to be quite general. This relation is phrased in terms of what we call the ‘mixing matrix’ of the group G and gate C. This matrix, which we denote by M, has entries

$$M_{\lambda ,\hat \lambda } = \frac{1}{{{\mathrm{Tr}}({\cal{P}}_\lambda )}}{\mathrm{Tr}}\left( {{\cal{P}}_\lambda {\cal{C}}{\cal{P}}_{\hat \lambda }{\cal{C}}^\dagger } \right)$$

(55)

for $\lambda ,\lambda \prime \in R_{\mathrm{G}}^\prime = R_{\mathrm{G}}\backslash \{ {\mathrm{id}}\}$ with ϕ_id the trivial subrepresentation of the PTM representation of G carried by |1〉〉 and where ${\cal{P}}_\lambda$ is the projector onto the subrepresentation ϕ_λ of ${\cal{G}}$. Note that this matrix is defined completely by C and the PTM representation of G. Note also that this matrix has only non-negative entries, that is $M_{\lambda ,\hat \lambda } \ge 0\quad \forall \lambda ,\hat \lambda$.

In the following lemma we will assume that the mixing matrix M is not only non-negative but also irreducible in the Perron-Frobenius sense.⁴⁴ Formally this means that there exists an integer L such that A^L has only strictly positive entries. This assumption will allow us to invoke the powerful Perron-Frobenius theorem⁴⁴ to prove in Theorem 3 that interleaved character randomized benchmarking works as advertised. Below Theorem 3 we will also explicitly verify the irreducibility condition for 2-for-1 interleaved benchmarking with the CPHASE gate. We note that the assumption of irreducibility of M can be easily relaxed to M being a direct sum of irreducible matrices with the proof of Theorem 3 basically unchanged. It is an open question if it can be relaxed further to encompass all non-negative mixing matrices.

Theorem 3

Consider the outcome $k_{\lambda^{\prime} }^m$ of an interleaved character randomized benchmarking experiment benchmarking group G, character group $\hat G$, subrepresentations $\hat \phi \subset \phi _{\lambda^{\prime} }$ for some λ′ ∈ R_G, interleaving gate C, and set of sequence lengths ${\Bbb M}$ and assume the existence of quantum channels ${\cal{E}}_C,{\cal{E}}$ s.t. $\tilde {\cal{C}} = {\cal{C}}{\cal{E}}_C$ and $\tilde {\cal{G}} = {\cal{E}}{\cal{G}}$ for all G ∈ G. Now consider the matrix $M({\cal{E}}_C{\cal{E}})$ as a function of the composed channel ${\cal{E}}_C{\cal{E}}$ with entries

$$M_{\lambda ,\hat \lambda }({\cal{E}}_C{\cal{E}}) = \frac{1}{{{\mathrm{Tr}}({\cal{P}}_\lambda )}}{\mathrm{Tr}}\left( {{\cal{P}}_\lambda {\cal{C}}{\cal{P}}_{\hat \lambda }{\cal{C}}^\dagger {\cal{E}}_C{\cal{E}}} \right)$$

(56)

for $\lambda ,\lambda^{\prime} \in R_{\mathrm{G}}^{\prime} = R_{\mathrm{G}}\backslash \{ {\mathrm{id}}\}$ where ${\cal{P}}_\lambda$ is again the projector onto the subrepresentation ϕ_λ of ${\cal{G}}$. If for ${\cal{E}} = {\cal{E}}_C = {\cal{I}}$ (the identity map) the matrix $M({\cal{I}}) = M$ (the mixing matrix defined above) is irreducible (in the sense of Perron-Frobenius), then there exist parameters A, f_λ′ s.t.

$$|k_{\lambda^{\prime} }^m - Af_{\lambda^{\prime} }^m| \le \delta _1\delta _2^m$$

(57)

with $\delta _1 = O(1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}}))$ and $\delta _2 = \gamma + O([1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}})]^2)$ where γ is the second largest eigenvalue (in absolute value) of M. Moreover we have that (noting that f_id = 1 as the map ${\cal{E}}_C{\cal{E}}$ is CPTP):

$$\left| {\frac{1}{{2^q}}\mathop {\sum}\limits_{\lambda \in R_{\mathrm{G}}} {{\mathrm{Tr}}} ({\cal{P}}_\lambda )f_\lambda - \frac{{2^q(F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}}) + 1)}}{{2^q + 1}}} \right|$$

$$\le O\left( {[1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}})]^2} \right)$$

(58)

Proof. Consider the definition of $k_{\lambda \prime }^m$:

$$k_m^{\lambda^{\prime} } = |\hat \phi |\mathop {{\Bbb E}}\limits_{\begin{array}{*{20}{c}} {\hat G \in {\hat{\mathrm G}}} \\ {G_1, \ldots ,G_m \in {\mathrm{G}}} \end{array}} \chi _{\hat \phi }(\hat G)\langle \langle Q|{\cal{E}}_{{\mathrm{inv}}}{\cal{G}}_{{\mathrm{inv}}}{\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_m$$

$$\times {\cal{C}}{\cal{E}}_C{\cal{E}} \ldots {\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_1\hat {\cal{G}}|\rho \rangle \rangle ,$$

(59)

where $G_{{\mathrm{inv}}} = G_1^\dagger C^\dagger \cdots G_m^\dagger C^\dagger$ and ${\cal{E}}_{{\mathrm{inv}}}$ is the noise associated to the inverse gate (which we assume to be constant). Using the character projection formula and Schur’s lemma we can write this as

$$k_m^{\lambda \prime } = \mathop {{\Bbb E}}\limits_{G_1, \ldots ,G_{m - 1} \in {\mathrm{G}}} \langle \langle Q|{\cal{E}}_{{\mathrm{inv}}}{\cal{G}}_1^\dagger {\cal{C}}^\dagger \cdots {\cal{G}}_{m - 1}^\dagger {\cal{C}}^\dagger$$

$$\times \left[ {\mathop {\sum}\limits_{\lambda _m \in R_{\mathrm{G}}^\prime } {\frac{{{\mathrm{Tr}}(P_{\lambda _m}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{\lambda _m})}}} {\cal{P}}_{\lambda _m}} \right]{\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_{m - 1}$$

$$\times {\cal{C}}{\cal{E}}_C{\cal{E}} \ldots {\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_1{\cal{P}}_{\hat \phi }|\rho \rangle \rangle .$$

(60)

Note now that in general ${\cal{C}}$ and ${\cal{P}}_{\lambda _m}$ do not commute. This means that we can not repeat the reasoning of Lemma 3 but must instead write (using Schur’s lemma again):

$$k_m^{\lambda^{\prime} } = \mathop {\sum}\limits_{\lambda _m \in R_{\mathrm{G}}^\prime } {\frac{{{\mathrm{Tr}}(P_{\lambda _m}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{\lambda _m})}}} \mathop {{\Bbb E}}\limits_{G_1, \ldots ,G_{m - 2} \in {\mathrm{G}}} \langle \langle Q|{\cal{E}}_{{\mathrm{inv}}}{\cal{G}}_1^\dagger {\cal{C}}^\dagger \cdots {\cal{G}}_{m - 2}^\dagger {\cal{C}}^\dagger$$

$$\times \left[ {\mathop {\sum}\limits_{\lambda _{m - 1} \in R_{\mathrm{G}}^\prime } {\frac{{{\mathrm{Tr}}({\cal{P}}_{\lambda _{m - 1}}{\cal{C}}^\dagger {\cal{P}}_{\lambda _m}{\cal{C}}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{\lambda _{m - 1}})}}} } \right]$$

$$\times {\cal{P}}_{\lambda _{m - 1}}{\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_{m - 2}{\cal{C}}{\cal{E}}_C$$

$$\times {\cal{E}} \ldots {\cal{C}}{\cal{E}}_C{\cal{E}}{\cal{G}}_1{\cal{P}}_{\hat \phi }|\rho \rangle \rangle .$$

(61)

Here we recognize the definition of the matrix element $M_{\lambda _{m - 1},\lambda _m}({\cal{E}}_C{\cal{E}})$. Moreover we can apply the above expansion to G_m−2,G_m−3 and so forth writing the result in terms of powers of the matrix $M({\cal{E}}_C{\cal{E}})$. After some reordering we get

$$k_m^{\lambda^{\prime} } = \mathop {\sum}\limits_{\lambda _1,\lambda _m \in R_{\mathrm{G}}^\prime } {\frac{{{\mathrm{Tr}}(P_{\lambda _m}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{\lambda _m})}}} [M^{m - 1}]_{\lambda _1,\lambda _m}\langle \langle Q|{\cal{P}}_{\lambda _1}{\cal{P}}_{\hat \phi }|\rho \rangle \rangle$$

where we have again absorbed the noise associated with the inverse G_inv into the measurement POVM element Q. Now recognizing that by construction ${\cal{P}}_{\hat \phi } \subset {\cal{P}}_{\lambda \prime }$ we can write $k_m^{\lambda \prime }$ as

$$k_m^{\lambda^{\prime} } = e_{\lambda^{\prime} }M^mv^T\langle \langle Q|{\cal{P}}_{\hat \phi }|\rho \rangle \rangle$$

(62)

where e_λ′ is the λ′th standard basis row vector of length $R_{\mathrm{G}}^\prime$ and $v = v({\cal{E}}_C{\cal{E}})$ is a row vector of length $R_{_{\mathrm{G}}}^\prime$ with entries $[v]_\lambda = \frac{{{\mathrm{Tr}}(P_{\lambda _m}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{\lambda _m})}}$. This looks somewhat like an exponential decay but not quite. Ideally we would like that M^m has one dominant eigenvalue and moreover that the vector v has high overlap with the corresponding eigenvector. This would guarantee that $k_m^{\lambda \prime }$ is close to a single exponential. The rest of the proof will argue that this is indeed the case. Now we use the assumption of the irreducibility of the mixing matrix $M = M({\cal{I}})$. Subject to this assumption, the Perron-Frobenius theorem⁴⁴ states that the matrix M has a non-degenerate eigenvalue $\gamma _{{\mathrm{max}}}(M({\cal{I}}))$ that is strictly larger in absolute value than all other eigenvalues of $M({\cal{I}})$ and moreover satisfies the inequality

$$\mathop {{\min }}\limits_{\lambda \in R_{\mathrm{G}}^\prime } \mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {M_{\lambda ,\hat \lambda }} \le \gamma _{{\mathrm{max}}}(M({\cal{I}})) \le \mathop {{\max }}\limits_{\lambda \in R_{\mathrm{G}}^\prime } \mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {M_{\lambda ,\hat \lambda }} .$$

(63)

It is easy to see from the definition of $M_{\lambda ,\hat \lambda }$ that

$$\mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {M_{\lambda ,\hat \lambda }} = \mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {\frac{1}{{{\mathrm{Tr}}({\cal{P}}_\lambda )}}} {\mathrm{Tr}}\left( {{\cal{P}}_\lambda {\cal{C}}{\cal{P}}_{\hat \lambda }{\cal{C}}^\dagger } \right)$$

(64)

$$= \mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {\frac{1}{{{\mathrm{Tr}}({\cal{P}}_\lambda )}}} \left( {{\cal{P}}_\lambda {\cal{C}}\mathop {\sum}\limits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {{\cal{P}}_{\hat \lambda }{\cal{C}}^\dagger } } \right)$$

(65)

$$= \frac{{{\mathrm{Tr}}({\cal{P}}_\lambda )}}{{{\mathrm{Tr}}({\cal{P}}_\lambda )}} = 1$$

(66)

for all $\lambda \in R_{\mathrm{G}}^\prime$. This means the largest eigenvalue of $M({\cal{I}})$ is exactly 1. Moreover, as one can easily deduce by direct calculation, the associated right-eigenvector is the vector v^R = (1, 1, …, 1). Note that this vector is precisely $v({\cal{E}}_C{\cal{E}})$ (as defined in Eq. (62)) for ${\cal{E}}_C{\cal{E}} = {\cal{I}}$. Similarly the left-eigenvector of $M = M({\cal{I}})$ is given by (in terms of its components) $v_\lambda ^L = {\mathrm{Tr}}({\cal{P}}_\lambda )$. This allows us to calculate that $k_m^{\lambda \prime } = \langle \langle Q|{\cal{P}}_{\hat \phi }|\rho \rangle \rangle$ if ${\cal{E}}_C{\cal{E}} = {\cal{I}}$, which is as expected.

Now we will consider the map ${\cal{E}}_C{\cal{E}}$ as a perturbation of ${\cal{I}}$ with the perturbation parameter

$$\alpha = 1 - \frac{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}}$$

(67)

with ${\cal{P}}_{{\mathrm{tot}}} = \mathop {\sum}\nolimits_{\lambda \in R_{\mathrm{G}}^\prime } {{\cal{P}}_\lambda }$. We can write the quantum channel ${\cal{E}}_C{\cal{E}}$ as ${\cal{E}}_C{\cal{E}} = {\cal{I}} - \alpha {\cal{F}}$ where ${\cal{F}}$ is some superoperator (not CP, but by construction trace-annihilating). Since $M({\cal{E}}_C{\cal{E}})$ is linear in its argument we can write $M({\cal{E}}_C{\cal{E}}) = M({\cal{I}}) - \alpha M({\cal{F}})$. From standard matrix perturbation theory [ref. ⁴⁵, Section 5.1] we can approximately calculate the largest eigenvalue of $M({\cal{E}}_C{\cal{E}})$ as

$$\gamma _{{\mathrm{max}}}(M({\cal{E}}_C{\cal{E}})) = \gamma _{{\mathrm{max}}}(M({\cal{I}}))$$

$$- \alpha \frac{{v^LM({\cal{F}})v^{R^T}}}{{v^Lv^{R^T}}} + O(\alpha ^2)$$

(68)

We can now calculate the prefactor $\frac{{v^LM({\cal{F}})v^{R^T}}}{{v^Lv^{R^T}}}$ as

$$\frac{{v^LA({\cal{F}})v^{R^T}}}{{v^Lv^{R^T}}} = \frac{{\mathop {\sum}\nolimits_{\lambda \in R_{\mathrm{G}}^\prime } {\mathop {\sum}\nolimits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {v_\lambda ^L} } M({\cal{F}})_{\lambda ,\hat \lambda }v_{\hat \lambda }^R}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}}$$

(69)

$$= \frac{{\mathop {\sum}\nolimits_{\lambda \in R_{\mathrm{G}}^\prime } {\mathop {\sum}\nolimits_{\hat \lambda \in R_{\mathrm{G}}^\prime } {{\mathrm{Tr}}} } (P_\lambda C^\dagger {\cal{P}}_{\hat \lambda }{\cal{F}})}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}}$$

(70)

$$= \frac{{{\mathrm{Tr}}\left( {{\cal{P}}_{{\mathrm{tot}}}{\cal{F}}} \right)}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}}$$

(71)

$$= \frac{1}{\alpha }\frac{{{\mathrm{Tr}}\left( {{\cal{P}}_{{\mathrm{tot}}}[{\cal{I}} - {\cal{E}}_C{\cal{E}}]} \right)}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}}$$

(72)

$$= 1$$

(73)

where we used the definition of α in the last line. This means that $\gamma _{{\mathrm{max}}}(M({\cal{E}}_C{\cal{E}})) = 1 - \alpha$ up to O(α²)corrections. One could in principle calculate the prefactor of the correction term, but we will not pursue this here. Now we know that the matrix $M({\cal{E}}_C{\cal{E}})^{m - 1}$ in Eq. (62) will be dominated by a factor (1 − α + O(α²))^m−1. However it could still be that the vector $v({\cal{E}}_C{\cal{E}})$ in Eq. (62) has small overlap with the right-eigenvector $v^R({\cal{E}}_C{\cal{E}})$ of $M({\cal{E}}_C{\cal{E}})$ associated to the largest eigenvalue $\gamma _{{\mathrm{max}}}(M({\cal{E}}_C{\cal{E}}))$. We can again use a perturbation argument to see that this overlap will be big. Again from standard perturbation theory [ref. ⁴⁵, Section 5.1] we have

$$\left\| {v^R({\cal{E}}_C{\cal{E}}) - v^R({\cal{I}})} \right\| = O(|\alpha |).$$

(74)

Moreover, by definition of $v^R({\cal{I}})$ and $v({\cal{E}}_C{\cal{E}})$ we have that $v^Rv({\cal{E}}_C{\cal{E}})^T = 1 - \alpha$. By the triangle inequality we thus have

$$\left\| {v^R({\cal{E}}_C{\cal{E}}) - v({\cal{E}}_C{\cal{E}})} \right\| = O(|\alpha |).$$

(75)

One can again fill in the constant factors here if one desires a more precise statement. Finally we note from Lemma 4 that

$$\alpha = 1 - \frac{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}}{\cal{E}}_C{\cal{E}})}}{{{\mathrm{Tr}}({\cal{P}}_{{\mathrm{tot}}})}} = \frac{{2^q}}{{2^q - 1}}(F({\cal{E}}_C{\cal{E}}) - 1)$$

(76)

This means that in the relevant limit of high fidelity, α will be small, justifying our perturbative analysis. Defining γ to be the second largest (in absolute value) eigenvalue of $M({\cal{E}}_C{\cal{E}})$, which by the same argument as above will be the second largest eigenvalue of $M({\cal{I}})$ up to O(α²) corrections, we get

$$|k_m^{\lambda^{\prime} } - \langle \langle Q|{\cal{P}}_{\hat \phi }|\rho \rangle \rangle - \gamma _{{\mathrm{max}}}(M({\cal{E}}_C{\cal{E}}))^{m - 1}\langle \langle Q|{\cal{P}}_{\hat \phi }|\rho \rangle \rangle | \le \delta _1\delta _2^m$$

with $\delta _1 = O(1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}}))$ and $\delta _2 = |\gamma | + O((1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}}))^2)$. Moreover, we have from Eqs. (68) and (76) that

$$\gamma _{{\mathrm{max}}}(A({\cal{E}}_C{\cal{E}})) = 1 - \frac{{2^q}}{{2^q - 1}}(F({\cal{E}}_C{\cal{E}}) - 1)$$

$$+ O\left( {[1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}})]^2} \right)$$

(77)

which immediately implies

$$\left| {\frac{1}{{2^q}}\mathop {\sum}\limits_{\lambda \in R_{\mathrm{G}}} {{\mathrm{Tr}}} ({\cal{P}}_\lambda )f_\lambda - \frac{{2^q(F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}}) + 1)}}{{2^q + 1}}} \right|$$

$$\le O\left( {[1 - F_{{\mathrm{avg}}}({\cal{E}}_C{\cal{E}})]^2} \right)$$

(78)

proving the lemma.

It is instructive to calculate the mixing matrix for a relevant example. We will calculate M for C the CPHASE gate and ${\mathrm{G}} = {\mathrm{C}}_1^{ \otimes 2}$ two copies of the single qubit Clifford gates. Recall from the main text that the PTM representation of ${\mathrm{C}}_1^{ \otimes 2}$ has three non-trivial subrepresentations. From their definitions in Eq. (10) and the action of the CPHASE gate on the two qubit Pauli operators it is straightforward to see that the mixing matrix is of the form

$$M = \left( {\begin{array}{*{20}{c}} {1/3} & 0 & {2/3} \\ 0 & {1/3} & {2/3} \\ {2/9} & {2/9} & {5/9} \end{array}} \right).$$

(79)

Calculating M² one can see that M is indeed irreducible. Moreover M has eigenvalues 1, 1/3 and −1/9. This means that for 2-for-1 interleaved benchmarking the interleaved experiment produces data that deviates from a single exponential no more than (1/3)^m (for sufficiently high fidelity) which will be negligible for even for fairly small m. This means that for 2-for-1 interleaved benchmarking the assumption that the interleaved experiment produces data described by a single exponential is good. We will see this confirmed numerically in the simulated experiment presented in Supplementary Fig. 2. Finally, we note that a similar result was achieved using different methods in ref. ^46,47