Abstract
What is the ultimate performance for discriminating two arbitrary quantum channels acting on a finite-dimensional Hilbert space? Here we address this basic question by deriving a general and fundamental lower bound. More precisely, we investigate the symmetric discrimination of two arbitrary qudit channels by means of the most general protocols based on adaptive (feedback-assisted) quantum operations. In this general scenario, we first show how port-based teleportation can be used to simplify these adaptive protocols into a much simpler non-adaptive form, designing a new type of teleportation stretching. Then, we prove that the minimum error probability affecting the channel discrimination cannot beat a bound determined by the Choi matrices of the channels, establishing a general, yet computable formula for quantum hypothesis testing. As a consequence of this bound, we derive ultimate limits and no-go theorems for adaptive quantum illumination and single-photon quantum optical resolution. Finally, we show how the methodology can also be applied to other tasks, such as quantum metrology, quantum communication and secret key generation.
Similar content being viewed by others
Introduction
Quantum hypothesis testing1 is a central area in quantum information theory,2,3 with many studies for both discrete variable (DV)4 and continuous variable (CV) systems.5 A number of tools6,7,8,9,10 have been developed for its basic formulation, known as quantum state discrimination. In particular, since the seminal work of Helstrom in the 70 s,1 we know how to bound the error probability affecting the symmetric discrimination of two arbitrary quantum states. Remarkably, after about 40 years, a similar bound is still missing for the discrimination of two arbitrary quantum channels. There is a precise motivation for that: The main problem in quantum channel discrimination (QCD)11,12,13,14,15 is that the strategies involve an optimization over the input states and the output measurements, and this process may be adaptive in the most general case, so that feedback from the output can be used to update the input.
Not only the ultimate performance of adaptive QCD is still unknown due to the difficulty of handling feedback-assistance, but it is also known that adaptiveness needs to be considered in QCD. In fact, apart from the cases where two channels are classical,16 jointly programmable or teleportation covariant,17,18 feedback may greatly improve the discrimination. For instance, ref. 19 presented two channels which can be perfectly distinguished by using feedback in just two adaptive uses, while they cannot be perfectly discriminated by any number of uses of a block (non-adaptive) protocol, where the channels are probed in an identical and independent fashion. This suggests that the best discrimination performance is not directly related to the diamond distance,20 when computed over multiple copies of the quantum channels.
In this work we finally fill this fundamental gap by deriving a universal computable lower bound for the error probability affecting the discrimination of two arbitrary quantum channels. To derive this bound we adopt a technique which reduces an adaptive protocol over an arbitrary finite-dimensional quantum channel into a block protocol over multiple copies of the channel’s Choi matrix. This is obtained by using port-based teleportation (PBT)21,22,23,24 for channel simulation and suitably generalizing the technique of teleportation stretching.25,26,27 This reduction is shown for adaptive protocols with any task (not just QCD). When applied to QCD, it allows us to bound the ultimate error probability by using the Choi matrices of the channels.
As a direct application, we bound the ultimate adaptive performance of quantum illumination28–35 and the ultimate adaptive resolution of any single-photon diffraction-limited optical system, setting corresponding no-go theorems for these applications. We then apply our result to adaptive quantum metrology showing an ultimate bound which has an asymptotic Heisenberg scaling. As an example, we also study the adaptive discrimination of amplitude damping channels, which are the most difficult channels to be simulated. Finally, other implications are for the two-way assisted capacities of quantum and private communications.
Results
Adaptive protocols
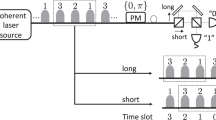
Let us formulate the most general adaptive protocol over an arbitrary quantum channel \({\cal{E}}\) defined between Hilbert spaces of dimension d (more generally, this can be taken as the dimension of the input space). We first provide a general description and then we specify the protocol to the task of QCD. A general adaptive protocol involves an unconstrained number of quantum systems which may be subject to completely arbitrary quantum operations (QOs). More precisely, we may organize the quantum systems into an input register a and an output register b, which are prepared in an initial state ρ0 by applying a QO Λ0 to some fundamental state of a and b. Then, a system a1 is picked from the register a and sent through the channel \({\cal{E}}\). The corresponding output b1 is merged with the output register b1b → b. This is followed by another QO Λ1 applied to a and b. Then, we send a second system a2 ∈ a through \({\cal{E}}\) with the output b2 being merged again b2b → b and so on. After n uses, the registers will be in a state ρn which depends on \({\cal{E}}\) and the sequence of QOs {Λ0, Λ1, …, Λn} defining the adaptive protocol \({\cal{P}}_n\) with output state ρn (see Fig. 1).
In a protocol of quantum communication, the registers belong to remote users and, in absence of entanglement-assistance, the QOs are local operations (LOs) assisted by two-way classical communication (CC), also known as adaptive LOCCs. The output is generated in such a way to approximate some target state.25 In a protocol of quantum channel estimation, the channel is labelled by a continuous parameter \({\cal{E}} = {\cal{E}}_\theta\) and the QOs include the use of entanglement across the registers. The output state will encode the unknown parameter ρn = ρn(θ), which is detected and the outcome processed into an optimal estimator.17 Here, in a protocol of binary and symmetric QCD, the channel is labelled by a binary digit, i.e., \({\cal{E}} = {\cal{E}}_u\) where u ∈ {0, 1} has equal priors. The QOs are generally entangled and they generate an output state encoding the information bit, i.e., ρn = ρn(u).
The output state ρn(u) of an adaptive discrimination protocol \({\cal{P}}_n\) is finally detected by an optimal positive-operator valued measure (POVM). For binary discrimination, this is the Helstrom POVM, which leads to the conditional error probability
where D(ρ, σ) := ||ρ − σ||/2 is the trace distance.4 The optimization over all discrimination protocols \({\cal{P}}_n\) defines the minimum error probability affecting the n-use adaptive discrimination of \({\cal{E}}_0\) and \({\cal{E}}_1\), i.e., we may write
This is generally less than the n-copy diamond distance between the two channels \({\cal{E}}_0^{ \otimes n}\) and \({\cal{E}}_1^{ \otimes n}\)
where2
with \({\cal{I}}\) being an identity map acting on a reference system r. The upper bound in Eq. (3) is achieved by a non-adaptive protocol, where an (optimal) input state ρar is prepared and its a-parts transmitted through \({\cal{E}}_u^{ \otimes n}\). Note that Eq. (3) is very difficult to compute, which is why we usually compute larger but simpler single-letter upper bounds such as
where F is the fidelity between the Choi matrices, \(\rho _{{\cal{E}}_0}\) and \(\rho _{{\cal{E}}_1}\), of the two channels.
Our question is: Can we complete Eq. (3) with a corresponding lower bound? Up to today this has been only proven for jointly programmable channels, i.e., channels \({\cal{E}}_0\) and \({\cal{E}}_1\) admitting a simulation \({\cal{E}}_u(\rho ) = {\cal{S}}(\rho \otimes \pi _u)\) with a trace-preserving QO \({\cal{S}}\) and different program states π0 and π1. In this case, we have \(p_n \ge [1 - D(\pi _0^{ \otimes n},\pi _1^{ \otimes n})]/2\).17 In particular, this is true if the channels are jointly teleportation covariant, so that \({\cal{S}}\) becomes teleportation and the program state is a Choi matrix \(\rho _{{\cal{E}}_u}\). For these channels, ref. 17 found that Eq. (3) holds with an equality and we may write \(||{\cal{E}}_0^{ \otimes n} - {\cal{E}}_1^{ \otimes n}||_\diamondsuit = ||\rho _{{\cal{E}}_0}^{ \otimes n} - \rho _{{\cal{E}}_1}^{ \otimes n}||\). More precisely, the question to ask is therefore the following: Can we establish a universal lower bound for \(p_n({\cal{E}}_0 \ne {\cal{E}}_1)\) which is valid for arbitrary channels? As we show here, this is possible by resorting to a more general (multi-program) simulation of the channels, i.e., of the type \({\cal{S}}(\rho \otimes \pi _u^{ \otimes M})\).
PBT and simulation of the identity
Let us describe the protocol of PBT with qudits of arbitrary dimension d ≥ 2. More technical details can be found in the original proposals.22,23 The parties exploit two ensembles of M ≥ 2 qudits, i.e., Alice has A := {A1, …, AM} and Bob has B := {B1, …, BM} representing the output “ports”. The generic ith pair (Ai, Bi) is prepared in a maximally entangled state, so that we have the global state
To teleport the state of a qudit C, Alice performs a joint measurement on C and her ensemble A. This is a POVM \(\{ {\Pi}_{C{\mathbf{A}}}^i\} _{i = 1}^M\) with M possible outcomes (see refs 22,23 for the details). In the standard protocol considered here, this POVM is a square root measurement (known to be optimal in the qubit case). Once Alice communicates the outcome i to Bob, he discards all the ports but the ith one, which contains the teleported state (see Fig. 2a).
The measurement outcomes are equiprobable and independent of the input, and the output state is invariant under permutation of the ports (this can be understood by the fact that the scheme is invariant under permutation of the Bell states and, therefore, of the ports). Averaging over the outcomes, we define the teleported state \(\rho _B^M = \Gamma _M(\rho _C)\), where ΓM is the corresponding PBT channel. Explicitly, this channel takes the form
where \({\mathrm{Tr}}_{\bar B_i}\) denotes the trace over all ports B but Bi.
As shown in ref. 22, the standard protocol gives a depolarizing channel4 whose probability ξM decreases to zero for increasing number of ports M. Therefore, in the limit of many ports \(M \gg 1\), the M-port PBT channel ΓM tends to an identity channel \({\cal{I}}\), so that Bob’s output becomes a perfect replica of Alice’s input. Here we prove a stronger result in terms of channel uniform convergence.26,27 In fact, for any M, we show that the simulation error, expressed in terms of the diamond distance between ΓM and \({\cal{I}}\), is one-to-one with the entanglement fidelity of the PBT channel ΓM. In turn, this result allows us to write a simple upper bound for this error. Moreover, we can fully characterize the simulation error with an exact analytical expression for qubits (see Methods for the proof, with further details given in Supplementary Section 1).
Lemma 1
In arbitrary (finite) dimension d, the diamond distance between the M-port PBT channel ΓM and the identity channel \({\cal{I}}\) satisfies
where \(f_e(\Gamma _M): = \langle \Phi |[{\cal{I}} \otimes \Gamma _M(|\Phi \rangle \langle \Phi |)]|\Phi \rangle\) is the entanglement fidelity of ΓM. This gives the upper bound
More precisely, we can write the exact result
where ξM is the depolarizing probability of the PBT channel ΓM. For qubits (d = 2), the “PBT number” ξM has the closed analytical expression
where smin = 1/2 for even M and 0 for odd M.
General channel simulation via PBT
Let us discuss how PBT can be used for channel simulation. This was first shown in ref. 21 where PBT was introduced as a possible design for a programmable quantum gate array.36 As depicted in Fig. 2b, suppose that Bob applies an arbitrary channel \({\cal{E}}\) to the teleported output, so that Alice’s input ρC is subject to the approximate channel
Note that the port selection commutes with \({\cal{E}}\), because the POVM acts on a different Hilbert space.21 Therefore, Bob can equivalently apply \({\cal{E}}\) to each port before Alice’s CC, i.e., apply \({\cal{E}}^{ \otimes M}\) to his B qudits before selecting the output port, as shown in Fig. 2c. This leads to the following simulation for the approximate channel
where \({\cal{T}}^M\) is a trace-preserving LOCC and \(\rho _{\cal{E}}\) is the channel’s Choi matrix (see Fig. 2d). By construction, the simulation LOCC \({\cal{T}}^M\) is universal, i.e., it does not depend on the channel \({\cal{E}}\). This means that, at fixed M, the channel \({\cal{E}}^M\) is fully determined by the program state \(\rho _{\cal{E}}\). One can bound the accuracy of the simulation. From Eq. (12) and the monotonicity of the diamond norm, we get
where δM is the simulation error in Eq. (9), with the dimension d being the one of the input Hilbert space. It is worth to remark that, while the simulation in Eq. (13) relies on a number of copies of the channel’s Choi matrix, it can be applied to an arbitrary quantum channel \({\cal{E}}\) without the condition of teleportation covariance.25
From port-based teleportation (PBT) to Choi-simulation of a quantum channel (see also ref. 21). a Schematic representation of the PBT protocol. Alice and Bob share an M × M qudit state which is given by M maximally entangled states \(\Phi _{{\mathbf{AB}}}^{ \otimes M}\). To teleport an input qubit state ρC, Alice applies a suitable POVM \(\{ {\Pi}_i\}\) to the input qubit C and her A qubits. The outcome i is communicated to Bob, who selects the i-th among his B qubits (tracing all the others). The performance does not depend on the specific “port” i selected and the average output state is given by \(\Gamma _M(\rho _C)\) where \(\Gamma _M\) is the PBT channel. The latter reduces to the identity channel in the limit of many ports \(M \to \infty\). b Suppose that Bob applies a quantum channel \({\cal{E}}\) on his teleported output. This produces the output state \({\cal{E}}^M(\rho _C)\) of Eq. (12). For large M, one has \({\cal{E}}^M \to {\cal{E}}\) in diamond norm. c Equivalently, Bob can apply \({\cal{E}}^{ \otimes M}\) to all his qubits B in advance to the CC from Alice. After selection of the port, this will result in the same output as before. d Now note that Alice’s LO and Bob’s port selection form a global LOCC \({\cal{T}}^M\) (trace-preserving by averaging over the outcomes). This is applied to a tensor-product state \(\rho _{\cal{E}}^{ \otimes M}\) where \(\rho _{\cal{E}}\) is the Choi matrix of the original channel \({\cal{E}}\). Thus the approximate channel \({\cal{E}}^M\) is simulated by applying \({\cal{T}}^M\) to \(\rho _C \otimes \rho _{\cal{E}}^{ \otimes M}\) as in Eq. (13)
PBT stretching of an adaptive protocol
Channel simulation is a preliminary tool for the following technique of teleportation stretching, where an arbitrary adaptive protocol is reduced into a simpler block version. There are two main steps. First of all, we need to replace each channel \({\cal{E}}\) with its M-port approximation \({\cal{E}}^M\) while controlling the propagation of the simulation error δM from the channel to the output state. This step is crucial also in simulations via standard teleportation18,26 (see also refs 37,38,39,40,41). Second, we need to “stretch” the protocol25 by replacing the various instances of the approximate channel \({\cal{E}}^M\) with a collection of Choi matrices \(\rho _{\cal{E}}^{ \otimes M}\) and then suitably re-organizing all the remaining QOs. Here we describe the technique for a generic task, before specifying it to QCD.
Given an adaptive protocol \({\cal{P}}_n\) over a channel \({\cal{E}}\) with output ρn, consider the same protocol over the simulated channel \({\cal{E}}^M\), so that we get the different output \(\rho _n^M\). Using a “peeling” argument (see Methods), we bound the output error in terms of the channel simulation error
Once understood that the output state can be closely approximated, let us simplify the adaptive protocol over \({\cal{E}}^M\). Using the simulation in Eq. (13), we may replace each channel \({\cal{E}}^M\) with the resource state \(\rho _{\cal{E}}^{ \otimes M}\), iterate the process for all n uses, and collapse all the simulation LOCCs and QOs as shown in Fig. 3. As a result, we may write the multi-copy Choi decomposition
for a trace-preserving QO \(\bar \Lambda\). Now, we can combine the two ingredients of Eqs. (15) and (16), into the following.
Port-based teleportation stretching of a generic adaptive protocol over a quantum channel \({\cal{E}}\). This channel is fixed in quantum/private communication, while it is unknown and parametrized in estimation/discrimination problems. a We show the last transmission an → bn through \({\cal{E}}\), which occurs between two adaptive QOs Λn−1 and Λn. This last step produces the output state ρn. b In each transmission, we replace \({\cal{E}}\) with its M-port simulation \({\cal{E}}^M\) so that the output of the protocol becomes \(\rho _n^M\) which approximates ρn for large M. Note that, in the last transmission, the register state \(\rho _{{\mathbf{ab}}a_n}\) undergoes the transformation \(\rho _{{\mathbf{ab}}b_n} = {\cal{I}}_{{\mathbf{ab}}} \otimes {\cal{E}}^M(\rho _{{\mathbf{ab}}a_n})\). c Each propagation through \({\cal{E}}^M\) is replaced by its PBT simulation. For the last transmission, this means that \(\rho _{{\mathbf{ab}}b_n} = {\cal{I}}_{{\mathbf{ab}}} \otimes {\cal{T}}^M(\rho _{{\mathbf{ab}}a_n} \otimes \rho _{\cal{E}}^{ \otimes M})\) where \({\cal{T}}^M\) is the LOCC of the PBT and \(\rho _{\cal{E}}\) is the Choi matrix of the original channel. d All the adaptive QOs Λi and the simulation LOCCs \({\cal{T}}^M\) are collapsed into a single (trace-preserving) QO \(\bar \Lambda\). Correspondingly, n instances of \(\rho _{\cal{E}}^{ \otimes M}\) are collected. As a result, the approximate output \(\rho _n^M\) is given by \(\bar \Lambda\) applied to the tensor-product state \(\rho _{\cal{E}}^{ \otimes nM}\) as in Eq. (16)
Lemma 2 (PBT stretching)
Consider an adaptive quantum protocol (with arbitrary task) over an arbitrary d-dimensional quantum channel \({\cal{E}}\) (which may be unknown and parametrized). After n uses, the output ρn of the protocol can be decomposed as follows
where \(\bar \Lambda\) is a trace-preserving QO, \(\rho _{\cal{E}}\) is the Choi matrix of \({\cal{E}}\), and δM is the M-port simulation error in Eq. (9).
When we apply the lemma to protocols of quantum or private communication, where the QOs Λi are LOCCs, then we may write Eq. (17) with \(\bar \Lambda\) being a LOCC. In protocols of channel estimation or discrimination, where \({\cal{E}}\) is parametrized, we may write Eq. (17) with \(\rho _{\cal{E}}\) storing the parameter of the channel. In particular, for QCD we have \(\{ {\cal{E}}_u\} _{u = 0,1}\) and the output ρn(u) of the adaptive protocol \({\cal{P}}_n\) can be decomposed as follows
Ultimate bound for channel discrimination
We are now ready to show the lower bound for minimum error probability \(p_n({\cal{E}}_0 \ne {\cal{E}}_1)\) in Eq. (3). Consider an arbitrary protocol \({\cal{P}}_n\), for which we may write Eq. (1). Combining Lemma 2 with the triangle inequality leads to
where we also use the monotonicity of the trace distance under channels. Because \(\bar \Lambda\) is lost, the bound does no longer depend on the details of the protocol \({\cal{P}}_n\), which means that it applies to all adaptive protocols. Thus, using Eq. (19) in Eqs. (1) and (2), we get the following.
Theorem 3
Consider the adaptive discrimination of two channels \(\{ {\cal{E}}_u\} _{u = 0,1}\) in dimension d. After n probings, the minimum error probability satisfies the bound
where M may be chosen to maximize the right hand side.
Not only this is the first universal bound for adaptive QCD, but also its analytical form is rather surprising. In fact, its tighest value is given by an optimal (finite) number of ports M for the underlying protocol of PBT.
Let us bound the trace distance in Eq. (20) as
where F is the fidelity between the Choi matrices of the channels. This comes from the Fuchs-van de Graaf relations42 and the multiplicativity of the fidelity over tensor products. Other bounds that can be written are
from the subadditivity of the trace distance, and
from the Pinsker inequality,43,44 where \(S(\rho ||\sigma ) = \mathrm{Tr}[\rho (\log _{2}\rho - \log _{2}\sigma )]\) is the relative entropy.4
If we exploit Eqs. (9) and (21) in Eq. (20), we may write the following simplified bound
In the previous formula there are terms with opposite monotonicity in M, so that the maximum value of the bound B is achieved at some intermediate value of M. Setting M = xd(d − 1)n for some x > 2, we get
One good choice is therefore M = 4d(d − 1)n, so that
In particular, consider two infinitesimally-close channels, so that \(F \simeq 1 - \epsilon\) where \(\epsilon \simeq 0\) is the infidelity. By expanding in \(\epsilon\) for any finite n, we may write
For instance, in the case of qubits this becomes \([\exp ( - 8n\sqrt \epsilon )]/4\), to be compared with the upper bound \([\exp ( - 2n\epsilon )]/2\) computed from Eq. (5). Discriminating between two close quantum channels is a problem in many physical scenarios. For instance, this is typical in quantum optical resolution45,46,47 (discussed below), quantum illumination28,29,30,31,32,33,34,35,48,49 (discussed below), ideal quantum reading,50,51,52,53,54 quantum metrology55,56,57,58,59 (discussed below), and also tests of quantum field theories in non-inertial frames,60 e.g., for detecting effects such as the Unruh or the Hawking radiation.
Limits of single-photon quantum optical resolution
Consider a microscope-type problem where we aim at locating a point in two possible positions, either s/2 or −s/2, where the separation s is very small. Assume we are limited to use probe states with at most one photon and an output finite-aperture optical system (this makes the optical process to be a qubit-to-qutrit channel, so that the input dimension is d = 2). Apart from this, we are allowed to use an arbitrary large quantum computer and arbitrary QOs to manipulate its registers. We may apply Eq. (27) with \(\epsilon \simeq \eta s^{2}/16\), where η is a diffraction-related loss parameter. In this way, we find that the error probability affecting the discrimination of the two positions is approximately bounded by \(B \gtrsim {\frac{1}{4}}\exp ( - 2ns\sqrt \eta )\). This bound establishes a no-go for perfect quantum optical resolution. See Supplementary Section 2 for more mathematical details on this specific application.
Limits of adaptive quantum illumination
Consider the protocol of quantum illumination in the DV setting.28 Here the problem is to discriminate the presence or not of a target with low reflectivity η ≃ 0 in a thermal background which has \(b \ll 1\) mean thermal photons per optical mode. One assumes that d modes are used in each probing of the target and each of them contains at most one photon. This means that the Hilbert space is (d + 1)-dimensional with basis \(\{ \left| 0 \right\rangle ,\left| 1 \right\rangle , \ldots ,\left| d \right\rangle \}\), where \(\left| i \right\rangle : = \left| {0 \cdots 010 \cdots 0} \right\rangle\) has one photon in the ith mode. If the target is absent (u = 0), the receiver detects thermal noise; if the target is present (u = 1), the receiver measures a mixture of signal and thermal noise.
In the most general (adaptive) version of the protocol, the receiver belongs to a large quantum computer where the (d + 1)-dimensional signal qudits are picked from an input register, sent to target, and their reflection stored in an output register, with adaptive QOs performed between each probing. After n probings, the state of the registers ρn(u) is optimally detected. Assuming the typical regime of quantum illumination,28 we find that the error probability affecting target detection is approximately bounded by \(B \gtrsim {\frac{1}{4}}\exp ( - 4nd\sqrt \eta )\). This bound establishes a no-go for exponential improvement in quantum illumination. Entanglement and adaptiveness can at most improve the error exponent with respect to separable probes, for which the error probability is \(\lesssim {\frac{1}{2}}\exp [ - n\eta /(8d)]\). See also Supplementary Section 3.
Limits of adaptive quantum metrology
Consider the adaptive estimation of a continuous parameter θ encoded in a quantum channel \({\cal{E}}_\theta\). After n probings, we have a θ-dependent output state ρn(θ) generated by an adaptive quantum estimation protocol \({\cal{P}}_n\). This output state is then measured by a POVM \({\cal{M}}\) providing an optimal unbiased estimator \(\tilde \theta\) of parameter θ. The minimum error variance Var\((\tilde \theta ): = \langle (\tilde \theta - \theta )^2\rangle\) must satisfy the quantum Cramer-Rao bound Var\((\tilde \theta ) \ge 1/\)\({\mathrm{QFI}}_\theta ({\cal{P}}_n)\), where \({\mathrm{QFI}}_\theta ({\cal{P}}_n)\) is the quantum Fisher information55 associated with \({\cal{P}}_n\). The ultimate precision of adaptive quantum metrology is given by the optimization over all protocols
This quantity can be simplified by PBT stretching. In fact, for any input state ρC, we may write the simulation \({\cal{E}}_\theta ^M(\rho _C) = {\cal{T}}^M(\rho _C \otimes \rho _{{\cal{E}}_\theta }^{ \otimes M})\), which is an immediate extension of Eq. (13). In this way, the output state can be decomposed following Lemma 2, i.e., we may write \(||\rho _n(\theta ) - \bar \Lambda (\rho _{{\cal{E}}_\theta }^{ \otimes nM})|| \le n\delta _M\). Exploiting the latter inequality for large n, we find that the ultimate bound of adaptive quantum metrology takes the form
where \({\mathrm{QFI}}(\rho _{{\cal{E}}_\theta })\) is computed on the channel’s Choi matrix. In particular, we see that PBT allows us to write a simple bound in terms of the Choi matrix and implies a general no-go theorem for super-Heisenberg scaling in quantum metrology. See Supplementary Section 4 for a detailed proof of Eq. (29).
Tightening the main formula
Let us note that the formula in Theorem 3 is expressed in terms of the universal error δM coming from the PBT simulation of the identity channel (Lemma 1). There are situations where the diamond distance \(\Delta _M: = ||{\cal{E}} - {\cal{E}}^M||_\diamondsuit\) between a quantum channel \({\cal{E}}\) and its M-port simulation \({\cal{E}}^M\) is exactly computable. In these cases, we can certainly formulate a tighter version of Eq. (20) where δM is suitably replaced. In fact, from the peeling argument, we have \(||\rho _n - \rho _n^M|| \le n\Delta _M\), so that a tighter version of Eq. (17) is simply \(||\rho _n - \bar \Lambda (\rho _{\cal{E}}^{ \otimes nM})|| \le n\Delta _M\). Then, for the two possible outputs ρn(0) and ρn(1) of an adaptive discrimination protocol over \({\cal{E}}_0\) and \({\cal{E}}_1\), we can replace Eq. (19) with
where \(\bar \Delta _M: = (||{\cal{E}}_0 - {\cal{E}}_0^M||_\diamondsuit + ||{\cal{E}}_1 - {\cal{E}}_1^M||_\diamondsuit )/2\). It is now easy to check that Eq. (20) becomes the following
In the following section, we show that \(\bar \Delta _M\), and therefore the bound in Eq. (31), can be computed for the discrimination of amplitude damping channels.
Discrimination of amplitude damping channels
As an additional example of application of the bound, consider the discrimination between amplitude damping channels. These channels are not teleportation covariant, so that the results from ref. 17 do not apply and no bound is known on the error probability for their adaptive discrimination. Recall that an amplitude damping channel \({\cal{E}}_p\) transforms an input state ρ as follows
with Kraus operators
where \(\{ \left| 0 \right\rangle ,\left| 1 \right\rangle \}\) is the computational basis and p is the damping probability or rate.
Given two amplitude damping channels, \({\cal{E}}_{p_0}\) and \({\cal{E}}_{p_1}\), first assume a discrimination protocol where these channels are probed by n maximally entangled states and the outputs are optimally measured. The optimal error probability for this (non-adaptive) block protocol is given by \(p_n^{{\mathrm{block}}} = [1 - D(\rho _{{\cal{E}}_{p_0}}^{ \otimes n},\rho _{{\cal{E}}_{p_1}}^{ \otimes n})]/2\) and satisfies
where \(F(p_0,p_1): = F(\rho _{{\cal{E}}_{p_0}},\rho _{{\cal{E}}_{p_1}})\) is the fidelity between the Choi matrices. In particular, we explicitly compute
It is clear that \(p_n^{{\mathrm{block}}}\) in Eq. (34) is an upper bound to ultimate (adaptive) error probability \(p_n({\cal{E}}_{p_0} \ne {\cal{E}}_{p_1})\) for the discrimination of the two channels.
To lowerbound the ultimate probability we employ Eq. (31). In fact, for the M-port simulation \({\cal{E}}_p^M\) of \({\cal{E}}_p\), we compute
where ξM are the PBT numbers defined in Eq. (11). For any two amplitude damping channels, \({\cal{E}}_{p_0}\) and \({\cal{E}}_{p_1}\), we can then compute \(\bar \Delta _M(p_0,p_1)\) and use Eq. (31) to bound \(p_n({\cal{E}}_{p_0} \ne {\cal{E}}_{p_1})\). More precisely, we can also exploit Eq. (21) and write the computable lower bound
In Fig. 4 we show an example of discrimination between two amplitude damping channels. In particular, we show how large is the gap between the upper bound \(p_n^{{\mathrm{block}}}\) of Eq. (34) and the lower bound in Eq. (37) suitably optimized over the number of ports M. It is an open question to find exactly \(p_n({\cal{E}}_{p_0} \ne {\cal{E}}_{p_1})\). At this stage, we do not know if this result may achieved by tightening the upper bound or the lower bound.
Error probability in the discrimination of two amplitude damping channels, one with damping rate p ≥ 0.8 and the other with rate p + 1%. We assume n = 20 probings of the unknown channel. The upper dark region identifies the region where the error probability \(p_n^{{\mathrm{block}}}\) of Eq. (34) lies. The adaptive error probability \(p_n({\cal{E}}_{p_0} \ne {\cal{E}}_{p_1})\) lies below this dark region and above the dotted points, which represent our lower bound of Eq. (37) optimized over the number of ports M. For comparison, we also plot the lower bound for specific M
Discussion
In this work we have established a general and fundamental lower bound for the error probability affecting the adaptive discrimination of two arbitrary quantum channels acting on a finite-dimensional Hilbert space. This bound is conveniently expressed in terms of the Choi matrices of the channels involved, so that it is very easy to compute. It also applies to many scenarios, including adaptive protocols for quantum-enhance optical resolution and quantum illumination. In order to derive our result, we have employed port-based teleportation as a tool for channel simulation, and developed a methodology which simplifies adaptive protocols performed over an arbitrary finite-dimensional channel. This technique can be applied to many other scenarios. For instance, in quantum metrology we are able to prove that adaptive protocols of quantum channel estimation are limited by a bound simply expressed in terms of the Choi matrix of the channel and following the Heisenberg scaling in the number of probings. Not only this shows that our bound is asymptotically tight but also draws an unexpected connection between port-based teleportation and quantum metrology. Further potential applications are in quantum and private communications, which are briefly discussed in our Supplementary Section 5.
Methods
Simulation error in diamond norm (proof of Lemma 1)
It is easy to check that the channel ΓM associated with the qudit PBT protocol of ref. 21 is covariant under unitary transformations, i.e.,
for any input state ρ and unitary operator U. As discussed in ref. 61, for a channel with such a symmetry, the diamond distance with the identity map is saturated by a maximally entangled state, i.e.,
where \(|\Phi \rangle = d^{ - 1/2}\mathop {\sum}\limits_{k = 1}^d | k\rangle |k\rangle\). Here we first show that
In fact, note that the map \(\Lambda _M = {\cal{I}} \otimes \Gamma _M\) is covariant under twirling unitaries of the form U ⊗ U*, i.e.,
for any input state ρ and unitary operator U. This implies that the quantum state ΛM(|Φ〉〈Φ|) is invariant under twirling unitaries, i.e.,
This is therefore an isotropic state of the form
where \({\Bbb I}\) is the two-qudit identity operator.
We may rewrite this state as follows
where ρ⊥ is state with support in the orthogonal complement of Φ, and F is the singlet fraction
Thanks to the decomposition in Eq. (44) and using basic properties of the trace norm,4 we may then write
where the last step exploits the fact that the singlet fraction F is the channel’s entanglement fidelity fe(ΓM). This completes the proof of Eq. (40).
Therefore, combining Eqs. (39) and (40), we obtain
which is Eq. (8) of the main text. Then, we know that the entanglement fidelity of ΓM is bounded as21
Therefore, using Eq. (48) in Eq. (47), we derive the following upper bound
which is Eq. (9) of the main text.
Let us now prove Eq. (10). It is known22 that implementing the standard PBT protocol over the resource state of Eq. (6) leads to a PBT channel ΓM, which is a qudit depolarizing channel. Its isotropic Choi matrix \(\rho _{\Gamma _M}\), given in Eq. (43), can be written in the form
where ξM is the probability p of depolarizing, |Φ〉0〈Φ| is the projector onto the initial maximally entangled state of two qudits (one system of which was sent through the channel), and |Φ〉i〈Φ| are the projectors onto the other d2 − 1 maximally entangled states of two qudits (generalized Bell states). Since the Choi matrix of the identity channel is \(\rho _{\cal{I}} = |\Phi \rangle ^0\langle \Phi |\), it is easy to compute
From the previous equation, we derive
where we have used \({\mathrm{Tr}}_2|\Phi \rangle ^i\langle \Phi | = d^{ - 1}\mathop {\sum}\limits_{j = 0}^{d - 1} | j\rangle \langle j|\) in the qudit computational basis {|j〉} and we have summed over the d2 generalized Bell states. It is clear that Eq. (52) is a diagonal matrix with equal non-zero elements, i.e., it is a scalar. As a result, we can apply Proposition 1 of ref. 62 over the Hermitian operator \(\rho _{\cal{I}} - \rho _{\Gamma _M}\), and write
The final step of the proof is to compute the explicit expression of ξM for qubits, which is the formula given in Eq. (11). Because this derivation is technically involved, it is reported in Supplementary Section 1.
Propagation of the simulation error
For the sake of completeness, we provide the proof of the first inequality in Eq. (15) (this kind of proof already appeared in refs 25,26). Consider the adaptive protocol described in the main text. For the n-use output state we may compactly write
where Λ’s are adaptive QOs and \({\cal{E}}\) is the channel applied to the transmitted signal system. Then, ρ0 is the preparation state of the registers, obtained by applying the first QO Λ0 to some fundamental state. Similarly, for the M-port simulation of the protocol, we may write
where \({\cal{E}}^M\) is in the place of \({\cal{E}}\).
Consider now two instances (n = 2) of the adaptive protocol. We may bound the trace distance between ρ2 and \(\rho _2^M\) using a “peeling” argument17,18,25,26,27
In (1) we use the monotonicity of the trace distance under completely positive trace-preserving (CPTP) maps (i.e., quantum channels); in (2) we employ the triangle inequality; in (3) we use the monotonicity with respect to the the CPTP map \({\cal{E}} \circ \Lambda _1\) whereas in (4) we exploit the fact that the diamond norm is an upper bound for the trace norm computed on any input state. Generalizing the result of Eq. (56) to arbitrary n, we achieve the first inequality in Eq. (15). Note that the previous reasoning can also be applied to a classically-parametrized unknown channel.
PBT simulation of amplitude damping channels
Here we show the result in Eq. (36) for \(\Delta _M(p) = ||{\cal{E}}_p - {\cal{E}}_p^M||_\diamondsuit\), which is the error associated with the M-port simulation of an arbitrary amplitude damping channel \({\cal{E}}_p\). From ref. 22, we know that the PBT channel ΓM is a depolarizing channel. In the qubit computational basis \(\{ \left| {i,j} \right\rangle \} _{i,j = 0,1}\), it has the following Choi matrix
where ξM are the PBT numbers of Eq. (11). Note that these take decreasing positive values, for instance
By applying the Kraus operators K0 and K1 of \({\cal{E}}_p\) locally to \(\rho _{\Gamma ^M}\) we obtain the Choi matrix of the M-port simulation \({\cal{E}}_p^M\), which is
where \(x: = \frac{1}{2} - \left( {1 - p} \right)\frac{{\xi _M}}{4}\), \(y: = \sqrt {1 - p} \left( {\frac{1}{2} - \frac{{\xi _M}}{2}} \right)\), \(z: = \left( {\frac{1}{2} - \frac{{\xi _M}}{4}} \right)\left( {1 - p} \right)\), and \(w: = \left( {\frac{1}{2} - \frac{{\xi _M}}{4}} \right)p + \frac{{\xi _M}}{4}\). This has to be compared with the Choi matrix of \({\cal{E}}_p\), which is
Now, consider the Hermitian matrix \(J = \rho _{{\cal{E}}_p^M} - \rho _{{\cal{E}}_p}\). If the matrix \(\phi = {\mathrm{Tr}}_2\sqrt {J^\dagger J} = {\mathrm{Tr}}_2\sqrt {JJ^\dagger }\) is scalar (i.e., both of its eigenvalues are equal), then the trace distance between the Choi matrices ||J|| is equal to the diamond distance between the channels ΔM(p) [62, Proposition 1]. After simple algebra we indeed find
where \(a_ \pm = \sqrt {1 - p} \sqrt {5 \pm 4\sqrt {1 - p} - p}\). Because ϕ is scalar, the condition above is met and the expression of ΔM(p) is twice the (degenerate) eigenvalue of ϕ, i.e.,
which simplifies to Eq. (36).
Data availability
The data sets generated in this study are available from the corresponding author upon reasonable request.
Code availability
The code used to generate data will be made available to the interested reader upon reasonable request.
Change history
02 August 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Helstrom, C. W. Quantum Detection and Estimation Theory. (Academic, New York, 1976).
Watrous, J. The theory of quantum information (Cambridge Univ. Press, Cambridge, 2018).
Holevo, A. Quantum Systems, Channels, Information: A Mathematical Introduction (De Gruyter, Berlin, 2012).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (Cambridge Univ. Press, Cambridge, 2010).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012).
Audenaert, K. M. R. et al. Discriminating states: the quantum Chernoff Bound. Phys. Rev. Lett. 98, 160501 (2007).
Calsamiglia, J., Munoz-Tapia, R., Masanes, L., Acin, A. & Bagan, E. The quantum Chernoff bound as a measure of distinguishability between density matrices: application to qubit and Gaussian states. Phys. Rev. A 77, 032311 (2008).
Pirandola, S. & Lloyd, S. Computable bounds for the discrimination of Gaussian states. Phys. Rev. A 78, 012331 (2008).
Audenaert, K. M. R., Nussbaum, M., Szkola, A. & Verstraete, F. Asymptotic error rates in quantum hypothesis testing. Commun. Math. Phys. 279, 251 (2008).
Spedalieri, G. & Braunstein, S. L. Asymmetric quantum hypothesis testing with Gaussian states. Phys. Rev. A 90, 052307 (2014).
Acin, A. Statistical distinguishability between unitary operations. Phys. Rev. Lett. 87, 177901 (2001).
Sacchi, M. Entanglement can enhance the distinguishability of entanglement-breaking channels. Phys. Rev. A 72, 014305 (2005).
Wang, G. & Ying, M. Unambiguous discrimination among quantum operations. Phys. Rev. A 73, 042301 (2006).
Childs, A., Preskill, J. & Renes, J. Quantum information and precision measurement. J. Mod. Opt. 47, 155 (2000).
Invernizzi, C., Paris, M. G. A. & Pirandola, S. Optimal detection of losses by thermal probes. Phys. Rev. A 84, 022334 (2011).
Hayashi, M. Discrimination of two channels by adaptive methods and its application to quantum system. IEEE Trans. Inf. Theory 55, 3807 (2009).
Pirandola, S. & Lupo, C. Ultimate precision of adaptive noise estimation. Phys. Rev. Lett. 118, 100502 (2017).
Pirandola, S., Bardhan, B. R., Gehring, T., Weedbrook, C. & Lloyd, S. Advances in photonic quantum sensing. Nat. Photon. 12, 724–733 (2018).
Harrow, A. W., Hassidim, A., Leung, D. W. & Watrous, J. Adaptive versus non-adaptive strategies for quantum channel discrimination. Phys. Rev. A 81, 032339 (2010).
Paulsen, V. I. Completely Bounded Maps and Operator Algebras (Cambridge Univ. Press, Cambridge, 2002).
Ishizaka, S. & Hiroshima, T. Asymptotic teleportation scheme as a universal programmable quantum processor. Phys. Rev. Lett. 101, 240501 (2008).
Ishizaka, S. & Hiroshima, T. Quantum teleportation scheme by selecting one of multiple output ports. Phys. Rev. A 79, 042306 (2009).
Ishizaka, S. Some remarks on port-based teleportation. Preprint at https://arxiv.org/abs/1506.01555 (2015).
Wang, Z.-W. & Braunstein, S. L. Higher-dimensional performance of port-based teleportation. Sci. Rep. 6, 33004 (2016).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017). Preprint at https://arxiv.org/abs/1510.08863 (2015).
Pirandola, S. et al. Theory of channel simulation and bounds for private communication. Quantum Sci. Technol. 3, 035009 (2018).
Pirandola, S., Laurenza, R. & Braunstein, S. L. Teleportation simulation of bosonic Gaussian channels: strong and uniform convergence. Eur. Phys. J. D. 72, 162 (2018).
Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463 (2008).
Tan, S.-H. et al. Quantum illumination with Gaussian states. Phys. Rev. Lett. 101, 253601 (2008).
Shapiro, J. H. & Lloyd, S. Quantum illumination versus coherent-state target detection. New J. Phys. 11, 063045 (2009).
Zhang, Z., Tengner, M., Zhong, T., Wong, F. N. C. & Shapiro, J. H. Entanglement’s benefit survives an entanglement-breaking channel. Phys. Rev. Lett. 111, 010501 (2013).
Lopaeva, E. D. et al. Experimental realization of quantum illumination. Phys. Rev. Lett. 110, 153603 (2013).
Zhang, Z., Mouradian, S., Wong, F. N. C. & Shapiro, J. H. Entanglement-enhanced sensing in a lossy and noisy environment. Phys. Rev. Lett. 114, 110506 (2015).
Barzanjeh, S. et al. Microwave quantum illumination. Phys. Rev. Lett. 114, 080503 (2015).
Weedbrook, C., Pirandola, S., Thompson, J., Vedral, V. & Gu, M. How discord underlies the noise resilience of quantum illumination. New J. Phys. 18, 043027 (2016).
Nielsen, M. A. & Chuang, I. L. Programmable quantum gate arrays. Phys. Rev. Lett. 79, 321 (1997).
Pirandola, S. End-to-end capacities of a quantum communication network. Commun. Phys. 2, 51 (2019). Preprint at https://arxiv.org/abs/1601.00966 (2016).
Laurenza, R. & Pirandola, S. General bounds for sender-receiver capacities in multipoint quantum communications. Phys. Rev. A 96, 032318 (2017).
Laurenza, R., Braunstein, S. L. & Pirandola, S. Finite-resource teleportation stretching for continuous-variable systems. Sci. Rep. 8, 15267 (2018). Preprint at https://arxiv.org/abs/1706.06065 (2017).
Cope, T. P. W., Hetzel, L., Banchi, L. & Pirandola, S. Simulation of non-Pauli channels. Phys. Rev. A 96, 022323 (2017).
Cope, T. P. W. & Pirandola, S. Adaptive estimation and discrimination of Holevo-Werner channels. Quantum Meas. Quantum Metrol. 4, 44–52 (2017).
Fuchs, C. A. & van de Graaf, J. Cryptographic distinguishability measures for quantum mechanical states. IEEE Trans. Inf. Theory 45, 1216 (1999).
Pinsker, M. S Information and Information Stability of Random Variables and Processes. (Holden Day, San Francisco, 1964).
Carlen, E. A. & Lieb, E. H. Bounds for entanglement via an extension of strong subadditivity of entropy. Lett. Math. Phys. 101, 1–11 (2012).
Tsang, M., Nair, R. & Lu, X.-M. Quantum theory of superresolution for two incoherent optical point sources. Phys. Rev. X 6, 031033 (2016).
Lupo, C. & Pirandola, S. Ultimate precision bound of quantum and subwavelength imaging. Phys. Rev. Lett. 117, 190802 (2016).
Nair, R. & Tsang, M. Far-field superresolution of thermal electromagnetic sources at the quantum limit. Phys. Rev. Lett. 117, 190801 (2016).
Cooney, T., Mosonyi, M. & Wilde, M. M. Strong converse exponents for a quantum channel discrimination problem and quantum-feedback-assisted communication. Comm. Math. Phys. 344, 797–829 (2016).
De Palma, G. & Borregaard, J. The minimum error probability of quantum illumination. Phys. Rev. A 98, 012101 (2018).
Pirandola, S. Quantum reading of a classical digital memory. Phys. Rev. Lett. 106, 090504 (2011).
Pirandola, S., Lupo, C., Giovannetti, V., Mancini, S. & Braunstein, S. L. Quantum reading capacity. New J. Phys. 13, 113012 (2011).
Dall’Arno, M. et al. Experimental implementation of unambiguous quantum reading. Phys. Rev. A 85, 012308 (2012).
Dall’Arno, M., Bisio, A. & D’Ariano, G. M. Ideal quantum reading of optical memories. Int. J. Quant. Inf. 10, 1241010 (2012).
Spedalieri, G. Cryptographic aspects of quantum reading. Entropy 17, 2218–2227 (2015).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439 (1994).
Braunstein, S. L., Caves, C. M. & Milburn, G. J. Generalized uncertainty relations: theory, examples, and Lorentz invariance. Ann. Phys. 247, 135–173 (1996).
Paris, M. G. A. Quantum estimation for quantum technology. Int. J. Quant. Inf. 7, 125–137 (2009).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222 (2011).
Braun, D. et al. Quantum enhanced measurements without entanglement. Rev. Mod. Phys. 90, 035006 (2018).
Doukas, J., Adesso, G., Pirandola, S. & Dragan, A. Discriminating quantum field theories in non-inertial frames. Class. Quantum Grav. 32, 035013 (2015).
Majenz, C. Entropy in Quantum Information Theory, Communication and Cryptography. PhD thesis, University of Copenhagen. (2017).
Nechita, I. et al. Almost all quantum channels are equidistant. J. Math. Phys. 59, 052201 (2018).
Acknowledgements
This work has been supported by the EPSRC via the ‘UK Quantum Communications Hub’ (EP/M013472/1) and by the European Commission via ‘Continuous Variable Quantum Communications’ (CiViQ, Project ID: 820466). The authors would like to thank Satoshi Ishizaka, Sam Braunstein, Seth Lloyd, Gaetana Spedalieri, and Zhi-Wei Wang for feedback.
Author information
Authors and Affiliations
Contributions
All authors contributed to prove the main theoretical results of the work. S.P. developed the basic idea and methodology, steered the research project, wrote the main manuscript and Supplementary Sections 4 and 5. R.L. wrote Supplementary Section 3. C.L wrote Supplementary Sections 2 and 4. J.P. contributed to refine Lemma 1 and to study the PBT simulation of amplitude damping channels, besides writing Supplementary Section 1.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pirandola, S., Laurenza, R., Lupo, C. et al. Fundamental limits to quantum channel discrimination. npj Quantum Inf 5, 50 (2019). https://doi.org/10.1038/s41534-019-0162-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0162-y
This article is cited by
-
From port-based teleportation to Frobenius reciprocity theorem: partially reduced irreducible representations and their applications
Letters in Mathematical Physics (2024)
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
-
Quantum-enhanced Doppler lidar
npj Quantum Information (2022)
-
Optical quantum super-resolution imaging and hypothesis testing
Nature Communications (2022)
-
Utilizing Adaptive Boosting to Detect Quantum Steerability
International Journal of Theoretical Physics (2022)