Uncertainty equality with quantum memory and its experimental verification

Abstract

As a very fundamental principle in quantum physics, uncertainty principle has been studied intensively via various uncertainty inequalities. A natural and fundamental question is whether an equality exists for the uncertainty principle. Here we derive an entropic uncertainty equality relation for a bipartite system consisting of a quantum system and a coupled quantum memory, based on the information measure introduced by Brukner and Zeilinger (Phys. Rev. Lett. 83:3354, 1999). The equality indicates that the sum of measurement uncertainties over a complete set of mutually unbiased bases on a subsystem is equal to a total, fixed uncertainty determined by the initial bipartite state. For the special case where the system and the memory are the maximally entangled, all of the uncertainties related to each mutually unbiased base measurement are zero, which is substantially different from the uncertainty inequality relation. The results are meaningful for fundamental reasons and give rise to operational applications such as in quantum random number generation and quantum guessing games. Moreover, we experimentally verify the measurement uncertainty relation in the presence of quantum memory on a five-qubit spin system by directly measuring the corresponding quantum mechanical observables, rather than quantum state tomography in all the previous experiments of testing entropic uncertainty relations.

Introduction

The uncertainty principle is one of the most important principle in quantum physics. It implies the impossibility of simultaneously determining the definite values of incompatible observables. The more precisely an observable is determined, the less precisely a complementary observable can be known. Based on the distributions of measurement outcomes, the quantum uncertainty relations can be described in various ways; see for instance refs. ^{1,2,3,4,5,6,7,8,9,10,11,12,13}

The uncertainty principle was first formulated via the standard deviation of a pair of complementary observables, known as the Heisenberg’s uncertainty principle¹ ΔxΔp ≥ ħ/2 for the coordinate x and the momentum p in an infinite dimensional Hilbert space. Later the Robertson−Schrödinger uncertainty inequality^2,3 presented an uncertainty relation for two arbitrary observables in a finite dimensional Hilbert space. Instead of the standard deviation of observables, the uncertainty principle can also be elegantly formulated in terms of entropies related to measurement bases. When a quantum system is projected onto a certain basis {|i_θ〉 |i = 1, 2, ⋯, d}, where θ labels the measured observable, the uncertainty of the measurement results has been characterized by the Shannon entropy $H_\theta = \mathop {\sum}\nolimits_{i = 1}^d - p_i\log _2p_i$, where p_i is the probability to obtain the ith basis state |i_θ〉. The larger the Shannon entropy H_θ is, the more uncertain the measurement results are. In terms of the Shannon entropies of the measurement results, the uncertainty principle can be formulated as $H_\theta + H_\tau \ge \log _2\frac{1}{c}$.⁴ Here 1/c quantifies the degree of complementarity of two observables θ and τ.

The above uncertainty relations only concern a single quantum system. By taking the entanglement with a memory system into account,¹⁴ an entropic uncertainty relation in the presence of quantum memory has been investigated in ref. ¹⁵. It has been shown that for a bipartite state ρ_AB, performing measurements on one of the subsystems A gives rise to the following relation

$$S(\theta |B) + S(\tau |B) \ge \log _2\frac{1}{c} + S(A|B),$$

(1)

where S(A|B) and S(θ|B) (S(τ|B)) denote, respectively, the conditional von Neumann entropies of the initial bipartite state ρ_AB and the final bipartite state ρ_θB (ρ_τB) after the measurement in the basis {|i_θ〉} ({|i_τ〉}). This uncertainty relation was further extended to the smooth entropy case.¹⁶ With considering the entangled quantum memory, these uncertainty relations have potential applications in entanglement witnessing and quantum key distributions (QKD).^15,17,18 However, the above results all concern measurements only on two observables and are given in inequality forms.

In this work, we consider projective measurements based on mutually unbiased bases (MUBs).^{19,20,21,22,23,24} The MUB measurements are complementary to each other in the sense that any pair of bases are maximally unbiased. They are deeply connected to the Born’s principle of complementarity²¹ and closely related to the wave-particle duality.^25,26 A complete set of MUBs consists of at most d + 1 observables, where d is the dimension of the state space. Comparing with the incomplete case, the advantage of a complete set of MUB measurements is informatively complete^23,24 and meaningful in quantum information progressing.²¹ It is therefore not surprising that a complete set of MUB measurements is crucial in entanglement detection.^27,28 It was also proved that using a complete set of MUBs is much better than using two observables in QKD.¹⁹

In ref. ⁶ an entropic uncertainty relation involving d + 1 MUB measurements has been obtained in terms of von Neumann entropy. However, it only dealt with a single system (in this case the von Neumann entropy is just the Shannon entropy of the measurement probability distributions), and the uncertainty relation is given by an inequality. In fact, the Shannon entropy is a natural measure of our ignorance regarding the properties of a classical system, because in classical measurements the observation removes our ignorance about the state by revealing the properties of the system which are considered to be pre-existing and independent of the observation. In contrast to classical measurements, one cannot say that quantum measurements reveal a pre-existing property of a quantum system. Therefore, the Shannon entropy could be thought of as “conceptually” inadequate in quantum physics.²⁹ In ref. ²⁶ the authors proposed a new measure of quantum information, which takes into account that the only features of quantum systems known before a measurement are the probabilities for various events to occur. It has significant physical meaning and various applications in quantum information processing such as quantum randomness, quantum state estimation, quantum teleportation and quantum metrology.^{30,31,32,33,34,35,36} Moreover, a series of works have been shown, together with many applications, that in single quantum system, the sum of the individual measures of information for MUBs is invariant under the choice of the particular set of complementary observations and conserved if there is no information exchange with environments.^{26,29,30,31,32,33,34,37,38,39,40,41,42}

In this article, we adopt the information measure proposed in ref. ²⁶ and consider the uncertainty relation in the presence of quantum memory. Interestingly, we find that if we take a complete set of MUB measurements into account, we can obtain an uncertainty equality that the sum of measurement uncertainties over all MUBs on a subsystem in the presence of quantum memory is equal to a fixed quantity determined by the initial state. It gives rise to a kind of conservation relation of the uncertainties related to these MUB measurements. We further show the elegant applications of our result in quantum guessing game and quantum random number generation. We also experimentally verify this uncertainty equality by directly measuring the uncertainties on a nuclear spin system. Our method avoids the tomography process and allows one to perform verification experiments in large quantum systems.

Results

Measurement of uncertainty relations

Let (p₁, p₂, …, p_d) be the probabilities for the d measurement outcomes. The lack of information about the jth outcome with respect to a single experimental trial is given by p_j(1 − p_j). The total lack of information regarding all d possible experimental outcomes is then given by $\mathop {\sum}\nolimits_{j = 1}^d {p_j} (1 - p_j) = 1 - \mathop {\sum}\nolimits_{j = 1}^d {p_j^2}$, which is minimal if one probability is equal to a unity and maximal if all the probabilities are equal. In fact, $1 - \mathop {\sum}\nolimits_{j = 1}^d {p_j^2}$ is nothing but 1 − Tr(ρ²), where ρ is the state after a quantum (projective) measurement, the linear entropy of the measured state. Therefore, the lack of information regarding all d possible experimental outcomes can be described by the linear entropy of a d-level quantum state ρ, S_L(ρ) = 1 − Tr(ρ²). S_L(ρ) ranges from 0 (when ρ is a pure state) to (d − 1)/d (when ρ is maximally mixed). Unlike that in ref. ²⁶, here we do not introduce a normalization factor to have a range between 0 and log₂ d, so the measure of uncertainty in terms of linear entropy does not have the unit of a “bit”. However, it quantifies uncertainty in a natural way: an uncertainty of 0 means the outcome is 100% certain while an uncertainty approaching 1 means the outcome is almost random.

For a bipartite state ρ_AB in a d × D (D ≥ d) dimensional composite Hilbert space, if system A is projected on to the basis {|i_θ〉 |i = 1, 2, ⋯, d}, the overall state of the composite system after the nonselective measurement^43,44 on A is given as

$$\rho _{\theta B} = \mathop {\sum}\limits_{i = 1}^d {\left| {i_\theta } \right\rangle _A} \langle i_\theta | \otimes _A\langle i_\theta |\rho _{AB}\left| {i_\theta } \right\rangle _A.$$

(2)

We can introduce the conditional linear entropy

$$S_L(\theta |B): = S_L(\rho _{\theta B}) - S_L(\rho _B) = {\mathrm{Tr}}(\rho _B^2) - {\mathrm{Tr}}(\rho _{\theta B}^2)$$

(3)

as a measure of the uncertainty about Alice’s measurement result given Bob’s state, where the reduced state ρ_B = Tr_A(ρ_θB) = Tr_A(ρ_AB) is independent of the measurement basis. It is straightforward to show that the conditional linear entropy S_L(θ|B) is always nonnegative. As an example, suppose ρ_AB is a maximally entangled pure state. Alice can perform a measurement on her system in any basis. The possible resulting states of Bob’s system are orthogonal to each other, and each possible resulting state is in one-to-one correspondence to Alice’s resulting state. Therefore, given Bob’s state, Alice’s measurement result can be determined with certainty. In this case S_L(θ|B) vanishes. If $\rho _{AB} = \mathop {\sum}\nolimits_{i = 1}^d {\sqrt {\lambda _i} } \left| {ii} \right\rangle$ is a partially entangled state written in its Schmidt bases, after Alice measures her system in the Schmidt basis, Bob’s possible resulting states are orthogonal to each other and the Alice’s measurement result is completely determined without uncertainty when Bob’s state is given. This is also confirmed by the vanishing conditional entropy as $S_L(\rho _{\theta B}) = S_L(\rho _B) = \mathop {\sum}\nolimits_i {\lambda _i^2}$. However, if Alice performs a measurement on a basis that is not the Schmidt basis, the possible resulting states of Bob’s system are not orthogonal and cannot be distinguished with certainty, and thus uncertainty of Alice’s measurement result exists even when Bob’s state is known. This fact is again confirmed by the observation that the conditional linear entropy is strictly greater than zero in this case. The conditional linear entropy is thus a good measure of the uncertainty about Alice’s measurement result given Bob’s state. It depends on the basis in which the measurement is performed in general. When Alice tries to find a basis to perform the measurement on her system so that Bob will know her result with minimum uncertainty, then using another MUB to perform the measurement will result in Bob having a large uncertainty about Alice’s result. However, the whole uncertainty running over all possible MUB measurements is fixed. This uncertainty relation is formulated in the following theorem (the proof involves subtle mathematical techniques, see Method A).

Theorem For any density matrix ρ_AB on a composite Hilbert space H_A ⊗ H_B of dimension d × D, we have the following uncertainty equality

$$\mathop {\sum}\limits_{\theta = 1}^{d + 1} {S_L} (\theta |B) = d\left( {{\mathrm{Tr}}(\rho _B^2) - \frac{1}{d}{\mathrm{Tr}}(\rho _{AB}^2)} \right)$$

(4)

when a complete set of d + 1 MUBs exists for the d-dimensional Hilbert space H_A.

The theorem shows that the total uncertainty related to the measurements over all d + 1 MUBs of a subsystem is exactly given by a fixed quantity, $d{\mathrm{Tr}}(\rho _B^2) - {\mathrm{Tr}}(\rho _{AB}^2)$, which is determined only by the initial bipartite state. This quantity is always nonnegative and can be viewed as the total measurement uncertainty of a subsystem, given the state of the other subsystem. Different from the uncertainty inequality (1) based on the von Neumann entropy, here we obtain the equality (4). Note that this equality (4) is also completely different from the one given in ref. ⁴⁵ which is based on only ONE positive operator-valued measure consisting of uniformly all the measurement operators of d + 1 MUBs (see Remark in Method A). In general, when there are only M MUBs available or when we are only interested in certain M MUBs, we always have the following uncertainty inequality,

$$\mathop {\sum}\limits_{\theta = 1}^M {S_L} (\theta |B) \ge (M - 1)\left( {{\mathrm{Tr}}(\rho _B^2) - \frac{1}{d}{\mathrm{Tr}}(\rho _{AB}^2)} \right).$$

(5)

With each additional MUB, the lower bound of total uncertainty is increased by a fixed amount ${\mathrm{Tr}}(\rho _B^2) - \frac{1}{d}{\mathrm{Tr}}(\rho _{AB}^2)$.

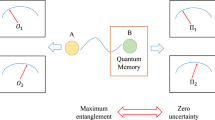
To illustrate the implications of the theorem, let us consider that Alice and Bob are both users of quantum technology. In order to make a hard decision on whether she should accept Bob’s invitation to see a film, Alice asks Bob to send her a qubit A. Alice can measure the qubit with the three (Pauli) observables σ_x, σ_y and σ_z at her choice. After the measurement, Alice announces her choice of the observable, and Bob is supposed to guess the Alice’s measurement results. Alice would accept (deny) Bob’s request if his guess is correct (wrong). Bob tries to gain Alice’s acceptance by entangling the qubit A with his local qubit B in the preparation stage. From the theorem, we know that the sum of uncertainties (of Bob’s guess at Alice’s measurement results given the state of B) in three different cases is equal to the quantity $Q = 2{\mathrm{Tr}}(\rho _B^2) - {\mathrm{Tr}}(\rho _{AB}^2)$ that is completely determined by the initial state ρ_AB. Bob can minimize the quantity Q by preparing an EPR state, thus win Alice’s acceptance with certainty, a result that cannot be obtained from an uncertainty inequality like the one based on Shannon entropy (see Fig. 1).

Fig. 1

a Sketch of the proposal. b Illustration of implications of the theorem. Alice chooses to measure one of the three Pauli matrices σ_x, σ_y and σ_z on qubit A, and then informs Bob her choice and requests him to guess her measurement outcome. In order to guess Alice’s measurement outcome with less uncertainty, Bob can entangle qubit A with a local qubit B before sending qubit A to Alice, so that to minimize the uncertainty

On the practical side, the theorem also provides possible applications in quantum random number generation, especially semi-self-testing quantum random number generators (QRNGs) which are more robust to device imperfections. In a typical setup of a semi-self-testing QRNG,^46,47,48 Alice and Bob share a quantum state ρ_AB, e.g., an EPR pair. If both parties are trusted, the measurement outcome of one party will be random to the other party when Alice measures in the computational basis and Bob measures in the diagonal basis. However, if one of the parties is corrupted, e.g., due to device imperfections, this scheme is broken. To show this, consider that one party switches to the same basis as the other party. A common solution is that each party randomly uses multiple basis, such as σ_x, σ_y, or σ_z basis.^46,47,48 Now, we consider the following semi-self-testing scenario. Alice first chooses a reference frame, and randomly performs measurements in one of the MUB basis. The reference frame is assumed to be reliably chosen, but Alice does not have a free will to randomly choose her measurement basis, i.e., the basis choice may be manipulated by an adversary who wishes to corrupt Alice’s randomness, such as Bob. Hence, the entropy of Alice’s random outcomes with respect to Bob is the smallest entropy S_L(θ|B) among all measurement choices. To maximize this quantity, the theorem shows that S_L(θ|B) should be equal for all θs. Thus, the maximum entropy of a semi-self-testing QRNG is $[d{\mathrm{Tr}}(\rho _B^2) - {\mathrm{Tr}}(\rho _{AB}^2)]/(d + 1)$. This limit on semi-self-testing QRNGs also cannot be obtained from an uncertainty inequality. Finally, note that entanglement-based QRNGs considered here have a higher randomness generation rate compared to prepare-and-measure QRNGs,⁴⁹ and cannot be analyzed by using the tools developed by Brukner and Zeilinger.²⁶

Experimental verification

To experimentally investigate the uncertainty conservation, a two-qubit system ρ_AB, chosen as the test system, is prepared in the following states:

$$\rho _{AB}(\alpha ,x) = x\left| {\psi _\alpha } \right\rangle \left\langle {\psi _\alpha } \right| + \frac{{1 - x}}{4}I_4,$$

(6)

where |ψ_α〉 = cos(α/2)|01〉 − sin(α/2)|10〉. These states are mixed states composed of one pure state with weight x and the maximal mixed state with weight (1 − x)/4. The parameters α characterizes the entanglement of the pure part and x characterizes the purity of the state. When α = π/2 and x = 1, the bipartite state is one of the Bell states. The other three Bell states can be obtained by local unitary operations while the linear entropy remains invariant under such transformations.

The key part of the experiments is to measure the system’s (conditional) linear entropy. Similar to the measurement of von Neumann entropy in previous experiments,^50,51 linear entropy can be indirectly measured by full quantum state tomography.⁵² However, this is inefficient for large-size quantum systems. Since the linear entropy is directly related to the purity Tr(ρ²) that can be directly obtained by Tr(ρ²) = Tr(V₂ρ ⊗ ρ)⁵³ with a copy of ρ, this allows us to employ an operational and direct way to experimentally verify the uncertainty conservation relation. Here the operator V₂ is the SWAP operation, i.e., V₂|ψ₁ψ₂〉 = |ψ₂ψ₁〉, that exchanges the states of two subsystems. By using one ancillary probe qubit to perform the interferometric measurement, we can directly obtain all the required information of the purities from the probe qubit, as shown in Fig. 2a.

Fig. 2

a Quantum circuit of directly measuring the purity. b Molecular structure for NMR quantum register. c Experimental schematic for verifying the measurement uncertainty relation. MUB measurements are performed on subsystem A to get ρ_θB, and meanwhile the same process is applied on the mirror subsystem A′. Then controlled-SWAP gates are performed for the measurements of the linear entropies S_L(θ|B) in LHS of Eq. (4). The purity information on the original state ρ_AB, i.e., the RHS of Eq. (4), are obtained without MUB measurement in the dashed lines. The purities of the bipartite system AB: ${\mathrm{Tr}}(\rho _{AB}^2)$ and ${\mathrm{Tr}}(\rho _{\theta B}^2)$, are obtained by two controlled-SWAP gates C_swap applying on subsystems AA′ and BB′ while only one C_swap is operated on subsystem BB′ (denoted by the solid line) for the purity of subsystem ${\mathrm{Tr}}(\rho _B^2)$ and ${\mathrm{Tr}}(\rho _{B|\theta }^2)$, where ρ_B|θ = Tr_A(ρ_θB)

Physical system

To verify the equation in the experiments, we used the sample named 1-bromo-2,4,5-trifluorobenzene as a five-qubit NMR quantum system which consists of two ¹H spins and three ¹⁹F spins, dissolved in the liquid-crystal N-(4-methoxybenzylidene)-4-butylaniline (MBBA). Spins H₃ and H₄ are labeled as the bipartite system ρ_AB, spins F₁ and F₂ as the copy system ρ_A′B′, and spin F₅ as the probe qubit ρ_probe. The effective Hamiltonian of the five-qubit system in double rotating frame is

$$H_{{\mathrm{NMR}}} = \mathop {\sum}\limits_{i = 1}^5 {\pi \nu _i\sigma _z^i} + \mathop {\sum}\limits_{1 \le j < k \le 5}^{} {\frac{\pi }{2}\left( {J_{jk} + 2D_{jk}} \right)\sigma _z^j\sigma _z^k} ,$$

(7)

where σ_z is the Pauli operator, ν_i is the chemical shift of spin-i and J_jk + 2D_jk is the effective coupling constant of spin-j and spin-k. The molecular structure is shown in Fig. 2b, and the relevant parameters are shown in Method B.

Experimental procedure

Figure 2c shows the experimental schematic for verifying the measurement uncertainty relations. It can be divided into four parts.

• 1. Preparing initial state. From thermal equilibrium state, we first initialized the system to a labeled pseudo-pure state (LPPS) $\rho _{{\mathrm {LPPS}}} = \frac{1}{{32}}I_{32} + \varepsilon \sigma _z^{{\mathrm {probe}}} \otimes \left| {0000} \right\rangle _{ABA{\prime}B{\prime}}\langle 0000|$ with selective-transition method,⁵⁴ where ε ≈ 10⁻⁵ is the polarization and I₃₂ is the 32-dimension identity matrix. There is no dynamical and measurement effect on the part of identity density matrix; thus in the following, we conventionally denote the state with the deviation density matrix,⁵⁵ ignoring the identity matrix. Then the product state ρ_AB(α, x) ⊗ ρ_A′B′(α, x) was prepared from |0000〉_ABA′B′ 〈0000|, where ρ_A′B′ is the copy of ρ_AB. We vary the weight x by rotation with different angles and a following nonunitary gradient pulse. The details of initialization process are shown in Method C.

• 2. Performing MUB measurements. The complete MUB measurements were implemented on subsystem A. For a two-dimensional system, the simplest case of MUBs are

  $$\begin{array}{*{20}{l}} {M_0 = \{ |0\rangle ,|1\rangle \} ,M_1 = \left\{ \frac{{|0\rangle + |1\rangle }}{{\sqrt 2 }},\frac{{|0\rangle - |1\rangle }}{{\sqrt 2 }}\right\} ,} \hfill \\ {M_2 = \left\{ \frac{{|0\rangle + i|1\rangle }}{{\sqrt 2 }},\frac{{|0\rangle - i|1\rangle }}{{\sqrt 2 }}\right\} .} \hfill \end{array}$$

  (8)

  They are just the eigenvectors of Pauli operators σ_x,σ_y and σ_z. In NMR, such MUB projective measurements can be emulated using pulsed magnetic field gradients.⁵⁶ Without interfering the unselected systems (B and its copy B′), we realized the MUB measurements on subsystem A and its copy A′ by the gradient echo technology,⁵⁷ i.e., by selective π pulses to the other spins, this dephasing operation (i.e., projective measurement of σ_z) can be selectively performed on some specific spins. It is in principle necessary to refocus all the evolutions under the internal Hamiltonian during the gradient echo. However, this sequence can be simplified when we only care about the purity of the crashed state. For example, the projective measurement of M₀ on spin F₂ (A) and H₄ (A′) are accomplished by $P_z^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}} = G_z - [\pi ]_x^{{\mathrm{F}}_{\mathrm{1}},{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}} - G_z - [\pi ]_{ - x}^{{\mathrm{F}}_{\mathrm{1}},{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}}$, where the evolutions under internal effective coupling Hamiltonian related to three qubits F₁, H₃ and F₅ are reserved during the pulse sequence. However, by some calculations, these undesired evolutions will lead to an error less than 2[1 − cos(2Δθ)] ≈ 0.065 on the purity measurements of the subsystem A or A′, mainly determined by the different evolutions on qubits F₁, H₃ due to the different effective coupling constants $J_{{\mathrm{F}}_{\mathrm{1}},{\mathrm{F}}_{\mathrm{5}}} + 2D_{{\mathrm{F}}_{\mathrm{1}},{\mathrm{F}}_{\mathrm{5}}}$ and $J_{{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}} + 2D_{{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}}$. Here $\Delta \theta = \pi [(J_{{\mathrm{F}}_{\mathrm{1}},{\mathrm{F}}_{\mathrm{5}}} + 2D_{{\mathrm{F}}_{\mathrm{1}},{\mathrm{F}}_{\mathrm{5}}}) - (J_{{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}} + 2D_{{\mathrm{H}}_{\mathrm{3}},{\mathrm{F}}_{\mathrm{5}}})]t_{G_z}/2$ with the duration $t_{G_z}$ of pulsed magnetic field gradient G_z. To perform projective measurements of M₁ and M₂ on specific spins, we first selectively rotate the spins with [π/2]_−y or [π/2]_x rotations, then performs the projective measurement of M₀, e.g., $P_x^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}} = [\pi /2]_{ - y}^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}} - P_z^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}}$ and $P_y^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}} = [\pi /2]_x^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}} - P_z^{{\mathrm{F}}_{\mathrm{2}},{\mathrm{H}}_{\mathrm{4}}}$.⁵⁶

• 3. Measuring the purities. After the MUBs on the subsystem A and A′, performing the quantum circuit in Fig. 2a will give the purity information on the resulting state ρ_θB after MUBs. For example, when two controlled-SWAP gates (C_swap) are applied to both subsystems AA′ and BB′, one gets the purity of the bipartite system AB: ${\mathrm{Tr}}(\rho _{\theta B}^2)$; when only one C_swap is applied to the subsystem BB′, one gets the purity of subsystem B: ${\mathrm{Tr}}(\rho _{B|\theta }^2)$ with ρ_B|θ = Tr_A(ρ_θB), as shown in Fig. 2c. Likely, the related purities of the original state ρ_AB: Tr(ρ_AB) and ${\mathrm{Tr}}(\rho _B^2)$, are obtained by the similar procedure without the MUBs. It can be noted the initial state of the probe qubit is different from the original method in Fig. 2a. We initialize the probe qubit as $\sigma _z^{{\mathrm {probe}}}$ in our experiment. However, this will not affect the measure of the purity by the quantum circuit U_qc in Fig. 2a, i.e.,

$${\mathrm{Tr}}[\sigma _z^{{\mathrm {probe}}}U_{{\mathrm {qc}}}(\sigma _z^{{\mathrm {probe}}} \otimes \rho \otimes \rho )U_{{\mathrm {qc}}}^\dagger ] = 2{\mathrm{Tr}}[V_2(\rho \otimes \rho )] = 2{\mathrm{Tr}}(\rho ^2).$$

Moreover, since the direct observable in NMR is σ_x, the final Hadamard gate can be canceled out by the readout operation. Therefore, through integrating the NMR spectra of the probe spin F₅, we directly measure the purities on the related states. By calculating the linear entropy, both sides of Eq. (4) are obtained without quantum state tomography.

Experimental results

The experimental results are shown in Fig. 3. As expected, the sum of uncertainties decreases to zero when the bipartite system is in maximally entangled state. With certain α, lower purity corresponds to higher uncertainty. From Fig. 3a, b, we can see that the experimental results are in accord with theoretical expectations and the uncertainty conversation relation holds with high precision. Figure 3c shows the final NMR spectra of the probe qubit for one certain initial state ρ_AB(π/4, 1). The sum of the integral values of all the peaks is read as the purity of the related state in our experiment, as shown in Fig. 3d.

Fig. 3

Experimental results of verifying the measurement uncertainty with the input states ρ_AB(α, 1) (a) and ρ_AB(π/2, x) (b). Red and blue dots represent the measured values of LHS and RHS of Eq. (4), respectively. The experimental data are rescaled by extracting the decoherence effect, shown by filled squares. The original data are shown in Method E. The dark gray curves are theoretical expectations. The bars are plotted from the infidelity of readout process. c Experimental NMR spectra of probe spin (F₅) for ρ_AB(π/4, 1). From bottom to up, the related resulting states after measurement are, respectively, ρ_AB, ρ_xB, ρ_yB, ρ_zB, ρ_B, ρ_B|x, ρ_B|y, ρ_B|z. d Measured purities of the resulting states shown in (c). Each purity is obtained from the sum of the integral values of the corresponding peak in (c)

In our experiments, to avoid the error accumulation and alleviate the influence of the decoherence, we used high-fidelity engineered quantum control pulses, which exploit the gradient ascent pulse engineering (GRAPE) algorithm,⁵⁸ to implement the quantum circuit in the experiments. The experiments for pure states contain eight GRAPE pulses with the total duration of about 74 ms, while for mixed states, we used 9~11 GRAPE pulses with total durations of 67−85 ms. We numerically optimized all GRAPE pulses with considering 5% ratio frequency (rf) field inhomogeneity, so that they are more robust in experiments. All GRAPE pulses used in the experiments have theoretical fidelities above 99.3%. Numerical simulations show that the imperfection of GRAPE pulses causes infidelity of 2−4% in the final states. Due to the short relaxation times of the liquid-crystal sample, the experiments suffer severe decoherence effect. We numerically simulated the dynamical process and estimated the attenuation factors caused by decoherence effect in the experiments.^59,60 Then we rescaled the experimental results. The details can be also found in Method E. In the numerical simulations, we found that transverse relaxation time T₂ plays a leading role in the decoherence process, while the longitude relaxation time T₁ has little influence. The imperfection in preparing the labeled PPS also causes some errors. The highest unexpected peak in the labeled PPS NMR spectrum of spin F₅ is about 3% intensity of the only expected peak.

Discussion

In conclusion, we have derived a novel entropic measurement uncertainty relation in bipartite systems with a quantum memory. It has been shown that after a complete set of MUB measurements on one partite, the total uncertainty on the other partite is exactly given by the purities of the initial system and the memory. Substantially different from the previous uncertainty relations with inequalities, we presented an equality of uncertainty relation for the case with a quantum memory, which implies direct applications to quantum random number generation and quantum guessing games. Moreover, the relation (4) is independent of the choices of the MUBs. Therefore, the relation (4) gives rise to a kind of conservation of measurement uncertainties, in the sense that (4) is invariant under the transformation of MUBs.

Our theorem gives an uncertainty equality relation for arbitrary dimensional bipartite systems consisting of a quantum system and a coupled quantum memory. It should be emphasized that, even for single-partite systems, it is already quite difficult to obtain an uncertainty equality relation for high-dimensional case. The high-dimensional bipartite case is much more complex than the case of single-partite one.^{26,29,30,31,32,33,34,37,38,39,40,41,42} Therefore, as one sees in Method A, it is not surprising that the derivation of our uncertainty relations needs subtle mathematical techniques.

With the help of one mirror system of the measured system and one additional probe qubit, we have provided the first experimental verification of this measurement uncertainty relation in an NMR quantum processor, where the experimental data of uncertainty quantities have been directly obtained by measuring the involved entropies without quantum state tomography. This method allows one to perform verification experiments in large quantum systems, and deal with the experimental data by standard statistical and information-theoretical methods. These results may give rise to significant applications in quantum information processing such as quantum metrology. For closed systems, it is well known that uncertainty relation determines the precision limit of quantum metrology based on complementary basis. For open systems, with B the environment and A the system to be measured, our equality presents a complete characterization of the precision limit for measuring the system under MUBs. Such precision limit or accuracy determined by uncertainty relations also appear in quantum computing when quantum gates like CNOT are physically implemented. Hence our results may highlight further studies on both fundamental problems in quantum mechanics and the applications.

Methods

A: Proof of the theorem

In a d-dimensional Hilbert space ${\cal{H}}$, let {|i_θ〉|i = 1,⋯, d} denote a basis labeled by θ. A set of M such bases is called mutually unbiased if

$$|\left\langle {i_\theta |j_\tau } \right\rangle |^2 = \frac{1}{d}$$

(9)

for any i, j = 1, 2, ⋯, d, and θ, τ = 1, ⋯, M with θ ≠ τ. When d is a power of a prime number, a complete set of d + 1 MUBs exists. When d is an arbitrary integer number, the maximal number of MUBs is unknown. For example, when d = 6, only three MUBs have yet been found. However, for any d ≥ 2, there exist at least three MUBs. For the purpose of this paper, we only assume that M MUBs are available in a d-dimensional Hilbert space, where M is less than or equal to the maximal number of MUBs that can exist.

In a composite Hilbert space ${\cal{H}} \otimes {\cal{H}}$ of two qubits, we construct the following M(d − 1) + 1 states,

$$|\Phi \rangle = \frac{1}{{\sqrt d }}\mathop {\sum}\limits_{i = 1}^d {|i_1\rangle _A \otimes \left| {i_1} \right\rangle _B^ \ast } ,$$

(10)

$$|\phi _{\theta ,k}\rangle = \frac{1}{{\sqrt d }}\mathop {\sum}\limits_{i = 1}^d {\omega ^{k(i - 1)}} |i_\theta \rangle _A \otimes \left| {i_\theta } \right\rangle _B^ \ast$$

(11)

with ω = e^2πi/d, k = 1, …, d − 1 and θ = 1, 2, …, M. Here |i_θ〉^* denotes the complex conjugate of |i_θ〉 with respect to the computational basis (which can be chosen as the first basis {|i₁〉} without loss of generality). It is straightforward to show that the M(d − 1) + 1 bipartite states defined in Eqs. (10) and (11) are normalized and orthogonal to each other.

Therefore, these M(d − 1) + 1 states can be used for constructing a basis in the composite Hilbert space ${\cal{H}} \otimes {\cal{H}}$. Since there are at most d² orthogonal states in a d²-dimensional space, one has M(d − 1) + 1 ≤ d², which implies M ≤ d + 1, i.e., there are at most d + 1 MUBs for a d-dimensional Hilbert space. When M = d + 1, i.e., a complete set of d + 1 MUBs in a d-dimensional space is available, the states defined in Eqs. (10) and (11) constitute a complete basis for the composite Hilbert space ${\cal{H}} \otimes {\cal{H}}$. On the other hand, when M < d + 1, one can complete a basis of the composite Hilbert space by adding p = (d − 1)(d + 1 − M) additional orthonormal states {|ϕ_α〉 |α = 1, ⋯, p}. The projector onto the subspace spanned by these additional states is denoted by ${\cal{P}}$, i.e.,

$${\cal{P}} = I \otimes I - \left| \Phi \right\rangle \langle \Phi | - \mathop {\sum}\limits_{\theta = 1}^M {\mathop {\sum}\limits_{k = 1}^{d - 1} {\left| {\phi _{\theta ,k}} \right\rangle } } \langle \phi _{\theta ,k}| = \mathop {\sum}\limits_{\alpha = 1}^p {\left| {\varphi _\alpha } \right\rangle } \langle \varphi _\alpha |.$$

(12)

It is obvious that ${\cal{P}} = 0$ when M = d + 1.

Let T₂ denote the partial transpose with respect to the computational basis of the second Hilbert space. One immediately has

$$(\left| \Phi \right\rangle \langle \Phi |)^{T_2} = \frac{1}{d}\mathop {\sum}\limits_{i,j = 1}^d {\left| {i_1} \right\rangle } \langle j_1| \otimes \left| {j_1} \right\rangle \langle i_1|.$$

(13)

As $\mathop {\sum}\nolimits_{k = 1}^{d - 1} {\omega ^{k(i - j)}}$ equals to −1 for i ≠ j and d − 1 when i = j, it is not difficult to show

$$\left( {\mathop {\sum}\limits_{k = 1}^{d - 1} {\left| {\phi _{\theta ,k}} \right\rangle } \langle \phi _{\theta ,k}|} \right)^{T_2} = \mathop {\sum}\limits_{i = 1}^d {\left| {i_\theta } \right\rangle } \langle i_\theta | \otimes \left| {i_\theta } \right\rangle \langle i_\theta | - \frac{1}{d}\mathop {\sum}\limits_{i,j = 1}^d {\left| {i_\theta } \right\rangle } \langle j_\theta | \otimes \left| {j_\theta } \right\rangle \langle i_\theta |.$$

(14)

Suppose ρ_AB is a bipartite state on the composite Hilbert space ${\cal{H}}_A \otimes {\cal{H}}_B$ of dimension d × D, and suppose {|i_θ〉_A} is the θth MUB in the d-dimensional Hilbert space ${\cal{H}}_A$, after system A is projected onto the θth MUB the overall bipartite state is written as

$$\rho _{\theta B} = \mathop {\sum}\limits_{i = 1}^d {\left| {i_\theta } \right\rangle _A} \langle i_\theta | \otimes _A\langle i_\theta |\rho _{AB}\left| {i_\theta } \right\rangle _A.$$

(15)

Given a bipartite state ρ_AB and a set of M MUBs in ${\cal{H}}_A$, we define an operator

$$\Gamma _{AB} \equiv I_A \otimes \rho _B + \frac{{M - 1}}{d}\rho _{AB} - \mathop {\sum}\limits_{\theta = 1}^M {\rho _{\theta B}}$$

(16)

on ${\cal{H}}_A \otimes {\cal{H}}_B$. This operator is Hermitian, and it has the following nice property.

Proposition When M = d + 1, the operator Γ_AB vanishes: Γ_AB = 0. When M ≤ d, it is nonnegative-definite

$$\Gamma _{AB} \ge 0.$$

(17)

In order to prove the proposition, we introduce an additional Hilbert space ${\cal{H}}_C$ of dimension d, and introduce a linear map ${\cal{F}}$ that maps operators on ${\cal{H}}_C$ to operators on ${\cal{H}}_A$, such that ${\cal{F}}(\left| {i_1} \right\rangle _C\langle j_1|) = \left| {i_1} \right\rangle _A\langle j_1|$ (i, j = 1,⋯, d). One can easily show that ${\cal{F}}(\left| {i_\theta } \right\rangle _C\langle j_\theta |) = \left| {i_\theta } \right\rangle _A\langle j_\theta |$ for θ = 1, …, M. Let ${\cal{F}}^{ - 1}$ denote the inverse map, and let $\rho _{CB} \equiv {\cal{F}}^{ - 1}(\rho _{AB})$ denote the corresponding state on ${\cal{H}}_C \otimes {\cal{H}}_B$ with respect to the state ρ_AB on ${\cal{H}}_A \otimes {\cal{H}}_B$. Therefore, the map ${\cal{F}}:\rho _{CB} \to {\cal{F}}(\rho _{CB})$ can also be conveniently written via a partial trace over system C

$$\begin{array}{c}{\cal{F}}(\rho _{CB}) = \mathop {\sum}\limits_{ij} {{\mathrm{Tr}}_C} \left\{ {\left[ {\left| {i_\theta } \right\rangle _A\langle j_\theta | \otimes \left| {j_\theta } \right\rangle _C\langle i_\theta |} \right]\rho _{CB}} \right\}\\ = \mathop {\sum}\limits_{ij} {\left| {i_\theta } \right\rangle _A} \langle j_\theta | \otimes \langle i_\theta |\rho _{CB}\left| {j_\theta } \right\rangle \\ = \rho _{AB}\end{array}$$

(18)

for any θ ∈ {1, ⋯, M}. Similarly, ρ_θB can be written as

$$\rho _{\theta B} = {\mathrm{Tr}}_C\left\{ {\left[ {\mathop {\sum}\limits_{i = 1}^d {\left| {i_\theta } \right\rangle _A} \langle i_\theta | \otimes \left| {i_\theta } \right\rangle _C\langle i_\theta |} \right]\rho _{CB}} \right\}.$$

(19)

Hence

$$\begin{array}{c}\mathop {\sum}\limits_{\theta = 1}^M {(\frac{1}{d}\rho _{AB} - \rho _{\theta B})} = \mathop {\sum}\limits_{\theta = 1}^M {{\mathrm{Tr}}_C} \left\{ {\frac{1}{d}\mathop {\sum}\limits_{ij} {\left| {i_\theta } \right\rangle _A} \langle j_\theta | \otimes \left| {j_\theta } \right\rangle _C\langle i_\theta |\rho _{CB}} \right\}\\ - \mathop {\sum}\limits_{\theta = 1}^M {{\mathrm{Tr}}_C} \left\{ {\mathop {\sum}\limits_i {\left| {i_\theta } \right\rangle _A} \langle i_\theta | \otimes \left| {i_\theta } \right\rangle _C\langle i_\theta |\rho _{CB}} \right\}\\ = - {\mathrm{Tr}}_C\left\{ {\left( {\mathop {\sum}\limits_{\theta = 1}^M {\mathop {\sum}\limits_{k = 1}^{d - 1} {\left| {\phi _{\theta ,k}} \right\rangle _{AC}} } \langle \phi _{\theta ,k}|} \right)^{T_C}\rho _{CB}} \right\}.\end{array}$$

(20)

We have used Eq. (14) to obtain the last equality. From Eqs. (13) and (18) with θ = 1, we also have

$$\frac{1}{d}\rho _{AB} = {\mathrm{Tr}}_C\left\{ {(\left| \Phi \right\rangle _{AC}\langle \Phi |)^{T_C}\rho _{CB}} \right\}.$$

(21)

From Eqs. (20) and (21) and the obvious relation I_A ⊗ ρ_B = Tr_C[(I_a ⊗ I_C)ρ_CB], we can rewrite Γ_AB as

$$\begin{array}{c}\Gamma _{AB} = I_A \otimes \rho _B - \frac{1}{d}\rho _{AB} + \mathop {\sum}\limits_{\theta = 1}^M {(\frac{1}{d}\rho _{AB} - \rho _{\theta B})} \\ = {\mathrm{Tr}}_C\left\{ {{\cal{P}}_{AC}^{T_C}\rho _{CB}} \right\}.\end{array}$$

(22)

Here the operator ${\cal{P}}_{AC}$ is the projector defined on ${\cal{H}}_A \otimes {\cal{H}}_C$ according to (12), i.e.,

$$\begin{array}{c}{\cal{P}}_{AC} = I \otimes I - \left| \Phi \right\rangle \langle \Phi | - \mathop {\sum}\limits_{\theta = 1}^M {\mathop {\sum}\limits_{k = 1}^{d - 1} {\left| {\phi _{\theta ,k}} \right\rangle } } \langle \phi _{\theta ,k}|\\ = \mathop {\sum}\limits_{\alpha = 1}^p {\left| {\varphi _\alpha } \right\rangle _{AC}} \langle \varphi _\alpha |.\end{array}$$

(23)

When M = d + 1, then p = 0, the states |ϕ_α〉_AC in ${\cal{H}}_A \otimes {\cal{H}}_C$ do not exist, both ${\cal{P}}_{AC}$ and Γ_AB vanish. When M ≤ d, we have

$$\begin{array}{c}\Gamma _{AB} = {\mathrm{Tr}}_C\left\{ {\mathop {\sum}\limits_{\alpha = 1}^p {\left( {\left| {\varphi _\alpha } \right\rangle _{AC}\langle \varphi _\alpha |} \right)^{T_C}} \rho _{CB}} \right\}\\ = \mathop {\sum}\limits_{\alpha = 1}^p {{\mathrm{Tr}}_C} \left\{ {\left( {\left| {\varphi _\alpha } \right\rangle _{AC}\langle \varphi _\alpha |} \right)^{T_C}\rho _{CB}} \right\}\\ = \mathop {\sum}\limits_{\alpha = 1}^p {{\mathrm{Tr}}_C} \left\{ {\left( {\left| {\varphi _\alpha } \right\rangle _{AC}} \right)^{T_C}\rho _{CB}\left( {\langle \varphi _\alpha |_{AC}} \right)^{T_C}} \right\}.\end{array}$$

The last equality is due to the fact that operators on ${\cal{H}}_C$ can have cyclic permutations under the partial trace over C. Let $\Theta _\alpha \equiv \left( {\left| {\varphi _\alpha } \right\rangle _{AC}} \right)^{T_C}\sqrt {\rho _{CB}}$, which are operators on ${\cal{H}}_A \otimes {\cal{H}}_C \otimes {\cal{H}}_B$. Then we have

$$\Gamma _{AB} = \mathop {\sum}\limits_{\alpha = 1}^p {{\mathrm{Tr}}_C} \left\{ {\Theta _\alpha (\Theta _\alpha )^\dagger } \right\}.$$

(24)

Since $\Theta _\alpha (\Theta _\alpha )^\dagger$ are always nonnegative-definite operators on ${\cal{H}}_A \otimes {\cal{H}}_C \otimes {\cal{H}}_B$, the operators ${\mathrm{Tr}}_C\left\{ {\Theta _\alpha (\Theta _\alpha )^\dagger } \right\}$ are nonnegative-definite operators on ${\cal{H}}_A \otimes {\cal{H}}_B$, so is their sum. Therefore Γ_AB ≥ 0. This completes the proof of the proposition.

According to the proposition, Γ_AB is a nonnegative-definite operator when M ≤ d, and it vanishes when M = d + 1. Hence, for any nonnegative-definite operator Π_AB on ${\cal{H}}_A \otimes {\cal{H}}_B$,

$${\mathrm{Tr}}_{AB}(\Gamma _{AB}{\Pi}_{AB}) \ge 0$$

(25)

when M ≤ d, and the inequality becomes an equality when M = d + 1.

Let Π_AB = ρ_AB, Eq. (25) yields

$$\begin{array}{c}0 \le {\mathrm{Tr}}_{AB}(\Gamma _{AB}\rho _{AB})\\ = {\mathrm{Tr}}(\rho _B^2) + \frac{{M - 1}}{d}{\mathrm{Tr}}(\rho _{AB}^2) - \mathop {\sum}\limits_{\theta = 1}^M {{\mathrm{Tr}}} (\rho _{\theta B}^2).\end{array}$$

(26)

Therefore,

$$- \mathop {\sum}\limits_{\theta = 1}^M {{\mathrm{Tr}}} (\rho _{\theta B}^2) \ge - {\mathrm{Tr}}(\rho _B^2) - \frac{{M - 1}}{d}{\mathrm{Tr}}(\rho _{AB}^2).$$

(27)

Adding $M{\mathrm{Tr}}(\rho _B^2)$ to the above inequality, we immediately have

$$\mathop {\sum}\limits_{\theta = 1}^M {({\mathrm{Tr}}(\rho _B^2)} - {\mathrm{Tr}}(\rho _{\theta B}^2)) \ge (M - 1)\left( {{\mathrm{Tr}}(\rho _B^2) - \frac{1}{d}{\mathrm{Tr}}(\rho _{AB}^2)} \right).$$

(28)

The inequality becomes an equality when M = d + 1. Thus, the theorem in the main text has been proved.

Remark: The approach we admitted here is methodologically similar to the one used in ref. ²⁶ (see also ref. ²⁹). In ref. ⁴⁵ an elegant uncertainty equality has also been presented based on ONE positive operator-valued measure consisting uniformly all the measurement operators of d + 1 MUBs. As we take into account all the d + 1 MUB projection measurements individually, our uncertainty relation is completely different from the one given in ref. ⁴⁵ In fact, the uncertainty relation in ref. ⁴⁵ cannot be applied to our QRNG self-testing scenario, because the equality derived in ref. ⁴⁵ holds only when the system is measured in one of the MUBs with uniformly random probability. While our equality holds no matter whether the MUB is uniformly chosen. Such a property is crucial in practical QRNG application, as one needs to restrict the input randomness to choose a mutually unbiased basis.

B: Quantum register

We used the sample named 1-bromo-2,4,5-trifluorobenzene as a five-qubit NMR quantum system which consists of two ¹H spins and three ¹⁹F spins, dissolved in the liquid-crystal N-(4-methoxybenzylidene)-4-butylaniline. The structure of the molecule is shown in Fig. 4. Due to the partial average effect in the liquid-crystal solution, the direct dipole−dipole interaction will be scaled down by the order parameter.⁶¹ In our sample, the partial average effect makes the direct dipole−dipole couplings of homonuclear spins much smaller than the difference between the chemical shifts of related nuclear spins, all the dipole−dipole Hamiltonians are reduced to the form of $\sigma _z^i\sigma _z^j$. Therefore, the effective Hamiltonian of the five-qubit system in rotating frame is

$$H_{{\mathrm{NMR}}} = \mathop {\sum}\limits_{i = 1}^5 {\pi \nu _i\sigma _z^i} + \mathop {\sum}\limits_{1 \le j < k \le 5}^{} {\frac{\pi }{2}\left( {J_{jk} + 2D_{jk}} \right)\sigma _z^j\sigma _z^k} ,$$

(29)

where σ_z is the Pauli operator, ν_i is the chemical shift of spin-i and J_jk + 2D_jk is the effective coupling constant of spin-j and spin-k. The relevant parameters are shown in Fig. 4.

Fig. 4

a Characteristics of the 1-bromo-2,4,5-trifluorobenzene molecule. The chemical shifts and effective coupling constants (in Hz) are on and above the diagonal in the table, respectively. The last two columns show the transversal relaxation times and the longitudinal relaxation times of each nucleus. b, c The thermal equilibrium ¹⁹F and ¹H spectra

C: Initial state preparation

We first initialized the quantum register into a labeled pseudo-pure state (LPPS) $\rho _{{\mathrm {LPPS}}} = \varepsilon \sigma _z^{{\mathrm {probe}}} \otimes \left| {0000} \right\rangle _{ABA{\prime}B{\prime}}\langle 0000| + 1/32I_{32}$ from the equilibrium state where ε is the polarization about 10⁻⁵. We just neglected the identity part because unitary and nonunitary operations all have no influence on it. We applied 30 unitary operators with the form $U = e^{ - i\beta _{ij}{\cal{V}}_{ij}}$ to redistribute the populations between energy levels i and j. Here ${\cal{V}}_{ij}$ is the single quantum transition operator between levels i and j, that is, a 32 × 32 matrix whose elements are zero except for two elements ${\cal{V}}_{ij}(i,j) = {\cal{V}}_{ij}(j,i) = 1/2$. According to the desired distribution, the angle β_ij were numerically calculated. In this produce, the unitary operators generated undesired coherence terms that were eliminated by a following field gradient pulse Gz. Accordingly, the LPPS ρ_LPPS was prepared.

In the following we only consider the deviation part $\sigma _z^{{\mathrm {probe}}} \otimes \left| {0000} \right\rangle _{ABA{\prime}B{\prime}}\langle 0000|$. The composite system was prepared into the state

$$\begin{array}{l}\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\alpha ,x) \otimes \rho _{A{\prime}B{\prime}}(\alpha ,x) = \sigma _z^{{\mathrm {probe}}} \otimes (x|\psi _\alpha \rangle \langle \psi _\alpha | + \frac{{1 - x}}{4}I_4)\\ \otimes (x|\psi _\alpha \rangle \langle \psi _\alpha | + \frac{{1 - x}}{4}I_4),\end{array}$$

from $\sigma _z^{{\mathrm {probe}}} \otimes |0000\rangle \langle 0000|$, where |ψ_α〉 = cos(α/2)|01〉 − sin(α/2)|10〉. In the case of x = 1, the bipartite systems are entangled where the rotation angle α varies from 0 to π/2 for producing different entanglement. α = 0 corresponds to separable state and α = π/2 corresponds to the maximally entangled state. Setting α = π/2 and scanning x from 0 to 1 with interval 0.25, we prepared the states with different mixedness. In preparing $\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\pi /2,x) \otimes \rho _{A{\prime}B{\prime}}(\pi /2,x)$, we divided it into 4 parts, i.e.,

$$\begin{array}{l}\sigma _z^{{\mathrm {probe}}} \otimes (\frac{{1 - x}}{4}I_2) \otimes (\frac{{1 - x}}{4}I_2),\\ \sigma _z^{{\mathrm {probe}}} \otimes (\frac{{1 - x}}{4}I_2) \otimes (x|\psi _{\pi /2}\rangle \langle \psi _{\pi /2}|),\\ \sigma _z^{{\mathrm {probe}}} \otimes (x|\psi _{\pi /2}\rangle \langle \psi _{\pi /2}|) \otimes (\frac{{1 - x}}{4}I_2),\\ \sigma _z^{{\mathrm {probe}}} \otimes (x|\psi _{\pi /2}\rangle \langle \psi _{\pi /2}|) \otimes (x|\psi _{\pi /2}\rangle \langle \psi _{\pi /2}|),\end{array}$$

(30)

and adopted the temporal averaging method⁶² to realize them. By summing the four output states, we obtained the desired state $\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\pi /2,x) \otimes \rho _{A{\prime}B{\prime}}(\pi /2,x)$. The pulse sequences for the state preparation are shown in Fig. 5a, b.

Fig. 5

a Quantum circuit of preparing $\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\alpha ,1) \otimes \rho _{A{\prime}B{\prime}}(\alpha ,1)$ from LPPS. The rectangles represent single-qubit rotations with angles α, π/2 and π along y-axis. Gz is the field gradient pulse along z-axis. b Pulse sequences for preparing $\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\pi /2,x) \otimes \rho _{A{\prime}B{\prime}}(\pi /2,x)$ with the temporal averaging method. The rotation angles δ_1,2,3,4 are arccos[(1 − x)²], arccos[x(1 − x)], arccos[x(1 − x)] and arccos(x²), which are used to adjust the coefficients of four parts in Eq. (30)

D: Experimental procedure

The total experimental procedure is shown in Fig. 6, including the LPPS preparation, the initial state preparation, MUB measurements and the readout of the purities. When the measurement is along y-axis, the first and last rotations in the MUB measurement part should be substituted by rotations along x and −x, and the angles remain also π/2. In the z-axis measurement case, these two rotations are omitted.

Fig. 6

Experimental pulse sequence. The LPPS preparation contains one GRAPE pulse and one z-axis gradient pulse. The GRAPE pulse is used to redistribute the populations and the field gradient pulse is used to eliminate the undesired coherences. The operation V(α, x) is to prepare the initial state $\sigma _z^{{\mathrm {probe}}} \otimes \rho _{AB}(\alpha ,x) \otimes \rho _{A{\prime}B{\prime}}(\alpha ,x)$. Its specific form is shown in Fig. 5. The solid blue rectangle is π/2 rotation along (−y)-axis in x-measurement and along x-axis in y-measurement. The dashed blue rectangles denote π/2 rotations with the opposite phases to those in solid blue rectangles. No need to operate them in z-measurement. The readout part contains two C_swap gates applying on subsystems AA′ and BB′. The dashed C_swap(AA′) is not required in reading out the purity of subsystem B

E: The attenuation factors caused by decoherence effect and experimental measured purities

Even through the high-fidelity GRAPE pulses in experiments, the experimental results are still severely affected due to the decoherence due to the long running times comparing to the T₂ relaxation times of nuclear spins.

In our experiments, the environmental noises are suitably modeled as Markovian, and the evolution of the system is given by the Lindblad master equation

$$\dot \rho = - i[H_{\mathrm S} + H_{\mathrm C}(t),\rho ] + \mathop {\sum}\limits_\alpha {\left( {2L_\alpha \rho L_\alpha ^\dagger - L_\alpha ^\dagger L_\alpha \rho - \rho L_\alpha ^\dagger L_\alpha } \right)} ,$$

(31)

where H_S is the system Hamiltonian, H_C(t) is the time-dependent external control Hamiltonian, and the operators L_α are Lindblad operators representing the coupling with the environment. The experiments are mainly affected by the dephasing process, and therefore $L_\alpha = \sqrt {\frac{{\gamma _\alpha }}{2}} \sigma _z^\alpha ,(\alpha = 1,...,5)$ and γ_α = 1/T_2α and

$$\dot \rho = - i[H_{\mathrm S} + H_{\mathrm C}(t),\rho ] + \mathop {\sum}\limits_\alpha {\gamma _\alpha } \left( {\sigma _z^\alpha \rho \sigma _z^\alpha - \rho } \right).$$

(32)

In the experiments, the high-fidelity GRAPE pulses we used are kinds of shaped pulses consisting of thousands of slices with a constant H_C(t_i) the duration of each slice, where δt is 2−25 μs. Consequently, for each slice, the state of the system can be approximately given by

$$\rho (t_{i + 1}) = \rho (t_i + \delta t) = \mathop {\sum}\limits_{\alpha = 1}^5 {\mathop {\sum}\limits_{i = 0}^1 {E_i^\alpha } } e^{ - i[H_{\mathrm S} + H_{\mathrm C}(t_{i + 1})]\delta t}\rho (t_i)e^{i[H_{\mathrm S} + H_{\mathrm C}(t_{i + 1})]\delta t}E_i^{\alpha \dagger },$$

(33)

where the Kraus operations

$$E_0^\alpha = \sqrt {\lambda _\alpha } {\mathbf{1}},E_1^\alpha = \sqrt {1 - \lambda _\alpha } \sigma _z^\alpha$$

(34)

with $\lambda _\alpha = (1 + e^{ - \gamma _\alpha \delta t})/2$.

Therefore, we numerically simulated the experiments, extracted the attenuation factors caused by decoherence effect and then rescaled the experiment results for verifying the uncertainty conversation relation in Fig. 3a, b. The un-rescaled original results are shown in Fig. 7a. From this we can see that even though the right and left sides of the uncertainty equation are all reduced, they almost equal each other. Figure 7b shows the directly measured purities of different states required in the uncertainty conversation relation.

Fig. 7

a The original results without rescaling of verifying the measurement uncertainty relation. The bars are plotted from the infidelity of readout process. b The directly measured purities. The hollow dots are the expected purities. The blue asterisks are the directly measured purities and the red ones are the rescaled results. The left five figures correspond to purities when the initial bipartite state is ρ_AB(α, 1) where α = 0, π/8, π/4, 3π/8, π/2 from top to bottom. And the right five figures correspond to ρ_AB(π/2, x) where x = 0, 0.25, 0.5, 0.75, 1 from top to bottom. In each figure, from left to right, they are ${\mathrm{Tr}}(\rho _{AB}^2)$, ${\mathrm{Tr}}(\rho _{xB}^2)$, ${\mathrm{Tr}}(\rho _{yB}^2)$, ${\mathrm{Tr}}(\rho _{zB}^2)$, ${\mathrm{Tr}}(\rho _B^2)$, ${\mathrm{Tr}}[(\rho _{B|x})^2]$, ${\mathrm{Tr}}[(\rho _{B|y})^2]$, ${\mathrm{Tr}}[(\rho _{B|z})^2]$, where ρ_θB (θ = x, y, z) are the resulting state after the complete MUB measurements on subsystem A, and ρ_B|θ = Tr_A(ρ_θB)