Introduction

Our device consists of a split Josephson junction terminating a two-wire transmission line, which itself is made of a linear chain of 4 × 104 junctions (Fig. 1a, b). The opposite end of the line is connected to a dipole antenna for performing local RF-spectroscopy. Recently it was shown that the collective electromagnetic modes of such chains are microwave photons with a velocity as low as v ≈ 106 m/s and wave impedance as high as Z∞ ~ RQ, where RQ = h/(2e)2 ≈ 6.5 kΩ is the superconducting resistance quantum.1 This was a significant step forward following the earlier experiments on electromagnetic properties of short Josephson chains.2,3,4,5,6,7 A propagating photon corresponds to a plane wave of voltage/current across/along the two chains, similarly to a coaxial cable. At low frequencies the dispersion is nearly linear and there is a band edge at about ωp/2π ≈ 20 GHz due to the Josephson plasma resonance of individual chain junctions. The split-junction differs from the rest once its Josephson energy EJ(Φ) and hence the plasma mode frequency ω0(Φ) is detuned below ωp by an external flux Φ through the loop. The anharmonicity of this mode is approximately given by the charging energy EC = e2/2CJ of the split-junction’s oxide capacitance CJ. For EC/h ≈ 300 MHz, a disconnected split-junction is similar to a conventional transmon qubit.8 The electromagnetic vacuum seen by such a transmon is formed by the standing wave modes of the finite length L transmission line.

Fig. 1
figure 1

a Optical image of the device, showing (left to right) the coupling antenna, sections of the Josephson transmission line, and the split-junction termination. b Distributed circuit model of the device. The system is probed from the opposite to the split-junction end. c Equivalent circuit model of a semi-infinite transmission line with the wave impedance Z∞ shunting the split-junction. d A lumped element equivalent circuit model of b for a finite-length line

Full size image

Cavity QED typically describes a reversible exchange of an excitation between a single resonant mode and a qubit at the vacuum Rabi frequency g.9,10,11 For a long transmission line, the excitation exchange can occur faster than the time 2L/v that takes the photon to traverse the line. This would dramatically modify the mode wave function, e.g. replacing a node of electric field with an antinode, because to establish it a photon must complete the round trip. The fact that a single atom (qubit) can alter the photon’s spatial profile motivated the term superstrong coupling in the original proposal.12 In the frequency domain, the condition for superstrong coupling is gρ > 1, where ρ = 2L/v is the density of vacuum modes (1/ρ is the free spectral range), which means the qubit exchanges an excitation with multiple vacuum modes simultaneously. For a single mode system, another regime beyond strong coupling takes place at g ~ ω0, which was termed ultrastrong coupling.13,14 In this regime the total number of excitations is no longer conserved, which leads to an entangled qubit-photon ground state.15 From the many-body physics perspective, the most intriguing scenario is the combination of ultrastrong and superstrong regimes, where formation of multimode entanglement is expected.16 In fact, quantum electrodynamics in this case maps onto the strongly correlated (Kondo-like) quantum impurity models of condensed matter physics.17,18,19,20,21,22 The advantage of simulating such models in a quantum optics setting is that, for sufficiently large gρ and g/ω0, the many-body effects can be completely developed, while each microscopic mode remains individually accessible due to the finite system size. Moreover, the system size itself becomes an experimental control knob.

Spectroscopic signatures of ultrastrong coupling were previously reported in experiments on flux qubits and transmons.23,24,25,26 The superstrong coupling condition gρ > 1 remains challenging even for circuit QED. A pioneering experiment in this direction was done by capacitively coupling a transmon qubit to a nearly one-meter long coplanar waveguide transmission line with Z∞ ≈ 50 Ω.27 The conditions gρ ≈ 0.3 and g ≈ 30 MHz were achieved and multimode fluorescence was observed under a strong driving of the dressed qubit. However, the coupling was too low to expect quantum many-body effects with single photons. In a recent experiment the coupling was increased to g ≈ 160 MHz by using a higher impedance transmission line (Z∞ ≈ 1.6 kΩ) made using Josephson junction chains.28 Unfortunately, the mode density was also reduced due to the limited chain length, resulting in gρ ≈ 0.4. Moreover, increasing the coupling requires reducing the parameter EJ/EC of the transmon, which comes at the price of charge noise decoherence.29,30 Besides circuit QED, hybrid quantum acoustic systems are promising for creating vacua with a high density of discrete modes.31,32

Remarkably, the coupling strength becomes practically unlimited with the galvanic connection used in our experiment.33 This is apparent in the L → ∞ limit, where the line, as viewed by the transmon, can be replaced by an ideal resistance Z∞ (Fig. 1c). The coupling is now characterized by the spontaneous emission rate Γ. On one hand (for a large but finite L) Fermi’s golden rule gives Γ = 2πg2ρ.34 On the other hand, correspondence principle requires that the excited state lifetime T1 ≡ 1/2πΓ is given by a classical expression T1 = Z∞CJ (the “RC” charge relaxation time). This gives Γ = 2.5 GHz/Z∞[kΩ], i.e. a typical transmon is overdamped by a conventional 50 Ω vacuum. Same effect takes place with flux qubits.35 The main innovation of our experiment is to utilize a high wave impedance (Z∞ ≈ 5–10 kΩ) in order to weaken the galvanic coupling to the range \(\Gamma \lesssim \omega _0/2\pi\) where the atomic transition is well-defined. The superstrong regime parameter \(g\rho = \sqrt {\Gamma \rho /2\pi }\) can be adjusted independently of Γ by varying the line length.

Results

In this work we achieved superstrong coupling with gρ ≈ 1.3 and we illustrate this by observing the phenomenon of spontaneous emission into a finite-size vacuum. As the parameter gρ grows above a unity, progressively more vacuum modes hybridize with the atom to the degree that the distinction between the two cannot be made. The spectrum no longer contains the individual 2g-splittings, and the atomic transition is replaced by a band of about Γρ states defining the spontaneous emission linewidth Γ. Clearly, reaching \({\mathrm{\Gamma }}\rho \gg 1\) is needed for the many-body physics, in the two relevant experiments \({\mathrm{\Gamma }}\rho \lesssim 1\).27,28 Here Γρ = 2π(gρ)2 ≈ 10, which allowed us to observe, for the first time, the radiative broadening of an atom by measuring the frequency shifts that it induced on a large number of individual vacuum modes.

We start with constructing a Hamiltonian model of galvanic light-matter coupling in our circuit. Accounting for the atom-induced distortions in the modes spatial profile can be challenging.36 Consequently, even for \({\mathrm{\Gamma }} \ll \omega _0\) the multimode Jaynes−Cummings model predicts divergent values of physical observables.37,38 Here we avoided these problems by choosing an appropriate circuit model of our system (Fig. 1d). An open section of a transmission line can be modeled by an infinite set of serial LjCj-circuits (j = 1, 2,…) connected in parallel. The frequency and characteristic impedance of each oscillator are given by ωj ≡ 1/(LjCj)1/2 = 2π(j − 1/2)/ρ and zj ≡ (Lj/Cj)1/2 = Z∞ωjρ/4, respectively.39 A weak wave dispersion can be taken into account by introducing a slow frequency dependence to both ρ and Z∞. We also introduce the bare transmon transition frequency ω0 = ((8EJEC)1/2 − EC/2)/ℏ and linearized impedance z0 = RQ(2EC/π2EJ)1/2. Defining the annihilation (creation) operators \(a_0(a_0^\dagger )\) for the bare transmon and \(a_j(a_j^\dagger )\) for the uncoupled bath modes, the Hamiltonian reads:

$$\begin{array}{*{20}{l}} {{H}/\hbar } \hfill & = \hfill & {\omega _{0}a_{0}^\dagger a_{0} - K(a_{0}^{\dagger} a_{0})^2 + \mathop {\sum}\limits_{j > {0}} \omega _{j}a_{j}^{\dagger} a_{j}} \hfill \\ {} \hfill & {} \hfill & { - (a_{0} + a_{0}^\dagger )\mathop {\sum}\limits_{j > 0} g_{j}(a_{j} + a_{j}^\dagger ) + \left( {\mathop {\sum}\limits_{j > {0}} \frac{{g_{j}}}{{\omega _{0}^{1/2}}}(a_j + a_{j}^\dagger )} \right)^{2},} \hfill \end{array}$$
(1)

where K = EC/2ℏ and individual couplings are given by gj = ω0(z0/zj)1/2/2.30 The vacuum Rabi frequency g is given by g = gj(ωj → ω0)/2π and we indeed confirm that Γ = 1/2πZ∞CJ.

The Hamiltonian (1) is a textbook Caldeira−Leggett model of a quantum degree of freedom interacting with an Ohmic bath.40 The last term is the rigorously derived “A2”-term of quantum optics. Note that in our model \(g_j^2\sim 1/j\), which regularizes perturbative series automatically, without the need for sophisticated analysis recently proposed for a capacitively connected transmon.37,38

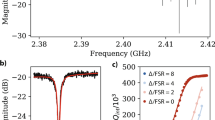
Spectroscopy data as a function of drive frequency and flux through the split-junction’s loop are shown in Fig. 2. We observe a dense set of regularly spaced resonances, with a mode spacing of about 1/ρ ≈ 50–60 MHz, which is disturbed periodically in flux (only a fraction of the period is shown). This flux-dependent disturbance is associated with the tuning of the transmon’s resonance across the spectrum of the transmission line. The unique feature of these data compared to previous multimode circuit experiments27,31 is that there are no individual vacuum Rabi splittings. In fact, at a fixed flux, the raw reflection trace vs. frequency contains no obvious sign of the atomic transition (Fig. 2b). However, upon tuning the flux, we observe that multiple resonances shift by nearly the same amount, indicating that many modes are equally sensitive to the tuning of the transmon (see three insets in Fig. 2a).

Fig. 2
figure 2

a Reflection magnitude as a function of drive frequency and flux through the loop. The color scale (not shown) is optimized to make the position of resonances maximally visible. The three insets have the same width along the frequency axis and correspond to the three boxed regions on the main plot. b An example slice of a at the external flux 0.525 × h/2e, shown by the horizontal dashed line, where the atomic resonance is expected at around 7 GHz

Full size image

A clear picture of an atom simultaneously coupled to many vacuum modes comes from extracting the density of states (DOS) conventionally defined as (π/L)/(ωj + 1 − ωj), where ωj is the measured frequency of jth mode. This quantity is readily available since every individual mode is frequency-resolved in our reflection spectroscopy. The obtained DOS has a broad peak, involving about 20 consequent modes, and slowly increasing with frequency background (Fig. 3a). From fitting the background to a simple model of transmission line DOS, we extract the bare junctions plasma frequency ωp/2π = 22.6 GHz and the wave impedance Z∞ = 4.9 kΩ (Methods). The peak line-shape fits well to a simple Lorentzian function with unit area, which correctly reflects one additional state coming from the transmon. The DOS peak position shifts with flux and perfectly follows the disconnected transmon’s resonance, assuming a reasonable junction asymmetry and that the maximal plasma frequency is that of the other chain junctions (Fig. 3c). Importantly, the fitted peak width is frequency-independent and matches the theoretical radiative linewidth Γ ≈ 1/2πZ∞CJ ≈ 600 MHz, within ±50 MHz. In a control experiment, we have checked that a device with a twice higher wave impedance, Z∞ = 9.8 kΩ, fabricated using a skinnier junction chain, narrows the DOS peak precisely by a factor of two (Fig. 3b).

Fig. 3
figure 3

a Single-particle density of photon states (DOS) vs. frequency (see text). The fluctuations are reproducible and reflect a small disorder in the junction parameters. The fit (solid line) is a combination of a Lorentzian resonance shape combined with the background transmission line DOS growing due to the van Hove singularity at the plasma frequency ωp/2π = 22.6 GHz. b DOS extracted for a device with Z∞ = 9.8 kΩ. c DOS from a plotted vs. flux. The two dashed lines indicate the fit to a transmon’s transition and a fixed width of the DOS peak

Full size image

To test the Hamiltonian (1) further, we measure the atom-induced photon−photon interactions. Neglecting the transmon’s nonlinearity at first, the Hamiltonian (1) is quadratic and can be diagonalized exactly to obtain the flux-dependent normal mode frequencies \(\tilde \omega _j(\Phi )_{}^{}\). The result very well reproduces the spectroscopy data in Fig. 2. Expressing the Kerr term in terms of the “quasiparticle” photon creation cj and annihilation \(c_j^\dagger\) operators, and keeping only energy-conserving terms, we can approximate the Hamiltonian (1) as:

$$H/h \approx \mathop {\sum}\limits_{j} \left( {\tilde \omega _{j}c_{j}^\dagger c_{j} - K_{j}(c_{j}^\dagger c_{j})^{2}} \right) - \mathop {\sum}\limits_{i \ne j} \chi _{i,j}(c_{i}^\dagger c_{i}c_{j}^\dagger c_{j}).$$
(2)

Here the Kj is the induced Kerr shift of the j-mode frequency due to a single photon, which plays the role of the on-site repulsion in Bose−Hubbard models.41 The χi,j is the induced cross-Kerr shift of the mode i due to a single photon in the mode j7 (Methods).

We verified the presence of the induced Kerr effect using high-power spectroscopy. The modes inside the DOS peak clearly shift much more in response to a high-power driving compared to the modes outside of it (Fig. 4a). At some threshold power, we observe that the resonances within the DOS peak snap onto their uncoupled values. This effect, standard in circuit QED,42 can be also explained as the split-junction effectively acquires an infinite inductance because the swing of its overdriven phase exceeds 2π.

Fig. 4
figure 4

a Power-dependence of the spectroscopy signal for the DOS peak at 7.12 GHz. The modes inside the DOS peak shift more strongly with power than the ones outside. b Dispersive shifts χi,j as a function of i-modes frequencies for a fixed second-tone driving of the mode j = 108 at 7.014 GHz, near the top of the DOS resonance (marked with an arrow). Blue markers indicate the same measurement for a largely detuned atom. Theory (solid and dashed lines) has no adjustable parameters except for the Y-axis scale (Methods). The error bars are the SD of the measured dispersive shifts. c Power-dependence of the shifts of selected modes indicated by matching markers

Full size image

The cross-Kerr interaction can be characterized more accurately. For a chosen flux bias, we drive a mode j = 108, corresponding to the peak in the DOS at a convenient atomic frequency around 7 GHz. The power is such that the mode is populated by an approximately one photon on average. The neighboring modes i = j ± 1, j ± 2,… are scanned with a low-power drive to obtain the resulting frequency shifts. This allows for a measurement of the dependence of χi,j on i − j and comparison with our perturbative calculation. The χi,j is maximal for the DOS peak maximum, and drops rapidly as the i-modes leave the Γ-neighborhood of the atomic resonance. Although the measured shifts have some fluctuations of the presently unknown nature, the overall data match the theory well using the photon number to drive power conversion as the only adjustable parameter (Methods).

Discussion

The origin of a weak \((K \ll \Gamma )\) photon−photon interaction strength is interesting and can be understood as follows. A mode of the bare transmon (a0) is approximately an equal superposition of Γρ ≈ 10 normal modes (cj) of the combined system. Normalization requires that each mode amplitude is 1/(Γρ)1/2. Therefore, the induced Kerr and cross-Kerr shifts per photon due to the quartic nonlinearity scale as EC/(Γρ)2 ~ EC/100, which agrees with the data (Methods). Somewhat counterintuitively, increasing the light-matter coupling in the microscopic Hamiltonian (1) leads to the dissolution of the transmon’s quartic nonlinearity over a large number of linear modes, thereby suppressing the many-body effects.

Fortunately, nonlinearity can be dramatically enhanced in our system by reducing the size of the split-junction such that \(E_{\mathrm J}/E_{\mathrm C}\sim 1\). Because of large quantum fluctuations of the Josephson phase, enabled by \(Z_\infty \sim R_{\mathrm Q}\),3 the series expansion of the cosine nonlinearity becomes invalid. Moreover, owing to the galvanic connection, the offset charge noise is eliminated by the large zero-frequency capacitance of the transmission line. In fact, for \(E_{\mathrm J}/E_{\mathrm C}\,\sim\,1\), our galvanic circuit QED system must be described by the boundary sine-Gordon quantum field theory. This quantum impurity model has a critical point at Z∞ = RQ.17,18 It plays an important role in a broad range of phenomena, from dissipative quantum phase transitions,43,44 to interacting electrons in one dimension.45 Alternatively, the small junction can be replaced by either a flux35 or fluxonium2,30,46,47 two-level-like qubits to implement the spin-1/2 Kondo impurity model in the bosonic representation.

In summary, we have demonstrated an ideal superconducting resistor, with a value exceeding resistance quantum RQ ≈ 6.5 kΩ, operating at frequencies beyond 10 GHz, and whose internal modes are frequency-resolved and hence are individually accessible. The spontaneous emission of a transmon qubit galvanically wired to it is not modified by the discreetness of the resistor spectral function at time scales shorter than the photon round trip time ρ, as long as the coupling to individual modes exceeds the mode spacing 1/ρ ≈ 50–100 MHz. The spontaneous emission linewidth is revealed by frequency shifts of the resistor’s individual modes. This situation defines a superstrong regime of light-matter coupling, relevant for exploring many-body physics with photons.

Methods

Device fabrication and measurement setup

The devices were fabricated on a highly resistive silicon substrate using the standard Dolan bridge technique. The process involves e-beam lithography on an MMA/PMMA bi-layer resist and the subsequent double-angle deposition of aluminum with the intermediate oxidation step. The spectroscopy measurements are done in a single-port reflection geometry using the wireless interface described in ref. 1 A global magnetic field was used to create a flux through the split-junction loop.

The density of states

The DOS in our system can be expressed as the sum of two contributions

$${\mathrm {DOS}}(\omega ) = \frac{1}{{2\pi v(1 - (\omega /\omega _{\mathrm p})^2)^{3/2}}} + \frac{1}{{2L}}\frac{\Gamma }{{(\omega - \omega _0)^2 + \pi ^2\Gamma ^2}}.$$

The first term is the DOS for photons in a bare “telegraph” transmission line. It is easily obtained from their dispersion relation \(\omega (k) = vk/\sqrt {1 + (vk/\omega _{\mathrm p})^2}\). The second term takes into account one additional state coming from the transmon. It is expressed as a Lorentzian function normalized by the double transmission line length so the integration over the full frequency range and the length results in exactly one. By fitting the measured DOS to the above expression we found the transmon’s resonance frequency ω0 and broadening Γ as well as the photons velocity v and cut-off frequency ωp.

Self- and cross-Kerr coefficients

In order to find the expressions for Kj and χi,j we start from the Hamiltonian (1) and limit the number of bath modes to N = 1000. Without the nonlinear term the Hamiltonian (1) can be diagonalized with a unitary transformation given by a matrix U. U is a block matrix, which ensures the commutation relations are preserved in the new basis \(c^\dagger ,c\).

$$\left( {\begin{array}{*{20}{l}} a \hfill \\ {a^\dagger } \hfill \end{array}} \right) = \left( {\begin{array}{*{20}{c}} u & v \\ { - v} & u \end{array}} \right)\left( {\begin{array}{*{20}{l}} c \hfill \\ {c^\dagger } \hfill \end{array}} \right).$$

Here a = (a0, a1, …, aN−1, aN)T, \(a^\dagger = (a_0^\dagger ,a_1^\dagger ,\ldots,a_{N - 1}^\dagger ,a_N^\dagger )^{\mathrm T}\), etc., and u, v are N + 1 by N + 1 matrices. We can now express the quartic transmon’s nonlinearity \(\sim (a_0 - a_0^\dagger )^4\) in the new basis. Counting the terms \((c_j^\dagger c_j)^2\) and \(c_i^\dagger c_ic_j^\dagger c_j\) we arrive at the expressions

$$\begin{array}{*{20}{l}} {K_j} \hfill & = \hfill & {\frac{1}{2}E_C(v_{1j}^2 - u_{1j}^2)^2/h}, \hfill \\ {\chi _{i,j}} \hfill & = \hfill & {2E_C(v_{1i}^2 - u_{1i}^2)(v_{1j}^2 - u_{1j}^2)/h}. \hfill \end{array}$$

We checked that the same results can be obtained in the perturbative calculation only starting from the linear circuit Hamiltonian.7

Measurement of the cross-Kerr shifts

The dispersive cross-Kerr interaction of photons caused by the Josephson junction nonlinearity appears as a mode frequency shift which is linear in the photon population of any other mode. We picked up the mode j = 108 and changed its photon population with the second microwave tone. For every other mode in the vicinity of the DOS peak we performed a set of reflection measurements with the second tone being consecutively on or off. The mode frequency in every measurement was found from the fit of the reflection coefficient, both the real and imaginary parts, to the damped LC-oscillator model. The shift is then defined as an average mode frequency change between the on and off state of the second tone. The procedure was repeated for various second-tone powers. To eliminate the detrimental effects of the flux jitter, we chose the shortest possible time between two consecutive measurements. Moreover, the frequency of the second tone was modulated with a time scale much smaller than the measurement time and with an amplitude larger than the jitter amplitude. This allowed us to create a constant population of the driving mode disregarding its frequency fluctuation. We performed the same measurements in the same frequency range but with the transmon’s resonance largely detuned. We found cross-Kerr shifts smaller by three orders of magnitude, which is consistent with our perturbative calculations of the bare transmission line nonlinearity. This consistency made the rough photon calibration possible.