Characterising the correlations of prepare-and-measure quantum networks

Abstract

Prepare-and-measure (P&M) quantum networks are the basic building blocks of quantum communication and cryptography. These networks crucially rely on non-orthogonal quantum encodings to distribute quantum correlations, thus enabling superior communication rates and information-theoretic security. Here, we present a computational toolbox that can efficiently characterise the set of input–output probability distributions for any discrete-variable P&M quantum network, assuming only the inner-product information of the quantum encodings. Our toolbox is thus highly versatile and can be used to analyse a wide range of quantum network protocols, including those that employ infinite-dimensional quantum code states. To demonstrate the feasibility and efficacy of our toolbox, we use it to solve open problems in multipartite quantum distributed computing and quantum cryptography. Taken together, these findings suggest that our method may have implications for quantum network information theory and the development of new quantum technologies.

Introduction

Quantum correlations^1,2,3 (namely, entanglement, nonlocality, steering correlations, etc) are essential resources in quantum information processing. In short, they are the reason why we see such unique advantages in quantum communication, cryptography, computing, and imaging. The general observation is that the stronger these correlations are, the more powerful quantum information becomes. This is especially the case for quantum communication⁴ and quantum cryptography,⁵ where stronger entanglement means higher quantum fidelity and stronger information security. For this reason, the characterisation of quantum correlations is an integral step in many quantum information protocols and a central research topic in quantum information science.

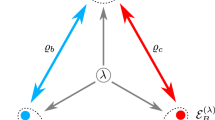
In this work, we are interested in characterising the quantum correlations of prepare-and-measure (P&M) networks, which are the basic building blocks of quantum communication and quantum cryptography. The central goal of a P&M quantum network is to send some classical message z over a quantum network to a group of receivers (see Fig. 1). This message could be anything, e.g., a secret key, elements of a database, or a signed certificate—it depends on the function of the protocol. Quantum encoding is done by preparing a quantum signal in one of the n predefined pure states, $\{ |\psi _z\rangle \} _{z = 1}^n$ (determined by the input z), and decoding is accomplished by making a measurement (sampled from a finite set of decoding settings) on the output quantum signal. For a generic P&M quantum network with k spatially separated receivers, we write p(a₁a₂…a_k|x₁x₂…x_k, z) to denote the probability of obtaining outcomes a₁a₂…a_k given decoding functions x₁x₂…x_k and message z. We use p to denote the entire list of input–output probability distributions.

Fig. 1

Scenario and assumptions. The behaviour of a two-receiver prepare-and-measure (P&M) quantum network is generally described by p = [p(ab|xy, z)], which expresses the probability of z transiting to outcomes a, b given measurement inputs x, y. In the quantum setting, the set of conditional probabilities are given by $p(ab|xy,z) = \langle \phi _z|E_x^aE_y^b|\phi _z\rangle$, with the constraint that 〈ϕ_z|ϕ_z′〉 = λ_zz′ is fixed. Our consideration hence assumes three conditions: (1) the set of code states are pure states, (2) the Gram matrix of these states is known, and (3) the receivers are independent of each other (they do not share any quantum resources, although classical randomness is allowed)

Our broad goal is to reveal the fundamental limits of P&M quantum networks without restrictions on the network and local decoding strategies. In particular, we are interested in identifying the set of quantum-realisable correlations p (henceforth called the quantum set) using only the knowledge of the quantum encoding scheme {|ψ_z〉}_z. In fact, as we shall show later, it is enough to use the inner-product information of the encoding scheme (instead of the complete specification) to achieve tight characterisation of the quantum network. This type of approach is particularly useful for analysing the performance of quantum communication and quantum cryptography. For instance, one can use the quantum set to derive lower bounds on the quantum network’s error probabilities.^6,7,8 These bounds essentially tell us what the encoding scheme could achieve in practice, be it for quantum cryptography, communication, or distributed computing purposes, as we shall demonstrate later.

Also, from the perspective of quantum information theory, this approach draws a direct connection between the distinguishability of quantum states and quantum correlations. More concretely, we first note that if the quantum encoding {|ψ_z〉}_z is completely orthogonal, i.e., 〈ψ_z|ψ_z′〉= δ_zz′, then p is generally unconstrained. That is, such encodings are classical states and hence can be arbitrarily copied—as such, there are no physical principles that could constrain the input–output probability distribution (except for the usual normalisation requirements). The interesting part comes when the encoding {|ψ_z〉}_z is non-orthogonal. In this case, there are two unique consequences. First, it is generally impossible for every receiver to learn the same information about z. This is due to the fact that one cannot clone non-orthogonal states,⁹ and consequently, there is a global trade-off between the amount of accessible information that each receiver can receive.^10,11 Second, no receiver can completely learn z even if he or she has received {|ψ_z〉}_z with perfect fidelity. This is because non-orthogonal states are fundamentally indistinguishable: there is no measurement that can discriminate them with perfect reliability.¹² Consequently, probability assignments like p(a = z|x) = 1 are forbidden. Taken together, these imply that, contrary to orthogonal (classical) encodings, correlations emanating from quantum encodings have non-trivial constraints (e.g., see quantum broadcasting^13,14).

Results

To solve the above characterisation problem, we propose a general computational method that is able to approximate (from the outside) the quantum set of any P&M quantum network. The approximation is based on a hierarchy of semidefinite relaxations, which is a generalisation and novel application of earlier research in quantum nonlocality.^{2,15,16,17,18,19,20} More specifically, we extend and generalise the hierarchy of semidefinite relaxations proposed in refs ^19,20 to the case whereby the quantum state shared between the receivers is not fixed. A key feature of our method is that it is semi-device independent (SDI).^{21,22,23,24,25,26,27} That is, the analysis provided is independent of how the network and measurements are implemented. The method only requires that the quantum encoding {|ψ_z〉}_z is characterised in terms of its Gram matrix, i.e., 〈ψ_z|ψ_z′〉 = λ_zz′, which in practice can be easily obtained by taking the inner products of the quantum code states (i.e., using their specifications).

The main advantage with this approach is that the dimension of the encoding system is no longer necessary in the analysis—using the inner-product information is enough to tightly characterise the quantum set. Indeed, the inner-product information is sufficient as it tells us how non-orthogonal the encoded states are and whether they are classical or not. As such, our approach is more practical than the standard SDI approach, which assumes the dimension of the quantum encoding system.^21,22,23,24 Notice that physical dimension is generally difficult to fix in practice as actual systems have multiple degrees of freedom. We remark that alternative SDI approaches based on bounded energy constraints²⁶ and the transmission of non-orthogonal binary states²⁷ have also been proposed. These have similar advantages as our approach, but present analyses using these approaches are so far limited to binary code states. It remains to be seen if these can be readily generalised to multiple code states, schemes that are often used in quantum technologies. In the following, we show that our method can be used to efficiently analyse any practical quantum communication protocol,²⁸ including those that use multiple infinite-dimensional code states.

To keep our presentation concise, we restrict the discussion to two-receiver P&M quantum networks (see Fig. 1); extension to larger networks is straightforward. Consider a P&M quantum task, where random code states are sent across a network to two independent receivers, called Alice and Bob, for measurement. For simplicity, we divide the task into two phases: a distribution phase and a measurement phase. In the first phase, a classical random source z is encoded into a quantum system |ψ_z〉 and distributed to Alice and Bob via an untrusted quantum network. For this type of transmission, it is useful to work in the purification picture, where state transformations are given by unitary evolutions.²⁹ That is, by working in a higher-dimensional Hilbert space, we may see the transmission as an isometric evolution that takes |ψ_z〉 to some pure output state |ϕ_z〉, which is now shared between the receivers and the network environment (the purification system). The key advantage of this picture is that while the dimension and possibly other properties of |ψ_z〉 may change after the transmission, the inner-product information of {|φ_z〉}_z remains the same: 〈ϕ_z|ϕ_z′〉 = 〈ψ_z|ψ_z′〉. Importantly, this means that our initial knowledge about 〈ψ_z|ψ_z′〉 = λ_zz′ is preserved in the transformed states.

In the measurement phase, Alice and Bob perform independent and random measurements on |ϕ_z〉 to gain information about z. Since there are only two receivers here, we revert back to the usual convention and denote Alice’s and Bob’s measurements by x and y and their corresponding measurement outcomes by a and b, respectively. Then, using the quantum Born rule, we have that the probability of observing outcomes a, b given measurements x, y and |ϕ_z〉 is

$$p(ab|xy,z) = \langle \phi _z|E_x^aE_y^b|\phi _z\rangle ,$$

(1)

where $\{ E_x^a\}$ and $\{ E_y^b\}$ are projective measurements satisfying the following properties: (i) for any x, $E_x^aE_x^{a^\prime } = 0$ for $a\not = a^\prime$, (ii) $\mathop {\sum}\nolimits_a E_x^a = {\Bbb I}$, (iii) $(E_x^a)^2 = E_x^a = (E_x^a)^\dagger$, and (iv) $[E_x^a,E_y^b] = 0$. We note that there is no loss of generality in assuming projective measurements here. Indeed, we can always lift any measurement to a projective one by working in a higher-dimensional Hilbert space; in our case this is possible since the dimension of the network is not fixed. The last property reflects the fact that Alice’s and Bob’s measurements are separable and hence the application of one has no effect on the outcome of the other.

Our characterisation problem is thus the following: Given an n × n Hermitian positive-semidefinite matrix λ, what is the corresponding quantum set p? We denote this set by ${\cal Q}(\lambda )$. In principle, solving this problem would require optimising over all possible quantum states and measurements in Eq. (1) subject to the constraints 〈ϕ_z|ϕ_z′〉 = λ_zz′. However, this task is computationally intractable: the dimension of the network is not fixed and thus could be infinite. To overcome this obstacle, we take inspiration from the characterisation techniques^{16,17,18,19,20} developed in Bell nonlocality research,^2,15 which is a special case of our problem. Recall that in a Bell experiment, local random measurements are made on a fixed source |ϕ〉 instead of a varying source |ϕ_z〉. Notably, it was shown in refs ^19,20 that the set of quantum probabilities derived from Bell experiments can be approximated via a hierarchy of membership tests. There, the basic idea is to bound the quantum set using a sequence of weaker (but tractable) characterisation tasks, which nevertheless still represent very well the original problem.

In this work, we show that a similar characterisation technique can also be devised for the general problem. More specifically, we give a general procedure for deriving (tractable) necessary conditions for any discrete-variable P&M quantum network. To start with, consider a quantum probability distribution $p(ab|xy,z) = \langle \phi _z|E_x^aE_y^b|\phi _z\rangle$, where 〈ϕ_z|ϕ_z′〉 = λ_zz′, and with $\{ E_x^a,E_y^b\} _{a,x,b,y}$ satisfying properties (i)–(iv). Let ${\cal S} = \{ S_1, \ldots ,S_m\}$ be a finite set of m operators, where each element is a linear combination of products of $\{ E_x^a,E_y^b\} _{a,x,b,y}$. Then define G to be the nm × nm block matrix

$$G = \mathop {\sum}\limits_{z,z^\prime = 1}^n G^{zz^\prime } \otimes \left| {e_z} \right\rangle \left\langle {e_{z^\prime }} \right|,$$

where $G_{(i,j)}^{zz^\prime } = \langle \phi _z|S_i^\dagger S_j|\phi _{z^\prime }\rangle$ for all z, z′ ∈ [n], i, j ∈ [m]. Here we denote by $\{ |e_z\rangle \} _{z = 1}^n$ the standard orthonormal basis of ${\Bbb C}^n$ and by $G_{(i,j)}^{zz{\prime}}$ the ij-entry of the matrix G^zz′. By construction, the matrix G is Hermitian and positive-semidefinite (PSD).³⁰ Furthermore, properties (i)–(iv) of the measurement operators and the inner-product constraints 〈ϕ_z|ϕ_z′〉 = λ_zz′ translate to linear conditions on the entries of G. To see this, we note that if the set ${\cal S}$ contains operators $\{ E_x^a\} _{a,x}$ and $\{ E_y^b\} _{b,y}$, then it can be easily verified that G satisfies

$$\begin{array}{l}\mathop {\sum}\limits_b G_{(a,x),(b,y)}^{zz} = \mathop {\sum}\limits_b p(ab|xy,z)\\ \mathop {\sum}\limits_a G_{(a,x),(a,x)}^{zz^\prime } = \lambda _{zz^\prime }.\end{array}$$

Therefore, for any discretely modulated P&M quantum network, it is always possible to define a PSD matrix that captures the original quantum model (1) in terms of constraints that are linear in its entries. Importantly, the existence of such a matrix provides us with a powerful means to check if a given p is of quantum origin. More specifically, we can use semidefinite programming (SDP) techniques³¹ to verify if p is in the set of compatible PSD matrices: if p is not a member, we conclude that it is not quantum realisable. However, successful membership does not necessarily mean p is of quantum origin. This is due to the fact that our characterisation method is a semidefinite relaxation³² of the original problem and hence can only provide an outer-approximation of ${\cal Q}(\lambda )$.

However, by introducing additional linear constraints via a hierarchical procedure, it is possible to gain a tighter characterisation of ${\cal Q}(\lambda )$. In particular, we could use the hierarchy proposed in refs ^19,20 to build a series of increasingly stringent membership tests, where the associated Gram matrix G grows bigger in each step and more constraints are generated. More precisely, we define a sequence of hierarchical sets ${\cal S}_1 = \{ E_x^a,E_y^b\}$, ${\cal S}_2 = {\cal S}_1 \cup \{ E_x^aE_{x^\prime }^{a^\prime }\} \cup \{ E_y^bE_{y^\prime }^{b^\prime }\} \cup \{ E_x^aE_y^b\} ,$ where ${\cal S}_k$ is defined inductively as the set of all operator sequences constructed from $E_x^a,E_y^b$ satisfying ${\cal S}_k \subseteq {\cal S}_{k + 1}$. This corresponds to a sequence of Gram matrices, G¹, G²,… with increasing size and constraints. Since the Gram matrix G^k of a particular kth step is at least as informative as a smaller sized Gram matrix G^k′, we conclude that the approximated set ${\cal Q}(\lambda )_k$ is a subset of ${\cal Q}(\lambda )_{k^\prime }$. Therefore, moving up the hierarchy gives a tighter approximation of the quantum set: ${\cal Q}(\lambda ) \subseteq {\cal Q}(\lambda )_k \subseteq {\cal Q}(\lambda )_{k - 1} \ldots$. In the online supplementary material, we prove that this hierarchy is in fact sufficient: it converges to the quantum set, $lim_{k \to \infty }{\cal Q}(\lambda )_k = {\cal Q}(\lambda )$. Nevertheless, in the applications below, we see that low-level approximations are already enough to achieve very tight bounds.

Applications

Our method can be applied to any quantum communication task that employs the P&M scheme. To illustrate this point, we provide two examples of application: (1) distributed quantum random access coding (QRAC)^33,34 and (2) quantum key distribution (QKD).^35,36

In the first, we consider a distributed computing task where two random bits z₀z₁ are encoded into a quantum state $\left| {\psi _{z_0z_1}} \right\rangle$ and sent to Alice and Bob for selective decoding. For the decoding part, Alice and Bob are each given a random position bit and their goal is to guess the input bit that is associated with the position bit. For example, if Alice receives x = 1, she has to guess the value of z₁ via measurement on her share of $\left| {\psi _{z_0z_1}} \right\rangle$. This task can be seen as a type of distributed quantum database, where network users can choose to learn any entry of the database; this includes the case whereby multiple users can choose to learn the same entry. To this end, we quantify the network’s ability to distribute information by Alice’s and Bob’s guessing probabilities, which we denote by p(a = z_x) and p(b = z_y), respectively.

At this point, it is useful to recall that if $\left| {\psi _{z_0z_1}} \right\rangle$ is a two-level quantum system (i.e., a qubit), then the best encoding strategy (in the case of the standard two-party QRAC) is to use the so-called conjugate coding scheme:³⁷ |ψ₀₀〉 = | + 〉, |ψ₁₀〉 = | + i〉, |ψ₀₁〉 = |−i〉, and |ψ₁₁〉 = |−i〉, where |±〉 and |±i〉 are the eigenstates of the Pauli operators ${\Bbb X}$ and ${\Bbb Y}$, respectively. This gives a guessing probability of $\left( {1 + 1/\sqrt 2 } \right)/2 \approx 0.853$,^33,34 which is optimal for qubit code states. Interestingly, using our method, we find that similar bounds can be established using only the Gram matrix information of the code states. In particular, we consider a set of code states {|ψ₀₀〉,|ψ₁₁〉,|ψ₁₀〉,|ψ₀₁〉}, whose Gram matrix is fixed to that of {|+〉,|−〉,|+i〉,|−i〉}, and ask what is Alice’s optimal guessing probability given Bob’s guessing probability is fixed. Our method predicts the following quantum boundary: (2p(a = z_x) − 1)² + (2p(b = z_y) − 1)² ≤ 1/2, which is drawn in Fig. 2. The SDP for this optimisation is given in the supplementary material.

Fig. 2

Distributed two-receiver quantum random access coding (QRAC). The boundary is generated using the first level of the semidefinite programming (SDP) hierarchy. In principle, the boundary is not necessarily tight, for ${\cal Q}(\lambda )_1$ may contain correlations that are not of quantum origin. However, in our case we show that the derived boundary is tight: it is saturated by the optimal asymmetric qubit cloning machine. Suppose the quantum code states are given by the conjugate coding scheme: |ψ₀₀〉 = |+〉|0〉,|ψ₁₀〉 = |+i〉|0〉,|ψ₀₁〉 = |−i〉|0〉, and |ψ₁₁〉 = |−〉|0〉. The quantum network is assumed to be an asymmetric cloning channel U_f: |0〉|0〉 → |0〉|0〉 and $|1\rangle |0\rangle \to \sqrt {1 - f} |1\rangle |0\rangle + \sqrt f |0\rangle |1\rangle$, where f ∈ [0, 1]. For the decoding, we assume that Alice and Bob perform the optimal QRAC qubit measurements: $E_x^a = ({\Bbb I} + ( - 1)^a({\Bbb X} + ( - 1)^{x + 1}{\Bbb Y})/\sqrt 2 )/2$, $E_y^b = ({\Bbb I} + ( - 1)^b({\Bbb X} + ( - 1)^{y + 1}{\Bbb Y})/\sqrt 2 )/2$. Using these and setting the left subsystem as Alice’s and the right subsystem as Bob’s, we have that $p(a = z_x) = 1/2 + \sqrt {(1 - f)/2} /2$ and $p(b = z_y) = 1/2 + \sqrt {f/2} /2$. These give (2p(a = z_x) − 1)² + (2p(b = z_y) − 1)² = 1/2, which is the quantum boundary predicted by the ${\cal Q}(\lambda )_1$ set

Three remarks are in order here. First, we see that the boundary (obtained from ${\cal Q}(\lambda )_1$) gives the same upper bound as ref. ³³ when one of the receivers is restricted to random guessing. This can be seen as the case in which one party receives $\left| {\psi _{z_0z_1}} \right\rangle$ with perfect fidelity and the other party receives a dummy state. Second, the boundary specifies a non-trivial trade-off function between Alice’s and Bob’s guessing probabilities, which is independent of their measurement strategies. This implies that the bound is absolute and cannot be improved upon with better measurement strategies, even if Alice and Bob are allowed to use shared randomness. Third, although our method can only provide an outer-approximation of the quantum set, it turns out that the first level of the hierarchy is already tight. More specifically, there is a concrete example, which saturates the boundary predicted by ${\cal Q}(\lambda )_1$; see Fig. 2 for more details. This example is given by the optimal asymmetric qubit cloning machine,³⁸ which optimally splits the qubit information between multiple parties (according to some predefined ratio); this is indeed a natural choice as the goal of the network is to preserve as much quantum information as possible for each party while splitting it.

In the second application, we prove the security of coherent-state QKD. Here, one of the receivers (Alice) is the eavesdropper (renamed to Eve) and her goal is to eavesdrop on the quantum channel connecting the transmitter and the other receiver (Bob). For concreteness, we first consider a phase encoded coherent-state QKD protocol,³⁹ which uses the encoding scheme $\left| {\psi _{z_0z_1}} \right\rangle :\left| {\psi _{00}} \right\rangle = \left| {\sqrt \mu } \right\rangle ,|\psi _{10}\rangle = \left| { - \sqrt \mu } \right\rangle,|\psi _{01}\rangle = \left| { i \sqrt \mu } \right\rangle$, and $\left| {\psi _{11}} \right\rangle = \left| { - i\sqrt \mu } \right\rangle$, where μ is the mean photon number of the coherent state. To maximise the sifting efficiency of the protocol, we use $\left\{ {\left| {\sqrt \mu } \right\rangle ,\left| { - \sqrt \mu } \right\rangle } \right\}$ for key generation and $\left\{ {\left| {i\sqrt \mu } \right\rangle ,\left| { - i\sqrt \mu } \right\rangle } \right\}$ for testing the security of the channel. Correspondingly on Bob’s side, we have that he uses measurement y = 0 for key recovery and measurement y = 1 for estimating the channel noise; we write ε₀ and ε₁ to denote the error probabilities observed in the key basis and the test basis, respectively. In this case, the sifting rate of the protocol tends to 1 (in the limit of infinite keys) when the probability of choosing the key basis goes to 1.³⁵

In the supplementary information, we show that the expected secret key rate (per signal sent) is

$$R_{{\mathrm{key}}}^\infty \ge {\mathrm{max}}\left\{ {0,p_{{\mathrm{det}}}\left[ {1 - h_2(\varepsilon _0) - h_2(\varepsilon _{{\mathrm{ph}}})} \right]} \right\},$$

(2)

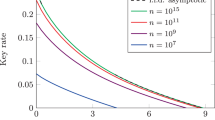
where ε_ph is the so-called phase error rate of the key basis,⁴¹ p_det is the probability of detection, and h₂(⋅) is the binary entropy function. The quantity of interest here is ε_ph, which is maximised assuming fixed system parameters (e.g., μ, ε₀, and ε₁). Crucially, ε_ph is a linear function of the matrix G, which allows us to use SDP technique. (For the explicit expression of ε_ph, we refer the interested reader to the supplementary information). Then, we use the second level of the hierarchy ${\cal S}_2$ and maximise ε_ph over the set of compatible probabilities in ${\cal Q}(\lambda )_2$. The outcome of the numerical optimisation is shown in Fig. 3 along with the simulation parameters. To benchmark our results against the best-known security analysis for the protocol, we also plot the security bound of ref. ⁴⁰ using the same constraints. From the figure, it is evident that our secret key rates are always higher than the ones given by ref. ⁴⁰. Importantly, this shows that our method significantly improves the security and feasibility of practical QKD, despite making only a few assumptions about the implementation. For completeness, we note that refs ^43,44 have also recently proposed a new security proof technique based on SDP (but using a completely different approach). In the case of the current protocol, their simulation outcomes are similar to ours, however, their method additionally requires that Bob’s measurements are fully characterised and an optical squashing model exists for the measurements.⁴⁵

Fig. 3

Phase encoded coherent-state quantum key distribution (QKD). We compare our secret key rate against the one given in ref. ⁴⁰. For the key rate simulation, we assume a detector dark count rate of p_dc = 10⁻⁷ and an intrinsic optical error rate of 2%. For a given channel loss 1 − η, the probability of detecting a signal is p_det = 1 − (1 − p_dc)² exp(−2ημ) and the error probability is ε = (p_dc + (1 − exp(−2μη))0.02)/p_det. Using these, we maximise the expected secret key rate (2). More precisely, we perform two optimisations. First, for a given μ we maximise the phase error rate over ${\cal Q}(\lambda )_2$ subject to the above constraints. This gives us a lower bound on the achievable secret key rate. Then, we optimise the secret key rate over μ. This gives us an estimate of the optimal secret key rate. Comparing with the secret key rate of ref. ⁴⁰ (red line), we see that our method predicts a higher secret key rate (blue line) for any loss point. For further comparison, we also plotted the collective beam-splitting attack bound with zero error⁴² (the top curve: black dashed line), which serves as an upper bound on the achievable secret key rate; note that this bound is not tight and it assumes zero errors

To demonstrate the ability of our method to handle non-standard QKD protocols, we consider the security of a modified coherent-one-way (COW) QKD protocol,^46,47 which is based on the transmission of time encoded coherent states {|0〉|α〉,|α〉|0〉,|α〉|α〉} with $\alpha = \sqrt \mu$. Here, the first two sequences of coherent states carry the secret bit (i.e., ‘0’ →|0〉|α〉 and ‘1’ →|α〉|0〉) and the last sequence is a test state used to estimate Eve’s information about the secret bit. For Bob’s measurements, we use the active switching measurement scheme proposed in ref. ⁴⁸ instead of the original passive switching scheme.⁴⁶ In this setup, Bob employs an optical switch to send the incoming states either into the data line or the monitoring line: the former measures the arrival time of the incoming states, whereas the latter measures the coherence (the interference visibility) between two adjacent states. The advantage of this scheme is that it yields higher detection probabilities than the passive scheme. Another major modification is that only the coherence of the test sequence |α〉|α〉 is measured. More specifically, the variant protocol does not measure the coherence between adjacent encodings (e.g., in cases like |0〉|α〉;|α〉|0〉 or |α〉|α〉;|α〉|0〉) like in the original protocol. This modification is largely motivated by earlier research, which showed that knowing the coherence information between adjacent encodings does not significantly improve the security of the protocol.⁴⁸ Importantly, in discarding these events, we have two benefits. First, the security analysis is greatly simplified, i.e., we only need to analyse a single encoding instead of a sequence of encodings, which can be unwieldy. Second, this opens up the possibility to explore scenarios whereby the mean photon number of the test sequence |α〉|α〉 is optimised. More concretely, we can now adjust the mean photon number of the test sequence to maximise the secret key rate. In the following, we will use |β〉|β〉 to represent the optimised test sequence.

Using the same approach as before (i.e., Eq. (2)), we compute the secret key rate of the variant protocol using a realistic error model that assumes an imperfect intensity modulator (on the transmitter side) and an imbalanced beam-splitter on the receiver side; see the description of Fig. 4 for more details. We first simulate the expected secret key rates of the protocol using the original COW QKD test sequence |β = α〉|β = α〉 with errors (red curve) and without errors (yellow curve). Both of these curves show that secret keys can only be distributed in the low loss regime (i.e., <4 dB loss; or equivalently 20 km of optical fibre length). Comparing with the collective beam-splitting attack curve⁴² (black dashed curve), we observe that the original COW QKD encoding may be suboptimal. To investigate this possibility, we use the flexibility of our method and further optimise |β〉|β〉 over a discrete set of ratios β/α to search for the best test sequence for a given loss point. We find that the improvement is highly significant. In the case with zero errors, the optimal ratio is β = α/2 and the tolerable loss is extended to >35 dB, which spells a ≥30 dB improvement over the original COW QKD encoding. The secret key rates (green curve) are also significantly higher and are close to the collective beam-splitting attack bound (in the low loss regime). In the case with errors, we also see similar improvements. More concretely, the optimised variant protocol is now able to distribute secret keys up to about 21 dB loss with errors, which translates to a fibre distance of about 110 km. In conclusion, our findings strongly indicate that it is much more secure to vary the mean photon number of the test sequence.

Fig. 4

Time encoded coherent-state quantum key distribution (QKD). For this simulation, we consider an error model that is based on imperfect intensity modulation and imperfect mixing of coherent states. On the transmitter’s side, we assume that the intensity modulator used to perform the on-off keying has finite extinction ratio, i.e., states are prepared as $\left| {\sqrt {1 - \delta } \alpha } \right\rangle$ and $\left| {\sqrt \delta \alpha } \right\rangle$ instead of |α〉 and $\left| 0 \right\rangle$. Here, we use δ = 0.01. On the receiver side, we assume that the beam-splitter in the measurement scheme of ref. ⁴⁸ has a ratio of 51/49 instead of the ideal 50/50. Using these component models and assuming that each detector has a dark count rate of p_dc = 10⁻⁷, we run the optimisation as per the previous QKD application and obtain four sets of data points using the original coherent-one-way (COW) QKD encoding and a new encoding strategy where the test sequence is optimised. For each of these, we compute the secret key rates with and without errors

Discussion

Taken together, our findings thus provide a powerful method to analyse the quantum set of any discretely modulated P&M quantum network, independently of how the network and decoding measurements are implemented. From the perspective of quantum information theory, the toolbox can help to reveal the fundamental limits of quantum communication and to analyse the performance of any quantum coding scheme. On the application side, the toolbox can be used to analyse the performance of quantum network protocols and the security of quantum cryptography, as evidenced by the three examples given above. Concerning the latter, it would be interesting to investigate how the toolbox could be utilised to solve other open problems in quantum cryptography, e.g., the security of round-robin differential phase-shift QKD⁴⁹ or continuous variable QKD protocols with discrete modulations.⁵⁰ Another interesting direction would be to extend the method to multiple transmitters like in the case of measurement-device-independent quantum cryptography.^{51,52,53,54,55,56} For instance, it would be interesting to see how our method can be used to analyse the security of phase-matching QKD,⁵⁶ which can break the fundamental distance limit of QKD using coherent states.