Abstract
Quantum computers, which take advantage of the superposition and entanglement of physical states, could outperform their classical counterparts in solving problems with technological impact such as factoring large numbers and searching databases. A quantum processor executes algorithms by applying a programmable sequence of gates to an initialized state of qubits, which coherently evolves into a final state containing the result of the computation. Although quantum processors with a few qubits have been demonstrated on multiple quantum computing platforms, realization of solid-state programmable quantum processor under ambient conditions remains elusive. Here we report a programable quantum processor that can be programmed with fifteen parameters to realize arbitrary unitary transformations on two spin qubits in a nitrogen-vacancy (NV) center in diamond. We implemented the Deutsch-Jozsa and Grover search algorithms with average success rates above 80%. The results pave the way to implement the programmable method in a large-scale quantum processor.
Similar content being viewed by others
Introduction
The ultimate goal of quantum information processing is to design a quantum processor that is capable of performing any given task. As with its classical counterpart, the versatility of quantum processors come from reprogramming the quantum logic gates to solve the given problem. Arbitrary operations on a multi-qubit system can be broken down into sequences of quantum gates.1,2,3 Reconfiguring these gate sequences provides the flexibility to implement a variety of algorithms without altering the hardware. A programmable quantum processor is more versatile than one designed for a fixed task. Programmable quantum processors based on a few qubits have been demonstrated using trapped ions,4,5 superconducting qubits6 and quantum-dot-based qubits,7 but the experimental realization of a solid-state programable quantum processor at room temperature remains elusive. Here, we demonstrate that with the electron spin and 14N nuclear spin of nitrogen-vacancy (NV) center in diamond one can combine initialization, readout, single- and two-qubit gates to form a programmable quantum processor that can perform quantum algorithms. NV centers in diamond have emerged as one of the promising candidates for implementing quantum technologies because they exhibit long coherence time and universal quantum gates with fault-tolerant control fidelity.8 Several algorithms have been demonstrated based on NV center. The quantum circuits employed in these studies are designed for the specific task.9,10 The programmable quantum processor is capable of realizing the target two-qubit unitary operation with a universal quantum circuit. In our work, arbitrary two-qubit unitary operation determined by external fields can be programmed and reconfigured with fifteen parameters.11
Results
As depicted in Fig. 1a, the NV center consists of a substitutional nitrogen atom with an adjacent vacancy site in the diamond crystal lattice. The ground state of NV center is an electron spin triplet state with three sublevels |mS = 0〉 and |mS = ±1〉. A static magnetic field is applied along the NV symmetry axis ([1 1 1] crystal axis) to remove the degeneracy between the |mS = +1〉 and |mS = −1〉 states, yielding the electron and nuclear Zeeman splitting. The Hamiltonian of the electron spin and the 14N nuclear spin system is
where Sz and Iz are the spin operators of the electron spin (spin-1) and the nuclear spin (spin-1). The electronic zero-field splitting is D = 2.87 GHz and the nuclear quadrupolar interaction is Q = −4.95 MHz. The two spins are coupled by a hyperfine interaction Azz = −2.16 MHz. The two-qubit quantum system is composed of |mS = 0, mI = +1〉, |mS = 0, mI = 0〉, |mS = −1, mI = +1〉, and |mS = −1, mI = 0〉 without considering the other spin levels. The four energy levels are denoted by |1〉, |2〉, |3〉 and |4〉 as shown in Fig. 1a. At the magnetic field strength of 500 G, the spin state of the NV center is effectively polarized to |mS = 0, mI = +1〉 when a 532 nm laser pulse is applied.12
Two-qubit programmable quantum processor in NV center. a Schematic atomic structure and energy levels of the NV center. The experiments are implemented on the two-qubit system composed of four energy levels within the dashed box (i.e., |mS = 0, mI = +1〉, |mS = 0, mI = 0〉, |mS = –1, mI = +1〉, and |mS = −1, mI = 0〉 denoted by |1〉, |2〉, |3〉 and |4〉). b Circuit diagrams for arbitrary unitary transformations. The brackets highlight the decomposition of arbitrary two-qubit operation into (C ⊗ D) · V · (A ⊗ B). R(θ, φ) corresponds to a rotation angle θ around the axis in the XY plane. φ denotes the angle between the axis and the X axis. Rz(φz) represents a rotation angle φz around the Z axis. The entangling two-qubit gate Uzz is exp(iπSz ⊗ Iz). c Realization of the single-qubit gates. The single-qubit rotations on the electron spin are realized by hard microwave pulses with fixed Rabi frequency of Ω1MW = 40 MHz. The duration of the pulses corresponds to the rotation angle θ. The single-qubit rotations on the nuclear spin are realized by decoherence-protected gates consisting of dynamical decoupling of the electron spin and nuclear spin driving during the time interval. The strength of the nuclear spin driving is determined by the rotation angle. The time τ corresponds to the interaction between electron spin and nuclear spin
Arbitrary single-qubit gates combined with applications of a maximally entangling two-qubit gate are sufficient for realization of universal two-qubit unitary operation. Our choice of a universal gate library consists of single-qubit gates and an entangling two-qubit gate, Uzz = exp(iπSz ⊗ Iz), which can be realized by the free evolution under the hyperfine coupling between electron spin and nuclear spin. We decompose a given two-qubit unitary operation U into U = (C ⊗ D) · V · (A ⊗ B) as shown in Fig. 1b, where V is a two-qubit gate and A, B, C, D are single-qubit gates. The decomposition follows a three-step procedure analogous to that in ref. 4. First, the matrix eigenvalues of V and U are matched to find the three parameters α, β and δ shown in the dashed rectangle in Fig. 1b. Second, the four remaining single-qubit gates, A, B, C and D, are found by mapping the eigenvectors of V and U to satisfied the equation U = (C ⊗ D) · V · (A ⊗ B). Finally, the single-qubit gates are parameterized by the decomposition Rz(φz,j) · R(θj, φj) for j = [A, B, C, D]. R(θj, φj) = exp[−iθj(cosφjSx + sinφjSy)], corresponds to a rotation of angle θ around the axis in the XY plane. φ denotes the angle between the axis of rotation and the X axis. Rz(φz,j) represents a rotation of angle φz,j around the Z axis. After the procedure discussed above, arbitrary two-qubit unitary transformations can be realized using the universal quantum circuit with fifteen parameters, which are α, β, δ, θA, φA, φz,A, θB, φB, φz,B, θC, φC, φz,C, θD, φD, and φz,D.
For the quantum processor, the two-qubit entangling gate, Uzz, is realized by the free evolution under the hyperfine coupling Hhf = 2πAzzSzIz. So the time duration of Uzz is 231.5 ns. The single-qubit rotations on the electron spin are realized by microwave (MW) pulses with fixed Rabi frequency of Ω1MW = 40 MHz. The pulses flip the electron spin practically independent of the nuclear spin state for the large Rabi frequency comparing to the hyperfine coupling Azz. The length of the MW pulse t is determined by the rotation angle θ as shown in the upper panel in Fig. 1c. Since the states of the electron and nuclear spin evolve and decohere at very different rates, decoherence-protected gates are implemented to realize the single nuclear spin rotation10 as shown in the lower panel in Fig. 1c. The XY-4 sequence is applied on the electron spin to protect the electron’s coherence. The states of nuclear spin is driven during the time between the decoupling pulses. A rotation of the nuclear spin, which is independent of the electron spin state, is constructed by choosing τ = 2nπ/Azz with integer n. Here we fixed τ = 2777.8 ns with n = 6 and the strength of the radio-frequency (RF) pulses is set as Ω1RF = θ/4τ. The rotation around the Z axis Rz(φz) is realized by adding a phase to the drive field for all subsequent gates.
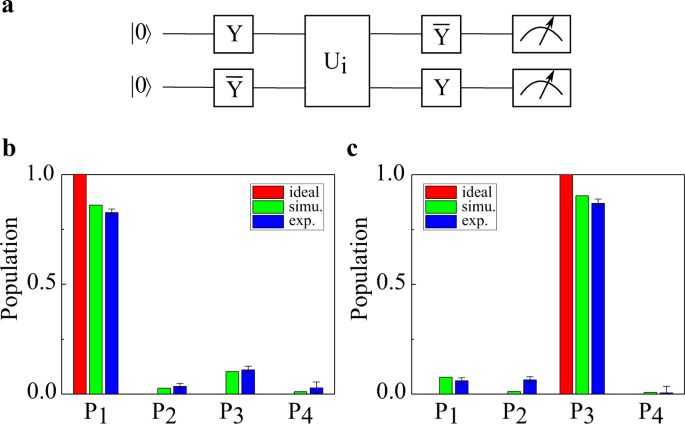
To exhibit the flexibility of the processor to generate unitary transformations, we first implement the Deutsch–Jozsa algorithm13 as an example. It has been employed in different systems to demonstrate the exponential speedup in distinguishing constant from balanced functions with respect to the corresponding classical algorithm.9,14,15,16,17,18,19 A function that has an n-bit input and a 1-bit output (f:0, 1, 2, …, 2n − 1 → 0, 1) is balanced when exactly half of the inputs result in the output 0 and the other half in the output 1, while a constant function assumes a single value irrespective of the input. The constant function (f(0) = f(1) = 0) and the balanced function (f(0) = 0, f(1) = 1) are mapped onto the unitary operators Ui with U1 = I and U2 = CNOT as shown in the quantum circuit in Fig. 2a, where the I denotes the identity and the CNOT is the controlled-NOT gate. A measurement of the populations, P = {P1P2P3P4}, of the final state determines if the function is constant or balanced. The populations, P, of the final state are determined by performing a set of measurements with different pulse sequences to redistribute the population of the final state. Comparing to the direct measurement of the final state, πe and πn pulses on the electron and nuclear spin respectively are also applied on the final state to flip the populations within the two-qubit system. The population of each energy level can be achieved from the resulting photoluminescence of these states. The entire quantum circuit combined with the flipping pulses can be treated as a unitary operator. This unitary operator is decomposed into the universal quantum circuit as shown in Fig. 1b following the three steps discussed above. The corresponding 15 parameters are shown in Table 1. Different unitary operators are implemented using the universal quantum circuit with different sets of parameters. Measurement of output P = {1000} indicates a constant function, while P = {0010} indicates a balanced function. In Fig. 2b, c, we show the measured population of each spin level of the final state after the Deutsch-Josza algorithm. The red bars indicate the ideal result, while the green bar is the simulation result considering the decoherence of the electron spin and the imperfect polarization (see Supplementary Information Section 2). The experimental results (blue bars) are in good agreement with the simulated results. The average success probability is 0.88(2) for constant and 0.93(2) for balanced functions.
Experimental demonstration of Deutsch-Josza algorithm. a Quantum circuit of Deutsch–Josza algorithm. Y \(\left( {\overline {\mathrm{Y}} } \right)\) indicates the π/2 (−π/2) rotation around the Y axis. The constant function and the balanced function are mapped onto the unitary operators U1 = I and U2 = CNOT, respectively. b, c The experimental results of Deutsch–Josza algorithm with constant and balanced functions, respectively. P1, P2, P3 and P4 denote the population of |1〉, |2〉, |3〉 and |4〉, respectively. The red bars are the ideal case. The green bars are the simulation results considering the imperfect polarization and the decoherence. The blue bars are the experimental results
Now we show that another quantum algorithm, named Grover search algorithm, can be executed by our programable quantum processor by just adjusting the 15 parameters. The Grovers search algorithm20 provides an optimal method for finding the unique input value x0 of a function f(x) that gives f(x0) = 1 and f(x) = 0 for all other values of x. It has been demonstrated in various systems.21,22,23,24 In the two-qubit version of this algorithm there are four input values, x ∈ (00, 01, 10, 11), resulting in four possible functions fij(x), with i, j ∈ (0, 1). These functions are mapped onto the C-Phase gate cUij that encodes fij(x) in a quantum phase, \(cU_{ij}\left| x \right\rangle = ( - 1)^{f_{ij}(x)}\left| x \right\rangle\). The C-Phase gate cUij is denoted by the oracle Ui as shown in the quantum circuit in Fig. 3a. The quantum circuits to realize the C-Phase gate cUij are designed specifically to the four cases in the conventional implementation of the two-qubit version of Grover search algorithm. In our work, the algorithm is demonstrated by the universal quantum circuit. The unitary operator of the four possible quantum circuit is programmed into the four sets of parameters as shown in Table 2. A measurement of the populations, P = {P1P2P3P4}, of the final state finds the state that has been marked. In Fig. 3b–e, we show the measured the population of each spin level of the final state after the Grover search algorithm of four possible oracle functions. The experimental results (blue bars) are in good agreement with the simulated results (green bars). The average success probability is 0.85(1), 0.82(2), 0.81(2), and 0.84(2) for four possible functions, respectively.
Experimental demonstration of Grover search algorithm. a Quantum circuit of Grover search algorithm. Four possible function fij(x) are mapped onto the oracle Ui which is the C-Phase gate cUij. b–e The results of Grover search algorithm characterized by the population of each spin level of the final state. P1, P2, P3, and P4 denoted the population of |1〉, |2〉, |3〉, and |4〉, respectively. The red bars are the ideal case. The green bars are the simulated case considering the imperfect polarization and the decoherence. The blue bars are the experimental results
Discussion
The algorithms presented here illustrate the computational flexibility provided by the solid-state spin-based quantum architecture at room temperature. The programmable quantum processor is capable of implementing arbitrary unitary operation on two qubits using the universal quantum circuit with altering the parameters. Substantial improvements could be made in the performance of the processor by using isotopically purified 12C, which would increase the coherence times of the qubits.25 Furthermore, dipolar coupling of electronic spins could mediate interactions between nuclear spins associated with different NV centers,26 offering a potentially scalable platform for information processing.27 Optical channels provide an alternate platform that is well suited to mediating interactions over macroscopic distances or in highly connected networks.28,29 With these improvements quantum computers with multiple qubits and fidelities above the fault-tolerance threshold should be realizable.
Methods
Experiment setup
Our experiment was performed on a [100] oriented NV center in bulk diamond with low concentration of nitrogen impurity (<5 ppb) and natural abundance of 13C isotope (1.1%). The sample was mounted on a home-built confocal setup (see Supplementary Information Section 1 for the schematic of the setup). Optical excitation was provided by a 532 nm green laser, which was gated by an acousto-optic modulator. The laser beam was double passed through the acousto-optic modulator to suppress the laser leakage. And then the laser was delivered through an oil objective. The red fluorescence from the NV center was collected by an avalanche photodiode. A solid immersion lens was utilized to enhance the photon detection efficiency. The magnetic field was aligned along the NV symmetry axis ([1 1 1] crystal axis) by a permanent magnet. At the static magnetic field of 500 G, the state of the two-qubit solid-state quantum processor can be effectively polarized to |mS = 0, mI = +1〉 with 532 nm laser pumping. After the optical pumping, 95% of the population occupied the |mS = 0〉 state of the electron spin and 98% of the population occupied the |mI = +1〉 state of the nuclear spin. The microwave and radio-frequency pulses were created by an arbitrary waveform generator. Power amplifiers were utilized to amplify the pulses. A broadband coplanar waveguide with 15 GHz bandwidth was installed for the microwave pulses on the NV center. The radio-frequency pulses were carried by a home-built coil.
Code availability
The codes that were used in this study are available from the corresponding author upon reasonable request.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Deutsch, D. Quantum computational networks. Proc. R. Soc. A 425, 73–90 (1989).
Barenco, A. et al. Elementary gates for quantum computation. Phys. Rev. A. 52, 3457 (1995).
Bremner, M. J. et al. Practical scheme for quantum computation with any two-qubit entangling gate. Phys. Rev. Lett. 89, 247902 (2002).
Hanneke, D. et al. Realization of a programmable two-qubit quantum processor. Nat. Phys. 6, 13–16 (2010).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016).
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244 (2009).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Rong, X. et al. Experimental fault-tolerant universal quantum gates with solid-state spins under ambient conditions. Nat. Commun. 6, 8748 (2015).
Shi, F. et al. Room-temperature implementation of the Deutsch-Jozsa algorithm with a single electronic spin in diamond. Phys. Rev. Lett. 105, 040504 (2010).
van der Sar, T. et al. Decoherence-protected quantum gates for a hybrid solid-state spin register. Nature 484, 82–86 (2012).
Shende, V. V., Markov, I. L. & Bullock, S. S. Minimal universal two-qubit controlled-NOT-based circuits. Phys. Rev. A. 69, 062321 (2004).
Jacques, V. et al. Dynamic polarization of single nuclear spins by optical pumping of nitrogen-vacancy color centers in diamond at room temperature. Phys. Rev. Lett. 102, 057403 (2009).
Deutsch, D. & Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. A 439, 553–558 (1992).
Chuang, I. L. et al. Experimental realization of a quantum algorithm. Nature 393, 143–146 (1998).
Ju, C. et al. Experimental demonstration of deterministic one-way quantum computation on a NMR quantum computer. Phys. Rev. A 81, 012322 (2010).
Bianucci, P. et al. Experimental realization of the one qubit Deutsch-Jozsa algorithm in a quantum dot. Phys. Rev. B 69, 161303 (2004).
Scholz, M., Aichele, T., Ramelow, S. & Benson, O. Deutsch-Jozsa algorithm using triggered single photons from a single quantum dot. Phys. Rev. Lett. 96, 180501 (2006).
Tame, M. S. et al. Experimental realization of Deutsch’s algorithm in a one-way quantum computer. Phys. Rev. Lett. 98, 140501 (2007).
Gulde, S. et al. Implementation of the Deutsch-Jozsa algorithm on an ion-trap quantum computer. Nature 421, 48 (2003).
Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325–328 (1997).
Jones, J. A., Mosca, M. & Hansen, R. H. Implementation of a quantum search algorithm on a quantum computer. Nature 393, 344–346 (1998).
Chuang, I. L., Gershenfeld, N. & Kubinec, M. Experimental implementation of fast quantum searching. Phys. Rev. Lett. 80, 3408 (1998).
Walther, P. et al. Experimental one-way quantum computing. Nature 434, 169–176 (2005).
Brickman, K. A. et al. Implementation of Grovers quantum search algorithm in a scalable system. Phys. Rev. A. 72, 050306 (2005).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383 (2009).
Bermudez, A., Jelezko, F., Plenio, M. B. & Retzker, A. Electron-mediated nuclear-spin interactions between distant nitrogen-vacancy centers. Phys. Rev. Lett. 107, 150503 (2011).
Yao, N. Y. et al. Scalable architecture for a room temperature solid-state quantum information processor. Nat. Commun. 3, 800 (2012).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Acknowledgements
We are grateful to D. Suter for valuable discussion. This work was supported by the National Key R&D Program of China (Grants No. 2018YFA0306600 and No. 2016YFB0501603), the CAS (Grants No. QYZDY-SSW-SLH004 and No. QYZDB-SSW-SLH005). X.R. thanks the Youth Innovation Promotion Association of Chinese Academy of Sciences for their support.
Author information
Authors and Affiliations
Contributions
J.D. proposed the idea. J.D. and X.R. designed and supervised the experiments. Y.Wu., Y.Wa. and X.Q. perform the experiments. Y.Wu., Y.Wa., X.R. and J.D. wrote the paper. All authors analyzed the data, discussed the results, and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, Y., Wang, Y., Qin, X. et al. A programmable two-qubit solid-state quantum processor under ambient conditions. npj Quantum Inf 5, 9 (2019). https://doi.org/10.1038/s41534-019-0129-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0129-z
This article is cited by
-
An efficient quantum partial differential equation solver with chebyshev points
Scientific Reports (2023)
-
Experimental demonstration of deterministic quantum search algorithms on a programmable silicon photonic chip
Science China Physics, Mechanics & Astronomy (2023)
-
Quantum simulation of parity–time symmetry breaking with a superconducting quantum processor
Communications Physics (2021)
-
Relaxation of a dense ensemble of spins in diamond under a continuous microwave driving field
Scientific Reports (2021)
-
Quantum-coherent nanoscience
Nature Nanotechnology (2021)