Introduction

Tremendous progress in realizing high-quality quantum bits at the few qubit level has opened a window for new challenges in quantum computing: developing the necessary classical control techniques to scale systems to larger sizes. A variety of approaches rely upon tuning individual quantum bits into the proper regime of operation.1,2,3,4,5,6,7,8,9 In semiconductor quantum computing, devices now have tens of individual electrostatic and dynamical gate voltages which must be carefully set to isolate the system to the single electron regime and to realize good qubit performance.4,10,11,12,13,14,15,16,17 A similar problem arises in the control of ion positions in segmented ion traps.18,19,20,21 Preliminary work to automate the laborious task of tuning such systems has primarily focused on fine tuning of analog parameters22,23 using techniques from regression analysis and quantum control theory.

We propose a new paradigm for automatic initialization of experiments that presently rely on human heuristics. While our approach is presented and evaluated in the context of tuning single and double dot devices, it can be easily adapted to other experimental scenarios, such as ion traps, superconducting qubits, etc. Although there has been recent progress in using computer-supported, algorithmic gate voltage control,23,24 the suggested approaches do not fully eliminate the need for human interference, as the decision of how to adjust gate voltages, based on the automatically obtained quantitative dot parameters and qualitative output, remains man-made. At the same time, tremendous progress in machine learning (ML) algorithms and automated image classification suggests that such techniques may be used to bootstrap the experimental effort from a de novo device to a fully tuned device, replacing the gross-scale heuristics, developed by experimentalists to deal with tuning of parameters particular to experiments.25,26,27 A quality simulated dataset allows us to train an ML algorithm to automatically classify the state of an experimental device. By combining it with optimization techniques, we establish a closed-loop system for experimental initialization without the need for human intervention.

In this work, we specifically consider the control problems associated with electrostatically defined quantum dots (QDs) present at the interface of semiconductor devices.28 Each QD is defined using voltages applied to metallic gate electrodes acting as depletion gates which confine a discrete number of electrons to a set of islands. We use ML and numerical optimization techniques to efficiently explore the multidimensional gate voltage space to find a desired island configuration, a technique we call “auto-tuning”. Toward this end, we use ML to recognize the number of dots generated in the experiment.

In order to improve on the accuracy, we work with convolutional neural networks (CNNs).26,29 CNNs are a class of artificial neural networks designed for efficient pattern recognition and classification of images. When trained on high-quality simulated data, CNNs can learn to identify the number of QDs. Once the neural network is trained to recognize dot configurations, we can recast the problem of finding a required configuration as an optimization problem. As a result, a neural network coupled to a optimization routine presents itself as a solution for determining a suitable set of gate voltages.

Training of an ML algorithm necessitates the existence of a physical model to qualitatively mimic experimental output and provide a large, fully labeled dataset. In this paper, we develop a model for transport in gate-defined QDs and train neural networks to identify number of islands under a given gate voltage configuration. We also describe the auto-tuning problem in the double dot to single dot transition regime. Finally, we discuss the performance of the recognition and auto-tuning for both simulated and experimental data. We report over 90 % accuracy for with very simple neural network architectures on all these problems, where accuracy is defined as the fraction of times when the predicted state agreed with the pre-assigned label.

Results

Electrostatically defined QDs offer a means of localizing electrons in a solid-state environment. A generic device, consisting of a linear array of dots in a two-dimensional electron gas (2DEG), is presented in Fig. 1a. Gate electrodes on top are used to confine electron density to certain regions, forming islands of electrons. The ends of the linear array are connected to reservoirs of electrons, i.e., contacts, which are assumed to be kept at a fixed chemical potential.

Fig. 1
figure 1

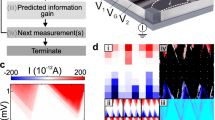
Schematic of a quantum dot device. a A generic nanowire connected to contacts with top gates. μ1 and μ2 are the chemical potentials of the contacts. b Potential profile V(x) along the nanowire. Alternating set of barrier and plunger gates create a potential profile V(x) along the nanowire. (N1, N2, N3, and N4 are the number of electrons on each island. Electrons can tunnel through the barriers between adjacent islands or the contacts. The filled blue areas denote regions of electron density.)

Full size image

By applying suitable voltages to the gates, it is possible to define a one-dimensional potential profile V(x). Alternating regions of electron density islands and barriers are formed, depending on the relation between the chemical potential and the electrostatic potential V(x) (Fig. 1b). Barrier gates are used to control tunneling between the islands while the plunger gates control the depths of the potential wells.

A fixed number of islands requires a specific number of gates. Since the voltage on each gate can be set independently, the state space for the gate voltages is \({\Bbb R}^m\), with m denoting the number of gates. By suitable choices of the gate voltages, it is possible to have a certain number of islands, each with a certain number of charges along the nanowire. We refer to the number of islands as the state. Though having a large number of gates implies a higher degree of control, it also presents a challenge in determining appropriate values for the gate voltages, given a required state.4

Standard techniques of assigning voltages to the gates rely on heuristics and experimental intuition. Such techniques, however, present practical difficulties in implementation when the number of gates increases beyond a modest number. Hence, it is desirable to have a technique, given a desired state of the device, to determine an appropriate voltage set without the need for actual intervention by an experimenter.

Machine learning30 is an algorithmic paradigm in artificial intelligence and computer science to learn patterns in data without explicitly programming about the characteristic features of those patterns. An important task in ML is classification of data into categories, generically referred to as a classification problem. The algorithm learns about the categories from a dataset and produces a model that can assign previously unseen inputs to those categories.

In supervised learning models, ML algorithms rely on labels identifying each element of a dataset to learn to classify data from a predefined and known representative subset (training data) into assumed categories (thus the term supervised). Once trained, the algorithm then generalizes to an unknown dataset, called the test set. Deep neural networks (DNNs) i.e., neural networks with multiple hidden layers, can be used to classify complex data into categories with high accuracy of over 90 %.26

The central aim of this work is to enable an automated approach to navigation and tuning of QD devices in the multidimensional space of gate voltages. Here, we define auto-tuning specifically as finding appropriate values for the gate electrodes to achieve a particular state. Identification of the state of the device is the first step in the tuning process. In light of the requirement for learning the state to achieve tuning and the success achieved with DNNs for data classification, we propose to use DNNs to determine charges and states of QDs. Once it is achieved, auto-tuning is reduced to an optimization problem to the required state and can be done with standard optimization routines.

Learning Coulomb blockade

We start our analysis from investigation of whether a machine can learn to identify the charge on a single QD (Fig. 2a), given the current as a function of VP (Fig. 2b). Formally, we define the broader problem of Learning Coulomb Blockade as:

Fig. 2
figure 2

Current and charge state simulations. a A single dot device model and potential profile V(x) along the nanowire with a single dot. b Simulated current and electron number N for a single dot exhibiting Coulomb blockade as a function of plunger gate voltage VP for a three-gate device. c A five-gate device used to model a double dot and potential profile V(x) with charges N1 and N2 on the two dots. d Simulated current flow at triple points and e honeycomb charge stability diagram in the space of plunger gate voltages (VP1, VP2) from the Thomas−Fermi model described in SM

Full size image

Problem \({\cal P}1\): Charge identification

Let I be the current at infinitesimal bias, V and Vi denote vectors of voltages applied to the gates, CS(V) be a vector of the number of electrons on each island, and N be the number of training samples. Given I(V) and a training set \({\cal T} = \left\{ {I({\boldsymbol{V}}_i),{\boldsymbol{CS}}({\boldsymbol{V}}_i)} \right\}_{i = 1}^N\), find a map \({\cal M}:I({\boldsymbol{V}}) \mapsto {\boldsymbol{CS}}({\boldsymbol{V}})\), such that, after being trained on the training set \({\cal T}\), \({\cal M}\) minimizes the error (or, equivalently, maximizes the accuracy)

$$Error = \frac{1}{{\left| {\cal E} \right|}}\mathop {\sum}\limits_i \left\Vert {{\boldsymbol{CS}}\left( {{\boldsymbol{V}}_i^\prime } \right) - M\left( {{\boldsymbol{V}}_i^\prime } \right)} \right\Vert_1$$
(1)

on the test set \({\cal E} = \left\{ {I\left( {{\boldsymbol{V}}_i^{\prime} } \right),{\boldsymbol{CS}}\left( {{\boldsymbol{V}}_i^{\prime} } \right)} \right\}_{i = 1}^{N^{\prime} }\), where the summation runs over all elements in the test set \({\cal E}\), \(\left| {\cal E} \right|\) denotes the size of the set \({\cal E}\), and \(\left\| \cdot \right\|_1\) is the 1-norm. While it is possible to define the error in terms of the zero-one loss or the 2-norm, since the charges are integers, the 1-norm was used.

In the case of a single dot, only one gate voltage, VP, is varied and the charge state is simply the number of electrons on the dot. Hence, V and CS are scalars. It is easy to see that this just amounts to learning to integrate the current characteristics and scaling to the appropriate charge number (Fig. 3a). The problem is said to be solvable if the map \({\cal M}\), learned using the neural network, has prediction accuracy greater than it would by uniformly random chance. In the single electron regime, say 1–10 electrons, this corresponds to a target accuracy of 50 % (for the simplest case of just two charge states; for k distinct states, the target accuracy would be \({\textstyle{{100} \over k}}\,\%\)).

Fig. 3
figure 3

Machine learning of Coulomb blockade. a Overview of the ML problem of going from current to charge state for a single dot. b Current vs. VP data for 100 different dots. Each row represents a separate device with distinct gate positions and physical parameters sampled from a Gaussian distribution around a mean set of parameters (see SM). c Corresponding charge vs. VP data for current data from b. d A sample current vs. VP curve given as input to the trained DNN. e The output from the DNN showing the predicted and actual charge states for sample in d

Full size image

We generated a training dataset for 1000 distinct realizations of the dots. Each sample point is a current and charge state vs. VP characteristic. Across the samples, parameters such as the gate positions, widths and heights are sampled from a Gaussian distribution with mean values in the parameter set (standard deviation for the Gaussian was set to 0.05 times the mean value; see Supplemental Material). Figure 3b, c shows sample current and charge data, respectively, of 100 such dots. The rationale behind generating a large dataset for the dots is twofold: having a variation in the dot parameters models the variations in different dots that are used in experiments and it presents a way to generate a generic training dataset for learning.

The ML problem is intended to map the current, given in Fig. 3b, to the charge state, shown in Fig. 3c. One can think of this as a regression problem from the vector of current values to the vector of charge values.

We used a DNN with three hidden layers31 and achieved 91 % accuracy for the charge state values (see Supplemental Material for a description of the computing environment). Here, the accuracy for a single current−gate voltage curve (see Fig. 3d, e) is calculated from the predicted charge state from the neural network and the charge state from the Thomas-Fermi model over the gate voltage range. This accuracy is then averaged over all the samples to produce an accuracy for the test set (see Eq. (1)). The size of input and output layers correspond to the number of points in the I(V) and CS(V). We used a 512-neuron input and 512-neuron output layer. The result from the output layer was rounded to the nearest integer to get the charge state. The hidden layers comprised 1024, 256 and 12 neurons, respectively. The outcome of the training is a set of biases and weights corresponding to each neuron that allow the calculation of the final output.

Interestingly, we observed that a successive decrease in the number of neurons across the hidden layers was critical to achieving a respectable accuracy. This suggests a redundancy of information encoded in the current characteristics that the network must learn to ignore when estimating the charge states.

We can visualize the learning by means of a validation set at the end of a fixed number of training epochs. We observed that in the initial training stages, the network learns the charge boundaries in the plunger voltage space of an average dot and then slowly starts to learn to identify charge states of individual dot samples.

We note that the problem identified above suffers from the charge-offset problem in the real world since the initial number of electrons on the dot might be unidentified. Hence, the network trained as a solution to Problem \({\cal P}1\) has limited applicability in experimental settings but nevertheless exemplifies that ML can, in principle, be applied to charge identification.

The charge number identification on the single dot also offers a trivial solution to identifying the state of the single dot. If the charge on the dot is non-zero, we can then conclude that a single dot exists whereas a zero charge implies a no dot device. The identification of state of the device with multiple islands from the current presents additional possibilities which we describe in the next section.

Learning state

The state is the number of distinct dots or islands that exist in the nanowire. We now consider a five-gate device which can exist in four possible states: Quantum Point Contact or a Barrier, single dot (SD), double dot (DD) and a short circuit (SC) (see Fig. 2c for the device model and Fig. 4a for the possible states). Different states are reached by changing the voltages VP1 and VP2. The voltages VB1, VB2, and VB3 are all fixed to −200 mV.

Fig. 4
figure 4

Current and state diagram for a double dot device. a Possible states in the five-gate device depending on the choices of the plunger gate voltages. b Current vs. (VP1, VP2) exhibiting varied features in the current depending on the underlying state of the nanowire. c State vs. (VP1, VP2)

Full size image

To quantify the definition of a state, we define a probability vector p(Vi) at each point Vi in the voltage space. The elements of p(Vi) correspond to the probability of being in each of the states as described above, i.e., p(Vi) = (pSC, pBarrier, pSD, pDD). For example, for a state of a single dot, the probability vector p(Vi) = (0, 0, 1.0, 0). For a region \({\boldsymbol{V}}_{\cal R}\) in the voltage space, \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) is defined as the average of the probability vectors for the points in the region.

We are interested in determining the state (i.e., distinguishing between SC, Barrier, SD and DD) for a given set of barrier and plunger gate voltages. Formally, we define the problem as follows:

Problem \({\cal P}2\): State identification for a full region

Let I be the current at infinitesimal bias, V and Videnote vectors of voltages applied to the gates, q(V) denotes a probability vector, and N be the number of training samples. Let’s define a full region as the maximum range of voltages that the device is simulated over. Given I(V) and a training set \({\cal T} = \left\{ {I({\boldsymbol{V}}_i),{\boldsymbol{q}}({\boldsymbol{V}}_i)} \right\}_{i = 1}^N\) with k possible device states over the full region, find a map p : V ↦ [0, 1]k, i.e., the probability vector p(V) at each point in the given voltage space, such that, after being trained on the training set \({\cal T}\), \({\cal M}\) minimizes the error (or, equivalently, maximizes the accuracy)

$$Error = \frac{1}{{\left| {\cal E} \right|}}\mathop {\sum}\limits_{\cal E} \left\Vert {{\boldsymbol{p}}\left( {{\boldsymbol{V}}_i^\prime } \right) - {\boldsymbol{q}}\left( {{\boldsymbol{V}}_i^\prime } \right)} \right\Vert_{2}^{2}$$
(2)

on the test set \({\cal E} = \left\{ {I\left( {{\boldsymbol{V}}_{i}^{\prime} } \right),q\left( {{\boldsymbol{V}}_{i}^{\prime} } \right)} \right\}_{i = 1}^{N^{\prime} }\). Again, the summation runs over all elements in the test set \({\cal E}\) and \(\left\| \cdot \right\|_2\) is the 2-norm.

The state diagram (see Fig. 4c) for each device has varying proportions between the possible states. The problem of state identification is solvable if the classifier can do a better prediction than it would be by chance on all states. Since the single dot state, which occupies the largest part of the state diagram, takes (44.3 ± 8.4) % of the full region, we define a required target accuracy of 45 %.

We generated a training set of 1000 gate configurations. Each sample point is the full two-dimensional map (100 × 100 pixels) from the space of plunger gate voltages (VP1, VP2) to current (see Fig. 4b for an example of such map). A state map corresponding to the current map presented in Fig. 4b is shown in Fig. 4c. The states are calculated via the electron density predicted from Thomas−Fermi model. The number of distinct charge islands in the electron density, separated by regions of zero electron density corresponding to the barriers, is used to infer the state of the nanowire (see Supplemental Material). Note that there is more than one way for some of the states to exist. For instance, lower voltages on the barrier B2 with respect to the barriers B1 and B3 or higher voltages on B1 and B2 as compared to B3; all lead to a single dot state (see Fig. 2c). Analogously to the single dot case, gate and physical parameters are sampled from a Gaussian distribution with mean values in parameter set (see Supplemental Material).

We note that Problem \({\cal P}2\) is a regression problem from the I(V) space to the space of probability vectors. The aim is to go from Fig. 4b to Fig. 4c. We used a neural network with three hidden layers similar to the one we employed for the single dot problem. The input and output layers are now of the size equal to number of points in the I(V) and CS(V) relationships, i.e., 100 × 100 pixels. It was possible to achieve 91 % on state values i.e., it was possible to reproduce the state map in Fig. 4c across different devices with the state label agreeing to 91 % with the actual values (see Eq. (2)).

As far as tuning the device is considered, it is not very useful to know the probability vector at each point in the voltage space. Hence, we move to defining a probability vector for a subregion as opposed to a single point in the voltage space.

Auto-tuning

We define the process of finding a range of gate voltage values in which the device is in a specific state as auto-tuning. The ability to characterize the state at any point in the voltage subspace provides a promising starting point for the automated tuning of the device to a particular state. In particular, having an automated protocol for achieving stable desired electron state would allow for efficient control and manipulation of the few electron configurations. In practice, auto-tuning compromises of two steps: (i) identifying the current state of the device and (ii) optimizing the voltage configuration to achieve a desired state. The steps are then repeated until the expected state is reached. For a device with m gates, this leads to a problem of finding an m-dimensional cuboid in the space of the m gate voltages. From an ML perspective, the recognition and tuning of the state can be expressed as the following two problems:

Problem \({\cal {P}}3a\): Averaged state identification for a subregion

Given \({I}\left( {{\boldsymbol{V}}_{\cal {R}}} \right)\), where \({\boldsymbol{V}}_{\cal {R}}\) is a subregion of the voltage space along with a training set \(\left\{ {{\boldsymbol{V}}_{{\cal R}_i},I\left( {{\boldsymbol{V}}_{{\cal R}_i}} \right),{\boldsymbol{p}}\left( {{\boldsymbol{V}}_{{\cal R}_i}} \right)} \right\}_{i = 1}^{N}\), find the average probability vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal {R}}} \right)\) of the region.

In a manner similar to target accuracy defined for \({\cal P}2\), the double dot subimages occupy the largest fraction of the distribution over the subimages in the dataset, and the problem has a solution with a target accuracy of 70 %.

Problem \({\cal P}3b\): Auto-tuning

Given the I(V) characteristics, an initial subregion in voltage space, and a desired dot state in terms of a probability vector pf, find (tune to) a subregion \({\boldsymbol{V}}_{{\cal R}_{\boldsymbol{f}}}\) with the desired dot state such that \(\left\Vert {{\boldsymbol{p}}_{\boldsymbol{f}} - {\boldsymbol{p}}\left( {{\boldsymbol{V}}_{{\cal R}_{\boldsymbol{f}}}} \right)} \right\Vert_{2}\,<\,\epsilon\), where \(\epsilon\) is an error threshold.

The idea behind auto-tuning in a two-dimensional space is presented in Fig. 5a, b. For the case of five-gate double dot device, defined in the Results section, we consider the restricted problem with two gates VP1 and VP2 being controlled and the barrier gates remaining fixed (see Fig. 2c). We start out in a double dot region and the desired dot state is set to be a single dot region.

Fig. 5
figure 5

Machine learning of double dot device. a Idea behind auto-tuning with I and II being the starting and ending subregions respectively. b Subregions encountered by the optimizer when auto-tuning to the single dot region, i.e., the destination probability vector p0 being set to (0, 0, 1, 0). c Design of the CNN for subregion identification. 30 × 30 pixel images are used as input to the CNN. d Starting subregion and end subregion in optimization described in b. The axes ticks denote the pixel index. e Probability vector predicted when subregion is of double dot type and probability vector predicted when subregion of single dot type for the regions in d

Full size image

State learning

As mentioned earlier, the first step in the auto-tuning process is the recognition of the existing state of the device. In a typical experiment, one has access only to a limited voltage regime, decided upon by the experimentalist. Such a region can be thought of as a subimage of the two-dimensional gate voltage map mentioned in the Results section. The identification of the averaged state of the device is an image classification task, with categories representing the different states of the nanowire (i.e., SC, Barrier, SD and DD).

Such problems, which have image classification at their core, have been successfully solved by CNNs.25,26 CNNs have one or more sets of convolutional and pooling layers, that precede the series of hidden layers (see Fig. 5c). A convolutional layer consists of a number of fixed size kernels which are convolved with the input. The weights in the kernel are determined by the training on the dataset. In order to reduce dimensionality of the input for faster operation and to effectively learn larger scale features in the input, a convolutional layer is generally followed by a pooling layer. A pooling layer takes in a subregion in the input and replaces it by an effective element in that region. A common pooling strategy is to let the effective element be the maximum element in the subregion which leads to the notion of a max-pooling layer.

The training set for the subregion learning was generated based on the set of 1000 full two-dimensional maps of I vs. (VP1, VP2) from the Results sections. Fifty thousand submaps of a fixed size (30 × 30 pixel) were generated. Ninety percent of the 50,000 samples were used as the training set and the rest were used to evaluate the performance of the network. We used tenfold cross-validation with the training set to estimate the performance of our classifier. We used the results from the cross-validation to estimate an average accuracy 97.3 %, with standard deviation of 1.4 %. The confusion matrix data describing the performance of the CNN classifier are presented in Table 1. Two examples of the subregions and corresponding probability vectors from the evaluation stage are presented in Fig. 5d, e, respectively.

Table 1 Confusion matrix
Full size table

For the training, we used two convolutional layers with kernels of size [5, 5]. The layers both had 16 kernels. Each convolutional layer was followed by a max-pooling layer, wherein the pool size was set to [2, 2]. The two hidden layers consisted of 1024 and 256 neurons. Rectified linear units (ReLU) with a dropout rate of 0.5 were used as neurons. Dropout regularization was introduced to avoid over-fitting.32 Finally, an Adam optimizer was used to speed up the training process.33

We found that the introduction of the convolutional layers was crucial in achieving better results in terms of both accuracy and efficiency. Here, accuracy is defined with the prediction of the state with the highest probability and efficiency is defined in terms of training time. We note that the state is predicted from the highest probability, though it might be possible that this highest probability is less than 0.5 (see Fig. 5e). Introducing more hidden layers did not affect the accuracy as much as introducing convolutional layers; this indicates that classification over the features seems to be a simpler task than producing an effective representation for the features.

Tuning the device

Having the state of the device identified for a subregion, the procedure of auto-tuning corresponds to a simple optimization problem. Let \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) be the probability vector of a given subregion and pf be the desired probability vector. Define \(\delta \left( {{\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right),{\boldsymbol{p}}_{\boldsymbol{f}}} \right) = \left\| {{\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right) - {\boldsymbol{p}}_{\boldsymbol{f}}} \right\|_2\). The problem of auto-tuning is then equivalent to minimization of \(\delta \left( {{\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right),{\boldsymbol{p}}_{\boldsymbol{f}}} \right)\) below a threshold \(\epsilon\) over the space of gate voltages.

We used COBYLA from the Python package SciPy34 as a numerical optimizer. The probability vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) was calculated using the neural network described in the Results section. The starting region was set initially in a double dot region, as can be seen in Fig. 5b. Around 15 to 30 evaluations of the probability vector using the CNN were required to ultimately find the required subregion (Fig. 5d, II in Fig. 5a) depending on the position of the initial subregion. The starting region was varied over the space of (VP1, VP2) and in each case it was possible to auto-tune to the required subregion.

Working with experimental data

We ran the CNN with the set of weights and biases established during the training on the simulated dataset described in the Results section on an experimental dataset for a three-gate device from our group35–37. The device used in the experiment had two barrier gates (B1 and B2) and one plunger gate (P). In this device, the barrier gates were also used as generic plunger gates. By choosing appropriate voltage values for the plunger (P) gate, the device could be operated as a single dot or a double dot device. The measured data consisted of 2D differential conductance maps in the space of barrier gate voltages (VB1 and VB2) for varied but fixed values of the plunger voltage (VP). Since the qualitative features are similar for a current map and a differential conductance map, we could feed in the differential conductance output into the CNN.

Identification of state in experimental data

For state identification, we considered small regions in the space of barrier voltage for a fixed plunger so that in each of the maps the device was in only one of the states, single or double dot. The maps were then taken at different values of the plunger voltage, ranging from −0.76 to −0.60 V. The barrier gates are varied from −1.44 to −1.34 V. Figure 6b shows the 2D maps for different values of the plunger voltage. A gradual transition from a single dot device to a double dot device is seen.

Fig. 6
figure 6

Auto-tuning. a The idea behind auto-tuning in the three-dimensional space of two barrier and plunger gate voltages. The successive squares represent the subregions encountered in the tuning process which are fed as input to the CNN. The arrow represents the direction of movement in going from an initial region to a final region. b Experimental data at different values of the plunger gate exhibiting a transition from a single dot state to a double dot state. c (Top row) The initial region (VP = −0.64 V) set in a single dot region. The optimizer coupled with the CNN tunes the device to a double dot state (VP = −0.73 V) i.e. the destination probability vector p0 being set to (0, 0, 0, 1). (Bottom row) The initial region set to a region (VP = −0.66 V) with no current through the device. The final state is again a double dot (VP = −0.72 V) as required. d The predicted state probability by the CNN as a function of VP. A clear transition is seen from single dot state to double dot state as is intuitively seen in the experimental data. The probabilities predicted from the CNN for the other states (barrier and short circuit) are smaller in comparison to the single or double dot probabilities and hence only the highest two probabilities corresponding to these states are shown for clarity. e Scatter diagram of initial (faded) and final (dark) positions in the voltage space for the test of the auto-tuning procedure on the simulated devices. The initial positions were chosen to be in the single dot state and required to tune to the double dot state. This test was repeated across all devices in the dataset and we observed an accuracy of 88.5 %

Full size image

Since our model produces the current value only qualitatively, the experimental data had to be re-scaled (by a constant number) prior to feeding into the CNN to match the simulated data. The CNN characterizes the state present in the device through a probability vector. Results for different values of the plunger voltage are shown in Fig. 6d. As can be seen, our CNN can effectively distinguish a single dot and a double dot state from the current maps.

Auto-tuning of the device to a double dot state

Since the device state could be predicted with reasonable accuracy, we considered tuning gate voltages from one state to another based on the experimental data. For this part, a dataset with a larger variation in barrier voltages was used. Figure 6a shows 2D maps of differential conductance vs. the barrier gate voltages (VB1 and VB2) for four different values of the plunger voltage. 2D subregions of these maps were used as input to the CNN in the tuning procedure.

We considered the auto-tuning of all three gate voltages (two barriers and the plunger). The final tuned state was set to a double dot region. See Fig. 6a for a visualization of the auto-tuning process. Two kinds of initial regions were considered: a single dot region (Fig. 6c, two top panels) and a region with no current (Fig. 6c, two bottom panels). In both cases, it was possible to find a set of barrier and plunger gate voltages that map to a double dot state (Fig. 6c, two right panels). Effectively, the CNN predicted the probability vector describing the device state (see Results section) from maps at different plunger voltages and the optimizer tuned the probability vector to a required form (in this case, a double dot).

We used the same optimizer as described in the Results section. The tuning process was completed within 40 to 50 iterations, depending on the initial region. Hence, the CNN coupled with an optimizer can be used with data from actual experiments for auto-tuning the device state.

To quantify the robustness and establish an accuracy for the optimization procedure, we performed the “auto-tuning” on the entire simulated dataset. For each device, a starting point was chosen in a uniform random fashion in the single dot region (see Fig. 6e) and the optimizer was set to converge to the double dot region. We observed 88.5 % accuracy for tuning to the double dot state, wherein a tuning is considered successful only if the final device state is double dot. Potential causes for failure included tuning into the boundaries of the phase diagram and regions which mimic local minima for the optimizer. Adding a preference for lower voltages using an artificial gradient or using a different norm to define the fitness function are possible solutions towards improving the tuning accuracy.

Discussion

Consider a QD device with a set of gate voltages. We showed that a neural network can be trained to predict a probability vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) describing the state of an arbitrary subregion in the voltage space. This predicted vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\), together with a destination probability vector, can be then fed to an optimizer controlling the space parameters in order to obtain the desired single or double dot state. We now describe how a generalized auto-tuner neural network can be implemented in an experiment to automatically adjust the parameters of the device to an expected state.

In particular, let’s assume that pf is the probability vector of the desired state. Starting in a random region of the voltage space, the trained CNN can predict a probability vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) for this region. A fitness function δ is then used to compare the predicted probability vector \({\boldsymbol{p}}\left( {{\boldsymbol{V}}_{\cal R}} \right)\) and the destination vector pf. By minimizing δ, the auto-tuning of the device takes place. An optimizer determines an optimal set of parameters that leads to a new subregion. The process is then repeated until the fitness has been minimized to a particular value.

Since the entire voltage space does not have to be explored, this implies a saving in terms of experimental time. Also, the process does not use human intervention at any step in the tuning of the dot signifying the use of auto in our definition of the auto-tuning problem.

We have presented novel techniques towards tuning of QD devices. Given that building scalable quantum computing devices is now on the horizon, we hope that such methods will present themselves as natural subroutines for construction of real devices and will do away the need to rely on heuristics. Hence, we outline two further problems: Inductive Learning and Charge Tuning that are more realistic and useful in an experimental setting and can be potentially tackled with ML.

Moving to learning and auto-tuning of multiple dots will present new challenges as a result of the higher dimensional space of gate voltages. This curse of dimensionality might detrimentally affect the design of auto-tuning algorithms. Pattern recognition in dimensions greater than two has not been studied extensively. Instead we propose a different solution that can be generalized based on an inductive strategy. We refer to it as Inductive Learning. We make use of the fact that gates which are spatially far apart are likely to be loosely coupled to each other. Hence, a strategy emerges in which we use the auto-tuning algorithm to tune the first two barrier gates. A second type of neural network will be used to tune the plunger gate. This will be repeated until all the single dots formed by two barriers and a plunger are tuned to the required configurations.

To use the QDs as qubits, it is required to have a specified number of electrons in each dot. In the Charge Tuning problem, we intend to tune charge states of the device. The capacitance matrix is an effective model of the device and it determines the quantitative size of features in the current output. For instance, in the case of a single dot, the capacitance matrix can be directly related to the charging energy of the device. For the double dot, the capacitance matrix elements determine the size of the honeycomb hexagons. Hence, establishing a learning algorithm for the capacitance matrix is the next logical step. A capacitance matrix along with the voltage values of the gate can be used to estimate the charge on the device. Estimation of the charge can then be coupled with an optimizer to tune the device to required charge values exactly like tuning the state as described in this paper. We refer to this process of learning the capacitance matrix and tuning the charge on the device as Charge Tuning.

We remark here that these further problems and any other that might arise may require different types of ML algorithms beyond just deep and CNNs described in this paper.

In conclusion, we have described a bare-bones physical model to calculate the capacitance matrix for a linear array of gate-defined QDs. We used a Markov chain model among the charge states to simulate transport characteristics under infinitesimal bias. Our model can qualitatively reproduce the current vs. gate voltage characteristics observed in experiments.

This model was used to train DNNs to learn the charge and state of single QDs from their current characteristics. We used a CNN to identify state of a double QD device from two-dimensional current maps in the space of gate voltages. We defined the auto-tuning problem for QD devices and described strategies for tuning single and double dot devices. The trained networks were tested on experimental data and successfully distinguished the single and double dot device states. We also demonstrated auto-tuning in a three-dimensional space of barrier and gate voltages on an experimental dataset.

Finally, we described how an auto-tuner network might be incorporated in an experiment and outlined further problems in tuning of QD devices. Moreover, our work presents an example of ML techniques, specifically CNNs, fruitfully applied to experiments, thereby paving a path for similar approaches to a wide range of experiments in physics.

Methods

Physical model of a nanowire

A prerequisite for training of neural networks is the availability of a training dataset which mimics the expected characteristics from a test set. We develop a model for electron transport under the Thomas−Fermi approximation to calculate electron density n(x) and current I (see Supplemental Material for details). This model allows us to construct a capacitance model for the islands given a potential landscape V(x) and the fixed Fermi level of the contacts. The potential profile, in turn, is determined by the voltages set on the gates (see Supplemental Material).

An infinitesimal bias is assumed to exist between the contacts. The discreteness in the number of electrons in the islands, along with inter-electronic Coulomb repulsion, leads to transport being blockaded across the nanowire. The charge configuration changes when there are two or more degenerate charge states. Such a degeneracy in energy leads to electron flow across the leads, i.e., current at an infinitesimal bias.

We model electron transport using a Markov chain among the charge states (N1, N2, …, Nk) of the k islands. Ni represents the number of electrons on the ith island. The rate of going from one state to another is calculated under a thermal selection rule set by the energy of the two configurations evaluated from the capacitance model and the tunneling rate. The tunneling rate is modeled as a product of the Wentzel–Kramers–Brillouin (WKB) tunnel probability38 across the barrier and classical attempt rate of electrons in the islands. From the steady-state configuration of the Markov chain, we calculate the current for a given potential landscape V(x) (see Supplemental Material). In all, this simplistic approach provides the minimum model to reproduce basic charge configurations and transport characteristics qualitatively for linear arrays of QDs.

As a check on the qualitative performance of our model, we consider three-gate and five-gate configurations, as shown in Fig. 2a, c, respectively. We consider a single island (two islands) defined using three (five) electrostatic gates, VBi, with i = 1, 2 (i = 1, 2, 3) and VPj with j = 1 (j = 1, 2). By changing the depth of the wells, electrons can tunnel in or out of the islands. At a given value of the gate voltage, a fixed integer number of electrons are assumed to exist on each island. Current flows through the device when two charge states have the same energy predicted by the capacitance model. In such a state, electrons tunnel through one of the contacts into the island (or tunnel between islands for a five-gate device) and tunnel out of the island through another contact. The direction of the electron flow is set by the sign of the bias applied across the leads.

In the simulation for the three-gate device (Fig. 2a), a single dot is present along the nanowire. The contact chemical potentials are fixed to μ1 = μ2 = 100.0 meV with respect to the conduction band minimum. An infinitesimal bias of 100 μeV is present across the leads. The barrier gates are assumed to be kept at a fixed voltage with VB1 = VB2 = −200 mV. The third gate, VP, is swept from 0 to 350 mV.

As can be seen in the current trace in Fig. 2b, Coulomb blockade is reproduced. Our model also allows us to predict the most probable charge configuration from the Markov chain analysis. We see that the charge configuration jumps to a different state exactly at the position of the current peaks. The steady increase in the height of current peaks is a result of lowering of the tunnel barriers on increasing VP. The decrease in spacing between adjacent current peaks with increasing values of VP is due to a slow increase in the capacitance of the dot with increasing electron number.

For the five-gate device, (Fig. 2c), the barrier voltages are set to VB1 = VB2 = VB3 = −200 mV. These values were chosen so that the device operates in a double dot configuration (Fig. 2c). We calculate the current as function of the two plunger gate voltages, VP1 and VP2. We reproduce the expected features for such a system,28 current flow only at triple points and honeycomb-shaped fixed-charge contours (Fig. 2d, e).

We note that while more sophisticated models should be used in future studies, we find our approach to be sufficient for showing how ML can help with the challenges outlined in the Results section.