Abstract
Detecting and controlling nuclear spin nano-ensembles is crucial for the further development of nuclear magnetic resonance (NMR) spectroscopy and for the emerging solid state quantum technology. Here we present the fabrication of a ≈1 nanometre thick diamond layer consisting of 13C nuclear spins doped with nitrogen-vacancy centres (NV) embedded in a spin-free 12C crystal matrix. A single NV in the vicinity of the layer is used for polarization of the 13C spins and the readout of their magnetization. We demonstrate a method for coherent control of few tens of nuclear spins by using radio frequency pulses, and show the basic coherent control experiments, Rabi oscillations and Ramsey spectroscopy, though any NMR pulse sequence can be implemented. The results shown here present an important step towards the realization of a nuclear spin based quantum simulator.
Similar content being viewed by others
Introduction
The concept of a quantum simulator originates from Feynman,1 where the idea is to use a well-controlled quantum system to simulate different types of Hamiltonians. While the first demonstrations of quantum simulator concepts have been realized already in ultra cold quantum gases2 and ion traps,3 a solid state implementation is still limited, though there has been some promising realizations of interaction Hamiltoninians using macroscopic nuclear spin ensembles4 (not scalable though due to the usage of pseudo-pure states), silicon photonics5 and using superconducting qubits.6 Solid state architecture realisation of this type of quantum device is important as it suggests good perspectives for scalability due to the well-developed semiconductor and nano-fabrication technology. A recent theoretical proposal and analysis demonstrate that a quantum simulator even for 2D spin systems is feasible on the basis of diamond quantum technologies.7
Two major challenges towards this realisation are the fabrication of a nano-ensemble of coupled nuclear spins and their polarisation (initialisation), coherent control and read-out. Important steps towards the latter goal have been taken during the last decades as the minimum number of nuclear spins that can be detected has been continuously decreasing. And finally coherent control over a single nuclear spin strongly coupled to a single electron spin has been demonstrated using optical8 and electrical detection.9 Later on first the detection of 104 nuclear spins on the diamond surface has been demonstrated10,11 and finally single spin sensitivity12,13,14 has been achieved.
Results
Here, we address the above mentioned challenges of fabrication of mono-atomic layers of nuclear spins and their control. Firstly, we propose an approach for fabricating clusters of nuclear spins. Secondly, we demonstrate a method for initialization, readout and control of few tens of nuclear spins. We fabricated by chemical vapour deposition (CVD) a nanometre thick diamond layer of 13C carbon atoms (nuclear spin I = 1/2) on two substrates, referred to as samples A and B, see Fig. 1. The growth conditions and procedure have been reported previously.15 First a 12C enriched (99.99%) diamond layer is grown via CVD on an ultra pure diamond substrate (E6 Ltd., electronic grade). On top of it a 13C (using >98.4% 13CH4) enriched layer is grown. In sample A (Fig. 1a) the layer is separated both from the substrate and from the surface by a 10 nm thick 12C enriched (nuclear spin free) diamond layer in order to reduce magnetic noise. The 13C layer was doped with nitrogen via δ-doping during the growth process to create single nitrogen-vacancy centres (NV) in the vicinity of the 13C layer.
In sample B (Fig. 1b) the cap and the buffer (close to the substrate) layers are 5 nm and 20 nm thick, respectively. This sample was implanted with nitrogen ions (15N+) to create NV centres in the vicinity of the 13C enriched region. Three implantation energies were used −5, 2.5 and 1 keV, resulting in an average depth of the nitrogen ions of 7, 3.5 and 1.4 nm, respectively.
Finally, the cap layer is used to protect the spin properties of the NV centres from the surface noise, which induces decoherence as reported previously.16
In both samples single NVs are coupled to few tens of nuclear spins, thus enabling polarization and read out of the magnetization of these small ensembles. Coherent control over the nuclear spins (demonstrated in sample A) is realized via radio frequency (RF) pulses allowing to perform NMR spectroscopy as well as to implement quantum gates. There are two major differences compared to our previous work.17 Firstly, we demonstate here coherent control over the 13C nuclear spins, whereas in ref.17 we show only nuclear spin polarisation and readout. Secondly, in the earlier report we studied a diamond sample with a natural abundance of 13C and naturally occurring NV centres, where no special fabrication process was applied. Here we perform a controlled fabrication of a 13C layer, which is deliberately doped with nitrogen atoms.
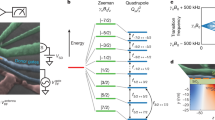
Confocal microscopy fluorescence imaging revealed the presence of single NVs in the 13C enriched layers of both samples. Optically detected magnetic resonance measurements of over 483 NV centres (sample A) and 584 NV centres (sample B) show strong coupling of the NVs to 13C nuclear spins. The spectra can be divided into four groups, distinguished by the number of 13C nuclear spins next to the vacancy, see Fig. 2.
The groups are defined as follows: NVs lacking a first-shell carbon spin (Fig. 2a) (group 1), NVs interacting with a single first-shell 13C spin, and showing a 130 MHz characteristic splitting (Fig. 2b) (group 1) and NVs interacting with two (group 3) or three (group 4) first-shell 13C spins showing three spectral lines (Fig. 2c) and four spectral lines (Fig. 2d), respectively. The latter group would dominate the observed spectra if all NV centres were embedded in a 100% abundance of 13C atoms. The probability of finding an NV centre of group k (k = 1, 2, 3, 4) is defined as pk, and the values obtained from the data for both samples are summarized in Table 1.
We note the larger number of NVs in groups p1 and p2 suggest the presence of two types of regions: one with high and one with low concentration of 13C spins at the microscopic level.
To quantify the overgrown layer at the nanometre scale, we fit a model whose principles are derived from the growth procedure. The predicted values for the probabilities for sample A are closer to the experimentally obtained ones compared to pi for sample B. It is not clear what is the reason for this, but still there is an agreement within 20% between the theory and the experiment. A detailed description is given in the Supplementary Material.
For each of the four groups, we extract the averaged line width of the ODMR spectra, and compare it with the one expected from simulation. In the simulated spectra, the interaction between the electron and the nuclear spins is extracted from an exact calculation of the hyperfine tensor18,19 for the nuclear spins, which are located within 1.5 nm from the NV centre. For nuclear spins which are further away, the dipole-dipole approximation is used. The line width Δν of the NV centres increases with the number of first-shell 13C spins, which has been observed previously20 and the distribution of Δν for the group 4 (three nuclear spins) is smaller than the one of group 2 and 3. Both features are reproduced by our model in a good agreement (Fig. 3) with the experimental data. More detailed analysis can be found in Supplementary Material.
Averaged linewidth of ODMR spectra of NV centres of sample A (blue markers) and sample B (we show only the 5 keV implantation). The error bars represents one standard deviation in the width of measured spectrum. The red markers are simulation with the optimal parameters (see Supplementary Material for more details)
NV centres from group 1 in sample A were chosen for the further experiments since in this diamond. A single NV 1 was chosen, having parallel and perpendicular components of the hyperfine interaction to 13C nuclear spins of \(A_{||}\sim A_ \bot \sim 50\,{\mathrm{kHz}}\) 21, measured both by XY821 and Hartmann-Hahn22 type of measurements (see also Supplementary Figure 3). From this interaction strength, the distance between the NV and the 13C layer is estimated to be 0.72 nm when dipolar interaction is assumed. The coherence time of this NV was found to be T2 = 50 μs. It is important to note, that according to the proposal7 it is not necessary to localise the nuclear spin cluster laterally. However, this still can be achieved, for example by applying the method proposed in ref.23
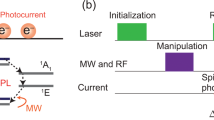
In order to obtain control over the nuclear spins, a robust method for the initialization (polarization) and readout of the nuclear spins is required. We have recently developed a technique to achieve this goal by utilizing a Hartmann-Hahn double resonance17 and here the main idea is given. The NV’s electron spin is driven by applying a spin locking sequence with a Rabi frequency Ω = ωL, where ωL is the Larmor frequency of the nuclear spins. At this condition there is transfer of polarization between the two systems, allowing to polarize and read out the state of a small ensemble of nuclear spins. The pulse sequence of this measurement named Polarization ReadOut via Polarization Inversion (PROPI) is depicted in Fig. 4a. It consists of two blocks of pulses and the working principle is the following. First we apply a laser pulse to initialize the NV centre into the \(\left| {m_s = 0} \right\rangle\) state. Then we apply a MW π/2 pulse to create the superposition state \(1/\sqrt 2 \left( {\left| {m_s = 0} \right\rangle + \left| {m_s = - 1} \right\rangle } \right)\) followed by a long MW pulse to keep the NV in this rotated basis (spin locking) to allow for resonant transfer of population between NV and nuclei. Afterwards a π/2 pulse is used to transfer the coherence to population difference, which is then read out by a second laser pulse. This sequence is repeated several hundred times and the signal is shown in Fig. 4b. We observe that with increasing number of steps, the fluorescence decays since the NV’s electron spin polarisation is transferred to the surrounding nuclear spins. After some time a saturation is reached, where the nuclear spins located in the vicinity of the NV centre are polarized parallel to the applied static magnetic field B0 (“up” state |↑〉17). Now if we change the phase of the first MW pulse by 180° in order to populate the opposite dressed state and we repeat the sequence, we observe a similar behaviour as there is again spin polarization transfer. The difference is that here the nuclear spin polarization is changed from parallel to anti-parallel to the magnetic field (“down” state |↓〉). If the nuclear spin polarization has not changed in between the two pulse blocks, then the area A↑ below the first curves will be equal to the area A↓ below the second curve. However, if there is a process affecting the nuclear spins (thermal relaxation, decoherence and spin diffusion, see below), then A↑ ≠ A↓. The sequence could be simplified if we remove the second pulse block and polarize the nuclear spins only in one state, for example in |↑〉. In this case the area below the curve will change due to some nuclear spin dynamics, for example if there is a time delay τ then A↑ ≠ A↑(τ). Both the PROPI sequence (Fig. 4a) and its simplified version can be used to initialize the nuclear spin ensemble and readout its magnetization, where we obtain similar results. First we demonstrate that the spin lattice relaxation (SLR) time T1 of the nuclear spins can be determined by using the simplified PROPI. For this purpose we introduce a time delay τSLR between the two polarization blocks, see Fig. 4a. Here we observe that A↑(τSLR) increases with increasing τSLR and a saturation is reached around 200 ms, see Fig. 4c. An exponential decay fit reveals T1 = 100 ms, a quite short value, which is probably due to the low magnetic field B0 = 458 G and the high local concentration of paramagnetic substitutional nitrogen (P1 centres, electron spin S = 1/2). Another possible loss of polarisation could be the nuclear spin diffusion out of the ensemble measured by the NV centre.
a PROPI pulse sequences. Here M = N = 200 and the length of the spin locking pulse was set to 20 μs. b NV fluorescence as a function of the number of polarization steps. c Spin lattice relaxation time measurement of a small nuclear spin ensemble revealing T1 = 100 ms. Compared to the sequence shown in a, only a polarization cycle towards one direction was used. Shown are therefore changes in A↑ when the time delay between two successive polarisation cycles is varied
Next we demonstrate coherent control over the nuclear spins using RF pulses. In Fig. 5a the pulse sequence is shown used to measure Rabi oscillations of the nuclear spin ensemble. Similar to the previous experiment it starts with a pulse block (see also Fig. 4a) to initialize the nuclear spins into the “up” state |↑〉. Afterwards we apply a single RF pulse resonant with the |↑〉↔|↓〉 transition. Then we apply a second pulse block, which polarizes the nuclear spin ensemble back into the |↑〉 state. In this work we used N = 100 = M = 100, in contrast to our previous work17, where usually N = 50 and M = 200. This is due to the fact, that the distribution of the nuclear spins is quite different in these samples. In ref.17 the diamond had a natural abundance of 13C, while in the current sample there is a nanometre thin layer of 13C enriched diamond. The NV’s fluorescence read out from this pulse block is depicted in Fig. 5b. This plot is actually a stack of same type measurements as shown in Fig. 4b. We find that the signal increases with increasing the length of the RF pulse τRF. If we take the area below the curves, we obtain the typical Rabi oscillations, shown in Fig. 5c. By halving the RF power we observe half of the Rabi frequency as expected, Fig. 5c, lower graph.
a Pulse sequence for performing nuclear spin Rabi experiments (M = N = 100). Raw b and processed data c from the PROPI measurement. In c Rabi oscillations are observed, which frequency decreases with decreasing RF amplitude (input at the RF amplifier) (upper to lower graph). Red lines correspond to cosine fits. A Rabi frequency of (19.1 ± 0.5)kHz (upper plot) and (9.5 ± 0.5)kHz (lower plot) is estimated
Finally we demonstrate NMR spectroscopy of a small nuclear spin ensemble. For this purpose we record the free induction decay (FID) of the ensemble (sometimes called Ramsey fringes) by using the pulse sequence depicted in Fig. 6a. After polarizing the nuclear spins into the |↑〉 state we apply a RF π/2 pulse to create the superposition state \(\left| \psi \right\rangle = 1/\sqrt 2 \left( {\left| \uparrow \right\rangle + \left| \downarrow \right\rangle } \right)\). We let this state evolve for a time τFID then we apply a second RF π/2 to convert it to a population difference. The latter is read out by the second pulse block on the NV centre. In Fig. 6b we show a typical FID of a 13C nuclear spin ensemble, when the NV was initialized in \(m_s = \left| 0 \right\rangle\) before the RF pulse. The exponential fit to the data reveals a nuclear spin phase memory time of \(T_2^ \ast = 2.5\,{\mathrm{ms}}\) which is probably limited by the spin relaxation time T1 of the NV. The latter undergoes relaxation towards Boltzmann equilibrium, where the |ms = ±1〉 states become populated. This results in changes of the nuclear spin Larmor frequency due to the hyperfine coupling since the latter is zero when the NV is in |ms = 0〉 state. This effect causes dephasing of the 13C nuclear spins. In addition, a high local concentration of P1 centres can also lead to nuclear spin dephasing.
If the NV is initialised into |ms = −1〉 state by applying a laser and a MW π pulse, then we observe a much shorter \(T_2^ \ast = 0.113\,{\mathrm{ms}}\) (Fig. 6c). This result can be explained by the fact, that the nuclear spins experience a magnetic field gradient of about 33 G/nm (at 0.72 nm distance), generated by the electron spin of the NV. This gradient shifts the resonance frequencies of the nearby nuclear spins and a broadening of the line of about 33 × 1.1 kHz/G = 36.3 kHz is expected, which agrees roughly with the value obtained from the experiment - \(1/\pi T_2^ \ast = 1/(0.113 \times \pi ) = 2.82\, {\mathrm{kHz}}\).
Discussion
In conclusion, we have demonstrated the fabrication of a nanometre thin 13C enriched diamond layer, where small nuclear spin ensembles are coupled to single NV centres. We present a method for coherent control of those ensembles by combining RF pulses and PROPI-based17 pulse sequences. Rabi measurements and NMR spectroscopy have been performed, revealing that the NMR line width depends strongly on the state of the NV centre during the free evolution time. This result confirms that the 13C nuclear spins are indeed in the close vicinity of single NV centres as expected from the CVD growth conditions. We believe that our work will find application in the emerging field of solid state quantum simulators, based not only on NV centres, but also on other physical systems involving a central electron spin and a nuclear spin bath, such as phosphor donors in silicon and semiconductor quantum dots.
Data availability
The authors declare that the main data supporting the finding of this study are available within the article and its Supplementary Information files. Additional data can be provided upon request.
References
Feynman, R. P. Simulating physics with computers. Int. Jour. Theor. Phys. 21, 467 (1982).
Bloch, I., Dalibard, J. & Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267 (2012).
Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516 (2016).
Álvarez, G. A., Suter, D. & Kaiser, R. Localization-delocalization transition in the dynamics of dipolar-coupled nuclear spins. Science 349, 846 (2015).
Wang, J. W. et al. Experimental quantum Hamiltonian learning. Nat. Phys. 13, 551 (2017).
Roushan, P. et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science 358, 1175 (2017).
Cai, J., Retzker, A., Jelezko, F. & Plenio, M. B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 9, 168 (2013).
Jelezko, F. et al. Observation of coherent oscillation of a single nuclear spin and realization of a two-qubit conditional quantum gate. Phys. Rev. Lett. 93, 130501 (2004).
Pla, J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334 (2013).
Staudacher, T. et al. Nuclear magnetic resonance spectroscopy on a (5-nanometer)3 sample volume. Science 339, 561 (2013).
Mamin, H. J. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557 (2013).
Mueller, C. et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 5, 4703 (2014).
Sushkov, A. O. et al. Magnetic resonance detection of individual proton spins using quantum reporters. Phys. Rev. Lett. 113, 197601 (2014).
Shi, F. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21 (2014).
Watanabe, H. & Shikata, S. Superlattice structures from diamond. Diam. Relat. Mater. 20, 980 (2011).
Staudacher, T. Enhancing the spin properties of shallow implanted nitrogen vacancy centers in diamond by epitaxial overgrowth. Appl. Phys. Lett. 101, 212401 (2012).
Scheuer, J. et al. Robust techniques for polarization and detection of nuclear spin ensembles. Phys. Rev. B 96, 174436 (2017).
Nizovtsev, A. P., Kilin, S. Y., Pushkarchuk, A. L., Pushkarchuk, V. A. & Jelezko, F. Theoretical study of hyperfine interactions and optically detected magnetic resonance spectra by simulation of the c291[nv]−h172 diamond cluster hosting nitrogen-vacancy center. New J. Phys. 16, 083014 (2014).
Nizovtsev, A. P. et al. Non-flipping 13 c spins near an nv center in diamond: hyperfine and spatial characteristics by density functional theory simulation of the c510[nv]H 252 cluster. New J. Phys. 20, 023022 (2018).
Mizuochi, N. et al. Coherence of single spins coupled to a nuclear spin bath of varying density. Phys. Lett. B 80, 041201(R) (2009).
Taminiau, T. H. et al. Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602 (2012).
London, P. et al. Detecting and polarizing nuclear spins with double resonance on a single electron spin. Phys. Rev. Lett. 111, 067601 (2013).
Lazariev, A. & Balasubramanian, G. A nitrogen-vacancy spin based molecular structure microscope using multiplexed projection reconstruction. Sci. Rep. 5, 14130 (2015).
Acknowledgements
This work was supported by the ERC Synergy grant BioQ, the EU (EQuaM, HYPERDIAMOND grant agreement No 667192), the DFG (SFB TR/21, FOR 1493) and the Volkswagenstiftung. BN is grateful to the Postdoc Network program of the IQST and to the Bundesministerium für Bildung und Forschung for receiving the ARCHES award. The work at ETH Zurich was supported by Swiss National Science Foundation (SNFS) Project Grant No. 200020 175600, the National Center of Competence in Research in Quantum Science and Technology (NCCR QSIT), and the DIAmond Devices Enabled Metrology and Sensing (DIADEMS) program, Grant No. 611143, of the European Commission. The work at Keio was supported in parts by KAKENHI (S) No. 26220602, SPS Core-to-Core Program, and Spin-RNJ.
Author information
Authors and Affiliations
Contributions
T.U., N.T., T.W., F.F., P.L., J.Z. carried out the experiments and analysed the data. P.L. provided the theoretical model. N.R. and J.M. performed the nitrogen ion implantation. H.W. and K.I. fabricated the diamond layers. B.N., T.U., N.T., and P.L. wrote the manuscript with feedback from all authors. B.N., M.B.P., and F.J. supervised and managed the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Unden, T., Tomek, N., Weggler, T. et al. Coherent control of solid state nuclear spin nano-ensembles. npj Quantum Inf 4, 39 (2018). https://doi.org/10.1038/s41534-018-0089-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0089-8
This article is cited by
-
Mapping a 50-spin-qubit network through correlated sensing
Nature Communications (2024)
-
Divergent Effects of Laser Irradiation on Ensembles of Nitrogen-Vacancy Centers in Bulk and Nanodiamonds: Implications for Biosensing
Nanoscale Research Letters (2022)
-
Power-law scaling of correlations in statistically polarised nano-NMR
npj Quantum Information (2022)
-
Algorithmic decomposition for efficient multiple nuclear spin detection in diamond
Scientific Reports (2020)
-
Spin coherence in two-dimensional materials
npj Computational Materials (2019)