The entropic cost of quantum generalized measurements

Abstract

Landauer’s principle introduces a symmetry between computational and physical processes: erasure of information, a logically irreversible operation, must be underlain by an irreversible transformation dissipating energy. Monitoring micro- and nano-systems needs to enter into the energetic balance of their control; hence, finding the ultimate limits is instrumental to the development of future thermal machines operating at the quantum level. We report on the experimental investigation of a lower bound to the irreversible entropy associated to generalized quantum measurements on a quantum bit. We adopted a quantum photonics gate to implement a device interpolating from the weakly disturbing to the fully invasive and maximally informative regime. Our experiment prompted us to introduce a bound taking into account both the classical result of the measurement and the outcoming quantum state; unlike previous investigation, our entropic bound is based uniquely on measurable quantities. Our results highlight what insights the information-theoretic approach provides on building blocks of quantum information processors.

Introduction

Manipulating the information content of a memory register has an associated thermodynamic cost: copying and erasing information can only be realized through physical operations whose implementation necessitates of appropriate resources.^1,2,3,4,5 Landauer’s principle epithomizes such cost by quantifying the minimum amount of work required to reset a memory^6,7 and thus entering the energetic balance of any physical process.

Controlling the conversion of information to energy will be key to the implementation of quantum-limited micro- and nano-engines and, in general, to the development of quantum technologies.⁸ In the light of Landauer’s principle, the simple act of monitoring a system through a quantum measurement implies a thermodynamic cost whose quantification has been the focus of recent debates.^{9,10,11,12,13,14,15}

These studies have reinforced the view that changes in information theoretic entropies serve as indicators of corresponding variations in physical entropies, whose origin can be traced back to dissipative phenomena. Thus, the observation of information flows resulting from a physical process helps establishing fundamental bounds to the thermodynamic cost of the process itself. This is even more relevant given that a direct assessment of quantities such as work, heat, and entropy is in general hard to perform. In addition, such fundamental bounds are useful for comparing the cost of different measurement strategies used to infer the information–thermodynamic balance of a given process, regardless of the details of the implementation. To this purpose, not only such fundamental bounds should comprehensively take into account all sources of entropy, but also they need to be cast in terms of quantities directly accessible to the experimenter.

Weak measurements offer a valuable chance to balance the degree of information acquired through a detection strategy and the disturbance to the state of the monitored system.^16,17 Such measurements are key for the control of the dynamics of a system, as experimentally demonstrated in the context of quantum metrology,^18,19,20,21 communication,^22,23,24 and error correction.^25,26 To date, weak measurements have generally been characterized by inspecting the classical information extracted through their use, and how this limits the quantum information preserved in the post-measurement state.^{24,27,28,29,30,31} A complete understanding of this tool in the information–thermodynamic sense has not been completely achieved. In fact, current efforts have focused on understanding how purely thermodynamic contributions can be distinguished by weakly measuring the system along quantum trajectories.¹³

Here we investigate both the informational and thermodynamic cost of generalized measurements in a photonic architecture.^27,32,33 Starting from the framework set in ref. ¹⁰, we introduce a figure of merit, the minimal energetic cost of measuring, which is attainable in a real experiment. Through the introduction of this quantitative instrument, we obtain a lower bound to the physical irreversible entropy associated with the act of observing, which is characteristic of and intrinsic to the measurement. The flexibility of our experimental apparatus allows for tuning the amount of information extracted from the system. Our measurement device can be tuned from the weak regime in which the state is only modestly perturbed, but little information is acquired, to the full strength regime encompassed by standard Von Neumann projections; these provide a large degree of information on the measured system, but its state is significantly altered. Our results show the energetic equivalence of performing measurements of arbitrary invasiveness on pure states. At variance with this, a weak measurement impacts in a less substantial way on the coherence of the quantum state of the measured system. Our endeavors, extending Landauer-like arguments, opens up the exploitation of generalized measurements in information-to-energy conversion processes.

Results

Measurement protocol

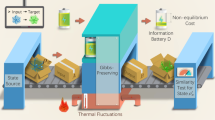
In Fig. 1, we show the salient features of our protocol. A quantum system, initially in the quantum state ρ _σ , is sent to a non destructive measurement device. Information is extracted by looking at an ancillary meter system, which we assume has initially been thermalized via the contact with a thermal bath at temperature T. As a result, the meter is prepared in the canonical Gibbs state $\rho _\mu = e^{ - \beta {\Bbb H}_\mu }{\mathrm{/}}{\Bbb Z}_\mu$, where β = 1/k_BT (here k_B is the Boltzmann constant), ${\Bbb H}_\mu$ is the free Hamiltonian of the meter, and ${\Bbb Z}_\mu = {\mathrm{Tr}}\left[ {e^{ - \beta {\Bbb H}_\mu }} \right]$ is the partition function (see Methods).

Fig. 1

Conceptual scheme of the protocol. After the meter is kept in contact with a thermal bath at fixed temperature T, the two systems interact through a unitary operator. It is possible to infer information on the signal by performing a measurement on the meter resulting in a classical and a quantum output

The measurement relies on the interaction of the signal and the meter ruled by a unitary operation U. The coupling links the two systems in such a way that a standard measurement on the meter delivers information on the state of the signal. Such information is in the form of a “classical” outcome k occurring with a probability p _k . The amount of classical information is then quantified by the Shannon entropy H({p _k }), associated with the probabilities p _k  = Tr[E _k ρ _σ ], where we have introduced the set of measurement operators E _k such that $\mathop {\sum}\nolimits_k {\kern 1pt} E_kE_k^\dagger = \mathbb{I}$. Remarkably, the Shannon entropy has a clear thermodynamic interpretation as formulated by Landauer’s principle: an agent having the signal at their disposal might try to extract work from it by exploiting the information gathered through the measurement performed over the meter. In the simplest instances, the amount of work extractable from the measurement scheme being considered is then k_BT(1 − H({p _k })).^34,35 However, the implementation of feedback results in some modifications of the expression.^36,37

We also have a “quantum” output, represented by the state of the signal $\rho _\sigma ^{(k)}$ after the interaction, conditioned on the outcome k. A complete information–thermodynamic analysis ought to take into account the transformation of the signal system after the meter measurement. A first analysis has been carried out in ref. ¹⁰: here we go beyond the context and results set by such seminal work to address quantities that are directly accessible to (and relevant for) the experimenter.

The key figure of merit is the Groenewold–Ozawa (GO) or quantum-classical (QC) information^38,39

$$I = S\left( {\rho _\sigma } \right) + H\left( {\left\{ {p_k} \right\}} \right) + {\cal I}_{\mathrm {post}}$$

(1)

This is the sum of three contributions: the quantum information on the initial preparation of the signal state, embodied by the von Neumann entropy S(ρ _σ ), the classical information resulting from the performance of the measurements, provided by the Shannon entropy H({p _k }), and the term

$${\cal I}_{\mathrm {post}} = \mathop {\sum}\limits_k {\kern 1pt} {\mathrm{Tr}}{\kern 1pt} \left[ {\left( {\sqrt {E_k} \rho _\sigma \sqrt {E_k} } \right){\mathrm{ln}}\left( {\sqrt {E_k} \rho _\sigma \sqrt {E_k} } \right)} \right],$$

(2)

which describes the mutual information linked to the post-measurement states and their probabilities up to a sign.⁴⁰ The energetic and informational balance resulting from the process being considered is condensed in the expression of the ensemble-average work $W_\mu ^{meas}$ needed for implementing the measurement itself. The balance can be cast into the form¹⁰

$$S_{\mathrm{irr}} \equiv \beta \left( {W_\mu ^{\mathrm {meas}} - {\mathrm{\Delta }}F_\mu } \right) \ge (I - H),$$

(3)

where ΔF _μ is the average variation in the Helmholtz free energy of the meter in the overall process, and S_irr is the irreversible entropy generated in the process of measuring. The complete information–thermodynamic balance can thus be understood in terms of a minimal irreversible entropy (see Methods), embodied by the left-hand side of the inequality above. This represents the minimal cost associated with the process of measuring, cast in the form of an unbalance between the GO (QC) information and the Shannon entropy.

In our experiment, we rely on Eq. (3) to explore how the lower bound on irreversible entropy is affected by the strength of the measurement. The role of the GO (QC) information in determining the efficiency of a feedback mechanism in a Maxwell-demon scenario has already been addressed.³⁷ In contrast, the implications of Eq. (1) in the analysis of quantum measurements have not been explored, nor the lower bound investigated experimentally. Our work contributes to both these points both at the theoretical and experimental level. Landauer’s principle, cast in the form of Eq. (3), makes the lower bound accessible from information theoretic considerations, avoiding possible complications entailed by the (in principle difficult) direct assessment of the irreversible entropy $S_{\mathrm{irr}} = \beta \left( {W_\mu ^{\mathrm {meas}} - {\mathrm{\Delta }}F_\mu } \right)$ at the ultimate limit, which we remark is not observable. The identification of tight bounds to S_irr is an open area of investigation^41,42 that is yet to deliver a bound able to provide a faithful estimate of the cost of acquiring or deleting information.

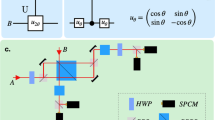
Here, we establish a minimal cost in terms of irreversible entropy in a two-photon experiment, with the aim of characterizing generalized measurements using information–thermodynamics. For our investigation, we use the experimental setup depicted in Fig. 2, where the polarization states photon pairs are used to encode the states of the signal and meter systems, assumed to be two-level system in the remainder of this work. The least (most) energetic state of each system is encoded in the horizontal $\left| H \right\rangle$ (vertical $\left| V \right\rangle$) polarization state of the respective photon.

Fig. 2

Experimental setup. The signal and meter photons are generated via a spontaneous parametric down conversion (SPDC) process through a β Barium-Borate crystal (Type I) pumped with a continuous-wave (CW) laser at 80 mW and wavelength 405 nm. We encode the logical states of each qubit in the horizontal and vertical polarization states $\left| H \right\rangle$ and $\left| V \right\rangle$ of each photon. The signal qubit is kept in the superposition state $\left| D \right\rangle = 1{\mathrm{/}}\sqrt 2 \left( {\left| H \right\rangle + \left| V \right\rangle } \right)$ while the meter starts in a $\left| H \right\rangle$ polarization state. The measurement strength can be adjusted with a rotation of the polarization of the meter performed via a half wave plate (HWP). The two photons then enter in an entangling C-Sign gate realized with partially polarized beam splitters (PPBSs) and HWPs (see Methods). The classical output is then measured in the diagonal basis while on the quantum output a quantum state tomography (QST) is performed

Experiment

Our experiment proceeds in four steps: (i) the signal is initialized in a superposition of its levels $\left| D \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| H \right\rangle + \left| V \right\rangle } \right)$ that is expected to deliver the highest entropy, while the meter is prepared in either the $\left| H \right\rangle$ or $\left| V \right\rangle$ state; (ii) the coupling is implemented by a controlled-sign (C-Sign) gate, which imparts a π-phase on the $\left| V \right\rangle _\sigma \left| V \right\rangle _\mu$ component only.^43,44,45 Its strength is effectively controlled by rotating the state of the meter by means of a half wave plate before the gate, set at a rotation angle θ. We can then create an entangled state of the two systems, so that a measurement on the meter will deliver information on the H/V component of the signal without destroying it; (iii) for different settings of θ, we measure the probabilities p _D and p _A of a standard polarization measurement performed on the meter. This allows us to compute the Shannon entropy associated to each coupling: we can then explore different regimes, ranging from strong von Neumann measurements to weak observations that minimally disturb the input signal state; (iv) we perform quantum state tomography (QST) of the signal photon conditioned on the outcome of the nondestructive measurement process. All relevant quantities are extracted from coincidence counts originating from a signal and a meter photon. This allows us to control the two out-coming states and use the results to evaluate the mutual information from the post-measurement states ${\cal I}_{\mathrm {post}}$ defined in Eq. (2).

First, we discuss the limiting case in which the meter is kept in the pure state $\left| H \right\rangle$. Our results are summarized in Fig. 3, where we show the Shannon entropy, the mutual information from the post-measurement states, and the GO (QC) information as functions of the angle θ corresponding to different measurement regimes. Clearly, θ = 0 corresponds to no coupling, while θ = π/8 corresponds to the von Neumann projective regime.^27,33 The interpolation between these two regimes has been investigated using a suitable lower bound^{24,27,28,29,30} based on the assessment of trade-offs between classical and quantum information at the outputs of the experimental apparatus. In our work, instead, we focus on how information theoretical entropies of either nature establish a lower bound on the physical irreversible entropy.

Fig. 3

Experimental behavior at T = 0. The experimental values of the Shannon entropy (purple), the GO (QC) Information (green), and the correlation term or mutual information of the post-measurement states (blue) are displayed in function of the measurement strength θ; the corresponding continuous lines represent the predictions for an ideal measurement. Vertical error bars take into account the Poissonian statistics of the measured counts and derived from a Monte Carlo (MC) routine

For all measurement strengths, the GO (QC) information (I) is expected to be equal to zero, given that the post-measurement entropy term reduces to the opposite of the Shannon entropy. We can develop an intuition for this result, considering that the information–thermodynamic balance of the process Eq. (3) should be governed only by the statistics of the measurement, which is the only source of entropy. The results of our experiment reported in Fig. 3 reveal that the strength of the measurement does not come into play when inspecting the balance provided by Eq. (3). Moreover, imperfections impact the experimental data by introducing an excess of von Neumann entropy on the post-measurement states of the signal, thus deviating from the theoretical expectations. Differently, the behavior of the Shannon entropy remains close to the predictions.

More generally, the state of the meter is assumed to be in a canonical distribution at temperature T, due to its interaction with a thermal bath. We simulate this mixed state by adding, with suitable weights associated to a temperature T, the concidence counts relative to the least ($\left| H \right\rangle$) and the most ($\left| V \right\rangle$) energetic states of the meter, while keeping the signal prepared in $\left| D \right\rangle$.^24,46

The GO (QC) information term is not directly accessible through the experiment. The reason is that the overall measurement apparatus actually performs distinct operations, depending on the preparation of the meter. The operator describing the post-measurement state of the signal when a meter photon prepared in $\left| H \right\rangle$ is injected is $M_k\rho _\sigma ^kM_k^\dagger {\mathrm{/}}p_k$ with $M_k^\dagger M_k = E_k$. Conversely, when a meter $\left| V \right\rangle$ is chosen, the state of the signal associated to the same output is now $N_k\rho _\sigma ^kN_k^\dagger {\mathrm{/}}p_k$, where $N_k = - i\sigma _yM_k$. However, we still have $N_k^\dagger N_k = E_k$. As the meter is kept in a mixed state, the measurement will output a mixture of the aforementioned states of the signal. The definition of the GO (QC) information in Eq. (1), instead, considers only the case where $M_k = N_k = \sqrt {E_k}$, thus resulting in the discrepancy between the expected and observed values of such contribution.

In order to go beyond such limitations and consider a figure of merit that is more faithful to the experimental setting being studied, we introduce a (related) figure of merit defined as⁴⁷

$$\tilde I = S\left( {\rho _\sigma } \right) + H\left( {\left\{ {p_k} \right\}} \right) + \mathop {\sum}\limits_k {\kern 1pt} {\kern 1pt} {\mathrm{Tr}}\left[ {\tilde \rho _\sigma ^k{\kern 1pt} {\mathrm{ln}}{\kern 1pt} \tilde \rho _\sigma ^k} \right],$$

(4)

where $\tilde \rho _\sigma ^k = 1{\mathrm{/}}{\Bbb Z}_\mu$$\left[ {e^{ - \beta \epsilon _{\mathrm{0}}}\left( {M_k\rho _\sigma M_k^\dagger } \right) + e^{ - \beta \epsilon _{\mathrm{1}}}\left( {N_k\rho _\sigma N_k^\dagger } \right)} \right]$ is the actual output state of the signal up to normalization. Such a state can be accessed experimentally by QST, and the resulting quantity $\tilde I$ can be used to modify Eq. (3). As it is straightforward to verify, we have $\tilde I < I_{}^{}$, which implies that we still have a meaningful bound (see Methods). An intuitive justification can be obtained by comparing Eqs. (1) and (4). In the former, the mutual information considers the quantum output conditioned to the ideal measurement operators $\sqrt {E_k}$. These only have an information theoretical meaning and represent a purified version of the actual physical states $\tilde \rho _\sigma ^k$ that neglects their dependence on the temperature of the meter. The modified GO (QC) information $\tilde I$ captures such an additional contribution to mixedness, which lowers the information content brought about by $\tilde I$, which hence provides a lower bound to I.

The results are summarized in Fig. 4, which shows how the increase in the temperature of the meter, thus its mixedness, reflects in the dispersion of the correlation term $\tilde I - H$. The data confirm that, in the ‘worst case scenario’ of injecting the state delivering the highest entropy, the degree of irreversibility generated by the implementation of the measurement addressed in our experiment is lower bounded by a quantity that is insensitive of the information gathered on the state of the signal through the meter. Thermodynamically, this implies that the minimum cost for the implementation of a measurement, as measured by the information-theoretical lower bound in Eq. (3) or the version proposed here involving $\tilde I$ is not linked to the back-action induced to the state of the probed system, but intrinsic in the act of measuring itself.

Fig. 4

Experimental behavior at T ≠ 0. The figure shows the comparison between the theoretical prediction and the experimental values against the temperature of the meter (β⁻¹) and the measurement strength (θ). Albeit the theoretical prediction does not depend on θ, experimentally we notice that for low temperatures the impact of the setup imperfections is more pronounced in the strong regime as degree of entanglement between the signal and the meter increases. As the temperature rises, this effect becomes negligible. Vertical error bars are smaller than the point size

On one hand, this calls for the research of bounds to the cost of measuring that are more sensitive to the explicit degree of back-action induced by the measuring step, much along the lines of recent attempts made in the context of the Landauer principle itself.^41,42,48 On the other hand, $\tilde I_{}^{}$ accounts explicitly for the impossibility of an experimental apparatus such as ours to distinguish among the conditional states resulting from the recording of a given measurement outcome. Its introduction highlights the need for experiment-tailored quantities apt to quantify appropriately the energetic and information balance. The second law of “information–thermodynamics”, cast in the form of Eq. (3), makes the lower bound accessible from information theoretic considerations, avoiding possible complications entailed by the direct assessment of the irreversible entropy at the ultimate limit. Our experiment gives us access to the possibility of estimating $W_\mu ^{meas}$ and ΔF _μ from the registered counts (see Methods), although this is not tantamount to measuring actual changes in thermodynamic quantities; remarkably, these are expected to be independent on the strength as well. Figure 5 illustrates the observed behavior of thermodynamic quantities for θ = 0.21: as the temperature raises, the work does not account for the increase in the Helmholtz free energy. These trends are reflected in the negative behavior of the irreversible entropy production S_irr, which can be justified by the fluctuation theorem, here compared with its information-theoretical lower bound: this is far from being strict, but provides information about the actual trend as a function of the initial temperature of the meter qubit.

Fig. 5

Upper panel: estimation of the work $W_\mu ^{\mathrm {meas}}$ (red points), and of the change in Helmholtz free energy ΔF _μ (green points), together with the predictions (solid lines). Lower panel: estimation of the irreversible entropy S_irr (blue points), compared to the direct measurements of $\tilde I - H$ (purple points). The solid lines correspond to the respective predictions

Conclusions

The physical act of measuring has a cost that can be interpreted, thermodynamically, in terms of an entropy production. Although the latter is typically not observable, it can be bound by information-theoretical quantities of easier experimental accessibility. This work aimed precisely at the experimental characterization of the minimum entropy cost necessary for the implementation of the measurement on the quantum state of an elementary system. Our experiment has been able to highlight the fundamental insensitivity of such entropic bound to the invasiveness of the measurement itself. Our approach is based on the use of generalized quantum measurements, spanning from weak to strong projective ones. It demonstrates the viability of such an important tool for experimental investigations on the information–thermodynamics of fundamental quantum processes.

Methods

Theoretical details

The free Hamiltonian of the meter is assumed to be, without loss of generality, ${\Bbb H}_\mu = \epsilon _0\left| H \right\rangle \left\langle H \right| + \epsilon _1\left| V \right\rangle \left\langle V \right|$, with $\epsilon _0$($\epsilon _1$) = 0(1). The key step of our protocol is represented by the interaction of the signal and the meter via the unitary operator ${\Bbb U}_{\sigma \mu } = {\Bbb N}_{\sigma \mu }({\Bbb I}_\sigma \otimes {\Bbb R}_\mu )$, which encompasses the rotation of the meter ${\Bbb I}_\sigma \otimes {\Bbb R}_\mu$ and the C-sign gate ${\Bbb N}_{\sigma \mu }$. It is worth remarking that the rotation allows to control the invasiveness of the measurement process^32,33 by rotating the state of the meter.

When the meter is in state $\rho _\mu = \left| H \right\rangle \left\langle H \right|$, the gate delivers a measurement operator acting like

$$M_k\rho _\sigma M_k^\dagger = \left| {\psi _k} \right\rangle \left\langle {\psi _k} \right|,$$

(5)

where:³³

$$\begin{array}{*{20}{l}} {\left| {\psi _0} \right\rangle = {\mathrm{sin}}\left( {2\theta + \frac{\pi }{4}} \right)\left| V \right\rangle _\sigma + {\mathrm{cos}}\left( {2\theta + \frac{\pi }{4}} \right)\left| H \right\rangle _\sigma } \hfill \\ {\left| {\psi _1} \right\rangle = {\mathrm{sin}}\left( {2\theta - \frac{\pi }{4}} \right)\left| V \right\rangle _\sigma - {\mathrm{cos}}\left( {2\theta - \frac{\pi }{4}} \right)\left| H \right\rangle _\sigma } \hfill \end{array}$$

(6)

are the states of the signal after the meter measurement. Such post-measurement states of the signal are useful for the calculation of the lower bound on the irreversible entropy, which does not depend on the von Neumann entropy of the signal state as ρ _σ is pure. In the limiting case of T → 0, the mutual information reduces to the opposite of the Shannon entropy, thus giving a null GO (QC) information. As the temperature of the thermal bath rises, the correlation term accounts also for the mixedness of the state of the meter, which can be only considered via Eq. (4).

The quantity in the left-hand side of Eq. (3) can be interpreted as an irreversible entropy $S_{\mathrm{irr}} = \beta \left( {W_\mu ^{\mathrm {meas}} - {\mathrm{\Delta }}F_\mu } \right)$. We have $W_\mu ^{\mathrm {meas}}$ = $\mathop {\sum}\nolimits_k {\kern 1pt} p_k{\kern 1pt} {\mathrm{Tr}}\left[ {\rho _k^\mu {\Bbb H}_\mu ^k} \right] - {\mathrm{Tr}}{\kern 1pt} \left[ {\rho _\mu ^{\mathrm {init}}{\Bbb H}_\mu } \right]$ where, $\rho _k^\mu = \left| k \right\rangle \left\langle k \right|$, ${\Bbb H}_\mu ^k = \epsilon _k\left| k \right\rangle \left\langle k \right|$, and $\rho _\mu ^{\mathrm {init}} = e^{ - \beta {\Bbb H}_\mu }{\mathrm{/}}{\Bbb Z}_\mu$. The average change in the Helmholtz free energy is ${\mathrm{\Delta }}F_\mu = \mathop {\sum}\nolimits_k {\kern 1pt} p_kF_\mu ^k - F_\mu ^{\mathrm {init}}$, in which $F_\mu ^k = - k_{\mathrm {B}}T{\kern 1pt} {\mathrm{ln}}{\kern 1pt} {\Bbb Z}_\mu ^k$. These lead to the following expressions

$$\begin{array}{l}W_\mu ^{\mathrm {meas}} = p_1{\bar{\mathrm \Delta }} + \epsilon _0 - \left\langle \epsilon \right\rangle ,\\ {\mathrm{\Delta }}F_\mu = p_1{\bar{\mathrm \Delta }} + \beta ^{ - 1}{\kern 1pt} {\mathrm{ln}}\left( {1 + e^{ - \beta {\bar{\mathrm \Delta }}}} \right),\end{array}$$

(7)

where ${\bar{\mathrm \Delta }} = \epsilon _1 - \epsilon _0$ and $\left\langle \epsilon \right\rangle = {\mathrm{Tr}}{\kern 1pt} \left[ {\rho _\mu ^{\mathrm {init}}{\Bbb H}_\mu } \right]$. Remarkably, in line with the lower bound in Eq. (3), the irreversible entropy does not depend on the invasiveness of the measurement process. In fact, we get the expression

$$S_{irr} = \beta \epsilon _0 - \beta \left\langle \epsilon \right\rangle - ln\left( {1 + e^{ - \beta {\bar{\mathrm \Delta }}}} \right).$$

(8)

The irreversible entropy and its lower bounds are shown in Fig. 6. The original Sagawa-Ueda bound sets a stricter limit to S_irr, and it is nearly saturated at high temperatures. However, its profile is flat in β⁻¹ and provides no information on the changes of irreversibility. The bound $\tilde I - H$, on the other hand, is less strict but provides indications on the irreversible behavior as a function of the temperature. Both bounds are insensitive to the measurement invasivity.

Fig. 6

Illustration of the Sagawa-Ueda and the modified lower bound vs S_irr. The irreversible entropy (blue surface) associated to the measurement process is bounded from below by I − H (gray surface), which, is not actually linked to directly measurable quantities. This prompts to introduce a modified GO (QC) information $\tilde I$ that is experimentally accessible. The modified lower bound $\tilde I - H$ is indicated as the purple surface

Experimental details

We built our investigation on the possibility to use pair of photons to encode both signal and meter systems. Photons are generated via a spontaneous parametric down conversion nonlinear process through a β barium–borate crystal (Type I): the source produces photon pairs at 810 nm when pumped with a 405 nm Continuous-Wave (CW) laser at 80 mW. The two photons interact in a C-Sign gate realized using partially polarized beam splitters with horizontal (vertical) polarization trasmittivity T_H(T_V) = 1(1/3) and Hadamard gates. This experimental gate acts transforming $\left| {HH} \right\rangle \to 1{\mathrm{/}}3\left| {VV} \right\rangle$, $\left| {HV} \right\rangle \to 1{\mathrm{/}}3\left| {VH} \right\rangle$, $\left| {VH} \right\rangle \to 1{\mathrm{/}}3\left| {HV} \right\rangle$, $\left| {V\,V} \right\rangle \to - 1{\mathrm{/}}3\left| {HH} \right\rangle$. Upon suitable normalization of the detected coincidence counts, we have the following probabilities p_D = (N_HD + N_VD)/N₀, p_A = (N_HA + N_VA)/N₀ with N₀ = N_HD + N_VD + N_HA + N_VA. These are instrumental to the evaluation of the Shannon entropies. Performing a QST procedure on the signal qubit after the measurement of the meter allows to obtain the experimental version of the $\tilde \rho _\sigma ^k$ density matrix in Eq. (4), giving us direct access to the mutual information from the post-measurement states. Thermodynamic quantities $W_\mu ^{\mathrm {meas}}$ and ΔF _μ could be obtained from the same counts, but these would rather represent informational estimates to which a thermodynamic meaning is attached.

Data availability

Data are available to any reader upon reasonable request.