Demonstration of Einstein–Podolsky–Rosen steering with enhanced subchannel discrimination

Abstract

Einstein–Podolsky–Rosen (EPR) steering describes a quantum nonlocal phenomenon in which one party can nonlocally affect the other’s state through local measurements. It reveals an additional concept of quantum non-locality, which stands between quantum entanglement and Bell nonlocality. Recently, a quantum information task named as subchannel discrimination (SD) provides a necessary and sufficient characterization of EPR steering. The success probability of SD using steerable states is higher than using any unsteerable states, even when they are entangled. However, the detailed construction of such subchannels and the experimental realization of the corresponding task are still technologically challenging. In this work, we designed a feasible collection of subchannels for a quantum channel and experimentally demonstrated the corresponding SD task where the probabilities of correct discrimination are clearly enhanced by exploiting steerable states. Our results provide a concrete example to operationally demonstrate EPR steering and shine a new light on the potential application of EPR steering.

Introduction

In the original discussion of Einstein–Podolsky–Rosen (EPR) paradox,¹ Schrödinger^2,3 described a quantum non-local phenomenon that Alice can steer Bob’s state through her local measurements. Since then, great efforts have been made to understand quantum nonlocality. It was not until 2007, Wiseman, Jones, and Doherty revisited Schrödinger’s discussion and formulated the concepts of quantum non-locality as quantum entanglement, EPR steering, and Bell non-locality in terms of quantum information tasks.^4,5 It is now clear that all steerable states are entangled, but not all steerable states exhibit the Bell non-locality,^4,5 which implies that EPR steering sits between quantum entanglement and Bell non-locality. This hierarchy also holds for all possible positive operator valued measures.⁶ EPR steering has recently drawn plenty of attention.⁷ For example, several theoretical studies including the verification of EPR steering based on steering inequalities⁸ and all-versus-nothing proof,⁹ no-cloning of quantum steering,¹⁰ temporal steering,^{11,12,13,14,15} quantification of steerability,^16,17,18 and one-way EPR steering¹⁹ have been reported as well as the corresponding experiments.^{20,21,22,23,24,25,26} There are also other interesting steering experiments, such as the high-order steering²⁷ and loophole-free steering.^28,29,30 Moreover, the parallel works based on the continuous variable systems^{31,32,33,34,35,36,37,38,39} have been reported.

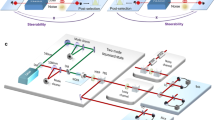
Similar to the necessary and sufficient verification of quantum entanglement with a quantum information task named quantum channel discrimination,⁴⁰ which refers to the task of distinguishing among different quantum operations,^41,42,43 EPR steering can be characterized necessarily and sufficiently based on a quantum task named subchannel discrimination (SD).¹⁷ As an extension of the quantum channel generally representing the physical transformation of information from an initial state to a final state in which the quantum operation is trace-preserving for all input states,⁴⁴ a subchannel is a completely positive operator that does not increase the trace in the density matrix space.¹⁷ A series of subchannels {Λ _h } _h , that constitute a channel Λ satisfying ${\mathrm{\Lambda }} = \mathop {\sum}\nolimits_h {\kern 1pt} {\mathrm{\Lambda }}_h$, can be treated as a decomposition of the channel into its different evolutionary branches with the corresponding probability Tr(Λ _h [ρ]) for any state ρ, as shown in Fig. 1a. Here, ${\mathrm{\Lambda }}_h[\rho ] = K_h\rho K_h^\dagger$, where the Kraus operators K _h are the explicit matrix descriptions of Λ _h and satisfy $\mathop {\sum}\nolimits_h K_h^\dagger K_h = {\mathbb{I}}$. The SD task allows one to distinguish in which subchannel the quantum evolution occurs, whereas this information is lost if the process is described simply in the framework of the quantum channel. Moreover, SD tasks might lead to the emergence of new quantum phenomena and applications in quantum information processing, such as the SD-based quantum key distribution.⁴⁵

Fig. 1

The process of subchannel discrimination (SD). a The collection of subchannels {Λ _h } _h composing a quantum channel Λ. b The protocol for realizing the Kraus operators K _ij using the entanglement-breaking channel (EBC) scenario. The state ρ is measured along the z direction with output result i after passing through the intermediate subchannel A _j . A new state is prepared based on the value of i. c The single-qubit protocol for SD in the case of two measurement settings. The unitary operation U related to the intermediate subchannels A₀ and A₁ is demonstrated with the qubit state ρ and an auxiliary qubit $\left| 0 \right\rangle$ which is finally measured along z with output result j. After the EBC, the measurement along a direction $\vec n$ is performed on the signal qubit, and the result b is obtained. d The two-qubit protocol for SD with multiple measurement settings. One of the two qubits, in a state ρ _AB , is sent to Bob, and the other is sent to Alice. On Bob’s side, the qubit passes through one of the unitary gates g _m with probability 1/m before the evolution K _ij . Alice chooses one of the measurement directions $\vec n_i$ based on the result b|g _m from Bob and obtains the result a

Recently, it has been proven that for any bipartite state, we can verify it is steerable if there exists an SD task in which the successful discrimination probability is enhanced by this state compared with the case employing single-qubit states; otherwise, if no such SD tasks exist, it is unsteerable.¹⁷ Also, such an SD task presents an operational method to characterize EPR steering. However, the detailed construction of such subchannels has not been investigated up to now. In this article, we design a feasible collection of concrete subchannels and experimentally demonstrate EPR steering with the corresponding SD task.

Results

SD task for the two-setting case

First, we would like to introduce the detailed SD task in the simplest case with two measurement settings. In this work, we consider a channel consisting of four subchannels Λ _ij (i, j = 0 or 1), where the corresponding Kraus operators are denoted by K _ij . We exploit an entanglement-breaking channel (EBC)⁴⁶ to limit the bound established in the single-qubit protocol. The Kraus operators K _ij are implemented with the EBC, as illustrated in Fig. 1b, where A _j (j = 0 or 1) is regarded as the intermediate subchannel and satisfies $K_{ij} = \left| i \right\rangle \left\langle i \right| \cdot A_j$ (i, j = 0 or 1) (see Methods). Since the information of i is included in the output ρ _out , the SD task is transformed into the task of distinguishing A _j based on i. To realize {A _j } _j , a unitary operation U is performed on a quantum system consisting of a target qubit in the state ρ and an auxiliary qubit initially in the state $\left| 0 \right\rangle$,⁴⁷ as shown in Fig. 1c. In this work, the operation is represented as follows,

$$U = \left( {\begin{array}{*{20}{l}} {A_0} \hfill & { - A_1} \hfill \\ {A_1} \hfill & {A_0} \hfill \end{array}} \right).$$

(1)

A _j is determined according to the output j measured along the z direction on the auxiliary qubit. The SD task in single-qubit protocol is completed by guessing j according to the output b that is measured along a direction $\vec n$ on the target qubit. Since the target qubit only carries the classical information after the EBC, $\vec n$ is optimized to be z to maximize the success probability $P_\rho ^{\mathrm{s}}$. With the input state ρ, the results of different strategies for guessing j are denoted by $p_\rho ^{c0},p_\rho ^{c1}$ (guessing j is the constant 0 or 1 regardless of b, respectively), $p_\rho ^{00},p_\rho ^{01}$ (guessing j = b or j = b ⊕ 1 where ⊕ represents addition modulo 2, respectively). The success probability is denoted as $P_\rho ^{\mathrm{s}} = {\mathrm{max}}\left\{ {p_\rho ^{c0},p_\rho ^{c1},p_\rho ^{00},p_\rho ^{01}} \right\}$, and the upper-bound probability P^s in the single-qubit case is obtained by optimizing the input state, which implies $P^{\mathrm{s}} = {\mathrm{max}}_\rho \left\{ {P_\rho ^{\mathrm{s}}} \right\}$.

We now consider the two-qubit Werner states ρ _AB ⁴⁸ with the form of,

$$\rho _{AB} = \eta \left| {\mathrm{\Phi }} \right\rangle \left\langle {\mathrm{\Phi }} \right| + (1 - \eta ){\mathbb{I}}{\mathrm{/}}4,$$

(2)

where η ∈ [0,1], $\left| {\mathrm{\Phi }} \right\rangle$ is the maximally entangled state, and ${\mathbb{I}}{\mathrm{/}}4$ is the maximally mixed state. As illustrated in Fig. 1d in the two-setting case (m = 1, and g₁ is identical), the task is that Alice guesses j and announces to Bob based on a which is obtained by measuring along $\vec n_i$ (chosen according to b). Since b ∈ {0, 1}, there are two directions $\vec n_i$ along which Alice can choose to measure. In this work, we follow two rules to design the SD tasks, i.e., (i) the success probability of maximally entangled state is 100%; (ii) the success probability of maximally mixed state is 50%. Thus, the success probability of SD task $P_{\rho _{AB}}$ equals to 1/2 + η/2. In the linear EPR steering inequalities, $C_n^{{\mathrm{LHS}}}$ denotes the bound established by the local hidden state model where n is the number of measurement settings.²⁰ In the case of n = 2, $C_2^{{\mathrm{LHS}}} = \eta _2^ \ast$ where $\eta _2^ \ast = 1{\mathrm{/}}\sqrt 2$ is the visibility bound of the Werner states. When $\eta > \eta _2^ \ast$, $\rho _{\rho _{AB}}$ is steerable. For the single-qubit protocol, by directly calculating, we find $P^{\mathrm{s}} = 1{\mathrm{/}}2 + C_2^{{\mathrm{LHS}}}{\mathrm{/}}2$ (see Section I of the Supplemental Material for details (See the Supplemental Material.)). Thus, if Bob finds $P_{\rho _{AB}} > P^{\mathrm{s}}$, the steerability from Alice to Bob is observed.

SD task for the multi-setting cases

EPR steering from Alice to Bob relates to the number of settings measured by Alice.^4,49 For some predictably steerable states, steering fails because of the very limited number of measurement settings.²⁵ To capture as much information about the states as possible to demonstrate EPR steering, it is necessary for Alice to apply multiple measurement settings to approach the predictions of infinite measurement settings. In this work, we consider the regularly spaced directions which are given by the Platonic solids with the number of measurement settings n corresponding to 2, 3, 4, 6, and 10.²⁰ Compared with the optimal measurement settings introduced in,⁴⁹ here, the two-setting and three-setting measurements are optimal and EPR steering can be affirmed necessarily and sufficiently. For other multi-setting cases, the optimal measurements don’t correspond to the regularly spaced directions and are difficult to realize in experiment. Moreover, the diffence between the results in this work and the predictions of the optimal measurements is very small (see Section I of the Supplemental Material (See the Supplemental Material.)). To experimentally realize such a task, on Bob’s side, the qubit equiprobably evolves through several unitary gates g _m before the Kraus operators K _ij , as illustrated in Fig. 1d, and the details can be found in Section I of the Supplemental Material (See the Supplemental Material.). The corresponding measurement setting based on Bob’s result b|g _m , which denotes that b is obtained under the gate operation g _m , is then implemented on Alice’s side. In fact, for each g _m , the SD process can still be regarded within the framework of two measurement settings. In the single-qubit protocol with n measurement settings, denoting $P_{m,\rho }^{\mathrm{s}}$ for each g _m , the total success probability is obtained as $P_n^s = {\mathrm{max}}_\rho \left\{ {\mathop {\sum}\nolimits_m {\kern 1pt} 1{\mathrm{/}}mP_{\rho ,m}^{\mathrm{s}}} \right\}$. Similarly, for the two-qubit state ρ _AB , $P_{\rho _{{{AB}}},{\kern 1pt} n} = \mathop {\sum}\nolimits_m {\kern 1pt} 1{\mathrm{/}}m{\kern 1pt} P_{\rho _{{{AB}}},m}$. Furthermore, similar with the two-setting case, we have $C_n^{{\mathrm{LHS}}} = \eta _n^ \ast$ and $P_n^{\mathrm{s}} = 1{\mathrm{/}}2 + C_n^{{\mathrm{LHS}}}{\mathrm{/}}2$ (see Section I of the Supplemental Material for details (See the Supplemental Material.)) when the multiple measurement settings are selected based on the Platonic solids.²⁰ As a result, the constructed SD task provides an operational method to characterize the steerability of Werner states. If the success probability of SD is enhanced by using the two-qubit state ρ _AB , i.e., $P_{\rho _{AB}} > P^{\mathrm{s}}$, then ρ _AB is steerable from Alice to Bob regardless of the number of measurement settings; otherwise, under n measurement settings performed by Alice, i.e., $P_{\rho _{{{AB}}},{\kern 1pt} n} \le P_n^{\mathrm{s}}$, Alice fails to steer Bob’s states.

Compared with the two-setting case in which there are four subchannels, the multi-setting cases can be regarded as multi-subchannel discrimination tasks where more subchannels consisting of gates g _m and the corresponding Kraus operators K _ij are required, and the reconstructed subchannels could be expressed as $K_{ijm}^\prime = K_{ij} \cdot g_m$. Following the similar method designing subchannels for Werner states, we can also create the corresponding subchannels for other types of two-qubit states, like the Bell diagonal states (see Section I of the Supplemental Material (See the Supplemental Material.)).

Experimental setup

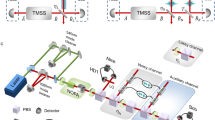
The unitary operation U shown in Fig. 1c can be decomposed into several parts, including two control-not (CNOT) gates (C_NOT1 and C_NOT2) and the other unitary evolutions E, V₁, V₂, and V₃, and implemented in an optical Sagnac-like interferometer (SLI), as illustrated in Fig. 2 (see Methods). And U could be expressed as

$$U = \left( {{\mathbb{I}}_C \otimes V_3} \right) \cdot C_{{\mathrm{NOT2}}} \cdot \left( {{\mathbb{I}}_C \otimes V_2} \right) \cdot C_{{\mathrm{NOT1}}} \cdot \left( {E \otimes V_1} \right),$$

(3)

where ${\mathbb {I}}_C$ is the identical operation on the control qubit. To obtain the bound P^s and verify the setup, the single-qubit protocol is performed with the input state denoted as $\rho (\theta ) = {\mathrm{cos}}{\kern 1pt} \theta \left| {\mathrm{H}} \right\rangle + {\mathrm{sin}}{\kern 1pt} \theta \left| {\mathrm{V}} \right\rangle$ where $\left| {\mathrm{H}} \right\rangle$ and $\left| {\mathrm{V}} \right\rangle$ represent the horizonal and vertical polarizations of the photons, respectively. For the two-qubit protocol, Werner states are prepared via the spontaneous parametric down conversion process by pumping the nonlinear crystal of periodically poled KTiOPO₄ (PPKTP) which is placed in a polarization Sagnac interferometer.⁵⁰ Here, $\left| {\mathrm{\Phi }} \right\rangle$ is prepared to be $\left( {\left| {\mathrm{HH}} \right\rangle + \left| {\mathrm{VV}} \right\rangle } \right){\mathrm{/}}\sqrt 2$. The experimental Werner states ρ _AB are prepared with an average fidelity of 98.3 ± 0.2%. The detailed experimental preparation can be found in Methods.

Fig. 2

Logic circuit and experimental setup. a The logic circuit for implementing U. b The integrated experimental setup. One photon is sent to Bob, and the other is sent to Alice. On Bob’s side, each one of the gates g _m before the Sagnac-like interferometer (SLI) is realized using a combination of a quarter-wave plate (QWP), a half-wave plate (HWP) and a QWP; the photons are measured along the z direction using an HWP and a polarized beam splitter (PBS). On Alice’s side, in the single-qubit protocol, the photons are detected directly to provide a coincidence signal. While, in the two-qubit protocol, Alice measures her photons along a direction $\vec n_i$ that is chosen based on the result b|g _m received from Bob. The photons on both sides are detected by single-photon detectors (SPD). Finally, Alice’s measurement result is sent to coincidence units, unit0 and unit1, to coincide with the corresponding results from port₀ and port₁, respectively. c The unit used to prepare the investigated entangled states. The polarization Sagnac interferometer is used to prepare the maximally entangled state $\left| {\mathrm{\Phi }} \right\rangle$ to be fed into the dual-wavelength PBS and HWP, i.e., HWP2. An additional unit M, in which the dashed gray part inserted with a long enough birefringent crystal (BC) assists in preparing the maximally mixed component ${\mathbb {I}}{\mathrm{/}}4$, is placed at the port to Alice to produce the mixed state ρ _AB . Two moveable shutters are used to adjust the parameter η. BS beam splitter, DM dichroic mirror. d Experimental realization of U with the SLI constructed from a homemade beam splitter, with half of it coated as a PBS and the other half coated as a non-polarized beam splitter (NBS)

Experimental results

In the case of two measurement settings, the results $p_\rho ^{c0},p_\rho ^{c1},p_\rho ^{00}$ and $p_\rho ^{01}$ are presented in Fig. 3a which show that the input states ρ(θ) should be optimized to obtain the upper-bound value P^s. More results in the single-qubit protocol with multiple measurement settings are presented in Section III of the Supplemental Material (See the Supplemental Material.). The Werner state ρ _AB is identified to be steerable when the SD performance is enhanced with $P_{\rho _{AB}} > P^s$, see Fig. 3b, c. By contrast, when $P_{\rho _{AB},{\kern 1pt} n} \le P_n^s$ (n = 2, 3, 4, 6, 10), Alice fails to steer Bob’s state via the corresponding SD task. As the number of measurement settings increases, the bound established for the single-qubit approach decreases, whereas the success probability achieved by employing steerable resources remains constant, as illustrated in Fig. 3d. All error bars in this work are estimated as the standard deviation from the statistical variation of the photon counts, which is assumed to follow a Poisson distribution. As the error bars on the experimental probabilities are very small, roughly 0.002, they are not shown in the figures.

Fig. 3

Experimental results for the SD task. a The probabilities of successful discrimination with single-qubit states in the case of two measurement settings. The curves and symbols represent the theoretical predictions and experimental results, respectively. b,c The experimental results in the two-qubit protocol with two and six measurement settings, respectively. The blue lines represent the theoretical predictions. The pink and green dots in b and c represent the corresponding experimental results, with the pink and green solid lines representing the single-qubit upper bounds for two and six measurement settings, respectively. The black dashed lines represent the single-qubit upper bound for the infinite number of measurement settings. d The comparison of the single-qubit upper bounds P^s with the results $P_{\rho _{{AB}}}$ obtained using the prepared maximally entangled state (blue dots) for different number of measurement settings. The success probabilities $P_{\rho _{{AB}}}$ are lower than the theoretical predictions, which can be primarily attributed to imperfect experimental manipulation. The brown squares represent the theoretical predictions of the upper bound for single-qubit states, whereas the experimental results are represented by the purple triangles. The bound P^s established for the single-qubit approach decreases, and it is very close to the value with infinite measurement settings when the number of measurement setting is equal to ten. The experimental error bars which are very small and not shown are estimated as the standard deviation

Moreover, by means of the SD task, the difference between EPR steering and entanglement can be characterized in an operational way. It is found that the success probability achieved using unsteerable Werner states ρ _AB cannot surpass the single-qubit bound when $\eta \le \eta _{10}^ \ast \approx 0.524$ in the case of ten measurement settings.²⁰ However, ρ _AB is still entangled when η > 1/3. This implies that the success probability of SD cannot be enhanced by using unsteerable entangled states, which is experimentally verified by the two pink dots in Fig. 4a. The concurrences of these two pink dots are measured to be 0.154 ± 0.008 and 0.223 ± 0.009, which verify that the states are entangled.⁵¹ We further investigate EPR steering with Bell-local states. Theoretically, the Bell inequality will be violated when $\eta > 1{\mathrm{/}}\sqrt 2$,⁴⁸ and according to ref. ⁵², ρ _AB is a Bell-local state when η ≤ 0.683. We measure the Bell-CHSH parameter S⁵³ which is shown as the function of $P_{\rho _{{AB}}}$ in Fig. 4b. The success probabilities of SD using three Bell-local states which are represented by the dark red dots in Fig. 4 are enhanced, and therefore, these states are steerable.

Fig. 4

Experimental results of investigating different kinds of correlations via the SD task. a The probabilities of successful discrimination for the case of ten measurement settings. The colored dots represent the experimental results, and the blue line represents the theoretical prediction. The dark red solid line and black dashed lines represent the upper bounds in the case of the single-qubit protocol for ten and infinite measurement settings, respectively. b The experimental results for the Bell-CHSH parameter S as a function of the success probability of SD, $P_{\rho _{{AB}}}$, in the case of ten measurement settings. The colored dots represent the experimental results. The green solid line represents the upper bound of local-hidden-variable model. The dark red dashed line represents the single-qubit upper bound. The experimental error bars which are very small and not shown are estimated as the standard deviation

Discussion

Based on the proof of the necessary and sufficient characterization of EPR steering, we designed and experimentally implemented an SD task to demonstrate EPR steering using two-qubit Werner states. The methods for decomposing a quantum evolution into sub-channels can be helpful for gaining a thorough understanding of complex open-system dynamics. The enhanced probabilities of successful discrimination achieved using EPR steering provides a concrete example of the application. Moreover, this practical task offers an intuitive means of operationally distinguishing the different concepts of quantum nonlocality.

Compared with the previous experiments using steering inequalities to investigate EPR steering, in which Bob measures along several directions when steered by Alice,^20,25 our work exhibits a particular feature that the measurement performed on Bob’s qubit is restricted to a single direction, which is z in this work. This feature implies that the SD task offers a convenient approach for identifying EPR steering. Another character of the SD task is the measurement sequence of Alice and Bob. In the previous works,^4,21 considering that Alice steers Bob, Bob performs the measurements after receiving the measurement results from Alice. However, in the SD task, the sequence is reversed, which means Alice begins to measure her qubit after Bob’s measurements.

As EPR steering can be regarded as the one-side device-independent quantum information task,⁴⁵ the steering-enhanced SD task, where Bob trusts his experimental device while Alice’s side is device-independent, shows the potential application in one-side device-independent quantum key distribution. Furthermore, in our work, the SD task on Bob’s side is implemented based on the one-way classical communication (from Bob to Alice). Considering the situation that Bell non-locality relates to the two-side device-independent quantum information task,^5,45 one might extend the SD task demonstrating EPR steering to investigate the Bell non-locality. For instance, a similar quantum information task referring to a bipartite SD problem (SD tasks on both sides) with two-way classical communications, which relates to the communication complexity problem,^54,55 might be used to characterize Bell non-locality in an operational way.

Methods

The detailed expressions of A _j and K _ij in the two-setting case

Following the theoretical method to determine A _j which is introduced in Section I of the Supplemental Material in detail (See the Supplemental Material.), we can obtain the expressions of A₀, A₁ in the two-setting case as below

$$A_0 = \left( {\begin{array}{*{20}{c}} {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} & {\frac{{{\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}{{\sqrt 2 }}} \\ {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} & { - \frac{{{\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}{{\sqrt 2 }}} \end{array}} \right),A_1 = \left( {\begin{array}{*{20}{c}} {\frac{{{\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}{{\sqrt 2 }}} & { - \frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} \\ {\frac{{{\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}{{\sqrt 2 }}} & {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} \end{array}} \right).$$

(4)

Considering the Kraus operators K _ij which satisfy $K_{ij} = \left| i \right\rangle \left| i \right\rangle \cdot A_j$ (i, j = 0 or 1), we can get

$$\begin{array}{l}K_{00} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} & {\frac{{{\mathrm{sin}}\frac{\pi }{8}}}{{\sqrt 2 }}} \\ 0 & 0 \end{array}} \right),\quad K_{01} = \left( {\begin{array}{*{20}{c}} {\frac{{{\mathrm{sin}}\frac{\pi }{8}}}{{\sqrt 2 }}} & { - \frac{1}{{4{\kern 1pt} {\mathrm{sin}}\frac{\pi }{8}}}} \\ 0 & 0 \end{array}} \right),\\ K_{10} = \left( {\begin{array}{*{20}{c}} 0 & 0 \\ {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}{\kern 1pt} \frac{\pi }{8}}}} & { - \frac{{{\mathrm{sin}}\frac{\pi }{8}}}{{\sqrt 2 }}} \end{array}} \right),K_{11} = \left( {\begin{array}{*{20}{c}} 0 & 0 \\ {\frac{{{\mathrm{sin}}\frac{\pi }{8}}}{{\sqrt 2 }}} & {\frac{1}{{4{\kern 1pt} {\mathrm{sin}}\frac{\pi }{8}}}} \end{array}} \right).\end{array}$$

(5)

For multi-setting cases, the corresponding expressions of A _j and K _ij can be obtained using the similar method which is shown in Section I of the Supplemental Material (See the Supplemental Material.).

Experimental implementation of the unitary operation U

We construct an inherently stable optical interferometer, namely, a Sagnac-like interferometer (SLI), to realize this operation U (see Fig. 2b). The path and polarization degree of freedom of the photons are used as the auxiliary qubit, which is initially in the state $\left| 0 \right\rangle$, and the probe qubit, respectively. A homemade beam splitter, of which one half is coated as a PBS and the other half is coated as a non-polarized beam splitter (NBS), acts as the input-output coupling element of the interferometer. Each single-qubit gate evolution of the probe qubit (the polarization of photons), i.e., V₁,V₂, and V₃, is realized through a combination of two HWPs. The operation E on the auxiliary qubit is realized by adjusting the ratio of the numbers of photons on the $\left| 0 \right\rangle$ and $\left| 1 \right\rangle$ paths, which is achieved by means of a continuously variable neutral density filter (CVF) crossing both paths. For the first CNOT gate, the path qubit is the control qubit, while the polarization is used as the target qubit. Thus, the polarization of photons on the $\left| 0 \right\rangle$ path remains the same, whereas the polarization on the $\left| 1 \right\rangle$ path reverses, meaning that the polarization $\left| {\mathrm{H}} \right\rangle$ is flipped to $\left| {\mathrm{V}} \right\rangle$ and $\left| {\mathrm{V}} \right\rangle$ is flipped to $\left| {\mathrm{H}} \right\rangle$. This process is realized by placing one HWP on each of the two paths; HWP0, located on the $\left| 0 \right\rangle$ path, is set at 0° for phase compensation, while HWP1 is set at 45° to reverse the polarizations of $\left| H \right\rangle$ and $\left| V \right\rangle$. The second CNOT gate is the inverse of the first CNOT gate; the polarization is treated as the control qubit affecting the target qubit, which is the qubit related to the path information. This gate is implemented in the PBS part of the homemade beam splitter. In detail, the $\left| {\mathrm{H}} \right\rangle$ polarization remains unchanged (retaining the same path information), while the $\left| {\mathrm{V}} \right\rangle$ polarization flips to the other path. The imperfect optical elements, especially the homemade beam splitter, would reduce the visibility of the interferometer and introduce system errors.

To realize {g _m } in the multi-setting cases, several wave plates including HWPs and quarter-wave plates (QWPs) are employed. This part is explained in detail in Section II of the Supplemental Material (See the Supplemental Material.).

Preparation of the experimental states

To obtain the single-qubit upper bound and verify the setup, we perform the SD task using the following single-qubit state ρ(θ),

$$\rho (\theta ) = {\mathrm{cos}}{\kern 1pt} \theta \left| {\mathrm{H}} \right\rangle + {\mathrm{sin}}{\kern 1pt} \theta \left| {\mathrm{V}} \right\rangle .$$

(6)

In this case, the photons on Bob’s side are prepared as the state expressed in Eq. (6), and the photons on Alice’s side are detected directly to provide coincidence signals. ρ(θ) are simply prepared with a half-wave plate (HWP) set at the angel θ/2 following a polarized beam splitter (PBS). The upper bound is then $P^{\mathrm{s}} = {\mathrm{max}}_{\rho (\theta )}\left\{ {P_{\rho (\theta )}^{\mathrm{s}}} \right\}$.

The investigated ρ _AB states are manufactured by combining the maximally entangled state $\left| \Phi \right\rangle$ and the maximally mixed state ${\mathbb{I}}{\mathrm{/}}4$. $\left| \Phi \right\rangle$ is prepared via the spontaneous parametric down conversion process where a χ⁽²⁾ nonlinear crystal of periodically poled KTiOPO₄ (PPKTP) is pumped by an ultraviolet laser with a peak wavelength of 404.1 nm and a spectrum width of 0.05 nm. The crystal is placed in a polarization Sagnac interferometer,⁵⁰ as illustrated in Fig. 2c. The dichroic mirror (DM) is designed to exhibit high transmission at 404 nm and high reflection at 808 nm. A dual-wavelength polarization beam splitter (PBS) is employed as the input-output coupling element of the Sagnac interferometer, and a dual-wavelength HWP set at 45° is used to change the vertically polarized component of the ultraviolate photon to the horizonal polarization to pump the PPKTP crystal. The crystal is placed in a thermoelectric oven with the temperature set at 28.5 ± 0.1 °C. The maximally entangled state $\left| {\mathrm{\Phi }} \right\rangle$ is prepared with a brightness of ~18,000 pairs s⁻¹ mW⁻¹, which is filtered using 3 nm bandwidth filters, and the state fidelity is 95.5 ± 0.4%. As shown in Fig. 2c, a part of the input of unit M still remains as the maximally entangled state $\left| {\mathrm{\Phi }} \right\rangle \left\langle {\mathrm{\Phi }} \right|$, and the other part is used to prepare the maximally mixed state ${\mathbb{I}}{\mathrm{/}}4$ with the dashed gray part in unit M. Two HWPs are set at 22.5° and a birefringent calcite crystal (BC) of 10 mm in length is employed to induce decoherence between the horizonal and vertical polarizations of the photons. The shutters are used to adjust the ratio between $\left| {\mathrm{\Phi }} \right\rangle \left\langle {\mathrm{\Phi }} \right|$ and ${\mathbb{I}}{\mathrm{/}}4$ to control the parameter η.

Data availability

All relevant data and program codes are available from the corresponding author upon the reasonable request.