Introduction

The wearable electronics industry is growing with many promising applications in health and performance monitoring. The’holy grail’ of wearable devices is long-term, continuous monitoring using the human body as a constant supply of energy to achieve self-powered operation or significantly extend the battery lifetime. To deliver a comprehensive understanding of the human condition, such devices can include multiple sensors monitoring different biomarkers and stressors in the environment. Long-term monitoring can significantly improve management of chronic diseases such as asthma and diabetes, and increase patients’ quality of life. The technology is of interest for other medical applications such as chronic pain management, geriatric care, and postoperative out-patient treatment. Without energy harvesting, these applications would require frequent charging of their batteries forcing users to remove their devices periodically. At best, this results in missed measurement opportunities, and at worst, it can cause noncompliance.

Thermoelectric generators (TEGs) that convert body heat to electrical energy provide a promising route to realizing self-powered wearable electronics as discussed in several review articles1,2,3. A TEG consists of a series of p-type and n-type semiconductor elements (so called ’legs’) that are electrically in series but thermally in parallel. When a TEG is placed on the human body, heat flows through the TEG and results in a temperature differential between the skin and the ambient. The temperature differential across the TEG produces a voltage, which can be applied to an external load. A standard TEG is a rigid device that sandwiches the thermoelectric elements between two rigid, electrically insulating but thermally conductive substrates (e.g., AlN). For wearable electronics, flexible, large area TEGs that conform to the human body are of interest. In recent years, a variety of approaches have been considered to realize flexible TEGs. These studies have focused on new flexible materials as well as conventional materials used in a variety of different architectures4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23. Unfortunately, many of these devices failed to match the performance of rigid TEGs either due to the lower quality of their thermoelectric materials or parasitic thermal and electrical resistances introduced by their device architectures.

This laboratory recently proposed an alternative flexible TEG manufacturing approach, which relied on the same rigid legs used in commercial TEGs24,25. The approach eliminated the need to develop new flexible thermoelectric materials allowing the flexible TEGs to employ the best available thermoelectric materials that have been perfected after decades of research. In this approach, the rigid legs are connected electrically in series using liquid metal interconnects embedded in a stretchable silicone elastomer. The liquid metal is a eutectic alloy of gallium and indium (referred to as EGaIn), composed of 75.5% Ga and 24.5% In26. Due to its water-like viscosity, EGaIn provides ultimate stretchability with negligible vapor pressure, and low toxicity. EGaIn is also easy to pattern using a variety of approaches including screen printing, spray coating through a stencil27 and 3D printing28. Due to its metallic electrical resistivity (2.94 μΩ.cm)29, the contribution of the EGaIn interconnects to the total TEG resistance is negligibly small. This is critically important for TEGs because the output power is inversely proportional to the device resistance. There is no other flexible interconnect material that can provide similar flexibility and device performance.

In a rigid TEG, the volume between the legs is typically filled with air, which has a very low thermal conductivity around 0.026 Wm−1 K−1 at room temperature30. This ensures that the majority of the heat flows through the thermoelectric legs, maximizing the temperature differential across the TEG and the output voltage it produces. In a flexible device, the same volume is typically filled with a flexible material, with 6–8× higher thermal conductivity than that of air31, providing an alternative path to heat flow. The impact of the filler material on heat leakage and TEG performance is the main focus of this paper. We present a stretchable aerogel–polydimethylsiloxane (PDMS) composite that leverages the insulating properties of a silica aerogel. Aerogels, with thermal conductivities as low as 0.018 Wm−1 K−1 32, are porous materials with ultra-low densities. While a typical aerogel is 99.8% air, its thermal conductivity can be lower than that of air due to the Knudsen effect33. Despite the fact that silica aerogel is a rigid and brittle material34, the composite is flexible and easily castable. In this paper, we demonstrate that aerogel inclusions in PDMS can reduce the thermal conductivity of the material by as much as 50% without a prohibitive increase in its stiffness. It is shown that the new composite effectively suppresses the heat leakage between the thermoelectric legs enabling power density levels approaching 35 μWcm−2 on the human wrist during walking.

Results and discussion

Impact of filler thermal conductivity on device performance

Figure 1(a) shows the cross-sectional view of a flexible TEG with EGaIn interconnects illustrating the heat leaking through the filler elastomer surrounding the legs. The thermal conductivity of the filler material as well as the device fill factor (i.e., the percentage of the total device area occupied by the legs) determine the amount of heat flowing through the filler around the legs. This leakage reduces the net heat flow through the legs and consequently, the temperature differential, ∆T that develops across them. Since the thermal conductivity of a typical elastomer is 6–8× higher than that of air, the effect can have a substantial impact on device performance.

Fig. 1: Heat leakage through the flexible filler and its impact on the temperature differential across the thermoelectric legs.
figure 1

a Cross-sectional microscope image of a flexible TEG with liquid metal interconnects. b A simple three-resistor thermal equivalent circuit of a TEG. c Cross-sections parallel and orthogonal to the interconnects illustrating simulated heat flow lines through the thermoelectric legs and the surrounding elastomer with three different thermal conductivities of (i) 0.15, (ii) 0.08, and (iii) 0.025 Wm−1 K−1. d Simulated temperature differential plotted as a function of module fill factor and elastomer thermal conductivity.

Full size image

The impact of the filler thermal resistance on ∆T can be explained by considering the simple three-resistor model shown in 1(b). In this model, the thermal resistance of the TEG, RTEG is in series with two parasitic resistances, Rbody on the body side and Rconvon the ambient side. Rbody embodies all parasitic thermal resistances on the hot side, including the contact resistance between the TEG and the heat source (e.g., human body). Rconv is mainly determined by convective cooling on the ambient side of the device. This simple model ignores the impact of Peltier heating/cooling as well as Joule heating, which are both second-order effects35. The temperature differential across the TEG can then be expressed as

$${{\Delta }}T = \left( {T_{{\mathrm{body}}} - T_{{\mathrm{amb}}}} \right)\frac{{R_{{\mathrm{TEG}}}}}{{R_{{\mathrm{body}}} + R_{{\mathrm{TEG}}} + R_{{\mathrm{conv}}}}}$$
(1)

where Tamb and Tbody are the ambient and body temperatures, respectively. The resulting open-circuit voltage, Voc is given by

$$V_{{\mathrm{oc}}} = - S{{\Delta }}T$$
(2)

where S is the average Seebeck coefficient of the thermoelectric materials used in the device. Therefore, to maximize the temperature differential, RTEG should be as large as possible relative to the total resistance in the denominator of Eq. 1. If all the available heat is flowing through the legs, RTEG is determined by the physical dimensions of the legs and the thermal conductivity of the material they are made of. With heat leaking through the elastomer, RTEG is effectively in parallel with the thermal resistance of the surrounding elastomer, resulting in a smaller TEG equivalent resistance, which causes ΔT to decrease35.

Three-dimensional thermal simulations were carried out in COMSOL MultiphysicsT M. Figure 1(c) shows the simulated heat flow lines through a single leg and the filler material around it. The simulation results are shown for two different orientations of the leg, parallel, and orthogonal to the electrical interconnects. We performed the simulations using three different filler thermal conductivities of (i) 0.15 Wm−1 K−1 (PDMS)31, (ii) 0.08 Wm−1 K−1, and (iii) 0.026 Wm−1 K−1 (air). The simulated device structure had 25 thermoelectric legs connected in series. The interconnect material was EGaIn, with a thermal conductivity of 25 Wm−1 K−136. The interconnects were encapsulated by a high thermal conductivity elastomer with a thermal conductivity of 1 Wm−1 K−1. The remaining simulation parameters, which closely match those of fabricated TEGs are tabulated Fig. 1(d). The flow lines indicate the direction as well as the magnitude of the heat flow. A higher concentration of lines in a specific location is indicative of a larger flux. As expected, heat leakage through the filler increases progressively with filler thermal conductivity.

With air between the legs, heat leakage around the legs is negligibly small. The simulations also demonstrate the heat spreading aspect of the EGaIn interconnects, which effectively increases the area for heat collection and rejection. Figure 1(e) shows the simulated ∆T across a 25-leg module as a function of the thermal conductivity of the filler material and the fill factor. The filler thermal conductivity values range from 0.02 to 0.15 Wm−1 K−1 (PDMS)31. The plot suggests that ΔT increases with decreasing filler thermal conductivity and increasing fill factor. We note that as the fill factor increases, the surface areas available for heat collection and heat rejection shrink resulting in larger external thermal resistances of Rconvand Rbody causing ΔT to drop. Not surprisingly, this effect is more prominent at lower filler thermal conductivities due to reduced heat leakage through the elastomer. The simulation results suggest that by optimizing the fill factor and the thermal conductivity of the filler material, more than 2× improvement in ΔT can be expected, which translates into a similar increase in the generated voltage according to Eq. 2. Since the output power scales with the square of the output voltage, the improvement observed in Fig. 1(e) is significant. This conclusion was the driving force for the effort presented in this paper.

Aerogel–silicone composite

In this work, we have considered the use of aerogel particles mixed in PDMS to produce a low thermal conductivity aerogel–silicone composite suitable as a filler material in flexible TEGs. The composite was formed by mixing aerogel particles in uncured PDMS. Figure 2(a) shows the cross-sectional optical microscope image of a typical composite. We can see that the sample is free of air bubbles and that the aerogel particles are uniformly distributed throughout the pictured area.

Fig. 2: Aerogel–silicone composite and its thermal conductivity.
figure 2

a A cross-sectional optical microscope image of the aerogel–silicone composite. b Thermal conductivity measurement system. c Thermal conductivity of the composite for two different aerogel particle sizes of 2–40 and 100–700 μm plotted as a function of the aerogel volume fraction. d A cross-sectional scanning electron microscope image of the aerogel–silicone interface.

Full size image

The thermal conductivity of the aerogel–silicone composite was measured using the so called absolute method in a system optimized for soft materials with thermal conductivity values less than 1 Wm−1 K−1. Figure 2(b) shows a simplified schematic of the measurement system. The tool consists of two parallel heat flow channels referred to as’measurement’ and’reference’ channels. The sample to be measured is sandwiched between two stainless-steel pillars in the measurement channel. Four thermocouples embedded in each pillar provide the temperature distribution along them. The temperature distribution is then used to determine the net heat conducting through the channel and the temperature differential that develops across the sample. The reference channel is identical to the measurement channel and holds a duplicate sample. The sole purpose of the reference channel is to eliminate heat leakage through the thermocouple wires. The wires from the eight thermocouples embedded in the pillars of the measurement channel are fed through small holes in the pillars of the reference channel. Since the two channels are thermally identical, both have the same temperature distribution, which eliminates any temperature drop across the thermocouple wires and heat conduction through them. The entire apparatus is installed in a vacuum chamber to eliminate convective heat losses.

Figure 2(c) shows the measured thermal conductivity of the composite as a function of the aerogel volume fraction. The change in thermal conductivity is shown for two different sized aerogel particles of 2–40 and 100–700 μm. As expected, the thermal conductivity decreases with increasing aerogel fraction for both aerogel particle sizes. With larger aerogel particles, the thermal conductivity decreases with increasing aerogel fraction in a linear fashion. It is significant that the reduction in thermal conductivity can be as high as 50% with the largest aerogel concentration used in this study. As illustrated in Fig. 1(c), such a drop in thermal conductivity can have a significant impact on the heat leaking through the elastomer and the ∆T across the device. It is interesting to note that with smaller particles, a considerable drop in thermal conductivity is observed only above an aerogel volume fraction of 40%.

To explore possible silicone diffusion into the aerogel particles, a sample was prepared by curing PDMS on a solid cylindrical aerogel piece with a diameter of 1 cm. After curing, the portion of the aerogel with no PDMS penetration was physically removed and the sample was sliced for cross-sectional SEM. The resulting SEM image is shown in Fig. 2(d). Unfortunately, the image does not reveal a clear PDMS-aerogel interface, which would have allowed an accurate measurement of the elastomer penetration into the solid aerogel. However, it appears that about 50 μm of aerogel remained intact on the elastomer, which suggests that some PDMS penetration has occurred. Even if we assume that the actual penetration is one tenth of this interface (i.e., 5 μm), we can calculate that the volume of an aerogel particle with a diameter of 30 μm would reduce to ~30% of its original volume. Since the size of the smaller particles is within 2–40 μm, the smaller particles would be completely absorbed in the elastomer. Therefore, we believe that PDMS penetration into the smaller aerogel particles can have a significant impact on the thermal conductivity of the composite. For larger aerogel particles, this volume reduction is negligibly small.

In flexible manufacturing, the viscosity of the uncured elastomer is an important parameter. In this particular application, the silicone needs to flow relatively easily to fill the volume between the legs. To study the impact of aerogel volume fraction on viscosity, rheological measurements were conducted. The measurements were conducted with an AR-G2 magnetic bearing rheometer (TA Instruments, USA), using a 20 mm diameter 2 cone and plate geometry. All tests were conducted under ambient conditions. In this experiment, a frequency sweep from 0.1 to 100 rad.s−1 at 2% strain was used to observe the elastic (G’)and viscous (G”) moduli. In addition, a flow sweep from 0.01 to 100 s−1, and then back to 0.01 was used to determine the shear rate dependent viscosity of the material. The reported viscosity values come from the up and down-sweep of the trials (i.e., the progression from low shear to high shear and the return from high shear to low shear).

Figure 3(a) shows the measured viscosity of the samples plotted as a function of the shear rate. We can see that both size and volume fraction of the aerogel particles can impact the composite’s viscosity. For the smaller, 2–40 μm particles, viscosity increases with the volume fraction, but it remains nearly independent of the shear rate; which implies Newtonian behavior. On the other hand, for the larger, 100–700 μm particles, the composite undergoes shear thinning (i.e., the viscosity decreases with shear rate). In this work, we have determined that the aerogel volume fraction has to be less than 50% to ensure reliable filling of the volume between the legs.

Fig. 3: Mechanical properties of uncured and cured aerogel–silicone composites.
figure 3

a Viscosity of the uncured elastomer. b Young’s modulus of the composite plotted against the aerogel volume fraction for two different aerogel particle sizes. c Percent elongation at break plotted as a function of the aerogel volume fraction. d Tensile strength of the composite plotted against aerogel volume fraction. Error bars indicate standard deviations.

Full size image

A NEXTECH DFS force gauge mounted on a NEXTECH MTS1 screw test stand was used to measure the mechanical properties of the aerogel–silicone composites including Young’s Modulus, elongation at break and tensile strength. The samples were rectangular in shape and were uniform in dimensions. The applied force was measured as a function of elongation for each sample up to the break point. The instrument has a safe operating range up to 50 N of applied force.

Figure 3(b) shows the Young’s modulus for cured composites with different aerogel volume fractions. The modulus measured for pure PDMS agrees with previously reported values37. As shown, the modulus is linearly increasing with the aerogel fraction for both small and large aerogel particle sizes. Nevertheless, even at a volume fraction of 50%, the composite remained reasonably flexible. It is also interesting to note that Young’s modulus measured for both large and small aerogel particle inclusions were similar at similar volume fractions. The general trend observed here agrees with previous reports that show a corresponding increase in Young’s modulus as a result of adding particulate matter38,39,40.

Figure 3(c) shows the percent elongation at break point as a function of the aerogel volume fraction. The plot only includes the data for samples prepared with large aerogel particles because the samples prepared with small aerogel particles did not approach fracture within the limits of our tool. The error bars represent 20% variation in the measured strain of three different samples with the same aerogel concentration. As anticipated, the maximum strain the sample can withstand decreases with increasing aerogel volume fraction. Nevertheless, the samples remain quite stretchable even at the largest aerogel concentration of 30%. At this concentration, the samples can withstand more than 40% strain, certainly beyond what is needed for a wearable TEG.

Figure 3(d) shows the tensile strength of the same samples as a function of the aerogel fraction. Again, we observe a small decrease in tensile strength of the composite as the aerogel volume fraction increases, which might be attributed to increased defect density at the interfaces between the aerogel particles and PDMS. The stresses for cavitation and debonding, two distinct failure phenomena, in an elastomer containing rigid inclusions (similar to our aerogel particles) was found to have an inverse dependence on particle diameter41.

Flexible TEGs with aerogel–silicone composite fillers

Figure 4(a) shows a cross-sectional view of a flexible TEG illustrating its four key components: (a) rigid p- and n-type thermoelectric legs, (b) EGaIn interconnects, (c) EGaIn encapsulation, and (d) the aerogel–silicone composite filler. The legs are connected in series via EGaIn liquid metal interconnects, which provide excellent stretchability as well as negligibly small interconnect resistance. The EGaIn interconnects are encapsulated by a high thermal conductivity elastomer, previously reported by this laboratory40,42. The elastomer not only enhances the mechanical integrity of the device without compromising the device performance by adding a large parasitic thermal resistance but it also acts as a heat spreader between the EGaIn interconnects. The rigid legs are surrounded by the aerogel–silicone composite, which secures them in place. Figure 4(b) shows the picture of a 64-leg TEG taken as it is flexed between two fingers. The high thermal conductivity elastomer encapsulating the EGaIn interconnects appears black due to graphene inclusion in the elastomer. The module was fabricated using smaller, 20–40 μm aerogel particles in order to be able to visualize the legs through the elastomer in these cross-sectional images. With smaller aerogel particles, the resulting elastomer is still somewhat hazy but still not as translucent as the elastomer shown in Fig. 2(a). A detailed description of the flexible TEG fabrication is provided in the Methods section.

Fig. 4: Flexible TEG.
figure 4

a Illustration highlighting the three key components of a flexible module including the EGaIn liquid metal interconnects, high thermal conductivity EGaIn encapsulation elastomer and low thermal conductivity aerogel–silicone filler. b A typical module flexed between two fingers.

Full size image

The preliminary electrical characterization of the flexible TEGs was carried out on a hot-plate. We measured the open-circuit voltage, Voc at different air velocities ranging from zero (natural convection) to 1.2 ms−1 (equivalent to walking speed) measured directly above the devices. An electric fan was used to produce lateral air flow. To achieve repeatable measurements, the 3-D printed wind tunnel shown in Fig. 5(a) was used. Each measurement was performed for approximately 5 min after placing the TEG on the hot-plate to provide sufficient time for the device to reach thermal equilibrium. Figure 5(b) shows the TEG open-circuit voltage, Voc as a function of the hot-plate temperature for a typical 64-leg flexible TEG. The ambient temperature, Tamb was 21.5 °C during the measurements. The plot clearly shows that, Voc is increasing linearly with the hot-plate temperature in all three cases. Since the ambient temperature is constant, this linear dependence is to be expected according to Eqs. 1 and 2. The slope of the line is determined by S and the magnitude of RTEG relative to the total thermal resistance. We can also see that the slope of the line is dependent on the air velocity. With no air flow, Rconv is determined by the heat transfer coefficient of the surface under natural convection. With air flow (i.e., forced convection), Rconv decreases, increasing the relative magnitude of RTEG. On the other hand, while the slope increases abruptly with 0.7 ms−1 of air flow, limited Voc improvement is gained by increasing the air velocity to 1.2 ms−1. This suggests that the heat transfer coefficient of the surface saturates above a certain air velocity, which was anticipated. In a previous publication from this laboratory, which focused on designing TEGs for wearable devices, we calculated the heat transfer coefficient of a heatsink surface at different air velocities as a function of the thermal conductivity of the material. It was shown that regardless of the thermal conductivity of the material, the heat transfer coefficient increased with air velocity saturating above 1 ms (typical walking speeds)43. Figure 6 shows the open-circuit voltage and power density of flexible TEGs fabricated using four different fill factors of 5, 7, 13, and 20%. The highest fill factor used in these devices was determined by the resolution of the sprayed EGaIn lines, which can be further improved by using a better stencil material and optimizing the separation between the stencil and the substrate. To study the impact of the filler thermal conductivity on device performance, we fabricated devices using three different filler materials of (i) pure PDMS with κ = 0.15 Wm−1 K−1; (ii) Aerogel–silicone composite with κ = 0.12 Wm−1 K−1, and (iii) Aerogel–silicone composite with κ = 0.08 Wm−1 K−1. In agreement with the simulation results, Fig. 6 reveals that the measured Voc consistently increases with decreasing filler thermal conductivity. On the other hand, the impact of fill factor on Voc appears to be negligibly small regardless of the filler thermal conductivity. We note that while a device with a smaller fill factor suffers from higher heat leakage through the filler, it also provides a larger surface area, which effectively decreases the parasitic thermal resistances, Rbody and Rconv shown in Fig. 1. Therefore, we believe the impact of heat leakage through the filler is partially compensated by the larger device area available for heat collection on the body side and heat rejection on the cold side.

Fig. 5: Impact of hot-plate temperature and air velocity on TEG open-circuit voltage.
figure 5

a Measurement setup consisting a wind tunnel placed on a hot-plate. b The dependence of the open-circuit voltage on hot-plate temperature and air velocity. Error bars indicate standard deviations.

Full size image
Fig. 6: Open-circuit voltage and power density of flexible TEGs versus air velocity.
figure 6

Different panels refer to different module fill factors of a 5%, b 7%, c 13%, and d 20%. Error bars indicate standard deviations.

Full size image

Power density levels produced by the TEGs were calculated from the measured Voc levels according to

$$P = \frac{{V_{{\mathrm{oc}}}^2}}{{4R_{{\mathrm{out}}}}}$$
(3)

where Rout is the output resistance of the TEG. The equation assumes that a matching load resistance is used to achieve maximum power transfer. Using a Z-Meter (DX 4090 by TEC-Microsystems), Rout was measured as 6.5 ± 0.5 Ω using AC excitation. The power density was simply calculated by dividing the power by the surface area of the device, which varies with the fill factor. Figure 6 indicates that While the fill factor’s impact on Voc is small, the power density is a strong function of this parameter due to the reduced surface area of the TEGs at higher fill factors. Increasing the fill factor from 5 to 20% results in 6–8× enhancement in power density at 1.2 ms−1. Interestingly, however, at 20%, Voc levels obtained with the two lower conductivity composites appear to be the same. We note that at this fill factor, the separation between two adjacent legs is about 900 μm, which is close to the size of the larger aerogel particles. We speculate that the larger aerogel particles may not allow uniform distribution of aerogel particles around the legs, which may be responsible for the observed behavior.

When a module is flexed, the length as well as the cross-sectional area of the EGaIn interconnects change. To determine the impact of bending on module electrical resistance, Rout of a typical module was measured using a Z-Meter during bending after repetitive bending cycles. The module resistance is an important parameter in determining the TEG performance since the generated power is inversely proportional to this resistance according to Eq. 3. For this measurement, a NEXTECH force gauge and screw test stand was employed to flex the modules in a repeatable fashion. The setup, including the Z-meter is shown in Fig. 7(a). A closeup image of the flexed TEG is shown in Fig. 7(b). The device has a fill factor of 20%. Figure 7(c) shows the module resistance after being subjected to repetitive bending cycles with a diameter of 6 mm. Each data point corresponds to the AC resistance measured after five bending cycles. The data indicate no sign of failure or any change in module resistance after 100 bending cycles. This result was anticipated because the module resistance is largely dominated by the thermoelectric legs. We note that with a resistivity of 2.94 μΩ-cm, EGaIn is ~3000 times more conductive than the thermoelectric materials used for the legs. Furthermore, the cross-sectional area of the interconnects is comparable to that of the legs and the interconnects are roughly 4× shorter than the legs.

Fig. 7: Flexible TEG electrical resistance.
figure 7

a Measurement setup used to measure the AC electrical resistance of a TEG while it is being flexed with a known force, b A closeup image showing the flexed TEG, c Electrical resistance measured after repetitive bending cycles. Each data point corresponds to the AC resistance measured after five bending cycles.

Full size image

To test the devices on the human body, a flexible TEG with a fill factor of 20% was incorporated into a wearable wristband made using EcoflexTM, another commercially available silicone. The wristband was attached with Velcro strips to help fasten the device securely on the wrist during the measurement. An Arduino Mega board with an SD card shield was programmed to act as a data acquisition system for continuous Voc measurement. The flexible TEG and the data acquisition board are shown in Fig. 8(a). For these measurements, we used the wind tunnel shown in Fig. 5(a) with the wrist serving as the heat source in place of the hot-plate. Figure 8 (b), (c) shows the measured Voc and the corresponding power density as a function of elapsed time. We can see that a very high voltage is generated immediately after placing the TEG on the wrist at t = 0. At this instant, the cold side of the TEG is at the ambient temperature and the resulting ∆T is the largest possible for the ambient temperature. However, ∆T drops rapidly as the cold side of the TEG warms up and the device reaches thermal equilibrium. We can see that the dependence of Voc on air velocity is similar to that observed on the hot-plate. Voc approximately doubles when the air velocity is raised from 0 to 0.7 ms−1 but increases only by a small amount when the air velocity is further raised to 1.2 ms−1, consistent with the measurements obtained on the hot-plate. At 1.2 ms−1, the power density generated on the wrist is ~35 μWcm−2, which is lower than the power density measured on the hot-plate for the same air velocity. This is caused by several factors including the lower skin temperature (30.6 °C) and higher ambient temperature (23.6 °C) causing Tamb − Tbody to drop by 3.4 °C. Another factor that can have an impact on ∆T is the larger thermal contact resistance between the flexible TEG and the body.

Fig. 8: Characterization of flexible TEGs on the wrist.
figure 8

a A flexible TEG worn on the wrist and the hand-held recording device. b Open-circuit voltage versus time measured on the wrist for three different air velocities of 0, 0.7, and 1.2 ms−1. c Corresponding power density values plotted against time.

Full size image

It is important to note however that these numbers represent the largest possible power densities that we can obtain with these TEGs. First and foremost, normal walking cannot create the steady and uniform air flow that a fan is designed to provide. Furthermore, with a larger band, the heat supplied by the human body will not be uniform over the area of a large flexible TEG. Factors such as proximity to muscle tissue and superficial veins influence the skin temperature44. Our measurements on the wrist obtained during normal walking were 30 to 50% lower than the power densities measured on the benchtop consistently. The experimental results reported here were obtained on the wrist of a 28-year-old male individual with average height and weight. It is important to note that the performance of TEGs on the human body will be dependent upon the location on the body as well as factors such as the physical activity level and the skin conductance. In a recent study, Thielen et al. demonstrated a significant drop in heat flux (and TEG generated power) in elderly and attributed the drop to increased skin resistance with aging45.

Table 1 shows recently reported power density levels for different flexible TEG technologies. As indicated in the table, some of these TEGs were characterized on hot-plates, some were worn on the human body and some were measured both ways. The term, bulk refers to flexible TEGs that employed rigid legs similar to those used in this work. For references that did not explicitly provide an ambient temperature, 27 °C (300 K) was assumed. The table provides the reported hot-plate temperatures as well as the resulting temperature differentials between the hot-plate and the ambient. We note that this is the extrinsic ∆T that appears across the entire device, i.e., the three thermal resistances, RTEG, Rbody, and Rconv in Fig. 1(b). References14,18,23,46,47,48,49, among others, that forced a specific ∆T across the device by attaching the cold side to a cooled metal plate (e.g., water cooling) were not included in the table since such a measurement ignores the impact of Rbody and Rconv, which can both be substantial for body-worn devices. All TEGs included in the table was characterized with no air flow (i.e., natural convection). Table 1 suggests that in general, flexible TEGs with rigid legs perform better than TEGs employing new flexible materials. This is especially true for TEGs characterized on the body. While it is intriguing to imagine thermoelectric materials that can simply be dispensed in liquid form, much future work is still needed for these materials to match the performance of established thermoelectric materials. Table 1 also suggests that flexible TEGs (including ours) do not perform on the body as well as they did on a hot-plate. Several factors are likely to contribute to this behavior. First, a hot-plate establishes a uniform heat flow throughout the device. On the body, factors such as proximity to muscle tissue and superficial veins influence the skin temperature44. Furthermore, it is easier to achieve a good thermal contact between the hot-plate and the TEG, whereas factors such as applied pressure and skin roughness can impact the contact resistance35. The table includes one of our TEGs with an aerogel–silicone composite filler characterized on a hot-plate as well as on the human wrist. The device had a fill factor of 20% and the thermal conductivity of the aerogel–silicone composite was 0.08 Wm−1 K−1. The table suggests that this aerogel–silicone TEG compares favorably to other flexible TEGs also built around rigid legs. Assuming these different TEGs have similar thermoelectric materials properties, differences between them can be attributed to physical dimensions of the legs, fill factor, electrical contact and interconnect resistances and the thermal conductivity of flexible materials used in their construction. Worn on the wrist, the devices presented in this report demonstrate power density levels as high as 35 μWcm−2 during walking. As such, a typical wristband with an area of 30 cm2 would achieve power levels as high as 1 mW, which is significant in our pursuit to power advanced wearables featuring multimodal sensing and wireless data transfer.

Table 1 Power density levels reported for different flexible TEGs measured without any air flow.
Full size table

Biocompatibility

Biocompatibility is a key concern for any wearable monitoring device. The materials used in our flexible modules include: (i) the silicone elastomer, (ii) EGaIn, (iii) Thermoelectric materials, and (iv) Metal contacts on thermoelectric legs. The use of silicones in medical industry is well established. In addition to their common use in breast implants for decades, silicones continue to be considered for a variety of new medical applications50,51,52,53,54.

Relative to silicones, our knowledge on biocompatibility of EGaIn is limited. Kim et al. studied cytotoxicity of EGaIn in an aqueous environment55. The study concluded that EGaIn was stable and reasonably safe without mechanical agitation. It was shown that cytotoxicity increased with sonication, which increased the In ion concentration. In another study, Lu et al. studied the in vivo toxicity of EGaIn nanoparticles. Important liver and kidney functions and blood indexes in mice were monitored over three months and no signs of toxicity were detected56. In a review article, Yan et al. reviewed applications of liquid metals in different biomedical applications including carriers for drug delivery, molecular imaging, enhanced cancer therapy, and medical devices including implantables57. In two recent studies, EGaIn was used to produce stretchable e-skin58 and electronic tattoo59.

We have not observed any evidence of EGaIn leakage through the elastomer during repetitive bending cycles. However, in a recent study by Zadan et al., EGaIn droplets embedded in PDMS were used to create the interconnects in a flexible thermoelectric module60. The elastomer was mechanically activated in order to create electrically conductive traces. This finding also suggests that an external physical force might also lead to tearing of the surface exposing the EGaIn bubbles embedded in the high thermal conductivity elastomer. Therefore, in the event of an accidental device rupture due to extreme external force, it is plausible to find EGaIn droplets coming in contact with the skin. Nevertheless, the results from the studies mentioned above on medical applications of the material are encouraging. While more work is clearly necessary to fully understand biosafety of EGaIn, the preliminary results suggest that the material is safe and it is suitable for wearable applications.

Commercial modules that employ thermoelectric materials such as bismuth chalcogenides and contact metals such as Ni and Sn are expected to be RoHS/REACH compliant, which implies that any material with documented evidence of health risk (e.g., Pb) is avoided. Thermoelectric modules built using these materials have been used on the body in numerous studies focusing on different aspects of module design. Finally, one of the strengths of the proposed approach is that it is not limited to a specific thermoelectric material. Therefore, the thermoelectric material employed in these flexible modules may be chosen considering both performance and biosafety. This includes new exploratory organic materials, which may eventually rival the performance of their inorganic counterparts after years of research and development.

Methods

Aerogel–silicone composite preparation

The aerogel–silicone composites reported in this paper were produced by mixing commercially available aerogel particles (from Aerogel Technologies, LLC) in PDMS (SylgardTM 184, Dow Corning). We used two different aerogel particle sizes of 20–40 μm and 100–700 μm (ENOVA™ Aerogel IC 3120). Both aerogels have the same pore surface area of 600–800 m2g−1 reported by the vendor. The PDMS base and the curing agent (10:1 ratio) were mixed in an orbital mixer (THINKY ARE-250) to achieve a homogeneous mixture without air bubbles. The desired volume of the aerogel powder (ranging from 10 to 50% of the total volume) was then added to the uncured PDMS and mixed in the same tool. The resulting mixture was found to be more viscous than plain PDMS, depending on the aerogel volume fraction. Beyond 50% for the small aerogel particles, and 30% for the large aerogel particles, the uncured elastomer was too viscous to work with. The aerogel-PDMS composite was cured on a hot-plate at 70 °C for 2 h.

Flexible TEG fabrication

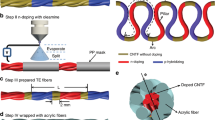
Figure 9(a) illustrates the process flow used to fabricate the flexible TEGs. The devices were made using commercially sourced, 0.7 × 0.7 × 3 mm sized p-type Bi0.5Sb1.5Te3 legs and n-type Bi2Se0.3Te2.7 legs. The Seebeck coefficient for both legs was ~220 μVK−1. The thermal conductivity values of the two legs were also similar, around 1.45 Wm−1 K−1. The n-type and p-type legs had different electrical conductivity values of 1100 and 820 S.cm−1, respectively. The legs were supplied with Ni/Sn metal stacks deposited prior to wafer dicing. The first step of the fabrication process involved placing the thermoelectric legs on a glass substrate featuring a double-sided sticky tape to prevent them from moving. We used a metal template to place the legs in their precise locations (Fig. 9(a-i)). After removing the template, the aerogel–silicone composite was poured between the legs, planarized and cured (Fig. 9(a-ii)). During this step, the glass substrate carrying the legs was placed in an appropriately sized plastic petri dish to contain the poured PDMS as it cured. To ensure that the uncured composite only filled the space between the legs, we pressed a second glass slide lined with a thermal release tape onto the legs. To visualize the distribution of aerogel particles between the legs, we used cross-sectional optical microscopy. The microscope image shown in Fig. 9(b) was obtained after physically removing the legs prior-to cross-sectioning. A device with a fill factor of 20% was used for this image. The picture clearly shows that while many aerogel particles were able to penetrate through the legs, the local aerogel density appears to vary throughout the cross-section, which is likely to have an impact on device performance. After curing the aerogel–silicone composite filler, the legs were inspected under an optical microscope for any elastomer residue left on the legs. The EGaIn interconnects were formed by spray coating EGaIn onto the Ni/Sn stack through a stencil made of a laser cut wax paper. The interconnects were then encapsulated by spray coating a thin (≈50-μm thick) layer of PDMS diluted to 50% by weight with n-hexane (95%, OptimaTM from Fisher Chemical), and curing the structure on a hot-plate at 140 °C for 30 min. (Fig. 9(a-iii)). Figure 9(c) shows the EGaIn interconnects formed on a 256-leg device with plain PDMS filler. The module has a fill factor of 20%. We note that the bubbles visible in the device are on or close to the surface and were introduced either during pouring or planarization. Figure 9(d) shows a similar module prepared with the larger, 100–700 μm aerogel particles. The 20% fill factor used to fabricate the modules corresponds to a leg separation of ~0.87 mm, which is close to the size of the larger aerogel particles. No measurable degradation in interconnect resistance was observed at least six months after fabricating the devices. Nevertheless, long-term stability of EGaIn interconnects on the contact metal is an important question, which needs to be explored before considering the proposed technology for mass manufacturing. After securing the interconnects with the thin, spray coated PDMS layer, a high thermal conductivity silicone elastomer consisting of graphene flakes and EGaIn was poured onto the device and cured to increase the thickness of the EGaIn encapsulation (Fig. 9(a-iv)). This final encapsulation layer improves the mechanical integrity of the device and the device performance by acting as a heat spreader on both sides of the device. The details of this elastomer and its application to flexible TEG fabrication can be found in recent publications by this laboratory40,42. After curing the encapsulation, the device was flipped and the EGaIn interconnects were formed on the opposite side (Fig. 9(a-v)) followed by encapsulation of the traces with the same high thermal conductivity elastomer (Fig. 9(a-vi)).

Fig. 9: Flexible TEG fabrication.
figure 9

a Process flow used to fabricate the flexible TEGs. b A cross-sectional microscope image of a TEG captured after physically removing the legs. c Top-view of EGaIn interconnects on a module built using pure PDMS as the filler. d Top-view of EGaIn interconnects on a module built using the aerogel–silicone composite filler.

Full size image