Introduction

Printed electronics (PE) has become a promising technology for the production of a wide range of flexible electronic components, ranging from photovoltaic devices, displays, sensors, and portable items to smart packaging1,2,3,4,5,6,7,8,9,10. The resulting functionality of these printed devices is highly dependent on the quality of the deposited ink. Nowadays, ink quality is mainly controlled based on defects8,9,10, including electrical properties6,11,12,13 surface morphology11,14,15,16, and ink distribution, which induces dimensional distortions8,17,18, such as enlargement or shrinkage. To increase the electrical functionality of printed devices, it is critical to monitor the dimensional distortions19, which have been tested extensively8,9,10. Currently, enlargement or shrinkage are monitored with optical microscopy (OM) under specific conditions, such as an appropriate illumination or along a particular direction, which might be problematic in an industrial environment15,20. Current approaches include defect detection realized by counting overlapping pixels or subtracting the expected image from the printed one8,9. These methods operate by using the on-site machine vision system to capture images of the final product, and then comparing them with the desired reference8,9,10. However, existing demonstrations include multistep image post-processing, which generates large data sets that are not easily handled in real time9. Therefore, a major challenge still remains in the mass production of PE devices for obtaining in-line feedback on print quality to ensure consistent production quality4,5.

Thanks to the non-destructive nature of terahertz (THz) light, which is generally defined between 100 GHz and 10 THz, and to its ability to penetrate through many optically opaque materials, such as plastic substrates, interest in THz time domain spectroscopy (THz-TDS) as a tool for quality control, as well as for non-invasive measurements, has increased considerably in recent years21,22,23,24,25,26,27. Further, some innovative approaches use metamaterials to enhance the interaction with the media under test, and therefore improve the detected sensitivity22,23,24,25. Since THz waves have submillimeter/millimeter wavelengths, THz metamaterials have relatively large dimensions (e.g., in the hundreds of microns), and are easily printed with current PE technologies26,27,28,13. Using this ability, we have recently introduced a simple strategy using a printed control bar with resonance in the THz frequency range to probe the electrical conductivity in the production of PE devices13. A key point of this strategy is the small printing area (<1 cm2) required to extract the conductivity information of ink during the printing process. However, the quality and functionality of printed devices also depend on geometric specifications, such as the printing precision of the width and length of the conductive traces. Such accuracy is directly related to the distribution of applied ink. In graphic printing, a physical model of the dot gain shows the difference between the actual and expected ink dot sizes29. This pattern is typically ~1 cm2 and is printed away from the main production line to provide a response proportional to the overall ink distribution as a function of the printing parameters. For the manufacture of printable electronics products, print quality correction is mainly carried out off-site, and consists in printing, by trial and error, a larger or smaller structure and/or stretching or compressing the original image to achieve the desired result. Therefore, to date, no real-time feedback strategy has been developed for adjusting the print production of printable electronic devices.

In this work, we study the ability of THz-TDS to track the printing accuracy and ink distribution of an industrial roll-to-roll press with the same physical model approach used in flexography. Fortuitously, the geometric properties of metamaterials strongly affect the transmission of an electromagnetic (EM) wave, through changes in its cell-unit, lattice, size, and other geometric parameters24,25, which is perfectly suited for this purpose. For this demonstration, two printing speeds and three geometric variations of the same pattern are used as feeding parameters. Our method uses the special EM transmission properties of a metallic checkerboard (MCB) pattern, which is made from conductive ink, and is rotated by 45∘. The rotation geometry was chosen to allow investigating self-complementary structures exhibiting complementary transmission properties, i.e., for the X- and Y-directions, according to Babinet’s principle. This phenomenon has been extensively studied for different frequencies, ranging from visible light to microwave radiations30,31,32,33,34,35. MCB yields simultaneous information about the lattice and unit cell variations and allows investigating the influence of the printing speed on the resulting distribution accuracy of deposited ink. A self-complementary structure has the peculiarity of presenting a flat response when it is perfectly printed. Otherwise, a small modification of its unit cells near self-complementarity produces a unique resonant signature35, which is highly suitable for tracking variations in printouts. Finally, to evaluate the ability of THz-TDS to follow the input printing parameters, we compared our results with those from standard visible OM.

Results

Visual approach

Figure 1a illustrates the set of designed samples, which contains three structures: (i) an inductive MCB (i-MCB), (ii) a perfect MCB, and (iii) a capacitive MCB (c-MCB), as explained in greater detail in the “Methods” section. The MCB is a self-complementary structure when c-MCB and i-MCB are complementary to each other. The designed structure was chosen to suit the spatial resolution characteristics of the printer. The predetermined period was the same in both directions p = px = py = 1 mm and for all structures. The size of the ink’s laps (+) or gaps (−) were varied between samples as follows: Δdc-MCB = −14 μm, ΔdMCB = 0 μm, Δdi-MCB = +14 μm and were kept constant in the X- and Y- directions (Δdx = Δdy). These three structures were fabricated using silver water-based ink from SunChemical (Sun AFT6700) on the polyethylene terephthalate (PET) substrate with two different printed speeds: 30 and 50 m/min. The production line was moving along the indicated Y-direction in Fig. 1. One-quarter of the visible images of the two printed sets are shown in Fig. 1b and c, respectively, where the black color represents the printed metallic ink (metallic patches) and the whitish color represents the substrate (voids). In Fig. 1b and c, visible images of size 10.24 × 10.24 mm2 and containing 4096 × 4096 pixels were obtained with a visible laser confocal microscope (model LEXT OLS4000), where 1 pixel corresponds to 2.5 μm.

Fig. 1: 2D optical microscopy characterization.
figure 1

a Designed samples, where black pixels correspond to ink and white is the substrate (voids): (i) i-MCB pattern with ink stretching of Δd = +14 μm; (ii) is the target MCB pattern for perfect transmission property; (iii) c-MCB pattern with ink compression of Δd = −14 μm. One-quarter of the visible images of the printed patterns obtained with a speed of b 30 m/min and c 50 m/min. d, e Extracted values of lattices and laps/gaps from visible images for X- and Y-directions, respectively. The horizontal and vertical lines show the standard deviation obtained from measuring Δd and p of five replicas for each structure. The red downward triangle, circle, and upward triangle show the design size of laps or gaps of i-MCB, MCB, and c-MCB, respectively. The dashed lines correspond to the designed dimensions of patterns.

Full size image

From a simple visual observation of Fig. 1, it is clear that none of the printed structures in Fig. 1b or c correspond perfectly to the designed ones in Fig. 1a, where all metallic patches are much bigger, and voids smaller. The visual analysis also clearly reveals the changes in pattern shapes for the two printing speed conditions. At a slower printing speed, far away from the optimized press run rate, printing quality printability is sub-optimal and printing conditions might be irregular. In the configuration press/ink/substrate, it appears that the ink tends to spread more, thus creating larger laps between each pattern. Meanwhile, increasing the print speed to approach optimal printing conditions gives better printability control and therefore produced patterns with sharper edges36. Especially for c-MCB printed at 50 m/min (c-MCB50), it can be seen that the lap sizes are smaller, with some gaps appearing between patches. Besides, we cannot identify variations in the lattice between all printed samples. Geometrical variation information provides an important insight into the printing performance, and is crucial for enabling the tuning of the desired final printed pattern. Theoretically, an accurate repetitive shape can be reached by seeking out the correct printing parameters. Here, we would like to highlight that the goal of our work is not to find the ideal printing conditions for the production of the perfect structure, but rather to precisely follow the printing variations.

For a more pragmatic assessment of the geometrical specifications of structures, we used Matlab software and counted the number of black or white pixels in order to extract the sizes of the lattice (px, py) and laps/gaps (Δdx, Δdy) for the X- and Y-directions (see Supplementary Fig. 1 for more details). From five replicas printed for each structure, we used the standard deviation to recover the variation in printing accuracy. Figure 1d, e summarizes the printing accuracy of the different structures and printing speeds, where the x-axis shows the size of laps/gaps and the lattice is plotted on the y-axis. The dashed lines correspond to the expected dimensions of the designed MCBs and the grid represents twice the spatial resolution limit of 5 μm. Figure 1d, e clearly confirms our simple visible observations, where slow printed samples have large bridges between patches, as compared to fast printing. These systematic assessments help in identifying the fact that printed patterns are not symmetric. There is always more ink in the Y-direction (Δdy), which means that the size of the patch is bigger on the Y- versus X-axis. Importantly, in Fig. 1d, e, we can see a small difference induced in the lattice for the different patterns and printing speeds. As is shown in the figures, the lattice size is always bigger in the Y-direction than in the X-direction. The extension of the lattice and patch sizes in the Y-direction relative to the X-direction is in good agreement with the placement of the print sheet relative to the direction of the production line. In general, compared to printing in the X-direction, the Y-direction is stretched during production17.

To summarize, a visual analysis with OM shows that the printing behavior can be controlled and observed from tiny induced changes in the feeding parameters, i.e. between the three cases presented in Fig. 1a i–iii. However, taking into account the large spatial variation of structures within a sample of about ±50 μm, OM allows differentiation of a change in printing on the order of 100 μm. For example, c-MCB’s Δdx is 30 ± 70 μm while MCB’s Δdx is 125 ± 30 μm. The second important conclusion that can be drawn is that the shape of printed patterns highly depends on the printing speed. For example, printing the patterns at a higher speed (50 m/min) produces shapes that are closer to the designed cases, but at the expense of a greater lattice and lap/gap size variability as compared to low printing speeds. In Fig. 1d, e, the c-MCB50 contains laps and gaps, and is the closest printed pattern to the perfect MCB shape, which is represented by the vertical black dotted line. As is shown above using microscopy analysis, ink distribution information can be extracted by testing a small print area. However, OM can be difficult to implement for quality control in an industrial environment as it is subject to special conditions for correct observation, such as a stabilized imager.

THz approach

The EM response of a metamaterial is controlled by the lattice and the dimensions of the unit cell comprising it24. Generally, changing the geometrical specifications represents a way to tune and determine whether the EM wave is transmitted, reflected, or absorbed25. Here, the designed MCBs behave as frequency selective filters, where an incident wavelength is approximately equal to one of the main dimensions of the unit cell (patch or voids), as well as to the lattice of the structure13. Based on the geometrical parameters of our designed patterns, we should have a maximum THz transmission for the i-MCB of around fΔdi-MCB = 0.22 THz, which corresponds to the size of the laps, and the first minimum THz transmission at fpi-MCB = 0.30 THz, which contains the lattice information. The i-MCB reveals a Fano-type resonance, where the transmission maximum is followed by a transmission minimum31. According to Babinet’s principle, the complementary of the i-MCB structure is the c-MCB structure, which must have reverse transmission properties at the same frequency. That means that we have a maximum THz transmission value (tending to 1) for i-MCB and a minimum THz transmission (close to 0) for c-MCB31. In the case of a perfect MCB, there should be no resonance, i.e., the same transmission (0.5) at every frequency, where half power is transmitted and half power is reflected31.

In Fig. 2a, to investigate EM responses in the Y- and X-directions, we simply rotated the samples at 90∘ while keeping the same THz polarization, as described in the “Methods” section. Based on the OM observation in Fig. 1b, c, all the printed samples contained mostly laps between each patch, and behave as i-MCB for EM light34. However, due to the asymmetric printing behavior for X- and Y-directions, we may expect different resonance responses as a function of lap size (i.e., between X- and Y-directions). To highlight the differences in printing behavior for the X- and Y-laps, Fig. 2a illustrates the different possible structures, with a magnification of the gaps/laps sizes for better vision. The major printing behavior found in our samples is illustrated in Fig. 2a–i, where laps in the Y-direction are bigger than those in the X-direction (Δdy > Δdx). Hence, according to previous work30,31,32,33,34,35, a sharper Fano resonance shifts toward a higher frequency is expected as the size of the laps increases. This shift results in an increase in transmission amplitude at the expected resonance frequency. Inversely, a widening of the peak resonance frequency with a shift to a lower frequency will occur with a reduction of the lap size. Indeed, a decrease of the transmission value at the expected resonance frequency will occur in such a case34,35 . This latter situation is outlined in Fig. 2a-ii, which corresponds to the interaction of an EM wave with c-MCB50 for the X-direction.

Fig. 2: 1D terahertz spectroscopy characterization.
figure 2

a Principle of electromagnetic field interactions with the samples in X- and Y-directions: (i) i-MCB antisymmetric pattern for X- and Y-directions; (ii) i-MCB and c-MCB behavior for Y- and X-directions, respectively. Normalized transmission of printed i-MCB, MCB, and c-MCB sample with b 30 and c 50 m/min. d, e Extracted values of lattices and laps/gaps from THz-TDS measurements for X- and Y-directions, respectively. The horizontal and vertical lines show the standard deviation obtained from measuring normalized transmission at 0.22 THz (TΔd) and the frequency minima (fp) of five replicas for each structure.

Full size image

To ascertain the EM properties of the printed MCB, we measured the normalized transmission responses using the THz-TDS system (detailed in the “Methods” section). Figure 2b and c presents examples of the normalized THz spectra from the samples presented in Fig. 1b and c, respectively. In these figures, a clear difference in THz transmission at the expected resonance frequency is found between the X- and Y- inspected directions, which agreed with the OM lap size observations in Fig. 1. For example, at a low printing speed for i-MCB (Fig. 2b), we can observe a small drop in transmission at 0.22 THz, from the Y- to X-direction, indicating a reduction in the lap sizes. However, by printing at higher speeds, we can see a clear drop in transmission, which is even more pronounced for the X- versus the Y-directions. By comparing Fig. 2b with Fig. 2c, we observe a clear change of the transmission properties between the different printing speeds, and see that it is in good agreement with OM measurements. On the other hand, the THz signature from the lattice remains unchanged at 0.27 THz, indicating that the variation of the lattice size was smaller than the spectral resolution of our THz system. It should be mentioned that for OM observations, a change in lattice of less than 6 μm with a large standard deviation was found. Nevertheless, from these transmission spectra, the most interesting case is certainly Fig. 2c (c-MCB), where laps and gaps coexist. In this case, the normalized transmission of the peak resonant response decreased drastically from 0.95 to 0.65, which is closer to the perfect transmission case condition of 0.5. Despite the small induced differences in lap/gap sizes between the designed patterns, i.e., from Δdi-MCB of +14 μm to Δdc-MCB of −14 μm, THz-TDS transmission measurements have succeeded in identifying the impact of variation of the initial patterns on the printing behavior.

To better evaluate the accuracy of the THz transmission measurements, we investigated the same five replicas used for the OM investigation and summarize the THz results for the X- and Y-directions in Fig. 2d and e, respectively. In the two figures, we are only interested in the transmission values at 0.22 THz (TΔdx,y), and in the frequency minima located close to 0.27 THz (fpx,y), which provide information on the laps/gaps and lattice signatures, respectively. The transmissions for laps/gaps are shown on the x-axis, while the y-axis represents the frequency response from the lattice size. To allow a direct comparison with OM results, the y-axis is depicted in a decreasing frequency order. A larger lattice size exhibits a lower resonant frequency response, whereas a smaller size resonates in the higher frequency range. From Fig. 2d, e, we can see that the lattice of the printed sample has a signature at a lower frequency than the design sample (depicted by the horizontal dashed line), which highlights the enlargement of the lattice, as was observed with OM. As with any other industrial tool, the printed electronic process is subject to great variations that continuously affect print quality. Here, the standard deviation of the THz results illustrates this existing condition as a function of the printing speed. In spite of these large variations, THz transmission, just like the OM results, allows a clear discrimination of the print quality according to the initial geometry of the print pattern. For example, in Fig. 2d, the largest standard deviation observed for Δdx is of the order of 20% over the normalized transmission value. Still, the THz data allow a greater discrimination between the c-MCB and MCB samples than that obtained by OM, i.e. a transmission of 0.32 ± 0.2 for the c-MCB and 0.75 ± 0.1 for the MCB. By calibrating these results with those obtained by OM: Δdx for c-MCB becomes 30 ± 40 μm while Δdx for MCB is 125 ± 20 μm. Given the 0.22 THz (λ = 1.36 mm) EM wavelength used to probe this variation, this spatial resolution performance far exceeds the diffraction limit imposed by the Rayleigh criterion37, confirming the remarkable ability of our method to achieve super-resolution detection in a far-field regime.

Intuitively, a large variation between similar samples should also mean a greater influence between the printed conditions and the THz transmission. To validate this hypothesis, we investigated the THz transmission behavior of c-MCB samples and compare our results with the percentage of metal occupancy revealed by OM observations. In Fig. 3, we evaluate the THz transmission for the X- and Y-directions of 14 samples, for a total of 28 measurements, with the same c-MCB print pattern. In this group of samples, five were printed at 30 m/min (the blue dots) and the rest at 50 m/min (the black dots). These results are plotted as a function of their metal occupancy rate measurements obtained by the OM method. Note that the metal occupancy depends on the amount of ink and its distribution, which for the MCB pattern, defines the number and sizes of gaps/laps. In that figure, the first striking observation is the growth of 10–90% in THz transmission, where the metal occupancy only changes from 55 to 61.5%. In addition, as it can be seen by the areas identified in dotted lines in Fig. 3a, a difference between the printing behaviors for the X- and Y-directions is easily discernible by the THz transmission measurement. This extreme sensitivity in THz response corresponds to the conversion of 60 gaps into laps, where the self-complementary transmission flipped from capacitive to inductive. As can be seen on the y-axis on the right side, a sample is composed of 100 gaps and perfectly follows a log scaling to match the observed transmission comportment (see Supplementary Fig. 2 for more details). In Fig. 3a, the initial stage of growth is approximately exponential, and then the growth slows to linear, and finally stops. This tendency of the THz transmission T can be described by the so-called logistic function (S-curve) defined by

$$T(\mathrm {MO})=\frac{L}{1+{\mathrm {e}}^{-k({\mathrm {MO}}-{\mathrm {MO}}_{0})}},$$
(1)

where L shows the maximum transmission value (L = 0.97), MO0 is the S-curve midpoint, and k is the steepness of the curve (k = 0.81). Here, the midpoint of the curve is 58.24%, which correspond to 0.5 in THz transmission. For the specific design of the MCB studied in this work, the midpoint at 58.24% defines a sensitivity range of 8% in the variation of metal occupancy, i.e. from 52 to 64%, as highlighted with the black arrow in Fig. 3a. Note that the sensitivity range and the midpoint can be modified by changing the parameters of the lattice and gap dimensions. Importantly, while the metal occupancy changes only for 8%, the THz transmission is varied through the entire range of sensitivity.

Fig. 3: 2D optical microscopy vs 1D terahertz spectroscopy.
figure 3

a Comparison between OM and THz-TDS results, where normalized transmission from THz-TDS is plotted as a function of the metal occupancy. The red line shows the fit with the logistic function. The black arrow shows the sensitive zone of metal occupancy. Illustration of the concept of spectral resolution for b optical microscopy and c THz-TDS.

Full size image

As can be observed in Fig. 3a, a transmission of 0.5 corresponds to 58.24% in metal occupancy, which is supposed to be for a perfect MCB case. However, this pattern contains 10 gaps out of 100 possible connections, and the rest are laps with sizes up to 100 μm. Basically, a balanced transmission/reflection condition occurs when the transmission of the overlapped patches compensates those with gaps. In other words, the presence of gaps has a greater influence on THz transmission than does the presence of laps (see Supplementary Fig. 2 for more details).

Discussion

The relationship between space and time resolution in our demonstration is quite appealing for quality control of printing conditions. It is well known that OM is designed to identify small elements. However, a larger field of view is required to achieve greater accuracy in order to resolve small changes in a structure that is periodic across positions in space, as illustrated in Fig. 3b. In our measurements, the size of the image is limited to 10.24 × 10.24 mm2, which means that the spatial frequency resolution is inherently set to ~0.1 cycle/mm. For THz-TDS measurements, a scan duration of 204.8 ps long provides a spectral resolution of 4.8 GHz. As we demonstrate in our work, when combined with metamaterials and especially for self-complementary structures, the spectral resolution of a THz-TDS system is converted into spatial resolution capability (as shown in Fig. 3c). Basically, any improvement in spatial resolution is solely a function of the duration of the temporal scan (i.e., no additional space is required). Remarkably, under certain conditions, THz spectroscopy of metamaterials can operate as a super-resolution far-field THz microscope.

To sum up, we have successfully revealed the printing behavior of an industrial roll-to-roll press with flexography printing units for PE device production using the single point THz spectroscopy method. Our strategy employs the self-complementary transmission principle of a small ~10 × 10 mm2 THz metamaterial. The THz information is able to track the geometrical accuracy and amount of ink of the printer with a similar level of precision as an optical microscope for visible light. In fact, 2D OM and 1D THz spectroscopy methods are in excellent agreement between each other. THz-TDS could be conveniently adopted for routine quality control of PE in industry, which should allow PE to maintain a required printing accuracy. Our results pave the way for a remote characterization tool to probe the dimensional accuracy and could ultimately be used as feedback parameters for improving the overall printing performances in real time.

Methods

Printing

Samples were printed by an industrial roll-to-roll press with flexography printing units (OMET Varyflex V2) using a silver water-based ink from SunChemical (Sun AFT6700) with adjusted viscosity and drying retardant. As it is shown in Fig. 4, the ink is put in contact with a micro-engraved cylinder (anilox), filling its cells, and is scraped with a doctor blade to assure that the cells are filled with a constant, controlled volume of ink at a rate of 12 billion cubic microns per square inch, which corresponds to 18.6 μm3/μm2. The ink is then transferred onto a printing form, which defines the pattern information. The inked pattern is then pressed against the PET substrate in the nip zone between the printing form and an impression cylinder. The ink transfer onto the substrate is performed with the lowest possible pressure20. The printing speed is varied between 30 and 50 m/min.

Fig. 4: Flexographic press principle.
figure 4

The inked pattern is pressed against the polyethylene terephthalate substrate in the nip zone between the printing form and an impression cylinder.

Full size image

Characterization techniques

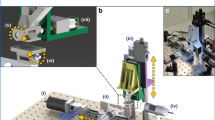
The images were taken with a confocal laser microscope LEXT OLS4000 in stitching mode, with a 5× objective lens with a 2 Megapixel charged coupled device camera. The THz-TDS setup was configured for spectroscopy in a transmission using an oscillator Ti:Sapphire laser (80 MHz, 400 mW, 810 nm, 40 fs) for pumping the commercial photoconductive antennas from Teravil used as emitter and detector, as shown Fig. 5. The PCA emitter and detector were placed in front of each other and a high resistivity hyper hemispherical silicon lens, located at the back of the emitter and detector, were used for fine alignment of the THz beam. To improve the dynamic range, the PCA detector was connected to a current amplifier (SR-5235) and a standard lock-in detection (SR-830) was performed with a mechanical chopper set at 330 Hz13. The samples were placed between the mechanical chopper and the PCA detector at a normal incidence of vertically polarized THz pulses with a peak frequency of 0.2 THz (see Supplementary Fig. 3 for more details).

Fig. 5: Terahertz time-domain setup.
figure 5

System based on photoconductive antennas for the generation and detection of terahertz waves in transmission mode. The blue arrow shows the polarization of THz light.

Full size image

Simulations and data processing

MCB was designed as a periodic structure, but due to the printing specifications, it has some irregularities, which have to be detected. To evaluate the variation of the size of laps/gaps and of the unit cell in the printing of MCB patterns, the images obtained were subjected to an appropriate post-processing analysis8,9,10. The real image was processed with a combination of low-pass and high-pass filters to eliminate noise, and were then transformed into a binary image. We simply rotated all MCBs by 90∘ relative to the THz beam polarization to scan in the Y- and X-directions. The normalized transmission can be inferred from a measurement of two transmitted THz pulses propagating through a substrate (Eref(t)) and through a sample (Esam(t)) in the time domain38. A ratio between the Fourier transform of the time-domain reference (Eref(ω)) and sample (Esam(ω)) waveforms gives the sample’s normalized transmission: T = Esam(ω)/Eref(ω).

The Finite-difference time-domain method using a linear polarized light and a periodic boundary condition was used for simulation of the expected transmission of i-MCBs and c-MCBs with varied voids (see Supplementary Fig. 4 for more details)13.