Introduction

Accurately resolving elemental distributions and morphological information inside functional materials at the nanoscale is critical for understanding their physical and chemical properties and for investigating the related device performances. Advances in multimodal imaging, combining measurements with different contrasts at the same time, have recently led to the ability to make maps of various properties of functional materials, which can be utilized to address their physical, chemical, and structural properties simultaneously1,2,3,4,5,6. As a powerful coherent imaging technique, X-ray ptychography can reconstruct complex phase information with high spatial resolution from coherent diffraction patterns of the functional materials, measured with overlapped X-ray probe positions7,8. When an appropriate phase retrieval method is applied, the incident X-ray probe profile and scanned sample information can be obtained with the same high spatial resolution9. X-ray fluorescence (XRF) can provide intrinsic trace element distributions within materials10. However, XRF is very sensitive to the incident X-ray beam profile information, resulting in lower spatial resolution than a ptychographic image from the same scanning experiment. For a scanning-probe XRF experiment, the resolution of the obtained XRF image is mainly limited by the size of the used X-ray beam profile, resulting from the convolution between the X-ray beam profile and the local illuminated region. Consequently, the related elemental analysis, for example, XRF tomography analysis which utilizes a series of XRF images by rotating the sample to obtain the three-dimensional inside morphological information of the measured sample, will suffer from the same low spatial resolution. Although many dedicated computational methods have been developed for image deblurring11,12,13,14, they are not suited for the current convolutional problem between the obtained XRF data and the known X-ray probe profile, where the physical relationship (discussed below) between the incident X-ray probe, low-resolution and high-resolution XRF data is not insured, due to the scanning process inherent to XRF microscopy.

Recently, the deep learning method has shown remarkable potential for solving many computational imaging problems15,16,17,18,19,20,21, such as phase retrieval22,23,24,25, phase unwrapping26, image denoising27,28, and image super-resolution29. Especially, the image super-resolution problem has been receiving increasing attention for decades. Computational deep residual networks exhibit outstanding performance in computer vision problems from low-level to high-level tasks30. These developed machine models can reconstruct a high-resolution (HR) image from one or more low-resolution (LR) images. However, the relationship between the input LR and the original HR image is usually a bicubic relation, aiming to generate a visually pleasing HR image from its degraded LR image. While plenty of image super-resolution algorithms based on ML have been proposed to tackle this problem, the application of the ML method to solve the convolutional problem between the X-ray beam profile and the XRF image is still a nascent field.

In this paper, we demonstrate an ML-based method to reconstruct super-resolved XRF images using multimodal raw XRF and ptychography data, measured simultaneously. The proposed residual dense network (RDN) model does not require numerical modeling and is instead based on training a generative RDN model to transform the LR XRF image, limited by its X-ray probe profile, to a super-resolved one. With this RDN model, we experimentally demonstrate that merging the X-ray probe profile from ptychography with the developed RDN model can reconstruct the HR XRF image with two different hard X-ray nanoprobes, focused by a Fresnel Zone Plate (FZP) and Multilayer Laue Lenses (MLLs), respectively. When applied for experimental LiNi0.6Mn0.2Co0.2O2 (NMC) particles, much better spatial-resolved elemental distributions were observed for the subsequent XRF tomography reconstruction using the obtained HR XRF images from different X-ray nanoprobes. This data-driven approach to enhance the spatial resolution of XRF microscopy can be applied to various other XRF imaging systems so long as the profile of the incident X-ray probe profile can be obtained. We believe that the current work represents a remarkable advancement in further improving the spatial resolution of XRF microscopy.

Results and discussion

Multimodal ptychography and XRF experiment

Generally, for an XRF mapping experiment in a fly-scan mode31,32,33, the collected XRF yield from different elements obeys the convolution equation:

$$Y_j\left({Z,{{{\mathbf{r}}}}} \right) = \sigma (Z,\lambda)\mathop {\int }\limits_{t_0}^{t_0 + {{\Delta }}t} \mathop {\int }\limits_{ - \infty }^\infty P\left({{{{\mathbf{r}}}} - {{{\mathbf{v}}}}t} \right)N\left({Z,\;{{{\mathbf{r}}}} + {{{\mathbf{r}}}}_{{{\mathrm{j}}}}} \right)dr\,dt,$$
(1)

where, σ(Z, λ) is XRF cross sections34, N(Z, r) is the elemental distribution of the measured sample, and P(r) is the X-ray probe intensity distribution (see Methods for details). rj is the jth X-ray nanoprobe scanning position on the sample, Z is the atomic number, λ is the wavelength of the incident X-ray, and Δt is the detector dwell time. Since the incident X-ray beam profile P(r) on the measured sample can be retrieved via ptychographic reconstruction by using the collected transmitted coherent X-ray diffraction patterns, it is possible to further utilize the obtained X-ray probe profile P(r) and the measured LR XRF image Yj(Z, r) to recover a high-resolution XRF image, where the corresponding resolution will be much closer to N(Z, r), compared to Yj(Z, r). During the scanning of the X-ray beam, the fine features presented in the probe function P(r), coupling to the XRF signal according to Eq. 1, represent a convolution operation that can be de-convolved with an appropriate computation, as we demonstrate here.

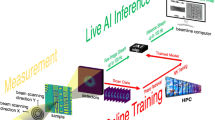
To demonstrate the technical feasibility of the proposed method, combined nano X-ray scanning experiments were conducted at the Hard X-ray Nanoprobe Beamline (HXN, 3ID) of the National Synchrotron Light Source (NSLS-II). As shown in Fig. 1, after being selected by a Si (111) monochromator, the monochromatic X-ray beam was pre-focused on the secondary source aperture (SSA) with a mirror in the horizontal direction and a set of compound refraction lens in the vertical direction. The microscope sits about 15 m downstream from the SSA, and an FZP with a 30-nm outmost zone width (or a pair of MLLs with higher resolution) was utilized to focus the monochromatic X-ray beam to a nano spot. The incident X-ray energy was set to 9 keV. During the measurements, 2D on-the-fly raster scans33 with the nanobeam were produced for both X-ray fluorescence images and far-field diffraction patterns. As shown in Fig. 1, a pixel-array detector was used to record transmitted far-field diffraction patterns, and an energy-dispersive detector (Vortex, Hitachi) was placed at 90° with respect to the sample to collect corresponding X-ray fluorescence signals. The obtained X-ray diffraction patterns were used to generate complex phase images and the incident X-ray wavefront information with a higher spatial resolution after the ptychographic reconstruction (see Methods for details). As a result, with this simultaneous measurement, the obtained X-ray wavefront information on the measured sample and X-ray fluorescence image was further utilized to reconstruct a higher resolution resolved XRF imaging using the proposed ML model.

Fig. 1: Schematic illustration of using the Hard X-ray Nanoprobe (HXN) beamline of NSLS-II for multimodal measurements.
figure 1

While the sample is raster-scanned by a nano-focused X-ray beam, both X-ray fluorescence images and transmitted coherent diffraction signals are collected simultaneously. A series of XRF maps and phase-contrast ptychographic images are collected while the sample is rotated in the beam to obtain 3D images. At the HXN beamline, the X-ray beam can be focused by an FZP or MLLs. The central beamstop is not shown to simplify the schematic.

Full size image

ML model training and testing

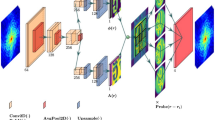
The architecture of the proposed RDN model is shown in Fig. 2a. It mainly includes three sub-modules: feature extraction, fusion, and up-sampling reconstruction35,36. The model directly uses the measured low-resolution XRF image as input. It fully utilizes all the hierarchical features extracted from the original LR XRF image to recover the original HR XRF image. In the model, the first two convolutional layers were used to extract the shallow features of the input XRF image. Then these extracted features are used as input to the following residual dense blocks (RDBs) to further extract hierarchical features with global feature fusion and global residual learning. After extracting local and global features in the LR space, an up-sampling reconstruction net is utilized to tune the result further fine in the HR space, which is mainly achieved by using three parallel RDBs. Here, the up-sampling operation (i.e., marked as “Upscale” in Fig. 2a) is performed by utilizing an Efficient Sub-Pixel Convolutional Neural Network37. Finally, following one more convolutional block (i.e., 3 × 3 convolution + LRLU + 1 × 1 convolution + LiSHT), the RDN model outputs the HR XRF image after stacking all the features obtained from the three parallel residual dense blocks in the HR space. Here, LRLU refers to leaky rectified linear unit. LiSHT refers to a non-parametric linearly scaled hyperbolic activation function which is applied at the final layer and is proposed by linearly scaling the Tanh activation function (see Methods for details)38.

Fig. 2: Architecture of our proposed residual dense network (RDN) for super-resolution X-ray fluorescence image reconstruction.
figure 2

a Overall layout of the ML model. b Detailed layout of residual dense block. For these RDBs, the input and output of each layer are fed into other layers as inputs. The curved lines show the feeding operations. Here, Conv represents the convolutional operation, and Conc refers to the concatenation of the feature map.

Full size image

Figure 2b shows the detailed architecture of RDB used in the proposed RDN model. The RDB is mainly based on the convolutional operation to extract features from its input, which consists of densely connected layers and local feature fusion with residual learning. In the RDB, each convolutional layer is connected directly with all the subsequent layers to preserve shallow and deep features that need to be preserved. Additionally, a global feature fusion is also used to adaptively preserve the hierarchical features in a global way. In the LR space, each RDBs has 16 convolutional blocks (i.e., 3 × 3 convolution + LRLU + BN, where BN refers to batch normalization), followed by a 1 × 1 convolutional layer to adaptively control the output information. The corresponding growth rate is 64 for the RDBs in the LR space. In the HR space, there are three parallel RDBs following the up-sampling operation and each RDBs has two convolutional blocks. The corresponding growth rate is 32.

As a typical ML-based method, the proposed RDN model attempts to learn a mapping function from a large amount of labeled data (i.e., paired LR and HR images prepared according to Eq. 1, see Methods for details) to predict the HR XRF image when an LR XRF image is input. To fully demonstrate the performance of our proposed RDN model, we applied two different types of focused hard X-ray beams to generate the training dataset for the RDN model. As shown in Fig. 3a, g the two different X-ray beam wavefronts are obtained via the ptychographic reconstructions from an FZP and MLLs at HXN, respectively (see Methods for details). The composition and structure of real-world materials can vary a lot from sample to sample. However, the relation between the measured LR XRF images and the measured materials can always be described by Eq. 1. To increase the diversity of the training dataset and the generality of the model, we use the Caltech-256 Object Category39 to prepare the training data for the RDN model, where the data has significantly different features. With the obtained hard X-ray nanoprobes and Caltech-256 Object Category database, two labeled XFR training datasets were constructed separately for the proposed RDN model (see Methods for details). According to Eq. 1, the LR images were generated by convoluting the HR images with the X-ray profiles obtained from ptychographic reconstruction and integrating signals from continuous probe shifting over scan steps modeling the on-the-fly data acquisition process (see Supplementary Fig. 1 for details).

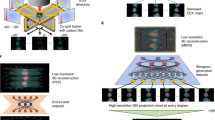
Fig. 3: The representative results for the performance of the RDN model in testing with different X-ray nanoprobes.
figure 3

a X-ray probe from an FZP. b, c Corresponding input testing LR XRF patterns from the FZP. d, e The ground truth. f, g The corresponding bicubic interpolation. h, i The predicted HR images from the RDN model. j X-ray probe from MLLs. k, l Corresponding input testing LR XRF patterns from the MLLs. m, n The ground truth. o, p The corresponding bicubic interpolation. q, r The predicted HR images from the RDN model. Here, the insets show the center marked by the red boxes.

Full size image

When training the model, we used a combined loss function (i.e., a combination of the mean square error and Pearson Correlation Coefficient, see Methods for more details) to optimize the model. The RDN model was implemented based on the PyTorch platform40 using Python. We adopted the Adam optimizer41 to optimize the weight and bias parameters of the model. The learning rate is initialized to 10-3 for all layers and decreases by half for every 15 epochs. During the training, the upscaling factor is determined by the ratio between the pixel size of XRF images (scanning step size) and the pixel size of the obtained X-ray probe profile from the ptychographic reconstruction. In this study, the upscaling factors are 7 and 10 in each dimension for the FZP and MLLs, respectively. Supplementary Fig. 2 shows the training and test loss as a function of the number of training epochs. The loss for the test data is gradually decreasing. After 50 training epochs, the loss for the test data is seen to reach 8.4 × 10−3, which illustrates that the proposed RDN model has provided a highly accurate reconstruction of the super-resolution XRF image from the corresponding low-resolution XRF image. To further demonstrate the performance of the trained RDN model, Fig. 3 shows four representative predicted results from test LR XRF images, which were not used for training the ML model.

As shown in Fig. 3b–i and Fig. 3k–r, we present the quantitative predictions from the trained RDN model as well as the images using the traditional bicubic interpolation with the same upscaling factor for the FZP and MLLs, respectively. Compared with their corresponding ground truth, these small features in the predicted images from the RDN model can be well reproduced. The proposed RDN model successfully reconstructs the detailed textures and edges compared with the original HR images. However, the obtained HR images from bicubic interpolation show a relatively poor performance compared with the results from the RDN model. As shown in Fig. 3, the calculated peak signal-to-noise ratios from bicubic interpolation are less than that from the RDN model. It should also be noticed that the physical relationship (i.e., Eq. 1) is not insured for the bicubic interpolation.

Comparison between experimental and resolution-enhanced XRF data

To demonstrates the ability of our RDN model on experimental data, we applied our RDN model to the experimental XRF datasets from NMC cathode material with compositional gradient structure from the core to the surface of the particle, using X-ray beams focused by an FZP and a crossed pair of MLLs, respectively. The concentration gradient NMC cathode material system in electrical vehicle applications has received much attention due to its high capacity, low cost, and long cycling life. This material system also offers tremendous scientific interest for entangled relation between microstructure/morphology with chemical heterogeneity and functionality, as the Ni-rich core provides high energy density and the Mn-rich surface enhances thermal and structural stability42,43. In addition, a chemo-mechanical degradation mechanism related to the formation of micro-cracks, voids, and fractures during cycling is considered the main drawback of this system44,45. Therefore, questions on how the primary particles aggregate to form second particles, how the cracks are initialized in the primary particle gap level during cycling, and how the elemental distribution (i.e., Ni, Mn concentration gradient structure changes) are changed during the cycling are critical for further understanding the structure-property relations and enhancing the electrochemical performance of this material. Such morphological/structural information requires high spatial resolution at the nanoscale and high chemical contrast to provide more precise information. Up to date, such investigations on this specific materials system utilize scanning/transmission electron microscopy techniques with cross-sectioned particles mostly46,47. However, this approach has many limitations, such as (1) requires many efforts in sample preparation (usually requires using a focused ion beam), (2) impossible for in situ investigation, (3) possible sample damage during the manipulation of the sample and to the electron beam, and (4) lack of data statistics due to the limited number of measurements. X-ray microscopy/imaging, a non-destructive technique, can overcome such limitations. Therefore, the high-resolution XRF/ptychographic imaging of concentration gradient NMC material in this study is not only a great case to prove our concept but also provides ground-truth information to answer many important scientific questions related to this materials system that could not be given from the previous studies.

The multimodal experiments were performed at the HXN beamline, as described in Fig. 1. During the measurement, the far-field coherent diffraction pattern was recorded simultaneously with the X-ray fluorescence signal at each scan position. The corresponding wavefronts of the incident X-ray beam can be obtained from ptychographic reconstructions. As shown in Fig. 3 and h, the profiles of the two X-ray probes have significantly different characteristics.

By using these two X-ray probes, the RDN model trained with the simulated LR and HR image pairs, was further applied to raw XRF projections at all angles for each tomography dataset. The enhanced XRF projection images were then used to reconstruct 3D XRF images by tomography reconstruction. The central slices of the 3D reconstructed structures are presented in Fig. 4 for using the FZP and MLLs, separately. As shown in Fig. 4, the proposed RDN model has successfully recovered a far more detailed chemical mapping of the elemental distribution inside the NMC particles, which can provide far better information on the micro-cracks, voids, and fractures of the sample compared with the directly measured LR XRF images. As the Nickel element concentration is >60% of the total for the NMC particle, the Ni XRF image should be representative of the major structural features. Indeed, in both cases (i.e., using the X-ray probe from the FZP and MLLs, respectively), the fine details in the enhanced XRF images are highly consistent with the structures obtained from the corresponding phase-contrast image using ptychography, as shown in Fig. 4. This consistency suggests that the image enhancement process imposed by the RDN model decouples the impact of the X-ray beam profile and the scanning scheme, which is similar to the reconstruction process in ptychography. In general, the resolution of a directly obtained XRF image depends not only on the X-ray beam intensity distribution but also on the scanning step size, which is caused by the convolution of the X-ray beam intensity and sample information. As shown in Fig. 4, the estimated resolution of the LR XRF image for the FZP by using two experimental datasets for each NMC sample48, is 94.8 nm and is 57.4 nm for MLLs (see Supplementary Fig. 3 for details). However, for the obtained HR XRF images shown in Fig. 4, the X-ray beam information has been deconvolved from the sample. Using the Fourier shell correlation (see Supplementary Fig. 4), we further estimated the resolution of these resolution-enhanced XRF images, as presented in Fig. 4. The corresponding resolution can be improved to 22.0 nm for the FZP and to 24.5 nm for the MLLs, respectively. In our experiments, as the X-ray probe size from the MLLs is smaller than that from the FZP, it will be expected that the performance of RDN model on the XRF image from the MLLs should be better than that from the FZP. This exception is probably due to a greater upscale factor (i.e., scanning step size) when the RDN model was applied to the XRF images from the MLLs, since the performance of the RDN model is dependent on the upscale factor. Nevertheless, enhanced spatial resolutions were observed on experimental XRF datasets from both the FZP and MLLs, respectively. From these comparative results, it can be concluded that the RDN model demonstrates high potential as a general method and provides comparably good enhancements for both probe profiles utilized.

Fig. 4: Comparison of experimental low-resolution XRF images and resolution-enhanced XRF images.
figure 4

In each image, the central slices of the 3D reconstructed structures of NMC particles are displayed. The experimental datasets were collected using different scanning X-ray probes, respectively. The left column shows the central slice of the raw XRF tomography reconstruction for the Nickel signal. The middle column shows the corresponding central slice of the 3D tomography reconstruction using the spatial resolution-enhanced Ni XRF results from the RDN model. The right column shows the central slice of the phase-contrast image from the ptychographic tomography reconstruction. Here, the insets indicate the area marked by the red boxes and all the scale bars are 2 μm.

Full size image

Furthermore, in realistic applications on different material systems, the quantitative elemental information encoded in the raw XRF data should be preserved during the image enhancement process. Thus, we further calculated the main elemental percentage concentration for the three major components (i.e., Ni, Mn, and Co) presented in the presented NMC particles (i.e., Fig. 4), which can help to understand the degradation mechanism of this material. Figure 5 shows the corresponding concentration distribution of the three main elements in these particles before and after applying the RDN model for the experimental XRF images from the FZP and MLLs, respectively (see also Supplemental Fig. 5 for the corresponding LR and HR XRF images). As presented, it can be seen that as the convolutional effect between the X-ray probe profile and XRF images is deconvolved, the RDN network redistributes the elemental concentration distribution slightly among these three main elements. However, the overall concentration distribution profiles of the three main elements remain similar after this image enhancement process. This further indicates the robustness of the proposed RDN model for enhancing the resolution of XRF images from different elements.

Fig. 5: Three main elemental concentrations of the NMC particles before and after the XRF image enhancement process.
figure 5

The main elemental concentration distributions of the NMC particles from directly obtained XRF images measured with the (a) FZP and (b) MLLs, respectively. c, d Corresponding main elemental concentration distribution of the NMC particles for the resolution-enhanced XRF images using the FZP and MLLs, respectively.

Full size image

Note that the RDN model training is solely performed on the simulated images. Thus, the capability of the RDN model might be restricted by the limitations in simulated training data. However, the RDN model can still perform excellently on these experimental data. When training the model, the RDN model attempts to learn a direct mapping function from the paired LR and HR XRF images dataset. Indeed, with all the above-demonstrated results, it can be concluded that the learned mapping function works remarkably well not only for these testing images but also for the experimental data. These results illustrate the robustness of the proposed RDN model. Because ML model is very easily parallelized, it can gain a speed advantage over the traditionally method. We expect a further improvement of the RDN model performance with a large and more diverse training dataset as well as incorporating the physical model for the training dataset, for example, including the self-absorption effect. Meanwhile, the proposed RDN depends sensitively on the exact X-ray beam profile due to the deconvolution nature of the problem. Thus, when the X-ray beam profile is changed, retraining the RDN model is required, but use of transfer learning (i.e., using the parameters from the pre-trained model) will speed up the analysis. Another prospect might be to further develop the current RDN model to include the incident X-ray beam profile as an input. Since the XRF experiment utilizes multimodal imaging, one can always use the corresponding ptychographic result as a reference to check the reliability of the HR XRF image. As a scanning-type method, the effective overlap ratio between the adjacent scanning spots plays a crucial role in determining the up limitation of the enhancement of the RDN model. When increasing the overlap ratio, the RDN model is expected to give a better enhancement, and vice versa. As multimodal imaging of functional materials continues to grow in importance, we believe our deep learning solution for enhancing the spatial resolution of an XRF microscope will see major opportunities not only in materials science, but in biomedical applications.

In conclusion, we have presented an ML approach to enhance the spatial resolution of scanning X-ray fluorescence images from focused hard X-ray beams by including information measured simultaneously by X-ray ptychography. Both simulated and experimental data were used to demonstrate the performance of our proposed RDN model to enhance the spatial resolution of XRF images as well as the related 3D tomographic reconstructions. Extensive benchmark evaluations demonstrate that our RDN approach can achieve better spatial resolution over state-of-the-art conventional scanning methods. The improved spatial resolutions are obtained with both simulated as well as experimental data. Especially when applied to the experimental data, we further showed that enhanced resolutions are observed for two different focusing methods, using the FZP and MLLs. Given the many important applications of XRF microscopy, we believe the current ML method will provide a new path for imaging both biological and functional materials via the scanning XRF method, which reveals element-specific chemical distributions in 3D. Our results show that the addition of probe information from ptychography coupled with the proposed ML-based computation method can obtain much higher resolution XRF tomography images, whose spatial resolution is mainly limited by the used incident X-ray probe size. This ML-enhanced method will likely see very broad applications in X-ray nanoprobe imaging and related research fields.

Methods

Sample preparation

Concentration gradient structured hydroxide precursor with an average composition of [Ni0.6Mn0.2Co0.2](OH)2 were synthesized via the coprecipitation method using a 20 L batch reactor. NiSO4·6H2O, CoSO4·7H2O, MnSO4·5H2O, NaOH, and NH4OH were used as starting materials. The prepared [Ni0.6Mn0.2Co0.2](OH)2 precursor was filtered, washed, and dried for 20 h at 100 ˚C. The dried precursor was mixed with LiOH·H2O, and portions of the mixture were calcined at 800 ˚C for 20 h under oxygen flow. Details of the synthesis method are described in the previous reports49,50.

Simultaneous data collection for Ptychography and XRF

The ptychography and XRF experiments were performed at the Hard X-ray Nanoprobe Beamline (HXN, 3ID) of the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory. The incident X-ray energy was set to 9 keV. The microscope sits about 15 m downstream from the SSA, and a Fresnel zone plate (Applied Nanotools Inc.) with 30-nm outmost zone width or MLLs51 were used to focus the beam to a nano spot. An energy-dispersive detector (Vortex, Hitachi) was placed at 90° horizontally with respect to the sample to collect fluorescence signals, and a pixel-array detector (Merlin, Quantum Detectors) was positioned 0.5 m downstream to record the transmitted far-field diffraction patterns. The simultaneously acquired far-field diffraction patterns were used to generate phase images with a higher spatial resolution via ptychographic reconstruction.

Ptychography and tomography data processing

The ptychographic reconstruction was completed by using a GPU-accelerated iterative method. Each 2D projection image was reconstructed with 1000 iterations of the Difference Map algorithm. 5 illumination modes were included in the reconstruction to handle the blurring introduced by the on-the-fly scan scheme27. The intensity summation of the obtained probes was used as the beam profile for training the RDN network. The tomography reconstructions for both the XRF and ptychographic images were performed by using the TomoPy package52 with 100 iterations of the ordered-subset penalized maximum likelihood algorithm. After tomographic reconstructions with the obtained LR and HR 2D XRF images, for the FZP, the LR 3D XRF image sizes are 120 × 105 × 120 with a voxel size of 66.7 nm and the corresponding HR 3D image sizes are 840 × 735 × 840 with a voxel size of 10 nm. For MLLs, the LR 3D XRF image sizes are 120 × 120 × 120 with a voxel size of 50 nm and the corresponding 3D HR image sizes are 1200 × 1200 × 1200 with a voxel size of 5 nm.

Training dataset and RDN model training

Typically, for the X-ray fluorescence mapping experiment in a step-scan mode, the collected X-ray fluorescence yield Y obeys that:

$$Y_j\left({Z,\;{{{\mathbf{r}}}}} \right) = \sigma (Z,\lambda )\mathop {\int }\limits_{ - \infty }^\infty P\left({{{\mathbf{r}}}} \right)N\left({Z,\;{{{\mathbf{r}}}} + {{{\mathbf{r}}}}_{{{\mathrm{j}}}}} \right)dr,$$
(2)

However, in a fly-scan mode, the XRF yield from a continuously moving sample becomes:

$$\begin{array}{ll}Y_j\left( {Z,\;{{{\mathbf{r}}}}} \right) = \sigma \left({Z,\lambda } \right)\mathop {\int }\limits_{t_0}^{t_0 + {{\Delta }}t} \mathop {\int }\limits_{ - \infty }^\infty P\left( {{{\mathbf{r}}}} \right)N\left({Z,\;{{{\mathbf{r}}}} + {{{\mathbf{r}}}}_{{{\mathrm{j}}}} + {{{\mathbf{v}}}}{{{\mathrm{t}}}}} \right)dr\,dt \\\qquad\quad\quad= \sigma \left({Z,\lambda } \right)\mathop {\int }\limits_{t_0}^{t_0 + {{\Delta }}t} \mathop {\int }\limits_{ - \infty }^\infty P\left({{{{\mathbf{r}}}} - {{{\mathbf{v}}}}t}\right)N\left({Z,\;{{{\mathbf{r}}}} + {{{\mathbf{r}}}}_{{{\mathrm{j}}}}} \right)dr\,dt,\end{array}$$
(3)

where, Δt is the detector dwell time and v is the scan speed. N(Z, r) is the elemental distribution of the measured sample, σ(Z, λ) is XRF cross sections, and P(r) is the X-ray probe intensity distribution. rj is the jth X-ray nanoprobe scanning position on the sample, Z is the atomic number and λ is the wavelength of the incident x-ray. According to Eq. 3, the labeled XRF training datasets were generated, using the Caltech-256 Object Category database with different hard X-ray nano probes, separately. The LR images were generated by convoluting the HR images with the X-ray probe and integrating signals from continuous probe shifting over scan steps, modeling the on-the-fly (step-scan) data acquisition process (see Supplementary Fig. 2 for the simulation and effect of different scanning methods on the LR image). For the FZP, each input LR image size is 105 × 120 with a pixel size of 66.7 nm, and the corresponding HR image size is 735 × 840 with a pixel size of 10 nm. For the MLLs, each input LR image size is 120 × 120 with a pixel size of 50 nm, and the corresponding HR image size is 1200 × 1200 with a pixel size of 5 nm. The X-ray probe image sizes are 128 × 128 for the FZP and MLLs, and the corresponding pixel sizes are 10 nm and 5 nm, respectively. For the FZP, the total number of the paired LR and HR images is 17640 and for MLLs, it is 17648. For both FZP and MLLs, when training the model, 95% of the paired LR and HR images were used to train the model, and the rest of them were used as validation. The test dataset was prepared and applied separately. To avoid overfitting, an early stop strategy was applied, whereby the test or validation loss should not be greater than two times the training loss. The batch size was 2.

The RDN model was implemented in PyTorch with Cuda, where the RDN model was initialized with the default initialization method in PyTorch. During the training, we applied the following loss function l, to optimize the weights and bias of the RDN model:

$$l = \frac{1}{{\alpha _1 + \alpha _2}}\left[ {\alpha _1L_1\left( {H_{{{\mathrm{p}}}},H_{{{\mathrm{g}}}}} \right) + \alpha _2L_2\left( {H_{{{\mathrm{p}}}},H_{{{\mathrm{g}}}}} \right)} \right],$$
(4)

where Hp is the predicted result from the RDN model and Hg is the corresponding ground truth. In Eq. 4, L1 is the modified correlation coefficients, which is defined as \(L_1( {H_{{{\mathrm{p}}}},H_{{{\mathrm{g}}}}}) = 1 - \frac{{\mathop {\Sigma }\nolimits_n ( {H_{{{\mathrm{p}}}} - \bar H_{{{\mathrm{p}}}}} ) ( {H_{{{\mathrm{g}}}} - \bar H_{{{\mathrm{g}}}}} )}}{{\sqrt {[ {\mathop {\Sigma }\nolimits_n ( {H_{{{\mathrm{p}}}} - \bar H_{{{\mathrm{p}}}}} )^2} ] [ {\mathop {\Sigma }\nolimits_n ( {H_{{{\mathrm{g}}}} - \bar x_{{{\mathrm{g}}}}} )^2} ]} }}\). L2 is the relative squared error, which is given as \(L_2 ( {H_{{{\mathrm{p}}}},H_{{{\mathrm{g}}}}} ) = \frac{{\mathop {\Sigma }\nolimits_n ( {H_{{{\mathrm{p}}}} - H_{{{\mathrm{g}}}}} )^2}}{{\mathop {\Sigma }\nolimits_n H_{{{\mathrm{g}}}}^2}}\). Generally, L1(Hp, Hg) is the statistical metric that measures the similarity between two variables53 and L2(Hp, Hg) is dominated by the strong part of a XRF image. Here, both α1 and α2 are set to 1 without bias.

On our current hardware, the network took about 60 h on average for 50 epochs of training. At the final layer of the RDN model, the non-parametric linearly scaled hyperbolic activation function is applied, whose expression is given by:

$${{{\mathrm{LiSHT}}}}\left( x \right) = x \times \tanh \left( x \right).$$
(5)

For the large positive inputs, the behavior of the LiSHT is close to the LRLU, i.e., the output is close to the input. The training process was conducted on a computer with two NVIDIA V100 GPUs and 256 GB of RAM. The PSNR used in the paper is defined as \({{{\mathrm{PSNR}}}} = 20 \times {{{\mathrm{log}}}}_{10}\left( {\frac{{{{{\mathrm{MAX}}}}}}{{{{{\mathrm{MSE}}}}}}} \right)\), where MSE = \(\frac{1}{{mn}}\mathop {\sum }\nolimits_{i = 0}^{m - 1} \mathop {\sum }\nolimits_{j = 0}^{n - 1} \left[ {I_1\left( {i,\;j} \right) - I_2\left( {i,\;j} \right)} \right]^2\) for 2D data, and MSE =\(\frac{1}{{lmn}}\mathop {\sum }\nolimits_{i = 0}^{l - 1} \mathop {\sum }\nolimits_{j = 0}^{m - 1} \mathop {\sum }\nolimits_{k = 0}^{n - 1} \left[ {I_1\left( {i,\;j,\;k} \right) - I_2\left( {i,\;j,\;k} \right)} \right]^2\) for 3D data. MAX is equal to 1. I1 and I2 are the corresponding input data.