Introduction

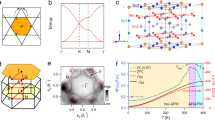
Kagome metals, consisting of a geometrically frustrated kagome sublattice, are fertile platforms for emergent topological states such as quantum spin liquids and quantum Hall states1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. Theoretically, electrons residing on the corner-shared triangle network create nontrivial quantum interference among the three sub-lattices and gives rise to flat bands, saddle points and Dirac fermions1,2,3,4,6,19,20. Studies of kagome metals have been focusing on these characteristic excitations; however, in the presence of multi-bands near the Fermi level, topological nodal lines can emerge and serve as an avenue to realize topological semimetals and insulators21,22. A widely studied example is the ferromagnetic shandite kagome-metal Co3Sn2S2, where the mirror symmetry protected nodal ring (Fig. 1a) breaks into Weyl nodes by its strong spin–orbit coupling (SOC)8,18,23,24,25,26,27,28,29,30,31,32,33,34. Here we show that the shandite kagome metals can host another nodal line, an endless Dirac-nodal line (Fig. 1b), in their electronic structure. Using density functional theory (DFT) calculations and symmetry-based indicator theories, we demonstrate that the nonmagnetic Ni3In2S2 is a topological semimetal with six endless Dirac-nodal lines near the Fermi level. The linearly dispersive band structure yields small effective mass and high mobility of the conduction electrons, which are responsible for a large magnetoresistance (MR) up to 2000% at 9 T. Our results uncover the diverse landscape of multiband kagome metals and suggest that the hole-doped Ni3In2S2 as a Dirac/Weyl semimetal platform for quantum effects.

Fig. 1: Crystal structure and electronic band structure for Ni3In2S2.
figure 1

a Weyl/Dirac points that can be obtained from nodal ring band crossings in the kagome lattice by tuning parameters like magnetism, spin–orbit coupling and breaking crystalline symmetries. b Topological (crystalline) insulator states obtained from nodal line band crossing after considering spin–orbit coupling. c, d Conventional cell and primitive cell for the kagome-lattice material Ni3In2S2. e Kagome layer in Ni3In2S2. f, g Three-dimensional BZ and surface BZ along z direction for Ni3In2S2. Throughout the manuscript, we use the primitive cell and the 3D BZ for theoretical calculations. h Spinless electronic band structure of Ni3In2S2 along some high-symmetry lines, with band crossings near the Fermi level highlighted by dashed circles.

Full size image

Results

Crystal structure, electronic bands, and topology of Ni3In2S2

The nonmagnetic shandite kagome-metal belongs to space group No.166 (\({{{\rm{R}}}}\bar{3}{{{\rm{m}}}}\)). The conventional cell and primitive cell of Ni3In2S2 are shown in Fig. 1c, d, respectively. Ni-atoms form a 2D kagome sublattice within the In-Ni layers, as shown in Fig. 1e. Figure 1f, g shows the three-dimensional Brillouin zone (BZ) of the primitive cell and two-dimensional surface BZ in the conventional cell, respectively. Throughout the manuscript, we use the primitive cell and the three-dimensional BZ for theoretical calculations, and the surface BZ for the angle-resolved photoemission spectroscopy (ARPES) measurement.

Figure 1h shows the DFT calculated band structure without SOC, since the SOC is small compared to the experimental resolution (details are in the Supplementary Materials). Two band crossings (highlighted by dashed circles) along T-H and Γ-S high-symmetry lines are identified near the Fermi level, EF. These crossings are composed mainly by the Ni 3d-orbitals (see Supplementary Materials). Since Ni3In2S2 preserves both time-reversal, \({{{\mathcal{T}}}}\), and inversion, \({{{\mathcal{P}}}}\), symmetries, these linear band crossings may belong to nodal lines/rings. To determine the topology of these linear crossings, we use symmetry-based indicator theories35,36,37 for further diagnosis. Figure 2 summarizes the diagnostic processes. Under the compatibility condition, we find the space group No. 148 is the maximum subgroup, having a nontrivial symmetry-based indicator group of \({{\mathbb{Z}}}_{2}{{\mathbb{Z}}}_{2}{{\mathbb{Z}}}_{2}{{\mathbb{Z}}}_{4}\), which is used to determine the complete topological information for the band crossings near the Fermi level35,36,37,38,39,40. Topological invariants for the symmetry-based indicator formulas of the space group No. 148 are:

$${z}_{2,i}\,=\,\mathop{\sum }\limits_{k\,\in\, {{{\rm{TRIM}}}}}^{{k}_{i}\,=\,\pi }\frac{{{{{\rm{N}}}}}_{-}(k)\,-\,{{{{\rm{N}}}}}_{+}(k)}{2}\,mod\,2,\,i\,=\,1,2,3,$$
(1)
$${z}_{4}\,=\,\mathop{\sum}\limits_{k\,\in\, {{{\rm{TRIM}}}}}\frac{{{{{\rm{N}}}}}_{-}(k)\,-\,{{{{\rm{N}}}}}_{+}(k)}{2}\,mod\,4,$$
(2)

where TRIM stands for the time-reversal-invariant momenta, and N±(k) represents for the number of bands that are even/odd under inversion symmetry at k.

Fig. 2: Topological diagnosis for the nodal lines in Ni3In2S2.
figure 2

a Diagnostic process for topological nodal lines in Ni3In2S2 by symmetry-based indicator theory and beyond (see text for more details). b Distributions of six endless node-line (red) and two node-ring (blue) band crossings in the first BZ, carrying π Berry phase. c Top view of the nodal lines and nodal rings in the BZ.

Full size image

Following Eqs. (1), (2), we obtain a series of topological invariants with z2,1z2,2z2,3z4 = (1110), meaning that there are 6 mod 12 nodal lines along the [111] direction36,37,41,42. This conclusion is confirmed by DFT calculations that show six endless Dirac-nodal lines along the [111] direction (red lines in Fig. 2b, c). These Dirac nodal lines carry a π Berry phase are protected by the \({{{\mathcal{PT}}}}\) symmetry. In addition to Dirac nodal lines, the DFT calculations reveal two nodal rings, similar to those observed in the magnetic Weyl semimetal Co3Sn2S2. These nodal rings have binding energies about 80 meV higher than those endless ones and can be understood by decomposing the symmetry-based indicator as z2,1z2,2z2,3z4 = (1110) = (1112) + (0002) with z4mod 4, where (1112) and (0002) uncover the 6 mod 12 Dirac-nodal lines along [111] direction and 2 nodal rings located at inversion-related momenta, respectively36,37.

Angle-resolved photoemission spectroscopy measurements

To study the electronic structure and its implications experimentally, crystals of Ni3In2S2 were grown and characterized as described in the Supplementary Materials. Single crystal X-ray diffraction confirmed the structure reported in ref. 43. The crystals are metallic with residual resistivity ratios near 130 K and showed Pauli paramagnetic behavior with no evidence of phase transitions between 2 and 300 K. To identify the theoretically predicted Dirac nodal lines, we performed ARPES measurements on the (001) surface of Ni3In2S2 crystals at 10 K. Figure 3a–c show the ARPES constant-energy plot with binding energy, EB = 0, 0.2, and 0.4 eV, respectively. The red dashed hexagon-network indicates the surface BZ. The data was collected at the photon energy, hν = 125 eV, corresponding to kz ~ 0 (see Supplementary Materials). The Fermi surface near the surface high-symmetry \(\bar{{{{\rm{M}}}}}\) point shows parallel lines connecting the first and second BZ. Moving to high binding energy, the parallel lines first evolve to a node near EB = 0.2 eV and eventually turn into an oval centered at the M point. These constant-energy plots suggest a Dirac point at the \(\bar{{{{\rm{M}}}}}\) point and is qualitatively consistent with the bulk electronic structure shown in Fig. 3d–f. We emphasize that DFT calculations use the primitive cell convention with a bigger BZ size compared with the surface BZ. Therefore the calculated electronic structure must be folded to the surface BZ, as shown in Fig. 3f. Figure 3g, h show the ARPES intensity plot along the surface \(\bar{{{{\rm{M}}}}}\,-\,\bar{{{{\rm{K}}}}}\) and \(\bar{{{\Gamma }}}\,-\,\bar{{{{\rm{M}}}}}\) direction, respectively. The Dirac-cone structure is clearly resolved along the \(\bar{{{{\rm{M}}}}}\,-\,\bar{{{{\rm{K}}}}}\) direction (Fig. 3g) and consistent with the DFT calculations. However the DFT calculated electronic structure shown in Fig. 3h is only partially resolved. We suspect this is due to the ARPES matrix element effect44 combined with the zone folding effect. As we show in Fig. 3f, the surface Brillouin zone is smaller than the bulk Brillouin zone. Consequently, the purple and green bands shown in Fig. 3h are folded from the bulk BZ and hence may show weaker intensity on the surface.

Fig. 3: Fermi surface and band dispersion obtained from ARPES measurements and DFT calculations.
figure 3

a–c Fermi surface mapping with energy of EF, EF − 0.2 eV and EF − 0.4 eV. \(\bar{{{\Gamma }}}\) is the center momenta in the first surface BZ. d–g DFT calculations on the Fermi surface mapping with kz = π, which correspond to the energies in (b–d). We note that the BZ in (a–c) are with hexagonal type lattice, i.e., conventional cell of Ni3In2S2, which will be three times smaller than the rhombohedral BZ used in the DFT calculation. BZ folding from the DFT calculated one (black hexagon) to the experimental one (red dashed hexagon) is shown in (f). g, h are two bulk band cutting marked in (c), with k∥ follow the yellow and blue lines, respectively.

Full size image

Transport property measurements

The observation of Dirac nodal lines near the Fermi level is expect to affect transport properties of Ni3In2S2. The small effective mass of the Dirac band is expected to significantly enhance the carrier mobility and yield giant magnetoresistance45,46,47. To confirm these effects, in Fig. 4b, c we show the transverse and longitudinal magnetoresistance MR(%) = 100[R(H) − R(0)]/R(0) measured at different temperatures indicated in the figures. The measurement orientations are shown in Fig. 4a. Indeed, we find that the longitudinal magnetoresistance at 1.8 K is non saturating up to 9 T and reaches value of 2000%, supporting a giant magnetoresistance induced by the Dirac nodal line. In the longitudinal geometry, the magnetoresistance is more than one order of magnitude smaller than that in the transverse geometry, consistent with the quasi-two-dimensional electronic structure. Similar magnetoresistance behavior in another crystal is shown in the Supplementary Material.

Fig. 4: Magnetic field dependence of the resistivity and magnetization of Ni3In2S2.
figure 4

a Relative orientations of the current I, magnetic field H, and crystallographic c-axis (conventional setting) for the magnetoresistance measurements. b, c Transverse and longitudinal magnetoresistance MR(%) = [R(H) − R(0)]/R(0) × 100 measured at the indicated temperatures. d Measured magnetization in blue with quantum oscillations clearly seen at higher fields. The oscillating part of the signal (red) is determined by subtracting a polynomial fit (cyan) to the measured data, and is shown over a small field range in (e). f Results of Fourier transforming of the oscillating component vs. 1/B.

Full size image

High carrier mobility is also evidenced by the clear quantum oscillations seen in the magnetization data in Fig. 4d. The presence of several frequencies in these de Haas-van Alphen oscillations is apparent in the small field range shown in Fig. 4e. Fourier transformation of the oscillating component vs. 1/B shown in Fig. 4f gives components corresponding to diameters of kF = 0.12, 0.15, 0.2, 0.22, and 0.247 in \(\frac{\pi }{a}\) (a is lattice constant) for the Fermi surface on kz = 0 plane, in agreement with the DFT calculation (see Supplementary Materials for details).

Discussion

Our theoretical and experimental results establish Ni3In2S2 as the first nonmagnetic kagome material hosting endless Dirac nodal lines near the EF. Ni3In2S2 is therefore a promising material platform to engineer diverse topological electronic states. In the atomic limit, Ni has an even number of electrons, making Ni3In2S2 an “insulator”. In the presence of SOC, Ni3In2S2 is actually a weak topological insulator with topological invariants of z2,1z2,2z2,3z4 = (1112). This indicates that there will be an even number of 2D Dirac cones. Indeed, surface calculations on the (001) surface shows 4 Dirac cones locating at each of the time-reversal-invariant momenta on the surface BZ (see Supplementary Materials). Ni3In2S2 may also turn into a strong topological insulator by making band inversions at the high-symmetry T-point through, e.g., external strain. Furthermore, the inversion and/or time-reversal symmetry-breaking will lift the band degeneracy and induce Weyl points in Ni3In2S2, such as doping of cobalt elements, which may induce a ferromagnetic phase transition and lead to a strong enhancement of physical properties like Nernst conductivity48,49. Finally, although multiple bands are crossing EF, previous studies of Dirac/Weyl semimetals9,47 have shown that the transport properties are determined by massless electrons near the Fermi level. As we show in Fig. 3, the experimentally determined Dirac-point is about 0.2 eV below EF and possibly responsible for the giant magnetoresistance in Ni3In2S2. Our DFT calculation shows that 0.65 e per unit cell is sufficient to bring the Dirac cone to the Fermi level for quantum transport behaviors47. This can possibly be realized by substituting Ni with ~20% Co or substituting In with ~30% Sn. Since In atom is nonmagnetic and contribute only small density of state near the fermi level, Sn substitution of In may induce less disorder effects. The magnetic Co substitution may, however, break the time-reversal-symmetry and give rise to Weyl points as those observed in Co3Sn2S28,23,24,25,26,27,28,29,30,31,32,33,34.

In summary, we observed endless Dirac nodal lines in kagome metal Ni3In2S2. Our results reveal a diverse topological landscape of multiband kagome metals and suggest Ni3In2S2 as a promising material platform to engeering topological electronic structures.

Methods

We performed first-principle calculations based on DFT50 within the Perdew–Burke–Ernzerhof exchange-correlation51 using the Vienna ab initio Simulation Package (VASP)52. The plane-wave cutoff energy is set to be 400 eV with a 11 × 11 × 11 k-mesh in the BZ for the self-consistent calculations, and all the calculations are made considering absence of SOC. Fermi surface and surface state calculations are performed using the tight-binding model of Ni3In2S2, which is obtained from maximally localized Wannier functions53. The lattice constants used in our calculation are a = b = 5.37 Å and c = 13.56 Å, which match with the experimental values of the atomic sites and the lattice constants. For the calculation with hole doping, we reduce the number of total valence electron by 0.65 e per unit cell and compensate it by a uniform background of positive charges via VASP.

The ARPES experiments were performed on Ni3In2S2 single crystals (see Supplementary Materials for growth and crystallographic details). The samples were cleaved in situ in a vaccum better than 5 × 10−11 torr. The experiment was performed at beamline 21-ID-1 at National Synchrotron Light Source II, Brookhaven. The measurements were taken with synchrotron light source and a Scienta-Omicron DA30 electron analyzer. The total energy resolution of the ARPES measurement is ~15 meV. The sample stage was maintained at low temperature (T = 15 K) throughout the experiment.

Transport and heat capacity data were collected using a Quantum Design Dyancool cryostat (see Supplementary Materials). Isothermal magnetization curves were also measured in this cryostat using the vibrating sample magnetometer option, while the temperature dependence of the magnetic susceptibility was measured using a Quantum Design MPMS3 usign the DC measurement option. Contacts for transport measurements were made using Epotek H20E silver epoxy.