Introduction

Polarons are quasiparticles that can form in polarizable materials by entanglement between charge carriers and lattice distortions1,2. An unbound electron or hole injected in a material can interact with the lattice vibrations (phonon). If the electron-phonon coupling is strong enough, the excess carrier induces local structural deformations associated with a potential well in which the carrier is self-trapped3,4. Polarons represent a long-standing yet still exciting field of research with profound impact in different disciplines ranging from physics to chemistry and material science. These charged quasiparticles play a pivotal role in several phenomena of practical importance such as carrier mobility5,6,7,8,9,10,11, surface reactivity12,13,14,15,16 and optical excitations17,18,19,20, as well as representing a testbed for the development of many theoretical models and numerical methods1. Small polarons, whose wave function is spatially confined within a few Ångström (Å) around their trapping site, are subjected to thermally-activated hopping processes, which enable polaron mobility. As a consequence, small polarons can travel through the material forming different spatial distributions (polaron configurations) that have a strong impact on the properties and functionality of the material21. Predicting favorable polaron configurations is key to correctly interpret experimental measurements and predict material’s behaviour, but it is a challenging task. Polaron ground-state distributions result from the balance between contrasting interactions, primarily polaron-polaron repulsion and the attraction between the negatively-charged polarons and the positively-charged donor defects (e.g., oxygen vacancies and/or dopants)22. Considering that polaron formation is favored on surface or near-surface sites, dimensionality effects and surface reconstruction also play a crucial role in defining the optimal polaron configuration, complicating the scenario even further14,21.

Material-specific properties of small polarons are typically computed by using first principles approaches in the framework of DFT and appropriate extensions22,23,24,25. The DFT modelling of defects-induced polarons is complicated by the need to adopt large supercells in order to attenuate artificial interactions between periodic images of the polaron, which hampers an efficient exploration of the huge configurational space and makes the calculations computationally very demanding26,27,28.

The routine approach to explore the polaron configurational space is based on a combination of manual selection and molecular dynamics (MD)22,29,30. This protocol involves a three-step procedure: (i) Generating a pool of initial structures, where the polaron trapping sites are manually selected (using different types of site-controlled strategies22,30,31); (ii) subsequent MD runs at temperatures high enough to activate small polaron hopping, thus allowing for a guided exploration of energetically favorable configurations; (iii) finally, a set of ground-state static DFT calculations for all inequivalent configurations found in the MD runs will determine the energetically favorable solutions at low temperature. This DFT-MD scheme can be easily automatized in a workflow, but the prohibitively long time required to execute MD runs on large supercells and the sporadic thermally-activated polaron hopping events, prevent an efficient exploration and restricts de facto the search to a limited subset of the full configurational space.

An alternative approach to bypass the extensive MD-simulations (step ii) would be to create a larger pool of manually-selected polaronic configurations in step i and directly determine their energy stability as in step iii. However, this strategy relies on human intuition that could bias the selection process of trapping sites, thus excluding possible favorable configurations from the investigated pool. Exhaustive searches including all possible symmetrically inequivalent configurations can be performed for the simplest cases, i.e., the dilute limit, where the amount of polarons is relatively low30. At higher defect concentrations, however, the combinatorial growth of configurations is excessive (i.e., dense limit). Therefore, random sampling approaches have to be used, which cannot guarantee the determination of the proper ground state. For this reason, alternative sampling methods are necessary to correctly describe the properties of materials hosting small polarons.

In this work we propose a data-driven strategy for an accelerated exploration of the polaron configurational space in order to predict the optimal trapping-site patterns for polarons. In recent years, machine learning (ML) has been used extensively in problems involving many combinatorial possibilities32, as in the cases of chemical compound space33, materials design34 and the calculation of potential energy surfaces and force fields35,36,37. ML approaches accounting for the electronic charge, spin, and oxidation states in materials have been recently designed using artificial neural networks38,39,40, however, their application to multi-polaron system has not been addressed yet. Here, we propose a simple kernel regression scheme41,42, with descriptors that embody the polaron-polaron and polaron-defects interactions, trained on minimal DFT datasets to assess the relative stability of the initial (few hundreds) polaron configurations. The trained ML algorithm can then be used to extend the exploration of the configurational space by systematically analyzing millions of configurations, going far beyond the limits of first principles MD or any alternative sampling approaches based entirely on DFT.

The proposed DFT+ML strategy is applied here to two prototypical polaronic materials considering different types of doping: the oxygen-defective rutile TiO2(110) surface12,15,22,29,43,44,45,46 and the Nb-doped perovskite SrTiO3(001) surface47,48,49. We show that the ML-aided search correctly identifies the ground-state polaron configuration for arbitrary carrier density (from the dilute to the dense limit), as confirmed by benchmark DFT tests on selected ML-predicted configurations. Our results show that our proposed method can be employed to efficiently determine the optimal polaron patterns in diverse polaronic materials, and can be trained to account for the interaction of polarons with different point-like defects (oxygen vacancies and dopants, but also interstitials and adatoms for example).

Results

Machine learning approach

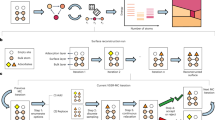
We start with a brief description of the ML-aided algorithm designed to predict the stability of multipolaron configurations (more details can be found in the Methods 4). The schematic protocol, shown in Fig. 1, involves a mapping between a general surface structure containing charge-donor defects (e.g., dopants or oxygen vacancies, Fig. 1(a)) and possible polaron hosting sites (typically transition metal ions) with a kernel-regression scheme. The connection is established by means of a simple descriptor (D) of local interactions (Fig. 1b, details provided in Descriptors section) which encode the spatial distance between the reference polaron to other polarons and point defects included within a cutoff sphere. This representation is used in a kernel regression scheme (Fig. 1(c)) to map a given many-polaron configuration to the corresponding polaron formation energy (Epol) as calculated by DFT (see Fig. 1(d)). In DFT the polaron formation energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) is defined as the total energy difference between the polaronic solution (\({E}_{{{{\rm{loc}}}}}^{{{{\rm{dist}}}}}\), with the excess charges localized in a locally distorted lattice sites) and the delocalized solution (\({E}_{{{{\rm{deloc}}}}}^{{{{\rm{undist}}}}}\), with all excess electrons uniformly delocalized over the lattice), \({E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}={E}_{{{{\rm{loc}}}}}^{{{{\rm{dist}}}}}-{E}_{{{{\rm{deloc}}}}}^{{{{\rm{undist}}}}}\)22. In our approach, the kernel regressor assigns a virtual single-polaron energy to every polaron in the configuration; the predicted single polaron energies are summed up to return the total polaronic energy of the test configuration, which can be compared to the Epol calculated by DFT.

Fig. 1: Schematic representation of the ML model.
figure 1

a Sketch of a polaron configuration in a generic atomic structural model. Possible polaron-trapping sites (blue circles), defects (dopants and atom vacancies, green and white circles, respectively) and schematic representations of polaron charge densities (yellow) are shown. The local interactions of the reference polaron with the defects and other polarons are indicated by arrows. b Descriptor representation \({\mathbf{D}_i^{\prime}}\) for every polaron in the configuration. The strength of the polaron-polaron and defect-polaron interactions are represented by colour gradient (from blue to pink, details in Descriptors section and Supplementary Methods). c Kernel functions k( ⋅ , ⋅ ) with parameters αi measure the similarity of the target-polaron descriptor \({\mathbf{D}^{\prime}}\) with the training-set samples Di , and assign a virtual single-polaron energy to every polaron in the configuration. d The ML-predicted single-polaron energies are summed up to return the total polaronic energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) of the configuration, which can be compared to the \({E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\).

Full size image

This scheme is used to first train the kernel regressor on an energy dataset of different polaronic configurations calculated by DFT. Then, the trained ML algorithm can be applied to polaron configurations not included in the DFT training database, in order to drastically expand the exploration of the configuration space. To ensure the quality of the predictions, the optimal polaron patterns identified by the ML algorithm can be ultimately tested and refined by few final DFT calculations.

In the following, we assess the quality and general efficiency of this computational strategy on rutile TiO2(110) and perovskite SrTiO3(001) surfaces by studying the relative stability of millions of possible polaron configurations with varying polaron concentration (i.e., various polaron densities), from the dilute to dense polaron limits.

Rutile TiO2(110)

The structural unit of rutile TiO2(110) is sketched in Fig. 2(a). The surface layer S0 consists of alternating rows of five- and sixfold-coordinated Ti atoms, referred to as TiA and TiB, respectively. Sub-surface and sub-sub-surface layers are indicated with the label S1 and S2, respectively. Ti atoms coordinated below the surface Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{A}}}}}\)/ Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{B}}}}}\) sites are labelled as A-/B-sites, respectively, with an additional subscriptlindicating the layer, e.g., Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\) refers to a TiA site located in the subsurface layer S1, whereas Ti\({}_{{{{\rm{S2}}}}}^{{{{\rm{B}}}}}\) indicates a B-type Ti located in S2. The surface terminates with two parallel rows of oxygen atoms oriented along the [001] direction, which are easily removable to form surface oxygen vacancies (VO). Each VO effectively donates two electrons that can be trapped in titanium sites converting two pristine Ti4+ ions into Ti3+ ions. Increasing the oxygen vacancy concentration \({c}_{{V}_{{{{\rm{O}}}}}}\) leads to higher densities of polarons. Due to the combinatorial growth of accessible polaron configurations with progressively larger amounts of polarons, finding the most favorable distribution of polarons is a very challenging task.

Fig. 2: Results of methodology when applied to TiO2(110).
figure 2

a Structural model of rutile TiO2(110) with the correpsonding labeling. b, c Comparison of DFT and ML-derived mean polaron energies \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) and \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) for the training data in a randomized split are shown in (b) and the validation and test data are shown in (c). The color encodes the corresponding defect concentration of each configuration. d Collection of the results of the nine omitted defect concentrations (validation of the extrapolation capabilities) and the exhaustive search are shown. The black dashed curve gives the convex hull of polaronic energies from the training database and dots show \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) for each configuration, where the size of the dots corresponds to the favorability of each configuration as assigned by the ML model. The convex hull from the exhaustive exploration at the DFT-level is given in solid black with triangles indicating the most stable configuration’s energy.

Full size image

Here we employ a 5 layers thick slab with a large 9 × 2 two-dimensional (2D) unit cell containing 36 Ti sites per layer14,21. Since the bottom two layers are fixed to bulk form (polaron inactive since no structural relaxation are allowed), this setup results in 108 potential trapping sites. We have inspected nine different defect concentrations starting from 1 VO per 2D unit cell (corresponding to \({c}_{{V}_{{{{\rm{O}}}}}}\) = 5.5%) up to 9 VO (\({c}_{{V}_{{{{\rm{O}}}}}}\) = 50%). Since polaron trapping at Ti sites follows a binomial distribution, the number of possible configurations ranges from ≈5 × 103 (2 polarons, \({c}_{{V}_{{{{\rm{O}}}}}}\) = 5.5%) to ≈1020 (18 polarons, \({c}_{{V}_{{{{\rm{O}}}}}}\) = 50%), without considering symmetries (see Supplementary Notes for a more detailed discussion).

To tackle this formidable problem, we rely on a previously generated MD polaron energy dataset14,21. It consists of 492 symmetrically-inequivalent polaron configurations, obtained by running MD simulations at nine different VO concentration levels (ranging from \({c}_{{V}_{{{{\rm{O}}}}}}\) = 5.5% up to \({c}_{{V}_{{{{\rm{O}}}}}}\) = 50%). Details on the database are provided in Supplementary Table 1. The MD-based dataset suggest that at low \({c}_{{V}_{{{{\rm{O}}}}}}\), polarons preferably localize at Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\) sites, while at higher defect and polaron concentration the S0 sites become comparatively more populated14,21.

To begin with, this DFT-MD database was split in train, validation, and test datasets (70%, 20%, 10%, respectively). The ML scatter plots shown in Fig. 2b, c show that the model can well reproduce the \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) with a mean square error MSE ≈ 1.2 ⋅ 10−4 for training, and MSE ≈ 1.3 ⋅ 10−4 for both validation and test (see Supplementary Table 5). We note that configurations at very shallow \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) (i.e., values higher than −0.2 eV) show larger errors, which we attribute to the lack of samples in the training dataset, owing to rare occurrence of these unfavorable polaronic solutions in the MD. In fact, these polaron energies correspond to configurations where a polaron is localized on the unstable Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{B}}}}}\) site. Since we aim to identify the optimal polaron configuration, this issue is not of great concern, but it highlights the need of a well representative sampling of the polaron configurational space. As we show in SrTiO3(001) section, a random sampling can overcome these limits of an MD-generated database.

To assess the validity of our method to predict configurations that strongly differ from the available training data, we have performed an additional test on unexplored polaron VO concentrations, by adopting the ’omitted defect concentration’ strategy described below. We constructed nine distinct test cases, one for each VO concentration level available in the MD database. In each of these cases, we limited the training dataset to samples belonging to only 8 of the 9 available defect concentrations. Finally, we tested the model on the remaining concentration, not used in the training. We analyzed qualitative and quantitative aspects of this procedure by conducting a direct comparison between ML-derived and target DFT energies for specific defect concentrations. We also compared the most stable configurations found via ML and via DFT-MD, by means of a convex hull diagram (reporting the most stable configuration at every defect concentration), to inspect whether ML is capable to deliver a qualitatively consistent energy landscape. This is particularly important for the case under study, since experimental measurements indicate that, for \({c}_{{V}_{{{{\rm{O}}}}}}\) ≈ 20%, highly defective TiO2(110) undergoes a 1 × 1 to 1 × 2 surface reconstruction, which can be connected to a lowering of the polaron energy with increasing \({c}_{{V}_{{{{\rm{O}}}}}}\)beyond a certain critical polaron concentration14,50.

The results are collected in Fig. 2(d) and in the Supplementary Fig. 5 and Supplementary Table 5. Even though we notice an apparent loss of precision for configurations that are different from those included in the training data, leading to larger systematic errors (the resulting MSE of \({\overline{E}}_{{{{\rm{pol}}}}}\) is of the order of 10−3 for all test concentrations), the ML model is still able to correctly identify the optimal arrangements of polarons from the MD dataset and find the correct minimum at \({c}_{{V}_{{{{\rm{O}}}}}}\) = 22%. This is shown by the dot sizes in Fig. 2(d), indicating the ML-predicted favorability of a configuration relative to other predicted configurations in the respective defect concentration. This result demonstrates that the DFT+ML scheme, trained with the available DFT dataset, is capable to predict with good accuracy the relative stability of solutions corresponding to different concentrations.

From these results, based on a ML-processing of the DFT-MD input database, we can conclude that a large-scale ML-based systematic search of new configurations (i.e., configurations not included in the original DFT database) should be feasible, provided that the final results are validated by a subsequent comparative DFT simulation. In this way, an accelerated ML exploration of the full configurational space would be possible, and only a small fraction of first principles calculations would be necessary, limited to the most favorable configurations found by ML. Different methods could be used to perform this exhaustive search in the configuration space, and find the optimal polaron arrangement for each concentration: Our designed ’exhaustive search’ strategy is described in the following.

Systematic search of configurations via ML

An efficient search in the entire configuration space needs to address the problem of the combinatorial growth of polaron configurations with increasing polaron density (increasing \({c}_{{V}_{{{{\rm{O}}}}}}\)). In our DFT calculations, the unit cell contains 108 possible Ti trapping site, leading to \(\left({108}\atop{18}\right)\approx 1{0}^{21}\) possible arrangements of polarons in the most defective case (\({c}_{{V}_{{{{\rm{O}}}}}}\) = 50%, 9 VO defects in our cell with 18 polarons). To cope with this huge combinatorial space, and avoid an inefficient blind search, we have developed a bottom-up searching strategy based on the concept of polaron building units. We have first trained our ML model on the entire DFT-MD database (492 inequivalent configurations). We have then addressed the problem of two polarons (lowest considered concentration, \({c}_{{V}_{{{{\rm{O}}}}}}\) = 5.5%) and predicted all \(\left({108}\atop{2}\right)=5778\) possible variants using the ML model, thus extending considerably the available DFT-MD database at that concentration. From these 5778 configurations we selected the 100 with the most favorable polaron energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) as calculated by ML, and used them as polaron building units to construct the polaron configurations at the next concentration level (\({c}_{{V}_{{{{\rm{O}}}}}}\) = 11.1%, 4 polarons). To this aim, we followed the same additive strategy, namely adding two additional polarons to each of the 100 two-polarons configurations, scrutinizing with the ML model all 106 not yet occupied hosting sites. Similarly to the previous concentration, also in this case only a subset of 100 distinct, energetically most favorable configurations has been used to build the next configurations (\({c}_{{V}_{{{{\rm{O}}}}}}\) = 16.7%, 6 polarons). The same protocol has been adopted for all higher concentrations. Finally, at each concentration the three best ML-predicted polaron configurations have been verified by performing a DFT run using ML-predicted pattern as input with a selective initialization of the occupation matrix (see Density Functional Theory section and Supplementary Methods). We refer to these final set of energies as exhaustive search ML-DFT energies.

The scheme described above allows for a quick calculation of roughly 4 ⋅ 106 configurational energies, excluding a larger number of highly unfavorable configurations, and keeping the computational cost constant among each defect concentration. The results are displayed in Fig. 2(d), where we show the comparison between the reference MD-DFT convex hull (input database, dashed line) and the best obtained ML-DFT energies at each concentration (full lines). In Supplementary Figs. 6 and 8a, b most stable configurations and the distribution of polarons to specific sites, respectively, are shown. Supplementary Table 7 and Supplementary Fig. 9 displays the energy distribution of the most relevant polaron configurations at \({c}_{{V}_{{{{\rm{O}}}}}}\)= 11.1%. The overall outcome is very satisfactory with a few positive aspects to note. First, the ML-aided DFT procedure finds a lowest absolute minimum not present in the MD database, clearly demonstrating the remarkable efficiency of the proposed ML scheme in exploring the configurational space. The absolute minimum is shifted from \({c}_{{V}_{{{{\rm{O}}}}}}\)= 22.2% to 27.8% resulting in a much smoother shape of the ML-derived convex hull. At defect concentrations lower than 22% the two curves essentially overlap, with the ML configurations all slightly lower than the best MD configurations (in this case with a modest improvement of few meV). More subtle are cases at \({c}_{{V}_{{{{\rm{O}}}}}}\) > 33%, where polarons start populating Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{B}}}}}\)-sites. This is due to a poor sampling of Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{B}}}}}\)-site in the MD simulations, and to a tendency at high concentration towards charge delocalization which impedes a site-specific assignment of the excess charge, pushing the system out of the polaron regime. This problem has been particularly obvious at the highest concentration, where we were not able to reproduce the low-energy configurations predicted by the ML-model in our DFT calculations (see missing data point of ML-DFT curve at \({c}_{{V}_{{{{\rm{O}}}}}}\) = 50%). As already mentioned, to avoid an unrealistic densely-packed arrangement of polarons or occupation of highly unfavorable trapping sites (unlikely to be observed in experiment51), TiO2(110) samples undergo a polaron-driven (1 × 1) → (1 × 2) structural reconstruction at \({c}_{{V}_{{{{\rm{O}}}}}}\) ≈ 20%14. Therefore, the apparent inefficiency of the ML search above the critical concentration is not an intrinsic deficiency of the designed strategy, rather it should be traced back to physical arguments that hamper the construction of a suitable database for an unrealistic situation. Forcing the structure to maintain the (1 × 1) symmetry leads to formation of Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{B}}}}}\) polarons, which are energetically not favorable, and tend towards charge delocalization and to polaron diffusion to the bulk (trapping at S2 sites)52. In this sense the present ML data provide further support and validation to the DFT-based description of the polaron-driven surface reconstruction discussed in ref. 14.

SrTiO3(001)

To assess the degree of transferability and generality of the proposed methodology we applied a similar scheme to Nb-doped SrTiO3(001), a different structure (atomically flat perovskite surface, see Fig. 3(a)) with different source of excess charge (chemical doping instead of VO), resulting in different type of interaction categories (see Descriptors section). To further generalize our DFT+ML procedure we decided to follow a different strategy to build the necessary DFT database. Instead of MD runs, which require long execution time and could result in an inefficient exploration of the configuration ground state, we have adopted a randomly generated polaronic database using the occupation matrix approach (see Density Functional Theory section, Supplementary Table 2 and Supplementary Methods). This procedure has few advantages as compared to the MD-sampling methodology. First of all, obtained samples are less correlated than in the MD-runs. Secondly, the bias towards low energy configurations, which are disproportionately more often visited in an MD-simulation, is removed. This should result in a more general model that has higher accuracy across all possible polaron patterns. Lastly, and most importantly, it fully bypasses the cost of the MD-simulations and only the structural relaxations for each distinct polaronic pattern has to be performed (see Supplementary Discussion). Following the same protocol as discussed in the previous section, we again performed a randomized split for training the model on the entire database, consisting of 379 polaronic configurations. Following this we assessed the extrapolation capabilities by testing the model on defect concentrations not present in the training data. Lastly, we performed an exhaustive bottom-up search for all defect concentrations, were we then evaluated most favorable predictions at the DFT-level.

Figure 3b, c show the results from the randomized data-split. The model is converged to a similar extent as in the case of TiO2 (\({\overline{E}}_{{{{\rm{pol}}}}}\) MSE of 5.7 ⋅ 10−5, 9.3 ⋅ 10−5 for training and test data, respectively), and, noticeable and unlike TiO2, the model delivers consistent accuracy at virtually all energies. This increased performance most likely originates from the less biased energy database obtained by the random sampling. In the case of omitted defect concentrations (relative favorability prediction shown in Fig. 3d), the model correctly extrapolates the low energy configurations for the omitted concentration based on the energies of the 4 included concentrations, and suffers to a smaller extent from systematic errors as compared to TiO2 (compare TiO2 and SrTiO3 cases in Supplementary Tables 5 and 6 as well as Supplementary Fig. 5).

Fig. 3: Collection of results when applying the methodology to SrTiO3(001).
figure 3

a Model of the surface slab and the corresponding labeling. Comparison of \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) and \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) for the training data in a randomized split are collected in (b) and the validation and test data are shown in (c). The color encodes the corresponding Nb-dopant concentration (cNb) of each configuration. d Collection of the results of the five omitted defect concentration cases and the exhaustive search are shown. The black dashed curve gives the hull of polaronic energies obtained from the training database and dots show \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) for each configuration, where the size of the dots corresponds to the ML-model’s assigned favorability of each configuration. The Nb-concentration dependent polaronic ground state energy from the exhaustive exploration is given solid black with triangles marking the ML-predicted configuration’s energy (all energies at DFT-level).

Full size image

Finally, we tested the efficiency of the exhaustive ML search, by exploring 2.25 ⋅ 106 nonequivalent configurations. The outcome (see dashed and full line in Fig. 3(d)), clearly shows that this ML-augmented scheme outperforms the standard random-database approach, as it finds multiple configurations lower in energy than the minima identified in the randomized search, at any polaron concentration. We confirmed the five lowest energies \({E}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) predicted by the ML exhaustive search at each Nb-concentration by a comparative static DFT-calculation and each of the ML-predicted polaron pattern was found more stable than the optimal pattern included in the training database. The most stable configuration predicted by ML (see Supplementary Fig. 7 for a collection of the most optimal polaron configurations) typically improved the mean polaronic energy \({\overline{E}}_{{{{\rm{pol}}}}}\) by 30 to 50 meV compared to the reference data. Interestingly, the results of the exhaustive ML search suggest a rationale for the most stable configuration based on a few simple rules: the energetically most stable configurations host polarons in the surface and subsurface layer, usually placed as close as possible to the Nb-dopants (preferably below or above a dopant rather than in the same atomic layer (see site distribution of favorable configurations collected in Supplementary Fig. 8(c)).

Discussion

In this paper we presented an ML-aided procedure to enhance and accelerate the identification of small polaron ground state configurations in multi-defect systems with varying defect concentration, by employing simple and general descriptors based on distance-dependent interaction categories and a standard kernel regression fed by a DFT energy database. We tested and discussed a few alternative protocols:

  1. (i)

    A conventional train/validation/test ML protocol.

  2. (ii)

    Omitted-defect concentration model, based on extrapolating the polaron energy for a given defect concentration from the DFT energies obtained at other concentrations.

  3. (iii)

    Exhaustive ML search. An exploration of the polaron configurational space based on a guided bottom-up selection of the most favorable configuration from all possible nonequivalent configurations at each given defect concentration.

We assessed the generality of the procedure by applying it to two different materials (TiO2(110) and SrTiO3(001)) with different types of defects (VO and Nb dopants) and adopting different strategies to construct the DFT database (MD and random sampling). Our data indicates that a randomized sampling approach is superior to MD-generated database which suffers from undesirable correlation between the MD-generated configurations and excessive computational cost. Importantly, the combination of random sampling and exhaustive ML search results in a robust algorithm that delivers very good results, as demonstrated for SrTiO3(001) where this procedure leads to a systematic improvement at all explored concentration: the exhaustive ML search finds configurations with lower 0-K DFT energy as compared to those included in the input database.

While our model has been applied to the identification of polaron configurations with static dopant/vacancy patterns, it can be further extended to consider optimized configurations with mobile point defects considering other type of defects (e.g. hydrogen adatom or Ti interstitials) and other materials9. In fact, the descriptor only relies on identifying polaron hosting sites with different local coordination and lattice symmetry and their relative position with respect to the surface, to structure a list of distances between polarons and defects. From this information, the descriptor structure can easily be attained for any material and only few parameters (i.e., number of included distances in each interaction category and cutoff radius) need to be determined to optimize the performance.

A final positive aspect offered by the proposed method is the arbitrary scalability with respect to the supercell size, enabling access to large scale simulations, where defect arrangements could be precisely aligned with experimental data, to determine likely polaronic configurations observed in surface imaging techniques. We note, however, that the unit cells used to train the ML model must be sufficiently large (e.g., at least as large as those used in this study, see Methods Section) in order to prevent spurious effects arising from the interaction of the charged point-defects with their periodic image in the DFT calculations. Also, qualitative extrapolations and interpolations to defect concentrations where no data is available and predictions seem plausible in the presented test cases and could be further developed.

Methods

Density functional theory

Density-functional theory (DFT) and first-principles molecular dynamics (MD) calculations were performed using the Vienna Ab-initio Simulation Package (VASP)53,54. For our DFT+U calculations we adopted the generalized gradient approximation with Perdew, Burke, and Ernzerhof parametrization (PBE)55, including an on-site effective U = 3.9 eV enacted on the d-orbitals of Ti atoms in the case of rutile TiO2 (previously determined by constrained random-phase approximation (cRPA)44) and U = 4.5 eV for SrTiO3, here enacted on the d-orbitals of Ti and Nb, in line with the cRPA value determined in previous works.56,57,58 Standard projector-augmented wave (PAW) potentials59,60 were used for Ti, Sr and Nb atoms, while oxygen was modeled adopting softer potentials to reduce convergence requirements on the energy cutoff. We used the Γ point only for the integration in the reciprocal space, and standard convergence criteria with a plane-wave energy cutoff of 250 eV21 for rutile TiO2, and 350 eV for SrTiO3.

The rutile TiO2(110) and SrTiO3(001) surfaces were modeled by super cells, containing five stochiometric layers in large two-dimensional 9 × 2 and 6 × 4 unit cells, respectively. The large lateral dimensions of the unit cells allow for a high number of possible polaron patterns, and reduce to a negligible extent the spurious interaction of charged point-defects with their image in the calculations with periodic boundary conditions21. The three surface layers and the corresponding labeling are shown in Figs. 2(a), 3(a). In both cases the bottom two stochiometric layers were kept fixed at bulk positions in order to mimic and retrieve the electronic and structural properties of the bulk. Oxygen vacancies (VO) on the two-fold coordinated O sites on the TiO2 surface, and Nb dopants replacing Ti atoms on the surface and subsurface SrTiO3 layers, were modeled at nine and five different concentration levels, \({c}_{{V}_{{{{\rm{O}}}}}}\) and cNb respectively. The defect positions were chosen such that inter-defect distances are maximized, and the concentrations are given in percentage with respect to the number of two-fold surface oxygen sites in TiO2 and the total number of Ti sites in SrTiO3. SrTiO3 is known to exhibit a wide variety of surface reconstructions, and it has recently been shown that flat bulk-terminated (001)-surface with surface defects can be stabilized using novel cleaving procedure61,62.

The polaronic localization sites were identified by inspecting the size of the local magnetic moments on Ti ions (larger than 0.5μB) and relaxations to 0 K have been performed from each distinct polaron localization pattern. In the case of rutile TiO2 nonequivalent polaron configurations were generated via MD at high temperature (700 K). Instead, to build a database of polaronic configurations in SrTiO3, for each concentration, an appropriate number of Ti sites within the top three layers were randomly chosen to host the polarons. For localizing the excess charge in the selected Ti hosting site we employed the occupation matrix control tool30. This tool allows us to constrain the electron density matrix of atoms in the cell directly, such that a polaron can be placed explicitly at the desired site, and in the desired orbital. Polaron configurations suggested by the exhaustive ML-aided search were always initialized via occupation matrix control, starting from initial occupation matrices taken from the training databases. Examples of occupation matrices are collected in the Supplementary Material in Section S2.

A final note on the calculation of the DFT polaron energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\): DFT calculations do not grant access to formation energies of individual polarons, but only to the total energy of all polarons in the unit cell. In order to compare polaron formation energies for configurations with different polaron concentration, we defined a mean polaronic energy \({\overline{E}}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}={E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}/{N}_{{{{\rm{pol}}}}}\), obtained by averaging over the number of polarons Npol in a given configuration. This operation allows us to compare the polaron energies obtained for different defect concentrations.

Descriptors

To design a suitable descriptor, we have exploited the fact that polaron energies are affected by two main interactions21:

  1. (i)

    Electrostatic interaction between charged defects: attractive interaction between negatively charged polarons and positively charged defects and polaron-polaron repulsion, both rapidly decreases with increasing spatial separation.

  2. (ii)

    Polaron orbital symmetry, determined by the local coordination and symmetry of the hosting site as well as by the distance from the surface layer (For example, in rutile TiO2(110) the distance-dependence of the polaron-polaron Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\)-Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\) interaction is different from Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\)-Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{A}}}}}\)21).

Based on these principles, we designed a descriptor composed of a list of pairwise polaron-polaron and polaron-defect interactions, defined by the corresponding inter-polaron and polaron-defect distances within a cutoff-sphere Rc around each polaron (defect: VO and Nb, for TiO2 and SrTiO3, respectively). In this way, fixed portions of the descriptor vector can be assigned to specific interaction categories. An interaction category always depends on the local coordination of the hosting site (e.g., Ti\({}_{{{{\rm{S1}}}}}^{{{{\rm{A}}}}}\)) and the local coordination of its interacting partner (e.g., Ti\({}_{{{{\rm{S0}}}}}^{{{{\rm{A}}}}}\)). Within each interaction category, a fixed number of preassigned slots n can be used, containing rescaled distances according to the expression:

$${f}_{{{{\rm{c}}}}}(d)=\left\{\begin{array}{ll}\frac{1}{2}\left(1+\cos \frac{\pi d}{{R}_{{{{\rm{c}}}}}}\right)\quad \quad &\,{{\mbox{if}}}\,\,d\le {R}_{{{{\rm{c}}}}}\\ 0\quad \quad &\,{{\mbox{else}}}\,\end{array}\right.$$
(1)

The rescaling allows that the vector is filled with zeros, were no interaction is present. For an exemplary description of the evaluation of a polaron descriptor see the Supplementary Methods. Mind that each descriptor corresponds to the environment of a single polaron. Therefore, the number of descriptors from the databases are 4368 and 2257 for TiO2 and SrTiO3, respectively.

We complete this section by providing a brief description of the resulting interaction categories for TiO2 and SrTiO3. More details can be found in Section S3 in the Supplementary Materials.

Interaction categories in TiO2(110)

In rutile TiO2 the three topmost layers contain hosting sites with two different local orientations, for a total of 36 interaction categories (Ti\({}_{{{{\rm{Si}}}}}^{{{{\rm{X}}}}}\)-Ti\({}_{{{{\rm{Sj}}}}}^{{{{\rm{Y}}}}}\), with X,Y ∈ {A, B} and i,j ∈ {0, 1, 2}). Due to the employed 9 × 2 supercell and the slightly different distance-dependence of stacked and non-stacked hosting sites of same local coordination21, we distinguish between stacked (A- or B-sites) and non stacked (\({{{\rm{A}}}}^{\prime}\)- or \({{{\rm{B}}}}^{\prime}\)-sites). This adds 18 additional interaction categories. Lastly, a category for the interaction with the VO is added for each differently coordinated sites (Ti\({}_{{{{\rm{Si}}}}}^{{{{\rm{X}}}}}\)-VO, with X ∈ {A, B} and i ∈ {0, 1, 2}), resulting in 60 possible interaction categories. Three shortest distances per interaction category and a cutoff radius of 15 Å resulted in optimal model predictions for this descriptor. The full list of interaction categories for TiO2 is given in the Supplementary Materials in Supplementary Table 3 and examples of interaction categories are collected in Supplementary Figs. 1, 2.

Interaction categories SrTiO3(001)

Cubic and atomically flat SrTiO3 has a more symmetrical structure, which results in a simpler descriptor. The three topmost layers contain identically coordinated hosting sites, leading to nine different interaction categories (TiSi-TiSj, with i,j ∈ {0, 1, 2}). However, a more fine grained distinction of polaron-dopant interactions is necessary, since dopants can in principle lay in any layer (unlike VO in rutile TiO2(110)). Therefore, we consider six additional interaction categories (TiSi-NbSj, with i ∈ {0, 1, 2} and j ∈ {0, 1}), resulting in a total of 15 different interaction categories with an optimal number of four included distances per category and a Rc = 13 Å. A full list of interaction categories for SrTiO3 is given in the Supplementary Materials in Supplementary Table 4 and examples of interaction categories are collected in Supplementary Fig. 1.

Machine learning model

We have used instance-based learning in form of kernel regression41, where a kernel-function k( ⋅ , ⋅ ) (or similarity measure) of the descriptor of interest \({\textbf{x}}^{\prime}\) and all descriptors xi of the training set is calculated and scalar multiplied with the optimized regression parameters α, giving a weighted mean of the target quantity based on similarity to training instances:

$$y^{\prime} =\mathop{\sum }\limits_{i=1}^{N}k({{{{\bf{x}}}}}_{i},{{{\bf{x}}}}^{\prime} ){\alpha }_{i}$$
(2)

We determine optimal regression parameters of each kernel regressor, corresponding to a specific type of polaron, via backpropagation and gradient-descent performed on the sum of each kernel regressors prediction. We found that training the regressors with a stochastic gradient descent variant results in better extrapolation capabilities than performing an exact fit. To optimize regression parameters of the different kernel regressors on the training data, the predicted energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}}\) is used to calculate the loss function with respect to the target polaron energy \({E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}}\) of the configuration from the training dataset . We employed an adapted mean squared error loss function J, where the error of each training sample is normalized to the number of polarons in the configuration (Npol,i).

$$J({E}_{{{{\rm{pol}}}}}^{{{{\rm{ML}}}}},{E}_{{{{\rm{pol}}}}}^{{{{\rm{DFT}}}}})=\mathop{\sum}\limits_{i}{({E}_{{{{\rm{pol}}}},i}^{{{{\rm{ML}}}}}-{E}_{{{{\rm{pol}}}},i}^{{{{\rm{DFT}}}}})}^{2}/{N}_{{{{\rm{pol}}}},i}$$
(3)

Without a normalization of the error to the number of polarons, the model tended to systematically underpredict energies at low defect concentrations, which can likely be attributed to a greater total number of polarons at high defect concentrations. More polarons result in a cumulative higher error and the model shifts towards providing a better fit for configurations with many polarons at high defect concentrations – compromising accuracy for configurations with fewer polarons. For the optimization of the loss function, an Adam optimizer63 has been used with a learning rate set to 0.0001, which resulted in slow yet consistent convergence of regression parameters (see Supplementary Fig. 3, also showing error convergence in dependence of training samples). It has been found that an initialization of regression parameters set to 0 resulted in a faster convergence than a random initialization. A batch size of 64 randomly chosen configurations per epoch, and a weight decay of 0.1 to enforce small regression parameters, also benefited convergence of the model to consistent performance throughout many tests. We used the Laplacian kernel

$$k({{{{\bf{x}}}}}_{i},{{{{\bf{x}}}}}_{j})=\exp \left(-\gamma \,| | {{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}| {| }_{1}\right)$$
(4)

for all models and found that a hyperparameter γ between 0.1 and 0.5 leads to optimal results (see Supplementary Fig. 4). The algorithm has been implementd using NumPy64 and Scikit-Learn65 for preprocessing, and PyTorch66 to perform the backpropagation and optimization of parameters.