Abstract
Nanoparticle corona phase (CP) design offers a unique approach toward molecular recognition (MR) for sensing applications. Single-walled carbon nanotube (SWCNT) CPs can additionally transduce MR through its band-gap photoluminescence (PL). While DNA oligonucleotides have been used as SWCNT CPs, no generalized scheme exists for MR prediction de novo due to their sequence-dependent three-dimensional complexity. This work generated the largest DNA-SWCNT PL response library of 1408 elements and leveraged machine learning (ML) techniques to understand MR and DNA sequence dependence through local (LFs) and high-level features (HLFs). Out-of-sample analysis of our ML model showed significant correlations between model predictions and actual sensor responses for 6 out of 8 experimental conditions. Different HLF combinations were found to be uniquely correlated with different analytes. Furthermore, models utilizing both LFs and HLFs show improvement over that with HLFs alone, demonstrating that DNA-SWCNT CP engineering is more complex than simply specifying molecular properties.
Similar content being viewed by others
Introduction
Antibodies are the most well-known nano-scale constructs capable of molecular recognition (MR) through adsorption to an intended target. Their generation and implementation since 1975 have enabled paradigm shifts in the biomedical sciences1. As the MR component of a large proportion of rapid tests and laboratory assays2, they are integral in chemical detection, food safety, and physiological sensing. One of their most recognizable applications is the home pregnancy test, where monoclonal antibodies against the human chorionic gonadotropin is used in a lateral flow assay3. As targeted therapeutics, or biologics, they are a widely produced class of pharmaceuticals that enable precision treatment of cancer and autoimmune conditions4. However, despite extensive use, their design still involves a selection process based on biological machinery5. Recently work has also explored synthetic MR design, including: nucleotide aptamers6, non-immunoglobulin protein scaffolds7, and molecularly imprinted polymers8. Potential limitations of these alternative approaches include: high cost, low stability, inability to detect different classes of molecules, and mostly importantly, the lack of a data driven method for design that is able to learn from past experimental results.
An emerging area of synthetic MR that involves the design of the nanomaterial corona phases (CP) is corona phase molecular recognition (CoPhMoRe)9. The CP of a nanoparticle is the thermodynamically-controlled coverage of a material’s surface formed from adsorbed molecules. These non-covalent modifications, whether from synthesis or the environment, often serve as the interface that determines a material’s properties10. In the case of single-walled carbon nanotubes (SWCNTs), their aqueous dispersion through adsorption of small molecules or polymers form surface CPs that can be capable of MR. Furthermore, the discovery that binding events can be transduced through the SWCNT’s intrinsic band-gap photoluminescence (PL)11 led to a series of studies that demonstrated promising photophysical detection of multiple classes of analytes, including: reactive species12, metal ions13, small molecules14, and biological macromolecules15. One advantage of such a system is that the SWCNT material functions of both MR and optical signal transduction sensor component, minimizing interfacial losses in other two-component designs.
SWCNT CoPhMoRe generation also faces a similar challenge of an enormous design space, starting with the need to formulate of a large library of unique CPs that can also stably disperse single SWCNTs in the solution phase16. Fortunately, single-stranded DNA molecules have been demonstrated to stably disperse SWCNTs and also are a common class of polymers that can be synthesized rapidly with molecular precision. Thus, DNA-SWCNTs have been a rich resource for MR design17,18. The nucleotide base (NB) dependent nature of interactions between DNA and SWCNTs have been studied both computationally19,20 as well as experimentally at the single-molecule21 and short motif level22. However, there currently exists no intuition to effectively design DNA CPs for the purposes of MR. The most common approach is a systematic enumeration of the sequence design space guided by global intuitions on sequence composition23. Considering that there are 4L permutations of DNA sequences (L being the sequence length), which then encodes for complex secondary and tertiary DNA structures that are also influenced by unique interactions from adsorption to the low-dimensional SWCNT, intuitive or random screening-based search methods are highly inefficient for converging on to promising targets.
Recently, machine learning (ML) techniques have been of considerable interest in exploring these complex materials design spaces. The goal of these methods are to perform classification and prediction tasks to optimize predefined metrics related to materials properties. In 2018, Yang et al. performed the first ML-based study of DNA-SWCNT, specifically for the application of sequence dependent SWCNT chirality separation in aqueous two-phase systems24. By limiting the DNA strand length to 12 NBs, 82 strands were modeled using a panel of learning algorithms to demonstrate a higher than 50% success rate of finding chirality separation sequences. To date, no such computational study or uniformly controlled large dataset exist for the evaluation of DNA-SWCNT CoPhMoRe development.
This work demonstrates an approach using ML in order to identify and inform DNA-SWCNT MR. Specifically, the goal is to use ML to predict which DNA sequences enable better SWCNT PL analyte responses for each specific experimental condition. A panel of previously untested analytes (cadmium, enrofloxacin, chloramphenicol and semicarbazide) were selected based on the need for rapid and quantitative testing technology for adulteration in the aquaculture supply chain25. To enable this ML approach, DNA-SWCNT PL spectra change from analyte exposure were collected to create the largest sensing response library to date for 176 randomly chosen DNA sequences in eight different experimental conditions. From this training data, ML predictions for DNA sensor responses were made using the following three steps. First, a convolutional neural network (CNN) was used to predict shorter-length DNA motifs correlated with photophysical responses, which we refer to as local structure predictions26,27,28. Second, independent features were created based on a principal components analysis (PCA) vectorization of 40 high-level features (HLFs) (e.g., molecular weight, melting point, dimers, etc.)29. Third, these HLF and CNN model outputs were then both used as independent features for gradient-boosted decision trees (GBDTs) in order to produce the final predictions regarding whether DNA sequences can produce promising sensor candidates for each analyte and sensing environment30. The study demonstrated that these ML models can significantly predict DNA-SWCNT MR with relatively few data points. Through interpretation of the HLFs significantly correlated with improved MR, general properties that increases sensor response can also be identified (e.g., decreasing melting temperatures, increasing adenine content, and decreasing thymine content). As a whole, we show that DNA-SWCNT sensors offer unique NB dependent MR capable of differentiating analytes and measurement conditions. While still a computationally and experimentally challenging problem, this work offers the systematic insights into DNA sequences effects and experimental design considerations for future computationally driven CoPhMoRe studies.
Results
Study organization and data collection
Many primary food supply chains (FSCs) are often a source of serious quality and safety problems. These issues can arise from substandard practices and poor operational conditions, but also intentional or economically motivated adulteration. Some of the specific agents presenting threats to human health in the aquaculture FSC include heavy metal contamination of water sources from industrial mining and antibiotic adulteration above acceptable levels25. Since FSCs are typically complex and change dynamically over time, part of determining the appropriate regulatory actions and ensuring consumer safety involves developing rapid testing capabilities to detect adulterants of interest. This study, based on a survey of aquaculture markets25, focuses on developing sensor elements against cadmium ions and three small molecule antibiotic species: enrofloxacin, chloramphenicol, and nitrofuran’s degradation product, semicarbazide. An analyte concentration of 100 μM was chosen for this study based on previous experience that kd values of SWCNT CoPhMoRes can be typically found in this range31,32. Optimization of sensitivity is usually a step performed after identifying promising targets. Additionally, a dataset containing previous published results of DNA-SWCNT sensors against arsenite (AS3+) and arsenate (AS5+)33, two other candidates of interest, were included in the computational analysis as comparison.
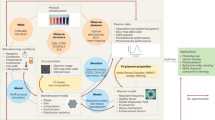
An overview of the paper’s methodological approach is shown in Fig. 1. This work revolves around computationally studying the DNA sequence dependence of DNA-SWCNT photophysical sensor constructs against the analytes of interest. SWCNTs synthesized from the high-pressure carbon monoxide (HiPco) method were used, which contain a range of different chirality small diameter SWCNT species that can be concurrently probed. Each sensor construct consisted of a colloidal aqueous dispersion of SWCNT using a single unique sequence of randomly generated single-stranded DNA, with the design space constrained to all DNA strands of length between 12 and 40 NBs. Shorter DNA lengths were not considered due to poor dispersion stability, potentially resulting in aggregation after analyte addition34. Longer DNA were not chosen due to increased CP stability with polymer length. While DNA stability may not be correlated with dispersion PL35, we hypothesize that a stable CP is potentially less likely to adsorb an analyte in a manner than modulate SWCNT emissions. However, despite using the limited sequence range, the design space is still considered innumerable from an experimental point of view at >1 × 1024 permutations just for DNA molecules of length 40.
1 First, DNA-SWCNT dispersions from a library of sequences. These sensor candidates were then tested against the analytes of interest under different pH conditions in this study, resulting in nIR spectral changes measured between 850 and 1250 nm. The model input is created by converting the before and after spectra from each analyte incubation into an optimizable score, Eq. (1) and Eq. (2), through the sensor response function. 2 The DNA sequences were encoded via 2 methods: direct vectorization/one-hot encoding or through calculations of common high-level features (HLFs). Using these two types of inputs, predictive models using gradient-boosted decision trees (GBDTs) were created. 3 Finally, the model is used to score potential MR designs and evaluated in out-of-sample analysis against laboratory results.
Each chosen DNA sequence was used individually to disperse SWCNT in aqueous solution via tip ultrasonication and purified through centrifugation using methods previously described36. While previous methods have utilized systemic evolution by dispersing SWCNT with a mixture of DNA sequences37, we chose a more homogeneous approach to eliminate additional complexity from interactions between library elements on the SWCNT.
UV-vis-nIR absorption spectroscopy was used to assess dispersion quality and concentration prior to sensing studies. The experiment itself was performed using a custom high throughput nIR spectroscopy setup, exciting samples consisting of either control or analyte at chosen experimental conditions with a 785 nm laser, and measuring PL in the range of 950–1250 nm.
Recent studies showed that SWCNT PL and analyte responses can be strongly dependent on solution and experimental conditions. To achieve the best controlled results and to minimize experimental variation from method error, the following standard experiment was developed:
-
The DNA CP is highly dependent of on solution pH, and likely adopts two different equilibrium conformations36. Specifically, pH 6 and 8 conditions were chosen for each DNA-SWCNT as two independent sensing states.
-
The test solution was buffered to 0.1 M ionic strength in sodium phosphate, and allowed to equilibrate for a minimum of 6 h against known dilution effects.
-
We have recently found that DNA-SWCNT PL quantum yield, defined photons emitted per particle, decreases with increasing excitation fluence. To mitigate this effect maximally without significantly increasing experimental time, excitation fluence at the sample was limited to and controlled at 1.67 mW μm^-2 for all experiments.
-
DNA-SWCNT is also known to associate to form loosely structured aggregates in solution38. To mitigate these effects, SWCNTs were diluted to 0.5 mg L^-1, lower than previous studies and were continuously agitated during analyte incubation.
-
SWCNT PL responses can also have kinetics on the order of hours39, especially in the case involving DNA and metal ions40. Thus, measurements were timed to be after exactly after 1 h incubation to assure both reproducibility and sufficient measured responses.
A total of 176 unique sequences were chosen as CP sensor candidates to test against 8 experimental conditions (combinations of 2 pHs and 4 analytes). One portion of the library was chosen randomly with respect to each NB, where each base choice was drawn with 1/4 probability. Another portion of the library was constructed from random pairs of NBs (e.g., AATTGGCC...). This bias was chosen due to the larger relative size of the SWCNT diameter to an individual NB, making two consecutive NBs more likely to modulate physical effects. To apply the newly proposed methods to an existing dataset in literature, sensor screening results against As3+ and As5+ was extracted from previous work, having 22 and 14 unique non-random DNA sequences, respectively.
Data processing and model inputs
In the PL experiments, a sensor response was defined as the change in PL emission spectra between a control condition and one incubated with analyte. Since the HiPco SWCNT sample contained a distribution of semiconducting SWCNT chiralities, the nIR emission spectra is a linear combination of individual chirality emission peaks. Given that each SWCNT chirality species’ emission peak can change in intensity, wavelength and/or broaden after analyte interactions, it was decided not to fit, or deconvolute, the spectra during analysis due to the number of fitting variables.
To convert optical spectral responses into optimizable numerical values (i.e., the dependent variable for the ML models), we defined two types of observably modified spectral features after analyte interaction: PL intensity and PL wavelength. To capture intensity modulations, an integrated normalized intensity change between the experimental and control was calculated. To capture the trend in wavelength modulations or peak shifts, a term describing the overall shape change of given a similar intensity change was calculated. The shape term was designed to be smaller when either one of the following conditions hold, based on a review of the typical variation between DNA-SWCNT sensor responses in our data sets:
-
The sensor response curve intensity is shifted up or down proportionally at all wavelengths (i.e., c(λ) = b*f(λ), \(\forall\lambda\), where \(b\in {\mathbb{R}}\)).
-
The highest peak of the sensor response curve, and the rest of the curve, are each shifted up or down proportionately at all wavelengths, but by different amounts (i.e., c(λ*) = b1*f(λ*) for λ* = arg maxλ(c(λ)), but c(λ) = b2*f(λ), \(\forall\lambda\) ≠ λ*, where \({b}_{1},{b}_{2}\in {\mathbb{R}}\))
The combined sensor response function is defined in Eq (1), with two components, an intensity term (left) and a shape term (right) Eqs. (2–3):
where the data wavelength range is between a and b, c(λ) is the PL spectra of the control DNA-SWCNT at wavelength λ, cmax is the maximum PL spectra of the control across all wavelengths, f(λ) is the PL spectra of the experiment sample at wavelength λ, fmax is the maximum PL spectra of the experiment sample across all wavelengths, and α the linear proportionality constant between the two sides of the sensor response function. The shape term is comprised of g(λ) and β, where g(λ) represents the proportional difference in intensity at wavelength λ compared to the highest peak, between the analyte and response curves, and where subtraction of the β term ensures a small shape term for the motivating examples described above.
The PL data was from this work was collected between 850 and 1250 nm. Since analyte interactions from MR can result in both PL intensity and/or wavelength changes as a function of experimental condition, an intuitive decision was made to assign both sides of the sensor response function with equal weight as to maximally capture any optimizable features. The value of α = 0.0113 was empirically determined by matching the ranges of measured values of the intensity and shape terms for the entire experimental dataset. (For more motivation and examples regarding the sensor response function, see Supplemental Materials).
To create the covariates (i.e., independent features) for the ML predictions, HLFs were calculated for all DNA sequences. These are commonly derived biophysical metrics for DNA molecules41,42. Some HLFs were directly calculated from the sequence primary structure, including strand lengths and percentages of each base type, while others required existing models of DNA structure. We assumed 25 °C and 0.1 M salt concentration when calculating non-covalent DNA interactions such as strand hybridization and hairpin formation. Lastly, thermodynamic properties were also predicted for the solution phase single-stranded DNA strands using well known models for ΔS ΔH, ΔG, and melting temperature. While it is difficult to know the exact influence of these derived solution features on DNA-SWCNT CPs, due to the close proximity of the strand to the unique hydrophobic and curved surface of the SWCNT, this prior knowledge likely significantly biases the CP structure and behavior. A description of each of the 46 HLFs is detailed in Supplementary Table 1.
Finally, the multiple HLFs defined in the form above are correlated with underlying physical properties, many of which in an interdependent manner. For example, changing sequence length modulates melting temperature and other thermodynamic properties in a similar underlying manner. We use PCA as a transform to simplify model inputs into orthogonal parameters. To perform this step in a manner that is representative of solution phase DNA, the 46 HLFs were calculated for one million randomly generated sequences of lengths 12–40 NBs. The resulting PCA coefficients were then used as a look-up to convert experimental HLFs into model inputs for each sequence that we refer to as HLF-principle components or HLF-PCs. As an added benefit, the first 9 principle components were able to capture over 95 percent of the total variation, and were chosen to reduce the number of features needed which can benefit ML model accuracy27. (See Supplementary Fig. 1 and Supplementary Fig. 2 for HLF-PC coefficients and variance.)
Model specification and training
The ML analysis relied on two-stage modeling for each experimental condition, summarized in Fig. 2. The rest of the section describes model specification, hyperparameters, and training in more detail.
The figure includes details regarding the dependent and independent variables used, and the purpose of each model in the analysis. The bottom shows the CNN architecture. First, DNA sequences were vectorized to create the model input using one-hot-encoding (OHE). Then the model input is run through a series of convolutional filters and pooling filters, where the number of such filters is a hyperparameter selected out-of-sample. The intuition behind the use of the CNN is to identify DNA motifs (small sub-sequences of DNA within the strand) that are involved in analyte responses by forming a 'local' structure for analyte adsorption.
CNNs were used to evaluate the effect of DNA local structure sequence dependence on analyte PL responses26,27. CNNs excel at certain tasks (e.g., image recognition) by identifying local structures in inputs (e.g., curves within images) and have successfully previously been utilized to predict transcription factor binding DNA motifs43. For this work, it was hypothesized that CNNs can identify DNA motifs responsible for binding sites against the target analyte, thus identifying features correlated with larger photophysical changes. Specifically, the hypothesis is that DNA motifs of 2–8 successive NBs might form some type of local -’binding point’ for the analyte to attach to based on relative molecular size or shape. To capture this relationship, CNNs with a single intermediate layer were chosen for evaluation. While a deeper CNN might be able to capture more complicated dynamics in sensor response, it would likely require significantly more training data than is available today.
Our CNN architecture is detailed in Fig. 2. CNNs were fit separately for each experimental condition using the sensor response in Eq. (1) as the dependent feature, one-hot encoding (OHE) of the DNA NBs as independent features, using rectified linear unit activation functions, minimizing mean squared error, and implemented with Tensorflow44. OHE refers to the direct vectorization of the DNA sequence into n × 4 matrices where n is the sequence length. By being trained separately on each experimental condition (analyte and pH), these CNNs are able to implicitly learn what DNA-SWCNTs produce better sensor responses for the chemical structure of each specific analyte. Various architectures of single-layer CNNs were considered, including number of convolutional filters cf ∈ {2, 4, 8, 16, 32, 64}, and motif sizes n ∈ {4, 6, 8} (filter size for pooling layers is set proportional to motif size). Multiple regularization hyperparameters were considered, including dropout d ∈ (0, 0.5) and number of training epochs ne ∈ {100, 150, 200, 250, 300, 350, 400, 450, 500}. Model hyperparameters were selected out-of-sample, using Bayesian optimization implemented with GPyOpt28,45. The CNNs architecture and independent feature encoding are displayed in Fig. 2. Out-of-sample CNN predictions were made for each experimental condition (analyte/pH) and DNA sequence, and used as an input to GBDTs. See the methods section for detailed information about how the CNNs were trained, hyperparameters were selected, and out-of-sample predictions were made.
Final predictions on DNA-SWCNT outcomes were made with GBDTs implemented with XGBoost30. GBDTs are ensemble models that fit decision trees stage-wise to minimize residual error. GBDTs were selected based on their ability to fit any function arbitrarily well given enough data (universality), and for their strong ability to learn complex interactions on small sized data sets that has been empirically supported by strong performance in data science competitions46. GBDTs were fit with the sensor response as the dependent feature, and HLF-PCs and local structure CNN predictions as independent features. GBDTs were also trained separately on each experimental condition (analyte and pH), therefore implicitly learning what DNA-SWCNTs produce better sensor responses for the chemical structure of each specific analyte. Hyperparameters to control model complexity and regularization included tree depth td ∈ {3, 4}, learning rate rho ∈ {0.01, 0.025, 0.05, 0.1}, and number of trees tn ∈ {100, 250, 500}. See the methods section for detailed information about how the GBDTs were trained, hyperparameters were selected, and out-of-sample predictions were made.
Evaluating predictive power and significant features
Out-of-sample predictions were evaluated for each experimental condition. Specifically, Pearson correlations of predicted and actual sensor responses were calculated for GBDTs trained with HLF-PCs as independent features. Corresponding p values were used to assess whether HLF-PCs can predict DNA-SWCNT outcomes. The analysis was repeated for GBDTs trained with both HLF-PCs and local structure CNN predictions as independent features. A p value was calculated for the difference of these two correlated Pearson correlation coefficients, to assess model improvement from the addition of CNNs47. Because the entire DNA-SWCNT library was randomly selected, this leave-one-out cross validation methodology gives an approximately unbiased estimator of the predictive power when generalizing the model across all possible DNA sequences of length 12–4048 [Chapter 7].
To determine significant features for the HLF-PCs, linear regression models were fit for each experimental condition, using HLF-PCs as independent features and sensor response function as the dependent feature. Linear regressions were selected due to their interpretable p values for each fitted model coefficient. This allows the HLF-PCs to be qualitatively evaluated in order to understand how HLFs impact DNA-SWCNT outcomes. As a robustness check, an ablation study was also performed for each experimental condition to evaluate the importance of each HLF-PC. Specifically, for each experimental condition one HLC-PC feature was removed at a time, and the increase in AIC score was recorded. HLF-PCs were then ranked based on the improvement in AIC score that each feature provides.
To assess the predictive power of the GBDTs as a function of the number of samples, the following analysis was performed. For each experimental condition where predictive power was previously established, and for any number of samples n ∈ {11, 16, 21, . . . , 176}, n DNA-SWCNT samples were randomly chosen and GBDTs were retrained to produce out-of-sample results for each sequence using the same methodology described. The Pearson correlation coefficient was then calculated for the predicted vs. actual sensor response. This process was repeated for 100 random samples for each value of n ≤ 36, and 25 random samples for all values of n ≥ 41 (to account for there being more variation in the Pearson correlation coefficient for smaller sample sizes).
Experimental output interpretation
One representation of the entire dataset’s PL response for each experimental condition is shown in Fig. 3. Here, HLFs of each sequence were first calculated. The Pearson correlation coefficient between HLFs and sensor response function (intensity, shape or total) is graphically shown for the cases where the p value < 0.05.
A color map is shown for the Pearson correlation coefficients (p value < 0.05) between each HLF based on experimental DNA sequences and sensor response function (Eq. (1)) that describes photophysical changes with analyte addition (red denotes positive correlation and blue with negative correlation). Sensor responses are further delineated as intensity, shape or total sensor response function for each experimental condition. Sections representing unique HLF groups are highlighted. Additional details for each individual HLF can be found in the Supplemental Materials.
The following set of observations can be made directly regarding the experimental results:
-
The pH 6 and 8 conditions, while using the same DNA CP, have different photophysical response correlations with the HLF panel and likely different surface structure interactions. Thus, these pHs were appropriately treated as separately optimizable experimental conditions.
-
Decreased DNA length, increased adenine content, and decreased cytosine content were positively correlated with improved PL responses. These properties were previously known to results in with more responsive and less stable DNA CPs13,36, supporting our choice of limiting sequence search to shorter strands.
-
While the intensity and shape sensor responses were generally congruent, they differed sufficiently and thus were necessary to provide orthogonal information to the algorithm.
-
The observed correlation between sensor response function and DNA secondary structure implies that strand-strand interactions play a major role in organizing the SWCNT CP.
-
Each experimental condition and analyte response appeared to have a unique HLF correlation combination, generally suggesting that the MR is mechanistically different and can be differentiable between the individual cases. Changes in PL emission spectra associated with these experimental conditions as populations were also observed to be uniquely different from each other (see Supplementary Fig. 3). This observed variation based on analyte composition and CP structure highlights the depth and utility of a CoPhMoRe system for engineering specific interactions.
Generally, if a HLF associated with a DNA CP is correlated to sensor responses for an experimental condition given a sufficient number of data points, then such sensors were likely DNA sequence optimizable. However, the lack of correlation does not necessarily entail poor sensing because there can exist photophysical PL modulating mechanisms that are DNA sequence independent and intrinsic to that of the SWCNT alone (for example, analytes that react directly with the SWCNT chemically while bypassing any selectivity imposed by the CP). While less can be concluded about the arsenic data due to the significantly lower number data points and the intuitive manner from which they were chosen, the observed correlation of sensor response with guanine and length were consistent with the conclusions of our previous study.
An analysis similar to Fig. 3 was also performed by separating sequences randomized via single vs. pairs of NBs (see Supplementary Fig. 6). The correlation maps from the two conditions are visually significantly different, indicating that they likely explore difference regions of the search space. A thorough investigation of nucleotide repeats should a topic for future work with larger sample numbers.
Result predictive power
For each experimental condition, GBDTs were trained and used to predict the out-of-sample sensor response for each DNA sequence (see methods section for model hyperparameters). Table 1 displays R2 and Pearson correlations between the predicted and actual sensor responses, and their corresponding p values. This was done with or without the local structure CNN predictions as model inputs.
GBDTs achieved statistically significant predictions for six of eight experimental conditions in the study, both with and without the local structure predictions from the CNN as model inputs. Predictions were significant for all analytes at pH 6, and for chloramphenicol and semicarbazide at pH 8. Pearson correlation coefficients were as high as 0.413 for semicarbazide at pH 8, with the corresponding R2 of 0.171 indicating that 17.1% of the variation in the sensor response can be explained by the model predictions. The corresponding p value of p = 1.22E−08 is convincing for the current study design. Furthermore, evidence was found that local structure CNN predictions can improve performance, and their inclusion as a model input improved correlations with statistical significance for two experimental conditions at the p < 0.05 significance level (semicarbiazide pH6 and enrofloxacin pH8). For the previously published arsenic data, with a smaller sample size, AS3+ achieved significant predictions and model improvement at the p < 0.1 significance level.
Evaluating significant features
To evaluate significant features and understand high-level properties that contribute to photophysical responses, a linear regression was fit for each experimental condition with HLF-PCs as independent features and the sensor response function as the dependent feature. This was done for all six experimental conditions from Table 1 with significant predictions at p < 0.05. Fitted model coefficients and statistical significance were shown in Table 2 below.
As a robustness check, an ablation study was performed for each experimental condition to evaluate the importance of each HLF-PC. Table 3 shows the most important features for each experimental condition ranked from most important to least (based on the relative improvement in AIC score due to each feature). The importance rankings support the significance analysis in Table 2.
Interpretation and overall observations
To interpret the significantly correlated HLF-PCs, the HLFs with higher magnitude coefficients for each PC were examined (See Supplementary Fig. 2 for graphical presentation). Each HLF-PC and some of their related physical properties are listed below (arrows represent the direction of correlation with the HLF-PC, letters ’A, T, G, C’ show the composition of individual or pairs of NBs, brackets ’()’ group base compositions that are modulated together):
-
HLF-PC 1: ↓ melting temperature with ↑ΔS, ΔH, and ΔG.
-
HLF-PC 2: ↑ melting temperature with ↑ (GC) and ↓ (A, T) in secondary structures.
-
HLF-PC 3: ↑ (G, C, GC) in dimers.
-
HLF-PC 5: ↓ G and ↑ (C, AC, TC).
-
HLF-PC 6: ↓ (A, AC) and ↑ (T, TC).
-
HLF-PC 8: ↑ (A,T) and ↓ (G, C, GC) in hairpins, and ↑ # of dimers.
-
HLF-PC 9: ↑ # of hairpins and dimers, ↓ A, T in hairpins, and ↓ # of NB in dimers.
For the set of experimental conditions, HLF-PC 2 and 6 were generally negatively correlated to sensor responses, which implicates increased photophysical responses for: decreased melting temperatures, increased adenine content, and decreased thymine content. HLF-PC 5 had the largest change in correlation between the two pH condition for a single analyte, chloramphenicol. The strongly negative correlation at pH 6, and strongly positive at pH 8, suggests significant effects of protonation on the CoPhMoRe constructs.
As a whole, these significant correlations with HLF-PCs can be used to improve the detection level of sensors while preforming fewer experimental iterations as compared to a random search. For example, the detection of semicarbazide at pH 8 is correlated with ↑HLF-PC 3, ↓HLF-PC 6 and ↑HLF-PC 9. Thus, subsequent sequence search libraries should bias toward: ↑ (G, C, GC) in dimers, ↑ (A, AC), ↓ (T, TC), ↓ # of hairpins and dimers, ↑ A, T in hairpins, and ↑ # of NB in dimers. It is important to note that while these characteristics were significantly correlated to the sensor response, they only explain a small portion of the variance within the known dataset. Thus, future guided searches must also include a large component of exploration.
The overall differences between the HLF-PC preferences for experimental conditions showed that DNA-SWCNT MR offered unique NB dependent selectivity. It is unsurprising that HLF of DNA molecules play a major role in their SWCNT-adsorbed structure, and thus subsequent analyte interactions. The improvement from the combined HLF-PC & CNN model from that of the HLF-PC alone is an objective demonstration of the intuitive idea that CP-based MR is more complex than simply specifying a polymer with a set of general properties. Even though, this improvement was only shown in 2 of the 8 cases, it is possible that a similar trend can be seen for the rest of the experimental conditions given a large enough sample size.
Assessing number of samples for predictive power
To study the effect of sample size on out-of-sample correlation for the 6 significant experimental conditions, we plot the average Pearson correlation coefficient between predicted and actual sensor response vs. the number of samples considered for the HLF-PC GBDTs (Fig. 4).
The effect of sample number is shown for the 6 significant experimental conditions: a Cd - pH 6, b Semicarbazide - pH 6, c Semicarbazide - pH 8, d Enrofloxacin - pH 6, e Chloramphenicol - pH 6, and f Chloramphenicol - pH 8. Each plot shows the average Pearson correlation coefficients produced by the GBDTs across random samples of size n drawn from the full database of 176 DNA-SWCNT experiments. The shaded regions show the 95% confidence interval for the average correlation coefficient for each value of n. Dashed lines show the sample size when statistical significance of p < 0.05 was reached for each experimental condition.
From Fig. 4, it was observed that the four experimental conditions at pH 6 all exhibit continued and steady improvement in the out-of-sample predictions as the number of samples increased. In contrast, both significant experimental conditions at pH 8 achieved higher correlations earlier at around 75 − 100 samples, but then had decreasing marginal returns in predictive power thereafter.
Generally, this sample size analysis can be used to aid the design of future studies against new analytes using the DNA-SWCNT system. The average number of samples to reach statistical significance was 126 for pH 6 and 49 for pH 8 experimental conditions (not including the pH 8 experimental conditions that did not reach statistic significance after 176 DNA-SWCNT experiments). Due to the size of the current dataset, the high-dimensionality of the search space and the nature of extrapolation, we are cautious to estimate the sample size required for a significant iterative improvement for the current experimental conditions. However, given the few samples required to arrive at models with significant correlations, this work can be used as an order-of-magnitude estimate of sample size for future unknown analytes.
Discussion
The CoPhMoRe design space spans a large range of molecular compositions as well as physical interactions between the analytes, kinetically trapped molecules and the nanoparticle. While there exist a large portfolio of studies on the development of SWCNT-based CoPhMoRe sensors, the complex and often transient mechanisms of interactions between the analyte and the sensor constructs present major challenges for both rational design and optimization of such systems. While the DNA CPs offer a molecularly defined library for sensor discovery, the number of sequence permutations, let alone secondary and tertiary structure from material adsorption, significantly complicates the search and optimization within this design space. Furthermore, the general knowledge gained in recent years regarding DNA and SWCNT interactions has not led to reliable methods of generating sensor elements.
While sensor candidates can be found through systematic or random searches, a ML guided method is potentially more adept at solving such a high-dimensional problem. We applied ML techniques in combination with a library of DNA-SWCNTs to study sensor development against analytes of interest in aquaculture. We restricted our search to DNA strand length of 12–40 NBs, and performed the largest CoPhMoRe screen to-date consisting of 176 sensors with 8 experimental conditions. Nevertheless, the number of unique sequences is currently innumerable from an experimental point of view. Our results showed that significant predictions can be made for 6 out of the 8 experimental conditions even for our extremely sparse number of data points compared to the dimension of the search space.
The DNA sequences for this study were modeled separately through HLF-PCs or CNNs, incorporating high-level or local structure features respectively. The CNN was constructed through OHE of DNA-NBs, with Bayesian hyperparameter optimization used to find appropriate model architecture and regularization given the amount of available data. HLF-PCs were constructed through PCA vectorization of broadly applied HLFs. Then they were then analyzed together via GBDTs, with out-of-sample predictions showing substantial promise in being able to predict sensor responses.
The fundamental difference between the HLF-PC and the CNN models is one of general known DNA properties vs. local sequence features. Interestingly, the combined HLF-PC & CNN model showed improvement over the HLF-PC model in two of the cases. This is statistical evidence for the importance of local features. While it is likely that most DNA-SWCNT CoPhMoRe photophysical responses were dictated by global DNA properties, there may exist an analyte dependent subset that hosts a more specific local feature dependent mode of MR.
Our results also reinforce the idea that each DNA-SWCNT offer multiple independent sensing states as a function of pH. In this study, sensors in pH 6 or pH 8 can be optimized uniquely against each of the analytes through the same sensor response function. Through HLF-PCs, we also found that general properties that improve the photophysical response of DNA-SWCNT such as: decreased melting temperatures, increased adenine content, and decreased thymine content. Additionally, the raw PL emission changes and the combination of significant HLF-PCs showed that the DNA-SWCNT platform interacted with different analytes in a spectrally and physically differentiable manner. Finally, our results showed that significant predictive models can be created with only about 50–100 samples, providing a starting point for future explorations into the design space. The fact that our model architecture achieved similar outcomes for different analytes and experimental conditions implies a degree of transferability for the utilization of this platform against future targets. In these future studies, we recommend that the methodological controls developed here be implemented to minimize the effect of experimental method error on model predictive power.
From an experimental point of view, the generation and testing of CPs is currently a bottleneck for the execution of ideal studies consisting of thousands of samples. Methods will need to be developed to bypass or automate the process of library SWCNT CP synthesis, sonication and centrifugation. A second area of potential improvement is the interpretation or vectorization of DNA sequences by taking into account additional information. Development of these methods will aid in re-scaling of the search space to focus on regions of interest. For example, the well-defined molecular structure of SWCNT should present CP structural biases. CP polymers can also self-self interact in adsorbed states on the SWCNT surface by wrapping around as a function of tube diameter. This opens up a new type of length-dependent interaction analysis. In these cases, having an adequate CP structural understanding through experimentation or simulation20,49,50 is needed. Similarly, additional information regarding DNA tertiary structure with or without a nanomaterial can be incorporated as independent variables in the model input. Third, while our results inform largely on interpretation of HLFs related to the influence of DNA on CP sensor development, model predicted NB sequences can ultimately be leveraged for more granular analysis provided that the models are derived from a larger dataset with higher predictive capability. For example, outputs from such models can be used to generate large sequence prediction libraries as input into deep-learning algorithms commonly employed in bioinformatics for the discovery of nucleotide-protein binding motifs51. Finally, with the capability of generating and testing large libraries, an application focused investigation into the effect of solvents and other solutes of the sensing mixture will allow for the optimization of sensor characteristics. This is especially important consideration preprocessing steps are often required for field samples, such as those collected in aquaculture testing.
To conclude, while nanomaterials’ unique physical and chemical properties provide promising environments for MR design, the size of the parameter search spaces and throughput of experiments are challenges well-suited for ML-based studies. This study demonstrated the feasibility of using ML models to analyze relatively few tightly controlled CoPhMoRe sensor studies to predict sensor-analyte interactions, contributing to the eventual goal of sequence-prescribed CP design.
Methods
Materials
All chemicals were purchased from Sigma-Aldrich (USA) unless stated otherwise. ssDNA sequences were purchased from Integrated DNA Technologies (IDT, USA). HiPCO Raw SWCNTs were used for all experiments and were purchased from Nanointegris (Batch HR27-104).
Preparation and characterization of SWCNT dispersions
SWCNT dispersions were prepared by combining 1 mg of SWCNTs and 1 mg of ssDNA in 1 mL of 100 mM NaCl solution. This mixture was tip sonicated (Qsonica Q500 with multi-tip add-on) while cooled by a pre-chilled rack with 0.125 in. probes for 30 min at a power of ~22 W (8 tips). Crude SWCNT dispersions were centrifuged two times at 16,000 g for 90 min to remove SWCNT bundles and other solid impurities. The top 80% of supernatant was collected after each round of centrifugation. Absorption spectra of SWCNT dispersions were collected (Cary 5000, Agilent Technologies) to approximate the concentrations of the post-dispersion stock solutions using the absorbance at 632 nm and an extinction coefficient of ϵ632 = 0.036(mg/L)−1cm−1 36.
SWCNT near-infrared fluorescence measurements
SWCNT stock solutions were diluted to a concentration of 0.5 mg/L in solutions of varying pH. These solutions were incubated at room temperature overnight to allow the systems to reach equilibrium prior to collecting fluorescence and/or absorbance measurements. Fluorescence measurements were conducted in triplicate in 96-well plates (Tissue Culture Plates, Olympus Plastics) using volumes of approximately 200 μL. SWCNT solutions were excited using a 785 nm diode laser (Invictus, Kaiser Optical Systems, MI), and a 20×/0.4 N.A. objective LD Plan Neofluar (Zeiss, Germany), and inverted microscope (Zeiss AxioVision). PL was collected using the same objective with using the same gratings and detector as above. Exposure time was held constant across was 60 s to have significant signal to noise. In all cases, fluorescence spectra were background corrected using SWCNT-free solution in an equivalent volume. During experiments in which an analyte was added, 2 μL of analyte solution was added to each well for the desired concentration and mixed on a rocking shaker for 1 h incubation at room temperature prior to collecting fluorescence measurements. Separate wells were designated as analyte-free controls.
PCA and HLF analysis
PCA was performed using the standard package in MATLAB via the SVD method (Natick, MA). Each HLF was first normalized by both the mean and standard deviation prior to PCA. Part of the HLF features were extracted using the oligoprop function in matlab. Additional references are provided in supplement.
Sensor response function-dependent variable
The combined sensor response function is defined as Eqs. (4–6):
The first term of the sensor response is designed to capture intensity modulations, by summing the normalized intensity change at each wavelength between the experimental and control was calculated. The second term is meant to capture total wavelength modulations or peak shifts, through a term describing the overall shape change of the same intensity change vector was calculated.
The second term (the shape term) is designed to be small when either one of the following conditions hold, based on a manual review of the noise typical of DNA-SWCNT sensor responses:
-
The sensor response curve intensity is shifted up or down proportionally at all points (i.e., c(λ) = b*f(λ), \(\forall\lambda\), where \(b\in {\mathbb{R}}\)).
-
The highest peak of the sensor response curve, and the rest of the curve, are each shifted up or down proportionately at all points, but by different amounts (i.e., c(λ*) = b1*f(λ*) for λ* = arg maxλ(c(λ)), but c(λ) = b2*f(λ),\(\forall\lambda\) ≠ λ*, where \({b}_{1},{b}_{2}\in {\mathbb{R}}\)).
The shape term accomplishes this by summing at each wavelength the difference in proportion between intensity for the wavelength and the highest peak of the analyte and response curves. This is accomplished with the g(λ) term. The subtraction of the β term ensures that when the highest peak of the curve is the same intensity, but the rest of the curve is shifted down proportionately at all points (i.e., c(λ*) = f(λ*) for λ* = arg maxλ(c(λ)), but c(λ) = b*f(λ), \(\forall\lambda\) ≠ λ*, where \(b\in {\mathbb{R}}\)), that β = g(λ), \(\forall\lambda\) ≠ λ*.
Supplementary Fig. 5 shows sensor response curves for four cases. In case (a), the sensor response curve is all shifted upwards proportionally, in case (b) the peak shifts up while the rest of the curve stays the same, in case (c) the peak stays the same while the rest of the curve shifts down, in case (d) the shape of the entire response curve is more visibly different than the rest, where the first and third peaks are lower while the second and fourth are higher. Intuitively, we would like the shape term of the sensor response function to be larger for case (d) than for other cases. This is true of the sensor response function defined in the paper, whose values are shown in Table 4 below. As expected, the shape term is much larger for curve (d), leading to the total sensor response function to be the largest, despite the intensity term being smaller for curve (d) than for curves (a) or (b).
Model specification - Gradient-boosted decision trees
The primary model used in this paper for DNA-SWNCT predictions, selected for its good performance on ML problems for small-scale data, is gradient-based boosting on decision trees (GBDTs)46. A simplified overview of how the model is trained is as follows. For a given experimental condition (analyte/pH), let y denote the vector of sensor responses for all DNA sequences, and let X denote the matrix of features (including either HLF-PCs, or HLF-PCs in addition to the local structure CNN predictions). The model is then iteratively built with simple decision trees trained on residual errors:
-
1.
Fit the stage 1 model (decision tree) f1(. ) on X, y, to minimize the residual sum of squares error.
-
2.
Calculate the first-stage residual errors Resid1 = S − f1(X).
-
3.
Fit a first-stage residual decision tree g1(. ) on X, Resid1, where the tree weights are fit to minimize the residual sum of squares error of f1(. ) + g1(. ) on X, y46.
-
4.
Set f2(. ) = f1(. ) + ρ*g1(. ), where ρ is the learning rate.
-
5.
Calculate the second-stage residual errors Resid2 = y − f2(X).
-
6.
Fit a second-stage residual decision tree g2(. ) on X, Resid2.
-
7.
Repeat until fM(. ) is trained.
Where the depth of each decision tree, the number of stages M, and the learning rate ρ are model hyperparameters to be set with cross-validation.
This model is implemented using the XGBoost library. The details for this Python package can be found in the conference paper accompanying the library30.
Model hyperparameters
This section provides additional details related to model hyperparameters, including selection methodology and the final hyperparameters used in the analysis.
Hyperparameter Selection - CNNs
The CNN in this paper uses the sensor response from Eq (1) as the dependent feature, and OHE of each DNA NB as the independent features. Various hyperparameters of single-layer CNNs are considered that relate to model complexity, including number of convolutional filters cf ∈ {2, 4, 8, 16, 32, 64}, and motif sizes n ∈ {4, 6, 8} (The filter size for the pooling layers is set proportional to the motif size, to reduce the number of model hyperparameters to be trained). Several regularization hyperparameters are also considered, including dropout d ∈ (0.0, 0.5) and number of training epochs ne ∈ {100, 150, 200, 250, 300, 350, 400, 450, 500}.
These CNN hyperparameters are selected out-of-sample, using Bayesian optimization implemented in Python with with GPyOpt and a 70%/30% training/test split in order to minimize residual squared-error28,45. It should be noted that while the final CNN model predictions were made out-of-sample by fitting the CNN separately on each experimental condition, the hyperparameters were selected using Bayesian optimization on the entire dataset at once to reduce computational time. The CNNs structure and the independent feature encoding are displayed in Fig. 2. Specifically, the following steps are taken:
-
1.
Bayesian hyperparameter optimization is initialized with motif size n = 6, number of convolutional filters cf = 32, dropout d = 0.0, and training epochs ne = 150.
-
2.
For a set of five trials, a 70%/30% training/test split of the DNA sequences is randomly produced, the CNN is trained using the current set of hyperparameters, and R2 is calculated out-of-sample on the test dataset for various experimental conditions.
-
3.
Based on the average R2 for all previous sets of trials in Step 2, a new set of hyperparameters is proposed using Bayesian optimization. At a high-level, these hyperparameters are selected to optimize the expected positive gain in R2, assuming that for unobserved sets of parameters the expected R2 can be predicted based on observed points, while the variation in this measure is proportional to how far away it is from observed points. Full mathematical details are given in28.
-
4.
Steps 2 and 3 are repeated for 20 iterations.
-
5.
The hyperparameter set achieving the highest out-of-sample R2 is selected for the final model.
Hyperparameter Selection - GBDTs
The final predictions for DNA-SWCNT outcomes were made with GBDTs, implemented with XGBoost. Various hyperparameters are considered to control model complexity and regularization, including tree depth td ∈ {3, 4}, learning rate rho ∈ {0.01, 0.025, 0.05, 0.1}, and number of trees tn ∈ {100, 250, 500}. Hyperparameters were then selected out-of-sample by performing a grid search. Specifically, the following steps were taken to select hyperparameters:
-
1.
Select an experimental condition, and all corresponding DNA-SWCNT data.
-
2.
For each possible set of model hyperparameters, do the following:
-
3.
For each DNA sequence in Step 1, a gradient-boosted decision tree is trained using the remaining DNA sequences as the training set (leave-one-out cross validation).
-
4.
Using the predicted sensor response from Step 3, and the actual experimental sensor response, calculate the Pearson correlation coefficient for the experimental condition and hyperparameters.
-
5.
Repeat Steps 1–4 for all experimental condition and all sets of model hyperparameters.
-
6.
For a given experimental condition, model hyperparameters are then selected to maximize the average Pearson correlation coefficient for all other analytes at the same pH (e.g., the model hyperparameters for chloramphenicol at pH 8 are selected to maximize the average Pearson correlation coefficient for enroflocaxin at pH 8, semicarbazide at pH 8, and cadmium at pH 8).
Final Hyperparameters - CNNs
Hyperparameters for CNNs were selected using the methodology described previously in this section. While the final CNN model predictions were made out-of-sample by fitting the CNN separately on each experimental condition, the hyperparameters were selected using Bayesian optimization on the entire dataset at once to reduce computational time. The final hyperparameters selected were convolutional filters cf = 4, motif size n = 4, dropout d = 0.027 and number of training epochs ne = 250. The small number of convolutional filters and motif sizes selected is unsurprising, given the fairly small number of laboratory experiments for different DNA sequences. However, even these simple CNNs were shown to be able to improve statistical power in some cases (see the results section in the main paper).
Final Hyperparameters - GBDTs
Hyperparameters for GBDTs were selected using the methodology described previously in this section. The final hyperparameters are shown in Table 5 below. The approach selected more sophisticated models (with a higher tree depth and lower learning rate) for the DNA-SWCNT sensors at pH6 than at pH8, which is consistent with the fact that the sensors exhibited greater responses at pH6.
Data availability
Data generated in the current study are displayed in the supplementary information. Experimental and processed data are available upon reasonable request addressed to the corresponding author.
Code availability
Code generated follow steps detailed in methods and supplementary information. Implementation code can be available upon reasonable request addressed to the corresponding author.
References
Liu, J. K. H. The history of monoclonal antibody development - Progress, remaining challenges and future innovations. Ann. Med. Surg. 3, 113–116 (2014).
LibreTexts. Laboratory analysis of the immune response. https://bio.libretexts.org/@go/page/5236/ (2021). Accessed: June 12, 2021.
Johnson, S. Chapter 2.4 - The home pregnancy test. In Cole, L. A. & Butler, S. A. (eds.) 100 Years of Human Chorionic Gonadotropin, 107–121 (Elsevier, 2020).
Singh, S. et al. Monoclonal antibodies: a review. Curr. Clin. Pharmacol. 13, 85–99 (2018).
Leenaars, M. & Hendriksen, C. F. M. Critical steps in the production of polyclonal and monoclonal antibodies: evaluation and recommendations. ILAR J. 46, 269–279 (2005).
Fickert, H., Fransson, I. G. & Hahn, U. Aptamers to Small Molecules. In The Aptamer Handbook, 94–115 (John Wiley & Sons, Ltd, 2006). Section: 4 _eprint:https://doi.org/10.1002/3527608192.ch4.
Martin, H. L. et al. Non-immunoglobulin scaffold proteins: Precision tools for studying protein-protein interactions in cancer. N. Biotechnol. 45, 28–35 (2018).
Zhang, J., Wang, Y. & Lu, X. Molecular imprinting technology for sensing foodborne pathogenic bacteria. Anal. Bioanal. Chemi. 413, 4581–4598 (2021).
Zhang, J. et al. Molecular recognition using corona phase complexes made of synthetic polymers adsorbed on carbon nanotubes. Nat. Nanotechnol. 8, 959–968 (2013).
Vilanova, O. et al. Understanding the Kinetics of Protein-Nanoparticle Corona Formation. ACS Nano 10, 10842–10850 (2016). Publisher: American Chemical Society.
Bachilo, S. M. et al. Structure-Assigned Optical Spectra of Single-Walled Carbon Nanotubes. Science 298, 2361–2366 (2002).
Ulissi, Z. W. et al. Spatiotemporal intracellular nitric oxide signaling captured using internalized, near-infrared fluorescent carbon nanotube nanosensors. Nano Lett. 14, 4887–4894 (2014).
Gillen, A. J., Kupis-Rozmysłowicz, J., Gigli, C., Schuergers, N. & Boghossian, A. A. Xeno Nucleic Acid Nanosensors for Enhanced Stability Against Ion-Induced Perturbations. J. Phys. Chem. Lett. 9, 4336–4343 (2018).
Dong, J. et al. A synthetic mimic of phosphodiesterase type 5 based on corona phase molecular recognition of single-walled carbon nanotubes. Proc. Natl Acad. Sci. 117, 26616–26625 (2020). Publisher: National Academy of Sciences Section: Physical Sciences.
Bisker, G. et al. Insulin Detection Using a Corona Phase Molecular Recognition Site on Single-Walled Carbon Nanotubes. ACS SENSORS 3, 367–377 (2018).
Haggenmueller, R. et al. Comparison of the Quality of Aqueous Dispersions of Single Wall Carbon Nanotubes Using Surfactants and Biomolecules. Langmuir 24, 5070–5078 (2008). Publisher: American Chemical Society.
Zhang, J. et al. Single Molecule Detection of Nitric Oxide Enabled by d(AT)(15) DNA Adsorbed to Near Infrared Fluorescent Single-Walled Carbon Nanotubes. J. Am. Chem. Soc. 133, 567–581 (2011).
Landry, M. P. et al. Single-molecule detection of protein efflux from microorganisms using fluorescent single-walled carbon nanotube sensor arrays. Nat. Nanotechnol. 12, 368–377 (2017).
Johnson, R. R., Johnson, A. T. C. & Klein, M. L. Probing the structure of DNA-carbon nanotube hybrids with molecular dynamics. Nano Lett. 8, 69–75 (2008).
Roxbury, D., Jagota, A. & Mittal, J. Structural characteristics of oligomeric DNA strands adsorbed onto single-walled carbon nanotubes. J. Phys. Chem. B 117, 132–140 (2013).
Manohar, S. et al. Peeling single-stranded DNA from graphite surface to determine oligonucleotide binding energy by force spectroscopy. Nano Lett. 8, 4365–4372 (2008).
Shankar, A., Mittal, J. & Jagota, A. Binding between DNA and carbon nanotubes strongly depends upon sequence and chirality. Langmuir: ACS J. Surf. Colloids 30, 3176–3183 (2014).
Ao, G., Streit, J. K., Fagan, J. A. & Zheng, M. Differentiating Left- and Right-Handed Carbon Nanotubes by DNA. J. Am. Chem. Soc. 138, 16677–16685 (2016). Publisher: American Chemical Society.
Yang, Y., Zheng, M. & Jagota, A. Learning to predict single-wall carbon nanotube-recognition DNA sequences. npj Comput. Mater. 5, 1–7 (2019). Number: 1 Publisher: Nature Publishing Group.
Jin, C. et al. Testing at the Source: Analytics-Enabled Risk-Based Sampling of Food Supply Chains in China. Manage. Sci. (2021). https://pubsonline.informs.org/doi/abs/10.1287/mnsc.2020.3839. Publisher: INFORMS.
Goodfellow, I. J., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016). http://www.deeplearningbook.org.
Bishop, C. M. Pattern Recognition and Machine Learning (Information Science and Statistics) (Springer-Verlag, 2006).
Bergstra, J. & Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 13, 281–305 (2012).
F.R.S., K. P. Liii. on lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2, 559–572 (1901). PCA beginnings.
Chen, T. & Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, 785–794 (ACM, New York, NY, USA, 2016). https://doi.org/10.1145/2939672.2939785.
Lee, M. A. et al. Implantable Nanosensors for Human Steroid Hormone Sensing In Vivo Using a Self-Templating Corona Phase Molecular Recognition. Adv. Healthc. Mater. 9, e2000429 (2020).
Salem, D. P., Gong, X., Liu, A. T., Akombi, K. & Strano, M. S. Immobilization and Function of nIR-Fluorescent Carbon Nanotube Sensors on Paper Substrates for Fluidic Manipulation. Anal. Chem. 92, 916–923 (2020). Publisher: American Chemical Society.
Lew, T. T. S., Park, M., Cui, J. & Strano, M. S. Plant Nanobionic Sensors for Arsenic Detection. Adv. Mater. (Deerfield Beach, Fla.) 33, e2005683 (2021).
Pinals, R. L., Yang, D., Lui, A., Cao, W. & Landry, M. P. Corona Exchange Dynamics on Carbon Nanotubes by Multiplexed Fluorescence Monitoring. J. Am. Chem. Soc. 142, 1254–1264 (2020). Publisher: American Chemical Society.
Jena, P. V., Safaee, M. M., Heller, D. A. & Roxbury, D. DNA-Carbon Nanotube Complexation Affinity and Photoluminescence Modulation Are Independent. ACS Appl. Mater. Interfac. 9, 21397–21405 (2017). Publisher: American Chemical Society.
Salem, D. P. et al. Ionic Strength-Mediated Phase Transitions of Surface-Adsorbed DNA on Single-Walled Carbon Nanotubes. J. Am. Chem. Soc. 139, 16791–16802 (2017).
Jeong, S. et al. High-throughput evolution of near-infrared serotonin nanosensors. Sci. Adv. 5, eaay3771 (2019).
Gong, X., Sharma, A. K., Strano, M. S. & Mukhopadhyay, D. Selective assembly of DNA-conjugated single-walled carbon nanotubes from the vascular secretome. ACS Nano 8, 9126–9136 (2014).
Kozawa, D. et al. A fiber optic interface coupled to nanosensors: applications to protein aggregation and organic molecule quantification. ACS Nano 14, 10141–10152 (2020). Publisher: American Chemical Society.
Li, W., Zhang, Z., Zhou, W. & Liu, J. Kinetic Discrimination of Metal Ions Using DNA for Highly Sensitive and Selective Cr3+ Detection. ACS Sens. 2, 663–669 (2017). Publisher: American Chemical Society.
SantaLucia, J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 95, 1460–1465 (1998). Publisher: National Academy of Sciences Section: Biological Sciences.
Sugimoto, N., Nakano, S.-i, Yoneyama, M. & Honda, K.-i Improved Thermodynamic Parameters and Helix Initiation Factor to Predict Stability of DNA Duplexes. Nucleic Acids Res. 24, 4501–4505 (1996).
Zeng, H., Edwards, M. D., Liu, G. & Gifford, D. K. Convolutional neural network architectures for predicting DNA-protein binding. Bioinformatics 32, i121–i127 (2016).
Abadi, M. et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems http://download.tensorflow.org/paper/whitepaper2015.pdf (2015).
Gpyopt: A bayesian optimization framework in python. http://github.com/SheffieldML/GPyOpt (2016).
Friedman, J. H. Greedy function approximation: a gradient boosting machine. Ann. Stat. 29, 1189–1232 (2001).
Meng, X.-L., Rosenthal, R. & Rubin, D. B. Comparing correlated correlation coefficients. Psychol. Bull. 111, 172 (1992).
Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning. Springer Series in Statistics (Springer New York Inc., 2001).
Roxbury, D., Mittal, J. & Jagota, A. Molecular-Basis of Single-Walled Carbon Nanotube Recognition by Single-Stranded DNA. Nano Lett. 12, 1464–1469 (2012). Publisher: American Chemical Society.
Roxbury, D., Jagota, A. & Mittal, J. Sequence-Specific Self-Stitching Motif of Short Single-Stranded DNA on a Single-Walled Carbon Nanotube. J. Am. Chem. Soc. 133, 13545–13550 (2011). Publisher: American Chemical Society.
Pan, X., Yang, Y., Xia, C.-Q., Mirza, A. H. & Shen, H.-B. Recent methodology progress of deep learning for RNA-protein interaction prediction. Wiley Interdiscip Rev.: RNA 10, e1544 (2019). _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/wrna.1544.
Acknowledgements
The work of the first and second authors was partially supported by a grant award from the Walmart Foundation (Agreement dated 10/17/2016). Daniel Lundberg, MIT graduate student, helped with part of the data analysis. Undergraduate students at MIT from the Undergraduate Research Opportunities (UROP) program, including: Kevin Avila, Alexa Stewart, Julie Yu, Sydney Kuo, and Babatunde Ogunlade, contributed partially to the laboratory experiments.
Author information
Authors and Affiliations
Contributions
X.G. and N.R. conceived the experiments and jointly wrote the paper. X.G. lead the lab experiments and interpretation of results, and N.R. leading the computational analysis. R.L. and M.S. supervised the experiment.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, X., Renegar, N., Levi, R. et al. Machine learning for the discovery of molecular recognition based on single-walled carbon nanotube corona-phases. npj Comput Mater 8, 135 (2022). https://doi.org/10.1038/s41524-022-00795-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00795-7