Introduction

Data storage and transport devices ranging from hard disk drives to flash memories, from CMOS to spintronic technologies are of crucial importance in today’s technological world. Usually, these devices are based on 2D structures approaching their limitations every day. 3D structures started to emerge over the past years, leading to significant improvements in both reducing the dimensions and increasing their efficiency, e.g., flash memories1,2. In these data storage devices, the third dimension is used by the simple stacking of the same 2D structures. Thus, the whole power of the additional third dimension is not utilized.

Over the past years, spin ices, a class of 3D materials, have been investigated in detail. Spin ices are frustrated systems where the magnetic moments are residing on the sites of a pyrochlore lattice, a lattice with corner-sharing tetrahedra, and commonly referred to as dipolar spin ices (DSI)3,4,5,6,7,8,9. Its degenerate ground state obeys the ice-rule, where two magnetic moments point to the center of the tetrahedra and two away from it. Switching a magnetic moment breaks the ice rule and creates a pair of magnetic charges in the centers of the vertices5,6. These magnetic charges, commonly referred to as emergent magnetic monopoles, can be separated with a finite energy cost and propagated through the lattice. In a classical analog to Dirac’s theory of magnetic monopoles10, monopole motion in spin ice leaves a trace called a Dirac String (DS), which is simply the chain of flipped magnetic moments connecting the two separated positive and negative magnetic poles. Theoretical and experimental studies have shown that the energetic ground state is degenerate, constrained by the ice rule and that the magnetic monopoles are connected via DS at low temperatures3,4,5,6,7,8,11,12.

In order to study the geometrical frustrations and the magnetic charges on the more controllable platform, 2D artificial spin ices (2DASIs) have been designed and investigated in detail13,14,15,16,17,18. There, lithographically patterned nanomagnets are arranged on different lattices. The most common ASI lattices are the square19,20,21,22 and kagome ices23,24,25,26. The dynamics in these systems has been extensively researched ranging from re-configurable wave band structures to tailored spin-wave channels27,28,29,30.

Further frustrated systems show similar properties including artificial colloidal ice, and particle spin ice systems, where the topological defects can be controlled and steered31,32,33,34.

In contrast to DSI, the reduced dimensionality and geometric frustration in square ice lift the degeneracy of the ice rule14,15,16,17,18,35,36, thus limiting monopole mobility. Note that a unique ordered ground state was theoretically predicted for DSI with zero total magnetization per cubic unit cell, being induced by long-range dipolar interactions between the magnetic moments37. However, the lift of degeneracy of the ground state is much higher for 2D systems. Various methods have been explored to regain spin ice degeneracy, including quasi three-dimensional lattices14,16,38,39,40,41,42,43 and interaction modifiers44. After early designs39 and realizations45 had envisioned a 3D artificial spin ice, the three-dimensional frustrated nanowire-lattice46 was manufactured by two-photon lithography47, in which charge propagation was later demonstrated48. However, in this lattice, the degeneracy of the ground state is still lifted, as the 3D structure consists of an interconnected nanowire lattice. In addition, the magnetic charges are connected via DS’s, which store energy due to the presence of domain walls at the vertex centers.

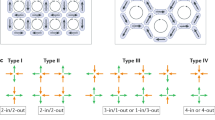
In this work, we combine the advantages of both DSI and ASI and present a 3DASI lattice, where numerical investigations are performed. Our lattice is a 3D nano-magnetic network of vertices consisting of four disconnected 3D magnetic ellipsoids with perfect Ising behavior enabling tension-free DS’s and unbound magnetic charges by recovering the lost degeneracy of the ice rule obeying states. Within this work, we refer to the vertices obeying the ice rule as the ground state. Vertices where three ising spins point towards or away from the center are referred to as Type III, and where all four elements point in or out of the center are called Type IV vertices. Here, magnetic monopoles are at the centers of the vertices which show a net magnetic charge. Namely, a Type III vertex hosts one magnetic monopole with charge Q = ±2qm, and a Type IV vertex hosts a magnetic monopole with charge Q = ±4qm49.

In the 3DASI lattice, we conserve the full accessibility of 2DASI and investigate numerically the propagation of emergent magnetic monopoles. We demonstrate that the difference in energy, required to create magnetic charges and their transport, is around 2 eV, which enables the controlled propagation of unbound charges. Considering the emergent magnetic monopoles as binary, mobile information carriers, the presented lattice demonstrates the steered motion of charge carriers in a 3D magnetic nano-network at room temperatures. The controllability of these charges paves the way toward a 3D magnetic network for data transport and storage.

Results

Modeling

In recent years, the direct-write technique of focused electron beam induced deposition (FEBID) has reached a high level of maturity for 3D nanofabrication. Many complex-shaped nano-architectures have become available, providing access to experimental investigations of curvature-, geometry-, and topology-induced effects in various disciplines, including magnetism, superconductivity, photonics, and plasmonics50,51,52,53,54.

Inspired by the recent developments in 3D optical lithography and focused particle 3D nano-printing by FEBID, we present a 3DASI lattice, where magnetic rotational ellipsoids are arranged along the main axis of a tetrahedron, resulting in an angle θ = arccos(−1/3) ≈ 109.5° between the elements, reproducing the Ice Ih crystal of the water ice3,5,9. Figure 1 illustrates the designed 3DASI lattice.

Fig. 1: 3DASI lattice.
figure 1

a 3D Illustration of the 3DASI lattice, and b the top view. The length of the ellipsoids L and maximal width w as well as the angle between the ellipsoids θ are depicted in (b). The circles between the ellipsoids are the cross-section of ellipsoids pointing in or out of the plane, as a consequence of the chosen top view.

Full size image

Note that in Fig. 1, we illustrate only the magnetic ellipsoids forming the lattice. In reality, the ellipsoids can be fabricated by direct-writing, i.e., FEBID, and interconnected with a magnetic insulator, e.g., platinum-51 or niobium-based55 compounds, as exemplarily illustrated in Supplementary Fig. 1. With FEBID as a suitable nanofabrication technique of the 3DASI lattice, the maximal width of the ellipsoids w can be reduced down to few tens of nanometers, while the length L can be chosen up to a few micrometers50,51,52,53.

Note that optical lithography techniques such as two-photon lithography have already been employed to fabricate three-dimensional magnetic structures such as nanowire lattices and magnetic buckyballs46,48,56,57.

We choose rotational magnetic ellipsoids as ASI elements because the self-demagnetizing field of the ellipsoids is homogeneous thus keeping the magnetic elements uniformly magnetized in the direction of the longer axis with no edge inhomogeneities58,59,60,61. Hence, our model shows nearly perfect Ising behavior and is suitable to separate and host magnetic charges. The maximal average deviation from a perfect uniformly magnetization for one ellipsoid in our model is found to be Δϕ ≈ 4 × 10−4 deg, where the interactions with nearest and next-nearest neighbors were encountered.

In this work, we restrict our model to three layers to conduct numerical experiments in feasible times. However, the region of interest is only the middle layer, meaning that we analyze the 3DASI lattice as a bulk system. Furthermore, the lateral dimensions are kept finite being confined only for the dynamic simulations of monopole propagation. Note that in finite-sized systems boundaries can be engineered to control the bulk behavior or introduce and confine defects in spin ice systems62,63.

Dirac strings and magnetic monopoles

Because of the symmetry of the tetrahedra, the degeneracy of the ice rule is not lifted in 3DASI. Consequently, the tension of the DS should vanish. To obtain an energy scale, we approximate the ellipsoids by magnetic dipoles with the dipole moment μ = MsV, where Ms is the saturation magnetization and V is the volume of the nanostructure. In this formulation, the dipolar interaction energy for each pair of magnetic dipole moments mi, mj at positions ri, rj in the lattice is given by the dipolar interaction energy

$${E}_{{{{\rm{dip}}}}}=\frac{{\mu }_{0}}{4\pi {\left|{{{{\bf{r}}}}}_{ij}\right|}^{3}}\left[{{{{\bf{m}}}}}_{i}\cdot {{{{\bf{m}}}}}_{j}-3\frac{\left({{{{\bf{m}}}}}_{i}\cdot {{{{\bf{r}}}}}_{ij}\right)\left({{{{\bf{m}}}}}_{j}\cdot {{{{\bf{r}}}}}_{ij}\right)}{{\left|{{{{\bf{r}}}}}_{ij}\right|}^{2}}\right]$$
(1)

with rij ≔ rj − ri and vacuum permeability μ0. Then from Eq. (1), we obtain the energy scale

$${J}_{NN}=\frac{3}{2\sqrt{2}}\frac{{\mu }_{0}}{\pi }\frac{{\mu }^{2}}{{a}^{3}}$$
(2)

as introduced in ref. 61, where a is the lattice constant.

From it we obtain the energy levels for the different vertex types, shown in Table 1. Note the degeneracy in the ice rule obeying vertices.

Table 1 Dipolar interaction energies in each vertex type in 2D and 3D ASI in units of JNN, which is JNN ≈ 0.43 eV for the chosen material and geometry parameters.
Full size table

Considering the monopole picture6, the magnetic ellipsoids can be approximated by the dumbbell model, which allows one to separate two magnetic monopoles in each magnetic ellipsoid. This model brings further corrections, as the nearest-neighbor exchange interactions within the vertices are also accounted. However, here we consistently compare the structural difference between the 2D and 3D artificial spin ice vertices, where the point dipole approximation covers the relevant interactions.

To consider a more complete model including further corrections to Eq. (1), we employ calculations via micromagnetic simulations with magnum.fe64, using material properties similar to the cobalt–iron (CoFe) alloys used in FEBID. Note that with this technique, the material parameters are already tunable52,65 for 2D structures, and advances are expected in the near future. We choose a saturation magnetization Ms = 800 kA m−1 and exchange stiffness constant Aex = 15.5 pJ m−1. The ellipsoids have the dimensions L = 100 nm, w = 20 nm, and a vertex-to-vertex distance of a = 120 nm, see Supplementary Fig. 2 for a detailed comparison between 2DASI and 3DASI elements. It is noteworthy that in our studies we especially focused on the 3D structures of sizes that have been demonstrated for platinum-based nanofabrications. Magnetic CoFe/CoFeB structures are larger, but the down-scaling is expected within the next years.

Figure 2a shows the calculated energies of all the possible vertices in 2DsASI and 3DASI. The latter show clearly the sixfold degeneracy of the ground state Type I/II. This degeneracy allows for magnetic charges to be separated because a tension-free DS is created, making them truly unbound. In Fig. 2a, we chose to plot all 24 = 16 possible configurations within a vertex. In reality, for vertices in the 3DASI lattice, there exists only one unique ground state configuration, the ice-rule configuration, up to symmetry operations, i.e., rotations and mirroring, always obeying the 2in–2out ice rule.

Fig. 2: Magnetostatic energies and minimum energy paths for propagation and separation of charges.
figure 2

a Total energies per vertex calculated with a micromagnetic treatment by taking into account energetic contributions of the exchange and demagnetization fields, where every possible magnetic configuration in a 2DsASI (circles) and in our 3DASI (squares) was considered, as illustrated in Supplementary Figs. 3, and 4, respectively. b Minimum energy paths to separate (magenta) the two magnetic charges by switching one ellipsoids magnetization in the ground state, and propagating it further through the lattice in a constant direction (green). The difference of saddle points and the corresponding minima yields the separation barrier ΔEs and propagation barrier ΔEp, while the energy of the lattice increases by 2Eq ≈ 2 eV due to the two additional charge defects. c Interaction energy between the magnetic charges after monopole separation and during propagation, which follows a 1/r Coulomb Law. d–h Schematic illustrations of the magnetization configurations for the ellipsoids in the DS with the positive (dark red) and negative (dark blue) charged magnetic monopoles. Snapshots of magnetizations are depicted in Supplementary Fig. 5, and animations for switching processes are available online.

Full size image

According to the original definition of emergent magnetic monopoles, the energy required to create a monopole-antimonopole pair (charge separation), should be larger than the energy required to propagate it6,10,16,66,67,68. We verify these properties by applying a full-micromagnetic model to calculate the energy barriers to separate and propagate the magnetic charges60,69,70. A detailed description of the full micromagnetic model and its application on 2DASIs is given in ref. 60.

Figure 2b illustrates the minimum energy paths (MEPs) for the switching processes within a DS. Starting from a lattice in the ground state, as illustrated in Fig. 2d), we separate two magnetic charges by switching the magnetization of one ellipsoid, and thus creating two Type III defects, which are depicted in Fig. 2e). The positive charge is then propagated to increase the length of the DS, shown in Fig. 2f–h. It can be seen, that the separation MEP (magenta) yields a separation barrier ΔEs approximately 2 eV higher than the propagation barriers ΔEp (green MEPs), which are nearly constant.

Note that the simplified and improved string method is a static method. Here, the energy landscape is reproduced in such a fashion, that the magenta curve in Fig. 2b is the energetically most favorable way to switch from state 0 to state 20, where two Type III defects are created. With these calculations, we are able to obtain direct visualization of the switching mechanism. Each state with energy E corresponds to a unique magnetic configuration that is reached within this transition. The reversal mechanisms are highly non-coherent and complex, being dictated by domain wall movements. Note that the reversal mode of magnetic elements can be an exchange or magneto-statically dominated61 and depend strongly on the chosen magnetic parameters. Impurities during the fabrication process, can lead to changes in the magnetic properties, and impact the reversal mode and transition kinetics of the system. With FEBID as a fabrication method, the parameters are freely tunable52,65, and thus the reversal modes can be tuned as well.

By separating the emergent monopoles, the energy of the system increases about 2Eq = 2 eV, which represents the energy increase due to Type III defects. Since we propagate only one charge, while the environment does not change, the energy of the system should stay constant during the propagation. This is possible in our 3DASI lattice due to the sixfold degeneracy of the ice-rule. Thus, propagating one magnetic monopole to the next vertex does not lead to tension in the DS. Note that, in non-degenerate 2DsASI, DS’s necessarily carry a tension. However, we need to consider the possible Coulomb interactions between magnetic charges5,6. In contrast to the classical DSI, this interaction can be neglected in comparison to the energy barriers in our 3DASI lattice6. Nevertheless, this energy is present in our lattice, as shown in Fig. 2c where we illustrate the gain in energy after the monopoles are separated and propagated as a function of the direct distance between the monopoles. After separation, the monopoles are at the centers of two neighbored vertices, whereas the distance between them is a = 120 nm. To obtain the interaction energies we calculate the demagnetization energies within the bulk layer for all energetic minima from Fig. 2b and subtract the energy where the system is in an equilibrium configuration with no magnetic monopoles (State 0). The obtained interaction energies follow a Coulomb law with shifted energy E ∝ 1/r, where r is the shortest distance between the monopoles6.

Note that these results are obtained at T = 0 K. In order to analyze the dependence of the stability and the propagation properties of a single monopole on both externally applied fields and temperature, we use the arbitrary field finite temperature micromagnetic analysis (FTM)71.

Arbitrary field FTM analysis

Starting from an initial magnetization state with one magnetic monopole of charge Q = −2qm, we calculate the energy barriers to switch the magnetization of different 3DASI elements under a uniform external magnetic field with μ0H = − μ0∣H∣ex. Here, μ0∣H∣ denotes the strength of the applied field, and ex is the unit vector along x. μ0∣H∣ is varied between 0 and 200 mT.

Commonly, magnetic monopoles are found in pairs. However, finite-sized systems allow trapping unpaired magnetic monopole at boundaries62. Similarly, the finite sizes of our lattice allow particular boundary ellipsoids to act as monopole injectors, and thus, single monopoles can be present in the lattice. Depending on the initial magnetic configuration of the middle layer, multiple monopoles with equal or opposite charges can be injected. For this particular initial state, we inject solely one monopole and are interested in its propagation in the desired direction without creating additional charges.

As illustrated in Fig. 3b, we consider different transitions, where the magnetic charge is propagated along X (blue arrow) and Y (orange arrow), or additional charges are separated in a neighbored vertex, where the separation in three different directions is considered, X (green arrows), Y and Z (red). By doing so, we cover all possible transitions in our lattice, where the existing charges with Q = −2qm are either propagated or additional monopole–antimonopole pairs are created at different locations. The initial magnetization configuration is the same as in Fig. 4e. Snapshots of magnetizations during switching processes for the relevant transitions are illustrated in Supplementary Fig. 6.

Fig. 3: Arbitrary field finite temperature micromagnetic analysis.
figure 3

a Dependence of the energy barrier on the applied external fields at T = 0 K to switch the magnetizations of different ellipsoids as depicted in (b). c Upper panel: the switching probability P at different temperatures for the relevant transitions from (b) calculated with FTM analysis, Eq. (3), where a Zeeman field with μ0∣H∣ = 180 mT, attempt frequency f0 = 50 GHz and pulse time tfinal = 0.15 ns were chosen. Lower panel: mean error rate of successful propagation correlated with the unintended separation, as given by Eq. (4).

Full size image
Fig. 4: Field-driven monopole propagation.
figure 4

Temporal evolution of the magnitude of the applied field (a) and of the averaged magnetization components (b) within the bulk layer during the x-propagation. The field is applied along −x in order to maximize the Zeeman energy acting on the ellipsoid whose magnetization should be switched. The field is turned off after t = 4.8 ns in order to transfer the magnetic charge to the next vertex controlling the propagation. c–e Schematic illustration of the monopole (dark blue) propagation. f–h Snapshots of the magnetization states from the output of the conducted micromagnetic simulations, where f illustrates the initial and g the final magnetic configurations. The magnetization evolution during the simulations is depicted at different times (white boxes) in (h). Color in f–h shows the x-component of the magnetization, as given by the colorbar.

Full size image

Figure 3a shows the calculated energy barriers as a function of the applied field strength for the transitions depicted in Fig. 3b. Our results indicate that the propagation barrier along X (blue, circles) is always lower than any other barrier. At vanishing fields, the barriers for propagation X and Y are equal, as demonstrated above. With the increasing field and approaching the coercive field, all barriers are lowering, ultimately, vanishing once the critical field is reached.

In the FTM analysis, described by Suess et al.71, a field-driven transition occurs with the switching probability

$$P=1-\exp \left(-{f}_{0}{t}_{{{{\rm{final}}}}}{e}^{\left(\frac{-{{\Delta }}E(H)}{{k}_{B}T}\right)}\right),$$
(3)

where f0 denotes the attempt frequency, ΔE(H) the energy barrier at a given field magnitude, kB the Boltzmann constant, tfinal the time of applied field pulse and T is the temperature.

To analyze the stability of the propagation at room temperature, we consider T = 300 K and calculate the associated probabilities where we choose μ0∣H∣ = 180 mT, f0 = 50 GHz, and tfinal = 0.15 s. f0 is chosen according to values considered in ASI literature72 and tfinal based on experimental expectations. Note that these two values appear only as a common factor in Eq. (3) and therefore other values for f0 can always be compensated by an appropriate choice of tfinal. The field strength μ0∣H∣ = 180 mT is chosen such that the switching barrier of the propagation is below 300kBT.

The upper panel of Fig. 3c illustrates the relevant probabilities for the switching possibilities depicted in Fig. 3b. Our results indicate that only the element of interest will change its magnetization, as its switching probability increases with the temperature, where Pprop(300 K) > 0.9. All the other probabilities are nearly zero at temperatures around T = 300 K. We chose to depict only the switching probabilities for the propagation and separation along x, as the other probabilities are lower than 1 × 10−15.

However, we still need to define the mean switching error rate

$${{{\rm{ERR}}}}(T)=1-{P}_{{{{\rm{prop}}}}}{\left(1-{P}_{{{{\rm{sep}}}}}(T)\right)}^{N},$$
(4)

which describes the probability for an unsuccessful propagation, i.e., falsely switch of one element leading to separation (or propagation failure due to insufficient thermal energy) in a lattice with N elements, where Pprob describes the propagation probabilities and Psep the separation probabilities.

In the lower panel of Fig. 3c, we see that the error rate significantly decreases after T = 290 K, as the X propagation probability increases to nearly 1. For T > 330 K the propagation is guaranteed, however the separation probability increases leading to an increment in the mean error rate. This indicates that the monopoles can be propagated in a controlled manner, in the desired direction, and that they can be accessed at temperatures around room temperature, improving the scalability and thermal stability of pyrochlore DSI.

Field-driven controlled monopole propagation

The controlled propagation can be achieved at any temperature, including T = 0 K if one adjusts the strength, direction, and duration of the globally applied magnetic fields. As illustrated in Fig. 3a, the energy barrier vanishes for large enough fields. To investigate this in a rather direct manner, we conduct numerical experiments, where we continue with our micromagnetic treatment and investigate the propagation of monopoles by applying pulses of external magnetic fields at T = 0 K.

We start from an initial system where the magnetic configuration is chosen in such a fashion that every vertex obeys the ice-rule, and thus it is in an energetic minimum. Reversing the magnetization in one boundary ellipsoid injects exactly one magnetic monopole with Q = −2qm, see Fig. 4c and f. After the injection, we confine the boundary ellipsoids as well as top and bottom layers and investigate the dynamics of the magnetic monopole propagation in a bulk lattice, see Supplementary Fig. 7.

We continue by applying a magnetic field along −x direction, as in the FTM analysis above. The field profile can be seen in Fig. 4a, where the magnitude of the applied field increases linearly over 4.8 ns from 160 to 208 mT and is then turned off abruptly after the propagation is successful.

Figure 4b shows the temporal evolution of the averaged magnetization components within the middle layer. Our results indicate that the magnetic charge is propagated to the next vertex via domain wall movements as predicted by our string method calculations and FTM analysis. Magnetization snapshots at chosen times from Fig. 4h show that until the critical field is reached, small deviations from the ising state are observed for the ellipsoids in the ground state, explaining the slow decrease in the average x-component of the magnetization from Fig. 4b. Once the applied field is large enough, the propagation takes place keeping the other vertices in the ground state, avoiding additional charge separations. By turning off the external field, we relax all the ellipsoids back to their ising state and control the propagation by demand. One can see in Fig. 4b that the average magnetization drops rather abruptly when the magnetic charge is propagated one vertex further with each step, demonstrating the free and controlled propagation of an unbound emergent charge in the presented lattice. In the Supplementary notes, we also discuss the magnetic charge being further propagated to the next x-row by applying the same protocol with a magnetic field along y and illustrate this propagation in Supplementary Figs. 8 and 9.

Discussion

We investigated micromagnetically a 3DASI lattice, which combines the advantages of classical 2DASI and pyrochlore DSI lattices, recovering the lost frustration and degeneracy of the ground state of the 2DsASI by enabling tension-free DS and thermally stable unbound magnetic monopoles.

In conclusion, string method simulations and FTM analysis show that the finite-sized 3DASI lattice allows the creation and propagation of magnetic charges, which can exist freely or in pairs being connected via tension-free DS at arbitrary temperatures. The interaction between two unbound magnetic monopoles follows a 1/r dependency showing further evidence for the presence of Coulomb interaction in our 3DASI lattice. We showed by numerical experiments, that a single unbound charge can be propagated by an external magnetic field, without creating additional magnetic charges.

Low-energy and ultra-fast switching in the 3DASI lattice, as well as the stability of emergent magnetic monopoles at room temperature and above, paves a way towards functional 3D magnetic nano-networks for data transport and storage. The controlled propagation of the magnetic charges is of high interest regarding the idea of magnetricity66,73, which might lead to further devices18.

Even though we focused only on the center layer and therefore regarded our model as a bulk lattice, the limitations of the z layers might show additional and equally interesting phenomena which will be investigated in detail in further work. By shaving off at a given z dimension, the lattice would have magnetic vertices, containing only three ellipsoids, which would always host a magnetic charge. The top and bottom layers could act as charge plasma layers, which might decharge in the middle layer, creating a magnetic capacitor.

Methods

String method

For each switching process, we start from an initial state and a final state interconnected via 19–20 magnetization states, corresponding to a coherent rotation of the magnetization of the element of interest. In a second step, the total energy of each image is driven a small step towards its energetic minimum. The energy contributions are the demagnetization energy, the exchange energy, and Zeeman energy (FTM analysis). The third step consists of cubic interpolation of the path, such that the magnetization states are equidistant according to an appropriate energy norm60,64,69. The last two steps are repeated until convergence is reached.

Micromagnetic simulations

By using the finite and boundary element method based simulation code magnum.fe64, we solve the Landau–Lifshitz–Gilbert (LLG) equation70:

$$\frac{\partial {{{\bf{m}}}}}{\partial t}=-\frac{\gamma }{1+{\alpha }^{2}}{{{\bf{m}}}}\times {{{\bf{{H}}}^{{{{\rm{eff}}}}}}}-\frac{\alpha \gamma }{1+{\alpha }^{2}}{{{\bf{m}}}}\times \left({{{\bf{m}}}}\times {{{\bf{{H}}}^{{{{\rm{eff}}}}}}}\right),$$
(5)

where α is the Gilbert damping constant, γ is the reduced gyromagnetic ratio, m is the magnetization unit vector, and Heff is the effective field term, which includes the considered energy contributions from demagnetizing, exchange, external and anisotropy fields (magnetic confinement). Vertex state energies are computed by calculating the demagnetizing and exchange energies from the relaxed structures (high damping α = 1). For the field-driven dynamic simulations, we also include global external fields and solve the LLG for a given time. In addition, the magnetization components are averaged within the middle (bulk) layer for each time step, as depicted in Fig. 4b.