Introduction

Bulk photovoltaic (BPV) effect1, which converts incident alternating optical field into direct electric current in centrosymmetric broken materials, has attracted tremendous attention during the past few decades for its easy manipulation and low energy cost. Comparing with conventional light-to-current conversion in a p–n junction between two semiconductors, BPV effect produces electric current everywhere light shines onto the material, which could significantly enhance the conversion efficiency and density. This bias-free approach does not need to deposit electrode contacts to the samples, so that impurities and interface effects can be reduced. From physics point of view, BPV effect is a second order nonlinear optical effect, which includes two photons (with frequency \(\omega\) and \(- \omega\); absorption and emission) and one electron (with moving velocity \(v\))2.

The BPV effect uses electron charge degree of freedom (DOF) to generate a biased electric potential in semiconductors3,4,5,6, which serve as promising electronic devices. In order to further increase the information read/write kinetics and storage density, one may resort to other DOFs of electron, such as its spin angular momentum. The study of the intrinsic spin and its induced magnetic moment is thus referred to as “spintronics”7,8,9, which has been shown to hold potential in the future miniaturized devices, especially in the field of quantum computing and neuromorphic computing. Roughly speaking, when the velocities of electrons in the spin up and spin down channels are different (\(v_ \uparrow - v_ \downarrow\, \ne \,0\)), there is a collective motion of electron spin and leads to a nonzero spin current.

In addition to spin, another DOF that could produce angular momentum and magnetic moment is the electron orbital, which describes the electron traveling around one or a few nuclei. It is an overlooked DOF because in most conventional materials, the orbital moment is significantly or completely quenched under strong and symmetric crystal field. However, when the symmetry and strength of crystal field are reduced, especially in low-dimensional materials, orbital DOF may play an important role in their magnetic properties, topological behaviors, and valleytronic features10,11,12,13. Similar as spintronics, this field is thus termed as “orbitronics”14,15, which is predicted to further enhance information read/write speed significantly. If the electron velocities carrying different orbital magnetic moments (and angular momenta) are different (e.g., \(v_{l_z} - v_{ - l_z}\, \ne \,0\)), then one could also expect an orbital current, analogous to spin current. Note that such an orbital current has been predicted in the linear response Hall effect picture16,17,18, in addition to spin Hall effect19,20 and valley Hall effect11,21,22,23.

In this work, we predict that in addition to nonlinear BPV effect, there exists a hidden orbital current, which carries colossal orbital moment when light shines onto two-dimensional (2D) nonmagnetic ferroelectric materials. We refer to this effect as bulk orbital photovoltaic (BOPV) effect, which is described by a second order nonlinear optical process. We use 2D ferroelectric group-IV monochalcogenide monolayers (GeS, SnS, GeSe, SnSe, GeTe, and SnTe)24,25,26,27,28 and group-V single elemental monolayer Bi(110)29,30 to illustrate our theory. This family of materials have been experimentally fabricated and proved to possess flexible and robust in-plane ferroelectrics31,32. They all belong to \(Pmn2_1\) space group, which contains a vertical mirror symmetry (\(\hat {\cal{M}}_x\)), and the electric polarization is along y. When linearly polarized light (LPL) (with their polarization direction along x or \(y\)) is irradiated onto them, conventional nonlinear BPV current is parallel or antiparallel to the polarization direction y, while the net BPV along x is zero, according to symmetry considerations. Nevertheless, we apply first-principles density function theory (DFT) calculations (see “Methods” section) and reveal that there exist unexpected hidden electron movements along the \(+ x\) and \(- x\) directions, which carries different orbital moments. Hence, one could expect a finite and pure BOPV current to be measured in the x-direction. Here, pure orbital current means that no electric charge current is mixed. We also show that the spin–orbit coupling (SOC) interaction could convert such orbital DOF based BOPV current into spin DOF, namely, bulk spin photovoltaic (BSPV) current (also along x)33,34,35,36. When circularly polarized light (CPL) is used, the conventional charge BPV current will be along x, while the BOPV and BSPV currents flow along \(y\).

Results

Photoconductivity and symmetry analysis

When light (propagating along out-of-plane direction z) irradiates onto the 2D materials, one could adopt closed circuit boundary condition37 and use electric field (E) as the natural variable. The BPV, BOPV, and BSPV effect can be evaluated by (Einstein summation convention adopted)

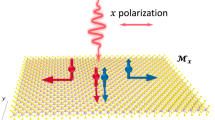
$$\begin{array}{l}{\cal{J}}^c\left( {\omega = 0} \right) = \sigma _{ab}^c\left( {0;\omega, - \omega } \right)E_a\left( \omega \right)E_b\left( { - \omega } \right),\\ {\cal{J}}^{c;L_i}\left( {\omega = 0} \right) = \sigma _{ab}^{c;L_i}\left( {0;\omega, - \omega } \right)E_a\left( \omega \right)E_b\left( { - \omega } \right),\\ {\cal{J}}^{c;S_i}\left( {\omega = 0} \right) = \sigma _{ab}^{c;S_i}\left( {0;\omega, - \omega } \right)E_a\left( \omega \right)E_b\left( { - \omega } \right).\end{array}$$
(1)

Here, \({\cal{J}}^c\), \({\cal{J}}^{c;L_i}\), \({\cal{J}}^{c;S_i}\) are conventional electric charge current, orbital current, and spin current density that propagate along the c-direction, respectively, and \(E_a\) (\(E_b\)) is electric field component (\(a,b,c = x,y\)). \(L_i\) and \(S_i\) are orbital and spin angular momentum components, respectively. Here, we focus on their z-component (\(i = z\)), which is most frequently measured and observed experimentally. Actually we have demonstrated that under glide plane symmetry \(\left\{ {\hat {\cal{M}}_z|\left( {\frac{1}{2}\frac{1}{2}0} \right)} \right\}\), the in-plane spin angular momentum component is suppressed in most k-points of the Brillouin zone (BZ)30. Now we focus on the \(\hat {\cal{M}}_x\) mirror plane constraints. One can apply a simple symmetry analysis to examine the non-dissipation response features of these coefficients. Under LPL (\(a = b = x,y\)), which does not break \(\hat {\cal{M}}_x\) symmetry, the charge current would also obey \(\hat {\cal{M}}_x\). Hence, \({\cal{J}}^x = \hat {\cal{M}}_x{\cal{J}}^x = - {\cal{J}}^x = 0\), so that both \(\sigma _{xx}^x\) and \(\sigma _{yy}^x\) are zero (symmetry forbidden). On the other hand, the vertical direction current \({\cal{J}}^y\) can be nonzero, hence the \(\sigma _{xx}^y\) and \(\sigma _{yy}^y\) are finite, indicating that BPV electric charge current only flows along \(y\). This is consistent with previous works38,39. However, since both \(L_z\) and \(S_z\) transform as pseudovectors – they flip their sign under \(\hat {\cal{M}}_x\). One thus expects that the \(\sigma _{xx}^{x;L_z}\), \(\sigma _{xx}^{x;S_z}\), \(\sigma _{yy}^{x;L_z}\) and \(\sigma _{yy}^{x;S_z}\) would become nonzero, while the \(\sigma _{xx}^{y;L_z}\), \(\sigma _{xx}^{y;S_z}\), \(\sigma _{yy}^{y;L_z}\) and \(\sigma _{yy}^{y;S_z}\) all vanish. These suggest that the zero-valued BPV current \({\cal{J}}^x\) actually do not indicate the electron motions are completely frozen in the \(x\)-direction. Instead, there exist hidden electron flows, which carry orbital and spin angular momentum rather than charge DOF. We illustrate this hidden spin/orbital photocurrent in Fig. 1(a). Since the charge photocurrent and spin/orbital angular momentum (or magnetic moment) photocurrent are perpendicular to each other, one may apply a four-terminal device to measure and observe them simultaneously.

Fig. 1: Bulk photovoltaic effect and microscopic picture.
figure 1

a Schematic plot of bulk angular momentum photoconductivity (BOPV and BSPV) effect. Unlike BPV that propagates along the mirror plane of monolayer GeS, the BOPV and BSPV currents carrying orbital and spin DOF information are traveling normal to the mirror plane (\({\cal{M}}_x\)) under light. A four-terminal device can be used to detect all these photocurrents. The yellow electrode measures charge DOF, while the blue electrodes are magnetic and could measure angular momentum DOF. b Interband transition (pink arrows) picture, where black arrows indicate angular momentum or magnetic moment from orbital and spin DOF. Solid and dashed curves represent occupied (valence) and unoccupied (conduction) bands of the semiconductor, respectively.

Full size image

We could calculate the nonlinear photoconductivity coefficients explicitly. According to the second order Kubo response theory and within the independent particle approximation framework5,40, one can compute the complex nonlinear photoconductivity from its band structure via

$$\chi _{ab}^{c;{\cal{O}}_z}(0;\omega, - \omega ) = \frac{{e^2}}{{\hbar{\,}^2\omega ^2}}{\int} {\frac{{d^3{\mathbf{k}}}}{{(2\pi )^3}}} \mathop {\sum}\limits_{lmn}^{{\Omega} = \pm \omega } {f_{\mathrm{ln} }\frac{{v_{nl}^av_{lm}^bj_{mn}^{c;{\cal{O}}_z}}}{{\left( {\omega _{nm} - {\mathrm{i}}/\tau } \right)\left( {\omega _{nl} + {\Omega} - {\mathrm{i}}/\tau } \right)}}}$$
(2)

This is based on a three band model that includes band-\(m\), \(n\), and \(l\). The phenomenological carrier lifetime \(\tau\) is taken to be 0.2 ps, and \({\mathrm{i}} = \sqrt { - 1}\). The direction scripts \(a,b,c = x,y\). \(f_{ln} = f_l - f_n\) and \(\omega _{nl} = \omega _n - \omega _l\) are the occupation and frequency difference between band-\(l\) and band-\(n\), respectively. Velocity parameter matrix component is defined as \(v_{lm}^a = \left\langle {l\left| {\hat v^a} \right|m} \right\rangle\) and the orbital (or spin) current operator is adopted to be \(j_{mn}^{c;{\cal{O}}_z} = \langle {m| {\{ {\hat v_c,\hat {\cal{O}}_z} \}} |n} \rangle = \frac{1}{2}\langle m |\hat v_c\hat {\cal{O}}_z + \hat {\cal{O}}_z\hat v_c| n\rangle\) with \(\hat {\cal{O}}_z = \hat L_z\) (or \(\hat S_z\)). For the charge current, it can be replaced by \(j_{mn}^c = \left\langle {m\left| {e\hat v_c} \right|n} \right\rangle\). The explicit k-dependence on these quantities are omitted. If during interband transition the \(j_{mn}^{c;L_z}\) or \(j_{mn}^{c;S_z}\) rises, it could lead to finite BOPV or BSPV current. We schematically plot this physical process in Fig. 1b. Note that this is different from the intra-band optical responses in doped semiconductors41.

Under LPL, the nonlinear photoconductivity in Eq. (1) can be evaluated as \(\sigma _{aa}^{c;{\cal{O}}_i} = \Re \chi _{aa}^{c;{\cal{O}}_i}\). For CPL irradiation (along \(z\)), the electric field takes the form \({\mathrm{i}}\left[ {{\mathbf{E}}\left( \omega \right) \times {\mathbf{E}}^{ \ast} \left( \omega \right)} \right]_z\), the response from CPL electric field phase (left or right handedness) can be evaluated by \(\sigma _{ab}^{c;{\cal{O}}_i} = \frac{1}{2}\Im ( {\chi _{ab}^{c;{\cal{O}}_i} - \chi _{ba}^{c;{\cal{O}}_i}} )\). We only include the electric field contribution (with ±i phase difference in the \(x\) and \(y\) components), since the optical response from magnetic field is generally ~4 orders of magnitude smaller than that from the electric field. Hence, electron excitations in the same spin channel is considered (without spin flipping), consistent with previous calculations on valleytronics10,21,42. We will focus on LPL-induced photoconductivity in the main text, and plot the CPL photocurrent responses in Supplementary Fig. 1. We can denote the numerator of Eq. (2) in the format \(N_{abc;z} = v^av^bv^c{\cal{O}}_z\), which can be used to determine the (dissipationless) symmetry allowed and forbidden responses. The time-reversal symmetry gives \(\hat {\cal{T}}v^a\left( {\mathbf{k}} \right) = - v^{a, \ast }\left( { - {\mathbf{k}}} \right)\) and \(\hat {\cal{T}}{\cal{O}}_z\left( {\mathbf{k}} \right) = - {\cal{O}}_z^ \ast \left( { - {\mathbf{k}}} \right)\), hence, one could have \(\hat {\cal{T}}N_{abc;z}\left( {\mathbf{k}} \right) = N_{abc;z}^ \ast \left( { - {\mathbf{k}}} \right)\) for a Kramers pair (here, ·* indicates complex conjugate of quantity \(\cdot\)). Integration over the first BZ yields a real number. As for mirror symmetry, since \(\hat {\cal{M}}_xv^x\left( {\mathbf{k}} \right) = - v^x\left( {{\tilde{\mathbf k}}} \right)\), \(\hat {\cal{M}}_xv^y\left( {\mathbf{k}} \right) = v^y\left( {{\tilde{\mathbf k}}} \right)\) (\({\tilde{\mathbf k}}\) is mirror symmetric image of \({\mathbf{k}}\), \(\tilde k_x = - k_x,\tilde k_y = k_y\)), and \(\hat {\cal{M}}_x{\cal{O}}_z\left( {\mathbf{k}} \right) = - {\cal{O}}_z\left( {{\tilde{\mathbf k}}} \right)\), we have \(\hat {\cal{M}}_xN_{aax;z}\left( {\mathbf{k}} \right) = N_{aax;z}\left( {{\tilde{\mathbf k}}} \right)\) and \(\hat {\cal{M}}_xN_{aay;z}\left( {\mathbf{k}} \right) = - N_{aay;z}\left( {{\tilde{\mathbf k}}} \right)\). The latter is odd under mirror operation. We thus prove that BOPV and BSPV currents only occur along the \(x\)-direction under \(x\) or \(y\)-LPL, consistent with previous analysis. In the long relaxation time approximation, one could demonstrate that LPL irradiation yields the BPV shift current and the CPL illumination generates an injection current for time-reversal symmetric systems. However, for the BSPV and BOPV, we find that the LPL-induced photocurrent is injection-like, which is proportional to the relaxation time \(\tau\). The CPL, on the other hand, induces shift-like current (see Supplementary Note 1 for detailed discussions)43.

DFT-calculated BOPV photoconductivity

Now we apply Eq. (2) to compute nonlinear photoconductivity in 2D nonmagnetic ferroelectric materials. Taking monolayer GeS as an example (Fig. 2a, band structure in Supplementary Fig. 2), we calculate its LPL-induced BOPV conductivity. In practice, the BZ integration in Eq. (2) is \({\int} {\frac{{d^3{\mathbf{k}}}}{{\left( {2\pi } \right)^3}}} = \frac{1}{V}\mathop {\sum}\nolimits_{\mathbf{k}} {w_{\mathbf{k}}}\), where \(V\) is the total volume of simulation supercell and \(w_{\mathbf{k}}\) is the weight of each k-point. In the 3D periodic boundary condition, the supercell of 2D materials contains an artificial vacuum space along \(z\), whose contribution needs to be eliminated. According to previous works, we rescale this result by using an effective thickness of the 2D materials, denoted as \(d\) (taken to be 0.6 nm), which is estimated by the layer-to-layer distance when these 2D materials are van der Waals stacked into bulk. Thus, we can rescale the photoconductivity by \(\sigma ^{2{\mathrm{D}}} = \sigma ^{{\mathrm{SC}}}h/d\), where \(\sigma ^{{\mathrm{SC}}}\) and \(h\) are the supercell-calculated conductivity and the supercell lattice constant along \(z\), respectively44,45. This makes the second order conductivity of 2D materials consistent with conventional quantities of 3D bulk materials. In the following, we will report the \(\sigma ^{2{\mathrm{D}}}\) values. As shown in Fig. 2b, one sees that consistent with our previous symmetry analysis, \(\sigma _{xx}^{y;L_z}\) and \(\sigma _{yy}^{y;L_z}\) are exactly zero through all optical frequency, while \(\sigma _{xx}^{x;L_z}\) and \(\sigma _{yy}^{x;L_z}\) are finite. Note that here we only focus on the out-of-plane angular momentum current, as these angular momenta are uni-directionally along \(z\) in most k points in the group-IV monochalcogenide monolayers with in-plane electric polarization (Supplementary Note 2). The spin-\(z\) component is even a good quantum number under SOC, which is quantized to be \(\pm \frac{1}{2}\) when the state is singly degenerate. This numerical results demonstrate that the nonlinear BOPV current flows along the \(x\)-direction, which is normal to the mirror plane. Our BPV conductivity calculation confirms that the \(x\)-direction charge current is zero (Supplementary Fig. 3), which also agrees with previous works. Thus, it suggests that the same amount of electrons carrying opposite \(z\)-component angular momentum are transporting along \(x\) and \(- x\) directions, which can be dubbed pure orbital current (charge current \({\cal{J}}^x = e( {v^{x;l_z} + v^{x; - l_z}} ) = 0\), orbital current \({\cal{J}}^{x;L_z} = l_zv^{x;l_z} - l_zv^{x; - l_z}\, \ne \,0\), where \(l_z\) is the averaged \(z\)-component angular momentum expectation value, similar as spin up and spin down in the spin DOF). As for the \(y\)-direction electron current, it is a pure charge current with \({\cal{J}}^y = e( {v^{y;l_z} + v^{y; - l_z}})\, \ne \,0\) and orbital current \({\cal{J}}^{y;L_z} = l_zv^{y;l_z} - l_zv^{y; - l_z} = 0\), indicating that all electrons are moving along the same direction (\(y\) or \(- y\)) and the amount of electrons carrying \(l_z\) and \(- l_z\) are the same. This is consistent with the illustrations in Fig. 1a.

Fig. 2: BOPV response of monolayer GeS.
figure 2

a Atomic geometry of monolayer GeS. b Calculated BOPV conductivity as a function of incident linearly polarized light frequency. c jDOS \(\tilde \rho (\omega,{\mathbf{k}})\) distribution in the first BZ at \(\omega = 2.83{\mathrm{eV}}\) and \(\omega = 2.17{\mathrm{eV}}\). d k-resolved BOPV conductivity \(\varsigma _{xx}^{x;L_z}({\mathbf{k}})\) (at \(\omega = 2.83{\mathrm{eV}}\)) and \(\varsigma _{yy}^{x;L_z}({\mathbf{k}})\) (at \(\omega = 2.17\,{\mathrm{eV}}\)).

Full size image

When the incident light energy is below the direct bandgap of monolayer GeS (1.91 eV), all photoconductivities are zero since no interband transition occurs. At incident optical energy of \(\hbar \omega = 2.83\,{\mathrm{eV}}\), the nonlinear BOPV conductivity \(\sigma _{xx}^{x;L_z}\) reaches a negative peak of \(- 636.2\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{\hbar }{{2e}}\). Here, the unit \(\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\) is that of nonlinear charge BPV conductivity, and \(\frac{\hbar }{{2e}}\) converts it to angular momentum, similar as that from the Hall conductance to the spin Hall conductance. If one measures magnetic moment, this unit becomes \(g\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{{\mu _B}}{{2e}}\), where \(g\) is Landé g-factor (\(g_L \simeq - 1\), \(g_S \simeq - 2\)) and \(\mu _B\) is Bohr magneton. In order to further examine its momentum space contribution, we first plot the k-resolved joint density of states (jDOS) \(\tilde \rho (\omega,{\mathbf{k}})\) at \(\omega = 2.83\,{\mathrm{eV}}\) (Fig. 2c, left panel). The jDOS reads

$$\rho _{cv}\left( \omega \right) = \frac{1}{{\left( {2\pi } \right)^2}}{\int}_{{\mathrm{BZ}}} {\tilde \rho (\omega,{\mathbf{k}})d^2{\mathbf{k}}} = \frac{1}{{\left( {2\pi } \right)^2}}{\int}_{{\mathrm{BZ}}} {\mathop {\sum}\nolimits_{c,v} {\delta \left( {\varepsilon _{ck} - \varepsilon _{vk} - \hbar \omega } \right)d^2{\mathbf{k}}} }$$
(3)

where \(\varepsilon _{nk}\) is eigenvalue of band-\(n\) at momentum \({\mathbf{k}}\), and \(c\) and \(v\) represent the conduction and valence bands, respectively. The integral is taking in the first BZ. According to Sokhotski-Plemelj formula, jDOS represents the resonant band transition between band-\(l\) and band-\(n\) in Eq. (2). One could see that \(\tilde \rho _{cv}\left( {\omega = 2.83\,{\mathrm{eV}},{\mathbf{k}}} \right)\) is mainly contributed around the \(\pm X\) and \(\pm Y\) points in the BZ. We next plot the real part of the integrand of Eq. (2), \(\varsigma _{xx}^{x;L_z}(\omega,{\mathbf{k}}) = \Re \mathop {\sum}\nolimits_{lmn}^{{\Omega} = \pm \omega } {f_{ln}\frac{{v_{nl}^xv_{lm}^xj_{mn}^{x;L_z}}}{{\left( {\omega _{nm} - {\mathrm{i}}/\tau } \right)\left( {\omega _{nl} + {\Omega} - {\mathrm{i}}/\tau } \right)}}}\) (Fig. 2d, left panel), integrating which over the first BZ yields \(\chi _{xx}^{x;L_z} = \sigma _{xx}^{x;L_z}\). One clearly sees that in the momentum space, \(\varsigma _{xx}^{x;L_z}(\omega,{\mathbf{k}})\) keeps the \({\cal{M}}_x\) symmetry, and is mainly contributed around \(\pm X\) and \(\pm Y\). The jDOS around Γ point does not contribute any significant photoconductivities. One can see that the BOPV fluctuates with respect to incident photon energy, and it could become zero at some specific energies (such as 2.63 eV for \(\sigma _{xx}^{x;L_z}\)). In order to see the origin of such zero photoconductivity, we plot \(\varsigma _{xx}^{x;L_z}({\mathbf{k}})\) at \(\omega = 2.63\,{\mathrm{eV}}\) in Supplementary Fig. 4. One could see that the two valleys (±Vx along Γ → ±X and ±Vy along Γ → ±Y) contribute oppositely to the conductivity. This could lead to valley-polarized photoconductivities without a net charge or orbital current flow, which invokes valley DOF in the system. When the \(y\)-polarized LPL is applied, it reaches a peak of \(913.95\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{\hbar }{{2e}}\) at \(\omega = 2.17\,{\mathrm{eV}}\). The k-resolved jDOS and \(\varsigma _{yy}^{x;L_z}(\omega,{\mathbf{k}})\) are shown in the right panels of Fig. 2c, d. Again, the distribution shows \({\cal{M}}_x\) symmetry, which locates around the two Vy valleys at \(\left( {0, \pm 0.54,0} \right)\) Å–1, but not around Γ.

BSPV photoconductivity

The SOC interaction that breaks the spin rotational symmetry usually splits the spin up and spin down degeneracy in the centrosymmetric broken systems (such as Rashba and Dresselhaus splitting). Here, we show that such spin polarization in band dispersion also produces finite BSPV effect. In Fig. 3a, we plot our calculated BSPV conductivity of monolayer GeS. Analogs to the BOPV, under LPL illumination, BSPV also flows along the \(x\)-direction, giving finite \(\sigma _{xx}^{x;S_z}\) and \(\sigma _{yy}^{x;S_z}\), while \(\sigma _{xx}^{y;S_z} = \sigma _{yy}^{y;S_z} = 0\). However, we find that the magnitude of BSPV conductivities are generally much smaller than that of the BOPV. Comparing Figs. 2b and 3a, one could see that the magnitude of BOPV conductivity is about one order of magnitude larger than the BSPV conductivity. For example, the \(\sigma _{xx}^{x;S_z}\left( {\omega = 2.83{\mathrm{eV}}} \right) = 113.37\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{\hbar }{{2e}}\) and \(\sigma _{yy}^{x;S_z}\left( {\omega = 2.17{\mathrm{eV}}} \right) = 3.60\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{\hbar }{{2e}}\), much smaller than the corresponding BOPV magnitudes at the same frequency range. We also plot their momentum space contributions (\(\varsigma _{xx}^{x;S_z}({\mathbf{k}})\) and \(\varsigma _{yy}^{x;S_z}({\mathbf{k}})\), in Fig. 3b), which show that they locate similarly as in the BOPV conductivities, and the \(\hat {\cal{M}}_x\) symmetry still retains. Note that these 2D ferroelectric monolayers possess four electron valleys in the first BZ (±Vx and ±Vy, near \(\pm X\) and \(\pm Y\)). Hence, we show that the photocurrent is mainly contributed from these valleys, which may provide promising and exotic physical properties among orbitronics, spintronics, and valleytronics.

Fig. 3: BSPV response of monolayer GeS.
figure 3

a BSPV photoconductivity component of monolayer GeS under LPL. b Momentum space distributions of the integrand \(\varsigma _{xx}^{x;S_z}(\omega = 2.83{\mathrm{eV}},{\mathbf{k}})\) and \(\varsigma _{yy}^{x;S_z}(\omega = 2.17{\mathrm{eV}},{\mathbf{k}})\).

Full size image

According to solid state physics theory, orbital moment in a bulk material is usually strongly quenched by strong and symmetric crystal field, so that it is the spin polarization that mainly contributes to the total magnetic moment. Hence, the orbital moment contribution is omitted in most cases. However, here we find that BOPV conductivity is generally much larger than that of BSPV. According to Eq. (2), the dominate interband transition contribution is from two-band transition, namely, \(|m\rangle = |n\rangle\), and the \(|l\rangle\) band lies on the other side of the Fermi level (hence \(f_{ln}\, \ne \,0\)). We will limit our discussion on this two-band model. Thus, the difference between BOPV and BSPV conductivities can be understood by comparing \(\left\langle {\left\{ {v_x,L_z} \right\}} \right\rangle\) and \(\left\langle {\left\{ {v_x,S_z} \right\}} \right\rangle\) for the low-energy bands (near Fermi level), which is determined by the velocity and orbital/spin texture. In order to illustrate it more clearly, we plot the k-space distribution of orbital and spin angular momentum (\(\left\langle {L_z} \right\rangle\) and \(\left\langle {S_z} \right\rangle\)) of the highest valence band (VB) and the second highest valence band (VB−1), as shown in Fig. 4a, b. Here, VB and VB−1 are actually Rashba splitting bands. One clearly observes that the \(\left\langle {L_z} \right\rangle\) distribution on the VB and VB−1 are similar, while the \(\left\langle {S_z} \right\rangle\) distribution on them show opposite values. This is because that the orbital texture is determined by the crystal field once the material forms, and changes marginally under SOC. On the other hand, the Rashba-type spin splitting yields that \(\left\langle {S_z} \right\rangle\) flips its sign between the VB and VB−1 at each k. We also plot the spin and orbital angular momentum distributions of the lowest two conduction bands in Supplementary Fig. 5, and similar results can be seen. The velocity texture distributions on VB and VB−1 are also similar (but not identical) (Fig. 4c). We plot \(\left\langle {\left\{ {v_x,L_z} \right\}} \right\rangle\) and \(\left\langle {\left\{ {v_x,S_z} \right\}} \right\rangle\) of bands near the Fermi level in Supplementary Fig. 6. From all these evidences, we show that the crystal field determined orbital responses are similar at the Rashba splitting bands, while their contributions to the spin responses are opposite (but not completely canceled due to small velocity distribution difference under Rashba splitting). Therefore, the BSPV conductivity is usually much smaller than that of BOPV.

Fig. 4: Rashba SOC effect on monolayer GeS BSPV photoconductivity.
figure 4

Momentum space distribution of a \(\left\langle {L_z} \right\rangle\), b \(\left\langle {S_z} \right\rangle\), and c velocity texture \(\left( {\left\langle {v_x} \right\rangle,\left\langle {v_y} \right\rangle } \right)\) of VB–1 and VB in the first BZ. d BSPV response function under different SOC strength parameter λ. Inset: The peak magnitude change of BSPV \(\sigma _{xx}^{x;S_z}\left( {\omega = 2.83\,{\mathrm{eV}}} \right)\) as a function of λ. Linear relation can be clearly seen. One has to note that the band dispersion will be significantly changed under very strong SOC, so that such linearity may not hold when λ is very big.

Full size image

SOC and polarization effects

In order to further understand the mechanism of BOPV and BSPV photoconductivities, we artificially tune the SOC interaction \(H_{{\mathrm{SO}}} = \alpha _{{\mathrm{SO}}}{\mathbf{S}} \cdot {\mathbf{L}}/\hbar ^2\) strength by multiplying a pre-factor \(\lambda \in [0,1]\). Here, \(\lambda = 0\) turns off the SOC, and \(\lambda = 1\) indicates full SOC. Since neither Ge nor S is heavy, the SOC effect is weak and the bandgap reduction under SOC is marginal (within 5 meV, Supplementary Fig. 7). We find that the BOPV (and BPV) conductivity marginally changes under different \(\lambda\) (see Supplementary Fig. 8). However, the BSPV conductivity linearly reduces to zero from \(\lambda = 1\) (full SOC) to \(\lambda = 0\) (no SOC), as shown in Fig. 4d. This clearly demonstrates that the BOPV effect is ubiquitous even without SOC since orbital texture originates from the crystal field, while SOC is crucial for BSPV effect in these nonmagnetic systems. Therefore, we could conclude that the BOPV effect arises when crystal is formed, and then it leads to BSPV effect through a finite SOC interaction (\(H_{{\mathrm{SO}}} \propto {\mathbf{S}} \cdot {\mathbf{L}}\)). Similar relation can also be seen in the orbital and spin Hall effects16. In magnetic systems, spin current could naturally emerge even without SOC. Note that very strong SOC may not necessarily imply further linearly enhanced BSPV, as the band dispersion would be significantly affected.

For the ferroelectric materials, one could easily apply external (electrical, mechanical, and optical) fields to modulate its polarization (for example, from \(P_0\) to \(- P_0\)). The transition barrier between different ferroic orders is usually a high-symmetric geometry, which is centrosymmetric and not electrically polarized (\(P = 0\)). We now examine the BOPV and BSPV photoconductivity under different electric polarizations. In Fig. 5, we plot the polarization dependent BOPV and BSPV photoconductivities. One clearly observes that all these conductivities diminishes at \(P = 0\) state. This is consistent with symmetry analysis, \(\hat IN_{abc;z}\left( {\mathbf{k}} \right) = - N_{abc;z}\left( { - {\mathbf{k}}} \right)\), where \(\hat I\) is inversion symmetry operator (angular momenta \(L\) and \(S\) are invariant under \(\hat I\)). We also note that when the polarization flips (corresponding to a 180°-rotation from \(P_0\) to \(- P_0\)), the photoconductivities reverse their flowing direction while keeping same magnitudes. If a 90°-rotation occurs, these conductivities also rotate 90°, flowing along the \(\pm y\)-direction. Hence, one could control the ferroic polarization order to manipulate the BOPV and BSPV photocurrents, as well as the BPV effect.

Fig. 5: Polarization effect.
figure 5

Polarization dependent a BOPV and b BSPV conductivity of monolayer GeS. The reversal of polarization \({\mathbf{P}}\) flips the photocurrent, while the high-symmetric structure (\(P = 0\)) forbids any photocurrents.

Full size image

Other analogous systems

We now calculate the BOPV and BSPV conductivities for other analogs, namely, monolayers GeSe, SnS, SnSe, GeTe, SnTe, and Bi(110). Note that even though the monolayer Bi(110) is a single elemental material, Peierls instability occurs due to strong s and p orbital hybridization, which leads to charge transfer within each atomic layer. Thus, the monolayer Bi(110) also shows in-plane ferroelectricity and fascinating optical properties. All these BOPV and BSPV photoconductivity results are shown in Fig. 6. For the BOPV conductivity, we observe clear similarities for all these systems, because their electronic band structure can be described by the same low-energy model30. By comparing the main peaks in Figs. 6a and 2b, we find that (for the group IV–VI systems) when the system is composed by small cation and large anion, the BOPV photoconductivity shows larger peak values (over \(10,000\frac{{\mu {\mathrm{A}}}}{{{\mathrm{V}}^2}}\frac{\hbar }{{2e}}\)). Hence, the monolayer GeTe exhibits the largest photocurrent responses, while the orbital photoconductivity of monolayer SnS is the smallest. However, the BSPV does not have such similarity as the SOC interaction strength (proportional to Z4) determines its responses.

Fig. 6: Photoconductivities of other systems.
figure 6

a BOPV and b BSPV conductivity coefficients of other similar 2D ferroelectric monolayers.

Full size image

Discussion

Before concluding, we would like to remark a few points. In our current calculation, we use DFT-based calculations and did not adopt more accurate many body calculation with exciton effects, due to their expensive computational demanding. We note that very recently Fei et al.6 have compared the DFT evaluated shift current (with bandgap shifted according to scissor operator scheme) and the more accurate many body calculations with exciton effect in both 3D perovskite and 2D monochalcogenide SnSe monolayer. They find that since the inverse of absorption coefficient (on the order of 103 Å) is much larger than the 2D material thickness (a few Å), the DFT-based results render very similar results with many body theory calculations. Our previous work also shows that the DFT calculations could yield qualitatively correct linear optical response functions in 2D group-IV monochalcogenides44. Hence, we here adopt the DFT-based electronic structure at the current stage, which is also usually used in most nonlinear optical response calculations.

Since the concept of orbital current was initially proposed in 200514, there have been several theoretical and computational studies on the orbital current and orbital Hall effect46,47,48. Intuitively, one could measure the orbital angular momentum accumulation at the edges of devices, but orbital hybridizations may hinder such measurement and make the observation very challenging. Hence, direct experimental evidences are still very rare and most studies are theoretical predictions. Recently, Yan and colleagues17 proposed an indirect detection method, which utilizes strong interfacial spin–orbit coupling from a contact and converts the orbitronic measurement into spintronic measurement. Two possible approaches can be considered: (1) One could induce spin polarization or spin current from the transverse orbital current in an edge connecting to a third lead with strong interfacial SOC atoms. Then the spin polarization and spin current can be detected via magneto-optical Kerr (or Faraday) effect and inverse spin Hall effect, respectively. (2) One could measure the magnetoresistance change when magnetization along \(z\) (\(M_z\)) of an external magnetic lead is flipped. In our work, our focus is to propose that the optically induced orbital current could generate spin current, under SOC interactions.

One may wonder how to classify the orbital current. Actually, the classification of orbital current (that carries orbital angular momentum) is theoretically challenging, as well as the exact classification of spin current. Rigorously speaking, only when the spin-z-component is a good quantum number and is thus quantized (for example, \(s_z = \pm \frac{1}{2}\)), one can well-define a spin current by separately evaluating the spin up and spin down conductivities, \(j^{{\mathrm{spin}}} = j^ \uparrow - j^ \downarrow\). However, this is generally not satisfied, especially when Rashba effect occurs in non-centrosymmetric systems and the \(s_z\) is usually not a good quantum number. Then the out-of-plane spin component expectation value is continuous, so that the spin current can hardly been properly defined. Nevertheless, we can follow this protocol and characterize orbital current according to the orbital angular momentum (\(l_z\) or \(m_l\)) it carries. This could provide more states than the up and down in spin current. However, such \(z\)-component angular momentum is generally continuous and a well-defined classification may not apply in this case. A possible route is to project orbital angular momentum operator onto valence band subspace (similar as for spin DOF), \({\Bbb L}^{\mathrm{v}}({\mathbf{k}}) = P\left( {\mathbf{k}} \right)\hat L_zP({\mathbf{k}})\) where \(P({\mathbf{k}})\) is projection operator49. If the spectrum of \({\Bbb L}^{\mathrm{v}}({\mathbf{k}})\) is fully gapped in the whole BZ, then the wavefunction can be classified into different angular momentum space accordingly. However, this is usually not easily satisfied, and more theoretical investigations are still required.

In the current work, we follow the conventional approaches to take a universal carrier relaxation time τ = 0.2 ps. Since the usual carrier relaxation time can be as long as a few picoseconds to even nanoseconds, this choice is conservative and would not overestimate photoconductivities. One has to note that in reality, τ varies under different environmental conditions, such as temperature, defects, disorders and impurities of the sample. Even in perfect crystals, the carrier lifetime varies for different bands at different k, so that an exact evaluation is challenging. Note that τ affects the smearing of the response function. In addition, according to Kramers–Kronig relation, the exact value would not greatly affect the real part of response function values, when the incident photon energy is away from resonant absorption regime. We expect experimental verifications that could not only determine the lifetime effect, but also the many body and exciton interaction effect.

We evaluate the photoconductivity according to Kubo response theory, which describes the sequential process. According to recent diagrammatic approach and Taylor expansion of the perturbed Hamiltonian on vector potential \({\mathbf{A}}\), it has been suggested that instantaneous processes could emerge50,51. However, they usually contribute marginally to bulk photogalvanic effect, especially in \(\hat {\cal{T}}\)-symmetric systems. Hence, we ignore such contributions in our current calculations. According to our previous discussion, \(\hat L_z\) is not conservative in this system, hence it does not fully obey continuous equation of motion. We could project \(\hat L_z\) onto the eigenenergy subspace by \(\hat {\cal{L}}_z = \mathop {\sum}\nolimits_n {\left| {\psi _{n{\boldsymbol{k}}}} \right\rangle \left\langle {\psi _{n{\boldsymbol{k}}}} \right|\hat L_z\left| {\psi _{n{\boldsymbol{k}}}} \right\rangle \left\langle {\psi _{n{\boldsymbol{k}}}} \right|}\)52, and the conservation law can be retained (\(\hat {\cal{L}}_z\) being a good quantum number). Our test calculations show that such projection provides qualitatively same results as reported here, where our symmetry analysis still holds.

Practically, ferroic materials usually contain multiple domains with domain boundary separating different polarization orders. In our current case, since the ferroelastic deformation strain is small, these domains prefer nearly 90° polarization directions at the two sides of the boundary. Hence, across the boundary, the local coordinate system (x and y) would swap. Since the photocurrents predicted in this work have strong (local) direction dependent selectivity, crossing the domain boundary would change the allowed BPV and BOPV (or BSPV) channels. For example, when a P0 parallel BPV current hit the domain boundary, it would become BOPV (and BSPV) current after transmission, because of a nearly 90° rotation of P0 on the other side of the boundary. Other orbital or spin current are reflected by the domain boundary to keep the electron and angular momenta conserved. Therefore, we propose that the domain boundary may serve as an angular momentum current filter or valve when light illuminates across ferroic domain boundaries.

In this work, we predict robust and pure bulk photovoltaic currents in the carrier orbital and spin degrees of freedom. Using nonmagnetic 2D ferroelectric materials (GeS and its analogs) as exemplary materials, we show that the mirror symmetry forbidden BPV conductivity actually contains hidden electron motions, which carries orbital moment flow with zero net electric charge current. Under SOC interaction, the photo-induced orbital current could generate spin current. Both of these currents are perpendicular to conventional BPV electric current, so that they can be purely and exclusively detected and used. When ferroic order switches, the photoconductivities rotate their directions accordingly. Ferroelectric domain boundary may serve as an effective angular momentum filter or valve when light shines on its both sides. We summarize such polarization and light dependent photovoltaic effects in Table 1. Our prediction of pure BOPV and BSPV effects can be detected and observed in experiments, and may provide potential ultrafast spintronic and orbitronic applications of 2D in-plane ferroelectric materials, in addition to their electronic features, especially when a four-terminal device is applied.

Table 1 Polarization dependent bulk (charge, spin, and orbital) photovoltaic conductivities.
Full size table

Methods

Density functional theory

We use first-principles density functional theory to calculate the geometric, electronic, and optical properties of 2D monolayer GeS and analogous systems, as implemented in the Vienna ab initio simulation package (VASP)53. The generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) form54 is adopted to treat the exchange correlation functional in the Kohn–Sham equation. A vacuum space of 12 Å along the out-of-plane z-direction is used, to eliminate the interactions between different periodic images. Projector-augmented wave (PAW)55 method is used to treat the core electrons, and the valence electrons are represented by planewave basis set, with a kinetic cutoff energy chosen to be 350 eV. The first Brillouin zone is represented by the Monkhorst-Pack k-mesh scheme56 with a (9 × 9 × 1) grid for geometric and electronic structure calculations. Convergence criteria of total energy and force component on each ion are set as 1 × 10−7 eV and 0.01 eV Å−1, respectively. Spin–orbit coupling interactions are self-consistently included in all calculations, unless otherwise noted. In order to evaluate the nonlinear optical conductivities, we fit the electronic structure by atomic orbital based tight-binding model in atomic orbital basis set (s and p orbitals), as implemented in the Wannier90 package57,58, and the optical conductivities are integrated on a denser k-mesh of (901 × 901 × 1) grid. The convergence of k-grid density is carefully tested. As for the estimate of orbital angular momentum contributed intra-atomically, we use \(|s\rangle = Y_0^0\), \(|p_x\rangle = \frac{1}{{\sqrt 2 }}\left( {Y_1^{ - 1} - Y_1^1} \right)\), \(|p_y\rangle = \frac{{\mathrm{i}}}{{\sqrt 2 }}\left( {Y_1^{ - 1} + Y_1^1} \right)\), and \(\left| {p_z} \right\rangle = Y_1^0\) as basis set and calculate their matrix components \(\left\langle {m|L_z|n} \right\rangle\), with the intra-atomic local orbital angular momentum \(L_z = {\mathrm{i}}\hbar \left( {\begin{array}{*{20}{c}} 0 & { - \frac{1}{2}\sigma _ - } \\ {\frac{1}{2}\sigma _ + } & 0 \end{array}} \right)\), where \(\sigma _ \pm = \sigma _x \pm {\mathrm{i}}\sigma _y\). The spin operators are proportional to conventional Pauli matrix, \(S_i = \frac{\hbar }{2}\sigma _i\), where \(\sigma _i\left( {i = x,y,z} \right)\) are Pauli matrices. We test and verify our calculation procedure by comparing with previous orbital momentum calculations and BPV effect computations.