Introduction

Tunable dielectrics is a type of functional materials whose dielectric permittivity (χ) can be adjusted by an external electric field E. The key parameter used to describe a tunable dielectric is the so-called dielectric tunability, η, which is defined as the relative change (%) of dielectric permittivity under an E field: \(\eta (E) = \frac{{\chi _0 - \chi \left( E \right)}}{{\chi _0}} \times 100{\mathrm{\% }}\). Here \(\chi _0\) is the zero-field or small-field dielectric permittivity while \(\chi \left( E \right)\) is the one under the field E. As a typical nonlinear dielectric, ferroelectrics are usually endowed with a high dielectric tunability, and hence have been broadly utilized in tunable dielectric devices. Recently, with the rapid developments in miniaturized and integrated tunable devices, such as phase shifters, oscillators, and filters, ferroelectric thin films showing a high η value have been extensively investigated1,2,3. PZT and some lead-free films including BaTiO34,5,6, (Ba, Sr)TiO31,7,8,9, and Ba(Zr, Ti)O310 are the center of focus based on their high dielectric permittivities. The reported η values are usually between 20 and 70%1,6,7,11,12.

Currently, there are a few issues that need to be addressed for the further development of tunable ferroelectric dielectrics. Firstly, BaTiO3-based ferroelectrics have a relatively low Curie temperature (<~120 °C) which has limited their applications, while the use of lead-based ferroelectrics (such as PZT) at elevated temperatures exacerbates the risk of toxic lead exposure. Secondly, the measured η values13,14,15,16,17,18,19 are usually not quantitatively explained, except for a few cases in bulk ceramics20,21. This is possibly due to the many practical factors affecting dielectric tunability in thin films, as well as disconnects between theorists and experimentalists. In this work, a coordinated effort integrating computational material design, material processing, and electrical characterization is reported for (001)-oriented epitaxial (K0.5Na0.5)NbO3 (KNN) films. As will be illustrated below, KNN in this structure is a promising material candidate for thin-film tunable dielectrics, owing to its lead-free composition, high Curie temperature, a sizable spontaneous polarization, and a large dielectric permittivity22,23,24,25.

Results and discussion

Dielectric tunability of a (001)-oriented tetragonal ferroelectric film

For a (001)-oriented tetragonal ferroelectric film of an epitaxial quality, its polarization P is aligned along the film normal under an external electric field E, the in-plane polarization, and electrical field components \(P_1 = P_2 = 0,E_1 = E_2 = 0\), while the out-of-plane ones are not, \(P_3 = P \,\ne\, 0,E_3 = E\). The in-plane strains extrapolated to the parent cubic phase, are \(\varepsilon _1 = \varepsilon _2 = u_m = \varepsilon _M^0 + Q_{12}(P_0^b)^2\)26, where \(\varepsilon _M^0\) is the effective in-plane misfit, i.e., the difference between in-plane lattice parameters of the clamped and free-standing films, Q12 is an electrostrictive coefficient, and \(P_0^b\) is the spontaneous polarization of the free-standing film or bulk. The Landau-Devonshire type (LD) thermodynamic potential of the film can be expressed as26:

$$\tilde G = a_1P^2 + a_{11}P^4 + a_{111}P^6 - EP + \frac{{\left\{ {\varepsilon _M^0 - Q_{12}\left[ {P^2 - \left( {P_0^b} \right)^2} \right]} \right\}^2}}{S}$$
(1)

where \(a_1,\;a_{11},\;a_{111}\) are the first, second, and third-order Landau coefficients determined under the stress-free condition, and S is the effective in-plane compliance given by \({\mathrm{S}} = s_{11} + s_{12}\), with \(s_{11}\), \(s_{12}\) being the elastic compliances of the parent cubic phase. These material-specific parameters can be obtained from experimental measurements. By using the combo coefficients below26,

$${\upalpha} = 2(a_1 - \frac{{2[\varepsilon _M^0 + Q_{12}(P_0^b)^2]Q_{12}}}{s}),\;\beta = 4\left( {a_{11} + \frac{{Q_{12}^2}}{S}} \right),\,\alpha _3 = 6a_{111}$$
(2)

We reduce Eq. (1) into

$$\tilde G = \frac{1}{2}\alpha P^2 + \frac{1}{4}\beta P^4 + \frac{1}{6}\alpha _3P^6 - EP + \frac{{[\varepsilon _M^0 + Q_{12}(P_0^b)^2]^2}}{S}$$
(3)

The equilibrium polarization under an electric field E can be obtained by minimizing the free energy in Eq. (3), i.e., \({\mathrm{d}}\tilde G/{\mathrm{d}}{P} = 0\), which leads to

$$E = {\upalpha}P + \beta P^3 + \alpha _3P^5$$
(4)

when E = 0, the film’s remnant polarization can be obtained, \(P_0^f = \sqrt {\frac{{ - \beta + (\beta ^2 - 4\alpha \alpha _3)^{1/2}}}{{2\alpha _3}}}\). Using a field-induced polarization \(p = P^f\left( E \right) - P_0^f\), the zero-field dielectric permittivity of the film (\(\chi _0^f\)) can also be obtained from an approximation of Eq. (4), taking into account only the first term,

$$E = \left[ {\alpha + 3\beta (P_0^f)^2 + 5\alpha _3(P_0^f)^4} \right]p$$
(5)
$$\chi _0^f = \frac{{\mathrm{d}p}}{{\mathrm{d}E}}|_{E = 0} = [\alpha + 3\beta (P_0^f)^2 + 5\alpha _3(P_0^f)^4]^{ - 1}$$
(6)

If the second-order term is taken into account, Eq. (4) reduces to

$$E = \gamma _1p + \gamma _2p^2$$
(7)

where \(\gamma _1 = (\chi _0^f)^{ - 1}\), \(\gamma _2 = 3\beta P_0^f + 10\alpha _3\left( {P_0^f} \right)^3.\)

From the solution of Eq. (7) we can obtain the dielectric permittivity under an applied electric field E,

$$\chi ^f\left( E \right) = \frac{{\mathrm{d}p}}{{\mathrm{d}E}} = \frac{1}{{\sqrt {\gamma _1^2 + 4\gamma _2E} }} = \frac{{\chi _0^f}}{{\sqrt {1 + \lambda _fE} }}$$
(8)
$${\mathrm{where}}\;\lambda _f = \frac{{4\gamma _2}}{{\gamma _1^2}} = 4(\chi _0^f)^2 \cdot \left[ {3P_0^f\beta + 10\left( {P_0^f} \right)^3{\upalpha}_3} \right]$$
(9)

It is noted that Eq. (8) reveals the nonlinear nature of the dielectric permittivity in a ferroelectric film. \(\lambda _f\) is the tunability factor of the ferroelectric film, which characterizes the rate of the nonlinear change of its dielectric permittivity. Consequently, the dielectric tunability \(\eta\) can be expressed as:

$$\eta = \frac{{\chi _0^f - \chi ^f\left( E \right)}}{{\chi _0^f}} \times 100{\mathrm{\% }} = 1 - \frac{1}{{\sqrt {1 + \lambda _fE} }}$$
(10)

From Eq. (10), it is clear that the dielectric tunability \(\eta\) has a positive correlation with \(\lambda _f\). The larger the \(\lambda _f\), the higher the reduced portion of \(\chi _0^f\), i.e., the higher the dielectric tunability \(\eta\) is, at a given electric field E. From Eq. (9), \(\lambda _f\) and hence \(\eta\) is determined by the directly measurable material properties \(\chi _0^f\) and \(P_0^f\), given that the material-specific parameters of \(a_{11},\;a_{111}\), \(S\) and Q12 are known (In principle, all three parameters λf, \(\chi _0^f\) and \(P_0^f\)are functions of the misfit strain \(\varepsilon _M^0\). They can be determined theoretically when the Landau coefficients (a1, a11, a111), the electrical/elastic/electromechanical properties (\(P_0^b\), s11/s12 and Q12) of the film material, as well as its misfit strain \(\varepsilon _M^0\) are all correctly determined. However, this is not always possible for theorists or convenient for experimentalists. In this work, for the selection of material, we used the experimentally measurable properties of \(\chi _0^f\) and \(P_0^f\), which are abundant in the literature, and a reduced number of material-specific parameters).

In Fig. 1 below, the tunability factors \(\lambda _f\) for some commonly used, (001)-oriented tetragonal ferroelectric films are presented as functions of \(\chi _0^f\) and \(P_0^f\). It clearly shows that, with an intermediate remnant polarization (\(P_0^f\) ~ 0.15 to 0.3), a large dielectric permittivity (second only to PZT 50/50 in this chart, \(\chi _0^f\) ~ 600–120018,25,27,28), (001)-oriented tetragonal KNN films display a large \(\lambda _f\) on the order of 10−6–10−7, corresponding to a dielectric tunability \(\eta\) ~ 59–86% under a typical electric field of 500 kV cm−1 (5 V on a 100 nm thick film). This is very promising for a lead-free ferroelectric.

Fig. 1: Relationship between λf, χf0, and Pf0.
figure 1

The relationship between λf, \(\chi _0^f\) and \(P_0^f\) of typical (001)-oriented tetragonal ferroelectric films, including BaTiO3, Ba(Zr0.3,Ti0.7)O3, BiFeO3, K0.5Na0.5NbO3, and Pb(Zr0.5Ti0.5)O3. The two open-circle points are experimental data from this work. The ellipses are drawn for the guidance of the eye.

Full size image

The Landau coefficients and other related parameters of the ferroelectric films in Fig. 1 are listed in Tables 1 and 2, for BaTiO3 (BTO)29, Ba(Zr0.3,Ti0.7)O3 (BZT 30/70)30, BiFeO3 (BFO)31,32,33 and Pb(Zr0.5Ti0.5)O3 (PZT 50/50)34 films, and (K0.5Na0.5)NbO3 (KNN) films35, respectively.

Table 1 Parameters used for BTO, BZT 30/70, BFO, PZT 50/50 films in Fig. 1.
Full size table
Table 2 Parameters of KNN films used in theoretical computations of this work35.
Full size table

Strain-stabilized (001)-oriented tetragonal KNN film

A modified-LD thermodynamic potential has been employed to predict the crystalline structure of an epitaxial KNN film35. The thermodynamic potential \(\tilde G\) of a single-domain epitaxial film under a constant-stress mechanical boundary condition can be written as36,37,38,39,40:

$$\begin{array}{l}\tilde G = a_1\left( {P_1^2 + P_2^2 + P_3^2} \right) + a_{11}\left( {P_1^4 + P_2^4 + P_3^4} \right) + a_{111}\left( {P_1^6 + P_2^6 + P_3^6} \right) + a_{12}\left( {P_1^2P_2^2 + P_1^2P_3^2 + P_2^2P_3^2} \right) + a_{123}P_1^2P_2^2P_3^2 + a_{112}\left[{P_1^4(P_2^2 + P_3^2) + P_3^4(P_1^2 + P_2^2) + P_2^4(P_1^2 + P_3^2)}\right] - \frac{1}{2}s_{11}\left( {\sigma _1^2 + \sigma _2^2 + \sigma _3^2} \right) - s_{12}\left( {\sigma _1\sigma _2 + \sigma _1\sigma _3 + \sigma _2\sigma _3} \right) - \frac{1}{2}s_{44}\left( {\sigma _4^2 + \sigma _5^2 + \sigma _6^2} \right) - Q_{11}\left( {\sigma _1P_1^2 + \sigma _2P_2^2 + \sigma _3P_3^2} \right)- Q_{12}\left[\sigma _1(P_2^2 + P_3^2) + \sigma _2(P_1^2 + P_3^2) + \sigma _3(P_1^2 + P_2^2)\right] - Q_{44}(\sigma _4P_2P_3 + \sigma _5P_1P_3 + \sigma _6P_1P_2) - \left( {P_1E_1 + P_2E_2 + P_3E_3} \right)\end{array}$$
(11)

where \(a_1,\,a_{11},\,a_{12},\,a_{111},\,a_{112}\,{\mathrm{and}}\,a_{123}\) are the first and high-order Landau coefficients determined under the stress-free condition. Pi (i = 1–3) and \(\sigma _j\) (j = 1–6) are the ith polarization and jth stress components, respectively. \(s_{11}\), \(s_{12}\), and \(s_{44}\) are the elastic compliances of the parent cubic phase, while Q11, Q12, and Q44 are the electrostrictive coefficients.

For an epitaxial oxide film, its in-plane strains decrease slowly with film thickness, after its initial relaxation via the formation of misfit dislocations in the first ~10–50 nm thick layer41,42. Therefore, for a few hundred nm thick or thicker oxide film, its in-plane strains are residual ones post relaxation, and can be considered as fixed/thickness-independent. Moreover, the stress components \(\sigma _3\), \(\sigma _4\), and \(\sigma _5\) are zero because of the film’s free surface. The relationship between the other in-plane strains \(\varepsilon _i\) (i = 1, 2, 6) and stress components can be obtained from the thermodynamic relations: \(\frac{{\partial \tilde G}}{{\partial {\upsigma}_1}} = - \varepsilon _1,\frac{{\partial \tilde G}}{{\partial {\upsigma}_2}} = - \varepsilon _2,\frac{{\partial \tilde G}}{{\partial {\upsigma}_6}} = - \varepsilon _{6.}\)

For a (001) ferroelectric thin film epitaxially grown in its cubic paraelectric phase on a (100)-oriented cubic substrate, the in-plane strains are \(\varepsilon _1 = \varepsilon _2 = u_m = \varepsilon _M^0 + Q_{12}(P_0^b)^2\) and \(\varepsilon _6\) = 0. So, the thermodynamic potential becomes37:

$$\begin{array}{l}\tilde G = a_1^f(P_1^2 + P_2^2) + a_3^fP_3^2 + a_{11}^f\left( {P_1^4 + P_2^4} \right) + a_{33}^fP_3^4 + a_{13}^f\left( {P_1^2P_3^2 + P_2^2P_3^2} \right)\\ + a_{12}^fP_1^2P_2^2 + a_{111}\left( {P_1^6 + P_2^6 + P_3^6} \right) + a_{112}\left[ {\left( {P_2^2 + P_3^2} \right)P_1^4 + \left( {P_1^2 + P_3^2} \right)P_2^4 + \left( {P_1^2 + P_2^2} \right)P_3^4} \right] + \\ a_{123}P_1^2P_2^2P_3^2 + \frac{{u_m^2}}{{s_{11} + s_{12}}} - \left( {P_1E_1 + P_2E_2 + P_3E_3} \right)\end{array}$$
(12)

where \(a_1^f = a_1 - \frac{{(Q_{11} + Q_{12})u_m}}{{s_{11} + s_{12}}}\), \(a_3^f = a_1 - \frac{{Q_{12}u_m}}{{S_{11} + S_{12}}}\), \(a_{11}^f = a_{11} + \frac{{s_{11}\left( {Q_{11}^2 + Q_{12}^2} \right) - 2Q_{11}Q_{12}s_{12}}}{{2(s_{11}^2 - s_{12}^2)}},\) \(a_{12}^f = a_{12} - \frac{{s_{12}\left( {Q_{11}^2 + Q_{12}^2} \right) - 2Q_{11}Q_{12}s_{11}}}{{s_{11}^2 - s_{12}^2}} + \frac{{Q_{44}^2}}{{2s_{44}}}\), \(a_{13}^f = a_{12} + \frac{{(Q_{11} + Q_{12})Q_{12}}}{{s_{11} + s_{12}}}\), \(a_{33}^f = a_{11} + \frac{{Q_{12}^2}}{{s_{11} + s_{12}}}\). \(a_1^f\), \(a_3^f\), \(a_{11}^f\),\(a_{12}^f\), \(a_{13}^f\) and \(a_{33}^f\) are the modified Landau coefficients of the film. The equilibrium thermodynamic states can be determined via minimization of \(\tilde G\) \(\left(\frac{{\partial \tilde G}}{{\partial P_1}} = 0,\frac{{\partial \tilde G}}{{\partial P_2}} = 0,\frac{{\partial \tilde G}}{{\partial P_3}} = 0\right)\). For a KNN film, all the parameters used in the calculations are listed in Table 2. The KNN film is in a tetragonal phase at room temperature (\(P_1 = P_2 = 0,\,P_3 = P \,\ne\, 0\)) when \(\varepsilon _M^0\) is between −1.0 and −2.0%. This result is consistent with the theoretical works reported in the literature35,37. For undoped (K0.5Na0.5)NbO3 films grown on a commonly used perovskite-type semiconductor substrate (SrTiO3, LaAlO3, (La,Sr)(Al,Ta)O3, etc.), this strain condition is readily achievable.

On the experimental side, there are several groups reporting strain- or composition-induced phases in (Kx,Na1−x)NbO3-based epitaxial films43,44,45,46. For example, Luo et al. revealed a strain-induced monoclinic phase in Li-43 and Mn-doped44 KNN films, which shows an enhance piezoelectric response. Helden et al.45 revealed a linear correlation between the phase transition temperature from a strain-stabilized monoclinic phase to the orthorhombic c-phase in (Kx,Na1−x)NbO3 films (x = 0.54–0.77), and the applied overall lattice strain from the sum of the anisotropic in-plane compressive misfit strains with the substrate. Shiraishi et al.46 showed a systematic reduction of the orthorhombic–tetragonal and tetragonal–cubic phase transition temperatures by increasing the Ta-dopant amount in thick epitaxial (K,Na)(Nb,Ta)O3 films deposited by using the hydrothermal method. Together, these works provided the foundation for engineering the phase structures in KNN films.

It is noted that, unlike those of well-studied ferroelectrics, such as PZT or BaTiO3, the material parameters of KNN in its LD potential are not all determined from experimental measurements35. To verify this material design, we used density functional theory (DFT) calculations47,48,49 to investigate the relative stability between the bulk orthorhombic and the strain-induced tetragonal phases.

As shown in Fig. 2a, the supercells with K and Na atoms orderly distributed along the [001] direction are adopted in our simulation. Moreover, two different phases, i.e., tetragonal P4mm and orthorhombic C2mm which contain 10 and 20 atoms, respectively, are considered for their relative stabilities under a biaxial strain. The misfit strain of the KNN structure can be represented by: \(\varepsilon _M^0\left( \% \right) = \frac{{a - a_0}}{{a_0}} \times 100{\mathrm{\% }}\), where a0 is the in-plane lattice parameter of the bulk stable phase of C2mm. The free energy-misfit strain diagram for the two phases is shown in Fig. 2b. It clearly shows that a compressive strain will destabilize the bulk C2mm phase, and induce the tetragonal P4mm phase. The transition point is at \(\varepsilon _M^0\) ~ −1.5%, fairly consistent with the prediction based on the LD thermodynamic computation35,37.

Fig. 2: Relevant results of DFT theoretical calculation.
figure 2

a Schematic diagram of ideal paraelectric KNN structure. The K/Na atom in the structure are ordered along [001] direction. The atoms in yellow, purple, green, and red are K, Na, Nb, and O, respectively. The unit cell in black frame and the supercell in red frame contains 10 and 20 atoms, respectively, and will be used in our calculation for different KNN phases, i.e., P4mm (10 atoms) and C2mm (20 atoms). b Free energies of the P4mm and C2mm phases as functions of the misfit strain.

Full size image

Analysis of microstructure and chemical states of the KNN films

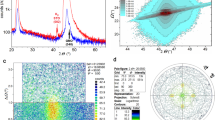
Based on the above analysis, we designed and obtained (001)-oriented tetragonal KNN films (150 and 500 nm thick) via RF magnetron sputtering on SrRuO3 (SRO)-buffered (100) SrTiO3 (STO) substrates, which showed a high tunability factor λf ~3 × 10−7, and a large dielectric tunability ~80%.

Figure 3 shows the microstructural characteristics of the KNN target and films. In Fig. 3a, except for the XRD peaks corresponding to a bulk orthorhombic phase of KNN50/5050, no other secondary phases were detected in the KNN ceramic target. The lattice parameters of the target are cpc = apc = 3.997 Å, bpc = 3.938 Å, respectively. In Fig. 3b, both KNN films show a (00l)-orientation with an out-of-plane lattice parameter of ~4.05 Å. Furthermore, in the (110) pole figure (Fig. 3c), the diffracted X-ray signals display a fourfold symmetry at a tilt angle of ~45°, indicating a heteroepitaxial growth of the KNN film with a (00l) out-of-plane orientation51. It will be revealed later, that these films have a tetragonal symmetry with a (00l)-orientation promoted by the SRO buffer layer, which lowered the surface energy of the (00l) crystalline plane. The 4.05 Å out-of-plane lattice parameter corresponds to an in-plane compressive strain of ~−1.8% (\(\varepsilon _{xx} = \varepsilon _{yy} = - \frac{{1 - \nu }}{{2\nu }}\varepsilon _{zz}\), \(\varepsilon _{zz}\) is the out-of-plane strain, \(\varepsilon _{zz} = \frac{{c_{\mathrm{film}} - c_{\mathrm{bulk}}}}{{c_{\mathrm{bulk}}}}\), \(c_{\mathrm{film}}\) and \(c_{\mathrm{bulk}}\) are the out-of-plane lattice parameters of the KNN film and bulk ceramic, \({\upnu}\) is the Poisson’s ratio, which is ~0.27 for KNN52). This compressive strain is responsible for the elongation of the out-of-plane lattice parameter and shortening of the in-plane a and b lattice parameters. Lastly, a representative AFM surface scan image of the 150 nm KNN film is shown in Fig. 3d. The film is dense and uniform, displaying a smooth surface with a root-mean-square (RMS) roughness of ~3.2 nm.

Fig. 3: Microstructure and morphology of KNN target and films.
figure 3

X-ray diffraction 2θ scan patterns of (a) the KNN ceramic target and (b) 150 nm- and 500 nm-thick KNN films; c the (110) XRD pole figure of the 500 nm KNN film; d an AFM surface scan image of the 150 nm KNN film.

Full size image

Figure 4a and e are representative cross-sectional bright-field TEM images of the 150 nm and 500 nm KNN film, respectively, which reveal clean and sharp interfaces in the KNN/SRO/STO heterostructure. The thicknesses of the SRO layer in both films were ~60 nm. In the high-resolution TEM images shown in Fig. 4b, c, f, and g, atomically coherent interfaces (marked by dashed white lines) between the (100) STO substrate and the SRO layer, SRO and KNN layers were revealed, validating a (00l) heteroepitaxial growth in the two films. Figure 4d is a selected area electron diffraction (SAED) pattern of the boxed region in Fig. 4c via a fast-Fourier transformation (FFT), while Fig. 4h is a SAED pattern directly taken from the circled region in Fig. 4e. The zone axis is [010] for both SAED patterns. The measured out-of-plane and in-plane lattice parameters of the KNN films were ~4.05 Å and ~3.93 Å, respectively. The sharp electron diffraction spots in Fig. 4d and h indicate that the films are of epitaxial quality, consistent with the XRD results displayed in Fig. 3.

Fig. 4: Cross-sectional microstructure of KNN films.
figure 4

Cross-sectional bright-field TEM images of the KNN/SRO/STO heterostructure with the KNN thickness of (a) 150 nm and (e) 500 nm; b–c and f–g are the high-resolution TEM images near the SRO/STO and KNN/SRO interfaces for the 150 nm and 500 nm thick KNN films, respectively; d and h are the selected area electron diffraction patterns of the boxed and circled regions in (c) and (e), respectively.

Full size image

Surface XPS spectra of the 150 nm KNN film were collected to analyze the valence states of the elements. The core-level elemental binding energies were all calibrated by using the carbon 1s peak (284.8 eV), and the XPS spectra were fitted by using the Avantage software. Figure 5a is the survey spectrum which showed clear signals from K, Na, Nb, and O, as well as a trace amount of the environment C. No fingerprints of any other element were found in the survey spectrum, which proved the chemical purity of the KNN film. Figure 5b is the core level K 2p XPS spectrum. The K 2p XPS peak from the K element in the KNN lattice splits into doublets (K 2p3/2 and K 2p1/2)53,54,55,56,57. There is a very weak second group of doublets, marked as K 2p‘3/2 and K 2p‘1/2, which can be attributed to a small amount of K existing in the form of K2O53,54,55,56,57. The existence of potassium oxide on the film surface is usually unavoidable53,54,55,56,57, which can be attributed to the effects of composition variation and different evaporation rates of the component species in the KNN target and film. Furthermore, the 1s core-level XPS spectrum of Na and the 3d core-level XPS spectrum of Nb are shown in Fig. 5c and d, respectively. The Na 1s peak is symmetrical and shows no split or shift of peak position. It is well fitted to the standard peak for the sodium element in the KNN lattice. On the other hand, the Nb peak splits into doubles (3d3/2 and 3d5/2) with a binding energy difference of ~2.7 eV, confirming the existence of Nb–O bonds and a Nb5+ valence state in the film58. Figure 5e is the O 1s core-level XPS spectrum, which is asymmetric and can be decomposed into three characteristic peaks, indicating the existence of three oxygen species on the film surface. The peak located at the low energy side (529.6 eV) is associated with the lattice oxygen (OL). The middle peak, located at 531.1 eV, corresponds to adsorbed oxygen on the surface (OS), which may have a variety of states, such as O−, O22−, etc. Lastly, the peak located at 532.2 eV is associated with oxygen vacancies (Ov)59. The formation of oxygen vacancies on the surface of a KNN film is commonly observed60,61, which can be attributed to the evaporation loss of volatile alkali ions55.

Fig. 5: Chemical properties of the KNN films.
figure 5

a survey spectrum and (b–e) narrow-scan spectra of (b) K 2p, c Na 1s, d Nb 3d, and (e) O 1s core levels from the 150 nm KNN film.

Full size image

Electrical performance

Figure 6a shows the measured P–E hysteresis loops of the two KNN films (@1 kHz). Both films display a remnant polarization of ~21 μC cm−2. In Fig. 6b, the measured dielectric permittivity χ-electric field E (χ-E) curve of the 500 nm film is well fitted by the theoretical results given by Eqs. (8) and (9), while that of the 150 nm film was offset from the computed χ-E curve by a small field/voltage (~0.225 V, inset of Fig. 6b). This small offset can be attributed to a non-negligible voltage drop across an interface capacitive layer. The effect of such an interface layer is schematically shown in Fig. 6c. A simple model of serially connected capacitors is used to illustrate the effect of film thickness on the voltage drop across a thin interface layer62. When the KNN film is thick enough, its capacitance becomes very low compared with that of the interface layer, and hence nearly 100% of the applied voltage drops across the KNN film. The interfacial voltage drop only becomes non-negligible when the film is much thinner (500 nm → 150 nm). After correction of this small offset, it is noted that there is only a small difference between the computed tunability factors \(\lambda _f\) (via Eq. (9)) of the two films, 3.05 × 10−7 m V−1 for the 500 nm film and 2.85 × 10−7 m V−1 for the 150 nm one, which can be attributed to their slightly different remnant dielectric permittivities (\(\chi _0^f\) ~ 860 and ~830 for the 500 nm and 150 nm KNN films, respectively). In addition, the dielectric loss tangent-electric field (tgδ-E) curve is also shown for the 500 nm film. The losses are in a reasonable range (~0.03 to ~0.1) except at the high negative bias end. This is possibly due to the asymmetric electrode interfaces62. Lastly, Fig. 6d displays the experimental and computed dielectric tunability-electric field (η-E) curves for the two KNN films. The experimental curves were derived from the χ-E data in Fig. 6b, while the theoretical curves were computed by using Eqs. (9) and (10), with a 0.225 V voltage offset correction performed for the 150 nm film. The experimental and theoretical dielectric tunabilities agreed fairly well with each other, especially in the high electric field end, where both curves saturate with an increasing field. The small gap between the experimental tunability and the theoretical one, which exists in the low-to-middle field range, can be attributed to charged defects in the films, which demand an extra amount of energy to be aligned with the applied electric field. Effects of these extrinsic charges diminish under a high electric field, hence the measured tunabilities (and dielectric permittivities as shown in Fig. 6b) behaved just like the theory predicted in the high field end. Number-wise, the designed high tunability values have been achieved in the KNN films. For the 150 nm-thick KNN film, the theoretical tunability η under an electric field of 6.5 × 107 (V m−1) (10 V) is 77.4%, while the measured η is 77.7%. For the 500 nm-thick KNN film, the computed and measured η values at 7.8 × 107 (V m−1) (39 V) were 80% and 81%, respectively. These numbers are the highest reported η values so far for KNN thin film dielectrics17,18,19,25,63.

Fig. 6: Electrical performance of the KNN films.
figure 6

a Polarization-electric field (P–E) hysteresis loops (measured @1 kHz); b measured and computed dielectric permittivity χ -electric field E (χ-E) curves of the 500nm-thick KNN film (\({\uplambda}_f\) = 3.05 × 10−7 m V−1 from Eq. 9), the inset shows the measured and computed χ-E curves (E > 0) of the 150 nm-thick film under 10V (\({\uplambda}_f\) = 2.85 × 10−7 m V−1 from Eq. 9). The dielectric loss tangent-electric field (tgδ-E) curves are also shown for the 500 nm film. c Schematic illustration of the effect of a capacitive interface layer on reducing the effective voltage across the KNN film. The thinner the KNN film, the larger the voltage drop on this interface layer. d Measured (@1 kHz) and computed dielectric tunabilities as functions of the bias field for the 500 and 150 nm (inset) KNN films.

Full size image

In this work, (001)-oriented, strain-stabilized tetragonal KNN thin films with a high dielectric tunability were successfully designed via computational approaches using the LD type thermodynamic potential and DFT calculations. These KNN films were epitaxially grown on SrRuO3-buffered (100) SrTiO3 substrates via RF magnetron sputtering. A high remnant polarization \(P_0^f\)(~21 μC cm−2) and a large small-field dielectric permittivity \(\chi _0^f\)(~830–860) were achieved in these films. The measured maximum dielectric tunabilities η (~75–80%) are in good agreement with the computed theoretical values. Moreover, their field dependences, i.e., the η-E curves, can be well described by our equation derived using the LD theory. These results suggest that, the dielectric tunability of a ferroelectric film, as its key performance parameter in tunable dielectrics, can be predicted using a computational approach.

Methods

DFT calculations

The DFT calculations were performed with the projector augmented wave (PAW) approach47, as implemented in the Vienna ab initio simulation package (VASP)48. The electron exchange-correlation functional was treated by generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE)49. The plane-wave cutoff and convergence criteria for energy and force are set to be 550 eV, 10−7 eV, and 0.01 eVÅ−1, respectively.

Sintering of the KNN ceramic target

The KNN 50/50 ceramic target was prepared by using a conventional solid-state reaction process. Na2CO3 (99.8%), K2CO3 (99%) and Nb2O5 (99.5%) were used as the raw materials with a molar ratio of 0.585:0.535:1.0. Amounts of excessive Na (17%) and K (7%) were determined based on sintering experiments leading to a stoichiometric KNN 50/50 ceramic target. The mixed raw materials were ball-milled for 24 h using alcohol as the dispersion medium, dried, and calcined at 850 °C for 6 h in air. Then the calcined powders were mixed with a binder of 5 wt% polyvinyl butyral (PVB) and pressed into pellets with a 60 mm-diameter and an 8 mm-thickness under a uniaxial pressing @ 10 MPa in a stainless-steel die. These pellets were then sintered at 1040 °C in air for 2 h after burning of the PVB binder at 650 °C for 5 h64. To avoid the formation of NaOH and KOH, the sintered target was kept in a vacuum cabinet.

Deposition of the KNN film

Single-crystalline substrates of (100) SrTiO3 (STO) as well as the SrRuO3 (SRO) ceramic target were provided by Anhui Institute of Optics and Fine Mechanics (Chinese Academy of Sciences, China). A base pressure of 2.0 × 10−4 Pa was achieved in a multi-target sputtering chamber prior to the sequential deposition of a bottom electrode (SRO) layer and a KNN film from the corresponding ceramic targets. KNN films of ~150 and ~500 nm thicknesses with a SRO layer of a fixed thickness ~60 nm were sputter-deposited in a mixed Ar/O2 atmosphere (1.2 Pa, Ar/O2 flow ratio = 3:1). During the sputtering process, the substrate temperature was held at 600 °C. Right after their depositions, the KNN thin film heterostructures were kept at 600 °C in 2.5 Pa pure oxygen for 20 min, to help reduce the oxygen vacancies. Metal-ferroelectric-metal (MFM) testing structures were formed after deposition of top electrodes (circular Au pads with ϕ = 200 μm), which were sputtered at room temperature via a shadow mask.

Characterization

The phase structures and crystallographic orientations of the KNN films were analyzed using standard X-ray 2θ-scans (in a commercial Rigaku Dmax-2500PC, Japan) and pole figure (R-156 Axis Spider, Smart Lab Rigaku, Japan; 40 kV, 200 mA). In the X-ray pole figure measurement, the (110) KNN peak was used. The 500 nm-thick film sample was rotated by varying the tilt angle ψ from 0° to 90°, and the azimuthal angle φ from 0° to 360° for every single ψ value. Nanostructures of the films were analyzed using transmission electron microscopy (TEM, JEOL JEM-2100HR) with cross-sectional samples prepared by using a focus ion beam (FIB) milling instrument (Scios2, FEI, USA). The surface morphology of the films was investigated by using an atomic force microscope (AFM, Micro Nano D-5A, with CSC21-AIBS AFM tips from Mikro Masch). The chemical bonding states of K, Na, Nb, and O were analyzed using X-ray photoelectron spectroscopy (XPS, Thermo Scientific ESCALAB 250Xi). The ferroelectric polarization-electric field (P–E) hysteresis loops were measured by using a Radiant Precision LC ferroelectric tester (Radiant Technology, USA). The capacitance (C)–voltage (V) (C–V) tests, which were used to extract the dielectric permittivity χ-electric field E (χ-E) curves, were carried out in a TH2828S LCR bridge (Tong hui Electronics, China), by superimposing a small AC signal (Vp-p = 1 V @ 1 kHz) on a DC bias voltage sweeping from its negative maximum to its positive maximum, and vice versa.