Abstract
The generation of multiphase porous electrode microstructures is a critical step in the optimisation of electrochemical energy storage devices. This work implements a deep convolutional generative adversarial network (DC-GAN) for generating realistic n-phase microstructural data. The same network architecture is successfully applied to two very different three-phase microstructures: A lithium-ion battery cathode and a solid oxide fuel cell anode. A comparison between the real and synthetic data is performed in terms of the morphological properties (volume fraction, specific surface area, triple-phase boundary) and transport properties (relative diffusivity), as well as the two-point correlation function. The results show excellent agreement between datasets and they are also visually indistinguishable. By modifying the input to the generator, we show that it is possible to generate microstructure with periodic boundaries in all three directions. This has the potential to significantly reduce the simulated volume required to be considered “representative” and therefore massively reduce the computational cost of the electrochemical simulations necessary to predict the performance of a particular microstructure during optimisation.
Similar content being viewed by others
Introduction
The geometrical properties of multiphase materials are of central importance to a wide variety of engineering disciplines. For example, the distribution of precious metal catalysts on porous supports; the structure of metallic phases and defects in high-performance alloys; the arrangement of sand, organic matter, and water in soil science; and the distribution of calcium, collagen and blood vessels in bone1,2,3. In electrochemistry, whether we are considering batteries, fuel cells or supercapacitors, their electrodes are typically porous to maximise surface area but need to contain percolating paths for the transport of both electrons and ions, as well as maintaining sufficient mechanical integrity4,5. Thus the microstructure of these electrodes significantly impacts their performance and their morphological optimisation is vital for developing the next generation of energy storage technologies6.
Recent improvements in 3D imaging techniques such as X-ray computed tomography (XCT) have allowed researchers to view the microstructure of porous materials at sufficient resolution to extract relevant metrics7,8,9,10. However, a variety of challenges remain, including how to extract the key metrics or “essence“ of an observed microstructural dataset such that synthetic volumes with equivalent properties can be generated, and how to modify specific attributes of this microstructural data without compromising its overall resemblance to the real material.
A wide variety of methods that consist of generating synthetic microstructure by numerical means have been developed to solve these challenges6. A statistical method for generating synthetic three-dimensional porous media based on distance correlation functions was introduced by Quiblier et al.11. Following this work, Torquato et al. implemented a stochastic approach based on the n-point correlation functions for generating reconstructions of heterogeneous materials.12,13,14,15,16 Jiao et al.17,18 extended this method to present an isotropy-preserving algorithm to generate realisations of materials from their two-point correlation functions (TPCF). Based on these previous works, the most widely used approach for reconstruction of microstructure implements statistical methods through the calculation of the TPCF2,19,20,21,22,23,24.
In the area of energy materials, interest has recently surged for generating synthetic microstructure in order to aid the design of optimised electrodes. The three-phase nature of most electrochemical materials adds an extra level of complexity to their generation compared to two-phase materials. Suzue et al.20 implemented a TPCF from a two-dimensional phase map to reconstruct a three-dimensional microstructure of a porous composite anode. Baniassadi et al.25 extended this method by adding a combined Monte Carlo simulation with a kinetic growth model to generate three-phase realisations of a SOFC electrode. Alternative algorithms for reconstruction of porous electrodes have been inspired by their experimental fabrication techniques. A stochastic algorithm based on the process of nucleation and grain growth was developed by Siddique et al.26 for reconstructing a three-dimensional fuel cell catalyst layer. This process was later implemented by Siddique et al.27 to reconstruct a three-dimensional three-phase LiFePO4 cathode. A common approach for generating synthetic microstructure of SOFC electrodes involves the random packing of initial spheres or “seeds” followed by the expansion of such spheres to simulate the sintering process28,29,30,31. Moussaoui et al.6 implement a combined model based on sphere packing and truncated Gaussian random field to generate synthetic SOFC electrodes. Additional authors have implemented plurigaussian random fields to model the three-phase microstructure of SOFC electrodes and establish correlations between the microstructure and model parameters4,32,33.
In the area of Li-ion batteries some authors have implemented computational models to adhere a synthetic carbon-binder domain (CBD) (usually hard to image) into XCT three-dimensional images of the NMC/pore phases34,35. An analysis of transport properties such as tortuosity and effective electrical conductivity prove the effect of different CBD configurations in the electrode performance. Other authors have implemented physics-based simulations to predict the morphology of three-phase electrodes. Forouzan et al.36 developed a particle-based simulation that involves the superposition of CBD particles, to correlate the fabrication process of Li-ion electrodes with their respective microstructure. Srivastava et al.37 simulated the fabrication process Li-ion electrodes by controlling the adhesion of active material and CBD phases. Their physics-based dynamic simulations are able to predict with accuracy the effect of microstructure in transport properties.
Recent work by Mosser et al.38,39 introduces a deep learning approach for the stochastic generation of three-dimensional two-phase porous media. The authors implement a type of generative model called Generative Adversarial Networks (GANs)40 to reconstruct the three-dimensional microstructure of synthetic and natural granular microstructures. Li et al.41 extended this work to enable the generation of optimised sandstones, again using GANs. Compared to other common microstructure generation techniques, GANs are able to provide fast sampling of high-dimensional and intractable density functions without the need for an a priori model of the probability distribution function to be specified39. This work expands on the research of Mosser et al.38,39 and implements GANs for generating three-dimensional, three-phase microstructure for two types of electrode commonly used in electrochemical devices: a Li-ion battery cathode and an SOFC anode. A comparison between the statistical, morphological and transport properties of the generated images and the real tomographic data is performed. The two-point correlation function is further calculated for each of the three phases in the training and generated sets to investigate the long-range properties. Due to the fully convolutional nature of the GANs used, it is possible to generate arbitrarily large volumes of the electrodes based on the trained model. Lastly, by modifying the input of the generator, structures with periodic boundaries were generated.
Performing multiphysics simulations on representative 3D volumes is necessary for microstructural optimisation, but it is typically very computationally expensive. This is compounded by the fact that the regions near the boundaries can show unrealistic behaviour due to the arbitrary choice of boundary condition. However, synthetic periodic microstructures (with all the correct morphological properties) enable the use of periodic boundary conditions in the simulation, which will significantly reduce the simulated volume necessary to be considered representative. This has the potential to greatly accelerate these simulations and therefore the optimisation process as a whole.
The main contributions of this work are listed below:
-
The implementation of a GAN-based approach for the generation of multi-phase 3D microstructural data.
-
Application of this method to two types of commonly used three-phase electrodes, resulting trained generators that could be considered as “virtual representations” of these microstructures.
-
A statistical comparison of the microstructural properties between the real and generated microstructures, establishing the effectiveness of the approach.
-
The development of a method, based on the GAN approach, for generating periodic microstructures, and the implementation of a diffusion simulation on these volumes to illustrate the impact of periodic boundaries.
-
The extension of this approach for the generation of arbitrarily large, multiphase, periodic microstructures.
Generative Adversarial Networks are a type of generative model developed by Goodfellow et al.40 which learn to implicitly represent the probability distribution function (pdf) of a given dataset (i.e., pdata).42 Since pdata is unknown, the result of the learning process is an estimate of the pdf called pmodel from which a set of samples can be generated. Although GANs by design do not admit an explicit probability density, they learn a function that can sample from pmodel, which reasonably approximate those from the real dataset (pdata).
The training process consists of a minimax game between two functions, the generator G(z) and the discriminator D(x). G(z) maps an d-dimensional latent vector \({\bf{z}} \sim {p}_{{\rm{z}}}({\bf{z}})\in {{\mathbb{R}}}^{d}\) to a point in the space of real data as G(z; θ(G)), while D(x) represents the probability that x comes from pdata.40 The aim of the training is to make the implicit density learned by G(z) (i.e., pmodel) to be close to the distribution of real data (i.e., pdata). A more detailed introduction to GANs can be found in Section A of the supplementary material.
In this work, both the generator \({G}_{{\theta }^{(G)}}({\bf{z}})\) and the discriminator \({D}_{{\theta }^{(D)}}({\bf{x}})\) consist of deep convolutional neural networks.43 Each of these has a cost function to be optimised through stochastic gradient descent in a two-step training process. First, the discriminator is trained to maximise its loss function J(D):
This is trained as a standard binary cross-entropy cost in a classifier between the discriminator’s prediction and the real label. Subsequently, the generator is trained to minimise its loss function corresponding to minimising the log-probability of the discriminator being correct:
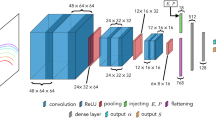
These concepts are summarised in Fig. 1. Early in training, the discriminator significantly outperforms the generator, leading to a vanishing gradient in the generator. For this reason, in practice instead of minimising \({\log}\,\left(1-D\left(G({\bf{z}})\right)\right)\), it is convenient to maximise the log-probability of the discriminator being mistaken, defined as \({\log}\,\left(D(G({\bf{z}}))\right)\)42.
Schematic showing the architecture of the DC-GAN for 2D microstructural data. Generalisation to 3D samples is conceptually straightforward, but difficult to show as it requires the illustration of 4D tensors. In each layer, the green sub-volume shows a convolutional kernel at an arbitrary location in the volume and the blue sub-volume is the result of that convolution. In each case, the kernel is the same depth as the one non-spatial dimension, c, but must scan through the two spatial dimensions in order to build up the image in the following layer.
The solution to this optimisation problem is a Nash equilibrium42 where each of the players achieves a local minimum. Throughout the learning process, the generator learns to represent the probability distribution function pmodel which is as close as possible to the distribution of the real data pdata(x). At the Nash equilibrium, the samples of x = G(z) ~ pmodel(z) are indistinguishable from the real samples x ~ pdata(x), thus pmodel(z) = pdata(x) and \(D({\bf{x}})=\frac{1}{2}\) for all x since the discriminator can no longer distinguish between real and synthetic data.
Regarding the microstructural image data, open-source nano-tomography data was used for both of the electrode materials considered in this study, which had already been segmented into each of their three respective phases (see Fig. 2). The first dataset is from a Li-ion battery cathode, comprising particles of a ceramic active material (nickel manganese cobalt oxide - NMC 532), a conductive organic binder (polymer with carbon black) and pores. This material is made by mixing the components in a solvent, thinly spreading this ink onto an aluminium foil and then drying. The second dataset is from an SOFC anode, comprising of a porous nickel/yttria stabilised zirconia (Ni-YSZ) cermet. This material is also made by mixing an ink, but this time it is deposited onto a ceramic substrate and then sintered at high temperature to bind the components together. Details of the sample preparation, imaging, reconstruction and segmentation approaches used can found in34 for the cathode and44 for the anode. The specifications of both datasets are shown in Table 1.
Two-dimensional (2D) images of the microstructures used as training sets in this work (L) Li-ion cathode, where the black phase represents pore, grey is NMC active material, and white is the organic binder; (R) SOFC anode, where the black phase corresponds to the pore, grey is Nickel and white is YSZ.
More than ten-thousand overlapping sub-volumes were extracted from each image dataset (Table 1), using a sampling function with a stride of 8 voxels. The spatial dimensions of the cropped volumes were selected based on the average size of the largest structuring element. The sub-volume size was selected to guarantee that at least two structuring elements (i.e., particular geometric shape that we attempt to extract from the XCT image) could fit in one sub-volume45. In the case of the Li-ion cathode, this structuring element corresponds to the particle size. In the case of the SOFC anode, “particle size” is not easy to define once the sample is sintered, so the sub-volume was selected based on the stabilisation of the two-point correlation function (TPCF). A more detailed discussion of the representativeness of the sub-samples chosen for training is given in Section G of the supplementary information.
Results
The two GANs implemented in this work, one for each microstructure, were trained for a maximum of 72 epochs (i.e., 72 complete iterations of the training set). The stopping criteria was established through the manual inspection of the morphological properties every two epochs. Supplementary Figs S9 and S10 of the supplementary data shows the visual reconstruction of both microstructures, beginning with Gaussian noise at epoch 0, and ending with a visually equivalent microstructure at epoch 50. The image generation improves with the number of iterations; however, as pointed out by Mosser et al.38, this improvement cannot be observed directly from the loss function of the generator and so the morphological parameters described above are used instead.
Before introducing the quantitative comparison of the real and synthetic microstructural data, the excellent qualitative agreement between them can be seen in Fig. 3, which shows six instances of both real and synthetic data from both the anode and cathode samples. Each slice consists of 642 voxels and is obtained from a 643 generated volumetric image. This qualitative analysis consisted of visually comparing some key features of the data. In the case of the Li-ion cathode, the structuring element in the microstructure (i.e., the NMC particles – grey phase) shows round borders surrounded by a thin layer of binder (white phase), and the phases seem distributed in the same proportion in the real and generated images. In the case of the SOFC, no structuring element is clearly defined; however, the shapes of the white and grey phases of the generated set show the typical shape of the real data which is particular for the sintering process in the experimental generation of these materials44.
In order to draw a comparison between the training and generated microstructures, 100 instance of each were randomly selected (64 × 64 × 64 voxels). The comparison results are presented in the following sections. Supplementary Figs S9 and S10 show 2D slices through generated volumes containing the max value in the phase dimension (rather than the label), which indicates the confidence with which it was labelled.
Lithium-ion cathode results
The results of the calculation of the microstructural characterisation parameters (i.e., phase volume fraction, specific surface area and TPB) for the three phases are presented in Fig. 4. For ease of comparison in a single figure, the results of the specific surface area analysis are presented in terms of the percentage deviation from the maximum mean area value among the three phases, Δ(SSA). In the case of the cathode, the maximum mean area, \({A}_{\max ,{\rm{mean}}}\), corresponds to the mean area of the white phase (binder) of the training set (\({A}_{\max ,{\rm{mean}}}=0.72 {\rm{\mu}} {{\rm{m}}}^{-1}\)) and all other areas, Ai, are normalised against this.
Microstructural characterisation properties for 100 training samples (blue) and 100 generated realisations (red) for the Li-ion cathode. In all cases, greater diversity is observed in the training set than the generated samples. Boxes show 25th–75th percentiles and the median. Black crosses show outliers.
The phase volume fraction, specific surface area and relative diffusivity show good agreement between the real and the synthetic data, particularly in the mean values of both distributions. These mean values and standard deviations are reported in Table 2. The distribution of relative diffusivity in the white phase is very close to zero due to the low volume fraction and resulting low percolation of this phase. For the TPB density, the mean of the generated set is nearly 10% greater than that of the training data; however, nearly all of the values for the synthetic data do still fall within the same range as the training set.
From Fig. 4 it is clear that the synthetic realisations show a smaller variance in all of the calculated microstructural properties compared to the real datasets. This is also shown in Supplementary Fig. S2, where the relative diffusivity is plotted against the volume fraction of the three phases.
The averaged S2(r)/S2(0) along three directions is shown in Fig. 5 for each of the three phases present in a Li-ion cathode. Since S2(0) represents the volume fraction ϕi of each phase, S2(r)/S2(0) is a normalisation of the TPCF that ranges between 0 and 1. In this expression, S2(r)/S2(0) stabilised at the value of ϕi. In all cases, the average values of S2(r)/S2(0) of the synthetic realisations follow the same trend as the training data. The black phase shows a near exponential decay, the grey phase presents a small hole effect and the white phase shows an exponential decay. A hole effect is present in a two-point correlation function when the decay is non-monotonic and presents peaks and valleys. This property indicates a form of pseudo-periodicity and in most cases is linked to anisotropy46,47. For the black and grey phases, the S2(r)/S2(0) values of the generated images show a slight deviation from the training set, however this value falls within the standard deviation of the real data.
SOFC anode results
Figure 6 presents the results of the SOFC anode microstructural characterisation parameters calculated for the training data and for the synthetic realisations generated with the GAN model. The Δ(SSA) was calculated using the same approach as described in the previous section, but in the case of the anode, the maximum mean area was the mean area of the white phase (YSZ) of the training set (\({A}_{\max ,{\rm{mean}}}=3.98\,\upmu {{\rm{m}}}^{-1}\))
The results in Fig. 6 show a comparable mean and distributions for the morphological properties calculated, as well as for the effective diffusivity of the training images and the synthetic realisations. Once again, the synthetic images show lower variance in the calculated properties than the training set. These mean values and standard deviations are reported in Table 3.
Once again, the difference in the diversity of synthetic images with respect to the training set can be clearly seen in Supplementary Fig. S3 where the effective diffusivity averaged over the three directions for each phase is plotted against its respective volume fraction.
The TPCF was calculated for the three phases along the three Cartesian directions. Figure 7 shows the value of S2(r)/S2(0) for the three phases present in the SOFC anode. The averaged results show an exponential decay in the black phase, a small hole effect47 in the grey phase and a pronounced hole effect in the white phase.
Periodic boundaries
Once the generator parameters have been trained, the generator can be used to create periodic microstructures of arbitrary size. This is simply achieved by applying circular spatial padding to the first transposed convolutional layer of the generator (although other approaches are possible). Figure 8 shows generated periodic microstructures for both the cathode and anode, arranged in an array to make their periodic nature easier to see. Additionally, local scalar flux maps resulting from steady-state diffusion simulations in TauFactor48 are shown for each microstructure. In both cases, the upper flux map shows the results of the simulation with mirror (i.e., zero flux) boundaries on the vertical edges, and the lower one shows the results of the simulation with periodic boundaries on the vertical edges. Comparing the results from the two boundary conditions, it is clear that using periodic boundaries opens up more paths that enable a larger flux due to the continuity of transport at the edges. Furthermore, this means that the flow effectively does not experience any edges in the horizontal direction, which means that, unlike the mirror boundary case, there are no unrealistic regions of the volume due to edge effects.
For both the Li-ion cathode (L) and the SOFC anode (R), periodic microstructures were generated by slightly changing the input to the generator. For each electrode, four instances are shown making the periodicity easier to observe. Also shown are local scalar flux maps generated from steady-state diffusion simulations in TauFactor with either mirror (top) or periodic (bottom) boundary conditions implemented on the vertical edges.
Discussion
This work presents a technique for generating synthetic three-phase, three-dimensional microstructure images through the use of deep convolutional generative adversarial networks. The main contributions of this methodology are mentioned as follows: The results from comparing the morphological metrics, relative diffusivities and two-point correlation functions all show excellent agreement between the real and generated microstructure. One of the properties that is different from the averaged value in both cases is the TPB density. Nevertheless, its value falls within the confidence interval of the real dataset. This comparison demonstrates that the stochastic reconstruction developed in this work is as accurate as the state-of-the-art reconstruction methods reported in the introduction of this article. One variation from previous methodologies is that GANs do not require additional physical information from the microstructure as input data. The methodology was developed to approximate the probability distribution function of a real dataset, so it learns to approximate the voxel-wise distribution of phases, instead of directly inputting physical parameters, which is significant; although inputting physical parameters in additional may be beneficial49.
Despite the accurate results obtained in terms of microstructural properties, a number of questions still need to be addressed. One of which involves the diversity in terms of properties of the generated data. Particularly in the case of the Li-ion cathode microstructure, the generated samples present less variation than the training set. This issue was already encountered by Mosser et al.39 and low variation in the generated samples is a much discussed issue in the GAN literature. The typical explanation for this is based on the original formulation of the GAN objective function, which is set to represent unimodal distributions, even when the training set is multimodal39,40,42. This behaviour is known as “mode collapse” and is observed as a low variability in the generated images. A visual inspection of the generated images as well as the accuracy in the calculated microstructural properties do not provide a sufficient metric to guarantee the inexistence of mode collapse or memorisation of the training set.
Figures 4 and 6 show some degree of mode collapse given by the small variance in the calculated properties of the generated data. Nevertheless, further analysis of the diversity of the generated samples is required to evaluate the existence of mode collapse based on the number of unique samples that can be generated50,51. Following the work of Radford et al.52, an interpolation between two points in the latent space is performed to test the absence of memorisation in the generator. The results shown in Supplementary Fig. S8 present a smooth transformation of the generated data as the latent vectors is progressed along a straight path. This indicates that the generator is not memorising the training data but has learned the meaningful features of the microstructure.
The presence of mode collapse and vanishing gradient remain the two main issues with the implementation of GANs. As pointed out by53, these problems are not necessarily related to the architecture of GANs, but potentially to the original configuration of the loss function. This work implements a DC-GAN architecture with the standard loss function; however, recent improvements of GANs have focused on reconfiguring the loss function to enable a more stable training and more variability in the output. Some of these include WGAN (and WGAN-GP) based on the Wasserstein or Earthmover distance54,55, LSGAN which uses least squares and the Pearson divergence56, SN-GAN that implement a spectral normalisation57, among others53. Therefore, an improvement of the GAN loss function is suggested as future work in order to solve the problems related to low variability (i.e., slight mode collapse) and training stability.
The applicability of GANs can be extended to transfer the learned weights of the generator (i.e., Gθ(z)) into (a) generating larger samples of the same microstructure, (b) generating microstructure with periodic boundaries, (c) performing an optimisation of the microstructure according to a certain macroscopic property based on the latent space z. As such, Gθ can be thought of as a powerful “virtual representation” of the real microstructure and it interested to note that the total size of the trained parameters, θ(G) is just 55 MB.
The minimum generated samples are the same size as the training data sub-volumes (i.e., 643 for both cases analysed in this work), but can be increased to any arbitrarily large size by increasing the size of the input z. Although the training process of the DC-GAN is computationally expensive, once a trained generator is obtained, it can produce image data inexpensively. The relation between computation time and generated image size is shown in Supplementary Fig. S7.
The ability of the DC-GAN to generate periodic structures has potentially profound consequences for the simulation of electrochemical processes at the microstructural scale. Highly coupled, multiphysics simulations are inherently computational expensive58,59, which is exacerbated by the need to perform them on volumes large enough to be considered representative. To make matters worse, the inherent non-periodic nature of real tomographic data, combined with the typical use of “mirror” boundary conditions means that regions near the edges of the simulated control volume will behave differently from those in the bulk. This leads to a further increase in the size of the simulated volume required, as the impact of the “near edge” regions need to be eclipsed by the bulk response. Already common practice in the study of turbulent flow60,61, the use of periodic boundaries enables much smaller volumes to be used, which can radically accelerate simulations. The flux maps shown in Fig. 8 highlight the potential impact even for a simple diffusion simulation and the calculated transport parameters of these small volumes are much closer to the bulk response when periodic boundaries are implemented.
Examples of generated periodic (and similar non-periodic) volumes for both the Li-ion cathode and SOFC anode can be found in the supplementary materials accompanying this paper and the authors encourage the community to investigate their utility. A detailed exploration of the various methods for reconfiguring the generator’s architecture for the generation of periodic boundaries, as well as an analysis of the morphological and transport properties of the generated microstructures compared to the real ones are ongoing and will be presented in future work.
An additional benefit of the use of GANs in microstructural generation lies in the ability to interpolate in the continuous latent space to generate more samples of the same microstructure. The differentiable nature of GANs enables the latent space that parametrises the generator to be optimised. Li et al.41 have implemented a Gaussian process to optimise the latent space in order to generate an optimum 2D two-phase microstructure. Other authors62 have used an in-painting technique to imprint over the three-dimensional image some microstructural details that are only available in two-dimensional conditioning data. This process is performed by optimising the latent vector with respect to the mismatch between the observed data and the output of the generator39,62. A potential implementation of the in-painting technique could involve adding information from electron backscatter diffraction (EBSD), such as crystallographic structure and orientation, into the already generated 3D structures, which would be of great interest to the electrochemical modelling community.
Future work will aim to extend the study by Li et al.41 to perform an optimisation of the 3D three-phase microstructure based on desired morphological properties by optimising the latent space. One proposed pathway to improve these optimisation process would involve providing physical parameters to the GAN architecture. This could be achieved by adding a physics-specific loss component to penalise any deviation from a desired physical property49. It could also involve giving a physical meaning to the z space through the implementation of a Conditional GAN algorithm63. With this, apart from the latent vector, the Generator has a second input y related to a physical property. Thus, the Generator becomes G(z, y) and produces a realistic image with its corresponding physical property
Concluding remarks
This work presents a method for generating synthetic three-dimensional microstructures composed of any number of distinct material phases, through the implementation of DC-GANs. This method allows the model to represent the statistical and morphological properties of the real microstructure, which are captured in the weights of the trained discriminator and generator networks.
A pair of open-source, tomographically derived, three-phase microstructural datasets were investigated: a lithium-ion battery cathode and a solid oxide fuel cell anode. Various microstructural properties were calculated for 100 sub-volumes of the real data and these were compared to 100 instances of volumes created by the trained generator. The results showed excellent agreement across all metrics, although the synthetic structures showed a smaller variance compared to the training data, which is a commonly reported problem for DC-GANs and mitigation strategy will be reported in future work.
Two issues encountered when training the DC-GANs in this study were instability (likely due to a vanishing gradient) and moderate mode collapse. Both issues can be attributed to the GANs loss function and solutions have been suggested in the literature, the implementation of which will be explored in future work.
Two particular highlights of this work include the ability to generate arbitrarily large synthetic microstructural volumes and the generation of periodic boundaries, both of which are of high interest to the electrochemical modelling community. A detailed study of the impact of periodic boundaries on the reduction of simulation times is already underway.
Future work will take advantage of the continuity of the latent space, as well as the differentiable nature of GANs, to perform optimisation of certain morphological and electrochemical properties in order to discover improved electrode microstructures for batteries and fuel cells.
Methods
This section outlines the architecture that constitutes the two neural networks in the GAN, as well as the methodology followed for training. It also describes the microstructural properties used to analyse the quality of the microstructural reconstruction when compared to the real datasets. The codes developed for training the GANs are open-source.
Pre-treatment of the training set
The image data used in this study is initially stored as 8-bit greyscale elements, where the value of each voxel (3D pixel) is used as a label to denote the material it contains. For example, as in the case of the anode in this study, black (0), grey (127), and white (255), encode pore, metal, and ceramic respectively.
In several previous studies where GANs were used to analyse materials, the samples in question had only two phases and as such, the materials information could be expressed by a single number representing the confidence it belongs to one particular phase. However, in cases where the material contains three or more phases, this approach can be problematic, as a voxel in which the generator had low confidence deciding between black or white may end up outputting grey (i.e., a value halfway between black and white), which means something entirely different.
The solution comes from what is referred to as “one-hot” encoding of the materials information. This means that an additional dimension is added to the dataset (i.e., three spatial dimensions, plus one materials dimension), so an initially 3D cubic volume of n × n × n, is encoded to a 4D c × n × n × n volume, where c is the number of material phases present. This materials dimension contains a ‘1’ in the element corresponding to the particular material at that location and a ‘0’ in all other elements (hence, “one-hot”). So, what was previous black, white, and grey, would now be encoded as [1,0,0], [0,1,0], and [0,0,1] respectively. This concept is illustrated in Supplementary Fig. S1 for a three-material sample, but it could trivially be extended to samples containing any number of materials. It is also easy to decode these 4D volumes back to 3D greyscale, even when there is uncertainty in the labelling, as the maximum value can simply be taken as the label.
GAN Architecture and Training
The GAN architecture implemented in this work is a volumetric version based on the deep convolutional GAN (DC-GAN) model proposed by Radford et al.52. Both generator and discriminator are represented by fully convolutional neural networks. In particular, the convolutional nature of the generator allows it to be scalable, thus it can generate instances from the pmodel larger than the instances in the original training set, which is useful.
The discriminator is composed of five layers of convolutions, each followed by a batch normalisation. In all cases, the convolutions cover the full length of the materials dimension, c but the kernels within each layer are of smaller spatial dimension than the respective inputs to these layers . The first four layers apply a “leaky” rectified linear unit (leaky ReLU) activation function and the last layer contains a sigmoid activation function that outputs a single scalar constrained between 0 and 1, as it is a binary classifier. This value represents an estimated probability of an input image to belong to the real dataset (output = 1) or to the generated sample (output = 0).
The generator is an approximate mirror of the discriminator, also composed of five layers, but this time transposed convolutions64 are used to expand the spatial dimensions in each step. Once again, each layer is followed by a batch normalization and all layers use ReLU as their activation function, except for the last layer which uses a Softmax function, given by Eq. (4)
where xj represents the jth element of the one-hot encoded vector x at the last convolutional layer.
It is well known that the hyperparmeters that define the architecture of the neural networks have significant impact on the quality of the results and the speed of training. In this work, although a formal hyperparameter optimisation was not performed due to computational expense, a total of 16 combinations between four hyperparmeters was performed. A statistical analysis between the real and generated microstructures was performed (as described in section 2), and the optimum architecture was chosen based on these results.
The generator requires a latent vector z as its input in order to produce variety in its outputs. In this study, the input latent vector z is of length 100. Table 4 summarises all of the GAN’s layers configuration described above, as well as the size, stride and number of kernels applied between each layer, and the padding applied around the volume when calculating the convolutions. As will be discussed later in this paper, although zeros were initially used for padding, the study also explores the use of circular padding, which forces the microstructure to become periodic.
In theory, a Nash equilibrium is achieved after sufficient training; however, in practice this is not always the case. GANs have shown to present instability during training that can lead to mode collapse42. Mescheder et al.65 present an analysis of the stability of GAN training, concluding that instance noise and zero-centred gradient penalties lead to local convergence. Another proposed stabilisation mechanism, which was implemented effectively in this work, is called one-sided label smoothing42. Through this measure, the label 1 corresponding to real images is reduced by a constant ε, such that the new label has the value of 1 − ε. For all cases in this work, ε has a value of 0.1.
An additional source of instability during training is attributed to the fact that the discriminator learns faster than the generator, particularly at the early stages of training. To stabilise the alternating learning process, it is convenient to set a ratio of network optimisation for the generator and discriminator to k: 1. In other words, the generator is updated k times while the discriminator is updated once. In this work k has a value of 2. In both cases (i.e., cathode and anode data) stochastic gradient descent is implemented for learning using the ADAM optimiser66. The momentum constants are β1 = 0.5, β2 = 0.999 and the learning rate is 2 × 10−5. All simulations are performed on a GPU (Nvidia TITAN Xp) and the training process is limited to 72 epochs (c. 48 h).
Microstructural characterisation parameters
The electrode microstructures can be characterised by a set of parameters calculated from the 3D volumes. These parameters include morphological properties, transport properties, and statistical correlation functions. To evaluate the ability of the trained model to accurately capture the pdf that describes the microstructure within the latent space, parameters were calculated from 100 instances of both the real and GAN generated data.
Morphological properties
Three morphological properties are considered in this work, each computed using the open-source software TauFactor48. These consist of the volume fractions and specific surface areas, as well as the triple-phase boundary (TPB) densities. More information about these parameters can be found in the supplementary information.
Relative diffusivities
The relative diffusivity, Drel, is a dimensionless measure of the ease with which diffusive transport occurs through a system held between Dirichlet boundaries applied to two parallel faces. In this study, it is calculated for each of the three material phases separately, as well as in each of the three principal directions in a cubic volume. It is directly related to the diffusive tortuosity factor of phase i, τi, as can be seen from the following equation,
where ϕi is the volume fraction of phase i, \({D}_{i}^{0}\) is the intrinsic diffusivity of the bulk material (arbitrarily set to unity), and \({D}_{i}^{{\rm{eff}}}\) is the calculated effective diffusivity given the morphology of the system. The tortuosity factors were obtained with the open-source software TauFactor48, which models the steady-state diffusion problem using the finite difference method and an iterative solver.
Two-point correlation function
According to Lu et al.12, the morphology of heterogeneous media can be fully characterised by specifying one of the various statistical correlation functions. One of such correlations is the n-point probability function Sn(xn), defined as the probability of finding n points with positions xn in the same phase12,13,14. Based on this, the so-called two-point correlation function (TPCF), S2(r), allows the first and second-order moments of a microstructure to be characterised14,39. Assuming stationarity (i.e., the mean and variance have stabilised), the TPCF is defined as the non-centred covariance, which is the probability P that two points x1 = x and x2 = x + r separated by a distance r belong to the same phase pi,
At the origin, S2(0) is equal to the phase volume fraction ϕi. The function S2(r) stabilised at the value of \({\phi }_{i}^{2}\) as the distance, r, tends to infinity. This function is not only valuable for analysing the anisotropy of the microstructure, but also to account for the representativeness in terms of volume fraction of sub-volumes taken from the same microstructure sample. In this work, the TPCF of the three phases is calculated along the three Cartesian axes.
Data Availability
The study used open-access training data available from references listed in the manuscript. Many instances of the generated data are available at https://github.com/agayonlombardo/pores4thought. All other generated data used is available from the authors on request.
Code Availability
All the codes used in this manuscript can be accessed via the following link https://github.com/agayonlombardo/pores4thought.
References
Weyland, M., Midgley, P. A. & Thomas, J. M. Electron tomography of nanoparticle catalysts on porous supports: A new technique based on Rutherford scatterin. J. Phys. Chem. B 105, 7882–7886 (2001).
Méndez-Venegas, J. & Díaz-Viera, M. A. Geostatistical modeling of clay spatial distribution in siliciclastic rock samples using the plurigaussian simulation method. Geofis. Int. 52, 229–247 (2013).
Fantazzini, P., Brown, R. J. S. & Borgia, G. C. Bone tissue and porous media: Common features and differences studied by NMR relaxation. Magn. Reson. Imaging 21, 227–234 (2003).
Moussaoui, H. et al. Microstructural correlations for specific surface area and triple phase boundary length for composite electrodes of solid oxide cells. J. Power Sources 412, 736–748 (2019).
Cooper, S. J., Bertei, A., Finegan, D. P. & Brandon, N. P. Simulated impedance of diffusion in porous media. Electrochim. Acta 251, 681–689 (2017).
Moussaoui, H. et al. Stochastic geometrical modeling of solid oxide cells electrodes validated on 3D reconstructions. Comput. Mater. Sci. 143, 262–276 (2018).
Holzer, L. et al. Microstructure degradation of cermet anodes for solid oxide fuel cells: Quantification of nickel grain growth in dry and in humid atmospheres. J. Power Sources 196, 1279–1294 (2011).
Eastwood, D. S. et al. The application of phase contrast X-ray techniques for imaging Li-ion battery electrodes. Nucl. Instrum. Methods Phys. Res. B 324, 118–123 (2014).
Ni, N. et al. Degradation of (La0.6Sr0.4)0.95(Co0.2Fe0.8)O3–δ Solid oxide fuel cell cathodes at the nanometer scale and below. ACS Appl. Mater. Interfaces 8, 17360–17370 (2016).
Pietsch, P. & Wood, V. X-ray tomography for Lithium ion battery research: A practical guide. Annu. Rev. Mater. Res. 47, 451–479 (2017).
Quiblier, J. A. A new three-dimensional modeling technique for studying porous media. J. Colloid Interface Sci. 98, 84–102 (1984).
Lu, B. & Torquato, S. N-Point probability functions for a lattice model of heterogeneous media. Phys. Rev. B 42, 4453–4459 (1990).
Yeong, C. L. & Torquato, S. Reconstructing random media. Phys. Rev. E Stat. Phys. Plasma Fluids Relat. Interdiscip. Top. 57, 495–506 (1998).
Yeong, C. L. & Torquato, S. Reconstructing random media. II. Three-dimensional media from two-dimensional cuts. Phys. Rev. E - Stat. Phys. Plasma Fluids Relat. Interdiscip. Top. 58, 224–233 (1998).
Manwart, C., Torquato, S. & Hilfer, R. Stochastic reconstruction of sandstones. Phys. Rev. E Stat. Phys. Plasma Fluids Relat. Interdiscip. Top. 62, 893–899 (2000).
Sheehan, N. & Torquato, S. Generating microstructures with specified correlation functions. J. Appl. Phys. 89, 53–60 (2001).
Jiao, Y., Stillinger, F. H. & Torquato, S. Modeling heterogeneous materials via two-point correlation functions: Basic principles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76, 1–15 (2007).
Jiao, Y., Stillinger, F. H. & Torquato, S. Modeling heterogeneous materials via two-point correlation functions. II. Algorithmic details and applications. Phys. Rev. E Stat., Nonlin. Soft Matter Phys. 77, 1–35 (2008).
Sundararaghavan, V. Reconstruction of three-dimensional anisotropic microstructures from two-dimensional micrographs imaged on orthogonal planes. Integr. Mater. Manuf. Innov. 3, 1–11 (2014).
Suzue, Y., Shikazono, N. & Kasagi, N. Micro modeling of solid oxide fuel cell anode based on stochastic reconstruction. J. Power Sources 184, 52–59 (2008).
Hasanabadi, A., Baniassadi, M., Abrinia, K., Safdari, M. & Garmestani, H. 3D microstructural reconstruction of heterogeneous materials from 2D cross sections: A modified phase-recovery algorithm. Comput. Mater. Sci. 111, 107–115 (2016).
Hasanabadi, A., Baniassadi, M., Abrinia, K., Safdari, M. & Garmestani, H. Optimization of solid oxide fuel cell cathodes using two-point correlation functions. Computational Mater. Sci. 123, 268–276 (2016).
Izadi, H. et al. Application of full set of two point correlation functions from a pair of 2D cut sections for 3D porous media reconstruction. J. Pet. Sci. Eng. 149, 789–800 (2017).
Hasanabadi, A., Baniassadi, M., Abrinia, K., Safdari, M. & Garmestani, H. Optimal combining of microstructures using statistical correlation functions. Int. J. Solids Struct. 160, 177–186 (2019).
Baniassadi, M. et al. Three-phase solid oxide fuel cell anode microstructure realization using two-point correlation functions. Acta Mater. 59, 30–43 (2011).
Siddique, N. A. & Liu, F. Process based reconstruction and simulation of a three-dimensional fuel cell catalyst layer. Electrochim. Acta 55, 5357–5366 (2010).
Siddique, N., Salehi, A. & Liu, F. Stochastic reconstruction and electrical transport studies of porous cathode of Li-ion batteries. J. Power Sources 217, 437–443 (2012).
Ali, A., Wen, X., Nandakumar, K., Luo, J. & Chuang, K. T. Geometrical modeling of microstructure of solid oxide fuel cell composite electrodes. J. Power Sources 185, 961–966 (2008).
Kenney, B., Valdmanis, M., Baker, C., Pharoah, J. G. & Karan, K. Computation of TPB length, surface area and pore size from numerical reconstruction of composite solid oxide fuel cell electrodes. J. Power Sources 189, 1051–1059 (2009).
Cai, Q., Adjiman, C. S. & Brandon, N. P. Modelling the 3D microstructure and performance of solid oxide fuel cell electrodes: Computational parameters. Electrochim. Acta 56, 5804–5814 (2011).
Bertei, A., Choi, H. W., Pharoah, J. G. & Nicolella, C. Percolating behavior of sintered random packings of spheres. Powder Technol. 231, 44–53 (2012).
Le Loc’h, G. & Galli, A. Truncated Plurigaussian method: theoretical and practical points of view. Proc. Geostatistics Int. Conf., Wollongong 96 1, 211–222 (1997).
Neumann, M., Osenberg, M., Hilger, A., Franzen, D. & Turek, T. et al. On a pluri-Gaussian modelfor three-phase microstructures, with applications to 3D image data of gas-diffusion electrodes. Computational Mater. Sci. 156, 325–331 (2019).
Usseglio-Viretta, F. L. E., Colclasure, A., Mistry, A. N., Claver, K. P. Y. & Pouraghajan, F. et al. Resolving the discrepancy in tortuosity factor estimation for Li-ion battery electrodes through micro-macro modeling and experiment. J. Electrochem. Soc. 165, A3403–A3426 (2018).
Trembacki, B. L., Mistry, A. N., Noble, D. R., Ferraro, M. E. & Mukherjee, P. P. et al. Editors’ choice—Mesoscale analysis of conductive binder domain morphology in Lithium-ion battery electrodes. J. Electrochem. Soc. 165, E725–E736 (2018).
Forouzan, M. M., Chao, C. W., Bustamante, D., Mazzeo, B. A. & Wheeler, D. R. Experiment and simulation of the fabrication process of Lithium-ion battery cathodes for determining microstructure and mechanical properties. J. Power Sources 312, 172–183 (2016).
Srivastava, I. Bolintineanu, D. S. Lechman, J. B. & Scott, A. Controlling binder adhesion to impact electrode mesostructure and transport, ECSarXiv. https://doi.org/10.1149/osf.io/ehdq6 (2019).
Mosser, L., Dubrule, O. & Blunt, M. Reconstruction of three-dimensional porous media using generative adversarial neural networks. Phys. Rev. E 96, 043309 (2017).
Mosser, L., Dubrule, O. & Blunt, M. J. Stochastic reconstruction of an oolitic limestone by generative adversarial networks. Transp. Porous Media 125, 81–103 (2018).
Goodfellow, I. et al. Generative adversarial network. https://arxiv.org/pdf/1406.2661.pdf (2014).
Li, X., Yang, Z., Brinson, L. C., Choudhary, A., Agrawal, A. & Chen, W. A deep adversarial learning methodology for designing microstructural material systems. Proceedings of the ASME 2018 International Design Engineering, 1–14 (ASME, 2018).
Goodfellow, I. NIPS 2016 Tutorial: generative adversarial networks. http://arxiv.org/abs/1701.00160 (2016).
Lecun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Hsu, T. et al. Mesoscale characterization of local property distributions in heterogeneous electrodes. J. Power Sources 386, A3403–A3426 (2018).
Blair, S. C. Berge, P. A. & Berryman, J. G. Two-point correlation functions to characterize microgeometry and estimate permeabilities of synthetic and natural sandstones. Lawrence Livermore National Laboratory Report, 1–30 (National Lab., CA, USA, 1993).
Journel, A. G. & Froidevaux, R. Anisotropic hole-effect modelling. J. Int. Assoc. Math. Geol. 14, 217–239 (1982).
Pyrcz, M. & Deutsch, C. The whole story on the hole effect. Geostatistical Assoc. Australas. Newsl. 18, 18 (2003).
Cooper, S. J., Bertei, A., Shearing, P. R., Kilner, J. A. & Brandon, N. P. TauFactor: An open-source application for calculating tortuosity factors from tomographic data. SoftwareX 5, 203–210 (2016).
Paganini, M., De Oliveira, L. & Nachman, B. Accelerating science with generative adversarial networks: An application to 3D particle showers in multilayer calorimeters. Phys. Rev. Lett. 120, 1–6 (2018).
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B. & Hochreiter, S. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 6627–6638 (2017).
Arora, S. Risteski, A. & Zhang, Y. Do GANs Learn the Distribution? Some Theory and Empirics. International Conference on Learning Representations (ICLR) 2018, 1–16 (ICLR, 2018).
Radford, A. Metz, L. & Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings, 1–16 (ICLR, 2016).
Wang, Z. She, Q. & Ward, T. E. Generative adversarial networks in computer vision: a survey and taxonomy. https://arxiv.org/abs/1906.01529 (2019).
Arjovsky, M. Chintala, S. & Bottou, L. Wasserstein GAN. https://arxiv.org/abs/1701.07875 (2017).
Gulrajani, I. Ahmed, F. Arjovsky, M. Dumoulin, V. & Courville, A. Improved training of Wasserstein GANs. https://arxiv.org/abs/1704.00028 (2017).
Mao, X. Li, Q. Xie, H. Lau, R. Y. Wang, Z. & Smolley, S. P. “Least Squares Generative Adversarial Networks”. 2017 IEEE International Conference on Computer Vision (ICCV), 2813–2821 (IEEE, Venice, 2017). https://doi.org/10.1109/ICCV.2017.304.
Yoshida, Y. & Miyato, T. Spectral norm regularization for improving the generalizability of deep learning. https://arxiv.org/abs/1705.10941 (2017).
Zhang, Y. et al. High-throughput 3D reconstruction of stochastic heterogeneous microstructures in energy storage materials. npj Comput. Mater. 5, 012003 (2019).
Zhang, D., Bertei, A., Tariq, F., Brandon, N. & Cai, Q. Progress in 3D electrode microstructure modelling for fuel cells and batteries: transport and electrochemical performance. Prog. Energy 1, 012003 (2019).
Lees, A. W. & Edwards, S. F. The computer study of transport processes under extreme conditions. J. Phys. C: Solid State Phys. 5, 1921–1928 (1972).
Henyš, P., Čapek, L. & Březina, J. Comparison of current methods for implementing periodic boundary conditions in multi-scale homogenisation. Eur. J. Mech., A/Solids 78, 103825 (2019).
Yeh, R. A. et al. Semantic image inpainting with deep generative models. Proc. 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, 6882–6890 (CVPR, 2017).
Isola, P. Zhu, J. Y. Zhou, T. & Efros, A. A. Image-to-image translation with conditional adversarial networks. Proc. 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, 5967–5976 (CVPR, 2017).
Dumoulin, V. & Visin, F. A guide to convolution arithmetic for deep learning. https://arxiv.org/abs/1603.07285 (2016).
Mescheder, L. Geiger, A. & Nowozin, S. Which training methods for GANs do actually converge? 35th International Conference on Machine Learning, ICML 2018, Vol. 8, 5589–5626 (ICML, 2018).
Kingma, D. P. & Ba, J. L. A method for stochastic optimization. 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, 1–15 (ICLR, 2015).
Acknowledgements
This work was supported by funding from both the CONACYT-SENER fund and the EPSRC Faraday Institution Multi-Scale Modelling project (https://faraday.ac.uk/; EP/S003053/1, grant number FIRG003). The Titan Xp GPU used for this research was kindly donated by the NVIDIA Corporation through their GPU Grant program. The authors would also like to thank various colleagues for their valuable comments: Prof. Stephen Neethling, Antonio Bertei, Tilman Roeder, Steven Kench, Vitaly Levdik, Donal Finegan and Harry Abernathy.
Author information
Authors and Affiliations
Contributions
A.G.L. wrote the code. S.J.C. supervised the project. S.J.C. and A.G.L. conceived the idea and performed the analysis. L.M. provided the theoretical foundations and expertise in GANs. N.P.B. offered supervision and guidance on the wider impact of the work. A.L.G. and S.J.C. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gayon-Lombardo, A., Mosser, L., Brandon, N.P. et al. Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries. npj Comput Mater 6, 82 (2020). https://doi.org/10.1038/s41524-020-0340-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0340-7
This article is cited by
-
Prediction of electrode microstructure evolutions with physically constrained unsupervised image-to-image translation networks
npj Computational Materials (2024)
-
Quantifying microstructures of earth materials using higher-order spatial correlations and deep generative adversarial networks
Scientific Reports (2023)
-
Bridging nano- and microscale X-ray tomography for battery research by leveraging artificial intelligence
Nature Nanotechnology (2022)
-
Super-resolving microscopy images of Li-ion electrodes for fine-feature quantification using generative adversarial networks
npj Computational Materials (2022)
-
Synthesizing controlled microstructures of porous media using generative adversarial networks and reinforcement learning
Scientific Reports (2022)