Introduction

Polymers are important dielectric materials that are often used for a wide range of applications, including high-energy-density capacitors1,2,3,4,5,6,7,8,9, high-voltage cables10, microelectronics11, and photovoltaic devices12,13. Each application requires a given range of the polymer dielectric constant ϵ, also referred to as the relative permittivity. High ϵ polymers are needed for high-energy-density capacitors and photovoltaic devices to allow facile charge extraction. On the other hand, polymers with low ϵ are needed in other applications, e.g., to reduce signal-delay time in microelectronics, and lower conduction loss in high-voltage cables. Extensive efforts are undertaken to optimize device performance by tailoring the ϵ of a given polymer. As a common example in the capacitor domain, many strategies have been proposed to increase ϵ of polymers via doping/coating high ϵ inorganic particles (e.g., BaTiO3)14,15, grafting/blending with highly polar polymers (e.g., polyvinylidene fluoride, PVDF)16 or metal-organic polymers17. However, such modifications are almost always accompanied with new challenges, e.g., reduced breakdown strength, high dielectric loss and increased film processing cost. Therefore, it is highly desirable to design pure all-organic polymers with tailored ϵ values4,8,18,19, while not compromising other attractive and necessary attributes.

ϵ is related to the electric polarization of a material under an alternating electric field20,21. It consists of three contributions, arising from electronic (ϵelec), ionic (ϵionic), and dipolar (ϵdiploar) polarization. Each of these polarization mechanisms have different response times, resulting in different contributions to the overall ϵ as a function of the applied frequency—above optical frequencies only ϵelec contributions are relevant, in THz regime both ϵelec + ϵionic contribute, and at lower frequencies all of the ϵelec + ϵionic + ϵdiploar contributions are significant. Thus, generally, ϵ decreases with an increase in the applied frequency (ignoring certain near-singularity artifacts at the resonant frequencies). This also suggests the significance of obtaining the complete frequency-dependent ϵ behavior for polymers, rather than a particular ϵ value at a single frequency. Extensive computational efforts have been made to compute the ϵ of polymers in the higher-frequency (THz) regimes7,22. For example, density functional perturbation theory (DFPT) has been used to compute the ϵ of crystalline polymers with acceptable accuracy7,22. However, this method is computationally expensive and restricted to small systems (<50 atoms). As a result, the computed ϵ can only account for ϵelec and ϵionic parts, excluding the ϵdiploar contributions arising from block- and chain-level changes in the polymers. Furthermore, the assumption of dense ordered crystalline structures commonly made in these computations (to allow for a small unit cell) leads to an overestimation of the ϵionic part. These issues can be partly solved by using large-scale classical molecular dynamics (MD) simulations23, but these are restricted to polymer systems with reliable classical force field.

Data-driven techniques are popular and powerful alternatives to build surrogate models for property prediction and material design, greatly accelerating the (discovery and application of new materials8,24,25,26,27,28,29. In the polymer domain, group contribution methods have been developed to predict various properties of polymers, such as ϵ21. However, major problems with this approach include the inability to generalize to new polymers containing functional groups outside the library of considered groups, and the disregard of sequence and connections of the constituting functional groups. A recent successful development has been to use hand-crafted features (also called descriptors or fingerprints) within the context of machine-learning (ML) models for polymer property prediction6,22,30,31,32. Although reliable ϵ-prediction models were developed in our previous work32, those are limited by the accuracy of the underlying DFPT dataset, especially due to the assumption of crystalline polymer structures (as mentioned above). More importantly, those models cannot predict the complete frequency-dependent ϵ behavior.

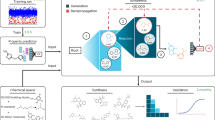
In this work, we develop an ML model to predict the frequency-dependent ϵ behavior of polymers, using a dataset of 1210 experimentally measured values at various frequencies (spanning 15 orders of magnitude). This is achieved using a 3-level hierarchical polymer fingerprinting scheme and the Gaussian process regression (GPR) algorithm to train the model, as shown in Fig. 1. The resulting ML model can accurately and rapidly predict ϵ of new polymer candidates across a wide range of frequencies, as validated using the performance on unseen test set. To better understand the ML models developed and derive simple chemical trends, we investigate the key chemical features that dominate the ϵ of polymers. Furthermore, to showcase the predictive power and the usefulness of the developed surrogate models, we computed the frequency-dependent ϵ of a candidate set of 11,000 unseen polymers manually accumulated from various available sources7,21,32,33,34. Another critical design property (glass transition temperature, Tg), reflective of the thermal stability of these polymers, was predicted using our previously developed ML model32. Using these two predicted properties, five representative polymers satisfying specific ϵ and Tg requirements are proposed for capacitor and microelectronic applications.

Fig. 1: Machine-learning workflow.
figure 1

Schematic of the workflow adopted to build general data-driven models of frequency-dependent ϵ for polymers.

Full size image

Results

Dataset and polymer fingerprints

As illustrated in Fig. 2a, 1210 experimental ϵ values belonging to 738 unique polymers were collected from the literature9,19,21,33,35,36,37,38,39,40,41,42 to train the ML models. These measurements were made at 9 frequency values (i.e., 60, 102, 103, 104, 105, 106, 107, 109, and 1015 Hz), at room temperature and under dry conditions. Here, ϵ values at 1015 Hz represent the optical frequency region and were obtained by taking the square of the experimental refractive index. Given the limitation of available experimental values, each polymer in Fig. 2a has ϵ values available at 1–8 frequency values. Furthermore, this 738-polymer dataset includes 11 elements, i.e., C, H, B, O, N, S, P, Si, F, Cl, and Br and various polymer classes, e.g., polycarbonates, polyimide, polyamide, polyolefins, polyvinyl, polyethers and polyesters. The ϵ distribution as a function of frequency (in Hz) is presented in Fig. 2a, along with the corresponding polymer count at each frequency. We note that the ϵ dataset ranges from 1.3 to 11 and is slightly unbalanced in terms of data count at different frequencies. This can be attributed to the difficulties experienced when making empirical measurements at various frequencies, but we believe that the data diversity is sufficient to build reliable regression models. The trends in ϵ values for 6 common and diverse polymers highlighted in Fig. 2a signify the importance of polymer chemistry. It is worth noting that ϵ of polar polymers like PVDF and polyvinyl alcohol (PVA) significantly decreases with an increase in frequency while for non-polar polymers, such as polypropylene (PP) and ETFE, ϵ is not sensitive to the applied frequency. Therefore, for the ML model to capture such trends accurately, it is essential that the dataset is representative and balanced in terms of polymer chemistry and count, respectively. More details on the ϵ dataset are provided in the “Methods” section.

Fig. 2: Experimental dielectric constant dataset and the chemical space of training and unseen datasets.
figure 2

a Experimental ϵ as a function of the frequency (unit, Hz), along with the data count at each frequency. The trends in ϵ values of six representative polymers are also shown using dashed lines. b Chemical space of the training set (738 polymers) considered this work (light blue squares), with respect to a larger unseen dataset of 11,000 polymers (gray circles), illustrated using the first two principal components (PC1 and PC2). A few representative polymer classes of the training dataset are highlighted with colored symbols.

Full size image

The next important step towards building accurate and reliable ML models is to generate relevant features that uniquely represent each polymer and also capture its frequency-dependent ϵ behavior. To capture the polymer chemistry, we used features from three hierarchical levels, i.e., (1) atomic-level fragments, (2) block-level fragments, and (3) chain-level features. A total of 411 chemical features were used to numerically fingerprint 738 polymers. Additionally, the frequency in log-scale (log F) was incorporated as the key feature to capture the frequency-dependent behavior, overall resulting in a 412-dimensional feature vector. Next, the least absolute shrinkage and selection operator (LASSO) method was adopted for dimensionality reduction and elimination of irrelevant features. The details on the fingerprinting scheme and the use of the LASSO method are included in the “Methods” section, while the final number of features retained for model development are summarized in Table 1.

Table 1 Details of ML models. NX is the number of features.
Full size table

To validate the generality, reliability and usefulness of the ML models developed in this work, the frequency-dependent ϵ of an unseen dataset of 11,000 candidate polymers previously synthesized elsewhere (but for which no dielectric characterization has been done)7,21,32,33,34, were predicted. This unseen dataset contains polymers distinct from the training dataset (of 738 polymers), but is made up of the same 11 elements, i.e., C, H, B, O, N, S, P, Si, F, Cl, and Br. Furthermore, the chemical diversity of this unseen dataset is quite similar to that of the training dataset (of 738 polymers), as illustrated in Fig. 2b using the first two (PC1 and PC2) components obtained from the principal component analysis (PCA) on chemical features of all polymers. The similarity of two datasets is further discussed using the agglomerative hierarchical clustering analysis in Supplementary Section 1. Note that the training dataset (light blue square) spans the chemical space well, indicating that it is representative of the unseen polymer dataset (gray circles). Several representative polymer classes of the training dataset are also labeled with colored symbols in Fig. 2b.

Frequency-dependent machine-learning models of dielectric constant

Considering that ϵ depends on both polymer-type and the applied frequency, the ML models (using the GPR algorithm) were trained in two different fashions with varying train-validation-test splits, referred to here as the (1) polymer-types-split (738 polymers) and (2) data-points-split (1210 points) approach. In the former split, the test set consists of completely different polymers than those in the training set, resulting in evaluation of ML performance on unseen polymer cases. While both random and stratified sampling methods were used in the latter to split train-validation-test sets across all polymers and all frequencies, as discussed in Supplementary Section 2.1. The random sampling method is selected in the present work due to the comparable ML performance of two sampling methods. For all models, fivefold cross-validation (CV) was used to avoid overfitting, and two error metrics, namely, root mean square error (RMSE) and the coefficient of determination (R2), were used to evaluate their performance.

Figure 3a1, b1 show the learning curves of the ML models trained using polymer-types-split and data-points-split methods, respectively. The average training and test RMSE of ϵ prediction as a function of training set size is plotted, with the error bars denoting 1σ standard deviation in the reported RMSE values over 50 runs. Results for both the cases, i.e., with all 412 features (GPR-XAll) and with those retained after LASSO dimensionality reduction (GPR-XLASSO) are included. As expected, the test RMSE decreases with an increase in training set size for all cases. We note that the GPR-XLASSO does a better job of improving the ML performance when trained using the data-points-split approach in comparison with the polymer-types-split approach. Further, a higher test RMSE of 0.67 resulted in polymer-types-split models using 90 % training set (664 polymers), while a test RMSE of 0.35 was obtained in data-points-split models (with 1089 training points). Considering the ϵ dataset ranges from 1.3 to 11, this amounts to an error of ≲7%. In addition to the LASSO feature reduction method, the recursive feature elimination (RFE) using linear support vector regression algorithm was used in the data-points-split model to backward eliminate irrelevant features. The corresponding learning curve is shown in Supplementary Fig. 4, revealing that the GPR-XLASSO model provides higher prediction accuracy.

Fig. 3: Machine-learning models of dielectric constant.
figure 3

ML models of ϵ based on polymer-types-split a and data-points-split b. a1 and b1 are learning curves trained using all features (GPR-Xall) and LASSO (GPR-XLASSO) reduced features, with the error bars denoting 1σ standard deviation in the reported RMSE values over 50 runs. a2 and b2 are parity plots using GPR-XLASSO and the 90% train set, where all frequency-dependent information of five polymers (PP, PET, PAN, PVC, and PDTC-HK511) were intentionally included in the 10% test set. Symbol sizes represent the frequency applied. a3 and b3 show Expt. vs ML predicted ϵ of PP, PVC and PAN in a2 and b2, respectively, with frequency = 60, 102, 103, 104, 105, 106, 107, 109, and 1015 Hz. The remaining two polymers (PET and PDTC-HK511) are available in Supplementary Fig. 5. Furthermore, the additional ML predicted ϵ values at 1012 Hz of these three polymers are shown. Error bars in a2, a3, b2, and b3 are predicted GPR uncertainties.

Full size image

To further validate the generality and accuracy of the two ML models, all frequency-dependent information of five common polymers, namely, polyethylene terephthalate (PET), polypropylene (PP), polyacrylonitrile (PAN), polyvinyl chloride (PVC) and PDTC-HK511, was intentionally included in the 10% test set (completely unseen by the 90% train set). These five polymers were selected based on their difference in polarity, wide range of ϵ values, and larger availability of frequency-dependent data. The resulting parity plots between ML prediction vs. experimental ϵ using the GPR-XLASSO models are portrayed in Fig. 3a2, b2. The error bars in these cases represent the GPR uncertainty and the size of markers denote the frequency applied. It can be seen that the R2 for the test set of polymer-types splits and data-points splits models is 0.74 and 0.92, respectively. The corresponding frequency-dependent ϵ behavior for PP, PVC, and PAN polymers is shown in Fig. 3a3, b3. The remaining two polymers (PET and PDTC-HK511) are available in Supplementary Fig. 5. It can be observed that frequency-dependent ϵ trend for PP and PAN are predicted fairly well using the polymer-type-split models, although the GPR uncertainties are slightly high due to absence of similar polymer chemistry within the training set. This issue is, however, greatly improved in the data-points-split model, wherein more polymer types (695) are included in the training set as compared to that in the polymer-type-split method (with 664 polymers).

A major benefit of the presented ML models is their ability to predict ϵ across a wide range of frequencies (60–1015 Hz). In Fig. 3a3, b3, we also show the ϵ predictions for the three unseen polymers at 1012 Hz, where empirical data is unavailable. The ML predictions can be seen to closely follow the available frequency-dependent ϵ trend. We also compare these models with our previous work utilizing DFPT-based computed ϵ values at THz frequency (denoted as ML-DFPT). As illustrated in Supplementary Fig. 6, the ML-DFPT predicted ϵ of PET, PP, and PVC are much higher than their corresponding experimental values at 109 Hz, leading to incorrect frequency-dependent ϵ trend; ϵ value should decrease with increase in frequency. The reason for this discrepancy is the overestimation of DFPT computed ϵ values, which are computed using unrealistic crystalline structures of polymers having unreasonably higher densities than realistic semi-crystalline or amorphous case. On the other hand, the present ML models utilize information available at different frequencies (both the lower regime and the higher optical region) to accurately predict the ϵ values at 1012 Hz.

Overall, Fig. 3 shows that the data-points-split-based ML models perform better than their polymer-types-split-based counterparts in terms of test RMSE, the error trends in the learning curve, and the prediction capability of five completely unseen polymers. Such observation is expected and understandable because of inclusion of fewer polymer types in the polymer-types-split training set. Moreover, in the data-points-split approach it is possible that the same polymers with different frequencies are randomly sampled in the training and the test sets, thus improving the ML performance. From a theoretical standpoint, these two ML models provide predictive capability of ϵ at two extremes: data-points-split model is appropriate for polymer cases with some known frequency-dependent ϵ values, while polymer-types-split model is applicable for completely new polymers with no ϵ information. With these systematic and careful studies, we believe that the random data-points-split approach is reliable and appropriate to be used to train the final predictive model with the entire dataset and CV.

Factors affecting dielectric constant

In addition to building the ML models, it is valuable to analyze the key features that correlate highly with the measured ϵ behavior in polymers. In the data-points-split approach, 53 features were retained from the initial set of 412 after LASSO-based dimensionality reduction. Figure 4 summarizes some representative features with strong negative or positive correlation with ϵ, with the corresponding coefficients available in Supplementary Fig. 7. As expected, there is a negative correlation between log F (frequency in log-scale) and ϵ with a coefficient of –0.93. Additionally, the presence of certain atomic- and block-level features, including CH2CH2, CF2CF2, benzene rings, CH3, CF3, (CH3)3, and CH2CH2CH, and chain-level features, such as the high number of 3-vertex carbon atoms, number of cyclic double bonds and presence of a purely single bond, lead to lower ϵ. The main reason being that these functional groups introduce zero or negligible net dipole moments but larger free volumes, resulting in small net dipole density and thus lower ϵelec. In contrast, the presence of polar groups, such as CH2CF2CH2, C–F, C–Cl, –OH, ketone, thioketones, NH, amide, pyridine, pyrrole, CH2CH2O, and various fragments including NH/amide could strongly enhance the electronic polarity (ϵelec) of polymers. Consequently, these positive (negative) correlated features can increase (decrease) the total ϵ across the entire frequency regime by controlling ϵelec. Furthermore, the structural arrangement of these functional groups strongly affects the polymer ϵ value, e.g., PVDF (CF2CH2CF2CH2) has an ϵ of 9.45 at 100 Hz while ETFE (CH2CH2CF2CF2) has an ϵ of just 2.6. Thus, it was essential to cover such special sequence-controlled block-level features in our fingerprinting scheme (e.g., CH2CH2CF2 and CH2CF2CH2) to distinguish polymers. Also, the chain-level features including the topological polar surfaces area of polar elements (e.g., O, N, S, F, and Cl) and the number of H-bond acceptors have a positive relationship with ϵ. These features can increase the ionic (ϵionic) and dipolar (ϵdipolar) parts by strengthening the H-bonding and dipole interactions between polymer chains, thus increasing the overall ϵ at THz and lower frequency regime. All these findings can be helpful guidelines for rational design of polymers with desired frequency-dependent ϵ values.

Fig. 4: Representative features affecting dielectric constant.
figure 4

Representative features having strong negative or positive correlations with ϵ. R represents an arbitrary chemical group of C, O, H, N elements, and log F denotes the log-scale frequency value used as a feature in the ML model.

Full size image

Application-specific polymers design with desired dielectric constant

Next, we move on to apply the developed ML model to discover novel polymers with desired ϵ for capacitors and microelectronic devices. As illustrated in Fig. 5a, the frequency-dependent ϵ of the 11,000 unseen candidate polymers in Fig. 2b were predicted using the GPR-XLASSO model trained on the full dataset (1210 points), the data-points-split approach and fivefold CV. We note that ϵ predictions can be made across a wide range of frequencies (e.g., 60, 102, 103, 104, 105, 106, 107, 108, 109, 1012, and 1015 Hz), although no training data is available at THz frequency. The inverse relation of predicted ϵ with frequency for these new polymers can be observed in Fig. 5a and further validations are shown in Supplementary Fig. 8.

Fig. 5: Machine-learning-predicted dielectric constant of 11,000 unseen polymers.
figure 5

a ML predicted ϵ at various frequencies (i.e., 60, 102, 103, 104, 105, 106, 107, 108, 109, 1012, and 1015 Hz) for 11,000 unseen polymers from Fig. 2b, along with their ML predicted Tg values. b Ten representative polymers with high Tg (≥450 K) selected from a, such that five polymers (ID 1–5) have high ϵ (≥5), and remaining five (ID 6–10) have low ϵ (2–2.5).

Full size image

To optimize polymer candidates for capacitor and microelectronic applications, in addition to ϵ, another critical design property, Tg, is considered. Polymers with high Tg are expected to be thermally stable, which is essential for these two applications9,43,44. Thus, in Fig. 5a, we also provide ML predicted Tg using our previously developed models32. Based on the past considerations appropriate for high-temperature energy density capacitors2,3,43,44, Tg ≥ 450 K was used as the first criterion to discover polymers for high-temperature applications. As mentioned earlier, polymers with high ϵ are required for capacitors, thus, 85 polymers with ϵ ≥ 5 (at 100 Hz) were selected from Fig. 5a expected to display high-energy density. As insulating films in microelectronic devices need polymers with low ϵ to decrease the signal-delay time, 191 polymers with ϵ in a range of 2.0–2.5 (at 100 Hz) were identified. For each application, the frequency-dependent ϵ of five representative polymers is shown in Fig. 5b. The corresponding monomer unit, and the ML-based ϵ (at 100 Hz) and Tg (in K) predictions are summarized in Fig. 6. Here, ID 1–5 represent cases with high ϵ for capacitors and ID 6–10 are polymers with low ϵ for microelectronic devices.

Fig. 6: Details of ten representative polymers.
figure 6

The monomer unit, and the ML predicted Tg and ϵ (at 100 Hz) of ten representative polymers shown in Fig. 5b. Polymers with ID 1–5 have high ϵ (≥5), while ID 6–10 are polymers with low ϵ (2–2.5). The associated ML prediction uncertainty is also provided.

Full size image

As shown in Fig. 5b, the frequency-dependent ϵ trend of ten polymers is correctly captured. Moreover, the monomer chemistry for the selected 5 polymer with high ϵ (ID 1–5) includes either amide, OH or C–Cl groups, agreeing with the positive correlation trend discussed above (and shown in Fig. 4). Similarly, the presence of CF3 group and benzene rings greatly decrease the polymer ϵ, as mentioned earlier and can be seen from the selected list of low ϵ polymer with amides groups (ID 6–8) and OH groups (ID 9) in Fig. 6. We also note that all of the selected 10 polymers contain rigid benzene rings, resulting in high Tg. Based on the prediction accuracy reached by our models on the unseen test set, the ability of the model to correctly capture inverse ϵ vs. frequency behavior, and the chemical arguments made above, we believe that these proposed ten polymers are good candidates for further experimental validations.

Discussion

Using an experimental ϵ dataset of 738 polymers (or 1210 data-points) at various frequencies, unique 3-level hierarchical polymer features and the GPR algorithm, we built a single ML model to accurately predict the frequency-dependent ϵ behavior of polymers. There are several advantages of the ML models presented here: first, it can predict ϵ of polymers across a wide range of frequencies (60–1015 Hz, excluding the resonant frequency regions). The single ML model developed here more accurately capture the inverse relationship between ϵ and frequency, compared with separate ML models for ϵ at different frequency regimes, as discussed in Supplementary Section 4. As the frequency in log-scale was used as a feature in the single ML model, the frequency-dependent trend was learned from the training data itself. Furthermore, we found the single ML model to be more generalizable for new cases, as it was trained using a larger polymer dataset. Additional advantages of having the frequency in log-scale as a feature is that it allows us to make ϵ predictions at any arbitrary frequency value, which is not possible with separate ML models. This complete frequency-dependent picture provides comprehensive information to assist rational design of new polymers. The present ϵ-prediction model is already implemented in our Polymer Genome platform (http://www.polymergenome.org).

Second, the predicted GPR uncertainty acts as a useful guide to know when the ML predictions can be trusted. The present ML model is more suitable for homo-polymers containing C, H, B, O, N, S, P, Si, F, Cl, and Br atoms. Also, higher uncertainties can be expected within the frequency range of 1010–1014 Hz owing to the unavailability of training data in this regime. These uncertainties can provide useful guidance for next experiments via active learning, with the newly generated data aiding model improvement45.

Third, key features that strongly affect the polymer ϵ behavior were analyzed, forming a crude first stage criteria to find polymers with the desired ϵ. To attain high ϵ, common polar groups, including C–F, –OH, C=O and amides, and rigid groups such as pyridine and pyrrole can be introduced into polymers. On the other hand, the introduction of non-polar groups (e.g., benzene rings and CH3) or functional groups with low polarization density (e.g., CF3) leads to low ϵ. However, we note that presence of some flexible polar groups may induce an unwanted high dielectric loss, which can be further eliminated by introducing additional screening criteria on other polymer properties, e.g., low dielectric loss and high breakdown strength.

Finally, ϵ and Tg of about 11,000 polymers have been predicted using the ML models developed in this and our previous work32, respectively, providing a huge pool of polymers for various applications. Using the Tg and ϵ as the screening criteria, 5 high and 5 low ϵ polymers are proposed for capacitors and microelectronic devices, respectively. While this work initiates a great opportunity to select polymers satisfying two properties, it can be easily extended to three or more properties.

Although we believe that the developed ML model is fairly accurate and universal, more efforts are envisioned in the future. First, Fig. 3 shows that a test RMSE of 0.67 and 0.35 is achieved for the polymer-types-split and data-points-split-based ML models using 90% training set and 10% test set, respectively. Therefore, it is expected that the average RMSE of predicted values for new cases ranges from 0.35 to 0.67. For polymers in applications requiring a high ϵ of 5–11, even the RMSE of 0.67 leads to an acceptable relative error of 6–13.4%. For applications require polymers with ϵ ranging from 2 to 3.5, the RMSE of 0.35 results in a relative error 10–17%, which is slightly high but acceptable. The relative error of some completely unseen polymers may reach to 19–33% with respect to the RMSE of 0.67. However, their predicted GPR uncertainties should also be high. Therefore, more data should be collected from literature either manually or using natural language processing techniques46 to improve the model performance and dataset diversity. Second, almost no empirical data is available in the THz region. First-principles MD simulations with the reactive force fields have been recently shown to accurately estimate ϵ values at THz frequencies using amorphous phases of polymers47. Such method can successfully overcome the problem of ϵ overestimation introduced because of the unrealistically higher densities of crystalline polymer models used in the DFPT method. There is a great opportunity to incorporate theoretical data to fill the empty THz region of our dataset. Third, new polymer features can be included at the morphological-level, e.g., molecular weights, cross-link and torsion angles, to represent more complicated polymer chemical space. Also, more advanced feature reduction methods can be developed to replace the present linear LASSO method.

Methods

Dataset

The experimental ϵ of 738 polymers, measured at room temperature, under dry conditions and at 9 frequency values, i.e., 60, 102, 103, 104, 105, 106, 107, 109, and 1015 Hz, were considered in this work. These values were taken from refs. 9,19,21,33,35,36,37,38,39,40,41,42. The ϵ measurements within the frequency range of 60–109 Hz is commonly made using the impedance analyzer, the precision inductance, and capacitance and resistance (LCR) meter18,42. ϵ values at 1015 Hz were obtained by taking the square of the experimental refractive index measured using refractometers. Since experimental conditions significantly impact the measured ϵ, we collected the data only when the measurements were made at room temperature (295 ± 5 K) and under dry conditions (with relative humidity <1%). We note that it is almost impossible to find consistent sample qualities across the literature, with the common variations observed in sample thickness and different order of polymer crystallinity. While such uncertainties are unavoidable in experimental datasets, we believe they are acceptable to train reliable ML models. For cases where multiple data-points were available we used the average ϵ value.

Our developed ML model was used to make prediction for a completely unseen dataset of roughly 11,000 homo-polymers that have previously been synthesized and reported (but for which no dielectric characterization has been done). This dataset is substantially diverse, containing numerous polymers classes, e.g., polyolefins, polyimides, polycuratedamides, polyvinyls, polyethers, polyesters, polydienes, polyoxides, and polycarbonates, but not more complex polymers such as copolymers, polymer blends, as well as ladder, cross-linked, and metal-containing polymers. Because of the evidence of past synthetic work, polymer candidates identified for specific applications from this candidate list using our model are expected to have good potential to be synthesized (again) and tested. This large dataset, which contains polymer identities, names/labels, and/or monomer representations, was collected from various available sources, including published articles, handbooks, and online repositories7,21,32,33,34.

Feature engineering

To build accurate and reliable ML models, it is important to include relevant features that numerically represent materials and collectively capture the trends in ϵ values across wide frequency range and across varying polymer chemistry. Our polymer fingerprinting scheme is based on a pre-defined list of possible components covering various length scales, including (1) atomic-level fragments, (2) block-level fragments, and (3) chain-level, i.e., extended features that capture higher level morphological information in polymers. The atomic-level fragments are specified by the generic label “AiBjCk”, representing an i-fold coordinated A atom, a j-fold coordinated B atom, and a K-fold coordinated C atom, connected in the specified order. For example, N3-C3-C4 represents a threefold coordinated N, a threefold coordinated carbon and a fourfold coordinated carbon. The block-level fingerprint components track the presence of 363 pre-defined building blocks that frequently occur in conventional polymers with some representative examples being C6H6, C=O, CH2, and CF2. More importantly, a series of triplet-blocks were defined to represent the specific structural arrangements of functional groups, e.g., CH2CH2CF2 and CH2CF2CH2. The occurrence of each block in the polymer repeat unit (monomer) normalized by the number of atoms (of the monomer) is used as a block-level fingerprint component. The chain-level features capture information at the highest length scale, including quantitative structure-property relationship (QSPR) and morphological features. The QSPR features, e.g., van der Waals surface area, topological polar surface area, and the fraction of rotatable bonds, were generated using the RDKit library. The morphological features, e.g., the length of the longest/shortest side chains with/without rings and the shortest topological distance between rings, were developed by us. Using this fingerprinting scheme, 155 atomic-level, 197 block-level and 59 chain-level features were generated for each of the 738 polymers, leading to a total of 411 chemical features for each polymer. Additionally, the frequency in log-scale (log F) was incorporated as a feature in the ML model development process, resulting in a total of 412 features. As per standard ML practices, all features were scaled from 0 to 1 during the model training.

The least absolute shrinkage and selection operator (LASSO) method was used to retain the relevant features by optimizing the regularization term to achieve the highest R2. Subsequently, the remaining features with non-zero coefficients were used to construct the ML models. For the LASSO dimensionality reduction scheme, all 412-dimensional features and the entire ϵ dataset was used. Furthermore, the group-shuffle-split and K-fold libraries implemented in sklearn python package were respectively used for the polymer-types-split and the data-points-split approach. The resulting number of feature (NX) is summarized in Table 1, including the frequency feature internally selected by the LASSO method.

To visualize the chemical diversity of the training (738 polymers) and the unseen (11,000 polymers) datasets adopted here, PCA was performed on the complete chemical features of these two datasets (706 features in total), excluding the frequency feature. The first two (PC1 and PC2) components are shown in Fig. 2b and used to analysis the similarity of two datasets with the agglomerative hierarchical clustering method. As illustrated in Supplementary Fig. 1, there are 90% shared chemical space of two datasets, revealing that the training dataset fairly covers the chemical space of the unseen dataset.

Gaussian process regression

We used the Gaussian process regression (GPR) with the radial basis function (RBF) kernel to train the ML models. In this case, the co-variance function between two materials with features x and \({\boldsymbol{x}}^{\prime}\) is given by

$$k({\boldsymbol{x}},{\boldsymbol{x}}^{\prime} )={\sigma }_{f}\exp \left(-\frac{1}{2{\sigma }_{l}^{2}}| | {\boldsymbol{x}}-{\boldsymbol{x}}^{\prime} | {| }^{2}\right)+{\sigma }_{n}^{2}.$$
(1)

Here, three hyperparameters σf, σl, and σn represent the variance, the length-scale parameter and the expected noise in the data, respectively. These were determined during the model training by maximizing the log-likelihood estimate. Further, as shown in Table 1, K-fold and group-shuffle-split methods with fivefold cross-validation were adopted in the polymer-types-split and the data-points-split models to avoid overfitting, respectively. The root mean square error (RMSE) and the coefficient of determination (R2) were used to evaluate the performance of the ML models. Further, learning curves (Fig. 3) were generated by varying the size of the training and the test sets to estimate the prediction errors on unseen data. Model performance (RMSE) was evaluated by averaging over 50 statistical runs with random training and test splits.