Interface enhanced functionalities in oxide superlattices under mechanical and electric boundary conditions

Abstract

In recent years, the inverse design of artificial materials, in the format of thin-films and superlattices, has been an active sub-field in material science. From a joint effort from both experiment and theory, scientists are searching for new engineering methods or design rules so that the materials can be custom designed with desired functionalities in theory before the materials are actually synthesized by epitaxial growth technique in laboratory. In this article, we provide a short summary of the recently proposed epitaxial strain and interface design approaches for the functional artificial oxide heterostructures. The underlying physical mechanism enabling the enhanced functional properties, such as ferroelectricity and multiferroics, are briefly reviewed. In particular, focused discussions are made on the proper treatments of both mechanical and electric boundary conditions when the oxide thin-films and superlattices are theoretically modeled by first-principles computer simulations.

Introduction

Last few decades have witnessed the explosive growth of new materials^{1,2,3,4,5,6,7,8}. A large portion of recently synthesized materials are contributed by the so-called artificial materials which cannot naturally exist. Such a significant progress has been facilitated by the advent and the maturity of modern thin-film technology⁹, for example, the pulsed laser deposition¹⁰ and the molecular beam epitaxy¹¹. Based on these advanced epitaxial techniques, it has become a routine work to make oxide superlattices or heterostructures in the laboratories. In particular, in these quasi one-dimensional materials of superlattices, sharp interfaces are formed which are defined by the atomic-level flat surface terraces bringing two distinct parent oxides into one artificial material⁸.

Equipped with the advanced synthesis techniques, scientists are now focusing on searching for materials with target properties. In practice, the functional properties include large ferroelectric (FE)¹² and ferromagnetic (FM) moments, piezoelectric¹², elastic, dielectric responses¹³, magnetoelectric, and spin-structural couplings^{7,14,15,16,17}, as well as tunable optical bandgap¹⁸. Very often, multifunctional properties are desired to be possessed in a single material for device applications. However, it implies an inverse design of materials, which poses a major challenge by itself. The difficulty lies at the fact that one need to search within the greatly expanded class of artificial materials. In oxide superlattice, one unique interface is formed by any two parent oxides. While, once the superlattices at the nanoscale are concerned, the complexity rapidly grows when one is facing almost infinite ways to select the particular interfaces and later, to arrange them into the superlattices¹⁹. The situation is even worse when one is provided by many choices of substrates in coherent growths of the heterostructures.

Clearly, efficient design principles are critically needed in order to guide the experimental exploration before the superlattice are actually grown in laboratory. In the past years, important inverse design principles have been proposed in theory^13,17,20 and later been verified in experiments^1,7,21,22,23. On the one hand, the motif of interface introduces an extra tuning knob to modify the symmetry of the heterostructures. The interfaces can naturally break the compositional inversion symmetry and generate the self-poling effects in the superlattice, which are used to induce or enhance the FE polarization and dielectric responses²⁴. On the other hand, the interface itself plays a key role to determine the functionalities of the superlattice. Different physical properties of bulk oxides strongly interact with each other, and the interface is at the forefront of the battle field where the reconstructions can lead to nontrivial physical effects. In the sparse interface limit, the interfaces are spread out and the overall properties of the superlattice are mainly governed by the long-range electrostatic interactions mediated by interfaces which is known as the electrostatic coupling effect and has been widely applied^24,25. However, in the dense interface limit, the short-range interactions will be decisive. The inversion symmetry can break right at the interface by two different types of structural distortions^26,27,28. Moreover, large electronic and structural reconstructions can occur at the interfaces. In some cases, the interfacial reconstructions can be utilized to stabilize some highly functional phases that are metastable in bulk materials⁸.

Ab initio calculations are actively involved throughout the arrival of interface design mechanism. Based on density functional theory (DFT)²⁹, first-principles calculations not only allow the initial quick validation of conceived design methods, but also give important qualitative or even quantitative inputs for future experiments. DFT can be dated back to 1960s, the theory rigorously projects the formidable many interacting electrons in condensed matter system onto an equivalent noninteracting one electron system. The successful application of DFT relies on the adopted level of exchange correlation (XC) functional approximations, which effectively describes the many-body effect of electrons. While the local density approximation (LDA)^30,31 underestimates the structural distortion, the generalized gradient approximation (GGA)³² suffers from the so-called super-tetragonality error and often overestimates the structure distortions³³. By satisfying all seventeen known exact constraints on semi-local XC functionals, the recently developed strongly constrained and appropriately normed (SCAN) meta-GGA functional^34,35 improves over the traditional LDA/GGA for structural, electric, and energetic properties of diversely bonded FE and multiferroic materials. The more expensive ab initio calculation based on the random phase approximation (RPA) has been only occasionally applied to study perovskite³⁶. The capability of DFT to describe functional materials has been greatly enhanced along with the development of electronic structure theory, such as modern theory of polarization, density functional perturbation theory (DFPT)^37,38,39,40, etc. The functionalities including intrinsic properties such as FE and FM moment which can be computed by standard DFT, or responses to various stimuli such as piezoelectric and dielectric constants calculable by DFPT.

While modeling the oxide superlattices, extra care should be taken on the mechanical and the electric boundary conditions. The mechanical boundary condition mainly refers to the epitaxial strain applied by the substrates. In the superlattice, the lattice constant of the substrate is usually different from that of bulk oxides⁴¹. As a result, either a compressive or a tensile strain is applied. The applied strain can be strongly coupled to the polar phonon mode^15,42,43 or the magnetic exchange interaction. Such couplings have been applied to engineer functional properties such as FE and FM in multiferroics^7,15,17. As far as the electric boundary condition is concerned, either a fixed electric (E) field or a fixed electric displacement (D) field is applied, which correspond to the close-circuit or the open-circuit condition in device applications^19,44,45,46. Furthermore, the correct treatment of electric boundary condition is also the key to describe the localized interface effect in insulating oxide superlattice. Such interface information can be extracted and used later to construct new superlattice for an inverse design purpose. In the above, throughout the superlattice, the D-field instead of E-field should be the uniform parameter due to charge continuity principle.

In this article, we firstly review the theoretical techniques in modeling the oxide thin-films and superlattices in section of “First-principles modeling and computational methods”, in which the recent methodology development enabling the calculations of insulating nonlinear materials under applied electric field and applied electric displacement field are reviewed. In the section of “Induced or enhanced functional properties under epitaxial strain”, we briefly describe the enhanced functionalities discovered by mismatch strains and the underlying physics. In the section of “Interface induced functional FE and multiferroic properties”, we review the four recently proposed interface design mechanism, which are the inversion symmetry breaking in tricolor superlattice in the section of “Compositional inversion symmetry breaking”, the electrostatic coupling mechanism in the section of “Electrostatic coupling effect via interfaces”, hybrid improper ferroelectricity in oxide heterostructure in the section of “Hybrid improper ferroelectricity”, and interface stabilized BiFeO₃-like structures in the section of “Interfacial reconstructions of structural instabilities”. The physical principles behind each of the above design rules are explained in detail.

First-principles modeling and computational methods

Mechanical boundary condition: epitaxial strain

Functional properties of oxide superlattices, such as FM^47,48, superconductivity^49,50, tunable optical band gap^18,51, FE^9,41,52,53, piezoelectricity^9,54,55, and multiferroicity^56,57,58,59, can be effectively optimized or even induced by the mechanical boundary conditions via the mismatch between bulk materials and the substrates on which the thin-films are grown. In general, the epitaxial strain η is defined as η = (a − a₀)/a₀, where a and a₀ are the in-plane lattice constants of the substrate and the bulk materials to be strained, respectively. More subtlety, the epitaxial strains can be further categorized as homogeneous or anisotropic bi-axial strain⁶⁰ if the two in-plane lattice constants are strained by same or different amounts, respectively. Over the last 2 decades, a vast number of perovskites have been successfully utilized as substrates in the synthesis of artificial thin-films^{41,61,62,63,64}. With such a broad range of lattice constants as shown in Fig. 1, the mismatch strain can be experimentally adjusted within [−3%, 3%] for many perovskites⁶⁴. However, in DFT calculations, the atomic modeling of such strained thin-films is rather straightforward, unlike the cases in the experiment. In order to mimic the coherent thin-film growth, the first-principles calculations should be performed by minimizing the total energy with the in-plane lattice constants clamped to be the same as the selected substrates, while all the other degrees of freedom including force on each atom as well as the stress along the growth direction should be fully relaxed. For materials with magnetic ordering, the modeling is slightly more complicated since the proper supercell size should be chosen in such a way that the particular type of antiferromagnetic (AFM) ordering^65,66 or the noncollinear spin configuration^67,68 are properly accommodated. However, it should be kept in mind that the coherent growth can be only achieved with the thickness below 10–20 nm⁴⁶. If it is above critical thickness, the strain energy would be relaxed to their natural bulk values^60,64, sometimes accompanied by the development of threading dislocations^46,64.

Fig. 1: Typical substrates that are used in the growth of perovskite oxide thin-film and superlattice.

Pseudo-tetragonal or pseudo-cubic lattice parameters (Å) for typical perovskite substrates, which include LuAlO₃⁶⁹, YAlO₃^63,70, PrSrAlO₄⁶³, LaSrAlO₄^63,71, LaAlO₃^63,72, LaSrGaO₄^63,73, NdGaO₃^74,75, LaGaO₃^74,76, SrTiO₃^63,74, KTaO₃^63,74, RScO₃^61,74,77, and RLuO₃^78,79 (R represents the rare-earth element).

Electric boundary condition: fixed applied electric field

For electronic device applications under short-circuit conditions⁴⁴, the applied external electric field is an important electric boundary condition for perovskite superlattices. Under vanishing applied electric field E = 0, the spontaneous polarization (P) is a key property of FE material, which can now be routinely computed based on the modern theory of polarization^80,81. The ionic contribution of polarization is straightforward, however, the electronic contribution should be computed via the Berry phase formulation given by $\varphi _n = {\mathrm{Im}}\left[ {{\int} {{\mathrm{d}}{\boldsymbol{k}} < u_{n{\boldsymbol{k}}}|\partial _k|u_{n{\boldsymbol{k}}} > } } \right]$, in which the Bloch-like wavefunctions u_nk from each occupied electronic band with index n over the Brillouin zone (k) are generated by the DFT ground state minimization⁸¹. In practice, the parallel transportation gauge is often adopted in the numerical implementation of the Berry phase calculation⁸¹. Moreover, important functional properties emerge in response to the applied finite electric fields in oxide superlattices, such as piezoelectricity or magnetoelectric couplings, in which the strong nonlinear effects were observed⁸². In order to properly treat the nonlinear responses, it is necessary to compute the electronic structure under the applied electric fields, which turned out to be nontrivial within the DFT framework^83,84,85,86. The difficulty lies at the fact that the macroscopic electric field results in a change of the electric potential under a lattice vector translation, which breaks down the periodicity underlying Bloch’s theorem and changes the qualitative character of the energy eigenstate⁸⁷. In addition, an external electric field tilts the conduction and valence bands in real space. As a result, it always trends to lower the energy of a system with bandgap by transferring electrons from valence band of one region to a conduction band of another region with the distance, which is known as the Zener tunneling effect^87,88. However, it was realized that the density matrix ρ(r, r′) and other local quantities remain periodic under translation by a vector R in the polarized ground state when the Zener tunneling is not significant under small applied electric fields. By imposing the periodicity in ρ(r, r′), Souza Íñguez, and Vanderbilt⁸⁶ proposed a practical approach to compute the “long-lived” electronic states under applied electric fields by minimizing the electric enthalpy functional $F({\boldsymbol{E}}) = E_{{\mathrm{KS}}}\left( {u_{n{\boldsymbol{k}}}} \right) - {\boldsymbol{E}} \cdot {\boldsymbol{P}}$. In the above, $E_{{\mathrm{KS}}}(u_{n{\boldsymbol{k}}})$ is the ordinary Kohn–Sham energy per unit volume under zero electric field, u_nk is the periodic part of Bloch function, and the macroscopic polarization P is composed by the ionic and electronic (Berry phase) contributions, respectively. To avoid a runaway solution associated with the Zener tunneling, a sparser k-space mesh should be chosen with $2\pi /\Delta k < E_g/|{\boldsymbol{E}}|$ in the practice calculation. As such, this method provides a first-principles computational framework to investigate many functional properties of materials under external electric fields.

Electric boundary condition: fixed applied electric displacement field

Fixed electric displacement (D) field is another important electric boundary condition in which the functional materials are often studied by first-principles calculations. The importance is mainly due to two factors. One is that the DFT calculation under constrained D field is directly corresponding to the open circuit condition for device applications^44,89. Another factor is that first-principles studies under this electric boundary condition provides a powerful theoretical tool to probe the metastable states and to utilize the locality of FE oxide thin-films and superlattices. Unlike the paraelectric (PE) systems, the FE materials are strongly nonlinear materials. The equation of states, such as the electric polarization and electric enthalpy, are multivalued as a function of applied electric field. Therefore, one could only obtain the stable structure corresponding to the global minimum of electric enthalpy functional (see discussion in the section of “Electric boundary condition: fixed applied electric field”) while the metastable and unstable states of FE materials are not accessible by the same approach. Fortunately, the above difficulty can be overcome by adopting the constrained D field in DFT calculations, in which the energy landscape U(D) becomes a single-valued function of D field allowing the complete probing of energy landscape including both stable and metastable regions^90,91,92. Moreover, the DFT calculations under constrained D-field are particularly useful in the modeling and interface design rules for FE oxide superlattices. In insulating FE perovskite superlattices, both local polarization and local electric field vary in different layers^44,89,93. However, the charge continuity principle (∇·D = 0) ensures that the electric displacement vector D is continuous along the growth direction, which is the [001] direction by convention. Therefore, the electric displacement field should be taken as the fundamental parameter that is uniform along the [001] direction, which has been conceptually proven for superlattice with continuous^19,44 or discontinuous polarity^89,94. Furthermore, the force-constant matrix of the insulating perovskite superlattice becomes short-ranged under constrained D-field. The locality principle enables one to extract the interface and bulk properties separately from the superlattices, which can be applied to inversely design perovskite superlattices of desired functional properties. Stengel et al.⁴⁴ have developed the fixed D-field methodology within the DFT framework. It is achieved by minimizing the energy functional, $U({\boldsymbol{D}},\nu ) = E_{{\mathrm{KS}}}(\nu ) + \frac{\Omega }{{8\pi }}[{\boldsymbol{D}} - 4\pi P(\nu )]^2$ where Ω is the cell volume, E_KS is the ordinary zero-field Kohn–Sham energy functional, and ν are the internal (both ionic and electronic) coordinates.

As one of the first applications, the DFT calculations with fixed D-fields have been applied by Hong and Vanderbilt to successfully probe the complex energy landscape and equation of states of PbTiO₃ (PTO)^90,95. The energy enthalpies U(D) and F(E) along [001], [110], and [111] directions are computed as functions of electric displacement field D and applied electric field E in Fig. 2a, b, respectively. Clearly, it can be seen that energy functional U(D) is a single-value function of D while energy functional F(E) is a multivalued function of E. Therefore, the DFT calculations with fixed D-fields can obtain not only the FE ground states with tetragonal symmetry as denoted by point 3 and 5 in Fig. 2a–c, but also the metastable states under applied (coercive) electric fields at point 2 and 4 as well as the unstable state at point 1 representing the hypothetical centrosymmetric phase of PTO with the P4/mmm space group symmetry. In stark contrast, DFT calculations with fixed-E electric boundary condition can only solve the equations of state for the stable and part of metastable regions; while the region 4→1→2 as shown in Fig. 2c, which has the negative dielectric permittivity χ = ∂P/∂E is unstable with respective to the applied electric fields and therefore it is inaccessible to the DFT calculation with fixed-E electric boundary condition. The authors also studied the structural stabilities of PTO as functions of D-fields⁹⁰ by exploring the contour energy surface U(D) of PTO with respect to constrained D-fields in both [100] and [010] directions. As shown in Fig. 2d, the four energy minima along ±[001] and ±[010] directions represent four of the six tetragonal (T) structures which are degenerate at DFT ground state; the four saddle points along [110] axis and the corresponding symmetry-equivalent directions depict the orthorhombic (O) phases. The energy barrier between T and O phases is significantly smaller than that between the T phase and the centrosymmetric (paraelectric) phase at the origin. It indicates that it will be much easier to switch the electric polarization in a tetragonal PTO along the path connecting state T→O→T than the path passing through the origin as shown in Fig. 2d. The contour energy surface U(D) as functions of constrained D-fields along [110] and [001] direction is also computed as plotted in Fig. 2e. In addition to the global energy minima and local minima corresponding to the T and O phases, four extra saddle points are also identified which correspond to the rhombohedral (R) phase with the polarization along [111] or symmetry-equivalent directions. Similarly, polarization rotation from tetragonal phase to rhombohedral phase via T→R→O path is found to be lower in energy compared to a direct switching through a paraelectric state at the origin. The small barriers connecting these minima with different orientations of polarization play a crucial role for the easy polarization rotation in PTO originating the large piezoelectric responses which has been predicted by previous theoretical studies^96,97.

Fig. 2: Energies computed by density functional theory in one typical ferroelectric oxide under constrained electric fields or constrained electric displacement fields.

In PbTiO₃ a energy U(D) as a function of electric–displacement (D) and b energy F(ξ) as a function of electric-field (ξ) of PTO along [001], [110], and [111] directions. c Electric polarization of a function of electric field P(ξ) along [001], [110], or [111] directions. d Electric Contour energy profile U(D) for D in the plane along the [100] and [010] directions. e Contour energy U(D) for D constrained in the plane determined by the [110] and [001] directions. All variables are in atomic units. In d and e, the minimum at T and saddle point at O represent tetragonal and orthorhombic states, respectively. Reproduced with permission from ref. ⁹⁰. Copyright [2011] {American Physical Society}.

Besides the ability to probe complex energy profiles of FE materials, the DFT calculations with fixed-D electric fields also provide a powerful scheme to explore the locality principles, which can be applied in the inverse design of oxide superlattices with desired functional properties. The perturbation in the electronic structure by the defects obeys the nearsightedness in the absence of long-range Coulomb interaction principle as shown by Prodan and Kohn⁹⁸. In this scenario, the interface can be considered as an effective defect and should only affect the properties of oxide superlattice in a well localized region, where else is determined by its bulk property. The fixed electric displacement field provides such a framework in demonstrating such locality principle, in which the long-range electrostatic interaction can be described by the uniform D field. In several extensive studies, it has been shown that the both the perturbed electric and structural properties by the interfaces are indeed well localized^19,99. The locality in polarization profile near the interfaces has been demonstrated in perovskite superlattice facilitated by the layer polarization analysis^100,101. Suppose the polarization is along the same direction of superlattice growth direction z or [001], the layer polarization of each AO (or BO₂) charge neutral layer with index j is defined by^19,101 $P_j = \frac{1}{S}\mathop {\sum}\nolimits_{\tau \in j} {Q_\tau } R_\tau - \frac{{2e}}{S}\mathop {\sum}\nolimits_{m \in j} {\bar z_m}$. Note that the sum is confined to the ionic and Wannier centers belonging to layer j. τ denotes ion cores with charge Q_τ located at R_τ and m denotes Wannier centers with charge −2e located at $\bar z_m$ and S is the in-plane base area. The layer polarization p_j has units of dipole moment per unit area, and satisfies the sum rule, i.e., the total polarization is exactly equal to the sum of layer polarizations $p_j = c^{ - 1}\mathop {\sum}\nolimits_j {p_j}$ where c = V/S is the supercell lattice constant along z direction. The locality principle was evidenced by the fact that layer polarization as a function of D field P_j (D) strongly depends on the local compositional environment. More specifically as shown in the Fig. 3, the BaO layer polarizations in SrTiO₃(STO)/CaTiO₃(CTO)/BaTiO₃(BTO) superlattices are mainly depended on the characteristic of the layer itself and its nearest layer chemical environment which are only weakly perturbed by the chemical environment of next nearest neighbors. Later, Swartz and Wu⁹⁹ have further shown that the local lattice deformation in terms of the layer height h_j (D), defined by $(\bar Z_{j + 1} - \bar Z_{j - 1})/2$, where $\bar Z_j$ is the average of z-coordinate ([001]) of all ions belonging to layer j basically shows the similar localized property as shown in Fig. 4. Later studies showed that other structural distortion such as the oxygen octahedral rotations and tilts^8,102 essentially follow the similar trend as described above. Such a locality principle has been utilized to build truncated cluster expansion model in order to accurately extract the electric and structural properties of interfaces as a function of D field. The above model is able to predict the electric, piezoelectric, and dielectric responses in superlattices with arbitrary sequences with an accuracy comparable to direct DFT calculation. Such a method paves the way to efficiently design oxide superlattice with desired functional properties.

Fig. 3: Localized electric property for a layer in a perovskite superlattices.

a Layer polarizations of BaO planes (relative to bulk BaTiO₃) as functions of electric displacement field (D) fields. b Layer polarizations of TiO₂ planes (relative to the average of layer polarization of TiO₂ planes in bulk BaTiO₃ and SrTiO₃) as functions of electric displacement field (D) fields. C, S, B, and T represent CaO, SrO, BaO, and TiO₂ layers, respectively. Results from first-principles calculations and model predictions are denoted by symbols and solid lines respectively. Reproduced with permission from ref. ¹⁹. Copyright [2008] {American Physical Society}.

Fig. 4: Localized lattice deformation for a layer in a perovskite superlattices.

Layer heights of TiO₂ in various chemical environments in PbTiO₃/SrTiO₃ superlattices. P, S, and T denote PbO, SrO, and TiO₂ layers in the superlattices. Symbols and solid lines represent the results of first-principles calculations and model predictions, respectively. Reproduced with permission from ref. ⁹⁹. Copyright [2012] {American Physical Society}.

Induced or enhanced functional properties under epitaxial strain

Ferroelectricity in thin films under epitaxial strain

In terms of lattice dynamics, the proper FE can be described by the soft mode picture^{103,104,105,106}. An unstable polar phonon mode at the Brillouin zone center freezes below the Curie temperature giving rise to the broken inversion symmetry with a lower symmetry. In conventional perovskite FE materials, such as BTO, PTO, and KNbO₃ (KNO)¹⁰⁶, the development of FE mode represents a delicate balance of Coulombic interactions. Ghosez et al.¹⁰⁷ decomposed the interatomic forces into the contributions from long-range dipole–dipole interaction and those from short-range repulsive interaction. The former one originates from long-range electrostatic interaction and favors a polar distortion, while the latter is attributed to the repulsions between electrons on adjacent ions favoring the nonpolar centrosymmetric phase. Interestingly, these two interactions vary rather differently as a function of interatomic distance r. It was argued that¹⁰⁸ the short-range repulsion forces increase more rapidly with the r⁻ⁿ dependence than the r⁻³ dependent long-range dipole–dipole counterpart while the interatomic distance r decreases under applied pressure, where n is a large number around 10¹⁰⁸. This theory is consistent with the recent DFT calculation, in which it was found that FE disappeared in bulk BTO with the decreased interatomic distance when cell volume became smaller under applied external pressure^96,107. This scenario is further evidenced by more recent first-principles calculations in which the short-range interatomic interaction was replaced by bulk BTO value, while the long-range dipole–dipole interaction is intact under applied high pressure. The series of calculations indicated that the polar instability becomes stronger due to the artificially suppressed short-range interatomic interactions¹⁰⁷. Therefore, adjustment of the interatomic distance is an effective way in tuning the FE. It could be achieved by the epitaxial strain in thin-films and superlattices based on modern thin film technology.

The application of epitaxial strain has been widely adopted to modulate the FE instability in perovskite thin films. As one of the early applications, Choi et al.¹⁰⁹ have grown BTO thin films on substrates of GdScO₃ and DyScO₃, which impose a compressive strain on BTO about −1.0% and −1.7%, respectively. As shown in Fig. 5, the compressive in-plane strain would elongate the lattice constant in c-axis, i.e., [001] direction. Under such mechanical boundary condition, the long-range dipole–dipole interaction is preferred relative to the short-range repulsion. As a result, the FE properties in these films are largely enhanced evidenced by the measured remnant polarization P_r of ~50 μC/cm² and ~70 μC/cm² on GdScO₃ and DyScO₃ substrate, respectively¹⁰⁹, which are almost two or three times the value of ~26 μC/cm² in natural bulk BTO. The enhanced FE in these compressed BTO thin-films are further supported by the enhanced FE structural phase transition temperature T_c, which were measured to be ~400 °C on GdScO₃ and ~540 °C¹⁰⁹ on DyScO₃, respectively. These results demonstrated a significant increase in the structural phase transition temperature of ~130 °C in bulk BTO. Not only it could be used to enhance FE, the applied epitaxial strain can be even used to induce FE in perovskite thin films that is PE in natural bulk format. For example, Zhang et al.¹¹⁰ theoretically explored the induced FE under both compressive and tensile strains in BaZrO₃ (BZO), which has a centrosymmetric cubic structure in unstrained bulk state. Their first-principles calculations suggested that BZO can develop out-of-plane [001] polarization comparable to that of BTO under compressive strain slightly larger than −2%; when the applied compressive strain is further increased to −4%, the induced FE polarization along [001] became as lager as 34 μC/cm², which is even larger than that of bulk BTO at room temperature. Under the tensile strain, their calculations further showed that an in-plane FE can develop. This is due to the elongated a–b axes that promotes the long-range dipole–dipole interaction within the a–b plane¹¹⁰.

Fig. 5: Functional properties of perovskite as ferroelectricity and its responses to external stimuli.

Schematic plots show the epitaxial strain effects on structure, magnetic, and electric properties of perovskite compounds.

In addition to its tunability on the magnitude of FE polarization, it was found that the orientation of polarization can also be effectively controlled as a function of the applied epitaxial strains^111,112,113. Diéguez et al.^111,112 investigated the polar properties of several bulk perovskite oxides, including BTO, BZO, PTO, and KNbO₃, etc. under epitaxial in-plane biaxial strains. The results are shown in Fig. 6. For all the structures considered, under sufficiently high compressive strain, the polarization always points towards the direction normal to the a–b plane. Furthermore, applied tensile strain tends to develop a component of polarization within the a–b plane. Due to the different FE directions that compressive and tensile strains promote, the resulting polarization vector is effectively rotated from [001] direction into in-plane direction when the epitaxial strain is gradually increased from compressive to tensile regions as shown in Fig. 6.

Fig. 6: Tunable crystal structure in perovskites by external stress.

Phase diagram in BaTiO₃, PbTiO₃, KNbO₃, and BaZrO₃ as functions of external stress and mismatch strain. a, aa, r, c, and p phases represent the perovskite structures with polarizations directed along [u00], [uu0], [uuv], [00v], and [000] directions. Reproduced with permission from ref. ¹¹¹. Copyright [2005] {American Physical Society}.

In the last section, we have mainly focused on the dependence of FE distortion on the applied epitaxial strains only. In those examples, applying epitaxial strains to thin-film perovskites is shown to be an efficient way to tune polarization in both the magnitude and the orientation. However, in the reality, other important structural distortions such as the antiferrodistortive (AFD) modes that associate with the oxygen octahedral rotations and tilts^{114,115,116,117} can coexist with the FE distortion. Emergent phenomena appear when the complex energy landscape is nontrivially modified since the various structural distortions can have distinct dependence on the applied epitaxial strain^114,118,119. For example, the lattice dynamics based on first-principles calculations showed that cubic STO is unstable under both polar and AFD distortions^114,118. However, STO is only PE at all temperatures. The structure of STO is cubic at room temperature and transforms directly into tetragonal I4/mcm symmetry incorporating AFD distortion associated with oxygen octahedral rotation around [001] axis below 105 K^120,121. The absence of FE was attributed to the quantum fluctuation that suppresses the FE phase¹²². Furthermore, Monte-Carlo simulation studied by Zhong and Vanderbilt¹²³ showed that the polar distortion is further suppressed by the competition between AFD and FE instabilities. Nonetheless, the weak FE instability of bulk STO is very sensitive to external stimuli too. Based on Landau–Ginsburg–Devonshire theory, Pertsev et al.¹²⁴ investigated the effect of epitaxial strain on the structural properties of STO thin-film. The density of Helmholtz free energy F of STO was expanded in terms of order parameters and their couplings which included misfit strain, FE and AFD structural distortions. In their work, single-domain thermodynamic equations of state in STO films under various strain and temperature conditions were obtained by searching over all minima of F with respect to the components of both the FE and AFD distortions. Furthermore, the temperature dependent second-order coefficients were fitted by the Barrett formula¹²⁵ and then extrapolated to higher temperatures. From the determined most energetically favorable phases, it was shown that STO films can become FE under certain applied strain as temperature is reduced from room temperature. The induced FE is due to the coupling between the polarization and strain, which favors the polar distortion along out-of-plane (in-plane) direction under applied compressive (tensile) strain, respectively. These predictions using phenomenological model were also confirmed by first-principles calculations. Antons et al.¹²⁶ studied the effects of the in-plane epitaxial strains on the dielectric response and FE of STO films by DFT calculations. Under applied compressive (tensile) strains which are larger than critical values, the STO films were found to transform into tetragonal (orthorhombic) phase with polarization developed along [001] ([110]) direction. Experimentally, Yamada et al.¹²⁷ examined the in-plane and out-of-plane FE in a compressively strained STO film by reciprocal permittivity via infrared reflection spectroscopy. Based on spectral analysis, it was concluded that the in-plane polar mode softens very slowly; while the spectral signal clearly indicated that the FE structural phase transition associated with an out-of-plane polarization appears below ~150 K, which is consistent with theoretical predictions¹²⁶.

Let us take a look at another example. Ground state of CTO has a nonpolar orthorhombic structure with Pbnm symmetry¹¹⁹, which is transformed from the cubic structure (Pm3̄m) through mode combinations of both M₃⁺ and R₄⁺ associated with oxygen octahedral rotations around [110] and [001] directions, respectively. Besides these AFD structural instabilities, first-principles calculations also identified that cubic CTO also has a strong zone center polar instability (Γ₄⁻ mode)^102,128,129 as evidenced by the imaginary frequency around ~120i cm^−1 129. However, the development of FE distortion is inhibited in the ground state of CTO due to the strong competition between antipolar distortion (X₅⁺ mode) and polar distortion (Γ₄⁻ mode)²⁸. Eklund et al.¹¹⁵ studied structural properties of CTO under epitaxial strain by DFT calculations. The polar structures, with space group symmetries of Pmn2₁ (polarization along a) and Pmc2₁ (polarization along b), were found to be stabilized under tensile strains as shown in Fig. 7. In particular, the Pmn2₁ structure can develop a large polarization of 46 μC/cm² under 4% tensile strain. Further analysis reveals that the oxygen octahedral rotations (M₃⁺ and R₄⁺ modes) as well as the antipolar distortion (X₅⁺ mode) are only little affected by the applied strains. Therefore, the induced FE in strained CTO films should mostly originate from the coupling between strain and polar instability as described above.

Fig. 7: Structural phase transition under applied epitaxial strain in CaTiO₃ determined by first-principles calculations.

The total DFT ground state energies of strained bulk CaTiO₃ from first-principles calculations as a function of applied misfit strain. Reproduced with permission from ref. ¹¹⁵. Copyright [2009] {American Physical Society}.

Multiferroic properties under epitaxial strain via spin-phonon coupling

In transition metal perovskites with open-shell cations on A or B sites, the magnetic exchange interactions are allowed by the f or d electrons. For example, in EuMO₃ (M = Ti, Zr, and Hf) with AFM ground state, the superexchange interactions between neighboring f electrons of the Eu²⁺ cations are mediated through the d electrons of M cations^130,131,132; whereas in AFM perovskites of AMnO₃ (A = Ca, Sr, and Ba), the superexchange among d electrons of Mn⁴⁺ are facilitated by the 2p orbitals of O anions^{42,43,133,134}. The strength of the superexchange interaction is sensitive to the orbital hybridization determined by the bonding geometry^42,43. Therefore, in multiferroic perovskites, the polar distortion that involves the magnetic cations potentially can be strongly coupled to the magnetic exchange interaction therefore spin orderings, which has been now known in the literature as the spin–phonon coupling effect^14,42,43,134. Currently, the design of new multiferroic materials by utilizing spin-phonon coupling is an active field. It is expected that artificial perovskites with AFM-PE ground state can be engineered into functional FM–FE state if the magnetic exchange interactions are sensitive to the low-lying polar mode that can be adjusted by the epitaxial strain.

The strain engineering via spin-phonon coupling was first proposed by Rabe and Fennie theoretically in EuTiO₃¹⁷. At room temperature, EuTiO₃ is PM with a cubic structure of Pm3̄m space group symmetry^135,136. At low temperature, the magnetic moment of Eu cation adopts G-type AFM ordering below the Néel temperature of T_N = 5.5 K¹³⁷. From first-principles calculations, the spin–phonon coupling effect is evidenced by the softening of the TO₁ polar phonon frequency about 7 cm⁻¹ when magnetic ordering is constrained to be FM ordering. The strong spin–phonon coupling is further confirmed by the experimental observation in which the static dielectric constant in EuTiO₃ undergoes significant increases as a function of increasing applied magnetic fields¹³⁷. Its electronic origin is due to that the magnetic exchange interaction via the hybridization of Eu-f and Ti-d electrons are strongly coupled to the polar distortion. According to the theoretical investigations by Birol and Fennie¹³¹, the magnetic ordering in EuTiO₃ is the competing results between the superexchange interaction and indirect exchange interaction which favor AFM and FM orderings, respectively¹³⁸. The former involves the virtual electronic hopping processes between Eu-4f and Ti-3d orbitals, which is sensitive to Eu-f and Ti-d local bonding environment. The latter can be described by two consecutive processes. Firstly, an intra-atomic electron hopping process from 4f to 5d orbital occurs for the same Eu cation, which is barely affected by structural distortion; it is followed by the exchange interaction between two neighboring Eu cations favoring the FM state. Under the polar distortion, the Eu-f and Ti-d hybridization environments are suppressed resulting in decreased superexchange interactions. On the other hand, the indirect exchange interaction favoring FM ordering is mostly determined by the distance between two Eu²⁺ cations only and less sensitive to the polar mode. As a result, polar distortion tends to drive EuTiO₃ from AFM–PE state to FM–FE state. Strain engineering in EuTiO₃ was proposed by Fennie and Rabe¹⁷ based on DFT calculations. Their calculations revealed that the infrared active TO₁ polar phonon mode is strongly coupled with both magnetic ordering and epitaxial strain as described above. When the applied epitaxial strain is larger than 1.25% the ground state of EuTiO₃ strained thin-film will become FM–FE via the spin–phonon coupling effect. By using the same mechanism, they argued that FM–FE state can also be stabilized by appllied magnetic field or electric field, which are estimated to be 1 T and 10⁵ V/cm⁻¹, respectively¹⁷. Later, the predictions were confirmed by experiments for an [001]-oriented EuTiO₃ film grown on DyScO₃ substrates by reactive molecular beam epitaxy technique⁵⁶. The DyScO₃ substrate exerts about +1.1% biaxial strain on EuTiO₃ film, which is close to the theoretically predicted critical strain to reach the FM–FE ground state as shown in Fig. 8. Temperature-dependent second harmonic generation measurements indicated that the EuTiO₃ film exhibits a PE to FE transition at 250 K. The temperature dependence of a magneto-optic Kerr effect shows that the same strained EuTiO₃ has a clear FM hysteresis loop under the Curie temperature of 4.24 K.

Fig. 8: Multiferroic phases induced by epitaxial strain in EuTiO₃.

a Predicted phase diagram of strained EuTiO₃ films with the biaxial strain ranging from −2% to +2%. b, c The ball-and-stick models of bulk EuTiO₃ and epitaxially strained thin-film EuTiO₃ on the DyScO₃ substrate respectively. Reprinted with permission from ref. ⁵⁶. Copyright (2010) Springer Nature.

Despite the above success, the practical application in strained EuTiO₃ films is still limited by the extremely low Néel temperature⁵⁶. The weak magnetic exchange energy is partially due to the fact that f electrons of Eu²⁺ are screened by 5s and 5p electrons in outer shells^130,138. While transition metal oxide perovskite, whose AFM magnetic ordering temperature governed by the superexchange interactions, can have much higher magnetic ordering temperatures, e.g., the Néel temperature in SrMnO₃^15,42 and CaMnO₃¹³⁴ are as high as 260 and 130 K, respectively. In transition metal perovskites, the superexchange interactions involve the d electrons hopping processes between neighboring B-site cations, which are facilitated by the hybridization between cation d and oxygen 2p orbitals. The resulting magnetic ground state prefers the AFM (FM) spin ordering when the B–O–B bond angle is close to 180° (90°), which is the phenomenological rule proposed by Goodenough, Kanamori, and Anderson^139,140,141. First-principles calculations revealed that polar modes in AMnO₃, such as the Slater mode in SrMnO₃, have a large projection on the B–O–B bond, which induced strong spin–phonon coupling effect^42,43,134. Therefore, one can expect that the AFM–PE ground state in many transition metal perovskites can be potentially engineered to be FE–FM state by the epitaxial strain through the spin–phonon coupling. SrMnO₃ is a prototypical transition metal perovskite with large spin–phonon coupling, which was evidenced by the softening of Slater phonon mode from 121 to 109i cm⁻¹ in cubic SrMnO₃ from constrained G-AFM and FM spin orderings. Lee and Rabe¹⁵ theoretically investigated the electronic and magnetic properties in SrMnO₃ films under various applied epitaxial strains. It was found that the tensile strain higher than 1% transforms SrMnO₃ from the PE/G-AFM ground state of Imma symmetry to the FE/G-AFM state of Ima2 symmetry with the in-plane FE polar distortion (Γ₄⁻ [110]). As the applied tensile strain further increases, the Γ₄⁻ [110] polar distortion continues to increase as shown in Fig. 9; meanwhile the magnetic ordering gradually changes from G-AFM to FM. The G-AFM phase with full anti-parallel spins on Mn cations is stable when the tensile strain is less than 2.0%. The C-AFM phase with about one-third parallel spins on Mn cations is energy favorable for the tensile strain range from 2 to 2.8%. The magnetic ordering further transforms to A-AFM at the tensile strain range from 2.8 to 3.4%, with two-third parallel spins on Mn sites. Finally, the FM–FE phase becomes the ground state as the tensile strain is larger than 3.4%. In their studies, SrMnO₃ films can also be driven into FM–FE ground state of I4cm under compressive epitaxial strain as large as −2.9%, in which the FE distortion (Γ₄⁻ [001]) is along out-of-plane direction. Interestingly, no intermediate phase was identified between PE–AFM and FE–FM under the compressive epitaxial strains.

Fig. 9: Multiferroic phases induced by epitaxial strain in SrMnO₃.

The total DFT ground state energies as functions of applied tensile epitaxial strains in SrMnO₃. Reproduced with permission from ref. ¹⁵. Copyright [2010] {American Physical Society}.

Tunable band gap under epitaxial strain

In open shell transition perovskites, the bandgap sometimes is closely associated with the onsite Coulomb interaction U and one-electron bandwidth W spanning the highest-occupied and lowest-unoccupied d orbitals near Fermi energy such as SrCoO₃. Roughly speaking, when U > W, an energy lowered by delocalizing electrons is unable to overcome the Coulomb blockade between neighboring sites, resulting in an insulator with band gap ≈ U − W; while for U < W, system is often found to be metallic^142,143. Comparing to the relatively insensitivity of U on the structural distortion, the bandwidth W is proportional to degree of hybridization of d-orbital at transition metal atom and p-orbital at an adjacent oxygen atom, which is very sensitive to its bond length and angle^43,142,143. Therefore, the applied epitaxial strain offers an opportunity to adjust the bandwidth W as well as the band gap in these transition metal perovskites. In particular, the crystal fields that arises from the electrostatic interaction between 3d and 2p orbitals can be adjusted via the polar distortion which changes the relative displacement between B-site atoms and their surrounding ligands. The subsequently rearranged energy levels can be used to tailor electronic states near Fermi level^144,145,146.

The bandgap tunability in SrCoO₃ has been studied by Lee and Rabe¹⁶ via first-principles calculations. SrCoO₃ has the cubic Pm3̄m symmetry at ground state which is FM below the Curie temperature T_c ~305 K. The FM ordering was found to due to the double exchange interaction that strongly depends on the d–p hybridization, whose strength is maximized for a 180º Co–O–Co bond angle. The strength of the double exchange is decreased in a restricted G-type spin configuration which is accompanied by the development of polar distortion^147,148. At the same time, the zone center polar phonon also undergoes a dramatic softening from FM to G-AFM driven by the strong spin-phonon coupling. Since the electronic structure of SrCoO₃ near the Fermi energy is composed of the Co-3d and O-2p bands¹⁴⁹, the bandwidth is largely affected by a FE distortion induced by the applied epitaxial strain. Considering the fact that the bandwidths of AFM and FM orderings are proportional to t²/U and t, respectively¹⁵⁰, where t is the hopping integral between two orbitals and in general, t is greater than t²/U. Therefore, the bandwidth is also decreased for the magnetic ordering changing from FM to AFM state. As a result, SrCoO₃ tends to have a finite band gap in the AFM state. The above scenario is consistent with the discoveries by first-principles calculations. Lee and Rabe¹⁶ found that the metallic FM–PE SrCoO₃ transforms into insulating G-AFM–FE multiferroic phase when the applied epitaxial compressive and tensile strains are greater than −0.7% and 3.2%, respectively. The origin of metal–insulator transition was proposed to be due to the bandwidth control via strain induced FE distortion as well as the influence from the magnetic ordering. At the phase boundary of −0.7%, its lattice constant shows up a 6.4% jump. Simultaneously polarization jumps from 0 to ~30 μC/cm², and bandgap changes from 0 to 0.23 eV. Varignon et al.¹⁵¹ recently proposed a different approach to tune the band gap by adjusting the electron orbital orderings though the indirect coupling between epitaxial strain and Jahn–Teller distortions. Jahn–Teller distortion is a common structural distortion that occurs in transition metal perovskites¹⁴⁶. In response to the crystal field, the electronic degeneracy is lifted by the elongation or contraction of chemical bonds between the transition metal ion and its surrounding ligands as schematically shown in Fig. 10, which also lowers the energy. The Jahn–Teller distortion itself is nonpolar, therefore it is not directly coupled to the external electric field. Interestingly, the authors reported an indirect Jahn–Teller distortion and epitaxial strain coupling mechanism. It was realized by the anharmonic lattice couplings between polar mode in bulk perovskite with Pb2₁m symmetry and Jahn–Teller distortion. The Pb2₁m symmetry is not common in bulk perovskites, but it can be stabilized via strain engineering to active a silent polar mode as shown in Fig. 10. They studied four highly strained perovskites which are SrTiO₃, BaMnO₃, BiFeO₃, and YMnO₃ respectively. In SrTiO₃, BaMnO₃, and BiFeO₃, splitting between the t_2g states were observed near the Fermi energy. The tensile strain increases (decreases) the in-plane (out-of-plane) distance between central transition metal ion and its surrounding oxygen anions. As a result, the crystal field level of d_xy orbital is lower than that of d_zx and d_yz orbitals, which displays the electronic ordering with a predominant occupation of the d_xy state. Similarly, Jahn–Teller distortion in YMnO₃ lifts the e_g orbital degeneracy and displays an orbital ordering and predominantly occupation of $d_{{\mathrm{x}}^2 - {\mathrm{y}}^2}$ orbital, which widens band gap under moderate electric field.

Fig. 10: Tunable bandgap under applied electric field in perovskite via Jahn–Teller distortion.

Jahn–Teller distortion (top right panel) and bandgaps (bottom right panel) as a function of applied electric field in SrTiO₃, BaMnO₃, YMnO₃, and BiFeO₃. The atomic displacements associated with polar and Jahn–Teller distortions are schematically shown on the top and bottom right panels respectively. Reproduced with permission from ref. ¹⁵¹. Copyright [2016] {American Physical Society}.

Interface induced functional ferroelectric and multiferroic properties

With the development of advanced epitaxial engineering techniques, layer-by-layer epitaxial synthesis of perovskite-based multicomponent superlattices has been made possible^152,153. This enables the experimentalists to precisely control thickness as well as the order of the constituent layers along stacking direction. As illustrated in Fig. 11, the dissimilar lattice parameters, chemical environments, electrostatic potentials, and structural instabilities belonging to individual bulk constituents can lead to diverse physical interplays at the interfaces^154,155,156. For instance, broken inversion symmetry can be designed by the species of perovskites in multicomponent superlattices¹³, which has a significant effect on FE properties^1,157,158. Furthermore, electrostatic coupling between constituent layers in superlattices are mediated by the interfaces¹⁵⁹, which tends to minimize the polarization mismatch of the constituent components in order to avoid large electrostatic energy penalty²⁴. The effect of electrostatic coupling is now routinely being applied to tune FE in multicomponent superlattices for desired polarization. In addition, emergent polar structural distortions appear on the interface as a result of competing structural instabilities among parent perovskites^160,161,162. In the above, structural distortions associated with octahedral rotations and tilts play important roles in FE properties of perovskites^163,164. Along this line, successful tuning of the amplitude even reconstructions of the oxygen octahedral rotations have been demonstrated recently^{165,166,167,168} through the modified chemical pressure¹⁶⁹ (ionic radius and chemical bonding) at the interface. In this section, we first focus on the FE induced by compositional breaking of inversion symmetry; next, we summarize FE enhancement in recent literature by utilizing the electrostatic coupling effect via the interfaces; subsequently, we briefly review the mechanism of hybrid improper FE and its application in perovskite superlattices^26,170; finally, we discuss the recent developed method to stabilize the highly polar FE phase on the interfaces through the reconstruction of oxygen octahedral rotations.

Fig. 11: Thin-film engineering approaches that induce or enhance ferroelectricity in perovskite thin-film and superlattices.

Figure schematically shows that the ferroelectric polarization can be induced or enhanced by applied external strain as discussed, chemical compositions that breaks inversion symmetry in tricolor superlattices, electrostatic interaction mediated by the interfaces in the superlattices, and structural reconstruction associated with oxygen octahedron, which are discussed in the section of “Ferroelectricity in thin films under epitaxial strain”, “Compositional inversion symmetry breaking”, “Electrostatic coupling effect via interfaces”, and “Interfacial reconstructions of structural instabilities”, respectively.

Compositional inversion symmetry breaking

For artificial perovskite superlattices, it was realized²² that the number of distinct species of parent perovskites, often referred as colors, can be used to break the inversion symmetry. The mechanism of broken inversion symmetry can be conveniently demonstrated by the interface dipole ${\boldsymbol{p}}_{{\mathrm{int}}}\left( {\boldsymbol{D}} \right) = \mathop {\sum}\nolimits_i {{\boldsymbol{p}}_i} \left( {\boldsymbol{D}} \right) - {\boldsymbol{p}}_i^0\left( {\boldsymbol{D}} \right)$, in which ${\boldsymbol{p}}i({\boldsymbol{D}})$ is actual ith layer polarization and ${\boldsymbol{p}}_i^0\left( {\boldsymbol{D}} \right)$ is a polarization of bulk constituent in that interface layer. As schematically shown in Fig. 12, the interface dipole must sum up to be zero to keep the inversion symmetry in bicolor superlattices; however, for the tricolor or multicolor superlattices with at least three species of perovskites, the sum of interface dipoles is nonzero due to the compositional symmetry breaking. It was proposed that the resulting self-poling effect could be used to enhance functionalities such as piezoelectricity in perovskite superlattices.

Fig. 12: Broken inversion symmetry and induced ferroelectricity in the tricolor perovskite superlattice.

Schematic plots demonstrate how the spatial inversion is broken by the number of species (colors) included in the superlattice. a The individual interface dipoles and the b overall interface dipole as a function of electric displacement field in bicolor BaTiO₃/SrTiO₃ bicolor superlattice. c The overall interface dipole as a function of electric displacement field in tricolor BaTiO₃/SrTiO₃/CaTiO₃ superlattices.

The inversion symmetry breaking in tricolor superlattice was proposed theoretically by Sai et al.^13,157. They have performed ground state DFT calculations for artificial ternary perovskite superlattices of (A_1/3A′_1/3A″_1/3)BO₃ and A(B_1/3B′_1/3B″_1/3)O₃ by assuming [001] as the superlattice growth direction. In their studies, BTO has been chosen as the parent perovskite. Specifically, they considered two model systems, the first system is isovalent substitutions on both A and B sites in (Ba_1/3Sr_1/3Ca_1/3)TiO₃ and Ba(Ti_1/3Zr_1/3Hf_1/3)O₃, respectively, and in the second system, they consider heterovalent substitution on the B site element in Ba(Sc_1/3Ti_1/3Nb_1/3)O₃. The compositionally induced inversion symmetry breaking can be clearly identified by the asymmetric FE double well potentials from the DFT calculations as shown in Fig. 13. By using energy difference between the minimum of the two wells, it was found that the induced asymmetricity in the heterovalent chemical substitution systems is much larger than that in the isovalent substitution systems. It indicates a larger magnitude of inversion symmetry breaking in the former. To better understand it, a pseudo-lattice model system Ba(B_1/3Ti_1/3B″_1/3)O₃ was built by the construction of artificial elements B and B″ with fractional nuclear charges Ti − δ and Ti + δ, respectively, which allows the gradual change of the heterovalent symmetry-breaking through the perturbation δ deviating from that of Ti (Z = 22). It was found that the strength of the symmetry breaking is very sensitive to the variation of δ in Fig. 13, which shows a cubic dependence. Such a sensitive dependence of the inversion symmetry breaking on the charge perturbation indicates that the FE and large piezoelectricity could be induced in tricolor superlattice which are only PE in bulk.

Fig. 13: Tilted double well potential in tricolor perovskite superlattice.

The ferroelectric double well potentials as functions of charge perturbation δ through the heterovalent substitution. Reproduced with permission from ref. ¹³. Copyright [2006] {American Physical Society}.

The compositional symmetry-breaking in tricolor superlattices has been confirmed later in experiments^1,22. Warusawithana et al. had grown CTO/STO/BTO tricolor superlattices using molecular beam epitaxy on STO substrates. They found a strong asymmetrical dielectric response due to compositional symmetry breaking²² based on the measured real part of the dielectric constants ε′ in (CTO)₁(STO)₁(BTO)₂(STO)₁(CTO)₁ and (CTO)₂(BTO)₄(STO)₂ superlattices, respectively. The inversion symmetry of the former is not broken by chemical composition, therefore the measured ε′ is an even function under the applied electric fields. On the other hand, the mirror symmetry of measure ε′ in (CTO)₂(BTO)₄(STO)₂ superlattice is broken as expected. At almost the same time, Lee et al.¹ also successfully grew a series of CTO/STO/BTO tricolor FE superlattices via the pulsed laser deposition technique. Significantly enhanced polarization was observed in some superlattices. Among the above, (STO)₂(BTO)₄(CTO)₂ sequence was found to have the maximum polarization¹. For this particular superlattice, the remnant polarization is determined to be 16.5 μC/cm² in experiments showing roughly 50% enhancement compared the estimated values based on electrostatic model.

A few years later, the compositional inversion symmetry breaking design method has been also applied on multiferroic artificial materials. At bulk level, both LaMnO₃ and SrMnO₃ are PE insulators with G-AFM ordering, in which the Mn atoms adopt t_2g³e_g¹ and t_2g³e_g⁰ electronic configurations respectively. As detected by the superconducting quantum interference device magnetometer, FM ordering emerges at the interfaces of artificial LaMnO₃/SrMnO₃ superlattice arising from the promoted double-exchange interactions from the charge-transfer between the e_g orbitals of LaMnO₃ and SrMnO_3. Due to its bicolor nature, the space inversion symmetry remains unchanged in in LaMnO₃/SrMnO₃ system. Kida et al. designed the tricolor superlattice composed of LaMnO₃, SrMnO₃, and LaAlO₃ that breaks the inversion symmetry^158,171. In such a superlattice space-inversion and time-reversal symmetries are both broken. Therefore, it possesses a toroidal moment defined as P × M, where P and M denote the polarization and magnetization, which allows the nonvanishing magnetoelectric tensor α_ij. The real and imaginary parts of α_ij are associated with the directional refraction and absorption of light intensity, respectively^172,173. The reversal of one of P, M, or light wavevector k (parallel or antiparallel to the toroidal moment) will result in a sign change of α_ij to modulate the refractive and absorptive light intensity, which is referred to as the optical magnetoelectric effect. The change of refractive light intensity was successfully detected in the LaMnO₃/SrMnO₃/LaAlO₃ tricolor sample by a reversal of the direction of magnetic field^171,172.

Electrostatic coupling effect via interfaces

The polar distortion is sensitive to the external electric fields. The electrostatic interaction generated by the uncompensated polarization charges at the interfaces provides an effective method to tune the FE instability in perovskite superlattices. At the interface of insulating superlattice, the electric displacement field, D = ε₀E + P, must be continuous along the stacking direction of the superlattice, which is known to be the electric boundary condition as discussed in the section of “Electric boundary condition: fixed applied electric displacement field”. In general, the polarization mismatch between the two constituent components will build polarization charge ∇·P at the interfaces and lead to large energy cost^24,46. In order to minimize the above electrostatic energy, the polarization mismatch should be reduced. In the FE/PE superlattices, the process is achieved by polarizing (depolarizing) the PE (FE) component through the long-range electrostatic interactions. As a result, a rather uniform local polarization profile instead of lager polarization mismatch forms in the superlattice along the stacking direction^{24,174,175,176,177,178,179,180,181,182}. In the case of bicolor FE/PE superlattices, if one chooses the incipient FE perovskite (sch as SrTiO₃ and KTaO₃) as the PE component, the FE can be induced or recovered by the poling effect via the interfaces. The electrostatic coupling mechanism has been widely applied in the design of FE or multiferroic perovskite superlattices in the last decade^{8,24,25,183,184,185,186,187}.

Polarization enhancement by electrostatic coupling was first demonstrated by Neaton and Rabe²⁴ in the epitaxial BTO/STO superlattices. They carried out DFT calculations for several five-period superlattices with the compositions of 4BTO/1STO, 3BTO/2STO, 2BTO/3STO, and 1BTO/4STO assuming the coherent growth on a STO substrate, as well as the bulk STO and strained bulk BTO. The space group symmetry P4mm of room temperature BTO is assumed for all the superlattices, which allows the development of polar distortions along superlattice growth direction. Without considering the electrostatic coupling effect, the overall polarization can be roughly estimated by the average over the polarization of each bulk constituent and its volume fraction in the superlattice. Since STO is PE, the estimated polarization should be therefore roughly proportional to the volume fraction of the BTO component. Surprisingly, the calculated polarizations of the superlattices by DFT are much larger than the above estimated value. In order to elucidate the underlying origin of the enhanced polarization in BTO/STO superlattice, the local polarization profile is computed based on the linear approximation as shown in Fig. 14a. Interestingly, the local polarization induced in STO layers is found to be comparable to that in BTO layers. Clearly, the discrepancy between the estimated and computed polarization suggested that the interface effect is very large. In order to quantitatively study the electrostatic coupling effect via the interface, a dielectric slab model was then proposed by Neaton et al.²⁴. Within the dielectric slab model, short circuit boundary condition is applied by the vanishing total potential drop across the superlattice by ${\boldsymbol{E}}_{{\mathrm{BTO}}}\ell _{{\mathrm{BTO}}} = - {\boldsymbol{E}}_{{\mathrm{STO}}}\ell _{{\mathrm{STO}}}$, in which E_BTO and E_STO are the electric fields within the BTO and STO layers, respectively and the $\ell _{BTO}$ and $\ell _{STO}$ denote the layer thicknesses of BTO and STO respectively. Based on this model, the resulting overall polarizations of the BTO/STO superlattice are therefore given by ${\boldsymbol{P}} = {\boldsymbol{P}}_{{\mathrm{BTO}}}^S/(1 + {\mathrm{\alpha \varepsilon }}_{{\mathrm{BTO}}}/{\mathrm{\varepsilon }}_{{\mathrm{STO}}})$, where $\alpha = \ell _{{\mathrm{STO}}}/\ell _{{\mathrm{BTO}}}$, and P_BTO^S is the polarization of strained bulk BTO, and ε_BTO and ε_STO are the dielectric constants of strained bulk BTO and bulk STO, respectively. The dielectric slab model correctly captures the interface mediated electrostatic coupling and predicts a nearly uniform local polarization profile along [001] in BTO/STO superlattices, which were consistent with results obtained from the DFT calculations as shown in Fig. 14b.

Fig. 14: Electric polarization profiles in BaTiO₃/SrTiO₃ superlattices.

a Computed polarization enhancement (P_λ/P₀) decomposition on each layer λ based on the Born effective charges and atomic displacements. b Overall enhancement as a function of α = ℓ_STO/ℓ_BTO computed from first-principles calculations (filled circle) compared with that from dielectric slab model (dashed line). Reproduced with permission from ref. ²⁴. Copyright [2003] {AIP Publishing LLC}.

The above design rule has also been applied onto other similar systems composed of a strong FE material and an incipient FE material with large dielectric constant, such as KNbO₃/KTaO₃ (KNO/KTO)^{183,184,185,186} and PTO/STO^25,187 superlattices. KNO is isostructural of BTO, and it adopts the tetragonal structure of P4mm symmetry with spontaneous polarization about 35μC/cm² above 488 K⁷⁴. At lower temperature, KNO adopts rhombohedral symmetry with polarization along [111]⁷⁴. On the other hand, KTO is also an incipient FE perovskite similar to STO. However, it does not develop an AFD transition but remains cubic at low temperature^74,188. In artificial KNO/KTO superlattices grown on KTO substrate, a large out-of-plane polarization is found to be induced in the KTO layers, which is due to the electrostatic coupling effect through the interfaces as discussed. In addition, it was found that the compressive strain exerted by the KTO substrate is not sufficient enough to drive the KNO constituents from rhombohedral phase into tetragonal phase^184,185. As a result, both out-of-plane and in-plane polarization components are found to be present in the KNO layers of the superlattice. The main difference between out-of-plane and in-plane polarization components is that the former varies continuously due to the fixed electric displacement field, while the latter allows abrupt changes through different layers. The design mechanism based on interface electrostatic coupling has also been successfully applied on the (PTO)_n/(STO)₃ system, where PTO is a tetragonal FE material with strong polarization at room temperature and STO is an incipient FE material^74,189. Similar to BTO/STO superlattice, out-of-plane polarization was found to be induced in the STO layers, and the local polarization profile can be well described by the dielectric slab model for n ≥ 3 when the interface atomic reconstruction can be neglected^25,190.

In the bicolor artificial superlattice, if bulk polarization of one constituent perovskite is along [001] direction while the other is long [110] direction, polarization in the interfacial layers will be observed to rotate from out-of-plane gradually to the in-plane direction due to the electrostatic coupling effect. As an example, Sinsheimer et al. fabricated artificial PTO/CTO superlattices on [001] surface of STO substrates using the off-axis radio frequency magnetron sputtering method¹⁹¹. For all superlattices fabricated, CTO thickness was fixed to be three layers, while the PTO thickness was varied. The tetragonality, FE, piezoelectric, and dielectric properties of PTO/CTO superlattices were measured as a function of the CTO volume fraction x = n_CTO/n_CTO + n_PTO as shown in Fig. 15, where n_CTO and n_PTO are number of CTO and PTO unit cells. It was observed that when x approaches to 0, polar properties of the superlattices are largely governed by the PTO layers in such a way that a large polarization along [001] direction is observed; for x closes to 1, the properties of superlattices are dominated by CTO constituents, and polarization along [110] direction is observed due to large tensile strain imposed by STO substrate as discussed in the section of “Ferroelectricity in thin films under epitaxial strain”. However, for 0 < x < 1, PTO/CTO superlattices develop a continuous polarization rotation from [001] to [110] as the thickness of PTO layers decreases, and their structures undergo consecutive phase transitions from T–M_C–M_A–O as shown in Fig. 15, where T represents tetragonal phase with polarization direct to [001] axis, M_C and M_A denote two monoclinic phases with polarizations along [u0v] and [uuv] (u < v) directions respectively, and O stands for orthorhombic phase with polarization point to [110] direction. Such a polarization rotation due to the electrostatic coupling between PTO and CTO layers gives rise to highly tunable dielectric and piezoelectric properties. As a result, the out-of-plane piezoelectric constant d₃₃ is greatly enhanced in the samples at the morphotropic phase boundary^97,192 of the T–M_C transition.

Fig. 15: Ferroelectricity related properties in PbTiO₃/CaTiO₃ superlattices.

a Tetragonality, b polarization, c dielectric constant, d piezoelectric coefficient, and e evolution of polarization vector as a function of CaTiO₃ volume fraction. Reproduced with permission from ref. ¹⁹¹. Copyright [2012] {American Physical Society}.

Hybrid improper ferroelectricity

Based on the nature of structural instability that gives rise to the polar distortion, FE materials can be classified into the so-called proper and improper ones. In proper FE materials, such as PTO or BTO, the polar distortion originates directly from the unstable polar phonon mode at Γ point of the Brillouin zone, which is the primary order parameter according to the Landau second order phase transition theory^104,193,194. The variation of energy with polar distortion around PE phase displays a characteristic of double-well shape in the proper FE, and the two energy minima with antiparallel polarization can be switched to each other through an external electric field without involving any other structural distortions. The microscopic origin of stabilizing force associated with proper FE distortion is closely related to the strong covalent bond or orbital hybridization between cation and anion¹⁹³. On the other hand, the polar mode in improper FE materials is not intrinsically unstable, but only becomes unstable after the development of the primary structural distortion which is usually zone-boundary phonon mode^160,195. For example, hexagonal YMnO₃¹⁹⁶ is a prototype of improper FE perovskite. Its polar mode is stable by itself in its centrosymmetric phase; it only becomes unstable after the development of zone-boundary mode with wave vector q = (1/3,1/3, 0), which triples the unit cell size to accommodate the rotation of the MnO₅ trigonal bipyramids and a buckling of the Y–O layers. The microscopic origin of improper FE can be related to the adjusted electrostatic interaction with the development of the primary structural distortion¹⁹⁷. Therefore, improper FE is also named after geometric FE. When an external electric field is applied to switch the improper FE, the polar mode together with the primary order parameter should be switched simultaneously⁹².

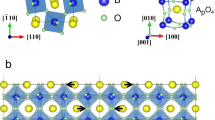
Recently, the so-called hybrid improper FE has emerged as an important new subcategory of the improper FE materials. As characteristic of hybrid improper FE, the development of polar distortion involves at least two nonpolar modes with distinct symmetries^170,198,199. The mechanism of hybrid improper FE has been demonstrated in the multiferroic Ca₃Mn₂O₇¹⁷⁰ belonging to the Ruddlesden–Popper family with a general formula of A_n+1B_nO_3n+1. Ca₃Mn₂O₇ consists of ABO₃ perovskite blocks stacking along [001] direction with an extra AO layer inserted every n (=2) cells as shown in Fig. 16a. The lattice dynamics studies show that the polar distortion is stable in its centrosymmetric phase with I4/mmm symmetry. However, a polar structural distortion (Γ₅⁻ mode) emerges upon the distortions associated with oxygen rotation (X₂⁺ mode) and tilt (X₃⁻ mode) develop simultaneously as shown in Fig. 16b–d. As a result, Ca₃Mn₂O₇ transforms into A2₁am FE phase. In addition, the energy landscape of the polar mode displays linear behavior after both oxygen octahedron rotation and tilt develop, which is consistent with the improper nature of FE through the symmetry allowed coupling term $\sim Q_{X_2^ + }Q_{X_3^ - }Q_{\Gamma _5^ - }$ that lowers the total energy in the FE phase, where Q denotes the mode amplitude.

Fig. 16: Crystal structure and structural distortions in hybrid improper ferroelectric materials of Ca₃Mn₂O₇.

a Ball-and-stick model of ferroelectric ground state structure of Ca₃Mn₂O₇ with A2₁am space group symmetry. b Structural distortion of oxygen octahedral rotation (X₂ mode). c Structure distortion of oxygen octahedral tilt (X₃⁻ mode). d Layer decomposition of polarizations within the plane along [110] direction. Figure 16a–c are reproduced with permission from ref. ¹⁷⁰. Copyright [2011] {American Physical Society}. Figure d is reprinted from ref. ²⁰⁰, Copyright (2012), with permission from Elsevier.

In perovskite superlattices, oxygen octahedral rotations and tilts are common structural distortions, which provides rich opportunities to induce polarization via the hybrid improper FE mechanism. The interface induced FE through the hybrid improper FE mechanism was first discovered experimentally in PTO/STO superlattices by Dawber et al.²⁵. In all 20 different superlattices under investigation, the thickness of STO layers was held fixed to be three cells, while the thickness of PTO layers was varied. According to the electrostatic coupling effect through interfaces as discussed in the section of “Electrostatic coupling effect via interfaces”, both the polarization and tetragonality of the superlattices are expected to be decreased as the PTO layer thickness decreases. A simple model was built, $E\left( {{\boldsymbol{P}}_{\mathrm{p}},\,{\boldsymbol{P}}_{\mathrm{s}}} \right) = xU_{\mathrm{p}}\left( {{\boldsymbol{P}}_{\mathrm{p}}} \right) + \left( {1 - x} \right)U_{\mathrm{s}}\left( {{\boldsymbol{P}}_{\mathrm{s}}} \right) + E_{{\mathrm{elec}}}\left( {{\boldsymbol{P}}_{\mathrm{p}},\,{\boldsymbol{P}}_{\mathrm{s}}} \right)$, in order to describe the FE in the superlattices by taking into account the electrostatic coupling effect through the interfaces. In the above, U_p(P_p) and U_s(P_s) represent the total energies of bulk PTO and STO as a function of their zero-field polarizations P_p and P_s which were obtained from DFT calculations, x = n_p/(n_p + n_s) is the PTO volume fraction and the last term is an electrostatic energy between the PTO and STO layers. As shown in Fig. 17a, this model agrees well with the DFT calculations when number of PTO layers (n_p) exceeds that of STO layers (n_s), n_p/n_s > 1. For n_p/n_s is less than 1, polarization predicted from the model vanishes, however, experimental measurement gave surprisingly nonzero polarization in those superlattices. In order to exclude the role of temperature effect in the unexpected recovery of FE, the total energies U_p(P_p) and U_s(P_s) in above electrostatic model were then replaced by the Helmoltz free energies¹⁹⁰. As shown in Fig. 17b–d, results from the revised model successfully predicted polarization, tetragonality and transition temperature for PTO/STO superlattices with n_p/n_s > 1, but still failed to reproduce the results in superlattices with low PTO volume fraction. Obviously, the failure of electrostatic coupling model in predicting FE of superlattices with ultra-thin PTO layer thicknesses indicates that electrostatic coupling alone is not sufficient, and some unexpected interface effect should take place here.

Fig. 17: Polarization, tetragonality and ferroelectric phase transition temperature of PbTiO₃/SrTiO₃ superlattices.

a Electric polarizations predicted by Landau–Devonshire phenomenological model and first-principles calculations as a function of the ratio between PbTiO₃ fraction and the SrTiO₃ fraction (n_p/n_s) in the superlattices. b The measured and predicted electric polarizations as a function of PbTiO₃ volume fraction in the superlattices based on positive up negative down experiment and Landau–Devonshire phenomenological theory, respectively. c Tetragonalities of two series of samples grown on 460 °C and 510 °C as a function of PbTiO₃ volume fraction in the superlattices. d Experimental (dots) and theoretical (solid lines) ferroelectric structural transition temperatures as a function of PbTiO₃ volume fraction in the superlattices. Reprinted with permission from ref. ¹⁹⁰. Copyright (2008) John Wiley & Sons, Inc.

In order to elucidate the interfacial origin of the unusual FE behavior in PTO/STO superlattices, Bousquet et al.¹⁶² carefully studied the structural distortions on the 1/1 superlattice based on DFT energy minimizations. The structural relaxation showed that 1PTO/1STO superlattice at ground state adopts a polar structure with P4bm symmetry. The polar structure can be considered as the combination of three distinct structural distortions added on the centrosymmetric reference structure with P4/mmm symmetry which are polar distortion (Γ₃⁻ mode), out-of-phase (M₄⁻ mode) and in-phase (M₂⁺ mode) octahedral rotations around [001] axis as shown in Fig. 18a–c, respectively. In order to study their relative importance in stabilizing the observed ground state, the three distortions have been systematically added onto the centrosymmetric reference structure. It was found that the polar structural distortion alone only has a relatively small energy gain as shown by the shallow FE double-well potential in Fig.18d. Surprisingly, the FE ground state is further stabilized when both of the in-phase and out-of-phase oxygen octahedral rotations are allowed to develop, which seem to be contradictive to the conventional belief that the AFD and FE distortions are in strong competition in perovskites¹²³. The following Landau free energy expansion the symmetry analysis reveals that the FE is actually promoted when two types of AFD modes are present via the trilinear coupling terms $Q_{\Gamma _3^ - }Q_{M_4^ - }Q_{M_2^ + }$ that greatly lowers the total energy in 1PTO/1STO supercell.

Fig. 18: Schematic plots demonstrating the induced improper ferroelectricity in 1PbTiO₃/1SrTiO₃ superlattice.

a Electric polarization along [001] direction is generated by zone center Γ₃⁻ mode. b Out-of-phase oxygen octahedral rotation is generated by zone boundary M₄⁻ mode. c In-phase oxygen octahedral rotation is generated by zone boundary M₂⁺ mode. d The calculated ground state total energies as a function of electric polarization by including Γ₃⁻ mode only, and Γ₃⁻ mode together with M₄⁻ and M₂⁺ all together. Figure 18a are reprinted with permission from ref. ²⁵, Copyright [2005] {American Physical Society}. Figure 18b–d are reprinted with permission from ref. ¹⁶². Copyright (2008) Springer Nature.

Similar distortions as observed in 1PTO/1STO supercell were also clearly identified at the interfaces in PTO/STO superlattices of other thicknesses, such as superlattices with 3/3, 5/3, and 7/3 periods. The appearance of the octahedral rotations can be attributed to the intrinsic structural instabilities at Brillouin zone boundary points in both PTO and STO in their cubic phases^104,114. As an incipient FE material, the bulk STO at ground state barely shows any FE polarization¹²², and has an octahedral rotation around the [001] axis. On the other hand, the appearance of the octahedral rotation in PTO is strongly dependent on the electric boundary condition. Hong and Vanderbilt⁹⁵ studied the complex energy landscape of STO and PTO perovskites as functions of varying applied electric displacement fields. It was found the AFD mode associated with the oxygen octahedral rotation in bulk PTO was absent in high electric displacement fields and recovered under at low electric displacement fields. A similar scenario occurs in PTO/STO superlattices when the STO portion is increased gradually in the experiment carried out by Bousquet et al.¹⁶².

A very similar effect induced by hybrid improper FE mechanism was also discovered at the interface of 1PTO/1PbZrO₃ short-period superlattice²⁰¹. A careful inspection of the relaxed ground state of the above interface only superlattice revealed that an interesting pattern of structural distortions emerged, which are oxygen octahedral tilts around [110] axis (R₁₁₀), and out-of-phase oxygen octahedral rotation around [001] axis (R₀₀₁). In terms of Glazer notation, the above structural distortions are referred to as a⁻a⁻c⁰ and a⁰a⁰c⁻, respectively²⁰². Based on Landau-type energy expansion facilitated by group theory analysis, the interface structure actually promotes FE polarization along [001] (P₀₀₁) and [110] axis (P₁₁₀) which was enable by a four-linear coupling term, ~Q_P001Q_P110Q_R001Q_R110 lowing the energy. If three of the four distortions are present, the fourth term which even was not unstable will be enhanced. Cleary, such induced FE belongs to improper FE in nature.

Beside the enhanced FE polarization in the FE/PE superlattice, the hybrid improper mechanism has also been applied onto inverse interface design of artificial FE materials from nonpolar perovskites only. As discussed above, the hybrid improper FE in Ruddlesden–Popper A₃B₂O₇ materials (such as Ca₃Mn₂O₇ or Ca₃Ti₂O₇) can be understood to arise from the non-cancelation of antipolar displacements of A-site cations^23,170,198. A similar antipolar displacement on A-site can be also found in many ABO₃ perovskites of Pnma phase such as CTO, which is a common crystalline symmetry in perovskites. The Pnma structure is evolved from the reference cubic structure with Pm3̄m symmetry via structural distortions including two distinct oxygen octahedral rotation patterns of a⁰a⁰c⁺ (Q_M) and a⁻a⁻c⁰ (Q_R), as shown in Fig. 19a, b, respectively. The antipolar distortion X₅⁺ (Q_X) develops at ground of CTO, through a symmetry-allowed trilinear coupling free energy term ~ Q_MQ_RQ_X that largely lowers the energy²⁸. Unlike the Ruddlesden–Popper systems, the oxygen octahedral connectivity is well preserved in Pnma structure, the octahedral rotations in bulk CTO cannot break the inversion symmetry. As a result, perovskite with Pnma symmetry yields an anti-polar ground state as shown in Fig. 19c. However, the above has been overcome by Fennie and Rondinelli recently²⁶. They theoretically designed the 1ABO₃/1A′BO₃ supercell based on nonpolar Pnma perovskites, which can be also considered as artificial double perovskites with two chemically distinct A-site species^26,200. The changes in the chemical environments allow the inversion symmetry breaking via the above improper FE mechanism. Similar to that in Ca₃Mn₂O₇, the antipolar displacements of two alternate AO layers along [001] direction no longer exactly equal to each other, leaving a nonzero residual overall polarization as shown in Fig. 19d. Since the inversion symmetry breaking originates from the non-cancelation of two distinct antipolar modes induced by two primary oxygen octahedral rotations, it is therefore classified as the hybrid improper mechanism^20,200. Furthermore, it was found that if the magnitudes of octahedral rotations and tilts are comparable in bulk ABO₃ and A′BO₃ then the antipolar A-site displacement will be similar. As a result, the overall polarization is small due to nearly canceled antipolar modes of AO and A′O layer. Therefore, it was proposed that a strong Pnma perovskite ABO₃ of small Goldschmidt tolerance factor and a weak Pnma perovskite A′BO₃ of large tolerance factor should be chosen in building the 1ABO₃/1A′BO₃ superlattice in order to achieve relatively large polarization. Due to the interface effect in nature, the total polarization is found to be maximized in the dense interface limit in 1ABO₃/1A′BO₃ systems²⁰. In addition, the FE transition temperature is determined by the structural phase transition with oxygen octahedral rotations and tilts, which is usually well above room temperature for many perovskites with Pnma structure^23,162,190. Therefore, the hybrid improper mechanism provides a promising way to design room temperature FE and multiferroic materials.

Fig. 19: Illustration of the hybrid improper ferroelectricity in artificial perovskite superlattices.

a Oxygen octahedral rotation around [001] direction. b Oxygen octahedral tilt around [110] direction. c Antipolar displacement (X₅⁺ mode) on A-site atoms. d Residual polarization arises from the non-canceled antipolar A-site displacements in 1LaGaO₃/1YGaO₃ superlattice. Reprinted from ref. ²⁰⁰, Copyright (2012), with permission from Elsevier.

Following the above design rule, ASnO₃/A′SnO₃ SLs (A, A′ = Ca, Sr, and Ba) are typical examples of improper FEs successfully predicted by first-principles simulations²⁰³. Because of the large radius of Ba atom, neither octahedral rotation nor tilt occurs in the BaSnO₃ layer. In contrast, the smaller sizes of A-site cations of Ca or Sr allow oxygen octahedral rotation and tilt to develop resulting in large antipolar structural distortion as represented by the in-plane A-site displacements in both CaSnO₃ and SrSnO₃ layers as previously described. As a result, FE polarizations of 10.379 and 2.778 μC/cm² are induced in both BaSnO₃/CaSnO₃ and BaSnO₃/SrSnO₃ superlattices. It should be noted that none of the them is polar by itself in natural ground state. Not surprisingly, BaSnO₃/CaSnO₃ has a larger polarization value than the latter due to the fact that CaSnO₃ is a stronger Pnma perovskite than that of SrSnO₃ as discussed. By the same token, the germinate based 1AGeO₃/1A′GeO₃ superlattice (A, A′ = Mg, Ca, Sr, and Ba) and 1LaGaO₃/1YGaO₃ have been predicted to be FE at room temperature²⁰. The hybrid improper FE mechanism has been also successfully applied onto Pnma perovskite with the B-site atom replaced by transition metal element with partially occupied d states in order to design novel multiferroic materials for desired magnetoelectric effect^204,205.

Based on first-principles calculations, Ghosh et al.²⁰⁴ have explored the structural and magnetic properties of the orthorhombic ferrite perovskite family of LnFeO₃, where Ln denotes a cation belonging to the lanthanide series or Yttrium. They found that 1LaFeO₃/1LnFeO₃ (Ln = Ce, Nd, Sm, Gd, Dy, Tm, Lu, and Y) supercells display both FE and FM properties at ground state. As expected, the FE polarization originates from the hybrid improper mechanism. LnFeO₃ (LaFeO₃) has a strong (weak) in-plane antipolar structural distortions due the much smaller cation size of Ln than that of La. Therefore, a nonzero in-plane polarization is induced from 2.2 μC/cm² for Ln = Ce to 11.6 μC/cm² for Ln = Lu, at the interfaces of the 1LaFeO₃/1LnFeO₃ superlattices due to the difference between the above two antipolar modes²⁰⁴. Surprisingly, the oxygen octahedral rotation and tilt can induce weak ferromagnetism due to the canted spins in G-AFM ordering of Fe atoms. Such canting arises from the Dzyaloshinskii–Moriya (DM)^206,207 exchange interactions between Fe spins. Moreover, DFT calculations suggested that these superlattices display a linear magnetoelectric effect larger than that observed in the prototypical magnetoelectric materials such as Cr₂O₃ and BiFeO₃. Based on the superexchange energies from first-principles calculations and mean-field theory, the magnetic transition temperature of 1LaFeO₃/1YFeO₃ was estimated to be close to the Néel temperature LaFeO₃ as high as ~740 K.

In addition, the hybrid improper mechanism was also successfully applied onto the inverse interface design of double perovskite superlattices. Similar to the Pnma phase perovskite, the double perovskite oxide can also adopt complex structural distortions combining oxygen octahedral rotation and tilt, adopting the a⁻a⁻c⁺ Glazer tilt pattern. As a result, the antipolar distortion similar to that in Pnma perovskite occurs in double perovskite oxides such as R₂NiMnO₆, which are FM insulators (R is a rare earth element), as shown in Fig. 20a^208,209. Zhao et al. have theoretically investigated the hybrid improper FE in R₂NiMnO₆/La₂NiMnO₆ short period superlattices²¹⁰. It was found that a spontaneous polarization is induced due to the different magnitudes of displacements between R and La associated with the antipolar displacement. Similar to that for perovskite 1ABO₃/1A′BO₃ superlattices, the interface induced polarization in R₂NiMnO₆/La₂NiMnO₆ increases as the ionic radius of rare-earth R decreases as shown in Fig. 20b. This is due to the enhancement of oxygen octahedral rotation and tilt in R₂NiMnO₆ through the trilinear coupling term. The polarization ranges from 1.4 to 9.2 μC/cm² for R = Ce, Pr, Nd, Sm, Gd, Tb, Dy, Ho, and Er. In particular, for Ce₂NiMnO₆/La₂NiMnO₆ short period superlattices, the combined DFT and Monte Carlo simulations predicted the Curie temperature to be 290 K as shown in Fig. 20c, which makes it a candidate of room temperature FE and FM materials.

Fig. 20: Crystal structure, electric polarizations, and magnetic phase transition temperatures of R₂NiMnO₆/La₂NiMnO₆ (R: rare earth element) superlattices.

a The ball-and-stick model of R₂NiMnO₆/La₂NiMnO₆ superlattices; the La³⁺, R³⁺, Ni²⁺, Mn⁴⁺, and O²⁻ ions are displayed as green, orange, cyan, purple, and red spheres, respectively. b The theoretical electric polarization, and c the predicted Curie temperatures as a function of the rare-earth ionic radius. Reprinted with permission from ref. ²¹⁰. Copyright (2014) Springer Nature.

Interfacial reconstructions of structural instabilities

As far as the structural distortion is concerned, only a few perovskites are dominated by polar mode, such as BTO, PTO, and KNO in its natural ground state. More complex structural distortions associated with the oxygen octahedral rotation and tilt usually occur ^{27,164,165,166,168}. The idealized cubic structure of perovskites can develop up to 15 distinct Glazer rotation patterns in total^28,169,211. The most common oxygen octahedral rotation patterns occur in the Pnma space group symmetry, such as CTO. The R3c symmetry, such as BiFeO₃ and LiNbO₃, is relatively less commonly seen in perovskites. The oxygen octahedral rotation pattern in Pnma perovskite can be depicted as the in-phase oxygen octahedral rotation around [001] axis and the oxygen octahedral tilt around [110] (a⁻a⁻c⁺ in Glazer notation), which originate from the structural instabilities at M and R points of Brillion zone, respectively. As we have discussed earlier in the section of “Tunable band gap under epitaxial strain”, the antipolar distortion X₅⁺ mode is strongly favored in Pnma perovskite due to the trilinear coupling mechanism, resulting in its paraelectric ground state. On the other hand, the oxygen octahedral rotation pattern in R3c can be described as the out-of-phase oxygen octahedral rotation around [001] axis combined with oxygen octahedral tilt around [110] axis (a⁻a⁻a⁻ in Glazer notation), both of which originated from the R point instabilities in the Brillion zone. The R3c perovskite is compatible with a large FE polarization. For example, the spontaneous polarization in BiFeO₃²¹² and LiNbO₃²¹³ are found to be 88.7 and 71 μC/cm², respectively. In particular, BFO is one of most studied room temperature multiferroic materials, in which the weak FM due to spin canting was recently confirmed in experiments^212,214. Unfortunately, compared to the widely spread Pnma perovskites, the perovskites with R3c symmetry are rarely seen^8,28,167.

However, recent theoretical studies suggested that, for many Pnma perovskites, the R3c structure is actually one of the low-lying metastable states²¹⁵. The energetics between its ground state with Pnma structure and metastable R3c structures have been systematically studied by Wang et al.⁸ recently by using CTO as the prototypical perovskite. In their work, they have proposed effective Hamiltonian models to describe the energy for ground state Pnma as well as metastable R3c phase of CTO, which was assumed to be coherently grown on the STO substrate. The effective Hamiltonian was built from the PE high-symmetry reference structure (P4/mmm) and the energies due to structural distortions in term of irreducible representations were considered by the Laudau type coupling terms facilitated by space group theory. All the coupling constants in the energy expansions were numerically fitted based on the inputs of DFT total energies with various frozen structural distortions. As expected, the ground state Pnma structure of CTO is found to be favored by a large trilinear coupling term (including in-phase octahedron rotation around [001], octahedron tilt around [110], and in-plane anti-polar mode) that significantly lower the total energy, which results in the antipolar mode with large A-site atom displacement. On the other hand, the R3c phase of CTO is promoted by a four-linear coupling term (including in-plane and out-of-plane FE modes, out-of-phase octahedron rotation around [001], and octahedron tilt around [110]), which largely lowers the total energy. Compared to the PE Pnma CTO, the R3c CTO has a slightly higher energy 0.211 eV/cell (contains 20 atoms) than the former. Wang et al.⁸ further derived the enthalpy functions of Pnma and R3c phases of CTO respective by assuming that the oxygen octahedron rotation and tilt angles are adjustable parameters under experimental conditions. Very interestingly, they found that the R3c structure of CTO becomes energetically more stable than the Pnma phase if the angles of octahedron rotation and, in particular, the octahedron tilt are significantly reduced.

The result by Wang et al.⁸ suggests that the functional R3c structure may actually be stabilized for many perovskites, which naturally exists as Pnma phase. However, the significant reduction in the oxygen octahedral rotation and tilt could not be easily achieved by the applied epitaxial strain. This is because the oxygen octahedral rotation and tilt angles are found to be only weakly tunable under mismatch strain¹¹⁵. On the other hand, the oxygen distortions are found to be highly dependent on chemical pressure which can be adjusted by the ionic radius, chemical bonding, and electronegativity¹⁶⁹. As a matter of fact, the amplitudes of the oxygen octahedral rotation and tilt are sensitively dependent on the ionic radii of the cations in ABO₃ perovskite. The above dependence can be quantified by the so-called Goldschmidt tolerance factor $t = (r_{\mathrm{A}} + r_{\mathrm{O}})/\sqrt 2 (r_{\mathrm{B}} + r_{\mathrm{O}})$, in which r_A, r_B, and r_O are ionic radii of A-site cation, B-site cation, and oxygen anion for a particular ABO₃ material, respectively²¹⁶. When t = 1, perovskites tend to retain high-symmetry structure without any distortions. When t > 1, A site ionic radii are much larger compare with B site, large A–O repulsive forces resist octahedral rotation and favor FE distortion with B site ions moving off center ^20,28,217. For t < 1, A site ionic radii are relatively small, under which the perovskites tend to develop large octahedral rotation and tilt^20,28,217. In perovskite superlattices, the proximity effect has recently been identified in both theory^102,117,218 and experiments⁸. It was found that for one ABO₃ with a small tolerance factor, its oxygen rotation and tilt will be significantly suppressed at the interfaces close to the second perovskite component with a relatively large tolerance factor.

Guided by the above mechanism, the stabilization of the R3c phase of CTO has been successfully realized at the interface of BTO/CTO superlattice through combined first-principles calculations and transmission electron microscopy by Wang et al.⁸. BTO is a perovskite with larger tolerance factor, which is strongly resistant to oxygen rotation and tilt at room temperature. Wang and co-workers investigated a number of nBTO/nCTO superlattices (n = 1…6). In particular, the structural distortions of 6BTO/6CTO was analyzed in detail as shown in Fig. 21. The perovskite component far away from the interfaces can be described by the bulk properties. In the BTO region in the superlattice, the structural distortion is mainly contributed by the polar distortion along [001] direction, which is consistent with the FE phase of BTO with tetragonal structure at room temperature. Whereas in the CTO region of the superlattice, the structure distortions are dominated by large in-phase oxygen octahedral rotation around [001] axis and tilt around [110] axis. As already described in the section of “Hybrid improper ferroelectricity”, this particular Pnma structure results in large antipolar mode as shown by the clear zigzag type A-site atom displacement which points to opposite direction for alternative layers along [110] direction. However, the oxygen distortion pattern undergoes a significant reconstruction at the interfacial layers. As a result, the oxygen octahedral in two alternating layers of CTO at the interface were surprisingly found to be out-of-phase, which are due to the largely suppressed oxygen rotation and tilt angles by the proximity effect. The new pattern of oxygen rotation and tilt is exactly the same as the R3c structure as predicted by the enthalpy function in the above paragraph. The enhanced FE was evidenced by the calculated larger polarizations 29.0 μC/cm² than the values predicted by the electrostatic coupling model 22.4 μC/cm² in the section of “Multiferroic properties under epitaxial strain via spin-phonon coupling”, which clearly indicates the interface enhanced FE.

Fig. 21: Layer by layer decomposed structural distortions and polarization in 6BaTiO₃/6CaTiO₃ superlattice.

R_Z^I, R_Z^O denote the in-phase and out-of-phase oxygen octahedral rotation around [001] direction respectively. P₁₁₀, P₀₀₁ represent the layer-by-layer decomposed polarization along [110] and [001] direction respectively. ADIS shows the atomic displacement of the A-site cations. R_xy describes the oxygen octahedral tilt around [110] direction. Reproduced with permission from ref. ⁸. Copyright [2016] {American Physical Society}.

Since the stabilization of the R3c structure takes place at the interfacial CTO layers, the enhanced polarization will depend on the density of the interfaces. As expected, the largest enhancement of polarization occurs in the 2BTO/2CTO supercell where the interface density is the maximum because the out-of-phase oxygen octahedral rotation requires a minimum number of two CTO layers. As the interface density decreases, the FE property is gradually dominated by the electrostatic coupling effect as we have discussed in the section of “Hybrid improper ferroelectricity”. The above theoretical prediction is consistent with the more recent experiments performed on the BTO/CTO superlattices^219,220. Jo et al. observed that the piezoelectric coefficient d₃₃ of 2BTO/4CTO is measured to be 54 pm/V as large as the piezoelectric response in bulk BTO at room temperature. It is established that the piezoelectric tensor is proportional to the remnant polarization P by d_ij = q_ijkP_jϵ_kj,²²¹ in which the d_ij, q_ijk, P_j, and ϵ_kj represent piezoelectric coefficient, electrostrictive coefficient, remnant polarization and elastic constant respectively. Considering the fact that 60% of the 2BTO/4CTO superlattice are composed of nonpolar CTO layers, the above experiment implies a significantly larger FE polarization than the conventional estimation based on the electrostatic coupling effect only. However, considering the above described interface effect, it is easier to understand this phenomenon. The oxygen octahedral network will be reconstructed to form R3c-like structure resulting in the enhanced FE as well as piezoelectricity.

Such a interface design mechanism has been applied onto other superlattices as well, such as 2BaTiO₃/2CdTiO₃, 2KNbO₃/2NaNbO₃, and 2KNbO₃/2AgNbO₃. In general, the DFT calculations show that the FE is enhanced by about 50–90%. Furthermore, based on first-principles calculations, Wang et al.⁸ have proposed that the above interface mechanism can be even used to induce large FE polarization in artificial perovskite superlattices which are built from non-polar perovskites only. For the proposed 1A′BO₃/1A″BO₃ superlattice, A′BO₃ is chosen to be strong Pnma structure with large in-phase rotation and tilt of oxygen octahedral, which is non-polar at ground state; on the other hand, A″BO₃ is a strong “cubic” like perovskite with tolerance factor (t ~1), so that neither the polar distortion or nor the oxygen octahedral rotation and tilt develop in A″BO₃. In the resulting 1A′BO₃/1A″BO₃ superlattices, the oxygen octahedral rotation and tilt are found to be suppressed in in A′BO₃ but are induced in A″BO₃ perovskite. Most interestingly, the resulting oxygen octahedral network at ground state exhibits out-of-phase octahedral rotation with octahedral tilt, which is exactly described by the R3c structure. Concomitantly, large polar distortions along [110] and [001] direction develop in all the proposed materials such as 1CdSnO₃/1BaSnO₃, 1CdHfO₃/1BaHfO₃, and 1CaZrO₃/1BaZrO₃. In the above proposed superlattices, the in-plane polarization is found to be roughly √2 times the out-of-plane component of polarization. This is exactly what one expects for the FE materials with R3c symmetry such as BiFeO₃. Because the prevalent Pnma structure in perovskite materials, this interface design mechanism introduces a new approach of designing novel functional materials. For example, if the FE could be recovered in orthogonal RFeO₃^{222,223,224,225} (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), the synthesis of room temperature multiferroic materials could be achieved.

Perspectives

In conclusion, we have reviewed the recent progress in the design mechanisms in order to achieve functional properties in perovskite based thin-films and superlattices. In the article, we have focused on the ferroelectricity and multiferroic, which are highly sensitive to the presence as well as the nature of the interfaces grown in the superlattices. Furthermore, the observed enhanced functionalities also represent a delicate balance between the long-range Coulombic interaction and short-range repulsion force or the competition among various magnetic orderings via the exchange interactions, which is further highly dependent on the particular mechanical and electric boundary conditions applied on the system. The modern thin-film technique provides an ideal playground to insert the designated interfaces in the superlattice by coherent epitaxial growth; at the same time, it can also implement the appropriate mechanical and electric boundary conditions through the choices of substrate and particular considerations in device fabrications. Over the last two decades, the first-principles calculations based on density functional theory have played a key role in conceiving the design rules of novel thin-film and superlattice as we have briefly reviewed. We have stressed that the comprehensive and proper treatments of mechanical and electric boundary conditions in theory are of crucial importance in validating those proposed design mechanisms.