Abstract
Chemical design of SiO2-based glasses with high elastic moduli and low weight is of great interest. However, it is difficult to find a universal expression to predict the elastic moduli according to the glass composition before synthesis since the elastic moduli are a complex function of interatomic bonds and their ordering at different length scales. Here we show that the densities and elastic moduli of SiO2-based glasses can be efficiently predicted by machine learning (ML) techniques across a complex compositional space with multiple (>10) types of additive oxides besides SiO2. Our machine learning approach relies on a training set generated by high-throughput molecular dynamic (MD) simulations, a set of elaborately constructed descriptors that bridges the empirical statistical modeling with the fundamental physics of interatomic bonding, and a statistical learning/predicting model developed by implementing least absolute shrinkage and selection operator with a gradient boost machine (GBM-LASSO). The predictions of the ML model are comprehensively compared and validated with a large amount of both simulation and experimental data. By just training with a dataset only composed of binary and ternary glass samples, our model shows very promising capabilities to predict the density and elastic moduli for k-nary SiO2-based glasses beyond the training set. As an example of its potential applications, our GBM-LASSO model was used to perform a rapid and low-cost screening of many (~105) compositions of a multicomponent glass system to construct a compositional-property database that allows for a fruitful overview on the glass density and elastic properties.
Similar content being viewed by others
Introduction
SiO2-based glasses are a group of materials known for its diverse applications as both structural and functional materials in various industrial fields1,2,3. Density and elastic moduli are two of the most common properties of SiO2-based glasses. Particularly, discovering new glass compositions to achieve high elastic moduli and low densities is of great interests for the development of strengthened and durable SiO2-based glass materials nowadays. Finding universal expressions or correlations to efficiently predict and further optimize densities and elastic moduli of SiO2-based glasses according to the chemical composition is not very straightforward due to their non-crystalline structures. Different from the crystalline materials, the elastic moduli of a SiO2-based glass are not only determined by the atomic bonding strength but also a complex function of many other physical properties at different length scales4,5,6,7, such as cation coordination, formation of atomic ring, chain, layer and polyhedral atomic clusters, and even the structural organization at mesoscopic scale, e.g. the formation of nanodomains4. Moreover, the additive oxides besides SiO2 introduce cations with various valence states, which not only change the cation-oxygen bonding strengths but also modify the degree of network polymerization. As a result, elastic moduli of the glass are complex functions of the chemical compositions of the additive oxides.
Through linear or polynomial regression analyses, many efforts have been devoted previously to fit the densities and elastic moduli with either the glass composition only8,9,10 or a single parameter related to atomistic structures, such as molar volume11 and the correlation length of x-ray diffraction peak5,12. Although these regression models were demonstrated to provide valid descriptions for some certain glass systems, they may have two major shortcomings that impede their usage in the practical design of new glass compositions. Firstly, the models are usually accurate for specific glass systems. Once the type of the additive oxides changed, the regression results may significantly be varied, or an alternative modeling method must be applied. As a result, it is difficult to extrapolate the developed models to capture the mixed effects of multiple additive oxides in the design space for industrial glass products. Secondly, for the models built on non-compositional variables, their outcomes are hard to be directly used for discovering new glass compositions, because it could be difficult to quantitatively interpret the optimization results with respect to glass chemistries. For example, elastic extremeness may occur at a certain correlation length of x-ray diffraction peak5,12, while it is still unknown what glass chemistries result in such correlation length. These shortcomings may originate from the fact that these models were usually built from regression algorithms based on presumed analytical formulas and a few variables that were predetermined relying on historical intuition and knowledge.
Machine learning (ML) techniques offer an alternative way to create predictive models that bridge the materials property of interest with its potential descriptors quickly and automatically13,14,15,16. In addition, the model created from ML does not require to rely on presumed fitting expressions or any historical intuition of material behaviors. As a result, the ML approaches can be a particularly powerful tool for modeling the property that is determined by many factors in a complex way with unclear underlying mechanisms. To date, the ML approaches have been widely used to build predictive models for a handful of materials properties and applications, including the modeling of elastic moduli of both crystalline17,18,19 and amorphous materials20,21,22,23,24. Using the artificial neural networks and genetic evolution algorithms, Mauro et al.20,24 recently showed that Young’s moduli of over 250 different glass samples can be accurately regressed and predicted using glass compositions as inputs. Most recently, by using glass composition as input descriptors, Yang et al. performed extensive studies to show that Young’s moduli of the CaO-Al2O3-SiO2 ternary glass system can be accurately predicted through several different ML models21. Additionally, in a recent work by Bishnoi et al., Young’s moduli of four important ternary glass systems were comprehensively studied and well predicted based on nonparametric ML regression models22. Furthermore, recent works by Lu et al. show that the densities and elastic moduli of the ZrO2-doped soda-lime borosilicate and calcium aluminosilicate glasses can be well predicted by a group of physical descriptors using quantitative structure-property relationship (QSPR) analysis25,26. All these recent works show great promise in the application of ML techniques on the chemistry design of advanced glass materials.
One could encounter several challenges to model densities and elastic moduli of SiO2-based glasses under a ML-based framework. A typical one would be the availability of sufficient quantities of training data to sample the predictive space. It could be harmful for extrapolative predictions if the training data are clustered around one or several particular regions of the design space. However, unfortunately, experimental data are usually clustered due to the constraints of practical manufacturing. This situation can be overcome by employing atomistic simulations such as molecular dynamics (MD) and molecular statics (MS) simulations, which were proved to be able to accurately compute the elastic moduli of many glassy systems5,7,27. Particularly, the MD simulations offer a promise of being able to predict the elastic moduli for the glass compositions that have not been experimentally synthesized20,28. As a result, one can achieve a compositionally homogenous sampling for any glass system of interest without the need of concerning the practical manufacturing constraints. However, even though the MD simulation is an effective and efficient tool, with current and near-term computing techniques, it can only access a limited fraction of discrete compositions in a practical design space that contains several (~5) oxide-components using tens of millions of CPU hours. Therefore, from the practical view, it is expected that the developed ML model is capable of giving reliable predictions over a large and even the entire compositional space despite the training is based on a limit set of data of lower-order systems (e.g., binary and ternary SiO2-based systems). To achieve this goal, the model cannot be purely empirical. A subtle set of descriptors should be constructed to include not only the information of glass composition but also the physical information related to the chemical characteristic of the components28, such as the parameters associated with atomic bond energies. In fact, several recently developed physic-based topological models have demonstrated quantitative connections between glass elasticity and the free energies associated with breaking different bond constraints between cations and anions25,26,29,30.
In this work, through merging ML approaches with high-throughput MD simulations, we aimed to develop a quantitatively accurate model to predict densities and elastic moduli of SiO2-based glasses according to the glass composition but across a complex compositional space. The effects of 13 types of additive oxides were investigated, namely Li2O, Na2O, K2O, CaO, SrO, Al2O3, Y2O3, La2O3, Ce2O3, Eu2O3, Er2O3, B2O3, and ZrO2. The training set was generated using MD simulations to homogenously sample the density and elastic properties of a part of the constituent binary and ternary systems. A set of descriptors was carefully constructed from the force-field potentials used for MD simulations and elemental mole fractions to include both physical and compositional information. Sequentially, enlightened by the previous work17, a statistical learning/predicting model was developed by implementing the least absolute shrinkage and selection operator31 with a gradient boost machine32 (GBM-LASSO). As a comparison, a traditional decision tree-based model (M5P)33,34 was also employed. By validating with a large amount (≫1000) of both simulation and experimental data, the GBM-LASSO model was demonstrated to have promising prediction capabilities on both densities and elastic moduli for the SiO2-based glasses not only within the composition range of the training set but also the high-dimension compositional spaces beyond the training set. The developed ML model could be useful for rapid glass composition-property screening that allows for a fruitful estimation and overview on the density and elastic properties of the general multi-component glass systems, especially the unexplored composition regions.
Results
Physics-informed descriptors
The successful application of ML approaches on the modeling of material properties requires the selection of an appropriate set of modeling variables or, namely, the descriptors for the property of interest. In general, the descriptors are expected to be capable of both sufficiently distinguishing each of the modeled compounds/materials and determining the targeted property. In this context, chemical compositions are straightforwardly used as one type of the most common descriptors as they are usually unique for each modeled material, and many material properties are eventually compositional dependent. In fact, several recent works have shown that using chemical compositions only as descriptors can describe the glass properties through the artificial neural network based ML algorithm20,21,22,35. However, only using compositional descriptors could make the model have limited extrapolative ability13,24,28.
Alternatively, one can construct the descriptors using a group of material feature parameters that have physical correlations with the targeted property. In this way, the resulting model could potentially capture the underlying physical mechanisms after training, and thus offer reliable predictions for the chemistries beyond the training set. These material quantities are generally classified into two categories, namely the chemical and structural feature parameters15,17. Chemical feature parameters are usually elemental properties, such as the effective ionic charge, atomic radius and weight, and electronegativity, which can be obtained by requiring the knowledge of the material chemistry only. Structural feature parameters, such as the atomic coordination number and bonding distances, and radial distribution function, require knowledge of the specific atomistic structures of the material (in addition to the chemistry), and they need to be determined experimentally or from atomistic simulations, such as MD simulations in the present work.
For fast mapping the glass properties in a complex computational space, it is not efficient to use both the chemical and structural feature parameters to construct descriptors. Densities and elastic moduli of the SiO2-based glasses are indeed strongly correlated with or determined by many of the glass structural features, such as atomic packing density, coordination numbers and ring sizes of network formers5,7,36,37,38,39,40,41. These structural feature parameters, however, are unknown for a given glass composition in the present work unless the MD simulations have been performed to obtain the corresponding atomistic structure. On the other hand, if the atomistic structure of a glass material is already known, there is no need to perform any ML-based predictions as the elastic moduli and density can be easily and quickly calculated via a MS simulation using the strain-stress method described in Methods Section. In fact, obtaining the glassy structure via MD simulations is the most time-consuming step when computing the density and elastic moduli of a SiO2-based glass. Thus, only the chemical quantities are considered for the construction of the descriptors for the ML model in the present work. As a result, the developed ML model is able to predict the properties by only requiring the information of the glass chemistry and without the need to run any additional MD simulations.
The construction of the descriptors should always start with the ones that are physically relevant to the material property of interest. In the MD and MS simulations, the interatomic interactions are determined by the force-field potentials. The calculated density and elastic moduli are actually derived quantities from many multilevel and intricate MD and MS runs. Therefore, the parameters of the force-field potentials can be a set of suitable candidates to construct the ML descriptors due to their intrinsic characteristics to describe the physical features of interatomic bonds.
In the present work, a set of self-consistent force-field potentials27,42,43,44,45,46,47,48,49,50,51 are employed to perform the MD and MS simulations. The potential consists of long-range Coulomb interactions and short-range interactions described in the Buckingham form52, which can be expressed as,
Here ri,j is the interatomic distance between atom i and j; qi and qj are the effective ionic charges of atom i and j, respectively; Ai,j, Bi,j, and Ci,j are the energy parameters of the Buckingham form between i and j. The values of the effective ionic charges and Buckingham parameters for each element are summarized in Table 1. Therefore, according to Eq. 1, the descriptors associated with the Coulomb interactions for a given glass composition is written as,
Here qm and qn denote the effective ionic charges listed in Table 1, which have values among −1.2, +0.6, +1.2, +1.8, and +2.4 e; \(c_{i_m}\) and \(c_{j_n}\) denote the mole fractions of the constituent elements i and j with effective ionic charge qm and qn, respectively. For example, for a glass that containing Na, K, Ca, and Sr, as the effective ionic charges are +0.6 e for Na/K and +1.2 e for Ca/Sr, respectively, the descriptor that corresponds to the Coulomb interactions between the ions with +0.6 and +1.2 e charges is calculated as \(u_{ + 0.6, + 1.2}^{{\mathrm{Coul}}} = \left( {c_{Na_{ + 0.6}} + c_{K_{ + 0.6}}} \right) \cdot 0.6 \cdot \left( {c_{Ca_{ + 1.2}} + c_{Sr_{ + 1.2}}} \right) \cdot 1.2\), where \(c_{Na_{ + 0.6}},c_{K_{ + 0.6}}\), \(c_{Ca_{ + 1.2}},{\it{{\mathrm{and}}}}\,c_{Sr_{ + 1.2}}\) are the elemental mole fractions of Na, K, Ca, and Sr, respectively. Because there are five different types of charge valences assigned for the elements that modeled in the present work, the total number of the Coulomb interactions descriptors, \(u_{q_m,q_n}^{{\mathrm{Coul}}}\), is \(C_5^1 + C_5^2\) = 15.
As shown in Eq. 1 and Table 1, the MD parameters associated with the Buckingham term describe the short-range interactions between each ion in a very complex way. Since we do not have a priori knowledge of how to combine these parameters to result in optimal modeling results, based on our previous experience17, the corresponding descriptors are constructed as a series of weighted Hölder means, from which the ML model selects the most useful descriptors for modeling and predicting the glass properties of interest. As shown in Table 1, there are three individual Buckingham parameters (i.e., Ai,o, Bi,o, and Ci,o) for each element to describe its short-range interactions with the O anions (including the O–O self-interactions). Among these three parameters, the Bi,o term influences the short-range interaction energy exponentially based on Eq. 1. Therefore, different from Ai,o and Ci,o, Bi,o is not directly used as the feature parameter for the descriptor construction. Instead, in order to accurately describe the exponential effects of Bi,o, we proposed to use a parameter, \(B_{i,O}^\prime\), for the descriptor construction. The \(B_{i,O}^\prime\) parameter is calculated from Bi,o,
where \(r_{i,O}^0\) is the distance where the first derivative of the Buckingham form becomes zero. Therefore, for each type of the ions, \(r_{i,O}^0\) is actually calculated from the values of Ai,o, Bi,o, and Ci,o. In addition, since Ci,o of Li has a zero value, extra procedures were applied to obtain the value of the \(r_{i,O}^0\) term for Li, which is described in detail in Supplementary Note 3. The calculated values of the \(B_{i,O}^\prime\) term for all the elements studied in the present work are summarized in Table 1, along with their MD parameters. Thus, the descriptors associated with the short-range interactions are eventually generated from Ai,o, \(B_{i,O}^\prime\), and Ci,o based on the glass composition (ci) as the following,
where \(u_p^x\) denotes the descriptors generated from the feature parameter xi,O associated with the Buckingham short-range interactions between the element i and O. There are three types of xi,O, Ai,o, \(B_{i,O}^\prime\), and Ci,o. Let \(S_{{\mathrm{ele}}} = \left\{ {{\mathrm{Si,O,Li,Na,K}} \ldots } \right\}\) be the set of the elements contained in the glass. Different values of p results in different Hölder means of x, which are the quartic-harmonic mean (p = −4), cubic-harmonic mean (p = −3), quadratic-harmonic mean (p = −2), harmonic mean (p = −1), geometric mean (p = 0), arithmetic mean (p = 1), Euclidean mean (p = 2), cubic mean (p = 3), and the quartic mean (p = 4), respectively. In addition, in Eq. 4, ci is the mole fraction of the glass constituent element i. Besides, we also consider the standard deviation of the arithmetic means (\(u_1^x\)) as a type of descriptors, which is calculated as,
Based on Eqs. 4 and 5, thirty distinct descriptors are generated in total from Ai,o, \(B_{i,O}^\prime\), and Ci,o (27 from Eq. 4, and 3 from Eq. 5). In addition, we include the multiplications between any two of the thirty descriptors as interaction terms to consider the non-linear relations among these descriptors. Finally, we also include the arithmetic mean of the atomic mass as an individual descriptor. As a result, overall 511 input descriptors are generated for the ML models, in which there are fifteen descriptors associated with long-range Coulomb interactions, thirty descriptors generated from the MD parameters of the Buckingham term and 465 corresponding interaction terms (including self-interactions, thus \(C_{30}^1 + C_{30}^2\) = 465), and one descriptor representing the mean atomic mass.
Regressions accuracy of training data
In the present work, the training dataset was generated by high-throughput MD simulations, which contains the densities, bulk and shear moduli (i.e., K and G) of 498 individual glass compositions in 11 binary and 20 ternary SiO2-based systems as summarized in Supplementary Table 5. In all, 11 types of additive oxides were considered, namely Li2O, Na2O, K2O, CaO, SrO, Al2O3, Y2O3, La2O3, Ce2O3, Eu2O3, and Er2O3. The ML models (i.e. GBM-LASSO and M5P models) were applied to learn each of the glass properties separately.
The densities from the MD-calculated training dataset are plotted in Fig. 1 against the corresponding regression results from the GBM-LASSO and M5P models. For the sake of a clear representation, the data points are grouped into four categories, which are pure amorphous SiO2, type-I glasses that only contain alkali and alkaline earth oxides as additives, type-II glasses that contain Al2O3 and other oxides, and type-III glasses that contain rare-earth and other oxides. As shown in Fig. 1, the glass densities produced from both GBM-LASSO and M5P models agree well with the results from MD calculations with root-mean-squared-errors (RMSE) as small as 0.0229 and 0.0325 g cm−3, respectively. It is also found that the distributions of the prediction residuals are close to norm distributions. Together with the histogram of residuals, Fig. 1 implies the ML models demonstrate the correlations of interests very well without any abnormal performance. The regression results of the two ML models on the bulk and shear moduli are also illustrated as parity plots shown in Figs 2 and 3. Still, good agreements are observed between the predictions from ML models and those from MD simulations in the training set. The residuals of the models also approximately follow normal distributions. The regression RMSEs of K and G of the GBM-LASSO model are 2.99 and 1.31 GPa, respectively, while 2.59 and 0.97 GPa for the M5P model. In addition, the GBM-LASSO model seems to yield slight underestimations on the glass samples with higher moduli, as shown in Figs 2a and 3a.
a Performance of the GBM-LASSO model. b Distribution of residuals between the GBM-LASSO predictions and the MD results of the training set. c Performance of the M5P model. d Distribution of residuals between the M5P predictions and the MD results of the training set. The curved lines in b, d are normal distributions constructed from the mean and the standard deviation of the residuals. The data points are grouped into four categories based on their glass chemistry, which are pure amorphous SiO2, type-I glasses that only contain alkane and alkane earth oxides as additives, type-II glasses that contain Al2O3 and other oxides, and type-III glasses that contain rare-earth and other oxides.
a Performance of the GBM-LASSO model. b Distribution of residuals between the GBM-LASSO predictions and the MD results of the training set. c Performance of the M5P model. d Distribution of residuals between the M5P predictions and the MD results of the training set. The curved lines in b, d are normal distributions constructed from the mean and the standard deviation of the residuals. The data points are grouped into four categories based on their glass chemistry by following the definitions Fig. 1.
a Performance of the GBM-LASSO model. b Distribution of residuals between the GBM-LASSO predictions and the MD results of the training set. c Performance of the M5P model. d Distribution of residuals between the M5P predictions and the MD results of the training set. The curved lines in b, d are normal distributions constructed from the mean and the standard deviation of the residuals. The data points are grouped into four categories based on their glass chemistry by following the definitions in Fig. 1.
Here, to further evaluate the regression accuracy of the ML models, we define the relative error as,
where XMD is the density or elastic modulus calculated from MD simulation and XML is the prediction from the GBM-LASSO or M5P model. As shown in Table 2, for both K and G, over 60% of the predictions from both ML models have a relative error of <5%, and over 90% predictions are within a relative error of <10%, indicating that excellent regression accuracy is achieved. Additionally, we find that the LASSO method has indeed significantly shrunk the size of the descriptor set. Among the 511 input descriptors, only 119, 127, and 87 descriptors are found to have non-zero regression coefficients when the ML models predict the glass density, K and G, respectively. It is also found that many of these descriptors have been multiply used for the LASSO regressions at different GBM iterative steps, indicating they are indeed important and useful to describe these glass properties.
Prediction capability
Since the ML models are only trained with a small set of data from MD simulations for the binary and ternary systems, providing reliable predictions out of the domain of the training set is quite crucial for the present models in terms of the future applications in the practical glass design spaces. Here, we randomly choose 11 ternary, 30 quaternary, 30 quinary, and 30 senary glass compositions that are not included in the training dataset to evaluate the prediction capabilities of the ML models in the compositional space beyond the training set. For each chosen composition, the GBM-LASSO and M5P models are applied to predict its density, K and G, and then MD simulations are correspondingly performed to validate the ML predictions. The validation results are shown as parity plots in Fig. 4. In addition, the prediction errors are analyzed and summarized in Table 3 in the same way as the error analysis of the training process (Table 2). On the one hand, it is found that the M5P model seems to yield large uncertainties when extrapolating. As shown in Table 3, the RMSEs of the predictions from the M5P model with respect to MD validations are 0.1774 g cm−3, 5.24 and 2.27 GPa for density, K and G, respectively, which are much larger compared to the RMSEs of the learning results listed in Table 2 (0.0325 g cm−3, 2.59 and 0.97 GPa for density, K and G). In addition, as shown in Fig. 4a–c, the data points in the parity plots of the extrapolative predictions are more scattered compared to the results of the training process (Figs 1c, 2c, and 3c). Particularly, as marked out in Fig. 4b, c, there are several predictions for the bulk and shear moduli that largely deviated from the MD results. Their relative errors are found to be over 20%. Moreover, it is worth to note that the M5P model is also trained by further decreasing the number of descriptors, which only resulted in a further increase in the training RMSEs but no significant improvements on the prediction RMSEs.
The predictions from the M5P and GBM-LASSO model are plotted versus the validation results from MD simulations. a–c Density, bulk and shear moduli predicted by the M5P model. d–f Density, bulk and shear moduli predicted by the GBM-LASSO model. The glass compositions used for the testing are from 101 randomly chosen ternary, quaternary and senary systems that are not included in the training set. The composition information of each data point can be found in Supplementary Table 6. The data points within the region between two black dot-dashed lines have relative errors less than 10%.
On the other hand, the developed GBM-LASSO model shows very promising prediction capabilities for multicomponent glass systems beyond the training set. As shown in Fig. 4d–f, the density, K and G predicted from the GBM-LASSO model are in very good agreement with the MD results. Nearly 85% of the predictions for K and over 90% for G have relative errors <10%. Moreover, as shown in Table 3, the RMSEs of the predictions from the GBM-LASSO model with respect to MD validations are 0.0536 g cm−3, 3.69 and 1.34 GPa for density, K and G, respectively, agreeing well to the training uncertainties of the model listed in Table 2. The results suggest that, after training with a small set of data for only binary and ternary systems, the developed GBM-LASSO model shows promising abilities to give reliable predictions for multicomponent k-nary glasses as long as their constituent oxides are included in the training set.
Moreover, we find the prediction range of the GBM-LASSO model can be possibly extended to cover more types of additive oxides by adding a small amount of related binary and ternary MD data to the training set. Here we use B2O3 and ZrO2 as examples, as the Buckingham potentials for boron and Zr have been recently developed by Du et al.43,53, which are also compatible with the set of MD potentials used in the present work. The original training set is slightly modified by adding a few new binary and ternary data with glass compositions containing B2O3 or ZrO2. Specifically, 7 binary and 21 ternary data are added with compositions from the xB2O3-(100-x)SiO2 (x = 5, 10, 15, 20, 25, 30, and 35) and xB2O3-yNa2O-(100-x-y)SiO2 systems (x, y = 5, 10, 15, 20, 25, and 30, and x + y ≤ 35), respectively. Also, for ZrO2, 13 new data are added to the training dataset, which are xZrO2-(100-x)SiO2 (x = 5, 10, 15, 20, 25, 30, 35) and xZrO2-(35-x)Na2O-65SiO2 (x = 5, 10, 15, 20, 25, 30). The GBM-LASSO model is re-trained with the corresponding new training set. Notably, the density, K and G of the newly added glass compositions are well reproduced by the new training dataset, and the overall RMSEs are just slightly varied (0.012 g cm−3 for density, 0.26 GPa for K and 0.30 GPa for G) from the values listed in Table 2. As shown in Fig. 5a, b, the non-linear effects of B2O3 on the bulk and shear moduli are accurately described for the xB2O3-(100-x)SiO2 and xB2O3-(30-x)Na2O-70SiO2 glasses after training. Moreover, the newly trained model can then be expanded to the multicomponent glasses that contain B2O3 and ZrO2. As shown in Fig. 5c, the ML predictions for several B2O3-containing compositions, which are not in the training set, are well confirmed by MD validations. Similar results are also observed for the ZrO2-containing glasses as shown in Supplementary Fig. 4. These results suggest that the developed GBM-LASSO has great potentials to be further expanded to cover more types of additive oxides in the future. To achieve such expansions, we only need a few of MD simulations to generate the binary and ternary data containing new types of oxides for the training set.
a, b Reproduction of the non-linear effects of B2O3 on bulk and shear modulus in the a xB2O3-(100-x)SiO2 and (b) xB2O3-(30-x)Na2O-70SiO2 glasses in the training set. c Predictions from GBM-LASSO versus MD results on the test set. The test set is composed of 15 randomly selected compositions for the B2O3-containing multicomponent glasses (detailed information is listed in Supplementary Table 7) that are not included in the training dataset.
We believe the outstanding prediction capability of the GBM-LASSO model may benefit from two aspects: the method of descriptor construction and the advantages of the regression algorithms employed in the model. As described in Eqs. 2–5, instead of directly using the chemical composition as descriptors, the present model constructs descriptors from the compositional averages of the MD potential parameters. As a result, these descriptors can not only smoothly map the entire design space as they are continuous functions of the glass compositions but also contain the information to reflect the intrinsic physical features of each component element, which are compositionally discrete. More importantly, the construction method ensures that the total number of the descriptors is invariant to the arity of the glass chemistry. In other words, it generates the same number of descriptors for any given glass composition, no matter how many types of additive oxides it contains, as long as the interatomic potentials based on Eq. 1 is used for MD simulations. In addition, most of the descriptors still have non-zero values even when the investigated glass contains only one or two types of additive oxides. As a result, this would allow the ML models to transform the extrapolation problems in the chemical compositional space into interpolation-like problems in the constructed descriptor space based on both glass composition and MD force-field parameters.
Furthermore, the GBM-LASSO model may also benefit from some unique features of the regression algorithms employed in the model. In principle, a good prediction ability means a model should avoid over-fitting performance and still achieve a regression accuracy as high as possible. In the present work, due to a relatively small size of the train set, the number of descriptors is almost the same as the number of training data. This results in a potential risk of over-fitting if all the descriptors are considered equally strong and used for regression. The LASSO regression method could be particularly useful to resolve this issue as it screens out the nonsignificant descriptors by setting their coefficient to zero. As a result, the risk of over-fitting could be efficiently reduced as the regression is actually produced by a much smaller number of descriptors.
Moreover, for a broader comparison, we also applied our descriptors and training/testing data with other two typical ML models, a frequently used GBM regression tree model (GBM-RT) implemented in the XGboost package54 and a model using the elastic net method55 under the GBM framework (GBM-EN). The prediction performances of these two models are described in detail in Supplementary Note 5. Comparing the prediction performances of all the test ML models (i.e., GBM-LASSO, GBM-EN, GBM-RT and M5P), it is noticed that GBM-LASSO/EN models generally show better performance than the tree-based models when predicting beyond the training set. One possible reason could be that the GBM-LASSO/EN models conduct continuous regression functions (LASSO and EN) by considering all the observations/descriptors simultaneously at each GBM-iterative step, and they do not perform data classification like the tree-based model. As a result, the regression processes enforce more smoothness than the tree-based models in the functions mapping continuous descriptors to observations, especially when the size of the training set is small and the targeted responses are continuous functions of descriptors. On the other hand, tree-based methods usually require hard thresholds on the classification boundary. This requirement could result in large prediction uncertainties for the untrained sample if one or several input descriptors have values very close to the classification boundary, especially when the model itself is trained with a small set of data but used for extrapolative predictions. For this reason, the GBM-LASSO model proposed in the present work could be advantageous for many of materials problems. In these cases, the properties of interests (e.g., density and elastic moduli) are reasonably continuous and smooth to the descriptors (e.g., compositions), but the training set is relatively small and established from the studies of sparse regions.
Comparison between ML predictions and experimental measurements
To further evaluate the model reliability, the predictions of the present GBM-LASSO model are validated with a large amount of experimental data across a multicomponent compositional space. Specifically, we collected the experimentally measured density and shear (G) and Young’s (E) moduli from the Sciglass 7.12 database, which in turn were gathered from academic literature and patents published up to May 201456, for the SiO2-based glasses containing the 12 additive oxides (i.e., Li2O, Na2O, K2O, CaO, SrO, Al2O3, Y2O3, La2O3, Ce2O3, Eu2O3, Er2O3, and ZrO2) that have been considered in the present work. When collecting the data, we constrained the composition of SiO2 to be no <50 mol%. In comparison, it is worth to note all the glass compositions in our MD training dataset have no <65 mol% SiO2. Overall 550 data points, including 142 binary, 303 ternary, 95 quaternary, and 10 higher-order data (oxide components more than four), were collected for G; 1010 data points, including 231 binary, 464 ternary, 157 quaternary, and 158 higher-order data, were collected for E; 4647 data points, including 1327 binary, 2483 ternary, 607 quaternary and 230 higher-order data, were collected for density. Moreover, ~30% of the data have the SiO2 composition less than 65 mol%, which can serve as a validation to test the extrapolation capability of the present ML model in the compositional space. In addition, among these collected data, some of them can correspond to the same or very similar glass compositions, but they are gathered from different literature sources, as the density and elastic moduli for those compositions have been measured multiple times previously.
For each of the collected experimental data point, we took the corresponding glass composition to predict the G, E and density using our GBM-LASSO ML model and compare them with the experimental values. The predicted E is calculated from predicted K and G as described by Eq. 10 in Methods Section. It is worth to mention that the GBM-LASSO model is still only trained with the MD training set, and the collected experimental data were not used for training. As shown in Fig. 6, the validation results are characterized as 2D-hexbin plots with the ML predicted results versus the experimental values. It is found that the predictions from the GBM-LASSO model generally agree well with the experimental measurements. Compared to the experimental values, over 50% of the model predictions have relative errors <7%, and ~90% predictions are with relative errors <15% for both G and E. In terms of density, the predictions from the ML model yields even better agreement with experiments, where over 80% of predictions have relative errors <3% and 96% of predictions are with relative error <6%.
Experimental data were collected from the Sciglass 7.12 database56. The GBM-LASSO model is only trained with the MD training set and the experimental data were not used for training. a Shear modulus; b Young’s modulus; c Density. The dashed line is the identity where the predictions are equal to the experimental values. The hexagonal unit with a hotter color means that there are more data points within the coverage area of the unit. The dashed-line circles in a mark out typical examples of prediction outliers caused by experimental data inconsistency.
Besides the general agreement between the ML predictions and experimental data, as shown in Fig. 6, it is noted that there are still scattered ML predictions that are largely deviated from the experimental values. After a careful analysis, we found that many of these prediction outliers should result from the inconsistency between the experimental data as they were gathered from different sources. In other words, the predictions of the ML model are in a good agreement with other sets of the experimental data with the glass compositions that are equal or close to the outliers. Here we show two typical examples as marked by the dashed-line circles in Fig. 6a. One set of the data there corresponds to a measurement on the Li2O-SiO2 binary glasses with Li2O contents ranging from 26 mol% to 40 mol%, in which shear modulus of the glasses were reported to range from 5.71 to 13.79 GPa57. In contrast, at the corresponding compositions, the ML model predicted that the shear moduli should be ~31–33 GPa, which are actually in very good agreement with the results of experimental measurements on similar glass compositions from other two studies58,59. Another set of data marked by the circle in Fig. 6 corresponds to a measurement on the Al2O3-Y2O3-SiO2 glasses60, where the ML model yields conflict predictions. However, in the meanwhile, the ML predictions on the Al2O3-Y2O3-SiO2 glass systems are also confirmed by other experimental measurements61,62,63 (More details are described in Supplementary Note 6). In addition, we acknowledge that, for some of the prediction outliers in Fig. 6, we still cannot have clear reasons as there are no other data available for comparison. These outliers can result from the inaccuracy of the MD simulations or the ML model when predicting the elastic moduli and densities for some specific glass chemistries. For example, it is found that the present ML model generally underestimates the densities of ternary glasses containing both Al2O3 and rare-earth oxides (i.e., Y2O3, La2O3, Eu2O3 and Er2O3).
More importantly, after we remove these outliers (i.e. 15 out of 550, 35 out of 1010, and 77 out of 4647 in total for G, E and density, respectively) that can be confidently regarded as the experimental inconsistency, the RMSEs of the predictions from the present GBM-LASSO model are 2.51, 6.67, and 0.0700 g cm−3 for G, E and D, respectively, which are reasonably small by considering the possible uncertainties of the experimental measurements. Such uncertainties are quite common in the Sciglass database due to different experimental methods and sources (one example is shown in Supplementary Fig. 2b). The general agreements between the ML predictions and experimental data shown in Fig. 6 further support the prediction reliability of the present GBM-LASSO model in a complex compositional space.
In addition, when validating with the experimental data for the B2O3-containing glasses from the Sciglass database, we found that the present GBM-LASSO model could have relatively large uncertainties in prediction accuracy. For example, the model predictions on the Young’s moduli of the B2O3-Na2O-SiO2 ternary glasses are found to agree with the experimental measurements from some certain groups64,65,66 (RMSE: ~6.33 GPa) but largely deviate from other experimental data in the Sciglass database (RMSE: ~15.05 GPa)56. There are two possible reasons for such fluctuations in prediction accuracy. First, the experimental data from different studies already contain large fluctuations in elastic moduli for glasses with similar chemical compositions67,68,69, indicating potentially large errors in some experiments. Second, the force-field potential of B2O3 employed in the present work can be inaccurate in terms of describing the elastic moduli. As reported by the developers of this B2O3 potential53, the MD predicted bulk, shear and Young’s modulus can be much higher than the experimental values in the B2O3-Na2O-SiO2 ternary system (up to 50% depending on the concentrations), although the variation trends with respect to the glass compositions are reproduced. However, because of the consistency between the MD results and our ML predictions (Fig. 5c), our developed GBM-LASSO model still has the capability to provide more reliable and accurate predictions for the B2O3-containing glasses, as long as compatible interatomic potentials that are more accurate on elastic properties are developed. Under that situation, one would only need to use the new interatomic potential to calculate a small amount of binary and ternary data and incorporate them into the training set.
Furthermore, the prediction capability of the GBM-LASSO model on elastic moduli is also evaluated by comparing it with a widely used physics-based model developed by Makishima and Mackenzie70,71, hereafter referred to as MM model. Noteworthily, the MM model requires the actual density of the glass as an extra input, but the present GBM-LASSO model can make predictions only according to glass compositions, which makes it more suitable to be used as a fast screening tool before practical syntheses. Additionally, in the MM model, the interactions between atoms are assumed to be fully ionic so that Young’s modulus can be derived from the Coulomb form of the electrostatic energy71. Such an ionic assumption could be problematic when it is applied for modeling the transition-metal oxides since the partially covalent characteristics of the metal-oxygen chemical bonds cannot be ignored. However, the covalent characteristics can be well captured by the Buckingham short-range interaction parameters in MD simulations, which are also used as input features to construct ML descriptors in the present work.
Indeed, compared to the MM model, it is found that the GBM-LASSO model yields considerable improvements on the elastic moduli predictions for the SiO2-based glasses containing transition-metal oxides. By using an experimental validation dataset collected from the Sciglass database, which is composed of multicomponent SiO2-based glasses with Y2O3 as one of the constituent components, the prediction RMSE of the GBM-LASSO model is calculated to be 10.16 GPa. As a comparison, the prediction RMSE of the MM model on the same dataset is as high as 22.42 GPa if the density-inputs are taken from the predictions of a widely used empirical regression model developed by Priven10, and 13.39 GPa if experimental densities are used as inputs. Similar results were also observed for the ZrO2-containing glasses, where the prediction RMSE of the GBM-LASSO model is 6.69 GPa, much smaller than that of the MM model, which is 10.55 GPa. More detailed information is provided in Supplementary Note 7.
As a further demonstration, we also performed an investigation in the Y2O3-SiO2 binary systems. Since there are no experimental measurements for this binary system, we performed ab initio MD simulations (AIMD) on bulk modulus (K) for several glass compositions to validate the results of our classical MD simulations. Due to the high computational costs, the AIMD simulations were not performed for predicting Young’s modulus. The calculation settings of the AIMD simulations are described in detail in Supplementary Note 8. As shown in Fig. 7, the bulk modulus predicted from the GBM-LASSO model agree well with both the classical MD and AIMD simulations. However, the predictions from the MM model largely deviate from the results of MD simulations using the glass densities no matter computed from classical MD simulations or predicted from the widely used empirical model developed by Priven10.
The bulk moduli predicted from the GBM-LASSO and MM models70 are in comparison with the calculations from the classical MD and AIMD simulations. The error bar of the AIMD results are generated from the results calculated under different applied strains.
Rapid screening of glass density and elastic moduli
The GBM-LASSO model developed in the present work is able to predict the density and elastic moduli of a given glass composition in a negligible fraction of a second, making it possible for a rapid and comprehensive screening on these properties in a complex compositional space. As an illustration, we apply the trained GBM-LASSO model to systematically map the distributions and variations of the densities and elastic moduli of Y2O3-doped soda-lime-alumina glasses. Specifically, a quinary compositional space composed of Na2O, CaO, Al2O3, Y2O3, and SiO2 is homogenously meshed with a compositional interval of 1.0 mol% and under a constraint that the concentration of SiO2 is no less than 65.0 mol%. The GBM-LASSO model is employed to predict the density, K and G for the glass composition at each mesh point. Overall, 82,251 compositions were studied by running the program on a regular personal computer (PC) in just a few hours. In contrast, tremendous computational powers (108–109 CPU hours) will be burned if purely using the MD simulations to generate the same amount of data.
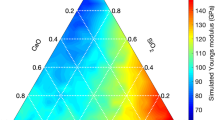
The prediction results are visualized in Fig. 8 as a 2D histogram plot with respect to density and Young’s modulus, E, which is calculated from predicted K and G. From a practical point of view, one would expect a structural glass to have Young’s modulus as high as possible, and meanwhile keep a relatively low density. From Fig. 8 we can know that most of the glasses in the Na2O-CaO-Al2O3-Y2O3-SiO2 system have Young’s moduli around 83 GPa and densities around 2.6 g cm−3. From the screening, it is also found that low Young’s moduli generally occur for the glasses with high Na2O contents, while the large additions of Al2O3 and Y2O3 result in a significant enhancement on Young’s moduli, which is consistent with the previous experimental observation61. As marked by the red-dashed-line circle in Fig. 8, one can achieve a series of glasses with Young’s moduli higher than 100 GPa and densities ranging from 2.5 to 3.1 g cm−3 by optimizing the contents of the additive oxides. In addition, from the screening results, one can also know that it is probably difficult to prepare glasses with densities lower than 2.4 g cm−3 but Young’s moduli larger than 80 GPa in this system. All in all, using the present developed GBM-LASSO model, a compositional-property database for any glass systems of interest can be rapidly generated as long as the corresponding force-field potentials are available and accurate enough to describe the structural and elastic properties. These databases allow the designers to have a fruitful overview on the density and elastic properties to enlighten their own design before experimental syntheses.
The 2D histogram plot is generated from 82,251 compositions, where the GMB-LASSO model is employed to predict the density and Young’s modulus. The content of SiO2 is constrained to be no less than 65 mol%. The hexagonal unit with a hotter color means that there are more glass compositions having density and E within the coverage area of the unit.
Discussion
In this work, we demonstrated a machine-learning framework to efficiently learn and predict densities and elastic bulk and shear moduli of SiO2-based glasses across a multicomponent compositional space, including 13 types of additive oxides, namely Li2O, Na2O, K2O, CaO, SrO, Al2O3, Y2O3, La2O3, Ce2O3, Eu2O3, Er2O3, B2O3, and ZrO2. Our framework combines a learning/predicting statistical model developed by implementing least absolute shrinkage and selection operator with a gradient boost machine (GBM-LASSO), high-throughput MD simulations to provide training data, and a diverse set of descriptors to generalize the chemistries of k-nary SiO2-based glasses. Notably, the descriptors are constructed from the force-field potential parameters used for MD simulations so that they have the capability to bridge the empirical statistical modeling with the underlying physical mechanisms of interatomic bonding. Consequently, even training with a simple dataset only composed of binary and ternary glass samples, the developed GBM-LASSO model exhibits promising prediction capability to allow for quick and accurate predictions on the density and elastic moduli for any k-nary glasses within the 14-component composition space. The GBM-LASSO model also has extendibility to cover new types of oxides through adding a small amount of related binary and ternary MD data to the training set.
The prediction reliability of the developed GBM-LASSO ML model is evaluated by validating with a large amount (»1000) of both simulation and experimental data. Furthermore, after comparing with other frequently used ML models, we found that the outstanding prediction capability of the GBM-LASSO model may benefit from both the way of descriptor construction and the advantages of the regression algorithms employed in the model. In addition, it is found that the GBM-LASSO model also yields considerable improvements on the elastic moduli predictions for the SiO2-based glasses containing transition-metal/rare-earth oxides compared to the widely used MM model70,71. Such improvements originate from the capacity of our ML model to accurately describe the partially covalent bonding characteristics between the transition metal and oxygen atoms. Finally, as an example of its the potential applications, we utilized the model to perform a rapid screening on 82,251 compositions of a quinary glass system to construct a compositional-property database that allows for a fruitful overview on the glass density and elastic properties.
The present work is focused entirely on the modeling of glass density and elastic moduli; however, our ML framework could also be advantageous for the study of other glass physical properties and structural features. Our future studies will be a ML modeling on a few of fundamental glass structural properties, such as bridge/non-bridge oxygen ratio and angle distribution, ring size distributions of the network formers and average coordination number and bond length of cations, which are well-known to be essential to understand many of the physical and mechanical behaves of the SiO2-based glasses. With the present work and more future works, a composition-structure-property database that sits nicely in the “Materials Genome Initiative” landscape28,72,73,74,75 is desired to be developed via ML techniques and serve as powerful tools for the practical design of new glasses in the future. More generally, the methods of descriptor construction and the ML framework introduced in the present work could also be advantageous for many other materials science problems, where the datasets are of modest size and extrapolative predictions in high-dimensional space are required from the learning based on the low-dimensional sparse regions.
Methods
Details of MD and MS simulations
To establish the initial training set (without including the B2O3-containing and ZrO2-containing glass data), high-throughput MD simulations followed by MS energy minimizations were employed to calculate the density, bulk and shear moduli over 498 different glass compositions. The compositions were from 11 binary and 20 ternaries systems, which are specified in Fig. 9. For each system, the mole fractions of the additive oxides species were varied from 0 mol% to 35 mol% for every 5 mol%, while the composition of SiO2 in the systems was kept no less than 65 mol%. For example, for binary systems, calculations were performed at seven compositions, which are xAnOm-(100-x)SiO2 with x = 0, 5, 10, 15, 20, 25, 30, and 35 mol%, respectively. For ternary systems, in addition to the compositions already calculated in constituent binary systems, calculations were performed at the compositions of xAnOm-yBkOl-(100-x-y)SiO2, where x, y = 5, 10, 15, 20, 25, and 30 mol% and x + y ≤ 35 mol%. AnOm and BkOl represent the additive oxides species.
In the present work, all the MD and MS simulations (including the simulations for generating both training and validation data) were performed using a set of interatomic potentials developed by Du and Cormack27,42,43,44,45,46,47,48,49,50,51, which are found to yield reliable predictions on the densities and elastic moduli of various SiO2-based glasses27,53,76,77,78. Another advantage of this potential set is that it covers the common oxides that include most of the industrial glass components. The potential consists of long-range Coulomb interactions and short-range interactions described in the Buckingham form52. The potential formula is expressed as Eq. 1 in Results Section and the values of the potential parameters are listed in Table 1 for each element. In this set of potential, the short-range interactions between cations are not considered since it is assumed that two cations cannot be the first-nearest neighbor ions/atoms. Moreover, it should be noted that, by following the method developed by Deng and Du53, one of the Buckingham parameters of the boron (B) ion, AB,O, was varied with the glass composition in each MD simulation in order to capture the changes in the partitioning between the BO3 and BO4 clusters caused by different chemical environments.
All the MD simulations were performed using the LAMMPS package79. Coulomb interactions were evaluated by the Ewald summation method, with a cutoff of 12 Å. The cutoff distance of the short-range interactions was chosen to be 8.0 Å. Cubic simulation boxes were constructed to consist of about 2100 atoms so that the mole fraction of each oxide species of the samples in the training set can be achieved. Initial atomic coordinates were randomly generated using the program PACKMOL80. The simulation protocol was initiated with relatively equilibration runs of 0.5 ns at 5000 K to remove the memory effects of the initial structure, followed by a linear cooling procedure with a nominal cooling rate of 5 K/ps to 3000 K in the canonical (NVT) ensemble. Then, the system was further equilibrated for 0.5 ns at 3000 K in the isothermal–isobaric ensemble (NPT with zero pressure) to allow a relaxation of the simulation box and atomic positions simultaneously. After this, a MD run with the microcanonical ensemble (NVE) was performed for another 0.5 ns to further equilibrate the system. After the equilibration at 3000 K, the system was gradually cooled down to 300 K through steps of 2500, 2000, 1000, 300 K with a nominal cooling rate of 0.5 K/ps under NPT condition. At each step temperature, the system was equilibrated for 0.5 ns under NPT condition, and then run with an NVE ensemble for another 0.5 ns. At 300 K, the system is equilibrated for 1 ns under NPT condition, which is then followed by a 0.5 ns NVE run. During the final 500,000 NVE steps, atomic configurations were recorded every 50 steps, and an average of the configurations was taken every 1000 records. Eventually, 10 (10 = 500,000/1000/50) atomic configurations of each glass composition were obtained and used for the further calculations of densities and elastic moduli. Recording multiple atomic configurations would allow us to avoid accidentally using a single unreasonable configuration that can lead to large errors in the following energy minimization calculations.
The elastic constants cij for a system are defined as the second derivative of the potential energy U at the corresponding local minimum (the curvature of the potential energy) with respect to small strain deformations, εi,
Based on the Voigt approximation81, which provides the upper bound of elastic properties in terms of uniform strains, the bulk modulus (K) of the system is calculated as,
and the shear modulus (G) is calculated as,
Based on K and G, the Young’s modulus (E) is given by,
With the glassy structures collected from the MD simulations, the density and elastic moduli were computed by means of the GULP code82. A Newton-Raphson energy minimization was performed at zero pressure and temperature to fully relax the output glassy structures from LAMMPS simulations. Then, the density was calculated theoretically by dividing the total system mass by the volume of the relaxed structure. For each glass composition, the GULP calculations were performed for all the 10 atomic structures obtained from the MD simulations, and then the average values of the density and elasticity calculations were taken as the final results. Most of the calculated elastic moduli and densities are well compared with available experimental data. The results are summarized in Supplementary Note 1 (Supplementary Figs 1–3). In addition, the effects of supercell size and initial input structures on the final simulation results were also tested, which is described in detail in Supplementary Note 2.
Statistical models for ML
To leverage the training data as wisely as possible, two types of statistical learning models, namely the GBM-LASSO and the M5P regression tree model33,34, were implemented in the present work to mathematically link the glass properties of interest (i.e., density, bulk and shear modulus) with the constructed descriptors.
The GBM-LASSO model was developed using the gradient boosting machine (GBM) technique32, which uses a gradient descent algorithm to iteratively produce a prediction model in the form of an ensemble of weak learning models. In the present work, the least absolute shrinkage and selection operator (LASSO)31 method was employed to generate the weak learning model at each GBM iterative step. The LASSO method is able to select the important input descriptors by identifying the non-important descriptors with zero regression coefficients and meanwhile keep regresses regularly, especially when the simple linear regression model such as ordinary least square (OLS) does not work due to a relatively small sample size compared with the number of descriptors. As a result, the high-dimension problem (with many potential input descriptors) is simplified to a lower dimension or OLS problem. This method is particularly useful to address the regression problem in the present work, since the size of the training set is small so that the number of the input descriptors is almost the same as the number of the training data (~500). At each GBM iterative step, the LASSO method can both select the descriptors that are most relevant to the glass property being learned and perform an ordinal linear regression using the selected descriptors. In addition, a learning rate of 5% was used to attenuate the LASSO regression term at each GBM iterative step. Moreover, in order to avoid over-fitting the training data, our GBM-LASSO model was also implemented with a 10-fold cross-validation and a conservative risk criterion developed by de Jong et al17. to determine the optimal number of the GBM iterations.
As a comparison to the developed GBM-LASSO model, we also applied a widely used regression tree model, known as M5P and implemented in the Caret/Weka data mining packages33,34, to the same training set. The M5P model was combined with a conventional decision tree model with the linear regression functions at the nodes. Specifically, the M5P model uses all of the descriptors for the linear regression performed at the tree nodes though it only uses partial descriptors for the tree establishment, which could be a problem when the number of the potential descriptors and the number of training data size are comparable. Therefore, in the present work, we first employed the M5P model to rank the importance of all the potential descriptors using the “varImp” function in the Caret package34. Then, the M5P model, including the final linear regression at each node, is run again with the top 100 descriptors that have been ranked from the first step. As a result, the number of descriptors used for the M5P model is comparable to the total number of the descriptors selected by the GBM-LASSO model. The tree structure of the present M5P model is optimized automatically using the prune function and 10-fold cross-validation resampling implemented in the Caret package34. For our specific learning problem, the M5P model has the advantage of being quickly trained.
Data availability
The data of the MD training and test sets are summarized in Supplementary Tables 5–7, and also available from a public open-access repository, Materials Commons (https://doi.org/10.13011/m3-4kwv-g523). The raw data of the MD simulations are available from corresponding author (qiliang@umich.edu) upon reasonable request.
Code availability
The codes that support the findings of this study are available from Materials Commons (https://doi.org/10.13011/m3-4kwv-g523). The ML models in the present work are also available as an open-access cloud computing platform at http://vglassdata.org.
References
Bansal, N. P. & Doremus, R. H. Handbook of glass properties. (Elsevier, 2013).
Wilson, J. & Low, S. B. Bioactive ceramics for periodontal treatment: comparative studies in the Patus monkey. J. Appl. Biomater. 3, 123–129 (1992).
Wallenberger, F. T. & Brown, S. D. High-modulus glass fibers for new transportation and infrastructure composites and new infrared uses. Compos. Sci. Technol. 51, 243–263 (1994).
Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 90, 3019–3039 (2007).
Pedone, A., Malavasi, G., Cormack, A. N., Segre, U. & Menziani, M. C. Insight into elastic properties of binary alkali silicate glasses; prediction and interpretation through atomistic simulation techniques. Chem. Mater. 19, 3144–3154 (2007).
Pota, M. et al. Molecular dynamics simulations of sodium silicate glasses: Optimization and limits of the computational procedure. Comput. Mater. Sci. 47, 739–751 (2010).
Jabraoui, H., Vaills, Y., Hasnaoui, A., Badawi, M. & Ouaskit, S. Effect of sodium oxide modifier on structural and elastic properties of silicate glass. J. Phys. Chem. B 120, 13193–13205 (2016).
Appen, A. A. Chemistry of glass Vol 10 (Khimiya, Leningrad, 1974)
Fluegel, A., Earl, D. A., Varshneya, A. K. & Seward, T. P. Density and thermal expansion calculation of silicate glass melts from 1000 °C to 1400 °C. Phys. Chem. Glasses-Eur. J. Glass Sci. Technol. Part B 49, 245–257 (2008).
Priven, A. I. General method for calculating the properties of oxide glasses and glass forming melts from their composition and temperature. Glass Technol. 45, 244–254 (2004).
Soga, N., Yamanaka, H., Hisamoto, C. & Kunugi, M. Elastic properties and structure of alkaline-earth silicate glasses. J. Non-Crystalline Solids 22, 67–76 (1976).
Pedone, A. & Menziani, M. C. Computational Modeling of Silicate Glasses: A Quantitative Structure-Property Relationship Perspective. in Molecular Dynamics Simulations of Disordered Materials: From Network Glasses to Phase-Change Memory Alloys (eds Massobrio, C., Du, J., Bernasconi, M. & Salmon, P. S.) 113–135 (Springer International Publishing, 2015). https://doi.org/10.1007/978-3-319-15675-0_5.
Mueller, T., Kusne, A. G. & Ramprasad, R. Machine learning in materials science: Recent progress and emerging applications. Rev. Comput. Chem. 29, 186–273 (2016).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. npj Comput. Mater. 3, 54 (2017).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Tanaka, I., Rajan, K. & Wolverton, C. Data-centric science for materials innovation. MRS Bull. 43, 659–663 (2018).
de Jong, M. et al. A statistical learning framework for materials science: application to elastic moduli of k-nary inorganic polycrystalline compounds. Sci. Rep. 6, 34256 (2016).
Evans, J. D. & Coudert, F. X. Predicting the mechanical properties of zeolite frameworks by machine learning. Chem. Mater. 29, 7833–7839 (2017).
Calfa, B. A. & Kitchin, J. R. Property prediction of crystalline solids from composition and crystal structure. AIChE J. 62, 2605–2613 (2016).
Mauro, J. C., Tandia, A., Vargheese, K. D., Mauro, Y. Z. & Smedskjaer, M. M. Accelerating the design of functional glasses through modeling. Chem. Mater. 28, 4267–4277 (2016).
Yang, K. et al. Predicting the Young’s modulus of silicate glasses using high-throughput molecular dynamics simulations and machine learning. Sci. Rep. 9, 8739 (2019).
Bishnoi, S. et al. Predicting Young’s modulus of oxide glasses with sparse datasets using machine learning. J. Non-Crystalline Solids 524, 119643 (2019).
Liu, H., Fu, Z., Yang, K., Xu, X. & Bauchy, M. Machine learning for glass science and engineering: A review. J. Non-Crystalline Solids. https://doi.org/10.1016/J.JNONCRYSOL.2019.04.039 (2019)
Onbaşlı, M. C., Tandia, A. & Mauro, J. C. Mechanical and Compositional Design of High-strength Corning Gorilla® glass. in Handbook of Materials Modeling: Applications: Current and Emerging Materials 1–23 (Springer International Publishing, 2018).
Lu, X., Deng, L., Gin, S. & Du, J. Quantitative structure–property relationship (QSPR) analysis of ZrO2-containing soda-lime borosilicate glasses. J. Phys. Chem. B 123, 1412–1422 (2019).
Lu, X. & Du, J. Quantitative structure-property relationship (QSPR) analysis of calcium aluminosilicate glasses based on molecular dynamics simulations. J. Non-Crystalline Solids 530, 119772 (2020).
Du, J. & Xiang, Y. Effect of strontium substitution on the structure, ionic diffusion and dynamic properties of 45S5 Bioactive glasses. J. Non-Crystalline Solids 358, 1059–1071 (2012).
Mauro, J. C. Decoding the glass genome. Curr. Opin. Solid State Mater. Sci. 22, 58–64 (2018).
Yang, K. et al. Prediction of the Young’s modulus of silicate glasses by topological constraint theory. J. Non-Crystalline Solids 514, 15–19 (2019).
Wilkinson, C. J., Zheng, Q., Huang, L. & Mauro, J. C. Topological constraint model for the elasticity of glass-forming systems. J. Non-Crystalline Solids: X 2, 100019 (2019).
Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 58, 267–288 (1996).
Friedman, J. H. Greedy Function Approximation: A Gradient Boosting Machine. in The Annals of Statistics 1189–1232 (Institute of Mathematical Statistics, 2001).
Rokach, L. & Maimon, O. Data mining with decision trees: theory and applications. (World scientific, 2014).
Kuhn, M. Caret package. J. Stat. Softw. 28, 1–26 (2008).
Cassar, D. R., de Carvalho, A. C. & Zanotto, E. D. Predicting glass transition temperatures using neural networks. Acta Materialia 159, 249–256 (2018).
Rouxel, T. Elastic properties of glasses: a multiscale approach. Comptes Rendus Mecanique 334, 743–753 (2006).
Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M. & Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 439, 419 (2006).
Yiannopoulos, Y. D., Varsamis, C.-P. E. & Kamitsos, E. I. Density of alkali germanate glasses related to structure. J. non-crystalline solids 293, 244–249 (2001).
Deriano, S., Rouxel, T., LeFloch, M. & Beuneu, B. Structure and mechanical properties of alkali-alkaline earth-silicate glasses. Phys. Chem. glasses 45, 37–44 (2004).
Lofaj, F., Dériano, S., LeFloch, M., Rouxel, T. & Hoffmann, M. J. Structure and rheological properties of the RE–Si–Mg–O–N (RE= Sc, Y, La, Nd, Sm, Gd, Yb and Lu) glasses. J. non-crystalline solids 344, 8–16 (2004).
Takahashi, S., Neuville, D. R. & Takebe, H. Thermal properties, density and structure of percalcic and peraluminus CaO–Al2O3–SiO2 glasses. J. Non-Crystalline Solids 411, 5–12 (2015).
Du, J. Challenges in Molecular Dynamics Simulations of Multicomponent Oxide Glasses. in Molecular Dynamics Simulations of Disordered Materials: From Network Glasses to Phase-Change Memory Alloys (eds Massobrio, C., Du, J., Bernasconi, M. & Salmon, P. S.) 157–180 (Springer International Publishing, 2015).
Lu, X., Deng, L. & Du, J. Effect of ZrO2on the structure and properties of soda-lime silicate glasses from molecular dynamics simulations. J. Non-Crystalline Solids 491, 141–150 (2018).
Cormack, A. N., Du, J. & Zeitler, T. R. Alkali ion migration mechanisms in silicate glasses probed by molecular dynamics simulations. Phys. Chem. Chem. Phys. 4, 3193–3197 (2002).
Du, J. & Cormack, A. N. The medium range structure of sodium silicate glasses: a molecular dynamics simulation. J. Non-Crystalline Solids 349, 66–79 (2004).
Du, J. & Corrales, L. R. Compositional dependence of the first sharp diffraction peaks in alkali silicate glasses: A molecular dynamics study. J. Non-Crystalline Solids 352, 3255–3269 (2006).
Du, J. & René Corrales, L. Understanding lanthanum aluminate glass structure by correlating molecular dynamics simulation results with neutron and X-ray scattering data. J. Non-Crystalline Solids 353, 210–214 (2007).
Du, J. Molecular dynamics simulations of the structure and properties of low silica yttrium aluminosilicate glasses. J. Am. Ceram. Soc. 92, 87–95 (2009).
Du, J. & Cormack, A. N. The structure of erbium doped sodium silicate glasses. J. Non-Crystalline Solids 351, 2263–2276 (2005).
Du, J. & Kokou, L. Europium environment and clustering in europium doped silica and sodium silicate glasses. J. Non-Crystalline Solids 357, 2235–2240 (2011).
Du, J. et al. Structure of cerium phosphate glasses: molecular dynamics simulation. J. Am. Ceram. Soc. 94, 2393–2401 (2011).
Buckingham, R. A. The classical equation of state of gaseous helium, neon and argon. Proc. R. Soc. Lond. A 168, 264–283 (1938).
Deng, L. & Du, J. Development of boron oxide potentials for computer simulations of multicomponent oxide glasses. J. Am. Ceram. Soc. 102, 2482–2505 (2019).
Chen, T. & Guestrin, C. Xgboost: A Scalable Tree Boosting System. in Proc. 22nd ACM Sigkdd International Conference on Knowledge Discovery And Data Mining 785–794 (ACM, 2016).
Zou, H. & Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 67, 301–320 (2005).
Mazurin, O. V. & Priven, A. I. Sciglass 7.12. (EPAM systems, Inc., 2014).
Rajendran, V., Khaliafa, F. A. & El-Batal, H. A. Investigation of acoustical parameters in binary X Li2O-(100-X) SiO2 glasses. Indian J. Phys. 69, 237–242 (1995).
Shaw, R. R. & Uhlmann, D. R. Effect of phase separation on the properties of simple glasses II. Elastic properties. J. Non-Crystalline Solids 5, 237–263 (1971).
Mohajerani, A. & Zwanziger, J. W. Mixed alkali effect on Vickers hardness and cracking. J. Non-Crystalline Solids 358, 1474–1479 (2012).
Oda, K. & Yoshio, T. Properties of Y2O3-Al2O3-SiO2 glasses as a model system of grain boundary phase of Si3N4 ceramics (Part 1). J. Ceram. Soc. Jpn. 97, 1493–1497 (1989).
Tanabe, S., Hirao, K. & Soga, N. Elastic properties and molar volume of rare‐earth aluminosilicate glasses. J. Am. Ceram. Soc. 75, 503–506 (1992).
Makehima, A., Tamura, Y. & Sakaino, T. Elastic moduli and refractive indices of aluminosilicate glasses containing Y2O3, La2O3, and TiO2. J. Am. Ceram. Soc. 61, 247–249 (1978).
Aleksandrov, V. I. et al. The production and some properties of high-melting glasses of the system B2O3-Al2O3-SiO2 (in Russian). Fiz. I khimiya Stekla 3, 177–180 (1977).
Appen, A. A. & Gan, F. Study of elastic and acoustic properties of silicate glasses. Zh . Pikladnoi Khimii 34, 974–981 (1961).
LaCourse, W. C. & Cormack, A. N. Glasses with transitional structures. Ceram. Trans. 82, 273–279 (1997).
Molot, V. A. The effect of composition on the mechanical properties of aluminosilicate, borosilicate and galliosilicate glasses. (Alfred University, 1992).
Karapetyan, G. O., Konstantinov, V. A., Maksimov, L. V. & Reznichenko, P. V. Structure of sodium borosilicate glasses from data of spectroscopy of Rayleigh and Mandelshtam-Brillouin scattering. Fiz. i Khimiya Stekla 13, 16–21 (1987).
Takahashi, K., Osaka, A. & Furuno, R. The elastic properties of the glasses in the systems R2O-B2O3-SiO2 (R=Na and K) and Na2O-B2O3. J. Ceram. Assoc., Jpn. 91, 199–205 (1983).
Imaoka, M., Hasegawa, H., Hamaguchi, Y. & Kurotaki, Y. Chemical composition and tensile strength of glasses in the B2O3-PbO and B2O3-SiO2-Na2O systems. J. Ceram. Assoc., Jpn. 79, 164–172 (1971).
Makishima, A. & Mackenzie, J. D. Calculation of bulk modulus, shear modulus and Poisson’s ratio of glass. J. Non-Crystalline Solids 17, 147–157 (1975).
Makishima, A. & Mackenzie, J. D. Direct calculation of Young’s moidulus of glass. J. Non-Crystalline Solids 12, 35–45 (1973).
White, A. The materials genome initiative: one year on. MRS Bull. 37, 715 (2012).
Liu, Z. Perspective on Materials Genome®. Chin. Sci. Bull. 59, 1619–1623 (2014).
Jain, A., Persson, K. A. & Ceder, G. Research update: the materials genome initiative: data sharing and the impact of collaborative ab initio databases. APL Mater. 4, 53102 (2016).
de Pablo, J. J., Jones, B., Kovacs, C. L., Ozolins, V. & Ramirez, A. P. The materials genome initiative, the interplay of experiment, theory and computation. Curr. Opin. Solid State Mater. Sci. 18, 99–117 (2014).
Ren, M., Deng, L. & Du, J. Bulk, surface structures and properties of sodium borosilicate and boroaluminosilicate nuclear waste glasses from molecular dynamics simulations. J. Non-Crystalline Solids 476, 87–94 (2017).
Ren, M. et al. Composition–structure–property relationships in alkali aluminosilicate glasses: a combined experimental–computational approach towards designing functional glasses. J. Non-Crystalline Solids 505, 144–153 (2019).
Xiang, Y., Du, J., Smedskjaer, M. M. & Mauro, J. C. Structure and properties of sodium aluminosilicate glasses from molecular dynamics simulations. J. Chem. Phys. 139, 44507 (2013).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. computational Phys. 117, 1–19 (1995).
Martínez, L., Andrade, R., Birgin, E. G. & Martínez, J. M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 30, 2157–2164 (2009).
Hu, Y.-J. et al. Effects of alloying elements and temperature on the elastic properties of W-based alloys by first-principles calculations. J. Alloy. Compd. 671, 267–275 (2016).
Gale, J. D. GULP: A Computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 93, 629–637 (1997).
Acknowledgements
Y.J.H. and Q.L. acknowledge support by the gift funding from Continental Technology LLC, Indianapolis, Indiana, USA. The high-throughput MD simulations were supported through computational resources and services provided by Advanced Research Computing at the University of Michigan, Ann Arbor. This work also used the Extreme Science and Engineering Discovery Environment (XSEDE) Stampede2 at the TACC through allocation TG-DMR190035.
Author information
Authors and Affiliations
Contributions
Y.J.H. and L.Q. proposed the methodology of descriptors construction. G.Z. and Y.J.H. conceived and implemented the statistical machine learning models. Y.J.H. and M.Z. performed the high-throughput MD simulations. B.B. performed the training of the GBM-RT model. Y.J.H., T.D.R., and G.Z. performed the screening work. Q.Z., Q.Z., Y.C, X.S., and L.Q. conceptualized and supervised the research project. M.d.J. assisted and provided guidance on the computer programing of the machine learning models. Y.J.H, G.Z., and L.Q. prepared the paper. All authors discussed the results and contributed to the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, YJ., Zhao, G., Zhang, M. et al. Predicting densities and elastic moduli of SiO2-based glasses by machine learning. npj Comput Mater 6, 25 (2020). https://doi.org/10.1038/s41524-020-0291-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-0291-z
This article is cited by
-
Thermal conductivity of glasses: first-principles theory and applications
npj Computational Materials (2023)
-
Predicting stress, strain and deformation fields in materials and structures with graph neural networks
Scientific Reports (2022)
-
Predicting glass structure by physics-informed machine learning
npj Computational Materials (2022)
-
Inverse design of truss lattice materials with superior buckling resistance
npj Computational Materials (2022)
-
Can ensemble machine learning be used to predict the groundwater level dynamics of farmland under future climate: a 10-year study on Huaibei Plain
Environmental Science and Pollution Research (2022)