A nonlinear magnonic nano-ring resonator

Abstract

The field of magnonics, which aims at using spin waves as carriers in data-processing devices, has attracted increasing interest in recent years. We present and study micromagnetically a nonlinear nanoscale magnonic ring resonator device for enabling implementations of magnonic logic gates and neuromorphic magnonic circuits. In the linear regime, this device efficiently suppresses spin-wave transmission using the phenomenon of critical resonant coupling, thus exhibiting the behavior of a notch filter. By increasing the spin-wave input power, the resonance frequency is shifted, leading to transmission curves, depending on the frequency, reminiscent of the activation functions of neurons, or showing the characteristics of a power limiter. An analytical theory is developed to describe the transmission curve of magnonic ring resonators in the linear and nonlinear regimes, and is validated by a comprehensive micromagnetic study. The proposed magnonic ring resonator provides a multi-functional nonlinear building block for unconventional magnonic circuits.

Introduction

Spin waves are collective excitations of spin systems in magnetic materials, which can be considered as a potential data carrier in future low-energy data-processing systems^1,2,3,4. This is due to their small wavelengths, down to a few nanometers^5,6, high frequencies up to a few terahertz⁷, ultralow losses^8,9, and abundance of associated nonlinear phenomena^10,11,12. These features make spin waves highly attractive for wave-based and neuromorphic computing concepts. Several important milestones were achieved in the realization of magnonic data-processing units, including logic gates^13,14,15, majority gates^16,17,18, a magnon transistor¹⁹, a phase shifter²⁰, building blocks for unconventional computing^21,22,23, auxiliary units for integrated circuits¹², magnonic directional couplers^24,25,26,27, and an integrated magnonic half-adder²⁵.

Here we propose a nanoscale nonlinear magnonic ring resonator. It is magnetic counterpart of the photonic ring resonator, which is considered as a universal unit and widely used in integrated photonic circuits²⁸, photonic quantum computing²⁹, and photonic neuromorphic computing³⁰. The concept of the magnonic ring resonator (see Fig. 1a) is similar to that of the photonic ring resonator³¹, except that spin waves, instead of light, are used to carry information. A magnonic ring resonator of submillimeter size has been studied in the linear regime using micromagnetic simulations as reported in ref. ³². Although such rather macroscopic ring resonators demonstrate certain interesting features due to multimode coupling and external field sensitivity, their functionality and size are hardly compatible with the current state of the complementary metal-oxide-semiconductor technology. Moreover, the presence of multiple modes such as width modes with different coupling strengths results in less effective energy transfer and makes it impossible for the device to operate in the so-called “critical coupling” condition. Here we study the single-mode nanoscale magnonic ring resonator using the critical coupling phenomenon and demonstrate its functionality analytically and by simulation, including linear and nonlinear operation regimes, as well as their anticipated applications. Despite the fact that this is a simulation, the recent progress in the realization of single-mode magnonic nano-conduits proves that the sizes chosen here can be realized based on the current nano-fabricating technology³³.

Fig. 1: Geometry and parameters used in the modeling.

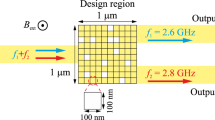
a Generic model of the magnonic ring resonator. The width of the waveguides is w = 100 nm and the thickness is h = 50 nm, the radius (from the center of the ring to the center of the waveguide) is R = 550 nm, the minimum gap between the ring and waveguide is δ = 20 nm. The dashed line shows the position of the reference plane. b Initial magnetization distribution of the investigated structure. The gray arrows and colors represent the in-plane orientations of the magnetization M.

Results and discussion

Theory and micromagnetic simulations of the linear regime

The basic configuration of the magnonic ring resonator consists of a ring of mean radius R and width w, and a straight waveguide of same width w, as shown in Fig. 1a. The static magnetization distribution of the magnonic ring resonator obtained from micromagnetic simulation is shown in Fig. 1b (details of the micromagnetic simulation method are described in “Methods”). For a sufficiently narrow ring, here w = 100 nm, the static magnetization is in the vortex state with the magnetization lying along the ring. Such a vortex state is the ground state in the presence of zero external fields (i.e., it corresponds to the global energy minimum) and it can be easily achieved in experiments^34,35, for instance, by controlling the variation of the external field (see Supplementary Figs. 1 and 2). The static magnetization of a straight waveguide is uniform and is along the waveguide, which is caused by a strong shape anisotropy and by the small cross-section. We consider Yttrium-Iron-Garnet (YIG) as the material of both the waveguide and the ring: it is chosen for its low damping, allowing for long-range spin-wave propagation³⁶. The used material parameters of YIG are described in “Methods.”

For the theoretical description of the power transmission in the ring resonator, we adopt a method typically used in optics and microwave electronics^31,37. Let us denote the complex amplitudes of input (output) spin waves in the waveguide and ring by a_1,2 (b_1,2), as shown in Fig. 1a. To define a reference plane, we use the position of the minimum distance between the ring and waveguide (see the dashed line in Fig. 1a), so that all a_i and b_i are the values, which would be at the point x = 0 if continuously extrapolated in the absence of coupling. If the coupling between the ring and waveguide is lossless, which is the case for pure dipolar coupling, it is described by the unitary scattering matrix³¹:

$$\left( {\begin{array}{*{20}{c}} {b_1} \\ {b_2} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \tau & {{\mathrm{i}}\kappa } \\ {{\mathrm{i}}\kappa } & \tau^* \end{array}} \right)\left( {\begin{array}{*{20}{c}} {a_1} \\ {a_2} \end{array}} \right)$$

(1)

The parameter κ is the coupling coefficient between the straight waveguide and the ring, which shows the fraction of the spin-wave amplitude coupled from the waveguide into the ring structure and vice versa. The parameter τ is the transmission coefficient across the coupling region, which shows the fraction of the spin-wave amplitude passed through the coupling region. The transmission coefficient τ is different from the transmittance T, which demonstrates the final transmitted power through all the structures and accounts for the interference in the ring. Naturally, |ĸ|² + |τ|² = 1, which reflects the lossless nature of the coupling. The calculation of the coefficients κ and τ for the dipolar coupled waveguides and ring is presented in “Methods.”

The complex amplitudes a₂ and b₂ are connected by the circulation condition: a₂ = b₂βe^iθ. Here, β = exp(−2πRΓ/v_gr) is the loss coefficient that describes which part of the spin-wave amplitude remains in the ring after one circulation, with Γ and v_gr being the spin-wave damping rate and group velocity in the ring, respectively (for details, see “Methods”). The parameter θ = 2πRk is the round-trip phase accumulation, where k is the wavenumber of the spin wave in the ring. The wavenumber is determined by the input spin-wave frequency, which is given by the dispersion relation ω_k in the ring and is normally different from the wavenumber in the straight waveguide.

Solving Eq. (1) together with the circulation condition, one finds the transmission T through the ring resonator structure:

$$T = \frac{{\left| {b_1} \right|^2}}{{\left| {a_1} \right|^2}} = \frac{{\beta ^2 + \left| \tau \right|^2 - 2\beta \left| \tau \right|\cos \left( {\theta - \psi } \right)}}{{1 + \beta ^2\left| \tau \right|^2 - 2\beta \left| \tau \right|\cos \left( {\theta - \psi } \right)}},$$

(2)

using the phase ψ = Arg[τ]. In our case of a straight waveguide and ring of the same cross-section, the phase is ψ = 0. At the resonance frequencies, at which θ = 2πn (n = 0, 1, 2, 3, … is the number of the resonance modes in the ring), the transmission T is equal to T = (β − |τ|)²/(1 − β|τ|)². The output signal vanishes completely if the transmission coefficient is equal to the loss coefficient, i.e., |τ| = β, which is the so-called case of “critical coupling.” The maximum transmission T in the critical case, which is reached when θ = (2n + 1)π, is equal to T = 4β²/(1 + β²)², and increases with β. Therefore, it is desirable to work in the range of β ≈ |τ| → 1 to achieve a large output power, i.e., to have small losses in the ring and weak coupling between the ring and the waveguide. However, a small loss and a small coupling increase the operational time of the resonator (time to reach the dynamic equilibrium)³⁸. Thus, optimal values of the transmission coefficient and the loss coefficient are in the range β ≈ |τ| ~ 0.6–0.9, which is the result of the trade-off between a large transmission and a short delay time for the ring resonator.

The coefficients κ, θ, and β depend on the spin-wave frequency. The coupling coefficient κ significantly depends on the gap between waveguide and ring. In our example simulations, the minimum gap, which is the closest distance between the waveguide and the ring, is fixed to δ = 20 nm for all simulations. The ring radius determines the separation between the ring resonance frequencies. To set the loss coefficient to a value close to the optimum of β ≈ |τ|, in our simulations we increased the Gilbert damping in the ring structure to α_G = 2 × 10⁻³. In an experiment, an increase of the YIG damping can be realized, for instance, by placing a normal metal on top of the ring to use the phenomenon of spin pumping³⁹. Please note that the parameters R, δ, and α_G are selected for the working frequency range from 2.6 to 2.8 GHz. These parameters can also be modified to obtain other frequency ranges that fulfill the critical coupling condition.

As an approximation of the ring dispersion relation, in principle, one can use the dispersion relation of a straight waveguide⁴⁰. For our case, it results in only a slight discrepancy of 80 MHz and the discrepancy becomes more negligible for R » w and kR » 1. In all the following calculations, we use a more accurate theory of the dispersion in the ring, as outlined in “Methods.” The spin-wave damping rate and group velocity, which determine the loss coefficient, are calculated from the dispersion relation.

The frequency dependencies of the transmission and the loss coefficient τ and β, together with the round-trip phase θ are shown in Fig. 2. In the chosen frequency range, the condition τ ~ β holds and the critical coupling condition is exactly satisfied at a frequency around 2.55 GHz (not shown in Fig. 2). The frequency dependence of the transmission coefficient is more pronounced because of a significant wavenumber dependence of the dynamic dipolar fields, generated by the spin waves propagating in the waveguide and the ring²⁴.

Fig. 2: Characteristics of the magnonic ring resonator.

Transmission coefficient (τ), loss coefficient (β), and round-trip phase cos(θ) as a function of frequency f.

The theoretical transmission curve of the whole ring resonator calculated according to Eq. (2), as well as the results of micromagnetic simulations are shown in Fig. 3a. In the simulation, the transmission T is defined by calculating the ratio of the spin-wave intensities in the straight waveguide behind and in front of the ring. Two resonance frequencies of the magnonic ring resonator are observed in this frequency range, which correspond to the 16th and 17th resonant mode. At these frequencies, the output signal is vanishing due to the destructive interference in the outgoing waveguide between the transmitted spin wave a₁τ and the coupled-back spin wave ia₂κ, which acquires the round-trip phase of θ = 2πn plus two π/2 phase shifts in the coupler (see Eq. (1)), being, in total, in antiphase to the first wave. At the resonance frequency, all the spin-wave power is concentrated in the ring (see Fig. 3b). In contrast, at the frequency of 2.724 GHz, which corresponds to θ = 2π × 16.5, the constructive interference conditions are satisfied and a large part of input power is transmitted, whereas only a small amount is circulating in the ring (Fig. 3b). A strong frequency dependence of the output power is important, as it allows one to realize notch filters with a magnonic ring and it enhances the sensitivity of the system to a nonlinear frequency shift.

Fig. 3: Transmission behavior of the magnonic ring resonator in linear regime.

a Theoretical (top panel) and simulated (bottom panel) normalized transmission T as a function of frequency f for different radii of the ring. b Snapshot of the out-of-plane component spin-wave amplitude m_z in the ring resonator with the radius of 550 nm for different excitation frequencies.

In addition, Fig. 3 shows the transmission curves for the rings having different radii. As expected, the resonance frequencies change and the resonance curves are shifted, while preserving their shape. The resonance frequencies, calculated analytically, are 20 MHz higher than those found from the micromagnetic simulations. Also, in the simulations, the critical coupling condition is satisfied in the range 2.65–2.68 GHz, as it is evident from the vanishing output at the resonance frequency, whereas theory indicates the critical coupling at a slightly different frequency of 2.55 GHz. These two weak discrepancies are mainly due to a slightly nonuniform width profile of the spin waves in the ring and the waveguide, and to a weak dipolar field generated by the straight waveguide, which slightly modifies the dispersion relation in the ring. Both effects are not taken into account in the theory. Furthermore, there is a certain difference in the maximum transmission energy between the simulations and the theoretical calculations, which is attributed to the propagation losses in the straight waveguide and the coupling area.

Reconfigurable magnonic ring resonator

In the previous section, the magnetization in the ring is oriented counterclockwise and the magnetization in the coupling region between ring and waveguide is aligned parallel. However, in the absence of an external field, the ring can exist in two stable magnetic configurations—clockwise and counterclockwise—as shown in the insets of Fig. 4. These two states lead to antiparallel and parallel magnetization configurations in the coupling region. The switching between these two states can be realized by controlling the tracks of the variation of the external field before reaching the remanent state (for details see Supplementary Figs. 1 and 2). The coupling strength, described by the coupling coefficient κ, depends strongly on the static magnetization configuration and affects significantly the transmission coefficient τ²⁴. The coupling strength is stronger for the antiparallel magnetization configuration and this results in the breaking of the critical coupling condition, i.e., |τ| ≠ β and, consequently, the transmission T at the resonance frequencies increases. Figure 4 shows the transmission curve for parallel and antiparallel alignments in which the transmissions at the resonance frequency of 2.662 GHz are 0.48% and 30.8%, respectively. The contrast between the two states can be further increased by optimizing the parameters of the ring resonator. For a future on-chip magnonic device, this switching can be realized by a local Oersted field created by direct current passing through a conducting wire, which is placed on top of the ring structure. This example shows that the symmetry break caused by the direction of the magnetization allows creating magnonic functionalities that are not available in the same form in, e.g., photonics.

Fig. 4: Reconfigurable magnonic ring resonator.

Simulated transmission T as a function of frequency f for different initial magnetization orientations. The insets show the initial magnetic configurations. The color-disk represents the in-plane orientations of the magnetization M.

Nonlinearity of magnonic rings

Magnonic systems are known to involve a variety of nonlinear effects, which open a way for the development of various nonlinear power-dependent devices. In general, all the parameters, which define the operation of the magnonic ring resonator, namely θ, β, and τ, are power dependent. However, it can be shown that the main impact of nonlinearities is caused by the nonlinear phase accumulation θ = θ(b), where b is the spin-wave amplitude, whereas the nonlinearities of the loss coefficient (due to the group velocity shift) and the coupling strength lead only to a small (second order) correction and, therefore, can be neglected in almost all experimentally achievable cases.

An increase of the spin-wave power results in a nonlinear shift of the spin-wave resonance frequency, $\omega _{k}\left( b \right) = \omega _{k}^{\left( {lin} \right)} + W_{k}\left| b \right|^2$, where W_k is the nonlinear shift coefficient. Consequently, a wave of a constant frequency possesses a power-dependent wavenumber k ≈ k₀ − (W_k/v_gr)|b|², which directly affects the phase accumulation during the spin-wave propagation. The integration over the ring yields the round-trip phase θ(b₂) = 2πR(k₀ − K|b₂|²), where $K=W_{k}(1-e^{-4 \pi \Gamma R/v_{gr}})/4 \pi \Gamma R \approx W_{k} \beta/v_{gr}$ is the averaged coefficient of the nonlinear shift of the spin-wave wavenumber. Then, Eq. (1) together with the circulation condition yields the following relation:

$$\left| {b_2} \right|^2 = \left| {a_1} \right|^2\frac{{\kappa ^2}}{{1 + \beta ^2\tau ^2 - 2\beta \tau \cos \left[ {\theta \left( {b_2} \right) - \psi } \right]}},$$

(3)

which implicitly determines the amplitude in the ring. The transmission T is given by the same Eq. (2), in which one should use the nonlinear phase accumulation θ(b₂) with the amplitude of b₂, found from Eq. (3).

The simulated transmission curves of the magnonic ring resonator for different excitation fields b_e are shown in Fig. 5 (bottom panel). A pronounced shift of the resonance frequency, at which transmission is minimum, is observed. A similar power-dependent transmission curve shift was observed in optical ring resonators^28,41,42. To plot the theoretical curves, we use a nonlinear frequency shift value of W = −2π × 2.6 GHz, which is calculated for a straight waveguide^25,43. As one can see, this approximation is reasonable and gives a similar shift of the transmission minimum position compared to the simulated results.

Fig. 5: Power-dependent transmission curve of the magnonic ring resonator.

Transmission as a function of spin-wave frequency for different values of the excitation field b_e (top panel: theory, bottom panel: simulation). Dashed magenta lines represent the second solution in the bistability range for b_e = 12 mT.

For a large-enough input spin-wave power, the transmission curve becomes bistable (see the magenta line in Fig. 5). The appearance of bistability is clear from Eq. (3), which, by expanding the denominator near the resonance frequency, has the same structure as the nonlinear ferromagnetic resonance curve, demonstrating the foldover effect^44,45. In the bistability range, the exact shape of the transmission curve depends on the experimental (simulation) conditions. The solid curves are obtained when all the simulations start from the same ground state. To access the dashed curve in the simulations, we gradually decrease the excitation frequency starting outside of the bistability range with a constant spin-wave amplitude. The small discrepancy between theory and simulation is mainly attributed to the nonlinear shift coefficient, which is extracted from a straight waveguide and not from the ring structure and the previously mentioned nonuniform spin-wave profile in the ring structure.

Nonlinear ring resonator for neuromorphic applications

In neuromorphic systems, the so-called “activation function” plays an important role. It describes how an incoming stimulus (here, the incoming spin-wave amplitude a₁) is transformed into the output signal (the outgoing spin-wave amplitude b₁) via a strongly nonlinear function. Thus, if the ring resonator should serve as a building block for neuromorphic spin-wave computing in a larger network composed of many resonators and interconnecting spin-wave waveguides and combiners, the activation function is characterized by the transmission T of the ring resonator, which should depend strongly on the input amplitude. For instance, in so-called spiking neurosynaptic networks, the “firing” of an artificial neuron, i.e., the emission of an output signal, takes place only if the input signal overcomes a certain threshold. This essentially means that the transmission T should be significantly large only if a certain incoming spin-wave input amplitude is overcome. Wave-based neuromorphic computing using such kind of function has been recently demonstrated for a full neuronal network in optics³⁰.

To characterize the activation function of the magnonic ring resonator, the spin-wave excitation frequency is fixed to f = 2.662 GHz, which coincides with the 16th resonance in the linear regime, as depicted in Fig. 5 by the vertical dashed line. The output spin-wave intensity nonlinearly depends on the input power, because this frequency does not correspond anymore to a resonance in the nonlinear regime. Figure 6a shows the relative transmission power for f = 2.662 GHz as a function of the excitation field amplitude b_e and the dynamic out-of-plane component of magnetization m_z (top axis). The transmission T is almost constant and below 1% in the excitation field range from 0.6 to 4 mT and then strongly increases from T = 0.78% at b_e = 4 mT to T = 51.5% at b_e = 13 mT due to the strong nonlinear shift and the steep slope of the transmission curve vs. frequency (compare to Fig. 5). A high contrast of around 18 dB between the output states is observed. This is reflected in the fact that by increasing the input spin-wave intensity by a factor of about 10, the transmitted intensity (absolute spin-wave output power) is increased by a factor of around 700. This strong nonlinearity can be achieved, as energy is stored in the ring at resonance. The contrast, threshold, and maximum transmission level can be tuned by adjusting the radius of the ring R, the transmission coefficient τ, and the loss coefficient β. As a further example for the use of the ring resonator for data processing, Fig. 6b shows a functionality that can be considered as a kind of “passivation function,” meaning that the transmitted intensity decreases with increasing input intensity. Due to the foldover effect shown in the transmission curve in the high-power region (see the magenta line in Fig. 5), the transmission T at the frequency of f = 2.638 GHz drops down from 68.6 to 14.2% by slightly increasing the excitation field from 10 to 12 mT. This functionality can be used to filter out the high-power spin waves or normalize the output spin-wave power, i.e., the absolute spin-wave output power could be made independent of the input spin-wave power in a certain power range. It is worth noting that the precession angle is only around 5° even for the high excitation field of 13 mT, which reveals the fact that the energy consumption is very low in the magnon domain.

Fig. 6: Nonlinear functionalities of the magnonic ring resonator.

Simulated transmission T at the fixed frequency of a f = 2.662 GHz representing an “activation function” and b f = 2.638 GHz representing a “passivation function” (power limiter) as a function of excitation field b_e and dynamic component of magnetization m_z, which linearly scales with b_e in the present field range.

In conclusion, a nanoscale nonlinear magnonic ring resonator is proposed and its functionality is demonstrated using micromagnetic simulations. The transmission curve of the ring resonator in the linear region is of a notch filter type due to the resonant critical coupling effect. Spin waves at resonance frequencies are stored in the ring and cannot pass through it, whereas spin waves of a frequency in between the resonances pass the ring resonator with only a small loss. Importantly, the nonlinear shift of the spin-wave resonance frequency and, consequently, of the spin-wave phase accumulation leads to a strong power dependence of the magnonic ring transmission curves. In this nonlinear regime, the resonance frequencies are shifted, the transmission curves become asymmetric, and, at large-enough input power, exhibit a bistability. The transmission at the linear resonance frequency shows a threshold-like behavior: a low-input spin-wave power is stored in the ring structure and the ring only generates an output if the input power exceeds a threshold. This functionality is useful for magnonic logic applications, for instance, in the field of neuromorphic computing. Very different transmission curves can be realized at frequencies not coinciding with the linear resonances. In addition, the transmission functions can be reconfigured by changing the alignment of the magnetization in the ring and the adjacent waveguide. The obtained results are supported by the developed analytical theory, which allows to calculate the ring resonator characteristics in both the linear and nonlinear regimes.

Methods

Spin-wave dispersion in a ring

The dispersion of spin waves in a magnonic ring can be calculated similarly to those of a vortex-state magnetic disk^46,47. It is noteworthy that the ring dispersion relation in the considered system is continuous, ω = ω_k, and spin waves with continuous wavenumbers k can propagate in it, as the ring resonator is not isolated. In our case, the width of the ring is sufficiently small⁴⁰, leading to an almost uniform (unpinned) spin-wave profile across the ring width, which greatly simplifies the calculations. In this approximation, the dispersion relation is given by

$$\omega _{k}^2 = \omega _{\mathrm {M}}^2\left( {\lambda ^2{k}^2 + {\it{F}}_{k}^{\left( {rr} \right)}} \right)\left( {\lambda ^2\left( {{k}^2 - R^{ - 2}} \right) + {\it{F}}_{k}^{\left( {zz} \right)}} \right),$$

(4)

where ω_M = γμ₀M_s, M_s is the saturation magnetization, γ is the gyromagnetic ratio, λ is the exchange length, and $\widehat {\mathbf{F}}_{k} = {\int} {{\int} {\widehat {\mathbf{G}}\left( {{\mathbf{r}}{\mathrm{,}}\,{\mathbf{r}}^\prime } \right)\exp \left[ {{\mathrm{i}}{k}R\left( {\phi - \phi ^\prime } \right)} \right]d{r}d{r}^\prime /\left( {2{\uppi}Rw} \right)} }$ is the effective dynamic demagnetization tensor with $\widehat {\mathbf{G}}\left( {{\mathbf{r}},{\mathbf{r}}^\prime } \right)$ being the magnetostatic Green’s function in the polar coordinate system⁴⁸ and the integration going over the ring surface. For an arbitrary wavenumber, the calculation of $\widehat {\mathbf{F}}_{k}$ is complicated. However, for k_n = n/R, which are the wavenumbers corresponding the resonant modes of an isolated ring, it is greatly simplified and yields

$${\it{F}}_n^{\left( {rr} \right)} = \frac{1}{{4Rw}}{\int}_0^\infty {f\left( kh \right)\left[ {I_{n + 1}\left( k \right) - I_{n - 1}\left( {k} \right)} \right]^2{k}d{k}} ,$$

(5)

$$F_n^{\left( {zz} \right)} = \frac{1}{{hRw}}{\int}_0^\infty {\left[ {1 - e^{ - {k}h}} \right]I_n^2\left( {k} \right)d{k}} ,$$

(6)

where $f\left( {{k}h} \right) = 1 - \left( {1 - \exp \left( { - {k}h} \right)} \right)/\left( {{k}h} \right)$, and we use the notation

$$I_n\left( {k} \right) = {\int}_{R - {w/2}}^{R + {w/2}} {J_n\left( {{kr}} \right){r}d{r}} ,$$

(7)

with the Bessel functions J_n. The function I_n(k) can be expressed via a combination of hypergeometric functions or calculated numerically. The complete continuous spin-wave dispersion ω_k can be numerically found by interpolation of the dispersion relations of the ring resonance frequencies $\omega_{k_n}$. The spin-wave group velocity is found via v_gr = dω_k/dk. The spin-wave damping rate is calculated using the following general formalism⁴⁹:

$${{\Gamma}}_{k} = \alpha _G\omega _{\mathrm {M}}\left( {\lambda ^2\left( {2{k}^2 - R^{ - 2}} \right) + F_{k}^{\left( {rr} \right)} + F_{k}^{\left( {zz} \right)}} \right)/2.$$

(8)

Coupling between waveguide and ring

The dynamics of spin-wave amplitudes a₁(x) and a₂(x) in coupled waveguides is described by the following system of equations²⁴:

$$\left\{ {\begin{array}{*{20}{c}} {v_{\mathrm {gr}}\frac{{da_1\left( x \right)}}{{dx}} = {\mathrm{i}}\omega _{\mathrm {c}}\left( x \right)a_2\left( x \right)} \\ {v_{\mathrm {gr}}\frac{{da_2\left( x \right)}}{{dx}} = {\mathrm{i}}\omega _{\mathrm {c}}\left( x \right)a_1\left( x \right)} \end{array}} \right.,$$

(9)

where ω_c is the coupling frequency, which has the meaning of a splitting between the symmetric and antisymmetric collective modes in the coupled waveguide. The difference in dispersion relations (and, consequently, in v_gr) in the waveguide and ring leads to only a small (second order) correction and is neglected here. The coupling frequency is given by

$$\omega _{\mathrm {c}} = \omega _{\mathrm {M}}\frac{{{\Omega}^{zz}F_{{\it{k}}_x}^{yy}\left( d \right) + {\Omega}^{yy}F_{{\it{k}}_x}^{zz}\left( d \right)}}{{\omega _{k}}}$$

(10)

and it depends on the coordinate x via the dependence of the distance between centers of straight and ring waveguides $d( x ) = d_0 + ( {R + \sqrt {R^2 - x^2} } )$ with d₀ = δ + w. The position-dependent angle between the waveguide and ring, and consequently between their static magnetizations, is not accounted for, as in the region that contributes most to the overall coupling, this angle is negligible. Here and below the tensors $\widehat {\mathbf{{\Omega}}}$, $\widehat {\mathbf{F}}$ and $\widehat {\mathbf{N}}_{k}$ are defined as in ref. ²⁴.

From the solution of Eq. (9), one finds the coupling and transmission coefficients, which enter into Eq. (1):

$$\tau = \cos \left( {2\overline \omega _{\mathrm {c}}R/v_{\mathrm {gr}}} \right),\,\kappa = \sin \left( {2\overline \omega _{\mathrm {c}}R/v_{\mathrm {gr}}} \right),$$

(11)

where $\overline \omega _{\mathrm {c}} = \left( {1/2R} \right){\int}_{ - R}^R {\omega _{\mathrm {c}}\left( x \right)dx}$ is the “averaged” coupling frequency. This equation can be used for any shape of the coupling area, e.g., if the ring is changed to a polygon. For the ring structure, the calculation of $\overline \omega _{\mathrm {c}}$ is greatly simplified (note that $\widehat {\mathbf{F}}\left( d \right)$ is an integral itself), noting that the coupling frequency decays fast with the separation d, so we can use the approximation d(x) ≈ d₀ + x²/(2R) and change the integration limits to (−∞,∞). Then,

$$\overline \omega _{\mathrm {c}} = \frac{{\omega _{\mathrm {M}}}}{{\omega _{k}}}\left( {{\Omega}^{zz}{\Phi}_{{\it{k}}_x}^{yy} + {\Omega}^{yy}{\Phi}_{{\it{k}}_x}^{zz}} \right),$$

(12)

where

$$\widehat {\mathbf{{\Phi}}}_{k_{x}} = \frac{1}{{\sqrt {2{\uppi}R} }}{\int}_0^\infty {\widehat {\mathbf{N}}_{k}}\cos \left( {{\it{k}}_yd_0 + \frac{{\uppi }}{4}} \right)\frac{{d{\it{k}}_y}}{{\sqrt {{\it{k}}_y} }} .$$

(13)

Micromagnetic simulations

The micromagnetic simulations were performed using the software package FastMag developed at the University of California, San Diego⁵⁰. This software uses a finite element method to solve the LLG equation and can use the power of modern Graphics Processing Units, which leads to the capability to handle ultra-complex geometries at a high speed⁵⁰. The finite element method is especially useful if non-rectangular systems such as the presented ring are simulated. The simulated structure of a magnonic ring resonator is shown in Fig. 1a. The parameters of the nanometer-thick YIG are obtained from the experiment as following³⁶: saturation magnetization M_s = 1.4 × 10⁵ A m⁻¹, exchange constant A = 3.5 pJ m⁻¹, and Gilbert damping for most of the structure α = 2 × 10⁻⁴, except for the ring structure. The Gilbert damping in the ring structure is increased to 2 × 10⁻³ to meet the critical coupling condition and the damping at the ends of the simulated structure is set to exponentially increase to 0.2, to prevent spin-wave reflection. The high damping region can be realized in the experiment by placing another magnetic material or a metal on top of YIG. The averaged cell size was set to 10 × 10 × 10 nm³, which is smaller than the exchange length of YIG (~16 nm) and the studied wavelength (~220 nm). To excite a propagating spin wave, a sinusoidal magnetic field b = b_esin(2πft) was applied over an area of 40 nm in length, with a varying oscillation amplitude b_e and microwave frequency f. The magnetization M_z(x,y,t) was obtained over a period of 250 ns, which is long enough to reach a stable dynamic equilibrium. The spin-wave intensity is calculated by performing a Fourier transform from 200 to 250 ns, which is long enough to resemble the condition of a dynamic equilibrium. The transmission T is defined by calculating the ratio of the spin-wave intensities in the straight waveguide behind and in front of the ring.