Introduction

The discovery of two-dimensional (2D) ferromagnetism in 20171,2 has initiated a vast interest in the field. The origin of magnetic order in 2D is fundamentally different from the spontaneously broken continuous symmetry that is responsible for magnetism in three-dimensional materials. In particular, the Mermin–Wagner theorem states that a continuous symmetry cannot be broken at finite temperatures in 2D and magnetic anisotropy therefore becomes a crucial ingredient for magnetic order in 2D. The first report on 2D ferromagnetism involved a monolayer of CrI31, which has a strong easy-axis orthogonal to the plane and has a Curie temperature of 45 K. In addition, few-layer structures of CrGeTe3 was reported to exhibit ferromagnetic order down to the bilayer limit2. However, for the case of a monolayer of CrGeTe3 magnetic order is lost due to the presence of an easy-plane, which comprises a continuous symmetry that cannot be broken spontaneously. Since then several materials have joined the family of 2D magnets. Most notably, CrBr33, which have properties very similar to CrI3 but with lower Curie temperatures of 34 K due to smaller magnetic anisotropy, Fe3GeTe2, which is metallic and has a Curie temperature of 130 K4, FePS35 which is antiferromagnetic with an ordering temperature of 118 K, and VSe2 where some evidence has been provided for ferromagnetic order at room temperature6 although the presence of magnetism is being debated7. In addition, several studies of magnetism in bilayers of various 2D materials have demonstrated that interlayer magnetic coupling can give rise to a plethora of new physical properties8,9,10,11,12,13,14,15.

Although the handful of known magnetic 2D materials have been shown to exhibit a wide variety of interesting physics, there is a dire need for discovering new materials with better stability at ambient conditions and higher critical temperatures for magnetic order. Such conditions are not only crucial for technological applications of 2D magnets, but could also serve as a boost for the experimental progress. In addition, the theoretical efforts in the field are largely limited by the few materials that are available for comparison between measurements and calculations. An important step towards discovery of novel 2D materials were taken by Mounet et al.16 where Density Functional Theory (DFT) was applied to search for potentially exfoliable 2D materials in the Inorganic Crystal Structure Database (ICSD) and the Crystallography Open Database (COD). More than 1000 potential 2D materials were identified and 56 of these were predicted to have a magnetically ordered ground state. Another approach towards 2D materials discovery were based on the Computational 2D Materials Database (C2DB)17,18,19, which comprises more than 3700 2D materials that have been computationally scrutinized based on lattice decoration of existing prototypes of 2D materials. The C2DB presently contains 152 ferromagnets and 50 antiferromagnets that are predicted to be stable by DFT. In addition to these high-throughput screening studies there are several reports on particular 2D materials that are predicted to exhibit magnetic order in the ground state by DFT20,21,22,23,24,25,26,27, as well as a compilation of known van der Waals bonded magnetic materials that might serve as a good starting point for discovering 2D magnets28.

Due to the Mermin–Wagner theorem a magnetically ordered ground state does not necessarily imply magnetic order at finite temperatures and the 2D magnets discovered by high-throughput screening studies mentioned above may not represent materials with observable magnetic properties. In three-dimensional bulk compounds the critical temperature for magnetic order is set by the magnetic exchange coupling between magnetic moments in the compound and a rough estimate of critical temperatures can be obtained from mean field theory29. In 2D materials, however, this is no longer true since magnetic order cannot exist with magnetic anisotropy and mean field theory is always bound to fail. The critical temperature thus has to be evaluated from either classical Monte Carlo simulations or renormalized spin-wave theory of an anisotropic Heisenberg model derived from first principles2,30,31,32. The former approach neglects quantum effects whereas the latter approximates correlation effects at the mean field level. It has recently been shown that the critical temperature of anisotropic 2D Heisenberg models can be accurately fitted to an analytical expression that is easily evaluated for a given material once the exchange and anisotropy parameters have been computed31,33. This approach has been applied to the C2DB resulting in the discovery of 11 new 2D ferromagnetic insulators that are predicted to be stable34. In addition 26 (unstable) ferromagnetic materials with Curie temperatures exceeding 400 K have been identified from the C2DB35. However, it is far from obvious that any of these materials can be synthesised in the lab even if DFT predicts them to be stable since they are not derived from experimentally known van der Waals bonded bulk compounds.

In the present work we have performed a full computational screening for magnetic 2D materials based on experimentally known van der Waals bonded materials present in the ICSD and COD. In contrast to previous high-throughput screening of these databases we evaluate exchange and magnetic anisotropy constants for all materials with a magnetic ground state and use these to predict the Curie temperature from an expression fitted to Monte Carlo simulation of the anisotropic Heisenberg model.

Results

Heisenberg models

The magnetic properties of possible candidate 2D materials are investigated using first principles Heisenberg models derived from DFT2,30,31,32,36. In particular, if a 2D candidate material has a magnetic ground state we model the magnetic properties by the Hamiltonian

$$H=-\frac{J}{2}\sum _{\langle ij\rangle }{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}-\frac{\lambda }{2}\sum _{\langle ij\rangle }{S}_{i}^{z}{S}_{j}^{z}-A\sum _{i}{({S}_{i}^{z})}^{2},$$
(1)

where J is the nearest neighbor exchange coupling, λ is the nearest neighbor anisotropic exchange coupling, A is the single-ion anisotropy, and 〈ij〉 denotes sum over nearest neighbors. J may be positive(negative) signifying a ferromagnetic (antiferromagnetic) ground state and we have assumed that the z-direction is orthogonal to the atomic plane and that there is in-plane magnetic isotropy. This model obviously does not exhaust the possible magnetic interactions in a material37, but has previously been shown to provide good estimates of the Curie temperature of CrI330,31 and provides a good starting point for computational screening studies.

The thermal properties can then be investigated from either renormalized spin-wave calculations29,30,31,38,39 or classical Monte Carlo simulations31,40, based on the model (1). Due to the Mermin–Wagner theorem the magnetic anisotropy constants are crucial for having magnetic order at finite temperatures and for ferromagnetic compounds the amount of anisotropy can be quantified by the spin-wave gap

$$\Delta =A(2S-1)+S{N}_{nn}\lambda$$
(2)

where S is the maximum eigenvalue of \({S}_{i}^{z}\) and Nnn is the number of nearest neighbors. This expression was calculated by assuming out-of-plane magnetic order and in the present context a negative spin-wave gap signals that the ground state favors in-plane alignment of spins in the model (1) and implies that the assumption leading to Eq. (2) breaks down. Nevertheless, the sign of the spin-wave gap comprises an efficient descriptor for the presence of magnetic order at finite temperatures in 2D, since a positive value is equivalent to having a fully broken rotational symmetry in spin-space.

For bipartite lattices with antiferromagnetic ordering (J < 0) the spin-wave analysis based on Eq. (1) (with out-of-plane easy axis) yields a spin-wave gap of

$${\Delta }_{{\rm{AFM}}}=-\left[S(J+\lambda ){N}_{nn}-(2S-1)A\right]\sqrt{1-{\gamma }^{2}},$$
(3)

with

$$\gamma =\frac{S{N}_{nn}J}{S{N}_{nn}(J+\lambda )-(2S-1)A}.$$
(4)

It is straightforward to show that ΔAFM is real and positive if (2S − 1)A > NnnSλ, real and negative if (2S − 1)A < NnnS(2J + λ) and imaginary otherwise. The latter case corresponds to favouring of in-plane antiferromagnetic order and negative real values correspond to favouring of ferromagnetic order (this may happen if λ is a large positive number even if J < 0). ΔAFM thus only represents the physical spin-wave gap in the case where it is positive and real. However, in the case of an imaginary spin-wave gap the norm of the gap may be used to quantify the strength of confinement to the plane. In the case of non-bipartite lattices we use the expression (3) as an approximate measure of the anisotropy. More details on this can be found in the Methods section.

In ref. 31 it was shown that the critical temperature for ferromagnetic order (J > 0) can be accurately obtained by classical Monte Carlo simulations of the model (1) and for S > 1/2 the result can be fitted to the function

$${T}_{{\rm{C}}}=\frac{{S}^{2}J{T}_{{\rm{C}}}^{{\rm{Ising}}}}{{k}_{{\rm{B}}}}f\left(\frac{\Delta }{J(2S-1)}\right)$$
(5)

where

$$f(x)={\tanh }^{1/4}\left[\frac{6}{{N}_{nn}}\mathrm{log}\,(1+c x)\right]$$
(6)

and  c= 0.033. \({T}_{{\rm{C}}}^{{\rm{Ising}}}\) is the critical temperature of the corresponding Ising model (in units of JS2/kB).

The expression (5) is readily evaluated for any 2D material with a ferromagnetic ground state once the Heisenberg parameters J, λ, and A have been determined. This can be accomplished with four DFT calculations of ferromagnetic and antiferromagnetic spin configurations including spin–orbit coupling. Specifically, for S ≠ 1/2 the exchange and anisotropy constants are determined by34,41

$$A=\frac{\Delta {E}_{{\rm{FM}}}(1-\frac{{N}_{{\rm{FM}}}}{{N}_{{\rm{AFM}}}})+\Delta {E}_{{\rm{AFM}}}(1+\frac{{N}_{{\rm{FM}}}}{{N}_{{\rm{AFM}}}})}{(2S-1)S},$$
(7)
$$\lambda =\frac{\Delta {E}_{{\rm{FM}}}-\Delta {E}_{{\rm{AFM}}}}{{N}_{{\rm{AFM}}}{S}^{2}},$$
(8)
$$J=\frac{{E}_{A{\rm{FM}}}^{\parallel }-{E}_{{\rm{FM}}}^{\parallel }}{{N}_{{\rm{AFM}}}{S}^{2}(1+\beta /2S)},$$
(9)

where \(\Delta {E}_{{\rm{FM}}({\rm{AFM}})}={E}_{{\rm{FM}}({\rm{AFM}})}^{\parallel }-{E}_{{\rm{FM}}({\rm{AFM}})}^{\perp }\) are the energy differences between in-plane and out-of-plane magnetization for ferromagnetic (antiferromagnetic) spin configurations and NFM(AFM) is the number of nearest neighbors with aligned (antialigned) spins in the antiferromagnetic configuration. For bipartite magnetic lattices (square and honeycomb) NFM = 0. However, several of the candidate magnetic materials found below contain a triangular lattice of transition metal atoms and in that case there is no natural antiferromagnetic collinear structure to compare with and we have chosen to extract the Heisenberg parameters using a striped antiferromagnetic configurations with NFM = 2 and NAFM = 4. Finally the factor of (1 + β/2S) in the denominator of Eq. (9) accounts for quantum corrections to antiferromagnetic states of the Heisenberg model where β is given by 0.202 and 0.158 for NAFM = 3 (honeycomb lattice) and NAFM = 4 (square and triangular lattices), respectively41. For S = 1/2 we take A = 0 and λ = ΔEFM/NS2 for J > 0 and λ = −ΔEAFM/(NAFM − NFM)S2 for J < 0. More details on the energy mapping analysis is provided in Methods below.

Computational screening of COD and ICSD

The first step in the computational screening is to identify potentially exfoliable 2D structures from the bulk materials present in ICSD and COD. In ref. 16 this was accomplished by identifying layered chemically bonded subunits followed by a calculation of the exfoliation energy from van der Waals corrected DFT. Here we will instead use a recently proposed purely geometrical method that quantifies the amount of zero-dimensional (0D), one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D) components present in a given material42. The method thus assigns a 0D, 1D, 2D, and 3D score to all materials and thus quantifies the 0D, 1D, 2D, and 3D character. The scores are defined such that they sum to unity and taking the 2D score >0.5 thus provides a conservative measure of a material being (mostly) composed of 2D components that are likely to be exfoliable.

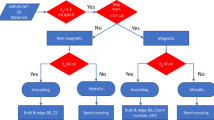
The ICSD and COD databases combined count more than 500,000 materials, but removing corrupted or incomplete entries and duplicates, reduces the number to 167,767 bulk materials42. Of these, a subset of 4264 are predicted to have a 2D score higher than 0.5 and these materials are the starting point of the present study. We then perform a computational exfoliation by isolating the 2D component and performing a full relaxation of the resulting 2D material with DFT. We restrict ourselves to materials that have a 2D component with less than five different elements and less than a total of 20 atoms in the minimal unit cell. Removing duplicates from the exfoliated materials then reduces the number of candidate 2D materials to 651 compounds. We find 85 materials with a ferromagnetic ground state and 61 materials with an antiferromagnetic ground state. A schematic illustration of the workflow is shown in Fig. 1. The fraction of materials, which are predicted to have a magnetic ground state is very close to that found by a similar screening study of the C2DB.

Fig. 1: Workflow.
figure 1

Schematic workflow of the computational screening for 2D magnets performed in the present work.

Full size image

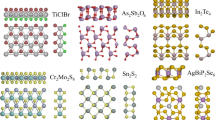
We find a wide variety of structures hosting a magnetic ground state. Several compounds are found to have the geometry of well-known binary prototypes such as CrI3 and NiI2 (the 1T phase of MoS2), but we also find several 2D materials with structures that have not previously been reported. In Fig. 2 we display a few of the most abundant magnetic prototypes as well as examples of more complex structures.

Fig. 2: Material examples.
figure 2

Atomic structures of a few representative materials. For every structure a 2 × 2 repetition of the primitive unit cell is shown.

Full size image

For all of the magnetic materials we calculate the nearest neighbor exchange coupling J, and the spin-wave gap Δ. The results are shown in Fig. 3 and specific materials will be discussed in detail below. The spin-wave gap is on the order of 0–4 meV for most materials whereas the exchange couplings fall in the range of 0–10 meV for the insulators but can acquire somewhat larger values for the metals. However, the energy mapping analysis is somewhat ill-defined for metals, since the electronic structure may change significantly when comparing energy differences between ferromagnetic and antiferromagnetic configurations. In particular, for insulators the spin per magnetic atom S is a well-defined integer that can be extracted from the ferromagnetic ground state without spin–orbit coupling. But for metals it is not clear what value to use in the model (1). In addition, it is not clear to what extend the Heisenberg model is suitable for a description of the magnetic properties of metals. We thus restrict ourselves to insulators in the following and then subsequently comment on promising metallic compounds.

Fig. 3: Exchange vs. anisotropy.
figure 3

Exchange coupling J and spin-wave gap Δ calculated for the magnetic 2D materials obtained from computational screening of ICSD and COD.

Full size image

Insulating 2D ferromagnets

In Table 1 we display the calculated exchange coupling constants and spin-wave gaps for ferromagnetic insulators with Δ > 0. Assuming in-plane magnetic isotropy these are the only insulators that will exhibit magnetic order at finite temperatures. For the compounds with S ≠ 1/2 we calculate the Curie temperatures according to Eq. (5).

Table 1 List of 2D ferromagnetic insulators (J > 0) with out-of-plane easy axis (Δ > 0).
Full size table

It is reassuring that the well-known Ising type 2D ferromagnets CrBr33 and CrI31 are reproduced by the screening. In addition, CrClO, CrCl3, MnO2, CoCl2, and NiI2 have previously been predicted to be ferromagnetic 2D insulators by DFT17,34,41. Multilayered CrSiTe3 has been reported to exhibit a large magnetic anisotropy in the direction perpendicular to the layers and a ferromagnetic phase transition has been observed at 33 K43. In addition, strained CrSiTe3 has very recently been predicted to comprise an ideal candidate for a 2D Kitaev spin-liquid44.

We also find 10 2D ferromagnetic insulators that has not previously been reported: CoCa2O3, CrHO2, Ni(ReO4)2, Co(ClO4)2, MoPO5, VAgP2Se6, Mn2FeC6N6, MnNa2P2F3O7, Mn3Cd2O8, and CuC4H4N2C2O2N4. Of particular interest is the compound CoCa2O3 (shown in Fig. 2), which is predicted to be ferromagnetic up to 57 K. However, it exhibits a rather small band gap of 40 meV, which may imply that the electronic structure could be sensitive to the choice of exchange-correlation functional. Such ambiguities have indeed been reported for FeCl3 and FeBr3, which are both predicted to be small-gap quantum anomalous Hall insulators by PBE, but trivial insulators by PBE+U as well as other GGA functionals18.

The largest exchange coupling constant in Table 1 is found for MnNa2P2F3O7 (11 meV), which appears highly promising. However, we do not have a reliable estimate for the critical temperature due to large in-plane anisotropy (only two nearest neighbors per Mn atom), which renders the inclusion of second-nearest neighbors crucial. A faithful estimation of the critical temperature would thus require a full Monte Carlo simulation of an extended Heisenberg model including in-plane anisotropy and exchange couplings for the second-nearest neighbors. This is, however, beyond the scope of the present screening study.

The materials NiRe2O8 (shown in Fig. 2) and CoCl2O8 are interesting variants of the common CdI2 prototype (for example NiI2 and MnO2) where the halide atom is replaced by units of ReO4 and ClO4, respectively. For 2D materials discovery based on computational lattice decoration such compounds opens the possibility of a wide range of new materials, since the number of possible ligands in the CdI2 prototype is dramatically increased.

We also wish to mention the compound CuC6H4N6O2, which is an example of a 2D metal-organic framework (MOF). It is composed of a rectangular lattice of Cu atoms connected by pyrazine (C4H4N2) and C2N4O2 units. Such 2D MOFs have recently attracted an increasing amount of attention and it has been shown that the quasi-2D MOF CrCl2(pyrazine)2 exhibits ferrimagnetic order below 55 K45. Due to the spin-1/2 nature of the magnetic lattice we cannot obtain a reliable estimate of the critical temperature of this material. Moreover, the material have large in-plane anisotropy and the second-nearest neighbors must play a crucial role since the nearest neighbor approximation gives rise to chains that cannot order themselves at finite temperatures. Nevertheless the sizable value of the intrachain exchange coupling (3.04 meV) could imply a critical temperature comparable to that of CrI3.

It should be stressed that the results of a screening study like the present one should be taken as a preliminary prediction. The first principles description of magnetic insulators is challenging for DFT since many of these exhibit strong correlation of the Mott–Hubbard type and the calculated Heisenberg parameters may be rather sensitive to the choice of functional32,34. We have tested the inclusion of Hubbard corrections for three representative materials in Table 1 using the U-values tabulated in ref. 34. For NiI2 it is well known that the magnetic anisotropy changes to in-plane magnetic order upon inclusion of Hubbard corrections34, which would render the material non-magnetic under the assumption of in-plane anisotropy and nearest neighbor exchange. In addition, we find that the exchange coupling is reduced to 1.82 meV if a Hubbard correction is included on the Ni d-orbitals. For CoCa2O3, the predicted critical temperature is increased to 226 K if a Hubbard correction is applied to the Co d-orbitals. Finally, for CrHO2 the critical temperature is largely unaffected by Hubbard corrections and we find that the Curie temperature changes to 48 K. It is, however, by no means clear that DFT+U provides a better description of the electronic structure in these cases and detailed benchmarking of the functional dependence of exchange and anisotropy parameters seems to be required in order to conclusively assess the quantitative accuracy of the predictions.

Itinerant 2D ferromagnets

For metallic materials the prediction of thermodynamical properties is more challenging since it is not obvious that the Heisenberg Hamiltonian (1) comprises a good starting point for the analysis. Nevertheless, the exchange coupling J and spin-wave gap Δ still provides rough measures of the magnetic interactions and magnetic anisotropy, respectively. Alternatively, one could specify the energy difference per magnetic atom in ferromagnetic and antiferromagnetic configurations as well as the energy cost of rotating the magnetic moments from the out-of-plane direction to the atomic plane. However, for the sake of comparison we have chosen to report the values of J and Δ resulting from the energy mapping analysis although it comprises a rather naive approach for metals. The value of S is obtained by rounding off the total magnetic moment per atom to nearest half integer and we then evaluate the critical temperature from Eq. (5), which is the prediction obtained by assuming a Heisenberg model description using the calculated parameters. The results are shown in Table 2 but it should be kept in mind that the exchange coupling constants and predicted critical temperatures in this case only provides a qualitative measure of the magnetic interactions.

Table 2 List of 2D itinerant ferromagnets (J > 0 and EGap = 0) with out-of plane easy axis (Δ > 0).
Full size table

Again, we rediscover a few materials (FeTe and VBrO) that were previously predicted to be ferromagnetic from computational screening of the C2DB. FeClO has recently been exfoliated to bilayer nanoflakes and were shown to retain the antiferromagnetic ordering known from the bulk material46. The discrepancy with our prediction of ferromagnetic order could either be due to an inaccurate description by PBE or due to the fact that the true antiferromagnetic structure of bulk FeClO is strongly noncollinear47, which is not taken into account in the present simplistic calculations.

We find a few materials with two nearest neighbors, implying a strongly anisotropic in-plane magnetic lattice. For example, VFC4O4(H2O)2 (shown in Fig. 2) is a MOF with hydrated alternating linear chains of V and F atoms interconnected by cyclobutanetetrone (C4O4) units. The intrachain exchange coupling is significant (22.3 meV), but a reliable estimate of the critical temperature requires inclusion of the interchain exchange, which is not addressed in the present study. We also find a few materials with nine nearest neighbors, which originates from a strongly buckled lattice of magnetic atoms and the analysis based on nearest neighbor interactions is expected to be insufficient in this case as well. We observe that several materials have predicted exchange couplings on the order of 10–50 meV, which far exceeds the values found for the insulators. But it should be emphasized that the comparison is not necessarily fair since the electronic structure of the antiferromagnetic state may be significantly different compared to the ferromagnetic state. Such differences will lead to large predictions for J that do not originate from magnetic interactions. Nevertheless, Table 2 provides a promising starting point for the discovery of 2D itinerant ferromagnets, but there is a dire need for a better theoretical framework that can quantitatively deal with the thermodynamical properties of itinerant magnetism in 2D.

We finally note that certain known itinerant 2D ferromagnets (VSe26 and CrGeTe32) are not present in Tables 1 and 2 due to in-plane magnetization, which results in a negative spin-wave gap in the present study. For the case of CrGeTe3 this is in accordance with the experimentally observed loss of magnetism in the monolayer limit whereas for VSe2 the origin of magnetic order is still unresolved7. In addition, we do not find the itinerant 2D ferromagnet Fe3GeTe24, which cannot be found in a bulk parent form in either the COD or ICSD.

Insulating 2D antiferromagnets

In the case of antiferromagnetic insulators we do not have a quantitative estimate of the Néel temperature given the nearest neighbor exchange coupling and spin-wave gap. However, it is clear that an easy axis (positive spin-wave gap) is required to escape the Mermin–Wagner theorem for materials with isotropic in-plane magnetic lattices. Moreover, although the formula for the critical temperature Eq. (5) was fitted to Monte Carlo simulations we expect that a rather similar expression must be valid for the Néel temperature of antiferromagnets. This is partly based on the fact that mean field theory yields similar critical temperatures for ferromagnetic and antiferromagnetic interactions in the nearest neighbor model and we thus use the expression (5) as a rough estimate of the critical temperatures for the antiferromagnet candidates found in the present work. In Table 3 we thus display a list of the antiferromagnetic insulators with positive spin-wave gap. In addition to the exchange coupling and spin-wave gap we also report the critical temperatures calculated from Eq. (5).

Table 3 List of 2D antiferromagnetic insulators (J < 0) with out-of-plane easy axis (Δ > 0).
Full size table

The most conspicuous result is the exchange coupling of VPS3, which exceeds 0.1 eV. However, while the use of the energy mapping analysis seems to be justified by the gapped antiferromagnetic ground state, the ferromagnetic configuration entering the analysis is metallic and may thus imply that the energy difference is not solely due to magnetic interactions. Nevertheless, the local magnetic moments in the ferromagnetic and antiferromagnet states are almost identical, which indicates that the large energy difference between the ferromagnetic and antiferromagnetic states originates in magnetic interactions.

We also observe that the V and Mn halides are predicted to be antiferromagnetic insulators with large exchange coupling constants. However, these compounds exhibits the CdI2 prototype where the magnetic atoms form a triangular lattice. In the present study we have only considered collinear spin configurations, but the true ground state of a triangular lattice with antiferromagnetic nearest neighbor exchange has to exhibit a frustrated noncollinear spin structure48. Second-nearest neighbors may complicate this picture and the true ground state of these materials could have a complicated structure. Moreover, it has previously been shown that the Mn halides are predicted to be ferromagnetic with the PBE+U functional, which underlines the importance of further investigating the predictions of the present work with respect to exchange-correlation functional, second-nearest neighbor interactions etc.

In analogy with the ferromagnetic insulators NiRe2O8 and CoCl2O8 the antiferromagnetic insulator CoRe2O8 comprises a variant of the CdI2 prototype (represented by the V and Mn halides in Table 3 where the halide atom has been replaced by ReO4.

NiC2O4C2H8N2, constitutes an antiferromagnetic example of a MOF with a rectangular lattice of Ni atoms connected by a network of oxalate (C2O4) and ethylenediamine (C2H4(NH2)2) units. Again, the material exhibits strong nearest neighbor interactions (across oxalate units), but the second-nearest interactions (mediated by ethylenediamine units) will play a crucial role in determining the critical temperature, which is predicted to vanish in the present study, being solely based on nearest neighbor interactions.

Finally, we remark that MnBi2Te4 in 3D bulk form has recently attracted significant attention as it has been demonstrated to comprise the first example of a magnetic Z2 topological insulator49,50. The bulk material consists of ferromagnetic layers with antiferromagnetic interlayer coupling. In contrast we predict that the individual layers exhibit antiferromagnetic order. Like the case of the Mn halides the sign of the exchange coupling constant changes upon inclusion of Hubbard corrections to the DFT description. We have tested that PBE+U calculations yields ferromagnetic ordering for U > 2.0 eV. In addition, we do not find the Ising antiferromagnet FePS35, since PBE without Hubbard corrections predicts this material to be non-magnetic in the minimal unit cell. In order to check the sensitivity we have chosen three representative materials in Table 3 and performed PBE+U calculations with U-parameters taken from ref. 34. In the case of VPS3, we find that the ground state remains antiferromagnetic but the critical temperature is reduced to 210 K. For CoRe2O8 the predicted critical temperature is increased to 202 and for VBr2 the predicted critical temperature is decreased to 53 K. It thus appears that the qualitative properties such out-of-plane easy axis and antiferromagnetic order are maintained, but the values for exchange and anisotropy constants may change by a factor of two if Hubbard corrections are included.

Itinerant 2D antiferromagnets

For completeness we also display all the predicted antiferromagnetic metals with Δ > 0 in Table 4. For S ≠ 1/2, we have provided rough estimates of the critical temperatures based on Eq. (5), but in this case it should be regarded as a simple descriptor combining the effect of exchange and anisotropy rather than an actual prediction for the critical temperature. Neither the energy mapping analysis or the Heisenberg model is expected to comprise good approximations for these materials. However, DFT (with the PBE functional) certainly predicts that these materials exhibit antiferromagnetic order at some finite temperature and Table 4 may provide a good starting point for further investigation or prediction of itinerant antiferromagnetism in 2D.

Table 4 List of 2D itinerant antiferromagnets (J < 0) with out-of-plane easy axis (Δ > 0).
Full size table

Full list of materials with a magnetic ground state

We conclude by providing a full list of all calculated 2D materials that exhibits a magnetic ground state. In Table 5 we list the predicted ferromagnetic insulators containing two elements and in Table 6 we list the ferromagnetic materials containing three, four, or five elements. For all materials we provide the COD/ICSD identifier for the bulk parent compound from which the 2D material was derived. We also state the spin S, the number of nearest neighbors Nnn, the exchange coupling J, the spin-wave gap Δ, and Kohn–Sham band gap EGap. For materials with S ≠ 1/2 and Nnn ≠ 2 we have calculated an estimated critical temperature from Eq. (5). In Table 7 we show all the antiferromagnetic compounds found in the computational screening. In addition, we found 11 materials (shown in Table 8) for which we were not able to evaluate exchange coupling constants. This was either due to problems converging the antiferromagnetic spin configuration (converged to ferromagnetic state), more than two magnetic atoms in the unit cell, or that the two magnetic atoms in the unit cell form a vertical dimer. All of the materials are, however, predicted to be magnetic and could comprise interesting magnetic 2D materials that are exfoliable from 3D parent compounds.

Table 5 List of 2D materials with a ferromagnetic ground state (within the PBE approximation) containing two elements.
Full size table
Table 6 List of 2D materials with a ferromagnetic ground state (within the PBE approximation) containing more than two elements.
Full size table
Table 7 List of 2D materials with an antiferromagnetic ground state (within the PBE approximation).
Full size table
Table 8 List of 2D ferromagnetic compounds, which did not allow for a simple estimation of a nearest neighbor exchange coupling constant.
Full size table

Discussion

We have performed a computational screening for 2D magnetic materials based on 3D bulk materials present in the ICSD and COD. We find a total of 85 ferromagnetic and 61 antiferromagnetic materials, which are listed in Tables 1–8. The strength of magnetic interactions in the materials have been quantified by the nearest neighbor exchange coupling constants and the magnetic anisotropy has been quantified by the spin-wave gap derived from the anisotropic Heisenberg model (1). Due to the Mermin–Wagner theorem only materials exhibiting an easy axis (positive spin-wave gap) will give rise to magnetic order at finite temperatures and these materials have been presented in Tables 1–4. For these we have also estimated the critical temperature for magnetic order from an expression that were fitted to classical Monte Carlo simulations of the anisotropic Heisenberg model.

The insulating materials are expected to be well described by the Heisenberg model and for S ≠ 1/2 we have evaluated the critical temperatures from an analytical expression fitted to classical Monte Carlo simulations. However, for simplicity this expression was based on a Heisenberg model with in-plane isotropy and nearest neighbor interactions only. This may introduce errors in the prediction of critical temperatures, but for any given material the approach is easily generalized to include other interactions and in-plane anisotropy, which will yield more accurate predictions for critical temperatures. In this respect the present approach to identify magnetic materials is rather conservative, since all materials with an in-plane easy axis are assumed to have an easy-plane and no magnetic order at finite temperatures. But such materials could potentially exhibit magnetic order due to in-plane anisotropy.

A more crucial challenge is related to the determination of Heisenberg parameters from DFT. We have already seen that PBE+U can modify the predictions significantly34 and even change the sign of the exchange coupling. Is is, however, not obvious that PBE+U will always provide a more accurate prediction compared to PBE (or other exchange-correlation functional for that matter) and benchmarking of such calculations is currently limited by the scarceness of experimental observations.

For antiferromagnetic insulators, we expect that classical Monte Carlo simulations combined with the energy mapping analysis will provide an accurate framework for predicting critical temperatures. In the present work we have simply used the expression (5) as a crude descriptor and leave the Monte Carlo simulations for antiferromagnets to future work. In general, the phase diagrams for antiferromagnets will be more complicated compared to ferromagnets48 and there may be several critical temperatures associated with transitions between different magnetic phases.

The case of itinerant magnets are far more tricky to handle by first principles methods. It is not expected that the applied energy mapping analysis comprises a good approximation for metallic materials and it is not even clear if the Heisenberg description and associated Monte Carlo simulations is the proper framework for such systems. A much better approach would be to use Greens function methods51,52 or frozen magnon calculations to access \(J({\bf{q}}) \sim {\sum }_{i}{J}_{0i}{e}^{i{\bf{q}}\cdot {{\bf{R}}}_{0i}}\) directly from which the magnon dispersion can be evaluated directly. It may then be possible to estimate critical temperatures based on renormalized spin-wave theory29 or spin fluctuation theory53.

Despite the inaccuracies in the predicted critical temperatures of the present work, all of the 146 reported magnetic materials constitute interesting candidates for further scrutiny of 2D magnetism. All materials are likely to be exfoliable from bulk structures and contains magnetic correlation in some form. Even the materials with an isotropic magnetic easy-plane that cannot host strict long-range order according to the Mermin–Wagner theorem, may be good candidates for studying KosterLitz–Thouless physics54. Moreover, such materials exhibit algebraic decay of correlations below the Kosterlitz–Thouless transition, which may give rise to finite magnetization for macroscopic flakes32,55.

Methods

Details on the energy mapping analysis

Here we provide the details of Eqs. (7)–(9) used to extract the Heisenberg parameters from first principles. The energy mapping analysis is based on ferromagnetic and antiferromagnetic configurations. We only consider nearest neighbor interactions and the number of nearest neighbors in the ferromagnetic configurations is denoted by Nnn. Only bipartite lattices allow for antiferromagnetic configurations where all magnetic atoms have antiparallel spin alignments with all nearest neighbors. For non-bipartite lattices we thus consider frustrated configurations where each atom has NFM nearest neighbors with parallel spin alignment and NAFM nearest neighbors with antiparallel spin alignment. Assuming a classical Heisenberg description represented by the model (1), the ferromagnetic (FM) and antiferromagnetic (AFM) DFT energies per magnetic atom with in-plane (∥) and perpendicular spin configurations are written as

$${E}_{{\rm{FM}}}^{\perp }=E_0-\frac{(J+B){S}^{2}{N}_{nn}}{2}-A{S}^{2}$$
(10)
$${E}_{{\rm{FM}}}^{\parallel }=E_0-\frac{J{S}^{2}{N}_{nn}}{2}$$
(11)
$${E}_{{\rm{AFM}}}^{\perp }=E_0+\frac{(J+B){S}^{2}({N}_{{\rm{AFM}}}-{N}_{{\rm{FM}}})}{2}-A{S}^{2}$$
(12)
$${E}_{{\rm{AFM}}}^{\parallel }=E_0+\frac{J{S}^{2}({N}_{{\rm{AFM}}}-{N}_{{\rm{FM}}})}{2},$$
(13)

where E0 represents a reference energy that is independent of the magnetic configuration. The Heisenberg parameters can then be calculated as

$$A=\frac{\Delta {E}_{{\rm{FM}}}(1-\frac{{N}_{{\rm{FM}}}}{{N}_{{\rm{AFM}}}})+\Delta {E}_{{\rm{AFM}}}(1+\frac{{N}_{{\rm{FM}}}}{{N}_{{\rm{AFM}}}})}{{S}^{2}},$$
(14)
$$\lambda =\frac{\Delta {E}_{{\rm{FM}}}-\Delta {E}_{{\rm{AFM}}}}{{N}_{{\rm{AFM}}}{S}^{2}},$$
(15)
$$J=\frac{{E}_{A{\rm{FM}}}^{\parallel }-{E}_{{\rm{FM}}}^{\parallel }}{{N}_{{\rm{AFM}}}{S}^{2}},$$
(16)

where \(\Delta {E}_{{\rm{FM}}({\rm{AFM}})}={E}_{{\rm{FM}}({\rm{AFM}})}^{\parallel }-{E}_{{\rm{FM}}({\rm{AFM}})}^{\perp }\) are the energy differences between in-plane and out-of-plane magnetization for ferromagnetic (antiferromagnetic) spin configurations.

However, we wish to base the energy mapping on the quantum mechanical Heisenberg model, which is less trivial. If we start with the sotropic Heisenberg model where spin–orbit coupling is neglected, the ferromagnetic configuration with energy EFM corresponds to an eigenstate with energy −JS2/2Nnn per magnetic atom, which is the same as the classical Heisenberg model. However, the antiferromagnetic configuration does not correspond to a simple eigenstate of the Heisenberg model. In particular, for bipartite lattices the Neel state where all sites host spin that are eigenstates of Sz is not the eigenstate of lowest (highest) energy of the Heisenberg Hamiltonian model with J < 0 (J > 0). Rather the classical energy corresponds to the expectation value of the Heisenberg Hamiltonian with respect to this state whereas the true ground state has lower (higher energy) leading to an overestimation of J if the energy mapping is based on the classical Heisenberg model. We have recently shown how to include quantum corrections to J for bipartite lattices using a correlated state, which has an energy in close proximity to the true antiferromagnetic ground state41. We note that the magnetic moments obtained with DFT support the fact that the DFT energy of the antiferromagnetic configuration represents a proper eigenstate of the Heisenberg model rather than the classical state. The result is the factor of (1 + β/2S) in Eq. (9).

Including spin–orbit coupling and magnetic anisotropy in the energy mapping complicates the picture since only one of the states \({E}_{{\rm{FM}}}^{\parallel }\), \({E}_{{\rm{FM}}}^{\perp }\) represents an eigenstate of the anisotropic Heisenberg model. On the DFT side this is reflected by the fact that only one of these configurations would be obtainable as a self-consistent solution and we have to calculate these energies by including spin–orbit coupling non-self-consistently. We thus retain the classical expression for the anisotropy constants, but include the quantum correction for the exchange constants. Is is, however, clear that the single-ion anisotropy term becomes a constant for any system with S = 1/2. In that case A does not have any physical significance and it cannot influence the values of \({E}_{{\rm{FM(AFM)}}}^{\parallel }\) and \({E}_{{\rm{FM(AFM)}}}^{\perp }\). We thus take A = 0 and λ = ΔEFM/NS2 for J > 0 and λ = −ΔEAFM/(NAFM − NFM)S2 for J < 0 in the case of S = 1/2. In principle, the two choices for λ should be equivalent and we have tested that they yield nearly the same value for a few spin-1/2 insulators, but in order to obtain full consistency with the spin-wave gap we use different expressions depending on the sign of J. In addition for S ≠ 1/2 the classical analysis leads to an inconsistency since the spin-wave gap (Eq. (2)) is not guaranteed to yield the same sign as −ΔEFM. This can be fixed by taking 2S → (2S − 1)S in Eq. (14), which leads to Eq. (7). Finally, the antiferromagnetic spin-wave gap (Eq. (3)) was derived for bipartite lattices and it is not possible to derive a gap for non-bipartite lattices in a collinear spin configuration, since such a state will not represent the true ground state and thus lead to an instability in the gap. However, we will apply the expression naively to non-bipartite lattices as well but taking Nnn → NAFM − NFM to ensure that the sign of the gap corresponds to the sign of −ΔEAFM.

Computational details

All DFT calculations were performed with the electronic structure package GPAW56,57 including non-self-consistent spin–orbit coupling58 and the Perdew–Burke–Ernzerhof59 (PBE) functional.