Introduction

High-entropy alloys (HEAs) have attracted ever-increasing research interest due to the huge unexplored compositional space and superior physical, mechanical, environmental, and functional properties1,2,3,4,5,6,7,8,9,10. Well-studied HEAs include the NiCoFeCrMn HEA and its subsystems2,4,7,11,12,13,14,15,16. Wu et al. found the equiatomic NiCoCr medium-entropy alloy (MEA) possesses even better mechanical properties than the well-studied NiCoFeCrMn HEA11,14,17,18,19. The excellent mechanical properties have direct connection with the dislocation and twin behaviors18,20,21, where atomic configurations with different ordering degrees (characterized by order parameters) can play an important role. The changes of ordering degrees driven by thermal energy can induce unusual temperature-dependent yield stress and electronic conductivity in Ni–Cr alloyed systems22,23,24. This phenomenon was referred to as the K-state effect by Thomas in 195122. The term “K-state” originates from German “Komplex Zustand” meaning “complex state”. It is generally used to describe a class of phenomena that the physical properties change abnormally with temperature, e.g., monotonic changes become nonmonotonic.

Recently, Jin et al. observed peaks in the specific heat curves of several subsystems of the HEA NiCoFeCrMn experimentally, but not all of them considered there showed such peaks. The observed peaks can be grouped into the well-known K-state phenomenon. An immediate question would be: why the peaks were observed in some of the alloys, such as the NiCoCr MEA, the peak of which is located around 940 K25? There are a number of underlying possibilities that may account for the phenomenon, including the interplay of the different entropy contributions. Although their experiments suggested that the magnetism does not contribute to the peak of this alloy26, the origin of the peak is not well understood, and detailed simulations are required to clarify its origin. In another work, Zhang et al. studied the configurational ordering of NiCoCr using the neutron scattering method27. They argued that Ni and Co are chemically similar atoms and suggested the existence of short-range ordering of Cr–Ni and Cr–Co pairs. To clarify this point, direct and quantitative information on the short-range ordering and its temperature dependence are required. In addition, the information for the Ni–Co pair is also unknown in their study, which is critical to justify whether the system can be treated as a pseudo-binary (PB) system or not13.

In order to obtain a deeper insight, the above issues need to be revisited and critically discussed. To this end, we propose to (i) simulate the specific heat curve and (ii) calculate the short-range-order (SRO) parameters in real space. These two aims can be realized simultaneously by using the Wang–Landau (WL) Monte Carlo (MC) algorithm28,29. The advantage of this MC algorithm is that it can effectively prevent walkers from being trapped in high density of state (DOS) regions, in contrast to the classic Metropolis MC method. The DOS is a distribution defined by the number of configurations as a function of system energy. The energies fed into the WL method can be calculated from either density functional theory (DFT)30 or the cluster-expansion (CE) method31,32,33, and we adopt the latter. For more details of the joint WL and CE method, please refer to ref. 34 and Supplementary Materials. In addition to the WL algorithm, simulated annealing (SA) is used to obtain a comprehensive understanding of the K-state phenomenon. Although the WL algorithm can give reliable and smooth specific heat curve and temperature-dependent SRO parameters, it cannot supply the configuration at a specified temperature that is accessible by the SA. The configurations are needed to calculate the SRO parameter in the reciprocal space, which can reveal fine atomic-scale details of the phenomenon. Moreover, the SA can also give other complementary information obtained using big supercells for crosschecking our WL results, such as the role of nearest-neighbor (NN) interactions.

Results and discussion

The CE Hamiltonians

In the CE method, parametrized Hamiltonians of N-component systems are employed to calculate the total energy of an arbitrary configuration σ33, i.e., \(E(\sigma )={\sum }_{\alpha }{J}_{\alpha }{\phi }_{\alpha }({\{{s}_{i}\}}^{N}),\alpha =0,1,2,\ldots\), where \({\phi }_{\alpha }({\{{s}_{i}\}}^{N})\) represents the product of the occupation variables si in cluster α and Jα is the effective interaction parameter for the cluster α. The occupation variables depend on both lattice sites and atomic species. The accuracy of total energies can be improved systematically by adding more terms and including more clusters. We consider two different CE Hamiltonians, i.e., one includes interactions up to three-body terms and the other up to two-body terms (see Supplementary Fig. S1 and Table 1). The two Hamiltonians include 19 and 15 effective cluster interaction parameters, respectively. The magnitudes of all the 3-body terms are <1 meV. The three-body Hamiltonian includes more interaction terms, so it has a smaller cross-validation score that measures the accuracy of a Hamiltonian. It describes the atomic interaction more accurately than its two-body counterpart. In order to double check the reliability, the two-body CE Hamiltonian is still considered in our calculations.

Table 1 The energy difference between the “ground state” and random structures computed by the two cluster-expansion Hamiltonians and DFT.
Full size table

The thermodynamic properties of NiCoCr by the WL algorithm

A low-temperature ordered structure can help the MC walker of WL algorithm efficiently explore the vast configurational space. The structure is not necessarily the true ground state. We find a “ground state” ordered structure with the lowest known energy after searching unit cells up to 12 atoms for NiCoCr using DFT. As is shown in Fig. 1, Ni and Co in this structure share two of the every three {001} planes and the third plane is completely occupied by Cr. The ordered structure of NiCoCr is 31 meV lower in energy than its random counterpart. The 2- and 3-body CE Hamiltonians predict almost the same values, which are 30 and 35 meV, respectively (see Table 1).

Fig. 1: The unit cell for the “ground state” of NiCoCr.
figure 1

The structure is of face-centered cubic type with Cr occupying a complete {002} layer and Ni and Co sharing the other two layers in a period of three layers.

Full size image

With this structure as the input of our joint WL and CE (WL-CE) method, the configurational DOSs of the MEA are calculated. The DOSs are then used to calculate the internal energies U, specific heats Cv, and order–disorder transition temperatures Tc. We run the simulations using a series of supercell sizes to ensure acceptable convergence in Tc. The transition temperatures are shown in Table 2 with respect to different Hamiltonians and supercell sizes, which are plotted in Fig. 2a. The transition temperature approaches the thermodynamic limit with increasing supercell size, which is very likely close to but <1200 K. The Binder cumulant of internal energies (VN)35 are calculated for the three different system sizes to get the transition temperature in the thermodynamic limit (see Fig. 2b). For a finite system of size N, \({V_N} = 1 - \left\langle {E_N^4} \right\rangle /3{\left\langle {E_N^2} \right\rangle ^2}\), and 〈〉 takes the ensemble average of a quantity. The Binder cumulant of the internal energies using the 3-body CE Hamiltonian gives Tc = 1120 K, which is 150 K lower than that calculated using the 240-atom supercell. Similarly, the Binder cumulant of internal energies using the 2-body CE Hamiltonian gives 1120 K, which is about 120 K lower than the value calculated with 240 atoms (see Supplementary Information).

Table 2 The transition temperatures calculated using different cluster-expansion Hamiltonians and system sizes.
Full size table
Fig. 2: Calculations of transition temperatures and specific heats.
figure 2

The transition temperature as a function of supercell sizes is shown in a, Binder cumulant of the transition temperature of configurational ordering in b, and the comparison of experimental specific heat and simulated specific heat (configurational entropy only) in c.

Full size image

The K-state phenomenon

The atomic origin of this peak is still unknown. In order to examine the role of configurational ordering transition in this phenomenon, we compare the locations of the simulated and experimental peaks, as shown in Fig. 2c. The majority part of the experimental specific heat (vibrational contribution) is fitted to the Einstein model and subtracted. Since the vibrational contribution alone does not affect the location of the peak, its subtraction helps better compare the phase transition temperatures. The locations of the theoretical and experimental peaks are very close, only with a discrepancy of 80–180 K.

This overestimation of the transition temperature is due to that vibrational and electronic entropies, and the possible interplay among the entropic contributions are not included in this calculation. Applying the Debye–Grüessen model with input parameters obtained from the DFT methods7,36, we calculate the vibrational and electronic entropies for both the ordered and disordered phases of NiCoCr (see Fig. 1). As is demonstrated by Supplementary Fig. S2, the ordered phase indeed has a smaller vibrational entropy than the disordered phase. This confirms that the difference between the total entropies of the ordered and disordered phases is underestimated when the vibrational entropy is ignored, which results in an overestimation of the transition temperature. Since the volumes of high-temperature disordered phases are usually larger than that of low-temperature ordered phases, this trend is expected to be common in alloys with ordering transitions. Hitherto the location of the peak is well explained by the configurational ordering transition, and the small discrepancy between the locations of experimental and simulated peaks finds its origin in the vibrational contributions. The more complicated interplay among the various entropic contributions is expected to be of secondary importance. By combining these results, we confirm the atomic ordering is the origin of the K-state phenomenon (i.e., the non-sharp peak) observed in the NiCoCr alloy.

The effect of volume expansion is difficult to be considered in the present lattice gas model. The three atomic species are of similar size, so it is reasonable to ignore the lattice distortion, as were done in a number of previous studies9,30,34. The good agreement of the experimental and simulated transition temperatures in these examples also partly support that these two factors may be ignored in systems consisting of atoms with comparable sizes.

The atomic origin of the K-state phenomenon

In the previous sections, we show that the K-state phenomenon can be well explained by the change of ordering degree in this extensively studied MEA. However, we do not know the underlying driving force of the ordering transition, i.e., the roles of the three elements in the process are unknown. To this end, the Warren–Cowley SRO parameters \({\alpha_{\mu ,\nu }^{i,j}}\) or its mathematically equivalent quantity \(1/{c}_{\mu }({q}_{\mu ,\nu }^{i,j}+{c}_{\mu }{c}_{\nu })\) are computed37,38 as a function of system energy and temperature. Generally, any configuration can be defined by occupation variables ξ. If a site i is occupied by an atom of type μ, \({\xi }_{\mu }^{i}=1\); otherwise \({\xi }_{\mu }^{i}=0\). Obviously, for a configuration \(\{{\xi }_{\mu }^{i}\}\), \({\sum }_{\mu }{\xi }_{\mu }^{i}=1\) and \(\langle {\xi }_{\mu }^{i}\rangle ={c}_{\mu }\). In real space, the Warren–Cowley SRO is defined as \({\alpha }_{\mu ,\nu }^{i,j}={q}_{\mu ,\nu }^{i,j}/{c}_{\mu }({\delta }_{\mu ,\nu }-{c}_{\nu })\), where \({q}_{\mu ,\nu }^{i,j}=\langle {\xi }_{\mu }^{i}{\xi }_{\nu }^{j}\rangle -\langle {\xi }_{\mu }^{i}\rangle \langle {\xi }_{\nu }^{j}\rangle\). Instead of directly using \({\alpha }_{\mu ,\nu }^{i,j}\), we define a new quantity, i.e., the renormalized SRO parameter \(1/{c}_{\mu }({q}_{\mu ,\nu }^{i,j}+{c}_{\mu }{c}_{\nu })\) in this study. The new quantity \(1/{c}_{\mu }({q}_{\mu ,\nu }^{i,j}+{c}_{\mu }{c}_{\nu })\) embraces the same information as the Warren–Cowley one and has an explicit physical meaning of average fraction of neighbors. We still call it SRO parameter in this context. The temperature is introduced through the Boltzmann distribution in a way similar to the specific heat.

The first six independent SRO parameters as functions of the system energy and temperature are shown in Fig. 3 (for the accurate three-body CE). The ranges of SRO parameters up to 2500K are listed in Table 3. Obvious changes are observed around the transition temperatures for the six SRO parameters, which is the origin of the peaks in the theoretical specific heat curves. Generally, all these parameters approach 1/3 with increasing temperature. A value of 1/3 just indicates that a phase may be in its completely random state, because some ordered states can also have this value. The randomness degree is not a simple function of the NN SRO parameters. We will calculate SRO parameters in the reciprocal space to justify and differentiate the two cases. Our real-space SRO parameters show that a Ni atom has fewer Ni neighbors but more Co and Cr. Similarly, a Co atom also has fewer Co neighbors and more Ni and Cr. The NN occupations of Co atoms do not change much with increasing temperature, particularly Ni–Co with probability within a narrow window. Cr–Ni binary alloys prefer ordering transitions that result in Ni2Cr ordered phase and K-state phenomenon22,24,25,39. The formation of Ni2Cr leads to significant changes in the SRO parameters of both Ni and Cr39,40 that holds for Cr–Co and Cr–Ni pairs as well. Zhang et al.27 found Ni and Co prefer to sit around Cr, which is confirmed by our WL MC results. Interestingly, in this process the chemical environment of Co does not significantly change, reflected by the temperature-dependent SRO parameters. The reason for this interesting feature will be given when the reciprocal-space SRO parameters are discussed.

Fig. 3: The short-range-order (SRO) parameters by two different Monte Carlo methods.
figure 3

The 6 independent renormalized SRO parameters \(N({q}_{\mu ,\nu }^{i,j}+{c}_{\mu }{c}_{\nu })\) of NiCoCr are computed using the 3-body CE Hamiltonian and the Wang–Landau Monte Carlo method for 108 atoms (a, b) and simulated annealing (SA) with the nearest-neighbor (NN) interactions (c). The SRO parameters as functions of the system energy and temperature are plotted in a and b, respectively. The transition temperature is shifted to its thermodynamic limit in b. The same results for the two-body CE Hamiltonian are referred to in the Supplementary Information. In c, a larger supercell of 6 × 6 × 6 (864 atoms) is adopted. The nearest-neighbor model yields qualitatively consistent results with our WL-CE model.

Full size image
Table 3 The ranges of the short-range-order parameters \(N({q}_{\mu ,\nu }^{i,j}+{c}_{\mu }{c}_{\nu })\) between 0 and 2500 K.
Full size table

In order to understand the changes of the SRO parameters, we adopt SA algorithm and the less accurate NN model to reproduce the results of Fig. 3b. This method allows us to use much larger supercell and identify the interactions that dominate the maximum change in the ordering degree. The NN interaction energies \({J}_{ij}^{NN}\) (meV/bond) is calculated by \({J}_{ij}^{{\rm{NN}}}=2\Delta {H}_{{\rm{f}}}/z\), where ΔHf is the formation energy per atom and z is the number of the NNs occupied by a different atomic species. In our choice of two-atom supercells, z = 8 not 12. The results for 864 atoms are shown in Fig. 3c. The SRO parameters generally have qualitatively consistent trends with that by the accurate WL-CE model. All the Cr-involved SRO parameters change more significantly than the others. This is due to the much stronger interactions of Cr–Ni (−19.1 meV/bond) and Cr–Co (−21.2 meV/bond) than that of Ni–Co (−1.1 meV/bond). Not only the changes of SRO parameters but also their magnitudes can be explained by the bond energies. Generally, the stronger the interaction between two elements, the higher their SRO parameter. However, the NN model gives larger changes of the Co-involved SRO parameters. This is different from the more accurate WL-CE model. Therefore, the actual values of SRO parameters are also substantially tuned by the associated bonds and many-body interactions.

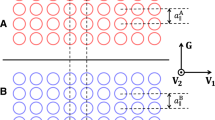
The concentration wave is a very useful concept to describe SRO, particularly when the wave is dominated by a small number of waves with wave vectors near some specific points in the Brillouin zone41. The locations of peaks in the reciprocal space give the dominant directions and wave vectors of the concentration waves. Therefore, the SRO parameters αμ,ν(k) in reciprocal space can reveal more details of the atomic origin of the K-state phenomenon (see Fig. 4). In reciprocal space, the SRO parameter \({\alpha }_{\mu ,\nu }({\boldsymbol{k}})={\sum }_{{n}_{{\boldsymbol{R}}}}{\alpha }_{\mu ,\nu }^{i,j}({\boldsymbol{R}}){e}^{2\pi {\boldsymbol{k}}{\boldsymbol{R}}}\), where nR is the number of shells included in the Fourier transform. We calculate αμ,ν(k) at 100, 900, and 1200 K using the SA algorithm and the 3-body CE Hamiltonian in order to accurately capture the ordering behavior. The parameters αμ,ν(k) at 100 K show strong 2/3[110] type ordering for Co–Cr and Ni–Cr pairs and [100] type ordering for Co–Ni pair. The 2/3[110] peaks become weak at higher temperatures and almost disappear above the transition temperature. This demonstrates that the Co–Cr and Ni–Cr pairs contribute to the ordering transition in a way similar to PB Cr alloys. The Ni–Cr pair is slightly stronger than Co–Cr, which is consistent with WL-CE results. In contrast, the [100] type peaks for Co–Ni remain almost unchanged up to 900 K and only decrease to 2/3 of its 100 K magnitude above the transition temperature. The strong peaks directly show that the Co–Ni pair distribution is not random in the NiCoCr alloy even above the transition temperature. This surprising feature not only explains the almost constant Co–Ni SRO parameter upon heating but also shows that NiCoCr cannot be treated as a PB system13.

Fig. 4: The finite-temperature short-range-order (SRO) parameters in reciprocal space.
figure 4

The SRO parameters of the nearest-neighbor pairs in reciprocal space αμ,ν(k) at 100, 900, and 1200 K are calculated by the 3-body CE Hamiltonian. The parameters αμ,ν(k) at 100 K show strong 2/3[110] type ordering for Co-Cr and Ni-Cr pairs, and [100] type ordering for Co-Ni pair. The 2/3[110] peaks become weak at higher temperatures and almost disappear above the transition temperature. In contrast, the [100] type peaks remain almost unchanged up to 900 K, and only decrease to 2/3 of its 100 K magnitude above the transition temperature. This feature shows that NiCoCr cannot be treated as a pseudo binary system.

Full size image

Revisit the role of the configurational entropy

The importance role of the configurational entropy has been identified statistically by the two Monte Carlo methods. We continue to use the method of proof by contradiction to check whether the role of the configurational entropy can be reasonably described by the PB model. Since Co and Ni are chemically similar, the three elements were considered as a PB system X2Cr (X = Co, Ni) by Zhang et al.13. If the their idea works, the change in configurational entropy during the process of first-order ordering transition is \(\Delta {S}_{{\rm{PB}}}=-{k}_{{\rm{B}}}\left(\right.(1/3)\mathrm{ln}\,(1/3)-(2/3)\mathrm{ln}\,(2/3)\left)\right.\approx 0.637{k}_{{\rm{B}}}\), which is 0.462kB smaller than 1.097kB of the ideal mixing. The transition temperature calculated using the configurational entropy of ideal mixing yields 320 K, which is about 1/3 of the experimental value 940 K. After considering the chemical similarity, the calculated value increases to 642 K, 2/3 of the experimental temperature. In contrast to these two thermodynamic models, our statistical WL-CE model gives a much closer value of 1070 K. If this transition is really of first order as in the PB model and driven by the configurational entropy, the “entropic change” for it is SWL ≈ ΔH/Tc = 0.035 eV/1070 K = 0.379kB, which is 0.6 × ΔSPB. But still, this value is much larger than that calculated by Schön et al.42. The reason is that the peak in the specific curve is not driven by the first-order transition between the ordered and random phases but an SRO transition. This was discussed in the previous sections. In the SRO transition, the configurational entropy is a continuous function of temperature, which is not considered in the thermodynamic model. If the configurational entropy is treated as a function of temperature (and also system energy, see Figs S3a and S4a), it will be smaller than the ideal value. All these numbers are summarized in Table 4.

Table 4 Comparison between statistical and thermodynamic models by assuming a first-order phase transition.
Full size table

We propose a joint technique to study the K-state phenomenon in the extensively studied NiCoCr MEA and find several novel aspects of this phenomenon. The theoretical transition temperature and the feature of specific heat are in good agreement with experimental ones, which confirms that the K-state phenomenon is due to ordering transition of chemical species. Atomic origins of the ordering transition are unveiled by two complementary Monte Carlo methods, i.e., the reordering of Cr–Ni and Cr–Co pairs drive the ordering transition, while that of Co–Ni changes weakly. This surprising feature is directly seen from the reciprocal-space SRO parameter, which shows that NiCoCr cannot be treated as a PB alloy. This is an excellent example to demonstrate the higher flexibility in coordinating atomic positions in ternary alloys than in binary alloys. The seemingly similar phenomena in the binary (e.g., Ni2Cr) and multicomponent alloys (e.g., NiCoCr) have very different atomic origin, which may be profuse for all multicomponent alloys with the K-state phenomenon. Our techniques include several efficient methods that can be directly used to study the other novel HEAs with K-state phenomenon, regardless of their component number.

Methods

A complete description of methodology details is supplied in Supplementary Information.