Introduction

Diamond is the hardest, stiffest and least compressible crystalline materials in the world. Understanding and further improving its hardness is scientifically fascinating and technologically important1,2,3. In the past few decades, numerous efforts have been made in these directions, both experimentally and theoretically4,5,6,7,8,9. It has been demonstrated that the hardness of the diamond can be improved by refining its grain size and/or twin thickness according to the well-known Hall–Petch effect10,11. For example, nanograined diamond (ng-diamond) with grain sizes of 10–30 nm has been reported as high as 110–140 GPa in Knoop hardness, significantly higher than that of single-crystal diamond4,5,12. Nanotwinned diamond (nt-diamond) with an average twin thickness (λ) of 5–8 nm, synthesized by compressing onion-structured precursors7,8, is recently reported to possess Vickers hardness of 175–200 GPa, setting a new world record. Can the hardness of nt-diamond be further increased? This is a fundamental scientific question for designing new superhard materials with potentially wide-ranging implications13.

The recent molecular dynamic (MD) simulations on nt-diamond indicated that the origin of the unprecedented hardness originates from two factors: high lattice frictional stress due to the strong sp3 C–C bonding and high athermal stress due to Hall–Petch effect14. Experimental and theoretical studies also show that twin boundaries (TBs) can continuously harden covalent materials with decreasing twin thickness (λ) to very small values (on the order of a few nm)7,8,15,16. Therefore, for covalent materials, a practical strategy to achieve superhardness is to introduce more TBs into the microstructure. Based on this idea, a novel intersectional nanotwinned diamond (int-diamond) model is constructed by inducing intersectional TBs into nt-diamond. After analyzing dislocation slip modes in individual int-diamond grains, the hardness of bulk int-diamond is calculated based on the Sachs model17. We find that the hardness of the int-diamond is much higher than that of the nt-diamond. This result is further verified by MD simulations. This work provides a new strategy for designing new super-hard materials in future experiments.

Results

Dislocation slip modes in int-diamond grains

For diamond, dominant dislocations are along the <110> directions slipping in the (111) plane with Burgers vector of \(\frac{1}{2}\) <110> for perfect dislocation and \(\frac{1}{6}\) <112> for glide-set partial dislocation14,18. According to the angle between Burgers vector and dislocation line direction, there are six types of dislocations: glide-set 0° perfect dislocations, glide-set 30° partial dislocations, glide-set 60° perfect dislocations, glide-set 90° partial dislocations, shuffle-set 0° perfect dislocations, and shuffle-set 60° perfect dislocations14. Among them, shuffle-set 0° perfect dislocation has the lowest critical resolved shear stress (CRSS) for dislocation motion and the lowest barrier strength when reacting with TBs14. Here the CRSS is defined as the threshold stress of dislocation motion, and the barrier strength is defined as the threshold stress of dislocation reaction with the TB when the activation energy reaches zero19. Therefore, at room temperature, the hardness of the diamond is primarily controlled by the behavior of shuffle-set 0° perfect dislocations16,20. Therefore, in the present study, the hardness of the int-diamond will be analyzed based on the behavior of shuffle-set 0° perfect dislocations.

In an int-diamond grain, two different orientation twin boundaries TB1 and TB2 coexist and interweaved, whose average twin thickness is λ1 and λ2, respectively (Fig. 1a)21,22. TB1 and TB2 segment the grain into domains with four different crystallographic orientations, that is, orientations D1, D2, D3, and D4. Among these different orientations, lattices of D1 and D2, D2 and D3, D3 and D4, and D4 and D1 are mirror images across TB1, TB2, TB1, and TB2, respectively. Consequently, the slip systems in an int-diamond grain can be expressed by a combination of four Thompson tetrahedra (in Fig. 1b): ABCD, ABCD1, A1BCD and A2BCD1, which correspond to D1, D2, D3, and D4, respectively. The combination of these four Thompson tetrahedra results in 39 slip systems in an int-diamond grain (Table 1). According to dislocation line directions and their slip plane orientations, the slip modes of shuffle-set 0° perfect dislocations in int-diamond are divided into four types: slip transfer (ST) mode, confined layer slip (CLS) mode, confined slip transfer mode I (CST-I) and confined slip transfer mode II (CST-II) modes, all of which are schematically plotted in Fig. 1b. For ST mode, the slip planes are parallel to either TB1 or TB2, and the respective dislocation lines are located within either TB2 or TB1. For CLS mode, the slip planes are parallel to either TB1 or TB2, while the respective dislocation lines are non-parallel to TB2 or TB1. For CST-I mode, both slip planes and dislocation lines are non-parallel to any TB. For CST-II mode, the slip planes are non-parallel to any TB, while the respective dislocation lines are located within either TB1 or TB2. As a result, the interactions of these slip modes with TBs are different. This leads to different CRSSs for the four slip modes. For ST mode, the dislocation-TB reaction is characterized by dislocations propagating within the TBs23,24, and the corresponding CRSS is determined by the lattice friction stress and barrier strength of shuffle-set 0° perfect dislocations reacting with the TBs25. For CLS mode, the dislocation motion is confined between two TBs and its CRSS can be evaluated by increased dislocation energy due to the dislocation line is left on the two TBs23,26. For CST-I mode, the shuffle-set 0° perfect dislocation is confined between two TBs and then become shuffle-set 60° perfect dislocation to parallel TB when it reaches TB because the initial dislocation line is non-parallel to TB. Finally, the shuffle-set 60° perfect dislocation interaction with TB to propagate through TB, and its CRSS is determined by the barrier strength of shuffle-set 60° perfect dislocations reacting with TBs and increased dislocation energy because produced dislocation on two TBs. For CST-II mode, although its dislocation motion is similar to that in CST-I mode, its barrier strength is determined by shuffle-set 0° perfect dislocations reacting with the TB. In order to obtain CRSSs for these slip modes, barrier strengths of shuffle-set 0° and 60° perfect dislocations reacting with TBs must be calculated first.

Fig. 1: Schematics of the int-diamond microstructure and its slip modes.
figure 1

a Structure schematic of int-diamond. Lattices of D1 and D2, D2 and D3, D3 and D4, and D4 and D1 are mirror images across twin boundary TB1, TB2, TB1, and TB2, respectively. GB is grain boundary. b Four dislocation slip modes in int-diamond: slip transfer mode (ST), confined layer slip mode (CLS), confined slip transfer mode I (CST-I), and confined slip transfer mode II (CST-II). c Schematic of shuffle-set screw perfect dislocation BD and AD reaction with TB when it reaches TB. d The stress-dependent activation energy of shuffle-set screw perfect dislocation BD and AD reaction with TB.

Full size image
Table 1 Slip system categories in int-diamond.
Full size table

Barrier strengths of dislocation reaction with TB

Shuffle-set 0° and 60° perfect dislocations reacting with TBs can be considered as a kink nucleation and migration process14,27,28 (Fig. 1c and Supplementary Fig. 1). The shear-stress dependent activation energy for kink nucleation and migration are calculated (detail in “Methods” section), and the results are plotted in Fig. 1d. With increasing shear stress, the activation energies for shuffle-set 0° and 60° perfect dislocations reacting with TB reach zero at shear stresses of 19 and 48 GPa, respectively. These stresses are considered the respective barrier strengths for shuffle-set 0° and 60° perfect dislocations. The twin intersecting points can provide the pinning obstacle for the slip of dislocation when the shuffle-set dislocation slip along the twin plane. However, in nt-diamond, the shuffle-set dislocations slip along twin plane energetically show no advantage over those along other slip planes16. Therefore, the shuffle-set dislocation is favor to slip along the slip planes rather than twin plane, and the pinning effect of intersecting points on shuffle-set dislocation motion is neglected in this work.

CRSS for ST mode

In ST mode, dislocation motions are blocked by TBs (inset of Fig. 2a)29. According to dislocation pile-up theory30, the CRSS (τcss) of this mode is expressed as the following:25

$$\tau _{{\mathrm{css}}}^{{\mathrm{ST}}} = \tau _0 + \left( {\frac{{\tau _{{\mathrm{TB}}}Gb}}{{\pi \lambda }}} \right)^{1/2},$$
(1)

where τ0 is lattice frictional stress; G is the shear modulus; b is the magnitude of the Burgers vector; λ is twin thickness of intersectional twin; τTB is the barrier strength of shuffle-set 0° perfect dislocations when reacting with the TB. Both modulus and stress are in GPa, and all length parameters are in nm.

Fig. 2: Critical resolved shear stress (CRSS) for different slip modes.
figure 2

a Calculated CRSS of slip transfer (ST) mode and confined layer slip (CLS) mode. A dislocation pile-up model and principles of virtual work is used for ST and CLS mode, respectively. b Calculated CRSS of confined slip transfer mode I (CST-I), and confined slip transfer mode II (CST-II). For CST-I and CST-II model, it can be considered as a superposition of ST and CLS modes. The inset is schematic of shuffle-set screw perfect dislocation AB, AD, BC and BD reaction with twin boundary TB1 and TB2. GB is grain boundary.

Full size image

With G = 540 GPa according to ref. 14, τTB = 19 GPa as calculated above and τ0 = 10.3 GPa (see “Methods” section) and assuming λ1 = λ2 = λ, twin thickness-dependent CRSS for ST mode is rewritten as the following:

$$\tau _{{\mathrm{css}}}^{{\mathrm{ST}}} = 10.3 + 28\lambda ^{ - 1/2},$$
(2)

which is plotted in Fig. 2a. This CRSS increases with decreasing twin thickness, and the trend and quantitative values are similar to that of ST mode in nt-diamond14.

CRSS for CLS mode

The CRSS for CLS mode can be calculated on the basis of the virtual work principle (Fig. 2), and it is expressed as: refs. 25,31

$$\tau _{{\mathrm{css}}}^{{\mathrm{CLS}}} = \tau _0 + \frac{{{\mathrm{Gb}}\left[ {1 - \nu \cos ^2(\phi )} \right]}}{{2\pi (1 - \nu )}}\frac{{\sin \theta }}{\lambda }\ln \frac{{\lambda \alpha }}{b},$$
(3)

where θ is the angle between the slip plane and the twin plane and λ is twin thickness; ν is Possion ratio; ϕ is the angle between the dislocation line and the Burgers vector, α is dislocation core parameter23.

With the corresponding parameters from ref. 14 and materials parameters of the diamond (listed in Supplementary Table 1), the CRSS for CLS mode is expressed as:

$$\tau _{{\mathrm{css}}}^{{\mathrm{CLS}}} = 10.3 + 22\frac{1}{\lambda }\ln \left( {\frac{{3.33\lambda }}{{0.25}}} \right).$$
(4)

Using Eq. 4, the CRSS for CLS mode is calculated and plotted in Fig. 2a. This CRSS increases with decreasing twin thickness, and the values are similar to that of CLS mode in nt-diamond14.

CRSS for CST-I mode

In CST-I mode, dislocation motions are confined by TB1 or TB2 and blocked by TB2 or TB1, respectively. Therefore, the corresponding CRSS is affected by both the Hall–Petch effect and the confined layer slipping effect. To obtain CRSS, both dislocation pile-up and CLS models are used (in Fig. 2b), and the CRSS for CST-I mode is expressed as:

$$\tau _{{\mathrm{css}}}^{{\mathrm{CST}} - I} = \tau _0 + \left( {\frac{{\tau _{TB}{\mathrm{Gb}}}}{{\pi \lambda }}} \right)^{1/2} + \frac{{{\mathrm{Gb}}\left[ {1 - \nu \cos ^2(\phi )} \right]}}{{2\pi (1 - \nu )}}\frac{{\sin \theta }}{\lambda }\ln \frac{{\lambda \alpha }}{b},$$
(5)

Where τ0 is lattice frictional stress, τTB is the barrier strength of shuffle-set 60° perfect dislocation reacting with TB, and ν is the Poisson ratio. All other parameters have been defined before.

Based on the parameters of the diamond from ref. 14 (listed in Supplementary Table 1), the CRSS of CST-I mode is expressed as:

$$\tau _{{\mathrm{css}}}^{{\mathrm{CST}} - I} = 10.3 + 45.3\lambda ^{ - 1/2} + 22\frac{1}{\lambda }\ln \left( {\frac{{3.33\lambda }}{{0.25}}} \right).$$
(6)

The resulting CRSS as a function of twin thickness is plotted in Fig. 2b. This CRSS increases with decreasing twin thickness. Because the CRSS is affected by both the Hall–Petch effect and the confined layer slipping effect, it can be considered as a superposition of ST and CLS modes. At the same twin thickness condition, this CRSS is higher than that of ST and CLS modes.

CRSS for CST-II mode

Similar to CST-I mode, the CRSS for CST-II is affected by both the Hall–Petch effect and the confined layer slipping effect; therefore, the CRSS for CST-II can be expressed by Eq. 5. The difference is that in this case, τTB refers to the barrier strength of shuffle-set 0° perfect dislocations reacting with TB. Based on Eq. 5 and the parameters of the diamond, the CRSS for CST-II mode is expressed as:

$$\tau _{{\mathrm{css}}}^{{\mathrm{CST}} - II} = 10.3 + 28\lambda ^{ - 1/2} + 22\frac{1}{\lambda }\ln \left( {\frac{{3.33\lambda }}{{0.25}}} \right).$$
(7)

The CRSS of CST-II mode thus calculated is plotted in Fig. 2b. Due to the lower barrier strength of shuffle-set 0° perfect dislocations, the CRSS is smaller than that of CST-I at the same twin thickness. Owing to the combined Hall–Petch and confined layer slipping effects, this CRSS is also higher than that of ST and CLS modes at the same twin thickness.

Hardness of bulk int-diamond based on the Sachs model

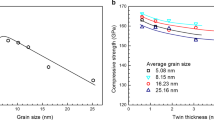
The Sachs model is a single-slip system model for mechanical properties of polycrystalline materials, and it is a particularly effective method to investigate the yield strength of polycrystalline materials with anisotropic slip systems17. For int-diamond, dislocations in multiple twin domains change directions and slip planes in such complex manner (as shown in Figs. 1 and 2) that the yield strength cannot be evaluated using a simple Taylor model32. Here, we model the yield strength of bulk int-diamond by considering 6000 grains on the basis of the Sachs model (see “Methods” section). Macroscopic yield strength is defined as the stress level at which 90% of the grains yield. The Vickers hardness is then assumed to be three times the compressive yield strength33,34,35,36,37. The resulting hardness of int-diamond increases with decreasing twin thickness (both λ1 and λ2), and is consistently higher than that of nt-diamond with the same twin thickness (λ1) and grain size (Fig. 3b). At a twin thickness of 0.62 nm, int-diamond reaches a hardness of 668 GPa, ~67% higher than that of the nt-diamond (401 GPa). These results indicate that the hardness limit for nt-diamond can be raised further by adding intersectional TBs in nt-diamond. Although the hardness limit of the int-diamond can be improved to 668 GPa, it is still below the theoretical hardness (~810 GPa) of diamond calculated by the 9τtheo, where the τtheo is the theoretical shear strength of diamond.

Fig. 3: Calculated hardness for int-diamond.
figure 3

a Fraction of yielded grains as a function of uniaxial stress. When the fraction of yielded grains reaches 90%, the corresponding uniaxial stress is defined as yield stress σy. The inserted figure is the statistical fraction of different slip modes occurring in the yielded int-diamond grains. b The calculated hardness of int-diamond compared with ng-diamond and nt-diamond. The inserted figure is the twin-thickness-dependent hardness of int-diamond and nt-diamond calculated by the Sachs model, together with the comparison of experimental measurements data7,8. Htheo is theoretical hardness of diamond calculated by the 9τtheo, where the τtheo is the theoretical shear strength of diamond.

Full size image

The fractions of different slip modes occurring in the yielded int-diamond grains are statistically analyzed, and the results are plotted in the insert of Fig. 3a. The fraction of grains yielded by ST mode slips increases whereas the fraction of grains yielded by CLS and CST-II mode slips decreases with decreasing twin thickness. Slips by CST-I mode are difficult to activate due to the high CRSSs, therefore the fraction of grains yielded by CST-I mode slips is essentially zero within the twin thickness range studied here. Hence, the hardness of bulk int-diamond is primarily due to slips in the ST, CLS, and CST-II modes with twin thicknesses up to 10 nm. As the CRSS of CST-II slip is higher than that of slip mode in nt-diamond, the hardness of int-diamond is higher than that of nt-diamond14.

Verification of int-diamond hardness by MD simulation

To further confirm the calculated results by Sachs model, the yield strength of polycrystalline int-diamond is studied by using MD simulation. The calculated stress-strain curve of the int-diamond is plotted in Fig. 4. The yield strength is equal to 165 GPa for int-diamond, 154 and 161 GPa for nt-diamond at twin thickness of 5.5 and 1.2 nm, and 140 GPa for ng-diamond, respectively. Although the strain rate (5 × 108 s−1) in MD simulation is higher than that of the experiment, these results qualitatively confirm that the yield strength of the int-diamond is larger than that of the nt-diamond, and further confirm the simulated results by our Sachs model.

Fig. 4: Calculated stress-strain curves of int-diamond, nt-diamond, and ng-diamond.
figure 4

The red, yellow, blue and cyan line is the stress-strain curve of int-diamond with twin thickness λ1 = 5.5 nm and λ2 = 1.2 nm, nt-diamond with twin thickness λ of 5.5 and 1.2 nm, and ng-diamond, respectively.

Full size image

Applicability of the int-diamond idea to synthesis

Huang et al.7 and Tao et al.8 have shown that, with properly selected precursory materials and under carefully controlled synthesis conditions, nano twins can be consistently introduced in ng-diamond. TEM observations show that in nt-diamond, a significant portion of the grains contains intersectional nanotwins, forming tweed-like pattern characteristic of the int-diamond (cf. Fig, 2 in ref. 7 and cf. Supplementary Fig. 2 in ref. 8). These observations suggest that int-diamond is readily manufacturable. The challenge is how to produce int-diamond consistently in bulk samples. Based on previous experimental results, two potentially important parameters to be grain size of the onion carbon precursors (highly deformed graphene layers in precursors increase the chance of TB formation in the diamond formation) and pressure and temperature conditions (high nucleation rates for diamond formation also increase the chance of producing TBs). Therefore, pre-deformation onion carbon precursors by uniaxial compression, large shear deformation38, and improvement of the synthesis pressure are a feasible method to form int-diamond in the experiment.

Discussion

We have examined the mechanical properties of diamond with a novel microstructure by introducing intersectional twin boundaries in ng-diamond. A total of 39 slip systems in four slip modes of this designer diamond (int-diamond) are systematically analyzed. Based on the critical resolved shear stress of the four modes, we calculate the hardness of bulk int-diamond using the Sachs model and show that int-diamond is much harder than nt-diamond. The hardening mechanism of int-diamond is attributed to the intersectional TBs, which block dislocations motions, resulting in increased CRSS. These results are further confirmed by direct polycrystalline MD simulations. This work provides a new strategy for designing new super-hard materials in experiments.

Methods

Barrier strength

The dislocation reaction with TB is a process of kink formation and migration, and it is schematically plotted in Supplementary Fig. 1. To simulate this process, a cuboid diamond twin structure model was first built. In this model, their x, y, and z axis are along diamond matrix’s .\([11\bar2]\), \([\bar 110]\), and [111] directions, the dimensions of x, y, and z axis are 20.9, 2.5, and 13.8 nm, respectively, and contains about 120000 carbon atoms. Next, a series of kinked shuffle-set 0° and 60° perfect dislocation with different kink pair widths was introduced in the twin plane of the cuboid diamond twin structure model by using dislocation displacement field method (in Supplementary Fig. 1)39,40.

MD simulations were then performed by using LAMMPS program41, and C–C bonding interactions were described by LCBOP potential42. Periodic boundary condition was only imposed along the y direction and the free surface was imposed in x and z directions. All these constructed structures were relaxed via energy minimization under different shear stress conditions. After relaxation, kink width dependent system energies were obtained and the maximum excess energy can be considered as kink formation energy (2Ef) at given shear stress. At the same time, a kink migration energy (Em) were calculated by using NEB method43. Finally, the activation energy Q of dislocation reaction with TB is obtained according to Q = 2Ef + Em27. The shear stress-dependent activation energy for dislocation reaction with TB is plotted in Fig. 1d. As shown in Fig. 1d, when the activation energy of dislocation reaction with TB reaches zero, the corresponding shear stress can be considered as the barrier strength for a dislocation reacting with TB.

Lattice friction stress

For shuffle-set 0° perfect dislocation slip in diamond, it also can be considered as a process of kink formation and migration, and the schematic for this process is plotted in insert of Supplementary Fig. 2. To simulate this process, a diamond structure model was built first. In this mode, its x, y, and z axis are along the \([11\bar 2]\), \([\bar 110]\) and [111] direction and with dimensions of 20.9, 2.5, and 13.8 nm, respectively. Then, a series of kinked shuffle-set 0° perfect dislocation with different kink pair widths were introduced in the slip plane located at the center of the diamond structure model. On the basis of these models, the shear stress dependent kink formation and migration energy is obtained by adding shear stress to the diamond structure model by using the method as described above (methods section of Barrier strength). Finally, the shear stress-dependent activation energy of shuffle-set 0° perfect dislocation slip in diamond is plotted in Supplementary Fig. 2. When the activation energy of the dislocation slip reaches zero, the corresponding stress is the lattice friction stress.

int-diamond hardness by using Sachs model

Sachs model is an effective method to investigate the yield strength for polycrystalline materials with anisotropic slip system. In Sachs model, the yield strength of each grain can be expressed as:

$$\sigma _n = \min \{ \sigma _n^1,\sigma _n^2,\sigma _n^3......\sigma _n^m\} ,$$
(8)

where the \(\sigma _n^m\) represents the yield strength of m-th slip system in n-th grain and it can be expressed as following:

$$\sigma _n^m = \frac{{\tau _m^{{\mathrm{CRSS}}}}}{{\mu _n^m}},$$
(9)

where the \(\tau _m^{{\mathrm{CRSS}}}\) is the CRSS of m-th slip system; \(\mu _n^m\) is the Schmid factor of m-th slip system in n-th grain.

In this work, a polycrystalline model with 6000 random orientations grains is considered. The yield strength for each grain can be obtained by using Eqs. 8 and 9. On the basis of these critical yield strength, we determine whether the grain yielded under a given uniaxial stress condition. As shown in Fig. 3a, the fraction of yielded grains increased with increasing uniaxial stress, when the fraction of yielded gain reaching 90%, the corresponding stress can be considered as the yield strength for this polycrystalline material. Further its hardness can be obtained by tripling its yield strength33,34,35.

MD simulation method for yield strength calculation

In this work, atomic models for int-diamond, nt-diamond, and ng-diamond were constructed by using Voronoi polyhedron method44. As shown in Supplementary Fig. 3, each model contains 20 grains with an average grain size of 16.23 nm. For int-diamond model, the twin boundaries TB1 have two types: Σ3(111) and Σ27(115) and twin boundary TB2 is Σ3(111). In this structure model, the fraction of twin boundary Σ3(111) is ~75%, and the fraction of twin boundary Σ3(111) can be further improved to asymptotically approach unity45. The twin thickness is 5.5 nm for TB1, and 1.2 nm for TB2. In the nt-diamond model, the twin thickness is 5.5 and 1.2 nm.

The MD simulations were then performed on these atomic models by using the popular LAMMPS code41, and atomic configurations were visualized and analyzed by using the OVITO package46. In this MD simulation, the C–C bonding interactions were described by Tersoff potential47, and the isothermal–isobaric (NPT) scheme was used48. The time-step is set as 0.001 ps, relaxation time is 200 ps. After structure optimization under 300 K and ambient pressure, the compressive deformation is applied along x direction under a constant strain rate of 5 × 108 s−1 with a total true strain of 0.3, and the corresponding stress-strain curves were recorded. The maximum stress in the recorded stress-strain curves can be considered as the corresponding yield strength.