Abstract
Atomically thin borophene has recently been synthesized experimentally, significantly enriching the boron chemistry and broadening the family of two-dimensional (2D) materials. Recently, oxides of 2D materials have been widely investigated for next-generation electronic devices. Based on the first-principles calculations, we predict the existence of the superconductivity in honeycomb borophene oxide (B2O), which possesses a high stability and could be potentially prepared by intrinsically incorporating oxygen into the recently synthesized borophene. The mechanical, electronic, phonon properties, as well as electron–phonon coupling of metallic B2O monolayer, have been systematically scrutinized. Within the framework of the Bardeen–Cooper–Schrieffer theory framework, the B2O monolayer exhibits an intrinsic superconducting feature with a superconducting transition temperature (Tc) of ~10.3 K, higher than many 2D borides (0.2–7.8 K). Further, strain can be utilized to tune the superconductivity with the optimal Tc of 14.7 K under a tensile strain of 1%. The superconducting trait mainly originates from the out-of-plane soft-mode vibrations of the system, which are significantly enhanced via the light O atoms’ incorporation compared to other 2D metal-boride superconductors. This strategy would open a door to design 2D superconducting structures via the participation of light elements. We believe our findings greatly bloom the 2D superconducting family and pave the way for future nanoelectronics.
Similar content being viewed by others
Introduction
Followed by theoretical prediction1, atomically thin borophene analogs of two-dimensional (2D) carbon materials, such as graphene, have recently been synthesized on Ag(111)2,3 and Au(111) substrates4. Due to the unique mechanical and electronic properties, borophene can be utilized in various applications, such as electrode materials in rechargeable batteries5,6,7,8,9, hydrogen storage10,11, sensor12,13,14, etc. These studies have significantly enriched the boron chemistry and broaden the family of 2D materials. It is known to be polymorphic metal monolayer with short covalent radius and sp2 hybridization, greatly different from its bulk phases with the semiconducting traits3,15. Furthermore, borophene is demonstrated to be an intrinsic superconductor16,17,18, showing an entirely different electronic property when compared with graphene. Next, intensive 2D superconductive borides, such as B2C19, Li2B720, tetr-Mo2B2, tri-Mo2B221, tetr-W2B2, hex-W2B222, AlB623, and XB6 (X=Ga, In)24, provide heretofore the diversity in the context of motifs, electron–phonon coupling (EPC) and superconductivity. However, the Tc, especially in 2D metal borides, is low to be only 0.2–7.8 K. This significantly necessitate the exploration of 2D boron-based superconductors with enhanced superconductivity.
It should be noteworthy that the electron-deficient property of B atoms makes B–B bonds unstable in borophene monolayer, particularly under oxygen-rich conditions25,26. This calls for the investigation of the possible 2D “BxOy” materials when exposed to oxygen. By scrutinizing the oxygen adsorption and dissociation on freestanding borophene, O-adsorbed borophene exhibits an enhanced stability via the strong B–O interactions27, in line with the characteristics of oxidation as reported in previous experiments2,3. These phenomena are ultimately in favor of the formation of 2D boron oxides under ambient conditions. Besides, oxidation could help to tune the physical and chemical properties of 2D materials as well28,29,30. Thus, borophene as electron-deficient monolayer is feasible to be embedded by oxygen via the formation of more stable B–O bonds31. It is in this way which the 2D boron oxides could be obtained potentially. Inspired by this, more attentions have been focusing on these 2D boron oxides. Using the particle-swarm optimization algorithm, zhang et al. have systematically explored the 2D boron oxide crystals, including compositions of B4O, B5O, B6O, B7O, B8O, possessing attractive electronic features31. Very recently, a 2D honeycomb boron oxide (B2O) with planar monolayer is proposed and exhibits intriguing topological phase transition when subject to external strains32. However, superconductivity in 2D boron oxides is yet to be reported experimentally and theoretically33,34,35,36. Considering the intrinsic superconductivity in borophene, the successful exploration of superconductivity in 2D boron oxides would not only bloom the 2D boron family but also feasibly facilitate the experimental explorations for realistic applications.
Inspired by prior successes in exploring superconductivity in borophene16,17,18,37,38,39, here we systematically study the superconductivity of 2D B2O monolayer with the lowest formation energy31. Using the first-principles calculations, the thermal and mechanical stability, electron structures, vibration modes, and superconductivity were discussed. The results show that B2O is not only a metallic monolayer but also an intrinsic superconductor with superconducting transition temperature (Tc) of 10.3 K that is higher than those of the mostly reported 2D borides. Such superconductivity is attributed to the out-of-plane soft-mode vibrations of O atoms. Moreover, under the tensile strain of 1%, a large softened vibration mode appears along M–X direction, that, leads to an increase of Tc by 40%, showing the tunability of superconductivity in B2O monolayer.
Results and discussion
The structure properties of B2O
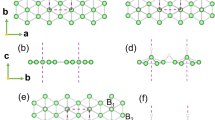
The artificial B2O monolayer in this work was verified to be the global minimum structure by adopting particle-swarm optimization40,41. B2O has a global minimum of energy of −6.80 eV/atom, ~0.48 and 0.50 eV smaller than the configurations with the 2nd and 3rd lowest energies, respectively (Supplementary Fig. 1a, b). However, the latter two structures are not dynamically stable, confirmed by the calculated phonon spectra (Supplementary Fig. 1c, d). Thus, we next only focus our attentions on the one with the global minimum energy. The title B2O monolayer crystallizes in the orthorhombic lattice with space group Cmmm (No. 65), possessing a C2v symmetry (Fig. 1a). The lattice parameters of B2O are a = b = 3.93 Å. The B atom adopts a slightly distorted trigonal coordination with the bond angles of 107.8 and 126.1° as shown in Fig. 1b. The B–B bond distance is 1.71 Å, comparable with that of δ6 (1.62–1.87 Å)42, χ3 (1.62–1.72 Å) and β12 borophene (1.65–1.75 Å)16. The bond length of B–O is 1.34 Å, significantly shorter than that of B4O (1.53 and 1.61 Å)31, indicating the lower bond energy and higher bond strength. The B–B and B–O bonds exhibit the strong covalent bonding traits (Fig. 1c), further favoring the high stability within the B2O plane.
a The planal structure of B2O monolayer. The rhombic primitive cell is labeled by the black dash line. The unit cell is indicated in green dash line. b The zoom-in B2O monolayer with bond distance and angle numbers is marked. c Electron localization function (ELF) of B2O monolayer with an isovalue of 0.5 a.u. d The difference charge density Δρ along the z direction of B2O. The yellow and cyan areas represent electron gains and losses, respectively. The isosurface value is set to be 0.005 a.u. The B and O atoms are indicated by blue and red ball, respectively.
The stability of B2O crystal
The stability of 2D crystals is very important in predicted structures. Here, the cohesive energy (Ecoh) and formation energy (Ef) are performed by
and
respectively, where \({E}_{{{\mathrm{B}}}_{{\mathrm{2}}}{\mathrm{O}}}\) is the total energy of primitive cell of B2O, and EB and EO are the energies of isolated B and O atom, respectively. The μB is the chemical potential of χ3 borophene, and the μO is the chemical potential of O2. The obtained Ecoh and Ef are calculated to be 2.43 and −0.99 eV, respectively, indicating the exothermic process and experimental feasibility under suitable external conditions. Besides, the evolution of the free energy obtained from ab initio molecular dynamics (AIMD) simulations is exhibited in Supplementary Fig. 2. The average value of the free energy remains nearly constant with small fluctuations during the entire simulation period at about 1500 K (Supplementary Fig. 2a). After 10-ps simulation, we found that there exists a sign of a structural disruption at about 1700 K (Supplementary Fig. 2b), producing a calculated melting temperature of 1500–1700 K. This melting temperature is higher than the previous report (1000 K)32, suggesting a higher thermal stability and thus the potential applications in extreme high-temperature environment.
To further assess the mechanical stability of our structure, we calculated the elastic constants Cij in the rectangle unit cell by
where Es is strain energy, and the tensile strain is defined as \(\varepsilon =\frac{{a}-{a}_{0}}{{a}_{0}}\), and a and a0 are the lattice constants of the strained and strain-free structures, respectively. εxx and εyy are the strains along the x and y directions, and εxy is the shear strain. The B2O belonging to orthorhombic crystal has four independent elastic constants: C11, C12, C22, and C66, corresponding to the second partial derivative of strain energy with respect to the applied strain. In order to calculate the elastic stiffness constants, the Es as a function of ε in the range of − 2% ≤ ε ≤ 2% were calculated. The results of the strain energy curves associated with uniaxial, biaxial, and shear strains are shown in Supplementary Fig. 3a. Then, the Cij can be obtained with the aid of the VASPKIT43, a post-processing program for the VASP code. Our calculations estimate C11, C12, C22, and C66 to be 42.57 N/m, 67.63 N/m, 237.59 N/m, and 11.58 N/m, respectively. Obviously, B2O monolayer satisfies the Born criteria44, C11 > 0, C66 > 0, and C11C22 – C\({}_{12}^{2}>\) 045, which further confirms the mechanical stability of B2O monolayer.
The in-plane Young’s moduli (Y) along the x and y directions are obtained with the help of elastic constants as: Y\({}_{x}={\frac{{{\rm{C}}}_{11}{C}_{22}\,-\,{C}_{12}^{2}}{{\rm{C}}}}_{22}=23.42\) N/m and Y\({}_{y}=\frac{{{\rm{C}}}_{11}{C}_{22}\,-\,{C}_{12}^{2}}{{{\rm{C}}}_{11}}=130.40\) N/m. Apparently, the Young’s moduli are comparable with TiN (143 N/m)46, MoS2 (123 N/m)47, phosphorene (24–103 N/m) and silicene (62 N/m)48. The Poisson’s ratio reflects the mechanical responses of the system against uniaxial strains and can be calculated as \({\nu }_{x}=\frac{{{\rm{C}}}_{12}}{{{\rm{C}}}_{22}}=0.29\) and \({\nu }_{y}=\frac{{{\rm{C}}}_{12}}{{{\rm{C}}}_{11}}=1.59\), indicating the large anisotropy in mechanical properties. To present a full understanding of the mechanical properties of B2O monolayer, we calculated the orientation-dependent Y and ν as a function of the polar angle θ (0–360°). For the orthogogonal 2D system, the strain parallel (ε∥) and perpendicular (ε⊥) to the θ direction induced by the unit stress σ(θ)(∣σ∣ = 1) can be expressed as49,50
and
respectively, where \(\Delta ={{\rm{C}}}_{11}{{\rm{C}}}_{22}-{{\rm{C}}}_{12}^{2}\), \(a=\cos\)(θ) and \(b=\sin\)(θ). Then, Y(θ) and ν(θ) are derived as
and
respectively. Clearly, both the variations of Y and ν show a spindle-like shape, indicating the fully anisotropic traits (Supplementary Fig. 3b, c). The Young’s modulus has a minimal value of 23.42 N/m along the x direction (θ = 0°), and a maximal value of 130.40 N/m along the y direction (θ = 90°). Meanwhile, the ν(θ) of B2O increases monotonically from 0.29 (θ = 0°) to 1.59 (θ = 90°). These anisotropies are associated with the bond interactions of B–B and B–O bonds in the two directions.
Electronic properties of B2O monolayer
In order to probe the nature of charge transfer of B2O monolayer, we also calculated the difference charge density Δρ, as shown in Fig. 1d. The charge transfer mainly occurs from less electronegative B to more electronegative O atoms. Although the σ states of O atoms gain electrons, whereas the π states partially loss electrons as well. There are significantly delocalized charge accumulations within B–O bond, indicating the covalent bonding feature. According to the Bader analysis51, the net charger transfer from B to O is 0.79 electron per atom, in consistence with above distribution of difference charge density. The ionic feature of B2O can be thus represented as B20.79+O1.58−, showing charge transfer predominantly from B to O atoms via B–O bonding interactions.
The B2O monolayer is metallic with two bands crossing the Fermi level (Fig. 2a), which is supported by the Fermi surface distributions along the high paths (Fig. 2b). From the orbital-resolved band structure, the bands around the Fermi level are mainly composed of the B-p and O-p orbitals. In Supplementary Fig. 4, we can clearly see that the orbital hybridization near the Fermi level mainly stems from B-px,y and B-pz states, followed by some contributions from O-px,y, O-pz, and B-s states. Thus, the metallic nature of B2O monolayer is essentially dominated by the B-p orbitals. In addition, two dirac cones (DCs) exist around the Fermi level. The orbital-resolved band structures of the B2O monolayer are presented in Supplementary Fig. 5 to understand the origin of DPs. The DC1 mainly consists of B-py and O-pz, and the DC2 involves the dominant contributions from B-pz and O-py. Nevertheless, the s, px orbitals of two atoms are not responsible for the formation of the DCs (Fig. 2a; Supplementary Fig. 5). The effects of spin-orbit coupling and Heyd–Scuseria–Ernzerhof (HSE06)52 are evaluated to play a negligible role in the formation of DCs32. Even, the DCs are still well maintained with strain reaching up to 3% (Supplementary Fig. 8b), indicating that the 2D B2O is a robust Dirac material. To assess the electronic transport properties of B2O monolayer, we further calculated the Fermi velocity (VF) within PBE level along Y–M by using the equation VF = \(\frac{\partial E}{\hslash \partial k}\), where the \(\frac{\partial E}{\partial k}\) is the slop of the linear band structure and the \(\hbar\) is the reduced Planck’s constant. The calculated VF closing to DC2 are 9.6 × 105 and 6.8 × 105 m/s, respectively, larger than and comparable with graphene (8.22 × 105 m/s)53. This high value of VF suggests B2O monolayer to be possess a ultrahigh carrier mobility and would facilitate the future electronics. To probe the effects of the percentage of Hartree–Fock (HF) functionals on electronic properties, screened exchange hybrid density functional of HSE06 were carried out as well (Supplementary Fig. 6). Upon increasing the fraction of HF in the HSE06 calculations, the dispersion of band structure shows a small variation when compared with the PBE results, and the main band traits, such as the two DCs, are maintained. This result suggests that HF plays a negligible role in the electronic structure of system. So, we only calculated and analyzed the superconductivity next on the PBE level.
Phonon and superconductivity of B2O crystal
The phonon spectrum of B2O monolayer shown in Fig. 3 reveals no imaginary phonon modes, indicating that the rhombic phase is kinetically stable, which is in line with previous result32. The phonon k ⋅ p theorem is used to sort the phonon branches based on the continuity of the eigenvectors of vibration modes54,55,56,
where \({e}_{k,\sigma }^{* }(j)\) is the displacement of atom j in the eigenvector of (k, σ) vibration mode, and Δ is a small wave vector. As indicated in Fig. 3a, the out-of-plane (ZA), in-plane transverse (TA), and in-plane longitudinal (LA) modes constitute the three acoustic branches for B2O.
According to the decomposition of the phonon spectrum with respect to the vibration directions of B and O atoms (Fig. 3a), three acoustic branches dominate the low-frequency region (below 400 cm−1), where the main contributions are from in-plane and out-of-plan of modes of O atoms. Meanwhile, the two lowest optical branches consisting of the out-of-plan of modes of B-z also make large contributions to this range. Generally, due to the subtle differences in atomic weight, the out-of-plane modes of B-z and O-z mostly occupy the low-frequency region. The mid-frequency region from 400 to 900 cm−1 are related entirely to the in-plane of modes of B-xy and the B-z. Moreover, the vibration frequencies larger than 900 cm−1 originate from the out-of-plan of modes of B-xy and O-xy. The highest vibration frequency, 1471 cm−1, is much larger than that of Mo2B2 (880 cm−1)21, W2B2 (920 cm−1)22, Li2B7 (1120 cm−1)20, AlB6 (1150 cm−1)23, β12 borophene (1200 cm−1)16,57, χ3 borophene (1290 cm−1)16,58, and B2C (1365 cm−1)19, it is even comparable with that of δ6 borophene (1411 cm−1)42. Such a high frequency is consistent with the strong covalent bonding, suggested by the former results of ELF (Fig. 1c) and projected phonon density of states (PhDOS) (Fig. 4a).
The results of the PhDOS, Eliashberg spectral function α2F(ω), the EPC constant λ, Tc, and the derivatives of Tc are presented in Fig. 4. The Eliashberg spectral function exhibits that four major peaks are located at 88.3, 119.3, 210.2, and 288.2 cm−1, respectively, in the low-frequency region. As shown in Fig. 3b, the low-frequency mode phonons contribute mainly to the EPC, accounting for 78.5% of the total EPC (λ = 0.75). The first peak of α2F(ω) is mainly responsible for this part, ~51.9% of the total EPC. In the frequency range of 83–120 cm−1, the large values of λqν along the M–X − Γ directions are visible and lead to the first two largest peaks of the α2F(ω) (Figs. 3b and 4b). As a consequence, λ(ω) increases rapidly in this range. In order to probe the underlying causes, we analyze the vibration modes with the largest value of λqν in this range (see Fig. 3b). Clearly, the out-of-plane vibrations of B and O atoms contribute to the increase of λqν. Besides, in mid-frequency region (400–800 cm−1), the phonons contribute the rest of the EPC by ~21.5%. However, the contributions of high-frequency phonons are negligible, which is similar to Mo2B221, W2B222, AlB623, β12 borophene16,57, and χ3 borophene16,58. Using the McMillian–Allen–Dynes formula59, the frequency-dependent superconducting transition temperature Tc(ω) is obtained from Fig. 4c. Its derivative also exhibits the four main peaks in low frequency, which consistent with distributions of α2F(ω). The B2O monolayer is a medium-coupling superconductor with λ of 0.75 according to the role proposed by Allen et al59. and possesses a Tc of 10.35 K, which is higher than those of LiC6 (5.9 K)60,61, C6CaC6 (4.0 K)62,63, and Cu-BHT (3.0 K)64 that their values of Tc were determined in experiments. Moreover, the Tc of B2O is also higher than recently reported 2D boride superconductors using a typical value of μ* = 0.1, such as Li2B7 (6.2 K)20, B allotrope (6.7 K)17, tetr-Mo2B2 (3.9 K), tri-Mo2B2 (0.2 K)21, tetr-W2B2 (7.8 K), hex-W2B2 (1.5 K)22, rect-GaB6 (1.7 K), rect-InB6 (7.8 K), hex-InB6 (4.8 K)24, and AlB6 (0.95 K)23. This increase of Tc can be rationalized by the fact that the vibrations of B atoms are significantly enhanced via incorporating light O atoms into the monolayer, in great contrast to the constraining effect associated with heavier metal atoms within 2D metal-boride superconductors. This provides clues for us to design 2D superconducting systems with light elements and opens the road toward further improvement of 2D superconducting feature. It is true that some intrinsic 2D stable B structures such as δ6 (27.0 K), χ3 (24.7 K), and β12 borophene (18.7 K)16 show superconductivity with higher Tc. This is not in contrast to our designing strategy of 2D superconductors via the participation of light elements: The pure 2D boron structures could be regarded the extreme phase of borides by introducing a more light "B" element into 2D sheet in the form of "BxB" when compared with the O’s incorporation in B2O monolayer. Here, the Tc of borophene is also calculated with μ* = 0.1. To explore the effect of the μ* on the Tc of B2O monolayer, we calculate the Tc by varing μ* from 0.08 to 0.15 (Supplementary Fig. 7). As expected, Tc would decrease monotonically decreasing form 11.9 K to 6.8 K upon the increase of μ*.
The oxidation process of black phosphorene could be well-controlled by the assistance of Laser65 and borophene has been successfully synthesized on the substrates3,4. Thus, the B2O monolayer may be obtained on borophene substrate by oxidation32. To simulate the real samples grown on substrates with different lattice constants, we applied the in-plane biaxial strain to the B2O monolayer. The biaxial strain can be calculated by \(\xi =\frac{{a}-{a}_{0}}{{a}_{0}}\times 100 \%\) (positive value means tensile strain, while negative one indicates compressive strain). In our calculations, the lattice constants are changed from −1% to 3%, and atomic coordinates are fully relaxed in each case. The band structures and phonon spectra are plotted in Supplementary Fig. 8. By confirmed the phonon spectra in Supplementary Fig. 8a, B2O is stable under the tensile strain from 1% to 3%. As indicated in Supplementary Fig. 8b, the tensile strain has few influence on the band structures around the Fermi level, the same as the N(EF) (Fig. 5b; Supplementary Fig. 8b). While, the phonon spectra shift to some extent under applied tensile strain. Especially, compared with freestanding sample, appearing a large soften mode along M–X at strain of 1%, is a good phenomena improving the superconductivity. The variations of superconductive parameters [N(EF), ωlog, λ, and Tc] under series of strain are exhibited in Fig. 5. Along with the increasing tensile strain, the ωlog first decrease until strain greater than 1%, and then it goes up conversely. While the λ and Tc vary in an inverse way, and the N(EF) varies a little. When tensile strain equals 1%, the λ and Tc can be increased to be 1.04 and 14.7 K, respectively, reaching the maximum values in this strain region. However, the bigger tensile strain suppresses the superconductivity. So, strain engineering offers an effective way to tune the superconductivity and facilitates the potential application in future nanodevices.
In summary, within the framework of the density-functional theory (DFT) and Bardeen–Cooper–Schrieffer (BCS) theory, we have systematically investigated the mechanical and electronic properties, phonon vibrations as well as superconductivity of the proposed 2D honeycomb borophene oxide, B2O. The B2O monolayer exhibits a high stability and possesses two Dirac cones near the Fermi level, and is an intrinsic BCS-type superconductor with a Tc of ~10.3 K. This Tc is higher than mostly reported boride superconductors. The superconducting trait is attributed to the out-of-plane vibration modes of B and O atoms. Upon applying a tensile in-plane strain of 1%, the Tc can achieve the maximum value of 14.7 K, which is associated with the large soften mode appearing along M–X direction in ZA branch. Thus, these interesting results would further trigger efforts on 2D superconducting materials.
Methods
First-principles calculations
The first-principles calculations based on the DFT were performed through the Vienna ab initio simulation package (VASP)66,67 and the Quantum-ESPRESSO code. After the full convergence tests, the exchange correlation interaction was simulated within the generalized gradient approximation (GGA)68,69 with the Perdew–Burke–Ernzerhof (PBE)70-type pseudopotential. The electronic wave functions were expanded via the plane wave basis set with a energy cutoff of 600 eV. The Γ-centered 15 × 15 × 1 k-point mesh were adopted using the Monkhorst–Pack method. To avoid the interaction between adjacent monolayers, the vacuum thickness was set to be 15 Å along the z direction. The structure were fully relaxed until the total energy and force on per atom were <10−5 eV and 0.01 eV/Å, respectively71,72. The EPC and superconductivity were calculated by the QE within the density-functional perturbation theory (DFPT)73 and the BCS theory74. The optimized norm-conserving Vanderbilt pseudopotentials75 were used to model the electron-ion interactions. The kinetic energy cutoff and the charge density cutoff of the plane wave basis were chosen to be 80 and 320 Ry, respectively. Self-consistent electron density was evaluated by employing 24 × 24 × 1 k mesh with a Methfessel–Paxton smearing width of 0.02 Ry. The phonon calculations were carried out on the 6 × 6 × 1 q mesh. Meanwhile, the convergences of λ and Tc are tested and shown in Supplementary Fig. 9, verifying that the q mesh of 6 × 6 × 1 is large enough to used in our calculations.
Structure screening and AIMD calculations
The particle-swarm optimization (PSO) scheme, as implemented in the CALYPSO code40,41, was adopted to search for the global minimum structure for the B2O compound. In the PSO calculations, both planar and buckled structures of B2O were considered, and the population size and the number of generations were set to be 30. Through the high-throughput calculations, thousands of different structures of B2O were generated and ranked by CALYPSO code in order of enthalpy from low to high. The electronic structure calculations were performed through the VASP. We also performed the AIMD simulations at a series of temperatures (300, 500, 700, 900, 1100, 1300, 1500, and 1700 K) with constant number, volume, temperature (NVT) ensemble, lasting for 10 ps with a time step of 1 fs to assess the thermal stabilities of B2O monolayer. The 3 × 3 × 1 supercell was adopted and the temperature was controlled using the Nosé–Hoover thermostat76.
Superconductivity calculations
Within the BCS and Migdal–Eliashberg theories77,78 framework, to examine the contribution to λ from individual phonon modes, the magnitude of the EPC λqν can be calculated by
where γqν, ωqν, and N(EF) are the phonon linewidths, the frequency of a lattice vibration with crystal momentum q in the branch ν and the density of states (DOS) at the Fermi level, respectively79. In addition, the phonon linewidths γqν can be estimated by
where ΩBZ is the volume of Brillouin zone (BZ); ϵkn and ϵk+qm are the Kohn–Sham energy, ϵF is the Fermi energy, and \({{\rm{g}}}_{{\boldsymbol{k}}n,{\boldsymbol{k}}+{\boldsymbol{q}}m}^{\nu }\) denotes the EPC matrix element. Moreover, according to the linear response theory59 the \({{\rm{g}}}_{{\boldsymbol{k}}n,{\boldsymbol{k}}+{\boldsymbol{q}}m}^{\nu }\) can be determined self-consistently. Subsequently, the Eliashberg electron–phonon spectral function α2F(ω) and the cumulative frequency-dependent EPC function λ(ω) can be calculated by
and
respectively.
The logarithmic average frequency \({\omega }_{\mathrm{log}\,}\) and the superconducting transition temperature Tc can be calculated as follows:
and
where μ* = 0.1, a typical value of the effective screened Coulomb repulsion constant16,57,80,81,82,83,84.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Zhang, Z., Yang, Y., Gao, G. & Yakobson, B. I. Two-dimensional boron monolayers mediated by metal substrates. Angew. Chem. Int. Ed. 54, 13022–13026 (2015).
Mannix, A. J. et al. Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs. Science 350, 1513–1516 (2015).
Feng, B. et al. Experimental realization of two-dimensional boron sheets. Nat. Chem. 8, 563 (2016).
Kiraly, B. et al. Borophene synthesis on Au(111). ACS Nano 13, 3816–3822 (2019).
Zhang, Y., Wu, Z.-F., Gao, P.-F., Zhang, S.-L. & Wen, Y.-H. Could borophene be used as a promising anode material for high-performance lithium ion battery? ACS Appl. Mater. Inter. 8, 22175–22181 (2016).
Chen, H. et al. First principles study of P-doped borophene as anode materials for lithium ion batteries. Appl. Sur. Sci. 427, 198–205 (2018).
Mortazavi, B., Dianat, A., Rahaman, O., Cuniberti, G. & Rabczuk, T. Borophene as an anode material for Ca, Mg, Na or Li ion storage: a first-principle study. J. Power Sources 329, 456–461 (2016).
Jiang, H., Lu, Z., Wu, M., Ciucci, F. & Zhao, T. Borophene: a promising anode material offering high specific capacity and high rate capability for lithium-ion batteries. Nano Energy 23, 97–104 (2016).
Jiang, H., Shyy, W., Liu, M., Ren, Y. & Zhao, T. Borophene and defective borophene as potential anchoring materials for lithium–sulfur batteries: a first-principles study. J. Mater. Chem. A 6, 2107–2114 (2018).
Chen, X., Wang, L., Zhang, W., Zhang, J. & Yuan, Y. Ca-decorated borophene as potential candidates for hydrogen storage: a first-principle study. Int. J. Hydrog. Energy 42, 20036–20045 (2017).
Sun, X. et al. Two-dimensional boron crystals: structural stability, tunable properties, fabrications and applications. Adv. Funct. Mater. 27, 1603300 (2017).
Xiao, H. et al. Lattice thermal conductivity of borophene from first principle calculation. Sci. Rep. 7, 45986 (2017).
Shukla, V., Wärnå, J., Jena, N. K., Grigoriev, A. & Ahuja, R. Toward the realization of 2D borophene based gas sensor. J. Phys. Chem. C. 121, 26869–26876 (2017).
Ranjan, P. et al. Freestanding borophene and its hybrids. Adv. Mater. 31, 1900353 (2019).
Zhang, Z., Penev, E. S. & Yakobson, B. I. Two-dimensional materials: polyphony in B flat. Nat. Chem. 8, 525 (2016).
Gao, M., Li, Q.-Z., Yan, X.-W. & Wang, J. Prediction of phonon-mediated superconductivity in borophene. Phys. Rev. B 95, 024505 (2017).
Zhao, Y., Zeng, S. & Ni, J. Superconductivity in two-dimensional boron allotropes. Phys. Rev. B 93, 014502 (2016).
Xiao, R. et al. Enhanced superconductivity by strain and carrier-doping in borophene: a first principles prediction. Appl. Phys. Lett. 109, 122604 (2016).
Dai, J., Li, Z., Yang, J. & Hou, J. A first-principles prediction of two-dimensional superconductivity in pristine B2C single layers. Nanoscale 4, 3032–3035 (2012).
Wu, C. et al. Lithium–boron (li–b) monolayers: first-principles cluster expansion and possible two-dimensional superconductivity. ACS Appl. Mater. Inter. 8, 2526–2532 (2016).
Yan, L. et al. Prediction of phonon-mediated superconductivity in two-dimensional Mo2B2. J. Mater. Chem. C. 7, 2589–2595 (2019).
Yan, L. et al. Novel structures of two-dimensional tungsten boride and their superconductivity. Phys. Chem. Chem. Phys. 21, 15327–15338 (2019).
Song, B. et al. Two-dimensional anti-van’t Hoff/Le Bel array AlB6 with high stability, unique motif, triple dirac cones and superconductivity. J. Am. Chem. Soc. 141, 3630–3640 (2019).
Yan, L. et al. Superconductivity in predicted two dimensional XB6 (X = Ga, In). J. Mater. Chem. C. 8, 1704–1714 (2020).
Li, L. H., Cervenka, J., Watanabe, K., Taniguchi, T. & Chen, Y. Strong oxidation resistance of atomically thin boron nitride nanosheets. ACS Nano 8, 1457–1462 (2014).
Lherbier, A., Botello-Méndez, A. R. & Charlier, J.-C. Electronic and optical properties of pristine and oxidized borophene. 2D Mater. 3, 045006 (2016).
Luo, W. et al. Insights into the physics of interaction between borophene and O2-first-principles investigation. Comp. Mater. Sci. 140, 261–266 (2017).
Butler, S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Georgakilas, V. et al. Noncovalent functionalization of graphene and graphene oxide for energy materials, biosensing, catalytic, and biomedical applications. Chem. Rev. 116, 5464–5519 (2016).
Yin, H., Liu, C., Zheng, G., Wang, Y. & Ren, F. Ab initio simulation studies on the room-temperature ferroelectricity in two-dimensional β-phase GeS. Appl. Phys. Lett. 114, 192903 (2019).
Zhang, R., Li, Z. & Yang, J. Two-dimensional stoichiometric boron oxides as a versatile platform for electronic structure engineering. J. Phys. Chem. Lett. 8, 4347–4353 (2017).
Zhong, C. et al. Two-dimensional honeycomb borophene oxide: Strong anisotropy and nodal loop transformation. Nanoscale 11, 2468–2475 (2019).
Van Delft, D. & Kes, P. The discovery of superconductivity. Phys. Today 63, 38–43 (2010).
Carenco, S., Portehault, D., Boissiere, C., Mezailles, N. & Sanchez, C. Nanoscaled metal borides and phosphides: recent developments and perspectives. Chem. Rev. 113, 7981–8065 (2013).
Uchihashi, T. Two-dimensional superconductors with atomic-scale thickness. Supercond. Sci. Tech. 30, 013002 (2016).
Brun, C., Cren, T. & Roditchev, D. Review of 2D superconductivity: the ultimate case of epitaxial monolayers. Supercond. Sci. Tech. 30, 013003 (2016).
Zhao, Y., Zeng, S. & Ni, J. Phonon-mediated superconductivity in borophenes. Appl. Phys. Lett. 108, 242601 (2016).
Li, G., Zhao, Y., Zeng, S., Zulfiqar, M. & Ni, J. Strain effect on the superconductivity in borophenes. J. Phys. Chem. C. 122, 16916–16924 (2018).
Shao, Z. et al. Ternary superconducting cophosphorus hydrides stabilized via lithium. npj Comput. Mater. 5, 1–8 (2019).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Zhao, Y. et al. Multigap anisotropic superconductivity in borophenes. Phys. Rev. B 98, 134514 (2018).
Wang, V., Xu, N., Liu, J.-C., Tang, G. & Geng, W. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Preprint at https://arxiv.org/abs/1908.08269 (2019).
Born, M. & Huang, K. Dynamical Theory of Crystal Lattices (Clarendon Press, 1954).
Mouhat, F. & Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90, 224104 (2014).
Zhou, L., Zhuo, Z., Kou, L., Du, A. & Tretiak, S. Computational dissection of two-dimensional rectangular titanium mononitride TiN: auxetics and promises for photocatalysis. Nano Lett. 17, 4466–4472 (2017).
Yue, Q. et al. Mechanical and electronic properties of monolayer MoS2 under elastic strain. Phys. Lett. A 376, 1166–1170 (2012).
Topsakal, M. & Ciraci, S. Elastic and plastic deformation of graphene, silicene, and boron nitride honeycomb nanoribbons under uniaxial tension: a first-principles density-functional theory study. Phys. Rev. B 81, 024107 (2010).
Wang, L., Kutana, A., Zou, X. & Yakobson, B. I. Electro-mechanical anisotropy of phosphorene. Nanoscale 7, 9746–9751 (2015).
Wang, V. & Geng, W. Lattice defects and the mechanical anisotropy of borophene. J. Phys. Chem. C. 121, 10224–10232 (2017).
Tang, W., Sanville, E. & Henkelman, G. A grid-based bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 21, 084204 (2009).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl 2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Wang, Z. et al. Phagraphene: a low-energy graphene allotrope composed of 5–6–7 carbon rings with distorted dirac cones. Nano Lett. 15, 6182–6186 (2015).
Liu, P.-F. et al. Hexagonal M2C3 (M = As, Sb, and Bi) monolayers: new functional materials with desirable band gaps and ultrahigh carrier mobility. J. Mater. Chem. C. 6, 12689–12697 (2018).
Huang, L. F., Gong, P. L. & Zeng, Z. Correlation between structure, phonon spectra, thermal expansion, and thermomechanics of single-layer MoS2. Phys. Rev. B 90, 045409 (2014).
Huang, L. F. & Zeng, Z. Lattice dynamics and disorder-induced contraction in functionalized graphene. J. Appl. Phys. 113, 083524 (2013).
Cheng, C. et al. Suppressed superconductivity in substrate-supported β12 borophene by tensile strain and electron doping. 2D Mater. 4, 025032 (2017).
Zhao, Y. et al. Multigap anisotropic superconductivity in borophenes. Phys. Rev. B 98, 134514 (2018).
Allen, P. B. & Dynes, R. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905 (1975).
Ludbrook, B. et al. Evidence for superconductivity in Li-decorated monolayer graphene. Proc. Nati. Acad. Sci. 112, 11795–11799 (2015).
Zheng, J.-J. & Margine, E. First-principles calculations of the superconducting properties in Li-decorated monolayer graphene within the anisotropic migdal-eliashberg formalism. Phys. Rev. B 94, 064509 (2016).
Ichinokura, S., Sugawara, K., Takayama, A., Takahashi, T. & Hasegawa, S. Superconducting calcium-intercalated bilayer graphene. Acs Nano 10, 2761–2765 (2016).
Margine, E., Lambert, H. & Giustino, F. Electron-phonon interaction and pairing mechanism in superconducting Ca-intercalated bilayer graphene. Sci. Rep. 6, 21414 (2016).
Huang, X. et al. Superconductivity in a copper (ii)-based coordination polymer with perfect kagome structure. Angew. Chem. Int. Ed. 57, 146–150 (2018).
Lu, J. et al. Bandgap engineering of phosphorene by laser oxidation toward functional 2D materials. ACS Nano 9, 10411–10421 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Blöchl, P. E., Jepsen, O. & Andersen, O. K. Improved tetrahedron method for brillouin-zone integrations. Phys. Rev. B 49, 16223 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Mat. 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum espresso. J. Phys.: Condens. Mat. 29, 465901 (2017).
Baroni, S., De Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1957).
Hamann, D. Optimized norm-conserving vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984).
Grimvall, G. The Electron-phonon Interaction in Metals, Vol. 8 (North-Holland Pub. Co., Amsterdam, 1981).
Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 89, 015003 (2017).
Dacorogna, M. M., Cohen, M. L. & Lam, P. K. Self-consistent calculation of the q dependence of the electron-phonon coupling in aluminum. Phys. Rev. Lett. 55, 837 (1985).
Zhang, X., Zhou, Y., Cui, B., Zhao, M. & Liu, F. Theoretical discovery of a superconducting two-dimensional metal–organic framework. Nano Lett. 17, 6166–6170 (2017).
Liu, P.-F. & Wang, B.-T. Face-centered cubic MoS2: a novel superconducting three-dimensional crystal more stable than layered T-MoS2. J. Mater. Chem. C. 6, 6046–6051 (2018).
Tu, X.-H., Liu, P.-F. & Wang, B.-T. Topological and superconducting properties in YD3 (D = In, Sn, Tl, Pb). Phys. Rev. Mater. 3, 054202 (2019).
Qu, Z. et al. Prediction of strain-induced phonon-mediated superconductivity in monolayer YS. J. Mater. Chem. C. 7, 11184–11190 (2019).
Yan, L. et al. Emergence of superconductivity in a dirac nodal-line Cu2Si monolayer: ab initio calculations. J. Mater. Chem. C. 7, 10926–10932 (2019).
Acknowledgements
L.Z. acknowledges the financial support from the University of Electronic Science and Technology of China. P.-F.L. and B.T.W. acknowledge the PhD Start-up Fund of Natural Science Foundation of Guangdong Province of China (Grant No. 2018A0303100013). L.Y. thanks Y.K.L. from Chinese University of Hong Kong for some discussions.
Author information
Authors and Affiliations
Contributions
L.Y. performed the conceptualization, data curation, and writing—original draft and validation. P.-F.L. performed investigation and validation. H.L. performed the formal analysis. Y.T. made software and investigation. J.H. did investigation. B.W. performed the supervision and validation. L.Z. performed the conceptualization, writing–reviewing, and editing. All authors discussed and analyzed the results and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yan, L., Liu, PF., Li, H. et al. Theoretical dissection of superconductivity in two-dimensional honeycomb borophene oxide B2O crystal with a high stability. npj Comput Mater 6, 94 (2020). https://doi.org/10.1038/s41524-020-00365-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-020-00365-9
This article is cited by
-
Strain-tunable Dirac semimetal phase transition and emergent superconductivity in a borophane
Communications Physics (2024)
-
Strong-coupling superconductivity with Tc above 70 K in Be-decorated monolayer T-graphene
Science China Physics, Mechanics & Astronomy (2024)
-
Chemically identifying single adatoms with single-bond sensitivity during oxidation reactions of borophene
Nature Communications (2022)
-
High-temperature phonon-mediated superconductivity in monolayer Mg2B4C2
npj Quantum Materials (2022)
-
Designing high-TC superconductors with BCS-inspired screening, density functional theory, and deep-learning
npj Computational Materials (2022)