Introduction

As our society’s need to store data continuously increases, we will soon reach the performance limits of current memory devices1. Magnetic skyrmions are widely believed to be one of the most promising candidates for next-generation memory technology. A magnetic skyrmion is a local whirl of spins in a magnetic material with a fixed chirality2,3. It is topologically protected against deformation into other magnetic states, and against disorder and perturbation. The stability of skyrmions, their small size and their responsiveness to tiny electrical current densities (~106A/m2), make these skyrmions ideal for enabling ultra-dense, low-energy memory devices3. One of the important mechanisms controlling the generation and stability of skyrmions and other magnetic topological defects4 is the Dzyaloshinskii–Moriya interaction (DMI)5,6.

Despite its fundamental importance, the microscopic origin of DMI in magnetic bilayers is not well understood. Originally derived for magnetic insulators, the theory developed by Moriya6 does not help us understand the trend of DMI observed in magnetic bilayers. Recent works have tried to uncover the microscopic origin of DMI in magnetic bilayers. One model proposes that the source of DMI in bilayers is the proximity-induced magnetic moments in the heavy metal(HM) layers7. However, this proposal is contradicted by another report8. Other interesting studies point out that HM–FM hybridization is a primary factor in controlling the strength of DMI9,10, with which our model agrees. However, the proposition of9 that the sign of DMI follows FM 3d band filling is contradicted by the large, negative DMI seen in Ir/Fe11,12 and both positive and negative signs of DMI reported for HM/Co8,13. Similarly, the proposal that DMI is controlled solely by the spin-polarized HM–5d states in Pt/FM10 is contradicted by experimental reports of opposite signs of DMI for Pt/Co14 and Pt/Ni15.

There is thus a gap in our understanding of the relationship of DMI with electronic structure, and of the mechanism by which DMI produces magnetic textures. This gap hampers our ability to design materials for enhanced DMI, or to control the strength or sign of DMI, which can help the development of controllable skyrmion technology16. In this paper, we address this gap and present a model to explain the microscopic origin of DMI in metallic bilayers. We calculate the DMI values in a series of heavy metal/ferromagnet (HM/FM) bilayers and explain the trend of DMI observed. In particular, we show that the value of DMI depends on two factors, namely, HM–FM hybridization and HM spin mixing terms. The latter are determined by the contribution of specific HM orbitals to the HM/FM bandstructure. We emphasize that the HM/FM bandstructure, and consequently the DMI sign, depends on the choice of both the FM as well as the HM. We also derive a theory for the mechanism by which spin orbit coupling (SOC) generates spin textures. Our results present a significantly new understanding of DMI. They also unveil important avenues to control the strength and sign of DMI, thereby advancing the controlled generation or annihilation of skyrmions.

Real world applications in emergent memory technology would ideally require skyrmions of size ≤10 nm that are stable at room temperature2. Ultrathin HM/FM films have been shown to host small skyrmions (~3–8 nm) stabilized by DMI, but so far they exist only at low temperatures (<30 K)12,17,18. On the other hand, HM/FM multilayer stacks can host skyrmions at room temperature, but so far they have been larger than 30 nm in diameter1,19,20,21,22. Recently, it has been proposed that frustrated magnets can also host skyrmions that are stabilized by competing ferromagnetic nearest-neighbor and antiferromagnetic next-nearest-neighbor interactions23,24,25,26. The existence of such skyrmions has been very recently shown for Gd2PdSi327. While these skyrmions are very small in size (approximately a few nms), so far, they have only been observed at low temperatures (<20 K) as well.

In HM/FM bilayers, the size and stability of DMI-stabilized-skyrmions is decided by the interplay between multiple variables, including, the DMI, the exchange constant, the out-of plane anisotropy and dipolar fields28,29,30,31. Therefore, to realize skyrmion based emergent memories, it will be important to identify materials with the appropriate combinations of these parameters. As a general rule, a large ratio of DMI to exchange constant encourages a quicker rotation of the spin, and reduces the size of the skyrmion (in the absence of interactions like edge effects)3. Thus, materials with enhanced values of DMI can host skyrmions that are stable at higher temperatures and small in size. Here, we report new bilayers that demonstrate giant DMI, up to twice the largest value known so far. We also present new material designs for magnetic multilayers that show enhanced DMI. We note that starting with an HM–FM bilayer with a giant interfacial DMI, fine tuning of DMI and exchange values is possible by further engineering of the stacks32,33. Large DMI also enables the formation of other chiral spin structures, like chiral domain walls, which are relevant to next-generation data storage devices34. Our results thus significantly advance the field by presenting new materials, which show promise for enabling skyrmion device technology.

Results

New materials with giant DMI

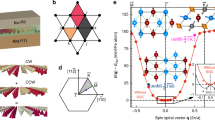
Our results for DMI are shown in Fig. 1. Our values show excellent agreement with literature, except for Re/Fe, where our DMI is roughly half that predicted by Simon et al.35. A significant result is the giant DMI seen in six bilayers, namely, Re/Fe, Os/Fe, Re/Co, Os/Co, Os/Ni and hexagonal Bismuth(hBi)/Ni. These materials show a DMI (d) up to twice the largest currently known values of 1.5 meV/atom for Co/Pt8, −1.9 meV/atom for Ir/Fe8 and −1.04 meV/atom for Ir/Co36. Note our predicted values of DMI (d) for these materials are 2.6 meV/atom for Co/Pt, −1.8 meV/atom for Ir/Fe and −1.8 meV/atom for Ir/Co. Predictions of large DMI in Re/Co, Os/Co, Os/Ni and hBi/Ni have not been reported before. As a possible quantum spin Hall material37, hexagonal Bi is particularly noteworthy, as it can help drive skyrmions via a large spin Hall current. A useful materials design strategy for enhancing DMI has been the addition of DMI of opposite sign from successive interfaces38,39, as implemented in Pt/Co/Fe/Ir multilayers. Our results make it possible to achieve even larger additive DMIs in simpler multilayer structures, such as Pt/Co/Os and Pt/Co/Re.

Fig. 1: Plots of Dzyaloshinskii–Moriya interaction (DMI) for a series of HM/FM bilayers (HM: Hf–Bi).
figure 1

Our DMI results are plotted with filled markers, whereas corresponding DMI values in literature are plotted using unfilled black markers. Circles represent Fe, squares represent Co and triangles represent Ni. Reference values are taken from ref. 35 for Re/Fe, Os/Fe Ir/Fe; from ref. 36 for Ir/Co; from ref. 8 for Pt/Co; from ref. 11 for Pb/Co; and from ref. 15 for Pt/Ni. The unit of D is mJ/(m−BM)2, where BM is the Bohr magneton.

Full size image

Discussion

We now present the analysis of our results and develop a model for the microscopic origin of DMI. We demonstrate that DMI depends on two parameters, HM–FM hybridization and the presence of specific HM orbitals in the bandstructure. We find that the strength of DMI is controlled by the relative alignment of HM–FM bands. Here we show that the sign of DMI is controlled by orbital contributions from the HM rather than the 3d orbital filling of the FM. Our work thus notably alters the current understanding of DMI in magnetic bilayers.

We now show that the strength of DMI (d) is principally determined by the HM–FM hybridization. To demonstrate this, we examine the projected density of states (p-DOS), plotted in Figs. 2, 3, and relative band alignments between the HM and FM layers. We define band overlap (BO) as the amount of overlap exhibited by the FM-3d bands with the HM–5d bands (6p bands) for the 5d (6p) series of HMs. We expect that the greater the BO, the greater the HM–FM hybridization. Upon visual inspection, we clearly see that d strongly depends on BO. In particular, a large BO is a necessary but not sufficient condition to obtaining large d. Since Fe, Co and Ni have d6–d8 electron configurations, the 3d–5d band overlap is maximized for Re, Os, Ir and Pt (d5–d8), giving rise to maximum DMI strength for these materials. Similarly for HM-6p elements, d increases for increasing BO. There are notable outliers, namely, Ir/Fe, Pt/Co and Pt/Ni (and hBi/Co for HM-6p) where the DMI obtained is smaller than what would be expected from BO alone. We explain the reason for these exceptions later.

Fig. 2: Plots of projected density of states (p-DOS) and band alignment for HM/Fe bilayers.
figure 2

P-DOS for Fe-3d is plotted in navy blue while p-DOS for HM–5d is plotted in cyan and that for HM-6p is plotted in magenta. Fermi energy is set at 0 eV.

Full size image
Fig. 3: Plots of projected density of states (p-DOS) and band alignment for HM/Co bilayers.
figure 3

P-DOS for Co-3d is plotted in navy blue while p-DOS for HM–5d is plotted in cyan and that for HM-6p is plotted in magenta. Fermi energy is set at 0 eV.

Full size image

For the HM–5d/Fe series, we observe a trend of ∣dβW/Fe∣ < ∣dAu/Fe∣ < ∣dRe/Fe∣ < ∣dOs/Fe∣. This is easily explained as the BO also increases in this order, as shown in Fig. 2. Similarly, for the HM–5d/Co series, we note a trend of ∣dHg/Co∣ ~ ∣dαW/Co∣ < ∣dPt/Co∣ < ∣dOs/Co∣ ~ ∣dRe/Co∣. This is explained by the large BO seen for Pt/Co, Os/Co and Re/Co, as shown in Fig. 3. The HM–Ni series also follows similar trends with increasing d for increasing BO. As noted before, Ir/Fe, Pt/Co and Pt/Ni have a smaller d than one would expect simply from BO. The only other outlier is Hg, which both for Fe and Co has a DMI which is small, but larger than expected from simply 3d–5d BO. Hg/FM results suggest that there might be other, smaller contributions to HM/FM hybridization in addition to the 3d–5d BO. For the HM-6p/FM series, the observed trend of ∣dTl/Fe∣ ≲ ∣dPb/Fe∣ ≲ ∣dBi/Fe∣ and ∣dTl/Co∣ < ∣dBi/Co∣ < ∣dPb/Co∣ both correlate well with the increasing order of BO. Overall, our results show that HM–FM band overlap has a significant control over the strength of DMI. We explain the cause of this relationship later.

The sign of DMI is important as it decides the sense of rotation of a magnetic texture. We note that DMI’s sign does not follow FM 3d band filling and can in fact change even for the same FM. Here we investigate the origin of this sign. We derive a theory for the mechanism by which SOC generates magnetic textures, and demonstrate that the sign of DMI is controlled by the relative presence of HM orbitals in the bandstructure. Our findings bring to light the source of the DMI’s sign and point to new pathways for controlling skyrmion chirality, with significant impact to future technology.

We use first order perturbation theory to derive the mechanism by which SOC leads to the creation of magnetic textures. We build upon an important previous work on the Berry phase theory of DMI40,41. According to this Berry phase theory, the rotation of the magnetic moment of an electron alters the free energy, via exchange interaction, and gives rise to DMI. Here we demonstrate how SOC leads to the rotation of magnetic moment in the first place, which subsequently creates magnetic textures and generates DMI. Our derivation applies specifically to the hedgehog-like (Néel) skyrmions found in magnetic multilayers42, as shown in Fig. 4.

Fig. 4: Schematics of crystal structure and a skyrmion.
figure 4

Panels a and b demonstrate a schematic of our structure of Pt/Co bilayer, where a shows the front view of the prerelaxed structure, which includes 10 Å of vacuum, and b shows the top view of the postrelaxed structure. Panel c shows a schematic of a Neel skyrmion.

Full size image

Consider a HM/FM bilayer system. In the absence of SOC, the FM has a constant magnetization. Let \({\psi }_{\vec{k}n}^{0}\) represent the unperturbed wavefunction of an electron delocalized over this bilayer.

$${\hat H_0}\left| {\psi _{\vec kn}^0} \right\rangle ={E}_{\overrightarrow{k}n}^{0}\left| {\psi _{\vec kn}^0} \right\rangle$$
(1)

We now turn on SOC, such that \(\hat{H}={\hat{H}}_{0}+{\hat{H}}_{{\mathrm{SOC}}}\). The new eigenstate representing the electron hopping between HM and FM is given by

$$\left|{\psi }_{{\vec k}n}\right\rangle =\left|{\psi }_{{\vec k}n}^{0}\right\rangle +{\sum \limits_{{\vec q},m}}\frac{\left\langle {\psi }_{{\vec k}+{\vec q}m}^{0}\right| {\hat{H}}_{{\mathrm{SOC}}}\left| {\psi }_{{\vec k}n}^{0}\right\rangle }{{E}_{{\vec k}n}^{0}-{E}_{\vec{k}+{\vec q}m}^{0}}\left|{\psi }_{{\vec k}+{\vec q}m}^{0}\right\rangle$$
(2)

Without loss of generality, we can assume the unperturbed FM has a magnetization along the z-axis and the perturbed magnetic moment rotates in the XZ plane. We now consider the component of magnetic moment of the perturbed state along \(\vec{x}\), up to first order

$$\langle {\hat{s}}_{x}\rangle ={\sum \limits_{\vec{q},m}}\left\langle {\psi }_{\vec{k}n}^{0}\right| {\hat{s}}_{x}\left| {\psi }_{\vec{k}+\vec{q}m}^{0}\right\rangle \frac{\left\langle {\psi }_{\vec{k}+\vec{q}m}^{0}\right| {\hat{H}}_{{\mathrm{SOC}}}\left| {\psi }_{\vec{k}n}^{0}\right\rangle }{{E}_{\vec{k}n}^{0}-{E}_{\vec{k}+\vec{q}m}^{0}}+C.C.$$
(3)

Taking the long wavelength limit of \(\vec{q}\to 0\).

$$\langle {\hat{s}}_{x}\rangle ={\sum \limits_{m \ne n}}\left\langle {\psi }_{\vec{k}n}^{0}\right| {\hat{s}}_{x}\left| {\psi }_{\vec{k}m}^{0}\right\rangle \frac{\left\langle {\psi }_{\vec{k}m}^{0}\right| {\hat{H}}_{{\mathrm{SOC}}}\left| {\psi }_{\vec{k}n}^{0}\right\rangle }{{E}_{\vec{k}n}^{0}-{E}_{\vec{k}m}^{0}}+C.C.$$
(4)

Writing \({\hat{s}}_{x}\) and \({\hat{H}}_{{\mathrm{SOC}}}\) in the spin basis (\(\left|\uparrow \right\rangle ,\left|\downarrow \right\rangle\)):

$$\left|\uparrow \right\rangle =\left[\begin{array}{c}1\\ 0\end{array}\right]\left|\downarrow \right\rangle =\left[\begin{array}{c}0\\ 1\end{array}\right]{\hat{s}}_{x}=\left[\begin{array}{*{20}{l}}0&1\\ 1&0\end{array}\right]{\hat{H}}_{{\mathrm{SOC}}}=\left[\begin{array}{*{20}{l}}\lambda {\hat{l}}_{0}/2&\lambda {\hat{l}}_{-}/2\\ \lambda {\hat{l}}_{+}/2&-\lambda {\hat{l}}_{0}/2\end{array}\right]$$
(5)

where \({\hat{l}}_{\pm }\equiv {\hat{l}}_{x}\pm \iota {\hat{l}}_{y}\quad {\hat{l}}_{0}\equiv {\hat{l}}_{z}\). We can write \({\hat{l}}_{\pm }\) in the d-orbital basis (\({d}_{{z}^{2}},{d}_{xz},{d}_{yz},{d}_{xy},{d}_{{x}^{2}-{y}^{2}}\)) as,

$${\hat{l}}_{+}=\left[\begin{array}{ccccc}0&\sqrt{3}&\iota \sqrt{3}&0&0\\ -\sqrt{3}&0&0&\iota &1\\ -\iota \sqrt{3}&0&0&1&-\iota \\ 0&-\iota &-1&0&0\\ 0&-1&\iota &0&0\end{array}\right]\,{\hat{l}}_{-}=\left[\begin{array}{ccccc}0&-\sqrt{3}&\iota \sqrt{3}&0&0\\ \sqrt{3}&0&0&\iota &-1\\ -\iota \sqrt{3}&0&0&-1&-\iota \\ 0&-\iota &1&0&0\\ 0&1&\iota &0&0\end{array}\right]$$
(6)

For an unperturbed wavefunction \({\psi }_{\vec{k}n}^{0}\) in the spin-up state, the only nonzero contributions to \(\langle {\hat{s}}_{x}\rangle\) come from \({\psi }_{\vec{k}m}^{0}\) in the spin-down state.

$$\begin{array}{l}\left|{\psi }_{\vec{k}n}^{0}\right\rangle =\left|{\phi }_{\vec{k}n}^{0},\uparrow \right\rangle ;\left|{\psi }_{\vec{k}m}^{0}\right\rangle =\left|{\phi }_{\vec{k}m}^{0},\downarrow \right\rangle \\ \langle {\hat{s}}_{x}\rangle =\lambda /2{\sum \limits_{m\ne n}}\frac{\left\langle {\phi }_{{\vec k}m}^{0}\right| {{\hat l}_{+}}\left| {\phi }_{\vec{k}n}^{0}\right\rangle }{{E}_{\vec{k}n}^{0}-{E}_{\vec{k}m}^{0}}+C.C.\end{array}$$
(7)

where \({\phi }_{\vec{k}}^{0}\) is the orbital part of the wavefunction. Similarly, for an unperturbed wavefunction \({\psi }_{\vec{k}n}^{0}\) in the spin-down state, we get:

$$\begin{array}{l}\left|{\psi }_{\vec{k}n}^{0}\right\rangle =\left|{\phi }_{\vec{k}n}^{0},\downarrow \right\rangle ;\left|{\psi }_{\vec{k}m}^{0}\right\rangle =\left|{\phi }_{\vec{k}m}^{0},\uparrow \right\rangle \\ \langle {\hat{s}}_{x}\rangle =\lambda /2{\sum \limits_{m\ne n}}\frac{\left\langle {\phi }_{\vec{k}m}^{0}\right| {{\hat l}_{-}}\left| {\phi }_{\vec{k}n}^{0}\right\rangle }{{E}_{\vec{k}n}^{0}-{E}_{\vec{k}m}^{0}}+C.C.\end{array}$$
(8)

Rotation of the magnetic moment of an electron, delocalized over the HM/FM interface, is caused by the spin orbit terms, \({\hat{l}}_{+}\cdot {\hat{s}}_{-}\) and \({\hat{l}}_{-}\cdot {\hat{s}}_{+}\). To obtain a continuous, self-sustained rotation in real space, spin-up and spin-down states should be rotated such that they pick up magnetic moments in opposite directions along the x-axis. This condition requires \(\langle {\phi }_{\vec{k}m}^{0}| \hat{{l}_{+}}| {\phi }_{\vec{k}n}^{0}\rangle\) to be opposite in sign to \(\langle {\phi }_{\vec{k}m}^{0}| \hat{{l}_{-}}| {\phi }_{\vec{k}n}^{0}\rangle\). Inspecting Eq. (6), we conclude that there are only three such terms, namely, \(\langle {d}_{xz}| {\hat{l}}_{\pm }| {d}_{{z}^{2}}\rangle ,\langle {d}_{xy}| {\hat{l}}_{\pm }| {d}_{yz}\rangle\) and \(\langle {d}_{x2-y2}| {\hat{l}}_{\pm }| {d}_{xz}\rangle\).

To further illustrate this mechanism, we consider a wavefunction hopping across the HM/FM interface. In the presence of SOC, whenever the electron hops to the HM atom, the three SOC spin mixing terms cause d-orbital transitions and rotate its magnetic moment (creating a swirling spin texture). As this electron hops to the FM, its rotated magnetic moment perturbs the wavefunctions of the FM via exchange interaction, altering the free energy and generating DMI40. The stronger the HM–FM hybridization, the stronger the perturbation of energy due to the hopping electron, the larger the DMI. The sign of DMI is decided by the interplay between these three SOC spin mixing terms and the strength of DMI is decided by the HM–FM hybridization. We note that this result does not support the model of10 where the source of DMI is identified to be transitions between dxz and dyz orbitals.

We now employ our theory to explain the trends of DMI sign observed in our calculations, thereby shining light on previously unexplained materials behaviour. According to our theory, three SOC transition terms, generate three separate DMI terms. The direction of each SOC transition will decide the sign of the corresponding DMI term, with opposite directions of transition leading to opposite DMI signs. The direction and strength of a transition, in turn, depends on the relative presence of HM orbitals (d1 and d2) in the bandstructure, before SOC is turned on. Specifically, the stronger the presence of d1, and the weaker the presence of d2, the stronger the transition from d1 to d2 would be, once SOC is turned on. The result of these inferences is that if we compare materials with similar crystal structures, their bandstructures and energy denominators (\({E}_{\vec{k}n}^{0}-{E}_{\vec{k}m}^{0}\)) are similar too. Consequently, it is the variation of relative presence of HM d orbitals that controls the net DMI sign.

With this in mind, we compare the contribution of d orbitals to the bandstructure for some chosen bilayers (Re/Fe, Os/Fe, Ir/Fe, Re/Co, Os/Co, Pt/Co, Os/Ni and Pt/Ni). These bilayers were selected from the bigger dataset for their large values of DMI and similar crystal structures. This enabled us to compare them to one another, as well as, easily demonstrate the mechanism behind DMI. We visually inspected the projected bandstructures in these materials, and found that the SOC transitions occur close to the K point in the Brillouin zone (BZ). The specific energy ranges over which the transitions occurred varied for different materials, but were generally found to be between −3 to −1 eV, or −4 to −2 eV below the Fermi level. Figure. 5 plots the difference in orbital contributions (p-DOS) from HM d orbitals around the K point, in the energy range corresponding to the bilayers. Keeping in mind that orbital contributions can only roughly capture SOC transitions, they turn out to be a good qualitative predictor of the sign of DMI. They also help explain why the three outliers mentioned above have DMI smaller than that predicted by BO alone.

Fig. 5: Plots for difference in orbital contributions (around K), and microscopic DMI.
figure 5

The difference between contributions of \({d}_{{x}^{2}-{y}^{2}}\) and dxz is plotted with magenta circles, and that between contributions of dxy and dyz is plotted with orange squares. Microscopic DMI is plotted using navy blue triangles for comparision.

Full size image

With regards to Fig. 5, a positive value of d1 − d2 contribution, signifies a likely transition from d1 to d2 and vice versa. For our chosen bilayers, we infer that dyz → dxy and \({d}_{xz}\to {d}_{{x}^{2}-{y}^{2}}\) transitions will generate negative DMI terms leading to counterclockwise rotation of spin. We observe from Fig. 5 that all our chosen materials show a dyz → dxy transition and a corresponding negative DMI term. However, early HMs tend to show a \({d}_{xz}\to {d}_{{x}^{2}-{y}^{2}}\) transition (negative DMI term) whereas late HMs show the reverse \({d}_{{x}^{2}-{y}^{2}}\to {d}_{xz}\) transition (positive DMI term). The sum of these DMI terms gives the final DMI. In Re/Fe, Os/Fe and Re/Co, both DMI terms are negative leading to a large negative net DMI. However, in Ir/Fe, Pt/Co and Pt/Ni, the two DMI terms have opposite sign and compete with one another. This explains why these outliers have a lower DMI than expected simply from BO. We do not observe any \(\langle {d}_{xz}| {\hat{l}}_{\pm }| {d}_{{z}^{2}}\rangle\) transitions. We note that Os/Ni also has competing transitions but shows a larger than expected DMI. Despite this exception, overall, the relative d-orbital contributions are a good qualitative predictor of the sign of DMI.

Our work has important implications as to the understanding of DMI and the control of skyrmions. First, our model also explains the correlation between DMI and orbital anisotropy reported recently43. According to our theory, DMI originates in spin mixing orbital transitions caused by SOC. Such transitions along with generating DMI will also naturally distort orbital shapes and alter orbital moments, leading to the correlation between DMI and orbital asymmetry observed. Second, our model suggests that DMI in bilayers can be controlled by tuning the HM–FM hybridization. A similar concept has been proposed for bulk ϵCo44. Third, the engineering of relative HM–5d orbital fillings, via strain and symmetry breaking, could provide a pathway for controlling the sign of DMI and the chirality of skyrmions. Control of skyrmions with an electric field would be a tremendous leap forward in the development of skyrmion technology.

Methods

Density functional theory calculations

We calculated the DMI using density functional theory (DFT) for a comprehensive series of HM/FM bilayers. Our choice of HM varied through the 5d and 6p series of elements, ranging from Hf to Bi. We chose the FM to be γ-Fe(111), Co(0001) or Ni(111). DFT calculations were performed using Vienna ab initio Simulation Package (VASP)45,46,47 with PAW-PBE pseudopotentials48. Taking the initial bulk structures from literature, we optimized their volume and constructed bilayers comprising of a monolayer of FM, a monolayer of HM and 10 Å of vacuum. A schematic of these structures is shown in Fig. 4. As the DMI in these bilayers is known to be interfacial11, using monolayers of FM and HM is sufficient to capture the essential physics. The in-plane lattice constant was fixed to that of the HM and the FM was strained to less than 5% to match. The calculations were converged with respect to kmesh and plane wave energy cut-offs. All structures were then relaxed till the Hellman–Feynman forces on all atoms were less than 0.01 eV/Å. DMI was the calculated using the mechanism described by Yang et al.8. The microscopic DMI (d) obtained from first principles was used to further calculate the micromagnetic DMI (D). An important caveat is that our calculations for DMI are performed with the assumption that the nearest neighbour (NN) DMI term is the dominant contribution to the total DMI. We make this assumption based on the expectation that the hopping terms between NN FM atoms (via HM), will in general be stronger than the hopping terms between next-nearest neighbours (NNN) FM atoms (via HM). According to our model, larger hopping terms will generally lead to stronger DMI. This picture should hold for our structures where there is a significant lattice mismatch between HM and FM layers and strong structural relaxation. It has been shown for chiral bulk materials49, that NNN DMI terms become less important than dominant NN DMI terms at nonzero magnetic fields. Therefore, we expect our results to be relevant to obtaining room temperature, small sized skyrmions at nonzero magnetic fields.