Unconventional topological phase transition in non-symmorphic material KHgX (X = As, Sb, Bi)

Abstract

Traditionally topological phase transition describes an evolution from topological trivial to topological nontrivial state. Originated from the non-symmorphic crystalline symmetry, we propose in this work an unconventional topological phase transition scheme between two topological nontrivial insulating states mediated by a Dirac gapless state, differing from the traditional topological phase transition. The KHgX (X = As, Sb, Bi) family is the first experimentally realized topological non-symmorphic crystalline insulator (TNCI), where the topological surface states are characterized by the Mobius-twisted connectivity. Based on first-principles calculations, we present a topological insulator–metal transition from TNCI into a Dirac semimetal (DSM) via applying an external pressure on KHgX. We find an unusual mirror Chern number C_m = −3 for the DSM phase of KHgX in the non-symmorphic crystal structure, which is topologically distinct from the traditional DSM such as Na₃Bi and Cd₃As₂. Furthermore, we predict a new TNCI phase in KHgX via symmetry breaking. The topological surface states in this new TNCI phase display zigzag connectivity, different from the unstressed one. Our results offer a comprehensive study for understanding how the topological surface states evolve from a quantum phase transition in non-symmorphic system.

Introduction

Understanding the fundamental physics in different phases of matter is one of the most important goals of condensed matter physics. A powerful route to understand an unrevealed phase is investigating the nature of a phase transition.^{1,2,3,4,5,6,7} Topological phases and topological phase transitions are new phenomena distinct from Landau’s phase transition⁸ and have attracted worldwide research interests because of their unusual fundamental physical properties as well as potential applications in next-generation electronics.^{9,10,11,12,13} Consequentially, searching for new type of topological phases in real materials and studying its phase transition become a research frontier in condensed matter physics and materials science.

In the past decade, many materials have been demonstrated to be a time-reversal symmetry-protected Z₂ topological insulator in both three-dimensional (3D) and two-dimensional systems.^8,14 Scientists also realize that additional crystalline symmetries play an important role in the topological classifications. Hence, various topological crystalline phases have been proposed and discovered, including the topological crystalline insulators (TCIs)^{15,16,17,18,19,20,21,22} and the topological semimetals (TSMs),^{5,6,7,23,24,25,26,27,28,29,30,31,32,33} which correspond to fully gapped and gapless bulk states, respectively. Recent works further raise a new class of TCI states in the time-reversal-invariant systems with spin–orbit coupling, which are protected by the non-symmorphic glide reflection symmetries.^{34,35,36,37,38,39} It was shown that, for a 3D insulating system under both glide reflection and time-reversal, a Z₄ invariant can be defined such that four topologically distinct phases can be identified under the symmetries,^36,37 called the topological non-symmorphic crystalline insulator (TNCI).⁴⁰ The topological surface states of TNCI exhibit exotic Mobius-twisted connectivity because the glide eigenvalue does not coincide with the 2π periodicity of the Brillouin zone (BZ).³⁶

The KHgX (X = As, Sb, Bi) family is recently predicted and confirmed as a TNCI both theoretically^38,39 and experimentally.⁴¹ However, the topological phase transition of this insulating phase remains still elusive. In this work, we investigate the topological phase transition in KHgX under external pressure and breaking symmetry via first-principles calculations based on density functional theory (DFT). Our calculations show a topological insulator–metal transition that KHgX transfers from TNCI into an unusual topological Dirac semimetal (DSM) phase under external stress within the non-symmorphic symmetry. More importantly, we find the mirror Chern number of this Dirac state is C_m = −3 on the k_z = 0 plane, which has never been found in previous Type-I and Type-II DSMs.^5,23,42,43 Furthermore, our calculation predicts that KHgX transfers into a new type of TNCI state distinct from the unstressed one when breaking the rotational symmetry. Consequentially, KHgX provides an unrevealed surface connectivity beyond the Mobius-twisted one. These intriguing topological phases and corresponding phase transitions may lead to brand new signatures in various experiments, including photoemission and scanning tunneling, as well as transport measurements, paving a way for experimental studies on new type of topological phases.

Results and Discussion

KHgX without stress

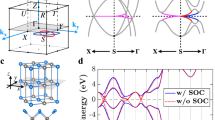
Experimentally KHgAs and KHgSb of the KHgX family (X = As, Sb, Bi) have been synthesized.^41,44 Figure 1a shows the crystal structure of KHgX in the space group P6₃/mmc (no. 194). The K atom acts as the electron donor while Hg and X form the honeycomb layer with weak interlayer interactions.⁴⁵ The alternatively stacking HgX honeycomb layers along the c axis indicates that the space group contains non-symmorphic symmetries. Taking K ion as the origin of the Cartesian coordinates, the space group can be generated by three symmetry operators: (1) The glide reflection $\hat M_y:(x,y,z) \mapsto (x, - y,z + c/2)$, i.e., a reflection by the y = 0 plane followed by a half translation parallel to c; (2) The six-fold screw rotation $\hat C_6$ : $(x,y,z) \mapsto (x\,{\mathrm{cos}}\,\theta - y\,{\mathrm{sin}}\,\theta ,x\,{\mathrm{sin}}\,\theta + y\,{\mathrm{cos}}\,\theta ,z + c/2)$ where $\theta = 2\pi /6$, i.e., a six-fold rotation along c-axis followed by a half translation; (3) The inversion through the origin $\hat P$ : $(x,y,z) \mapsto ( - x, - y, - z)$. Here $\hat M_y$ and $\hat C_6$ are non-symmorphic symmetries involving a fractional translation that cannot be removed by different choices of the origin. All the crystal symmetries of the Hamiltonian can be written in terms of the above generators together with the translation operator $\hat t(x,y,z)$ of the Bravais lattice. The Hamiltonian also exhibits the time-reversal symmetry $\hat T$ since KHgX is non-magnetic.

Fig. 1

The lattice structure, Brillouin Zone, and band structures of KHgAs and KHgBi. a Top: The primitive unit cell of KHgX under the space group P6₃/mmc. Bottom: Top view of the crystal structure, where the black arrows define the orientation of the Cartesian coordinate used in this work. b The bulk BZ, (010)-surface BZ (gray plane), and (100)-surface BZ (blue plane). Here (010) or (100) refers to the surface normal vector in terms of the Cartesian coordinate. In the bulk BZ, the k_z = 0 plane is colored by red. c, d The calculated band structure of KHgAs and KHgBi, respectively, with the optimized lattice constant. The red dots indicate the contribution from the Hg-s orbitals

Symmetries play important roles in this work such that: (a) The $Z_4$ invariant is defined under $\hat M_y$ and $\hat T$; (b) The mirror Chern number is defined under $\hat M_z$, where $\hat M_z = \hat t(0,0,2c)\hat P(\hat C_6)^3$ is the reflection (not glide) by the $z = c/4$ plane, namely, the HgX layer; (c) The rotational symmetry ($\hat C_6$ or $\hat C_3$) together with $\hat P$ and $\hat T$ protect the Dirac node (DN) under stress, where $\hat C_3 = \hat t(0,0, - c)(\hat C_6)^2$ is the three-fold rotation (not screw). In the following, given a symmetry operator $\hat h$, a path or plane in the bulk or surface BZ is called invariant under $\hat h$ if all the k on this path or plane satisfy $\tilde h{\mathbf{k}} = {\mathbf{k}} + {\mathbf{G}}$ where $\tilde h$ is the 3 × 3 matrix acting on the Cartesian coordinate and G is a vector of the reciprocal lattice. On such $\hat h$ invariant path or plane, common eigenstates of the Hamiltonian $\hat H({\mathbf{k}})$ and the symmetry operator $\hat h$ can be found.

Figure 1c, d show, respectively, the calculated band structures of stress-free KHgAs and KHgBi based on the optimized lattice constants (Table 1) with minimum and maximum spin–orbit coupling strength among the KHgX family. A common feature of the KHgX band structures is the two occupied Hg-s bands as can be seen along Γ−A. In fact, these Hg-s bands show inverted energy order compared to that of KZnP,^38,45,46 where the latter is adiabatically connected to the atomic limit. Owing to such non-trivial band inversion, it was predicted that the unstressed KHgX exhibits gapless surface states characterized by the hourglass flow connectivity^38,39 (also called the Mobius-twisted connectivity^36,37). Previous works^38,39 have demonstrated the non-trivial topology of KHgX from Wilson loop spectra. Here we instead unveil the topological properties of KHgX from another viewpoint through the Z₄ invariant and mirror Chern number as discussed below.

Table 1 Geometrically optimized lattice constants (in Å) from DFT calculations

Owing to the symmetries of $\hat M_y$ and $\hat T$, the Z₄ invariant χ ∈ {0, 1, 2, 3} is well defined for the orthorhombic BZ of KHgX. Following the conventional approach, we carry out the Wilson loop calculations for KHgBi in different phases as discussed in section II of the Supplementary Information (SI-2). The one-to-one relation between the Wilson loop spectrum and the topological invariant χ is clearly seen. Here we also provide a new gauge-independent formula of this invariant, Eq. S14 in SI-3. We will adapt this equation in this work because it is more suitable for numerical calculations. On the other side, the mirror Chern number $C_{\mathrm{m}} = (C^{ + i} - C^{ - i})/2 \in {\Bbb Z}$ is well defined on the two $\hat M_z$ invariant planes k_z = 0 and k_z = π/c, where C^±i is the Chern number of the subspace such that

$$C^{ \pm i} = \frac{1}{{2\pi }}{\int}_{k_z = 0} {F^{ \pm i}} ({\mathbf{k}})\cdot d{\mathbf{a}}$$

(1)

in which $F^{ \pm i}({\mathbf{k}})$ is the Berry curvature of the occupied $\hat M_z$ eigenstates (with eigenvalues ±i). However the mirror Chern number on $k_z = \pi /c$ plane must vanish since the subspace spanned by $\hat M_z$ eigenstates at $k_z = \pi /c$ is symmetric under $\hat P\hat T$, making the Berry curvature zero.^38,47 In the following, “mirror Chern number” or “C_m” refers to the one defined on k_z = 0 plane. The relation between C_m and χ will also be addressed in the next section (Eq. 5). By using the effective tight-binding model described in the “Method” section, we numerically calculate these topological invariants and conclude that χ = 2 and $C_{\mathrm{m}} = - 2$ for stress-free KHgX. For the bulk terminations that preserve $\hat M_y$, χ = 2 ensures that the gapless surface states display the Mobius-twisted connectivity,^36,37 drawing the same conclusion as ref. ³⁸. We have noticed that ref. ³⁸ argues $C_{\mathrm{m}} = 2$ instead of −2. The sign ambiguity may arise since the integral (Eq. 1) depends on the surface orientation, and here we set $d{\mathbf{a}}|| + k_z$ when performing the integration.

KHgX under stress

Interestingly, KHgX transforms into a DSM after gap closing. We schematically illustrate this phase transition in Fig. 2a–c for KHgX around Γ. Figure 2a shows the unstressed case or the so-called TNCI phase with χ = 2 and C_m = −2. By applying suitable stress while preserving the symmetries of the space group, Fig. 2b demonstrates the critical point of the phase transition, where the gap between the conduction (CB) and valence (VB) band vanishes. By further enhancing the stress so that the CB (VB) goes downward (upward) with increasing band overlaps, in general any band crossing points can be gapped out due to band hybridizations.⁴⁸ However, it is not the case for Γ → A, along which the hybridization is forbidden. The path Γ → A is invariant under $\hat C_6$, where the CB (the red band in Fig. 2a–c belonging to the representation Δ₉) and VB (the blue band belonging to Δ₇) have the $\hat C_6$ eigenvalues given as

$$\begin{array}{l}{\mathbf{CB}}:\;\{ e^{i\pi /2},e^{ - i\pi /2}\} ,\\ {\mathbf{VB}}:\;\{ e^{i\pi /6},e^{ - i\pi /6}\} .\end{array}$$

(2)

Fig. 2

Schematic illustration of band structures in topological phase transitions and calculated band structures under stresses. a–d Schematic band structures of KHgX around Γ for illustrating the topological phase transition. e, f The calculated band structure of KHgAs and KHgBi under the uniaxial stress along c, respectively. The red dots indicate the contribution from the Hg-s orbital

Here the phase factor exp(−ik_zc/2) arising from the half translation is omitted, and these eigenvalues are degenerate in pairs due to $\hat P$ and $\hat T$. Having different $\hat C_6$ eigenvalues, the CB and VB do not hybridize along Γ → A owing to the orthogonal theorem.⁴⁹ Therefore, a four-fold degenerate band crossing point (i.e., the DN) is formed along Γ → A once the CB has energy lower than VB, realizing the DSM phase (Fig. 2c). Note that the CB and VB also have different eigenvalues under the three-fold rotation $\hat C_3$, given by the square of Eq. (2). We remark that the DN of the stressed KHgX is protected by $\hat C_6$ (or $\hat C_3$), $\hat P$, and $\hat T$, in the sense that the node cannot be gapped out by symmetry-preserving perturbations. In Fig. 2e, f, we show the calculated band structure of KHgAs and KHgBi under the uniaxial stress along c (the in-plane stress is relaxed to zero). We find that the DSM phase is realized when the uniaxial stress exceeds Δc/c₀ = 0.085 (2.23 GPa) for KHgAs; Δc/c₀ = 0.140 (2.86 GPa) for KHgSb; Δc/c₀ = 0.115 (1.56 GPa) for KHgBi, where Δc refers to the lattice distortion parallel to c while c₀ refers to the ideal lattice constant (Table 1).

The Z₄ invariant is not well defined for the DSM phase of KHgX since there is a gapless point, the DN, along Γ → A, However, we can still consider the mirror Chern number. During the phase transition process, the two inverted Hg-s bands at Γ and A are unaffected by the stress since they are fully occupied deeply below the Fermi level (Figs 1c, d, and 2e, f). As the DN is formed at the Fermi level along Γ → A, a band inversion is also created at Γ. In addition to the aforementioned two inverted Hg-s bands below the Fermi level, there are triple times of band inversion at Γ for the DSM phase, implying an interesting mirror Chern number C_m = −3. To confirm this conjecture, we express the Chern number C^±i (Eq. 1) of the subspace as^50,51

$$C^{ \pm i} = \frac{3}{{i\pi }}\ln \left[ {\mathop {\prod}\limits_{n \in {\mathrm{occ}}.} {( - 1)} \eta _n^{ \pm i}(\Gamma )\theta _n^{ \pm i}(K)\zeta _n^{ \pm i}(M)} \right]{\mkern 1mu} mod\,6,$$

(3)

where $\eta _n^{ \pm i}(\Gamma )$ is the $\hat C_6$ eigenvalue of the occupied $\hat M_z$ eigenstate at Γ (with $\hat M_z$ eigenvalue ±i), while $\theta _n^{ \pm i}(K)$ and $\zeta _n^{ \pm i}(M)$ is of the $\hat C_3$ and $\hat C_2 = t(0,0, - c)(\hat C_6)^3$ eigenvalues at K and M, respectively. As the DN is formed, the highest occupied state at Γ changes from $\Gamma _7^ -$ to $\Gamma _9^ +$ (Fig. 2a–c). The $\hat C_6$ eigenvalues of the doubly degenerate states $\Gamma _7^ -$ and $\Gamma _9^ +$ were given in Eq. (2). Because $\hat M_z = \hat t(0,0,2c)\hat P(\hat C_6)^3$, both the $\Gamma _7^ -$ and $\Gamma _9^ +$ states with $\hat C_6$ eigenvalues of, respectively, exp(−iπ/6) and exp(−iπ/2) have common $\hat M_z$ eigenvalues of +i. As the highest occupied state changes from $\Gamma _7^ -$ to $\Gamma _9^ +$, we have $\Delta C^{ + i} = - 1$ according to Eq. (3), which immediately implies $\Delta C^{ - i} = + 1$ under $\hat T$. Knowing that C_m = −2 before the band inversion, this results in C_m = −3 for the DSM phase.

Owing to the non-trivial mirror Chern number obtained here, the DSM phase of KHgX exhibits protected surface states distinct from other DSMs, such as Na₃Bi⁵ and Cd₃As₂.²³ To demonstrate, we consider the (010)-surface of the stressed KHgBi with Δc/c₀ = 0.115, where (010) refers to the surface normal vector in terms of the Cartesian coordinates. The surface BZ and the surface band structure are shown in Figs 1b and 3a, respectively. The (010)-surface preserves the symmetry $\hat M_z$, under which C_m is defined. Accordingly, along $- \overline X \to \overline \Gamma \to \overline X$ of the surface BZ, to which the bulk k_z = 0 plane projects, there should exist three pairs of counter-propagating surface states with opposite $\hat M_z$ eigenvalues due to C_m = −3.^16,17 These non-trivial surface states can be clearly observed in Fig. 3a (see the schematic illustration in the lower inset). Owing to C_m < 0, the surface states with $\hat M_z$ eigenvalues +i propagate toward the −x direction.¹⁶ On the other hand, along $\overline \Gamma \to \overline Z$, the bulk-projected DN appears, which is emphasized by the white dashed circle in Fig. 3a. Moreover, there is a surface band connecting to this bulk-projected DN from $\overline Z$. When viewed from the Fermi surface as presented in Fig. 3b, the connected surface bands become a pair of Fermi arcs. More precisely, in Fig. 3b, there is a pair of Fermi arcs (labeled by I and II) connecting the two bulk-projected DNs (yellow dots) located along $- \overline Z \to \overline \Gamma \to \overline Z$. Such Fermi arc surface states have been widely observed in many DSMs^5,23,43,52 although there is no topological origin.^52,53,54 Nonetheless, for the DSM phase of KHgX, the Fermi surface is guaranteed to intersect the high-symmetry line $- \overline X \to \overline \Gamma \to \overline X$ by (at least) six times due to C_m = −3.

Fig. 3

Topological surface states and Fermi arcs. a The calculated (010)-surface band structure of the stressed KHgBi with Δc/c₀ = 0.115. (see “Method”). The red color represents the bulk projected bands. The upper inset is a zoom-in of the calculated surface band structure along $- \overline Z \to \overline \Gamma \to \overline X$ with ±i indicating the $\hat M_z$ eigenvalues of the surface states. The lower inset is a schematic illustration of the surface band structure along $- \overline X \to \overline \Gamma \to \overline X$ with blue and red lines representing, respectively, positive and negative eigenvalues of $\hat M_z$. b Constant energy cut at the Fermi energy (i.e., the Fermi surface). The two yellow dots indicate the position of the bulk-projected Dirac nodes, which are connected by a pair of Fermi arcs labeled by I and II

Generally speaking, a DSM phase can be regarded as a critical point on the topological phase diagram, which transforms into various topological distinct phases via symmetry breaking.^5,24,43 Starting from the DSM phase of KHgX, an interesting phase can be realized by breaking the rotation ($\hat C_6$ and $\hat C_3$) while keeping all the other symmetries. As we now show, the resulting phase is a TNCI with χ = 3 and C_m = −3. Rotational symmetry breaking has the effect of gapping out the DN along Γ → A (Fig. 2d), while the mirror Chern number C_m, as a topological invariant, is left intact. Therefore, we still have C_m = −3 after rotational symmetry breaking, the same as the DSM phase. On the other hand, the Z₄ invariant is now well defined since the DN has been gapped out and which can be inferred through³⁶

$$\chi = \nu _{k_z = 0}{\kern 1pt} {\mathrm{mod}}\,2,$$

(4)

where $\nu _{k_z = 0}$ is the Z₂ invariant^55,56 defined on the k_z = 0 plane. We have $\nu _{k_z = 0} = 1$ since C_m = −3 is odd.¹⁶ Equation 4 determines χ ∈ {0, 1, 2, 3} up to modulo 2, implying that χ = 1 or 3 after rotational symmetry breaking. A general relation between the mirror Chern number and the Z₄ invariant is also suggested by Eq. (4), i.e.,

$$C_{\mathrm{m}} = 2n \Leftrightarrow \chi = 0,2\quad {\mathrm{while}}\quad C_{\mathrm{m}} = 2n + 1 \Leftrightarrow \chi = 1,3$$

(5)

where $n \in {\Bbb Z}$. To determine the actual χ value (1 or 3) after rotational symmetry breaking, we resorted to the DFT calculation, where we confirmed χ = 3 based on the proposed formula (Eq. S14). However, it should be emphasized that χ is a modulo 4 invariant; therefore, there is an ambiguity between χ = 1 and 3, which depends on the orientation of the surface and line integrals in Eq. S14 (or S10) for the definition of the invariant. This ambiguity also arises when the domain of the BZ (Eq. S1) is shifted by $k_z \mapsto k_z + n \times 2\pi /c$ where n is some odd integer.⁵⁷ Nonetheless, once the orientation or domain of the BZ is fixed, different χ values still describe distinct topological phases.^36,57

Here we note that the band gap of KHgX, which is sensitive to the lattice constant,⁴⁶ can be manipulated by stress. We have systematically investigated the phase transition parameters such as the spin–orbit coupling strength as well as the interlayer spacing by replacing variant species to realize the topological phases in the stress-free condition. As shown in SI-1 and Fig. S1, the stress-induced band gap modulation can be achieved through replacing the big X anion by the small P anion or replacing the large K⁺ cation by the smaller Na⁺ or Li⁺ cations without applying stress. We have found three candidates KHgP, NaHgAs, and LiHgSb, which are DSMs with the mirror Chen number of −3 at their equilibrium volumes (SI-1).

Evolution of the surface band topology

We have shown that by varying the stress and breaking the rotational symmetry, KHgX undergoes the topological phase transition: TNCI (χ = 2, C_m = −2) → DSM (C_m = −3) → TNCI (χ = 3, C_m = −3), in which χ is ill-defined for the DSM phase. Each phase exhibits unique gapless surface states resulting from the non-triviality of χ or C_m. Here we demonstrate how the surface band topology of KHgX evolves during the topological phase transition. Since χ is defined under $\hat M_y$ and $\hat T$ while C_m is defined under $\hat M_z$, we will focus on the (100)-surface (Fig. 1a) that preserves both $\hat M_y$ and $\hat M_z$. The (100) is the only surface that keeps $\hat M_y$; meanwhile due to the rotational symmetry, there are also another two glide reflections given by $\hat C_3\hat M_y(\hat C_3)^{ - 1}$ and $(\hat C_3)^2\hat M_y(\hat C_3)^{ - 2}$, under which the Z₄ invariant can be defined. Therefore, the following discussion also applies to the set of symmetrical equivalent surfaces $\{ 2\bar 1\bar 10\}$ (Miller–Bravais index).

Below we consider KHgBi under stress, in which the phase transition from TNCI (χ = 2, C_m = −2) to DSM (C_m = −3) occurs around Δc/c₀ = 0.115. Figure 4a shows the TNCI surface band structure with Δc/c₀ = 0.100 less than the critical value. Consistent with the χ = 2 topology,^36,37 there exist gapless surface states along the closed path $\tilde Y \to \tilde T \to \tilde Z \to \tilde \Gamma \to \tilde Y$ where the Mobius-twisted connectivity can be observed along the two $\hat M_y$ invariant paths $\tilde Y \to \tilde T$ and $\tilde Z \to \tilde \Gamma$. In addition, along the $\hat M_z$ invariant path $- \tilde Y \to \tilde \Gamma \to \tilde Y$, there exist two pairs of counter-propagating surface states with opposite $\hat M_z$ eigenvalues, consistent with C_m = −2. Here the surface states with $\hat M_z$ eigenvalues +i propagate toward +y since C_m < 0. If we consider the $(\bar 100)$-surface instead, then these “+i surface states” will propagate toward the −y direction.

Fig. 4

Evolution of surface states in topological phase transitions. a–d Topological phase transition of the calculated (100)-surface band structure in KHgBi under stress and symmetry breaking. e–g The schematic illustration of surface band structure in each topological phase. Green and brown lines indicate the surface states with different $\hat M_y$ eigenvalues. The label ±i indicate the $\hat M_z$ eigenvalues of the surface states depicted in blue and red, respectively. Dotted, dashed, and solid lines represent the first, second, and third pair of the surface states, respectively. The other surface state of each pair locates along $- \bar Y \to \bar \Gamma$ and is not shown here. a, e The topological non-symmorphic crystalline insulator (TNCI) phase with χ = 2 and C_m = −2 with Δc/c₀ = 0.100. The Mobius-twisted connectivity can be observed along $\tilde Y \to \tilde T$ and $\tilde Z \to \tilde \Gamma$, shaping like an hourglass (The shape spoils along $\tilde Z \to \tilde \Gamma$; however, the same topology remains.). b, f The Dirac semimetal (DSM) phase with C_m = −3 under the stress Δc/c₀ = 0.115. The Mobius-twisted connectivity along $\tilde Z \to \tilde \Gamma$ is spoiled owing to the occurrence of the bulk-projected Dirac node (DN). A magnified view for the DN is also provided in c. d, g Another TNCI phase with χ = 3 and C_m = −3, transformed from the DSM phase by breaking the rotational symmetry. The quantum spin Hall effect can be observed along $\tilde Z \to \tilde \Gamma$

With the stress up to Δc/c₀ = 0.115, KHgBi turns into the DSM phase with C_m = −3. Figure 4b shows the surface band structure along the path $\tilde Z \to \tilde \Gamma \to \tilde Y$, which is different from the previous phase (Fig. 4a). Along the $\hat M_y$ invariant path $\tilde Z \to \tilde \Gamma$, the occurrence of the bulk-projected DN breaks the Mobius-twisted connectivity and makes the Z₄ invariant undefined for the DSM phase. While along the $\hat M_z$ invariant path $\tilde \Gamma \to \tilde Y$, the two surface bands labeled as I and II no longer degenerate at Γ but connect to the bulk states. As such, we now have three pairs of counter-propagating surface states along $- \tilde Y \to \tilde \Gamma \to \tilde Y$ instead of two pairs, consistent with the change from C_m = −2 to C_m = −3.

Finally, upon breaking the rotational symmetry, KHgBi undergoes the phase transition from DSM (C_m = −3) to another TNCI phase (χ = 3, C_m = −3) as shown in Fig. 4d. The resulting surface band structure is nearly identical to the DSM phase (Fig. 4b, c) except the bulk-projected DN is gapped out. In Fig. 4d, a reference line drawn inside the gap will intersect the surface band(s) by odd number of time(s). This implies the surface band topology along the $\hat M_y$ invariant path $\tilde Z \to \tilde \Gamma$ is identical to the quantum spin Hall (QSH) effect,⁸ consistent with χ = 3 topology.^36,37 In addition, there also exist three pairs of counter-propagating surface states along $- \tilde Y \to \tilde \Gamma \to \tilde Y$ since C_m = −3 (see Fig. 4g), the same as the DSM phase.

Figure 4e–g schematically demonstrate the phase transition in KHgX. Starting from the TNCI phase with χ = 2 and C_m = −2 in Fig. 4e, the surface states along $\tilde Y \to \tilde T$ and $\tilde Z \to \tilde \Gamma$ display the Mobius-twisted connectivity with two pairs of counter-propagating surface states along $- \tilde Y \to \tilde \Gamma \to \tilde Y$ with opposite $\hat M_z$ eigenvalues. Figure 4f shows the DSM phase with C_m = −3 over the critical stress, where the Mobius-twisted connectivity along $\tilde Z \to \tilde \Gamma$ is broken by the bulk-projected DN with an extra pair of counter-propagating surface states along $- \tilde Y \to \tilde \Gamma \to \tilde Y$. Another TNCI phase with χ = 3 and C_m = −3 given by breaking the rotational symmetry is depicted in Fig. 4g, where the bulk-projected DN is gapped out, and now the surface bands along $\tilde Z \to \tilde \Gamma$ connect in a zigzag way equivalent to the QSH effect.

In summary, the KHgX (X = As, Sb, Bi) family is the first experimentally realized TNCI, where the topological surface states are characterized by the Mobius-twisted connectivity. We diversify the topological phase diagram of KHgX by introducing two new phases based on first-principles calculations. By applying stress, KHgX undergoes a topological insulator–metal transition from the TNCI phase with C_m = −2 into the DSM phase with a non-trivial mirror Chern number C_m = −3 in the non-symmorphic crystal structure. Via symmetry breaking, the DSM phase transforms into another new TNCI phase with C_m = −3 hosting the QSH effect. The change in the connectivity of the surface bands provides a direct justification of the topological phase transition, and manipulating the band gap is the key to realize these predicted new topological phases.

Method

The bulk electronic structure calculations were performed using the VASP package⁵⁸ based on the DFT. The generalized gradient approximation of Perdew–Burke–Ernzerhof⁵⁹ was used for the exchange correlation functional. The cutoff energy of 800 eV and the BZ sampling grid of 12 × 12 × 6 were used in this work. The topological invariants were calculated by using the effective tight-binding Hamiltonian constructed by the WANNIER90 code⁶⁰ on the basis of the DFT wavefunctions. The initial projections of the Wannier orbitals were selected as Hg-s and X-p (X = As, Sb, Bi). The surface states were obtained from the surface Green function of the semi-infinite system based on the iterative method.⁶¹