Introduction

High-throughput material synthesis and rapid characterization are necessary ingredients for inverse design and accelerated material discovery.1,2 X-ray diffraction (XRD) is a workhorse technique to determine crystallography and phase information, including lattice parameters, crystal symmetry, phase composition, density, space group, and dimensionality.3 This is achieved by comparing XRD patterns of candidate materials with the measured or simulated XRD patterns of known materials.4 Despite its indispensable utility, XRD is a common bottleneck in materials characterization and screening loops: 1 hour is typically required for XRD data acquisition with high angular resolution, and another 1–2 hours are typically required for Rietveld refinement by an expert crystallographer, assuming the possible crystalline phases are known. It is widely recognized that machine learning methods have potential to accelerate this process; however, practical implementations have thus far focused on well-established materials,5,6,7 require combinatorial datasets spanning among various phases,8,9 or require large datasets,5,10 whereas material screening using the inverse design paradigm often involves less-studied materials, spanning multiple classes of different material/phase compositions, and smaller prototype datasets.

Typically, experimental XRD pattern data are analyzed by obtaining descriptors such as peak shape, height, and position. Matching descriptors of the test pattern to known XRD patterns in crystalline databases allows the identification of the compound of interest.4 Refinement methods such as Rietveld refinement and Pawley refinement have been used for decades to analyze experimental XRD patterns.4 For novel compounds in thin-film form, however, the use of Rietveld refinement is limited due to the lack of reference patterns in material databases, as well as unknown film textures. The direct-space method, statistical methods, and the growth of single crystals have been used to obtain crystal symmetry information for novel materials,7,11,12,13,14 but the significant iteration time, feature engineering, human expertise, and knowledge of specific material required makes these methods impractical for high-throughput experimentation, where sample characterization rates are of the order of one material per minute or faster,2,15 explored over various material families.

An alternative approach consists in using machine learning methods to obtain more robust spectral descriptors and quickly classify crystalline structure based on peak location and shape in the XRD pattern. Breakthrough methods have been developed for the similar problem of phase attribution in combinatorial alloys,16,17 but only few studies have been developed for solution-processed material screening, such as perovskite screening, where phase attribution is usually not as important as correct classification of materials into groups according to crystal parameters. The most successful methods10,18 for material screening use convolutional neural networks (CNNs) trained with hundreds of thousands of XRD powder patterns simulated with data from the Inorganic Crystalline Structure Database (ICSD). Further CNN and other deep learning algorithms have been employed to obtain crystalline information for other kinds of diffraction data.19,20,21 In a couple studies, noise-based data augmentation, a common technique of image preprocessing for machine learning, has been used to avoid overfitting in a broader kind of X-ray characterization problems20,22,23 and more broadly in other fields such as Tramission Electron Microscopy imaging;21 however, the augmentation procedure has not been based in physical knowledge of actual experimental samples. Furthermore, the best-performing machine learning methods developed up-to-date for XRD analysis do not allow any kind of interpretation by the experimentalists,10 hindering improvements of experimental design.

While similar approaches produce good results for crystal structure classification, we have found that applying them to high-throughput characterization of novel solution-processed compounds is generally not practical, given the limited access to large datasets of clean, preprocessed, relevant, XRD spectra. Furthermore, most materials of interest developed in high-throughput synthesis loops are thin-film materials. The preferred orientation of the crystalline planes in thin-films causes their experimental XRD patterns to differ from the thousands of simulated XRD powder patterns available in most databases.24,25 Thin-film compounds usually will present spectrum shifting and periodic scaling of peaks in preferred orientations, reducing the accuracy of machine learning models trained with powder data,8,9,26 even in the cases when noise-based data augmentation techniques are used.18

Considering these challenges, we propose a supervised machine learning framework for rapid crystal structure identification of novel materials from thin-film XRD measurements. For this work, we created a library of 164 XRD patterns of thin-film halide materials extracted from the >100,000 compounds available in the ICSD27; these 164 XRD patterns include lead halide perovskite28,29 and lead-free perovskites-inspired materials.30 These XRD patterns were manually classified among different crystal dimensionalities using ICSD information. Based on this small dataset of relevant XRD powder patterns extracted from the ICSD and an additional 115 experimental XRD patterns, we propose a model-agnostic, physics-informed data augmentation to generate a suitable and robust training dataset for thin-film materials, and subsequently test the space group and dimensionality classification accuracy of multiple machine learning algorithms. A one-dimensional (1D) implementation of an “all convolutional neural network” (a-CNN)31 is proposed, implemented and identified as the most accurate and interpretable classifier for this problem. We propose a new way to use class activation maps (CAMs),32 computed from the weight distribution of a global average pooling layer and adapted to the context of our problem, to provide interpretability of root causes of classification success or failure to the experimentalist. Subsequently, the effect of the augmented dataset size and the XRD pattern granularity is investigated. Our proposed methodology could be applied to other crystal descriptors of thin-film materials, such as lattice parameters or atomic coordinates, as long as labeled information is available.

Our contributions can be summarized as: (a) development of physics-informed data augmentation for thin-film XRD, which successfully addresses the sparse/scarce data problem, breaching the gap between the thousands of XRD patterns in crystalline databases and real thin-film materials, (b) development of highly interpretable, highly accurate, a-CNN for XRD material screening, (c) proposal of average class activation maps as a feasible interpretability tool in CNNs trained on spectral data.

Results and discussion

Framework for rapid XRD classification

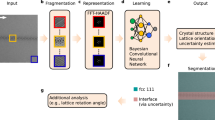
The framework developed for rapid classification of XRD thin-film patterns according to crystal descriptors is shown in Fig. 1a. The methodology makes use of both experimental and simulated XRD patterns to train a machine learning classification algorithm. A simulated dataset is defined by extracting crystal structure information from the ICSD. The experimental dataset consists of a set of synthesized samples, which are manually labeled for training and testing purposes. The datasets are subjected to data augmentation based on the three spectral transformations shown in Fig. 2.

Fig. 1
figure 1

General framework and a-CNN architecture. a Schematic of our X-ray diffraction data classification framework, with physics-informed data augmentation. b Schematic of the best-performing algorithm, our all convolutional neural network

Full size image
Fig. 2
figure 2

Physics-informed data augmentation: schematic of the physics-informed data augmentation algorithm, which accounts for the particularities of thin-film XRD spectra, as described by the subsequent transformations stated in Eqs. 1–3

Full size image

The crystal descriptors of interest, space group and crystal dimensionality, are chosen because of their importance for material screening in accelerated material development. In many inorganic material systems, the crystalline dimensionality—i.e., a generalization of the crystalline symmetry into 0-dimensional (0D), 1D, 2D, or 3D symmetry— constitutes a figure of merit for experimental material screening as it correlates with observed charge-transport properties.33 In perovskites and perovskites-inspired materials, for instance, 3D crystalline structures have been shown to have good carrier-transport properties for solar cells and light-emitting diode applications,33,34 whereas 3D–2D mixtures have been found to have greater stability in lead halide perovskites than pure-phase 3D crystals.35 With further detail, the space group number describes the standardized symmetry group of a configuration in space, classifying crystal symmetries into 230 groups. Identifying the space group number of a sample provides crystal information beyond dimensionality, including atomic bonding angles and relative distances, which are believed to be of importance for predicting material properties.36 In this specific study, the framework relies on the relation between XRD patterns and the crystal descriptors of interest. For example, among perovskite-inspired materials for photovoltaic applications, 3D cubic lead halide perovskites of multiple compositions show distinct features in their XRD patterns compared with 2D layered bismuth perovskites.37,38

Typically, the powder XRD pattern is used to identify space group through Rietveld refinement, but the compression of crystalline 3D crystallographic information into a 1D diffraction pattern causes the space group to be impossible to determine unambiguously in certain low-symmetry phases, independently of the measurement technique.39 In this work, the space groups of interest are able to be determined from XRD information only.

To better account for noise measurement and the physical difference between randomly oriented powder patterns and experimental thin-film patterns, the patterns were subjected to a process of data augmentation based on domain knowledge. Subsequently, both augmented experimental and simulated XRD pattern datasets are used for testing, training and cross-validation of machine learning algorithms.

Figure 1b shows the architecture of the final a-CNN, which is proposed and identified as the best-performing machine learning algorithm in subsequent sections.

Experimental measurement and labeling of XRD patterns

The experimental dataset consists of 75 XRD patterns for dimensionality classification, summarized in Supplementary Table S1, and 88 XRD patterns for space group classification, summarized in Supplementary Table S2. A total of 115 unique labeled XRD patterns are considered among both datasets. For this work, perovskites-inspired 3D materials based on lead halide perovskites (space group \(Pm\bar 3m\)), tin halide perovskite (I4/mcm), cesium silver bismuth bromide double perovskite (\(Fm\bar 3m\)), bismuth and antimony halide 2D (\(P\bar 3m1\), \({\it Pc}\), \({P2}_{1}{\!/\!a}\)), and 0D (P63/mmc) perovskite-inspired materials are synthesized and used as training and testing dataset. The details of the synthesis and characterization methodology are described in great detail in our experimental study.40 Supplementary Fig. S1 shows the t-Distributed Stochastic Neighbor Embedding representation of the XRD patterns labeled with dimensionality and space group, providing evidence of the complexity of the classification problem.

In this case, Rietveld refinement is restricted due to the unknown preferred orientation and texture of the thin-film samples. In consequence, the XRD patterns are subjected to peak indexing and the dimensionality and space group are labeled based on ICSD data.

Data mining and simulation of XRD patterns

The simulated training dataset consists of 164 compounds extracted from ICSD with a similar composition, expected crystal symmetry, and space group as the synthesized materials of interest. All the possible single, double, ternary, and quaternary combinations of the elements of interest were extracted during database mining. The compositions of all the materials of interest along with labeled dimensionality and space group information is available in Supplementary Table S3. The fundamental crystal descriptors extracted from the material database are used to simulate XRD powder patterns with random crystalline orientations, as explained in the Methods section.

Data augmentation based on domain knowledge

Experimental thin-film XRD patterns vary greatly compared to simulated, idealized, randomly oriented XRD patterns. Due to expansions and contractions in the crystalline lattice, XRD peaks shift along the 2ϴ axis according to the specific size and location of the different elements present in a compound, while maintaining similar periodicity based on crystal space group.3,8,26,41 In addition, for thin-film samples, the XRD pattern can be shifted due to strain in the film induced during the fabrication process.42 Polycrystalline thin-films are also known to have preferred orientations along certain crystallographic planes. The preferred orientation is influenced by the crystal growth process and the growth substrate,24 and is common for most solution-processing and vapor-deposition fabrication methods. Ideal random powders contain multiple grains without any preferred global orientations, thus all crystallographic orientations are represented evenly in the peak intensity and periodicity of the XRD pattern. As a consequence of their preferred orientations along crystallographic planes, thin-film XRD relative peak intensities are scaled up periodically in the preferred plane orientation, and scaled down periodically or even eliminated in the non-preferred orientations.

To increase the size and robustness of the limited training dataset and to account for these fundamental differences between real thin-films and simulated XRD powder patterns, we perform a three-step data augmentation procedure based on physical domain knowledge:

(1) Peak scaling, (2) Peak elimination, and (3) Pattern shifting. These transformation are described in detail in Methods. Figure 2 summarizes the data augmentation steps and its effects on a representative pattern. Given the hyperparameters S and ε in Eqs. 1–3 in the Methods section, 2000 patterns are augmented from the simulated dataset, and 2000 patterns are augmented from experimentally measured spectra.

We choose to perform physics-informed data augmentation instead of explicit regularization for the following reasons: (1) data augmentation has been found to be more robust at avoiding overfitting than explicit regularization when using convolutional neural networks,43 (2) data augmentation is model-agnostic, allowing our approach to successfully bridge the gap between experimental XRD patterns and thousands of XRD patterns available in databases without depending on a specific model that might not generalize well in all cases (no-free-lunch theorem), and (3) physics-informed data augmentation allows high interpretability, and is found to be more robust than traditional noise-based data augmentation approaches (Supplementary Table S6).

Classification results and a-CNN

Preprocessed, augmented experimental data, and augmented simulated data are fed into various supervised machine learning algorithms for training and testing purposes. The best-performing algorithm is evaluated. The XRD patterns are classified into three crystal dimensionalities (0D, 2D, and 3D) and seven space groups (\(Pm\bar 3m\), I4/mcm, \(Fm\bar 3m,P\bar 3m1\), \({Pc}\), P21/a, and P63/mmc).

For this purpose, we represent the XRD pattern as either a vector or a time series. For each kind of data representation, different classification algorithms are considered. Using a vector representation of the XRD pattern, the following classification methods are tested: Naive Bayes, k-Nearest Neighbors, Logistic Regression, Random Forest, Decision Trees, Support Vector Machine, Gradient Boosting Decision Trees, a Fully Connected Deep Neural Network, and an a-CNN with a global pooling layer.44,45,46 The XRD patterns are also analyzed as a time series with a normalized Dynamic Time Warping (DTW) distance metric47 combined with a k-Nearest Neighbors classification algorithm, which was found in literature as the most adequate metric for measuring similarity among metal-alloy XRD spectra.7,26

The problem of novel material development is inherently a multi-class classification problem, in which the classes for training and testing purposes can often be imbalanced as some material families are better characterized than others (e.g., lead-based perovskites are better represented in material databases than newer lead-free perovskites).38 Common metrics for binary classification such as accuracy might not be the most adequate in this context.45 The final choice for adequate metrics depends on the relative importance of false positive and false negatives in minority and majority classes, according to the goals of the experimentalist. For method development in this work, we consider the following metrics: subset accuracy, defined as the number of correctly classified patterns among all test patterns, and F1 score. F1 score in this problem can be interpreted as the weighted harmonic mean of precision and recall; the closer it is to 1.0, the higher the classifier’s precision and recall.45 Intuitively, precision is the ability of the classifier not to produce a false positive, whereas recall is the ability of a classifier to find all the true positives. An F1 metric is calculated for each class label, and it is combined into an overall score by taking either the micro or the macro average of the individual scores. The macro average calculates the mean of the metrics of all the individual classes, hence treating all classes equally. The micro average adds the individual contribution of all samples to compute the overall metric.

When there is class imbalance, accuracy and F1 micro score characterize the classifier’s performance over all classes, whereas F1 macro emphasizes the accuracy on infrequent classes.45 Thus, a natural choice for high-throughput experiments across multiple material classes seems to be accuracy/F1 micro score, except in those cases when we are especially interested in analyzing an infrequent material class, being F1 macro a more representative metric in that case. In this work, we choose to report the classification accuracy and both F1 micro and F1 macro, whereas recall and precision results are included in the Supplementary Information (Supplementary Tables S4 and S5).

We measure the performance of the dimensionality and space group classification methods based on three different approaches of splitting the training and testing datasets:

Case 1: Exclusively simulated XRD patterns are used for testing and training. Fivefold cross-validation is performed.

Case 2: The simulated XRD patterns are used for training, and the experimental patterns for known materials are used for testing.

Case 3: All of the simulated data and 80% of the experimental data are used for training, and 20% of the experimental data are used for testing. Fivefold cross-validation is performed.

Each one of the training/testing cases mentioned earlier are tested for crystal dimensionality and space group prediction accuracy and micro/macro F1 score. The results are reported in Table 1. In each cell, the crystal dimensionality classification metric is reported first, followed by the metric for space group classification. Case 1, presenting fivefold cross-validation results of the simulated dataset, has the highest accuracy as it does not predict any experimental data and thus is free of experimental errors for both crystal descriptors. Case 2 performs the experimental prediction solely based on simulated patterns, thus having the lowest accuracy. Finally, Case 3 has a significant higher accuracy than Case 2 for both crystal dimensionality and space group prediction. F1 scores follow these trends as well.

Table 1 Results of the ML algorithms under consideration
Full size table

In general, the model’s accuracy and F1 score is lower for space group classification than that for crystal dimensionality classification. This discrepancy is caused by the lower number of per-class labeled examples for space group classification compared to crystal dimensionality classes. Class imbalance can also systematically affect the training performance of the classifier, to avoid this issue, we performed an oversampling test with synthetic training data according to,48,49 and observed little discrepancy of accuracy between the balanced and imbalanced datasets after fivefold cross-validation.

The use of experimental data as part of the training set increases the model’s accuracy and robustness. This fact can be explained by the high variability of experimental thin-film XRD patterns, even after data preprocessing. The relatively high accuracy with the relatively small number of experimental samples (on the order of 10–102) confirms the potential of our data augmentation strategy to yield high predictive accuracies even with small datasets. Supplementary Table S6 in the Supplementary Information compares our strategy with traditional noise-based augmentation approaches, and shows an average increase of classification accuracy of >12% absolute.

Naturally, the F1 macro score is systematically lower than the F1 micro score, reflecting the impact of misclassification of those dimensionality and space group classes with less training examples. However, the F1 macro score is still fairly high for most classifiers. This fact reflects the importance of adequate experimental design to achieve good generalization among classes.

For all three test cases, the a-CNN classifier performs better than any other classification technique. The 1D a-CNN architecture implemented is composed of three 1D convolutional layers, with 32 filters each, and strides and kernel sizes of 8, 5, and 3 units, respectively. The activation function between layers is ReLu. A global average pooling layer50 (acting as a weak regularizer) and a final dense layer with softmax activation is used. The loss function minimized is binary cross entropy. We use early stopping with a batch size of 128 during training, and use the Adam optimizer algorithm to minimize the loss function. The CNN is implemented in Keras 2.2.1 with the Tensorflow background. Figure 1b contains a schematic of the proposed a-CNN architecture.

Our a-CNN architecture, in contrast with other CNNs, does not have max pooling layers between convolutional layers, and also lacks a set of dense layers in the final softmax classification layer. These modifications, in contrast with the architectures used in,10,18 significantly reduces the number of parameters in the neural network, allows faster and simpler training, and are less prone to overfitting. Another advantage of our implementation is the possibility to extract CAMs from the weight distribution of the global average pooling layer. This characteristic of the network, properly adapted to our problem, allows us to visualize how the classified XRD patterns are mapped to the weight distribution at the end of the a-CNN. The results are further discussed in the interpretability subsection.

The a-CNN trained after data augmentation has an accuracy of >93 and 89% for crystal dimensionality and space group classifications, respectively. As far as we know, the accuracy is among the highest described in literature for space group classification algorithms, comparable to those trained with thousands of ICSD patterns and manual labeling by human experts,10,51 and is also comparable to similar approaches in other kinds of diffraction data.8,19 The neural network seems to be the most adequate method for high-throughput synthesis and characterization loops, as it also performs relatively well in terms of algorithm speed and in conditions of class imbalance. In the future, our methodology can be extended to other materials systems, and may include other crystal descriptors as predicted outputs, such as lattice parameters and atomic coordinates.

Furthermore, the a-CNN performs better than the traditional k-nearest neighbors method using DTW. In our test case and dataset, the differences between thin-film and powder spectra seem not to be captured properly by DTW alone. Arguably, DTW could be more useful if a larger XRD thin-film pattern dataset is available for k-Nearest Neighbors classification, or if it exists greater similarity between XRD patterns of the same class, allowing the DTW warping path to be better captured within the DTW window under consideration.26 CNNs have been found to perform better than DTW for classification of time series, which is consistent with our results.52

Effect of augmented dataset size

The size of the dataset is critical for obtaining a high accuracy and F1 score. To explore the effect of augmented dataset size, the a-CNN accuracy was computed for various combinations of augmented experimental patterns (i.e., number of augmented XRD spectra originated from the 88 measured spectra, varying S and ε in Eqs. 1–3) and augmented simulated dataset sizes (i.e., number of augmented XRD spectra originating from the 164 simulated ICSD spectra). Figure 3a, b summarizes this sensitivity analysis for Case 3 training/testing conditions for dimensionality and space group classification. Twenty different fivefold cross-validation runs were performed to calculate the 1-standard deviation error bars for each data point.

Fig. 3
figure 3

Accuracy of the a-CNN model with augmented data: line plot showing mean Case 3 a-CNN accuracy, as a function of the number of augmented patterns (Methods, Eqs. 1–3) included in the training set, for (a) dimensionality classification and (b) space group classification. The x axis shows augmented experimental data (based on the original experimental XRD patterns), and the legend shows simulated data (based on the 164 simulated powder diffraction patterns obtained from the ICSD). The error bars correspond to one standard deviation from the mean

Full size image

In general, as the size of the experimental and augmented datasets increase, the mean accuracy quickly approaches the asymptotic accuracy reported in Table 1. This trend reaffirms and quantifies the importance of data augmentation for the predictive accuracy of our model.

The critical augmented dataset size seems to be around 700 augmented spectra. The model’s accuracy is more sensitive to the augmented experimental dataset size, likely because most of the dataset variance comes from the experimental XRD patterns. The data augmentation of the simulated dataset causes the accuracy to grow monotonically in Fig. 3b; however, this trend is not satisfied in the case of Fig. 3a, where no augmented simulated data seems on average to perform the best. We hypothesize that augmenting simulated data could actually introduce excessive noise to the model, hampering classification when the number of possible classes is small.

Figure 3 illustrates that if no data augmentation is used (i.e., the origin, 0, 0), the predictive accuracy could be below 50% for space group and below 70% for dimensionality. Our physics-informed data augmentation directly increase accuracy by up to 23% in the case of dimensionality and 19% in the case of space group classification. This result reinforces the need for data augmentation for sparse/scarce datasets, as is typical with early-stage material development.

Impact of data coarsening

To evaluate the trade-offs between accuracy and XRD acquisition speed, we investigate how data coarsening of the XRD pattern impacts the accuracy of ML algorithm prediction. In Fig. 4, we report Case 3 accuracy with increasing 2ϴ angle step size. The baseline step size of the 2ϴ scan in our XRD patterns is 0.04°. Data coarsening is performed by selectively removing the data with increasing step sizes and rerunning the augmentation and classification algorithms. For crystal dimensionality and space group classification, the highest accuracies are achieved at 0.04–0.08°, whereas 85%+ accuracy is achieved when the 2ϴ step size is 0.16° or less for both cases. Using the larger step size, the XRD pattern acquisition time can be reduced by 75%, allowing the full spectra to be measured and classified in <5.5 min with our tool setup.

Fig. 4
figure 4

Reducing XRD pattern acquisition time: simulation of the trade-off between XRD pattern acquisition rate and predictive accuracy. Accuracies for crystal dimensionality and space group predictions are estimated by coarsening the XRD spectrum 2ϴ step size for Case 3 conditions. The error bars correspond to one standard deviation from the mean

Full size image

Interpretability using CAMs

Class activation maps (CAM) are representations of the weights in the last layer of a CNN, before performing classification. A CAM for a certain class and pattern indicates the main discriminative regions (in our case, peak and series of peaks in the XRD pattern) that the network uses to identify that class.32 Details of the CAM computation are included in the Methods section.

A similar approach has been followed to interpret and improve object recognition in images and videos using 2D CNNs.32 A single pattern or image produces a unique CAM revealing the main discriminative features. In addition, in the context of our problem, we propose to generalize CAMs to all training samples within a class by averaging over each of the computed CAM weights for all training samples within a class, as explained in the Methods section. This averaging procedure is justified as the location and periodicity of discriminative peaks within a class varies only slightly along all labeled samples in the training set, and can be extended to many spectral measurement techniques. This average CAM allows to visualize the main discriminative features of an XRD pattern that were used to classify all the training data belonging to a certain class.

By comparing the CAM for a single pattern with the average CAM for given class, we can identify the root causes of correct and incorrect classification by the a-CNN. Figure 5 illustrates this procedure for XRD patterns of space group classes Class 2 (P21/a) and Class 6 (\(Pm\bar 3m\)). Figure 5a, b shows the average CAM maps of Class 6 and Class 2 space groups. Figure 5c shows the CAM of an individual, correctly classified XRD pattern. If we compare the individual CAM with Class 6 Average CAM, we can see that the neural network is identifying the same reference pattern as most of Class 6 samples, which translates into classification as Class 6. In contrast, Fig. 5d shows an incorrectly classified XRD pattern, which was determined to belong to Class 6 by the CNN, when in reality it belongs to Class 2. A comparison of the individual CAM with the average CAMs of classes 6 and 2 reveals that the misclassified CAM is more similar to Fig. 5a than Fig. 5b. A closer look to the misclassified patterns, shows that the periodicity of peaks before 30° and the relative lack of peaks between 30° and 50° (likely caused by mixed phases), are causing the misclassification.

Fig. 5
figure 5

Class activation maps for misclassification interpretability: class activation maps (CAMs) generated by the a-CNN architecture, representing space group classification of Class 2 (P21/a) and Class 6 (\(Pm\bar 3m\)). (a, b) correspond to maps generated by averaging all training samples in a certain class, whereas (c, d) correspond to the CAMs of correctly classified and incorrectly classified individual patterns, respectively. The correctly predicted pattern of (c) is explained by the similarity of its CAM to the average CAM of Class 6; whereas, the incorrectly prediction (d) can be explained by comparing its CAM with the average CAMs of classes 2 and 6

Full size image

Several representative misclassification cases are identified and included in the Section VII of Supplementary Information. In our work, by comparing the CAM of wrongly classified cases with the average CAM of all training data within certain class, we conclude there are three main causes for failed classification. The first cause is the mixture of phases in the sample, which increases the chance of the CAM of a particular pattern differing from the average class CAM. The second cause is lack of XRD patterns in the per-class training data. We only have <5 patterns in certain space group classes, thus the average CAM of minority classes has only a limited number of discriminative features compared to majority classes, increasing the testing error. The third cause of misclassification is missing peaks, or too few peaks, present in the XRD pattern; because of the lack of enough discriminative features, the CAM of the incorrectly labeled pattern could be ambiguously similar to two or more average class CAMs, causing the misclassification.

After the experimentalist identifies these root causes of error, they can be mitigated by increasing the number of experimental training points for certain classes or increasing the phase purity of the material coming from the synthesis and solution-processing procedure.

Summary of contributions

In this work, we develop a supervised machine learning framework to screen novel materials based on the analysis of their XRD spectra. The framework is designed specifically for cases when only sparse datasets are available, e.g., early-stage high-throughput material development and discovery loops. Specifically, we propose a physics-informed data augmentation method that extends small, targeted experimental and simulated datasets, and captures the possible differences between simulated XRD powder patterns and experimental thin-film XRD patterns. A few thousand augmented spectra are found to increase our classification accuracy from <60 to 93% for dimensionality and 89% for space group. The F1 macro score is also over 0.85 for various algorithms, reflecting the model’s capacity to deal with significantly imbalanced classes.

When trained with both augmented simulated and experimental XRD spectra, a-CNNs are found to have the highest accuracy/F1 macro score among the many supervised machine learning methods studied. Our proposed a-CNN architecture allows high performance and interpretably through CAMs. The use of our proposed average CAMs, allow to identify the root cause of misclassification, and allow the design of a robust experiment. Furthermore, we find that the neural network model tolerates coarsening of the training data, providing future opportunities for online learning, i.e., the on-the-fly adaptive adjustment of XRD measurement parameters by taking feedback from machine learning algorithms.15

Our approach can be extended to XRD-based high-throughput screening of any kind of thin-film materials, beyond perovskite and perovskite-inspired materials. Since most material databases lack information for various kinds of novel materials, the data augmentation approach to tackle data scarcity can be broadly applied. The underlying difference between XRD patterns of thin-films and powders is common to a broad range of materials and is commonly seen in most thin-film characterization experiments. The high interpretability of our approach could allow future work in semi-supervised or active learning, allowing the CAM maps to guide manual XRD refinement or actual XRD experiments. The framework may also be extended beyond XRD classification, to any spectrum containing information-rich features that require classification (XPS, XRF, PL, mass spectroscopy, etc.). The advantages of our approach include: (1) interpretable error analysis; (2) a data augmentation strategy that enables fast and accurate classification, even with small and imbalanced datasets.

Methods

Measurement and preprocessing of experimental XRD patterns

The XRD patterns for each sample are obtained by using a parallel beam, X-ray powder diffraction Rigaku SmartLab system53 with 2ϴ angle from 5 to 60° with a step size of 0.04°. The tool is configured in a symmetric setup. We preprocess the raw XRD patterns to reduce the experimental noise and the background signal. For this purpose, the background signal is estimated and subtracted along the 2ϴ axis, and the spectrum is smoothed conserving the peak width and relative peak size applying the Savitzky-Golay filter.54 A representative example of a preprocessed and raw XRD spectra is included in Supplementary Fig. S2.

Simulation of powder XRD patterns

The powder XRD simulations are carried out with Panalytical Highscore v4.7 software based on the Rietveld algorithm implementation by Hill and Howard.55,56 The XRD crystal is assumed to have fully random grain orientations. The unit cell lattice parameters, atomic coordinates, atomic displacement parameters, and space group information are considered for the structure factor calculation in the Rietveld model.

Physics-informed data augmentation

Suppose we describe the series of peaks in an XRD pattern by a discrete function \(\left( {2\theta } \right):I \to {\Bbb R}^ +\), which maps a set of discrete angles I to positive real numbers \({\mathbb{R}^+}\) corresponding to peak intensities. We augment the data through the following sequential process of transformations \(\Phi _{S,c}^1,\Phi _S^2\), and \(\Phi _\varepsilon ^3\):

Random peak scaling is applied periodically along the 2ϴ axis to account for different thin-film preferred orientations. A subset of random peaks at periodic angles S is scaled by factor c, such that

$$\Phi _{S,c}^1 = \left. {c\cdot f} \right|_S + \left. f \right|_{I\backslash S}$$
(1)

Random peak elimination (with a different randomly selected S than Eq. 1) is applied periodically along the 2ϴ axis, to account for different thin-film preferred orientations, such that

$$\Phi _S^2 = \left. {0\cdot f} \right|_S + \left. f \right|_{I\backslash S}$$
(2)

Pattern shifting by small random value ε along the 2ϴ direction to allow for different material compositions and film strain conditions, such that

$$\Phi _\varepsilon ^3 = f\left( {2\theta - \varepsilon } \right)$$
(3)

CAMs

We perform global average pooling in the last convolutional layer. The pooling results are defined as \(\mathop {\sum }\limits_x f_k\left( x \right)\) where fk (x) is the activation of unit k at convolution location x. The pooling results \(\mathop {\sum }\limits_x f_k\left( x \right)\) are subsequently fed into the softmax classifier. The class confidence score, thus can be computed as:

$$Sc = \mathop {\sum}\nolimits_k {w_k^c} \mathop {\sum}\nolimits_x {f_k\left( x \right)} = \mathop {\sum}\nolimits_x {\mathop {\sum}\nolimits_k {w_k^Cf_k\left( x \right)} }$$
(4)

We define \(M_C\left( x \right) = \mathop {\sum}\nolimits_k {w_k^c} f_k\left( x \right)\), as the CAM for class C, where \(w_k^C\) is the weight of unit k of the last convolution layer of class C. Therefore, Sc can be rewritten as:

$$Sc = \mathop {\sum}\nolimits_x {Mc\left( x \right)}$$
(5)

MC (x) directly indicates the importance of the activation at the discrete location x for a given XRD pattern in class C.

In the context of XRD and other spectral measurements, the location of relevant intensity peaks is likely to be displaced only little from sample to sample within a certain class. Thus, the CAMs for all samples within a class are similar, and could be averaged to obtain the discriminative features during activation. Thus, we can define average CAMs for class C as \(\bar M_C\left( x \right)\):

$$\bar M_C\left( x \right) = \frac{1}{n}\mathop {\sum }\limits_{i = 0\, \in C}^n M_{C_i}\left( x \right)$$
(6)

where n corresponds to the training patterns labeled as class C.