Introduction

Ferroelectric materials are very often split into domains, areas that differ in the direction of spontaneous polarization.1,2 Domain walls (DW)—very thin regions separating domains—play an essential role in the electrical, electromechanical, and optical properties of ferroelectrics. For example, a high wall mobility promotes fast polarization switching of the material.3 Until recently, although the structure of ferroelectric walls was addressed both in theory and experiment, researchers mainly cared about ferroelectric walls as borders between adjacent domains, rather than finite-thickness areas exhibiting certain internal structure. However, with a shift of the researchers’ attention from the micron to nanometer scale, one got interested in the “inner” properties of ferroelectric and, in general, ferroic DWs. Specifically, DWs were considered in the context of nanoelectronics.4

One of the “inner” properties of ferroic walls is their ability to carry some bound charge, which is apt to be screened with free carries. Walls carrying bound charge are termed charged domain walls (CDWs). Remarkably, the screening takes place even in the case where the adjacent domains are insulating.5 Keeping in mind that the walls are often easily movable, CDWs can be viewed as ultrathin movable conductive sheets embedded into an insulating material.

The pursuit of nano-electronic applications motivated CDW studies in the 21st century. CDWs have been documented in many ferroelectrics, including perovskite and non-perovskite oxide materials, polymer compositions, and improper ferroelectrics. A conductivity wall/domain contrast up to 13 orders of magnitude has been recently reported.6 A number of methods enabling CDW engineering have been developed, and first device prototypes exploiting CDWs appeared.7,8

Various CDW issues were reviewed in refs 9,10,11. Not competing with these articles, in the present paper, we are aiming at a synoptic presentation of the main concepts behind the understanding of CDWs, combined with a brief and updated review of important findings in the field.

Basic information about CDWs

For two adjacent domains 1 and 2 with polarizations P1 and P2, the bound charge with the surface density

$$\sigma _P = \left( {{\boldsymbol{P}}_2 - {\boldsymbol{P}}_1} \right) \cdot {\boldsymbol{n}}_1,$$
(1)

is present at the wall separating them. Here n1 is the wall normal unit vector pointing inside domain 1. Since the bound charge creates electrostatic fields in the domains, which is energetically costly, DWs do not carry often any bound charge. Such walls are called neutral domain walls (NDWs). DWs with non-zero bound charge σP are called CDWs. The head-to-head (H–H) configuration in adjacent domains leads to a positive charge (Fig. 1a, b, d). Tail-to-tail (T–T) CDWs (with reversed arrows in Fig. 1a, b, d) are charged negatively. The head-to-tail walls, illustrated by Fig. 1c, can also carry bound charge; its sign depends on the wall orientation.

Fig. 1
figure 1

Schematic of charged domain walls for tetragonal perovskite ferroelectrics. Arrows show directions of spontaneous polarization. a 180° non-ferroelastic weakly charged domain wall (WCDW). b 180° non-ferroelastic strongly charged domain wall (SCDW). c 90° ferroelastic WCDW. d 90° ferroelastic SCDW. Small deviations of WCDWs from their electro-neutral orientations (shown with dashed lines) are exaggerated. Twist in (c) and (d) schematically shows the difference in spontaneous strains between ferroelastic domains

Full size image

The presence of bound charge leads generally to its screening with free charges—electrons, holes, and/or mobile ions. This screening can be regarded as a distinctive feature of CDWs. It is useful often to distinguish two types of CDWs: strongly charged (SCDWs) and weakly charged (WCDWs). SCDWs cannot exist without charge screening because the electric field of the bound charge would destabilize ferroelectricity. WCDWs might exist as stable objects without charge screening, though the latter is very likely. In the cases when the difference between SCDWs and WCDWs is not crucial, we will use the general abbreviation CDWs.

DWs slightly deviating from the electro-neutral orientations are typically WCDWs. They are illustrated by Fig. 1a, c. DWs in improper ferroelectrics, where the spontaneous polarization P0 is not the order parameter, belong to WCDWs irrespectively of the orientation. Here, the electric field cannot destabilize ferroelectricity, it only reduces the value of P0.3,12,13 DWs in recently introduced hyperferroelectrics14,15,16 can also be regarded as WCDWs. Remarkably, NDWs can carry a distribution of the bound charge, while the total charge is zero.17,18

In typical and most important proper oxide ferroelectrics, CDWs essentially deviating from the electro-neutral orientation are SCDWs. This case is illustrated by Fig. 1b, d. In such materials, the stabilization of SCDWs requires almost complete screening of the bound charge with free charges.13 This fact is of prime importance for the studies and practical harnessing of SCDWs.

It is also useful to distinguish the situations where the walls are ferroelastic (the adjacent domains differ in the spontaneous strain) and non-ferroelastic (the spontaneous strains are the same). They are illustrated by Figs. 1 c, d and 1 a, b, respectively. Elastic forces prevent rotation of ferroelastic walls contributing to the CDW stability.19 Most of experimentally accessed SCDWs are ferroelastic.

CDW observations

In view of the high energy of their formation, CDWs were only occasionally mentioned in the past.20,21,22,23,24 In the 2000’s, research activity focused on oxide interfaces4,25 revived the interest in electronically compensated CDWs as potential hardware of reconfigurable conducting paths. To date, CDWs are documented in many ferroelectrics, using different experimental techniques. Below, we overview the accumulated experimental findings, highlighting the results promising for applications and/or essentially contributing to the physics of CDWs (see the section 'Theoretical insights into CDW properties').

Since the 1980s, transmission electron microscopy (TEM) techniques has allowed experimentalists to resolve the shapes of DWs and identify their charged parts. In particular, CDWs were observed in KNbO3 crystals26 and Pb(Zr,Ti)O3 (PZT) ceramics.22 Presently, high-resolution and scanning TEM techniques allow for observation of individual atomic displacements and, hence, give information about the internal CDW structure. With these techniques, CDWs were documented in single crystals of LiNbO3,27 YMnO3,28 and (Ca,Sr)3Ti2O7,29,30 thin films of BiFeO3,8,31,32,33 PbTiO3,34 and PZT,35,36,37,38,39,40 and ceramics of BiFeO3,41 (K,Na)NbO3,42 TmMnO3,43 and LuMnO3.43 TEM techniques, supplemented by analyses of the energy losses of electrons (EELS) were employed recently to detect elemental components of the material in the vicinity of CDWs.30,38,39,40,41 Other methods were also in use: scanning electron microscopy for observations of the intersections of CDWs with etched surfaces of LiNbO3 crystals,44 high-resolution X-ray photoemission electron microscopy to visualize and characterize conducting DWs in ErMnO3,45 low-energy electron microscopy (electron backscattering) to image CDWs in LiNbO3 crystals.46

High-resolution TEM studies have provided crucial information about the widths of domain walls. Figure 2a shows one of the images obtained in such studies. This image enabled evaluation of the CDW thickness (5–10 nm) against (1–2 nm) for the NDW in PZT ultra thin films.35 This experimental finding corroborates the theoretical insights and estimates and supports the approach currently used for the description of CDWs which are roughly one order of magnitude thicker than NDWs (see the section 'Theoretical insights into CDW properties').

Fig. 2
figure 2

Observation of ferroelectric CDWs. a High-resolution TEM image of a 180° CDW in ultra thin Pb(Zr0.2Ti0.8)O3 film, after ref. 35 (scale bar, 1 nm). This image enabled evaluation of a large thickness (5–10 nm) of the wall. Red line indicates the CDW center. b, c CDWs in La-modified BiFeO3 thin films visualized via scanning probe microscopy. b Amplitude image of PFM signal in the vertical mode, which gives positions of the walls (scale bar, 1 μm). c Conductive-AFM image of the same area, after ref. 48. d 90° CDWs (vertical alternating dark and bright stripes) in \(\langle 110\rangle _{\mathrm{c}}\) oriented BaTiO3 crystal observed with optical microscopy by an intensity analysis of transmitted non-polarized light (scale bar, 100 μm). The contrast is conditioned by the rotations of the optical indicatrices of ferroelastic domains. After ref. 68

Full size image

Different variants of scanning probe microscopy were extensively used in the studies of CDWs on the mesoscale. A combination of piezo-force microscopy (PFM) with conductive atomic force microscopy (c-AFM) was found to be an efficient tool for CDW identification.47 Using such an approach, CDWs in BiFeO3:La thin films were documented.48 Here, the information about the phase and amplitude of signals in the vertical and lateral modes enables one to locate the positions of CDWs. Figure 2b shows an amplitude image of PFM signal in the vertical mode. It gives the positions of the walls while they were identified as SCDWs, using the phase of this signal combined with the PFM signal in the lateral mode (not shown). An enhanced conduction of these walls was documented, using c-AFM (Fig. 2c). In combination and separately, PFM and c-AFM techniques were also applied for CDW observation in PZT,38,40,49,50 BiFeO3,31,48,51 and PST52 thin films, ErMnO3,53,54 LiNbO3,55,56 HoMnO3,57 YbMnO3,58 and Cu3B7O13Cl59 crystals, BiFeO3 ceramics,41 hybrid improper ferroelectric (Ca,Sr)3Ti2O7,60 and organic ferroelectrics.61

Other scanning techniques employed for CDW visualization are: Kelvin-probe force microscopy in HoMnO3,57 microwave impedance characterization in Pr(Sr0.1Ca0.9)2Mn2O7,62 scanning spreading resistance microscopy in BiFeO3,8 and local Hall effect in YbMnO3.58

On the millimeter scale, CDWs can be detected optically in the reflection and transmission configurations. The first one is relevant to experiments with BaTiO3 and PbTiO3,21 LiNbO3,24,63,64,65,66 and Pb5Ge3O11.23,67 As for the transmission configuration, CDWs in (110)c and (111)c cuts of BaTiO3 crystals (hereafter the subscript c indicates the pseudocubic reference frame) were observed both in polarized and non-polarized (Fig. 2d) light.13,68,69,70,71,72 Non-ferroelastic 180° CDWs were also identified in transmitted polarized light in PbTiO3 and LiNbO3 crystals.21,56,65

CDWs were also observed, using other optical methods: The two-beam photorefractive coupling and directional light scattering in Sn2P2S6,73 surface laser intensity modulation in LiNbO3,24 second-harmonic generation in Pr(Sr0.15Ca0.85)2Mn2O7,74 Cherenkov second-harmonic generation in LiNbO3,75,76 Raman confocal microscopy in LiNbO3, LiTaO3, and SBN,77,78 and optical microscopy in LiNbO366 and Pr(Sr0.15Ca0.85)2Mn2O7.74 Raman scattering was also employed to determine the local symmetry in the vicinity of CDWs in LiNbO3, LiTaO3,77,78 BaTiO369 and (K,Na)NbO3.79

Theoretical insights into CDW properties

Here, we overview the available theoretical knowledge on such important properties of CDWs as concentrations of screening charges, the wall thicknesses, and the formation energies. These properties and their interrelations will be considered mainly for SCDWs. Modeling of CDW conductivity is reviewed in the section 'CDW conductivity'.

For SCDWs with representative polarization P0 = 30 μC/cm2 and wall width w = 10 nm,13,35,80 the screening charge concentration can be estimated as 2P0/ew ≈ 3 × 1020 cm−3, where e is the elementary charge. This is an extremely high value for nominally insulating wide-bandgap ferroelectrics. The screening charges can be electrons, holes, or/and mobile ions. For electron–hole (e–h) screening, high concentrations caused by band bending at the wall usually results in degeneracy of the fermion gas.81

For e–h screened SCDWs in typical proper ferroelectrics, the wall widths are expected to be appreciably larger than those in the case of NDWs. Along with the gradient energy in Landau theory,82 which promotes widening of DWs, for SCDWs, there exists an additional widening mechanism.80,83 It is conditioned by a decreasing dependence of the kinetic energy81 of free electron (hole) gas on DW thickness w. This widening mechanism is found to be strong, leading roughly to about an order-of-magnitude increase of the SCDW width compared to that relevant to NDWs.80,83,84 This result was obtained with different calculation methods for 180° SCDWs within the Landau theory coupled to the quasi-classical Thomas–Fermi model85 for the free-charge concentration. It was also shown that in the morphotropic boundary type materials (e.g., BaTiO3 at room temperature), 90° SCDWs are expected to be yet a few times thicker than 180° SCDWs.86 This is due to reduction of the excess order-parameter energy, owing to electron screening. The above estimate for 180° SCDWs corroborates the results of the comparative high-resolution TEM studies of NDW and SCDW in PZT (see the section 'CDW observations').

A more advanced treatment of 180° SCDWs was offered by combining the Landau theory with the self-consistent Hartree approximation for screening electrons.87 It has revealed a generic discrete quantum structure of CDWs and the condition for employment of the Thomas–Fermi approximation. Specifically, the electron motion perpendicular to the walls is quantized such that the electron energy spectrum exhibits a finite number of subbands related to free electron propagation along the wall (Fig. 3a). This spectrum can cause specific light absorption associated with CDWs. It was shown also that the Thomas–Fermi approximation holds true when more than three electronic subbands are present. This is the case for typical oxide ferroelectrics. The true quantum screening regime with less than four electronic subbands looks interesting but exotic nowadays.

Fig. 3
figure 3

General quantum and spatial properties of CDWs. a Schematic electronic structure of the wall, EF is the Fermi energy, Ej(k) is the dependence of the electron energy on the inwall wavevector for the j-th subband, and Δe is the difference between the energy at the wall center and the Fermi level (the core energy drop). The levels with energies Ej(k) ≲ EF are filled with electrons. b Schematic band-bending diagram showing position of the CB edge in the presence of electrostatic potential φ for a 180° CDW of the H–H type. The spatial structure of the wall includes the core and tails; we is the CDW width, le is the tail length, and EC refers to the case φ = 0. After ref. 87

Full size image

The above considerations imply that the ferroelectric possesses electronic states only below the valence band (VB) edge EV and above the conductive band (CB) edge EC. However, any real material possesses localized electronic levels (traps) within the bandgap. Experiments show that the effective trap concentration Nt varies around 1017 cm−3 in nominally undoped ferroelectrics.88 It was shown analytically and numerically84,87 that the presence of traps leads to modification of the SCDW structure: The wall consists of a relatively narrow core, containing most of the screening charge, and some tails (Fig. 3b) so that the potential decays far from the core. The width of the core is close to the wall width w, obtained with neglected traps,80,87 while the tail length \(\ell\) is much larger than w. For a H–H CDW (electron screening), the most important parameters—the width we, the tail length \(\ell _{\mathrm{e}}\), and the core energy drop Δe (Fig. 3b)—are found to be80,87

$$\begin{array}{ccccc}\\ w_{\mathrm{e}} \simeq & 1.3\left( {\hbar ^6\varepsilon _{\mathrm{f}}^3/P_0m_{\mathrm{e}}^3e^5} \right)^{1/5}\cr \\ \ell _{\mathrm{e}} \simeq & 0.4\sqrt {\varepsilon _{\mathrm{f}}\left( {E_C - E_F} \right)/e^2N_t} \cr \\ \Delta _{\mathrm{e}} \simeq & 4.35\left( {\hbar ^6P_0^4/\varepsilon _{\mathrm{f}}^2m_{\mathrm{e}}^3} \right)^{1/5},\\ \end{array}$$
(2)

where εf ≫ 1 is the dielectric constant, me is the effective electron mass, and EF is the Fermi energy. The condition of degeneracy of electrons is kBT ≪ Δe. For a T–T CDW, it is sufficient to replace me by the hole mass mh and EC−EF by EF−EV. For representative parameters P0 = 30 μC/cm2, εf = 500, \(m_{\mathrm{e}}/m_{\mathrm{e}}^0 = 0.3\) (\(m_{\mathrm{e}}^0\) is the free electron mass), Nt = 1017 cm−3, and EC−EF = 1.5 eV we obtain: we ≃ 7 nm, \(\ell _{\mathrm{e}} \simeq 1\) μm, and Δe ≃ 0.4 eV. These rough estimates also show that the SCDW width w exceeds the width of NDWs by nearly one order of magnitude. The theoretical prediction of the tails has yet to be verified in an experiment.

The formation energy is a vital characteristic of CDWs, for it controls the possibility of their spontaneous appearance and deliberate creation of them. For typical proper oxide ferroelectric treated as a defect-free dielectric, the formation energy (per unit area) of an individual electron (or hole) screened SCDW in an isolated sample can be estimated80 as \(W \simeq 2P_0E_g/e\) whereas Eg = EC−EV is the bandgap. The same estimate is valid for creation of a couple of walls: electron screened SCDW + hole screened SCDW. This estimate has a simple interpretation: for the full screening, one should transfer 2P0/e electrons [per unit area] across the bandgap, paying the energy penalty Eg/e per electron. A more elaborate treatment87 provides expressions for the formation energies for the electron (We) and hole (Wh) screened CDWs:

$$W_{\mathrm{e}} \simeq 2P_0\left( {E_C - E_F} \right)/e,\hskip 4pt W_{\mathrm{h}} \simeq 2P_0\left( {E_F - E_V} \right)/e.$$
(3)

Note that We + Wh = W. Since the electronic energies entering these expressions are \(\simeq 1\hskip 4pt {\mathrm{eV}}\), these values are roughly two orders of magnitude larger than the typical NDW energies.80 The above large formation energy rises a questions about feasibility of CDWs. Experimental observations of CDWs motivate one to look for energetically less costly screening scenarios, avoiding the electron transfer across the bandgap.

A possibility of reduction of CDW energy occurs if defects providing free carriers are mobile. Specifically, in n-type materials, electrons needed for screening of the bound charge at H–H CDWs can be collected from a macroscopically large area avoiding the electron transfer across the bandgap.13 At the same time, the ionized donors can be used for screening of T–T CDWs. Evidently, an analogous scenario works for p-type materials. In such “mixed” free-carrier/ion screening scenarios, substantially smaller wall-formation energies than for the e–h screening are expected.13,89 These screening scenarios entail a clear manifestation. In the case of a quasi-periodic H–H/T–T CDW pattern, the minimal possible period is expected to be a decreasing function of concentration of the defects providing free carriers. This prediction corresponds to the experimental data obtained for CDW structures in BaTiO3 crystals possessing variable concentration of oxygen donor-like vacancies13,68 (see also the section 'CDW engineering').

An alternative way to avoid the over-bandgap electron transfer is to use super-bandgap illumination as a mean to produce screening electrons and holes. A theory of this mechanism of SCDW formation was recently offered.90 It can be considered as a generalization of the previous results,80,87 which explores the concept of intensity-dependent quasi-Fermi levels for electrons and holes.91 This scenario has been implemented experimentally.72

Above we restricted ourselves to infinite one-dimensional CDWs. What happens if a CDW connects two electrodes? This brings us to a qualitatively different 2D case, which is relevant not only to the basics, but also to the conductivity issues to be considered in the section 'CDW conductivity'. The matter is that the application of an equipotential electrode to the crystal surface flattens the band bending (Fig. 3b) in the vicinity of the electrode. On the other hand, this bending is the driving force for the free-charge accumulation at the wall.68 Thus, the electron (hole) gas at CDWs can be disconnected from the electrodes with dielectric gaps. However these gaps can be essentially narrowed or even closed in the presence of a d.c. electric field. This is illustrated by Fig. 4 obtained by phase-field modeling.68 In addition, the d.c. field can facilitate tunneling through the gaps.

Fig. 4
figure 4

Color-scale maps of the phase-field calculated free-electron concentration at a H–H CDW in BaTO3 contacted with an electrode.68 a Short-circuited configuration, the electron gas is disconnected from both electrodes with dielectric gaps. b Under applied voltage of 12 V, one of the gaps is closed while the other becomes much narrower, facilitating electron tunneling. After ref. 68

Full size image

The above discussion was dealing with theoretical insights into SCDWs. As for WCDWs, most attention was paid to improper ferroelectrics of the hexagonal manganite type, like ErMnO3. The wall structure was probed using the Landau theory92 in combination with ab initio calculations93 while the effect of screening charge was ignored. The experimental profiles for NDWs and CDWs in ErMnO392 were approximated using the phenomenological model92 while the documented small differences between the thicknesses of NDWs and CDWs was attributed to the effect of the crystalline anisotropy.

Ab initio calculations within the density-functional theory (DFT) for CDWs is a less developed but rapidly growing activity. Most of DFT calculations are relevant to NDWs, see, e.g., refs 47,94,95. DFT simulations of CDWs represent a more complicated problem owing to the necessity to account for long-range correlation effects and trap recharging. Ab initio calculations53 were performed for a 10-unit-cell stack of YMnO3, which contains one H–H and one T–T wall. In these materials, P0~6 μC/cm2, which, taking the wall width w = 10 nm,92 leads to a still appreciable bound charge concentration of 2P0/ew ≈ 0.6 × 1020 cm−3. If this charge is screened with the e–h free carriers, to provide such screening, the Fermi level at the CDW should be quite close to the edge of the VB (or CB). This was observed in ab initio simulations,53 where the Fermi level contacted VB. This should promote the conduction at T–T walls screened by holes, which is consistent with the experimental observations53 (see the section 'CDW conductivity').

The advantage of ab initio simulations is a possibility of engineering of new materials. Recently, a concept of hyperferroelectrics—a new class of proper ferroelectrics which are not destabilized by unscreened depolarization field was introduced.14 The possible CDWs in these materials may be naturally stable, as confirmed by first-principles calculations of H–H and T–T walls in ABC-type hexagonal hyperferroelectrics.16 However, scarce data on CDWs in hyperferroelectrics still need additional validation. Ab initio simulations are efficiently employed for bandgap design: the impact of CDWs on the bandgap width was addressed in organometal halide perovskites, which is of interest in the context of photovoltaics.96

It should be mentioned that, for a CDW, besides the formation energy its stability is important. As was mentioned in the section 'Basic information about CDWs', elastic effects contribute to stability of ferroelastic CDWs. At the same time, even being screened, CDWs exhibit positive formation energy. This means that, unless the boundary conditions prevent disappearance of the walls, any CDW configuration has to be regarded as metastable. The decay mechanisms can be very complicated. In practice, depending on the type of ferroelectric, the temperature, etc., the decay time can range from a fraction of second to years.

CDW conductivity

The very large conductivity of CDWs in nominally insulating ferroelectrics is relevant both to the fundamental knowledge and applications in nanoelectronics.4,47,68 Here we represent first the main theoretical insights into CDW conduction properties and consider then the relevant experimental data.

In the case of e–h screening, CDW conductivity is expected to be due to the freedom of movement of the compensating electrons or holes in the wall plane. Since the concentrations of compensating free carriers at CDWs can readily be above 1020 cm−3, large metallic-like inwall conductivity is expected. This simple idea, expressed in 1973,5 lies in the basis of all available models of CDW conductivity. In the case of mixed electron-ion screening, the ion-screened CDW is expected to possess a relatively small conductivity because of low ion mobility.

Let n = n(z) be the concentration of the compensating charge carriers (electrons or holes) for positively or negatively charged walls as a function the coordinate z in the direction perpendicular to the wall. The specific bulk conductivity σ can be expressed as σ = eμn, where μ is mobility of the screening carriers. It is implied that the current flows along the wall, i.e., we deal with a quasi-2D effect. The specific surface CDW conductivity reads \(\sigma _S = e\mu \bar nw\), where \(\bar n\) is the average over z concentration of compensating carriers and w is the CDW width.

Determination of n(z) and w requires modeling of CDW structure. In practice, inclined 180° CDWs, characterized by the inclination angle θi between the wall plane and the polarization direction, see Fig. 1a, b, are important. The total bound charge to be screened is 2P0sinθi in this case, and the width w is expected to be weakly dependent on θi for not very small inclination angles. Thus, we have roughly \(\bar nw \approx 2P_0{\mathrm{sin}}\theta _i\). This feature is consistent with the results of continuum numerical simulations for LiNbO3 crystals.84,97

This above continuum medium model of CDW conductivity is oversimplified. First, we know that the discrete quantum subband structure depicted in Fig. 3a is generic for CDWs. A part of the subbands can be filled with electrons (holes) and, thus, excluded from the charge transport. For this reason, the total concentration of conductive charge carriers can be substantially smaller than 2P0sinθi. This can explain the results of recent experiments with CDWs in YbMnO3 crystals.58 Second, the mobility μ can differ substantially from the value expected for the 3D band transport in metals. This can be due to (i) roughness of the CDW and (ii) 2D character of the electron scattering processes.

Often, CDW conduction experiments run in tip configurations when the electric current flows between a continuous bottom electrode and a tip top electrode. Here, the total resistance extracted from the I–V characteristic can be approximated by R = F/σS where F ≈ 0.72·log(5d/a) is a dimensionless geometric factor accounting for a sharp convergence of stream lines of the current density from continuous bottom electrode to the tip.6 Fortunately, it depends weakly on the ratio of the sample thickness d to the tip contact length a facilitating estimates of σS and σ from experimental data.

The presence of a large CDW conductivity does not ensure that it is easily available via Ohmic contacts. As we have seen in the section 'Theoretical insights into CDW properties', dielectric gaps are possible between the electrodes and highly conductive electron gas at the wall. These gaps depend generally on the applied d.c. voltage V and the work-function difference between the crystal and metal. Thus, complicated I–V characteristics are generally envisaged.

Turning to the experimental side, we mention first that an elevated conductivity of SbSI crystals owing to the presence of CDWs was reported already in 1976.20 At that time, it did not attract a strong interest. Such an interest arose in 2009 after the report of high local conductivity of domain walls in BiFeO3 crystals.47,98 However, the walls investigated were nominally neutral. A stimulating result, relevant to CDWs, dates from 2012 when a large conductivity was detected at transient CDWs of nucleating nano-domains in PZT thin films.50 The conductivity contrast between the walls and the bulk reached ~104. This discovery triggered a research endeavor to detect and explore similar phenomena in other systems.

An important advance was achieved with 90° CDWs in BaTiO3 stabilized by the ferroelastic clamping.68 Experiments were conducted with a set of pad electrodes covering either H–H, or T–T CDWs, or bulk areas (Fig. 5a). Conductivity of the T–T CDWs showed no difference compared to the bulk. However, conductivity of the H–H CDWs was found to be much higher than that of the bulk. This is illustrated by Fig. 5a. Using the data of Fig. 5a, the conductivity of the H–H CDWs was evaluated to be 108–1010 times higher than that of the bulk. Furthermore, this conductivity exhibited a metallic-type decreasing temperature dependence. A remarkable feature of this CDW conductivity was the threshold behavior of the I–V dependence (see the section 'Theoretical insights into CDW properties'). Such a behavior is explained within the CDW theory. The absence of large conductivity at T–T CDWs is in agreement with the electron/ion screening scenario for CDWs in BaTiO3: the H–H CDWs are screened by highly mobile electrons while T–T walls are screened by much less mobile oxygen vacancies (see the section 'Theoretical insights into CDW properties').

Fig. 5
figure 5

CDW conductance in BaTiO3 a and LiNbO3 b, c crystals. a I–V characteristic for different regions of the crystal: with a H–H SCDW, with a T–T CDW, and without walls. Insert shows schematically the experimental configuration comprising \(\langle 110\rangle _{\mathrm{c}}\) oriented BaTiO3 crystal with CDWs; top pad electrodes (Pt) are shown with circles while the continuous bottom electrode is not shown. After ref. 68. b, c I–V characteristics for different CDW configurations in LiNbO3: an array of 1464 parallel CDWs sandwiched between top (Ag) and bottom (Cr) electrodes b and an array of 32 parallel CDWs contacted by two Cr pads patterned from the bottom electrode c. After ref. 6

Full size image

Using the c-AFM method, CDW conductivity was also detected in BiFeO3 thin films.48 The current flowing through H–H CDWs was more than three orders of magnitude larger than that flowing through the bulk or through NDWs. Figure 2b, c show a PFM image of the domain structure and the corresponding map of electric current. Conducting lines are clearly seen at H–H CDWs. The H–H CDWs exhibited a non-thermally-activated conductivity, which contrasted with a thermally-activated conductivity of 71° nominally neutral walls.

Ferroelastic bent CDWs in PZT also exhibit non-thermally-activated conductivity. Narrow feroelastic domain inclusions limited with a pair of weakly bent ferroelectric walls were addressed. In view of their weak bending, the walls are expected to be WCDWs. Using high-resolution cryogenic c-AFM, clear current maxima corresponding to each of the two bent DWs limiting narrow inclusions were identified.38 Also, a correlation between the local concentration of charged dopants and the CDW conductance was established using the EELS TEM technique.40

In 2017, record-breaking conductivity was reported for 180° CDWs in LiNbO3 crystals,6,76,99 while the earlier studies reported only transient currents66 and d.c. conductivity under super-bandgap illumination.55 We highlight here the results from ref. 6. In this work, inclined (θi ≈ 1°) positively charged walls (and also arrays of such walls) were engineered, using biased μm-sized tips. Conductance was measured, using different configurations of electrodes made of different materials. The conductance of a wall array measured between a bottom Cr electrode and Ag-paste top electrode was reported to be of rectifying type (Fig. 5b). The measurements where the wall was contacted with two bottom Cr electrodes yielded the ohmic behavior (Fig. 5c). The data of Fig. 5c were used to evaluate the specific surface resistance of CDWs and their bulk conductivity σ. With the wall width w = 10 nm, the latter was estimated as σ ≈ 0.02(Ωcm)−1. This value exceeds the dark conductivity of LiNbO3 by at least 13 orders of magnitude. While the CDW thermally-activated conductivity was highly stable for T ⪅ 70 °C, it decayed gradually and irreversibly at higher temperatures. This can be interpreted by the replacement of the e–h screening with the ionic charge compensation via thermo-activated migration of charged defects.

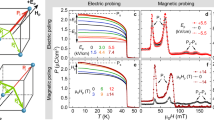
CDW conductance in improper ferroelectrics drew considerable attention as well, hexagonal manganites were of prime interest here. In these materials, DWs are interlocked with structural antiphase boundaries resulting in a full spectrum of DW orientations, ranging from neutral to maximally charged. Figure 6 illustrates this situation for ErMnO3 crystals.53 As seen from conducting-AFM contrast in Fig. 6, CDWs in hexagonal manganites demonstrate both increased (T–T) and suppressed (H–H) conductivities. The enhanced conduction of T–T walls demonstrated in this figure is consistent with the results of ab initio calculations (see the section 'Theoretical insights into CDW properties'). Similar conductive behavior was reported in hybrid improper ferroelectric Ca2.46Sr0.54Ti2O7.60 Despite their suppressed conductivity at relatively low applied voltages, H–H CDWs can be switched into a conductive state when a threshold voltage is exceeded, as demonstrated for ErMnO3.100

Fig. 6
figure 6

CDW conductance in improper ferroelectric ErMnO3. The c-AFM scan shows suppressed conductance at H–H walls (dark), enhanced conductance at T–T walls (bright), and a continuous transition between these two states with changing inclination angle (scale bar, 2 μm). Arrows show the direction of P0. After ref. 53

Full size image

Recently c-AFM conduction experiments were advanced to include local Hall measurements.58 This was done as applied to T–T CDWs in YbMnO3 crystals. The positive sign of screening charge carriers (holes) and their mobility μ ≈ 50 cm2/Vs, relevant to the band transport, were established. Remarkably, the estimated concentration of screening holes (~1016 cm−3) was found to be about four orders of magnitude below the value of 2P0/ew for w = 10 nm. This can be qualitatively interpreted as a manifestation of the quantum subband structure of the wall (see the section 'Theoretical insights into CDW properties').

CDW engineering

A lot of efforts were put into engineering of CDW patterns in the tetragonal phase of BaTiO3 crystals.13,68,72 The basic method used was the frusrative poling:13,101 a thin crystal plate is brought into the tetragonal phase under a dc electric field normal to it, which equally favors two or more tetragonal domain states. For the [110]c oriented field, the preferable tetragonal states are poled along [010]c and [100]c directions, while, for the [111]c orientation, the preferable states are poled along [010]c, [100]c, and [001]c. Frusrative poling not necessarily leads to CDW formation since NDWs with lower energy per unit area can be generated as well. To avoid the preference of the system to form NDWs, one should reduce the formation energy of CDWs in question.

Frusrative poling was implemented on crossing the border to tetragonal ferroelectric phase from cubic or orthorhombic phases. Since the interphase borders on the field/temperature (E–T) diagram are inclined, they can be crossed either by variation of E (Fig. 7a, line 2) or T (Fig. 7a, lines 1 and 3).

Fig. 7
figure 7

Engineering of CDWs in BaTiO3 crystals and BiFeO3 films. a Schematic field/temperature (E–T) phase diagram of BaTiO3 for \(\langle 111\rangle _{\mathrm{c}}\) or \(\langle 011\rangle _{\mathrm{c}}\) orientations of frusrative field. The borders between the cubic (C), tetragonal (T), and orthorhombic (O) phases are shown with straight lines. Lines (with arrows) 1, 2, and 3 show sequence of changes of E and T used for engeneering of 90° CDWs in refs 13,68,72, respectively. b Engineering of CDWs in [001]c films of BiFeO3:La using trailing field.102 The map of sign of [100]c component of the spontaneous polarization (dark—positive, bright—negative). The as-grown film exhibits random domain states (scale bar, 1 μm). The right and left parts of the film are treated with a biased AFM tip, moving along zig-zag lines. This creates an effective trailing field102 directed along red arrows. The vertical components of the field under the AFM tip combined with the effective trailing field brings the left and right parts of the film into single-domain states. The in-plane polarization components are shown with P0-marked arrows. Once two encountering domains (shown with homogeneous colors) merge, a CDW forms. After ref. 48

Full size image

In the case of 〈110〉c poling of nominally stoichiometric BaTiO3 and the cubic/tetragonal border, the preferable domain states can be separated either with a NDW parallel to the plane of the plate or with a CDW normal to it. Though, the energy per unit area of NDWs is smaller than that of CDWs (see the section 'Theoretical insights into CDW properties'), a smaller area of a CDW reduces the formation energy of the latter.

In ref. 13 for \(\langle 111\rangle _{\mathrm{c}}\) poling (the (E–T) “trajectory” is shown in Fig. 7a with line 3), the competing NDWs and CDWs had approximately the same areas. Nevertheless, CDW patterns were generated, by using samples with elevated oxygen deficiency, proving the enhanced concentrations of free elections and mobile donors (oxygen vacancies), which promote the mixed elecron/ion screening scenario with essentially reduced CDW energy (see the section 'Theoretical insights into CDW properties'). A remarkable correlation between the charge concentration and the domain size was reported, which is consistent with the theoretical prediction for this scenario. Yet another approach to the reduction of the CDW formation energy was employed in ref. 72. Here, for \(\langle 111\rangle _{\mathrm{c}}\) poling in nominally stoichiometric BaTiO3, the orthorhombic/tetragonal phase border was crossed along line 1 in Fig. 7a, under a super-bandgap illumination that reduces the CDW formation energy (see the section 'Theoretical insights into CDW properties'). One should note that the CDW patterns in (111)c plates are always stable under a moderate electric field (~1 kV/mm), while after removal of the field the domain patterns may persist for a long time or disappear quickly, depending on the sample.

In the view of utilizing CDWs for nanocircuitry, CDW nanoscale manipulation in La-doped BiFeO3 thin films is of special interest.48 As-grown films exhibit a random mixture of domain states (central part of Fig. 7b). The films were scanned with a biased AFM tip, which followed special trajectories creating an effective trailing field.102 Such a scanning leads to formation of two encountering domains (Fig. 7b). Merging the encountering domains yields a CDW.48 In this approach, the tip-geometry-enhanced electron tunneling into the ferroelectric film was exploited to promote an efficient screening of the bound charge and reduce the CDW formation energy. Some results of characterization of the CDW pattern created in this way are shown in Fig. 2b, c. This method was also applied to CDW engineering in (Pb,Sr)TiO3 thin films.52 In this work, along with the trailing electric field, the formation of CDWs was also controlled with poling using patterned electrodes.

Next we consider specific features of CDW engineering in LiNbO3. They are due to two interrelated factors—specific ferroelectric properties103 and persistent experimental efforts toward optical applications.27,65,104,105 Domain walls in this material can be neutral, weakly, and strongly charged. Commercially available periodic domain structures, designed for optical applications, possess predominantly neutral or almost neutral DWs. However, there are numerous experimental tools for production of CDWs with a tunable angle θi between the wall and its electro-neural orientation, which controls the bound charge.

Stable H–H CDWs with the inclination angle θi = 90° were obtained first without application of electric fields by a severe heat-treatment close to the Curie temperature (≈1200 °C) with subsequent cooling down.106 Field-assisted poling of commercially available z-cut LiNbO3 wafers combining tip and continuous electrodes leads to inclined H–H CDWs with θi ⪅ 1°.6,55,76 The origin of the inclinations is not quite clear; most probably, they are due to expansion of the field stream lines toward the continuous electrode. The inclination angle can be varied by doping with Mg and thermal treatments.

A different method for fabrication of various domain structures leading to CDWs is known as prohibited poling.107,108,109,110,111 It can be exemplified as follows: a UV laser heats locally (on the μm scale) + z-face of a LiNbO3 sample close to the Curie point. After cooling down, the sample shows no signs of domain inversion. However, during subsequent field-assisted repoling of the sample at room temperature, the exposed area remains non-inverted (prohibited poling), as shown schematically in Fig. 8a. The resulting domain structure possesses a CDW whose inclination angle θi varies from 90° at the maximum depth to 0° near the surface. Experimental evidences of such domain patterns are obtained by etching, PFM, and electron microscopy methods (Fig. 8b, c).

Fig. 8
figure 8

Domain structure of a UV treated sample of LiNbO3 after its subsequent repoling. a Schematic front view for created domain line. The inclination angle of CDW θi varies from 90° at the maximum depth to 0° at the surface. b Geometrical scheme of the repoled and then wedge polished sample. c Top view of the wedge polished and etched sample imaged with scanning electron microscopy (scale bar, 1 μm). After refs 108,111

Full size image

The physical mechanism behind the inhibition poling effect is, most probably, a local increase of the coercive field during the UV exposition because of high-temperature out-diffusion of lithium.109 Remarkably, the CDW formation occurs pretty fast (on the scale of minutes), whereas diffusion of ions is extremely slow in lithium niobate.103 This indicates that electrons are responsible for the charge screening.

Now we address CDW engineering in improper ferroelectrics. The available data suggest that spontaneous CDW formation53,59,60 occurs quite often. However, CDW engineering was only recently carried out in Cu-Cl boracite ferroelectrics.59 In this material, the spontaneous polarization and spontaneous strain are linearly coupled. Exploiting this property of the material, quadrant domain structures were created with application of about 1 GPa pressure in the middle of the quadrant. The structure contained NDWs as well as H–H and T–T 90° CDWs, the T–T walls were found highly conductive. It was shown that this way injected CDWs can also be displaced by applying a properly oriented dc electric field.

CDW functionalities

Harnessing CDWs in prototypes of electronic devices can be viewed as an ultimate practical goal of the scientific activity in the field. On the way toward applications, conductance control via unique properties of CDWs received appreciable attention.7,8,58,100,112,113,114,115,116,117 Below we consider simple examples of CDW exploitation.

Nanodevices could be designed such that the high conductivity of the wall could be created or erased on demand to provide resistive switching. Such an idea can be implemented either in the parallel-plate-capacitor configuration8,112 or coplanar capacitor configuration.7

With (110)c oriented films, the coplanar capacitor configuration was chosen to provide up to 103 on/off ratio.7 Here, in the on regime, the coplanar electrodes were connected with a wall that contained both neutral and charged segments. The resistance was determined by the neutral segments because of their relatively small conductivity. This prototype of nonvolative ferroelectric domain wall memory was scalable to below 100 nm, exhibited excellent endurance and retention characteristics, and a multilevel data storage capacity. Thus, an important step toward integrated multi-terminal nanoscale DW devices was made. Employment of configurations with very low CDW resistance will enable one to proceed to much higher on/off ratios.

The functionality of the parallel-plate setup made of a (100) BiFeO3 film was shown to be essentially controlled by the presence of a CDW.8 The schematic of such a setup is shown in Fig. 9.

Fig. 9
figure 9

Resistive switch using CDW in BiFeO3 (BFO) film on TbScO3 (TSO) substrate with (La,Sr)MnO3 (LSMO) electrode. a Configuration containing only NDWs (109° DW and 180° DW). b Configuration containing also a segment CDW (71° CDW). Both configurations are stable in absence of applied voltage. The configuration with a CDW segment is up to 105 times more conductive than the other. By applying positive or negative voltage to the tip one can switch between two configurations thus providing the resistive switching with the “on/off” ratio up to 105. After ref. 8

Full size image

Here the configuration shown in Fig. 9a does not contain CDWs. By applying positive voltage to this configuration one can generate a segment of CDW (Fig. 9b), the length of which increases as a function of voltage. After the voltage removal, the modified configuration stays unchanged while by applying a large enough negative voltage, the system is then brought back to the original configuration. Thus, the system exhibits a switching instability. If the CDW segment is large enough (more than 20% of the film thickness in this experiment), the across-the-film conduction of the two states differs up to 5 orders of magnitude. The elevated conduction of the “on” state is controlled by two factors: the high conductivity of the CDW segment and the conductivity of the 180° NDW, which is enhanced due to the impact of the electrostatic potential created by the charge at the CDW segment.

Manipulation of charge transport in H–H CDWs in improper ferroelectrics like hexagonal manganites was also demonstrated. In semiconducting ErMnO3, an electric-field control switching between resistive and conductive states was documented.100 In YbMnO3, the T–T CDW conductance was manipulated with external magnetic field.58

The suppressed conductivity of some DW parts in hexagonal manganites is of interest in view of potential application for nano-capacitors, particularly in YMnO3, where insulating CDWs had conductivity contrast up to 500 with respect to the bulk.113 Along with enhanced conductivity and other potential functionalities, CDW enhanced piezo-response was also actively analyzed.69,70,71,101,118,119,120

Summary and outlook

The last decade was marked by a tremendous progress in investigation of ferroelectric CDWs. The field has evolved into a vast area of experimental and theoretical studies with promising results for applications. To date, CDWs have been documented in both bulk crystals and thin films. Numerous experimental techniques operating at the nanoscale were applied to (developed for) the fabrication and identification of various walls (weakly and strongly charged, inclined, etc.) and for analysis of their properties. Giant CDW conductivity, with up to 13 orders of magnitude enhancement as compared to the bulk, is now reliably detected for numerous materials. The possibilities of creation, displacement, and annihilation of CDWs, as well as a number of applications, have been demonstrated. An impressive amount of theoretical studies have been performed employing analytical and numerical studies within the Landau theory and also ab initio DFT simulations. It is possible now to judge about the charge screening mechanisms inherent in CDWs, about their widths (~10 nm), energy, quantum structure, the effect of light, etc.

Despite this impressive progress, the studies of CDWs are still at their infancy and it is too early to compare CDW funtionalities with other systems, e.g., memristors. This is greatly due to diversity and complexity of the subject matter. Thus, we expect a gradual maturation of the field. This inlcudes a deeper penetration into the nanoscale, more control with nano-fabrication techniques, better spatial resolution, and specialization of experimental methods as applied to particular materials. We also expect quantization and a better control of tip-related measurements of CDW conductivity. On the theoretical side, we hope to see specialization of the ab initio theory as applied to the actual charge screening mechanisms, an analysis of the impact of the quantum structure of CDWs on the 2D conductivity, and account for the effect of the wall roughness on the carrier mobility. Involvement of light into various CDW properties also looks highly promising. The fundamental differences between the properties of CDWs and NDWs will be clarified.

As for future applications of CDWs, the general trend here is indeed in miniaturization of the tip-related CDW configurations. Along this way, prototypes of novel reconfigurable functional elements, such as field and stress controlled memory cells, logical elements, and data storage devices, are anticipated. Switch from two- to three-terminal prototypes and fabrication of array structures are also envisaged. Performance of these devices, including such issues as low switching energy, high electrical tunability, memristive functionality, scaling behavior, speed, and endurance and retention characteristics will be considered and improved.