Strain-mediated voltage-controlled switching of magnetic skyrmions in nanostructures

Abstract

Magnetic skyrmions are swirling spin structures stabilized typically by the Dyzaloshinskii-Moriya interaction. The existing control of magnetic skyrmions has often relied on the use of an electric current, which may cause overheating in densely packed devices. Here we demonstrate, using phase-field simulations, that an isolated Néel skyrmion in a magnetic nanodisk can be repeatedly created and deleted by voltage-induced strains from a juxtaposed piezoelectric. Such a skyrmion switching is non-volatile, and consumes only ~0.5 fJ per switching which is about five orders of magnitude smaller than that by current-induced spin-transfer-torques. It is found that the strain-mediated skyrmion creation occurs through an intermediate vortex-like spin structure, and that the skyrmion deletion occurs though a homogenous shrinkage during which the Néel wall is temporarily transformed to a vortex-wall. These findings are expected to stimulate experimental research into strain-mediated voltage control of skyrmions, as well as other chiral spin structures for low-power spintronics.

Introduction

Magnetic skyrmions typically exhibit a cycloidal or helical spin rotation along the radial plane from one perpendicular direction to the other, known as a Néel Skyrmion or a Bloch skyrmion, respectively. The topological charge number¹ $Q = \left( {1/4\pi } \right){\int} {\mathbf{m}} \cdot \left( {\partial _x{\mathbf{m}} \times \partial _y{\mathbf{m}}} \right)dxdy$ (where m denotes the normalized local magnetization) has a magnitude of about 1 in both types of skyrmions, 0.5 in a magnetic vortex, and 0 in a ferromagnetic state. Nanoscale skyrmions in magnetic materials are typically stabilized by Dyzaloshinskii-Moriya interaction (DMI), which arises either intrinsically within a bulk lattice or due to the proximity to an adjacent heavy-metal (Fig. 1a).^2,3,4

Fig. 1

Architecture. a, Schematic of the interfacial DMI in juxtaposed magnetic and heavy-metal layers. S₁ and S₂ denote the spins of two neighboring atoms in the magnetic layer that are exchange coupled through an atom of large spin-orbit coupling (SOC) in an adjacent heavy-metal layer. D₁₂ is the DM vector which is parallel to the interface and perpendicular to the triangle of the three atoms. b, Heterostructures for strain-mediated voltage (U)-controlled switching of magnetic skyrmions: (from top to bottom) a capping layer; a ferromagnetic (FM) nanodisk with perpendicular magnetic anisotropy (PMA) and robust magnetoelastic coupling; a heavy-metal (HM) underlayer; a piezoelectric layer; an electrode. The capping layer can be a non-magnetic oxide or a dissimilar heavy metal to enhance the PMA and/or the interfacial DMI strength. c, Schematics of two degenerate Néel skyrmions induced by interfacial DMI with a positive average strength D

The ability to use external stimuli to control (e.g., switch, move) a magnetic skyrmion underpins its potential application in spintronics, such as a skyrmion-based magnetic random access memory⁵ or a race-track memory.⁶ Various stimuli have been used, e.g., magnetic fields,^7,8 electric currents,^{6,9,10,11,12,13,14,15,16,17} laser,^18,19 voltages,^20,21,22,23 and stress.^{24,25,26,27,28,29,30} Among them, using voltages or strains are particularly promising because the heat dissipation in both schemes is negligible. Notably, repeated skyrmion creation and deletion induced by voltages^21,22 or stress^25,30 have been demonstrated. However, these reports^21,22,25,30 all involve a simultaneous application of a bias magnetic field to stabilize the skyrmion, which would hamper the device miniaturization because it is challenging to localize a magnetic field on a chip.

Here we propose an architecture that integrates a multilayer magnetic nanostructure with an underlying piezoelectric layer, where the former consists of a magnetic ultrathin nanodisk sandwiched by a capping layer and a heavy-metal underlayer (Fig. 1b). In this architecture, we computationally demonstrate a repeated creation and deletion of an isolated Néel skyrmion by voltage-induced strains without using any magnetic fields. Note that recent experimental observations have demonstrated that an isolated magnetic skyrmion can be stable in the absence of magnetic fields in a magnetic nanostructure with a 3D geometric confinement.^31,32 Here we limit our discussion to the case where a net DMI arises only from the magnet/heavy-metal interface. In this case, the formation of a Néel skyrmion is more favorable than a Bloch skyrmion, which can be seen from the expression of the interfacial DMI free energy (Eq. 4 in Methods). Figure 1c schematically shows the two degenerate spin structures of an isolated Néel skyrmion with downward (Q = −1) and upward (Q = 1) cores, assuming the effective interfacial DMI strength D in Eq. (4) is positive.

Using a 1.1-nm-thick Co₂₀Fe₆₀B₂₀ (CoFeB) nanodisk as an example, we computationally identified the ranges of disk diameter and D where an isolated Néel skyrmion is stable or metastable. Upon applying a voltage across the piezoelectric layer (Fig. 1b), the induced strain can be transmitted to the CoFeB disk and modulate its magnetic free energy via magnetoelastic coupling^{33,34,35,36,37} and possibly the D. Our simulations then show that, if (1) a ferromagnetic state and a Néel skyrmion are stable or metastable under zero magnetic fields and (2) the gap between the energy levels of these two states is not too large, the voltage-induced strain alone can drive a non-volatile switching from the ferromagnetic state to the skyrmion (creation) and vice versa (deletion).

Results

Stability and size of an isolated Néel skyrmion in a magnetic nanodisk

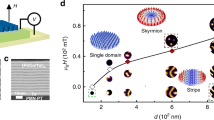
Figure 2a shows the computed stability diagram of three types of spin structures under different disk diameters and D. These three structures, represented by differently line patterns, include an isolated Néel Skyrmion, a quasi single domain (QSD, a ferromagnetic state with titled spins near edges), and a stripe domain with Néel walls; see exemplary structures alongside the diagram. In areas where three line patterns overlap, all three spin structures can exist at equilibrium: the structure having the lowest intrinsic free energy density f_intrin (see definition in Methods) is considered as thermodynamically stable while the other two metastable. Areas where two line patterns overlap can likewise be understood. Stable QSD, skyrmion, and stripe are colored blue, green, and yellow, respectively. For example, a skyrmion can exist at equilibrium wherever the three line patterns overlap, but it is thermodynamically stable only in the green area (i.e., relatively large disk diameter together with an intermediate D). Notably, a stable Néel skyrmion is always accompanied by two other metastable spin structures (i.e., all the green area hosts three line patterns) and generally only shows a slightly smaller f_intrin than the stripe domain and/or the QSD (see top panels of Fig. 2b-c).

Fig. 2

Thermodynamic stability diagram. a, Stability diagram of the quasi single domain (QSD), Néel skyrmion, and Néel stripe (represented by different line patterns) as a function of the CoFeB disk diameter and the interfacial DMI strength D. Typical spin structures are shown on the right. Areas of stable (i.e., ground-state) QSD, skyrmion, and stripe are colored blue, green, and yellow, respectively. Areas with overlapping line patterns indicate the existence of one or two metastable spin structures in addition to the stable spin structure. Color bar m_z denotes local normalized perpendicular magnetization. Dependence of the intrinsic magnetic free energy density f_intrin and the skyrmion diameter d_Sk on b, the interfacial DMI strength D, and c, the CoFeB disk diameter. The disk diameter is 220 nm for all cases in b, while the D is 0.75 mJ/m² for all cases in c. When D < 0.75 mJ/m² in b and when disk diameter < 140 nm in c (marked by blue crossed circles), the skyrmion exhibits a notably higher energy level than the other spin structures. These highly metastable skyrmions appear at equilibrium in simulations only when the in-plane size of a simulation cell is relatively small (i.e., 0.5 nm). The vertical line in b marks the critical interfacial DMI strength D_c ( ≈ 0.7 mJ/m²) for a 220-nm-diameter 1.1-nm-thick CoFeB disk

The size of an isolated Néel skyrmion is also strongly influenced by the D and the magnetic disk diameter. As shown in Fig. 2b, under the same disk diameter of 220 nm, the skyrmion diameter (d_Sk, defined as the diameter of the line m_z = 0⁶) increases nonlinearly from about 40 nm to 150 nm upon increasing D from 0.4 mJ/m² to 3 mJ/m². Such a nonlinear feature becomes appreciable when D is larger than a critical value D_c, which was analytically estimated (see Supplemental Note S1) to be about 0.7 mJ/m² for the 220-nm-diameter disk (marked by broken line). Similar nonlinear features also appear in the cases of other disk diameters that have different D_c (see Supplemental Fig. S1a-b). These nonlinear features appear because the edge confinement tends to suppress the growth of a skyrmion when D > D_c.³⁸

Furthermore, when the disk diameter increases from 80 nm to 720 nm at D = 0.75 mJ/m², d_Sk increases almost linearly from about 16 nm to 500 nm (see Fig. 2c). This indicates a nontrivial role of edge confinement on the d_Sk in the range of disk diameters investigated, because d_Sk would otherwise remain the same whether the hosting magnetic disk is large or small.³⁸ As d_Sk increases, the feature of the local magnetization profile changes from a compact-skyrmion-type (where the Néel wall thickness is similar to d_Sk) to a bubble-type (Néel wall thickness &mle;d_Sk), as shown in Fig. S1c-d. Note that the stability of such an isolated skyrmion reduces when the disk diameter exceeds 300 nm, evidenced by the associated slight increase of the f_intrin (top panel of Fig. 2c). The value of 300 nm is close to the analytically calculated spin cycloid period $L_0 = 2\pi ({2A_{{\mathrm{ex}}}/D})$ (where A_ex is the Heisenberg exchange coefficient), about 318 nm for D = 0.75 mJ/m². Associated with the reduced stability of one isolated Néel skyrmion at large disk diameters, the formation of multiple isolated Néel skyrmions in the same disk becomes more favorable (see Supplemental Fig. S2). In fact, multiple isolated Néel skyrmions have been experimentally observed in a 2-µm-diameter Pt/Co/Ta disk at zero magnetic fields.¹³ Roughly speaking, one isolated Néel skyrmion in a disk can be stable if the disk diameter is not significantly larger than L₀.³⁸

Strain-mediated creation and deletion of one isolated skyrmion

Using a 220-nm-diameter CoFeB disk with D = 0.75 mJ/m² as an example, we show that switching of an initial QSD to a skyrmion (creation) requires the application of a minimum biaxial in-plane isotropic tensile strain ε_app of about 0.4% (see inset of Fig. 3a). The initial QSD state was obtained after the application and subsequent removal of a large perpendicular magnetic field. The temporal evolution of Δf_intrin (the bottom of Fig. 3a) shows that the skyrmion creation occurs through a dynamically oscillating process, going through multiple transitional states. Here the transitional states are defined as where the Δf_intrin peaks during the oscillation. The time when Δf_intrin reaches its highest peak (~34.5 kJ/m³) is denoted as t_ts. At t = t_ts, a vortex-like spin structure appears (Fig. 3b), corresponding to a Q value of about 0.4 (note that |Q| = 0.5 in an ideal in-plane vortex). Spin structures at the initial (t = 0 ns) and the equilibrium states (t_eq = 22.37 ns, see definition in Methods) are also shown in Fig. 3b, while a complete skyrmion creation process is shown in Supplemental Video S1. The thermodynamic condition for passing the highest transitional state (t = t_ts) is written as,

$${\mathrm{\Delta }}f_{{\mathrm{tot}}}\left( {t_{{\mathrm{ts}}}} \right) = {\mathrm{\Delta }}f_{{\mathrm{intrin}}}\left( {t_{{\mathrm{ts}}}} \right) + {\mathrm{\Delta }}f_{{\mathrm{elast}}}\left( {t_{{\mathrm{ts}}}} \right) < 0.$$

(1)

Fig. 3

Skyrmion creation. a, Temporal evolution of the m_z (volume average of the normalized perpendicular magnetization), Q (the topological charge number), and the change of the intrinsic magnetic free energy density ${\mathrm{\Delta }}f_{{\mathrm{intrin}}}\left( t \right) = f_{{\mathrm{intrin}}}(t) - f_{{\mathrm{intrin}}}(t = 0)$ when a biaxial in-plane isotropic (ε_app = ε_xx = ε_yy) tensile strain of 0.4% is applied (see inset) to the 220-nm-diameter CoFeB disk and then kept on. The gray dots, as well as the downward arrows mark the initial state (t = 0), highest transitional state (t = t_ts), and the equilibrium state (t = t_eq). b, Corresponding spin structures at these three time stages showing a strain-mediated skyrmion creation. The interfacial DMI strength D = 0.75 mJ/m²

When ε_app = 0.4%, Δf_elast(t_ts) is about −35.7 kJ/m³, yielding a negative Δf_tot(t_ts). Temporal evolution of the Δf_elast (the change of elastic energy density), as well as other energy densities contributing to the Δf_intrin are shown in Supplemental Fig. S3a, which shows that the skyrmion creation is driven by the minimization of elastic, stray field, and interfacial DMI energy at the expense of increasing the exchange and anisotropy energy. As shown in Fig. 3b, an upward-core Néel skyrmion (Q ≈ 1) appears at equilibrium. However, a degenerate downward-core skyrmion (Q ≈ −1) can appear under different ε_app and D (see Fig. S3b-c and analyses therein).

Our simulations also show that, starting from the same QSD state, the equilibrium spin structure would be a vortex-like spin structure (|Q| reduces toward 0.5) instead of the desirable Néel skyrmion when ε_app is relatively large (see Supplemental Fig. S4). In this case, more spins would lie within the horizontal plane to minimize the elastic energy and meanwhile form a vortex to minimize the stray field energy, at the expense of increasing the interfacial DMI energy.

We further found that a minimum biaxial in-plane isotropic compressive ε_app of about −0.24% (see inset of Fig. 4a) is required to switch a skyrmion to a QSD state (deletion) in a 220-nm-diameter CoFeB disk with D = 0.75 mJ/m². The initial skyrmion structure (t = 0, shown in Fig. 4b) was obtained by evolving the skyrmion at t = t_eq (Fig. 3b) to equilibrium under zero strain. Compared to the multiple transitional states in the case of skyrmion creation, only two appreciable transitional states need to be passed (see the evolution of Δf_intrin in Fig. 4a). The Δf_intrin at the highest transitional state (where t = t_ts = 1.22 ns) is about 5.25 kJ/m³, while the Δf_elast(t_ts) is about −7.63 kJ/m³. Based on Eq. (1), Δf_tot(t_ts) is negative, ensuring the pass of highest transitional state. Analyses on the individual evolution profiles of contributing energy terms (similarly to Fig. S3a) show that the strain-mediated skyrmion deletion is driven by the minimization of elastic, exchange, and anisotropy energy, at the expense of increasing the interfacial DMI and stray field energy. Spin structures at the highest transitional state (t = t_ts) and upon the completion of switching (t = t_sw = 1.63 ns) are also shown in Fig. 4b. Here the t_sw is defined as the time when the skyrmion diameter reduces to zero. A complete skyrmion deletion process is shown in Supplemental Video S2. Figure 4b along with the video demonstrates that the skyrmion deletion occurs through a homogeneous shrinkage, during which the Néel wall is temporarily transformed into a vortex wall to minimize the stray field energy. Such a vortex wall can be seen in the spin structure at t = t_ts, and more clearly in the video.

Fig. 4

Skyrmion deletion. a, Temporal evolution of the m_z, Q, and ${\mathrm{\Delta }}f_{{\mathrm{intrin}}}$ when a biaxial in-plane isotropic compressive strain of −0.24% is applied (see inset) to the 220-nm-diameter CoFeB disk and then kept on. The gray dots, as well as the downward arrows mark the initial state (t = 0), highest transitional state (t = t_ts), and the completion of switching (t = t_sw, at which the skyrmion diameter reduces to zero). b, Corresponding spin structures at these three time stages showing a strain-mediated skyrmion deletion. The interfacial DMI strength D = 0.75 mJ/m²

Based on the mechanisms discussed above, we have further simulated a non-volatile and reversible switching between a skyrmion and a QSD (i.e., repeated skyrmion creation and deletion) using pulses of bipolar in-plane isotropic strains (Supplemental Fig. S5). The minimum duration of the tensile strain pulse for creating the skyrmion is found to be the time when Q increases to about 1 for the first time (~3 ns, see Fig. 3a). The minimum duration of the compressive strain pulse equals t_sw.

Discussion

The top panel of Fig. 5a shows the critical strain for skyrmion creation as a function of D under the same disk diameter of 220 nm. There are two main messages. First, there exists a range of D (0.75 ~ 1.75 mJ/m²) only within which a skyrmion can be created from an initial QSD. When D is relatively small (0.4 ~ 0.5 mJ/m²) where the skyrmion state has an appreciably higher energy level than the other states (Fig. 2b), the equilibrium spin structure resembles an in-plane magnetic vortex (see Supplemental Fig. S6). This is because the switching is dominated by the minimization of elastic energy, similarly to the cases when ε_app is relatively large (Fig. S4). When D is relatively large (2–2.25 mJ/m²) where the Néel stripe has a lower energy level than the skyrmion (Fig. 2b), the equilibrium spin structures would then be a Néel stripe (also see Fig. S6). This is because at large D, the minimization of interfacial DMI free energy plays a more important role in the overall process of energy minimization, such that more Néel walls would form at equilibrium. When D ≥ 2.5 mJ/m², the initial QSD becomes unstable (Fig. 2b).

Fig. 5

On critical strains. Influence of a, the interfacial DMI strength D, b, the disk diameter on the critical (minimum) strains for skyrmion creation and deletion. A constant disk diameter of 220 nm is used for cases in a, a constant D of 0.75 mJ/m² is used for cases in b

Second, the magnitude of critical strain generally decreases with increasing D, resulting from the reduced energy level of transitional states (Supplemental Fig. S7a). The latter is consistent with the reducing stability of the initial QSD at large D (Fig. 2b). However, a plateau appears at intermediate D values (1.0–1.5 mJ/m²). This is because the number of transitional states increases with D increasing from 1 to 1.5 mJ/m² (also see Fig. S7a), which offsets the reduction of critical strains.

The bottom panel of Fig. 5a shows the critical strain for skyrmion deletion as a function of D under a constant diameter of 220 nm. Different from the creation process, the magnitude of critical strain increases without a plateau as D increases. This is due to the correspondingly higher energy level and the emergence of more transitional states (see Fig. S7b), both of which would increase critical strains. The higher energy level is an indicator of the enhanced stability of the skyrmion (Fig. 2b).

Having demonstrated that the D-dependence of critical strains is related to the D-dependent thermodynamic stabilities of the skyrmion and QSD, we further simulate the critical strains as a function of the diameter of the CoFeB nanodisk (d_disk) under a constant D of 0.75 mJ/m² (Fig. 5b). For the case of skyrmion creation, there are likewise two main messages. First, there exists a window of disk diameter (140–480 nm) only within which the skyrmion can be created from a QSD. When d_disk is relatively small (80–140 nm), the skyrmion comes highly metastable (Fig. 2c) primarily due to the high stray field energy, and cannot be created by applying tensile ε_app. Instead, an in-plane vortex-like spin structure appears at equilibrium (see Supplemental Fig. S8), which exhibits lower stray field energy than a skyrmion. When d_disk is large (e.g., 720 nm), a circular stripe domain appears at equilibrium (see also Fig. S8). Second, the magnitude of critical strain generally decreases due to the reduced stability of the initial QSD at large d_disk. A plateau appears at intermediate disk diameters (240–300 nm), which likewise results from the competition between the lower energy level and the emergence of more transitional states during the kinetic process (see Supplemental Fig. S9a). The same principle can be applied to understand the increasing critical strain for skyrmion deletion without a plateau (see the bottom panel of Fig. 5b). In this case, the energy level becomes higher and more transitional states appears at large d_disk (see Fig. S9b), both would increase the critical strain. Overall, it can be concluded that the critical strains for creating and deleting an isolated Néel skyrmion (Fig. 5) are primarily determined by the thermodynamic stabilities of the skyrmion and the QSD (Fig. 2).

The energy consumption E_cons of a strain-mediated voltage-controlled skyrmion switching is estimated as the minimum energy required to charge the piezoelectric capacitor,³⁹ i.e., E_cons = 0.5PAU. Here P denotes the electric polarization of the piezoelectric under a driving voltage U; A is the area of the top electrode of the piezoelectric. Consider an epitaxial Pb(Zr_0.2Ti_0.8)O₃ (PZT) nanoisland as the piezoelectric. Our previous phase-field simulations⁴⁰ have shown that a biaxial in-plane strain of larger than 1% can be achieved in a cuboid-shaped PZT nanoisland of 400 nm (length) × 400 nm (width) × 100 nm (thickness) through voltage-induced 90° ferroelectric domain switching. Notably, the bipolar biaxial in-plane strain required for skyrmion creation and deletion can be accessed by engineering the size/shape of the PZT nanoisland and its misfit strain with the substrate, under a driving voltage of ~1 V.⁴¹ Taking P = 0.75 C/m² for the PZT nanoisland⁴² and U = 1 V, E_cons ≈ 6 fJ for A ≈ 0.015 μm² (i.e., the surface area of a 140-nm-diameter CoFeB disk, which is used as a top electrode of the PZT nanoisland). E_cons can be reduced to ~0.5 fJ if using a separate 40-nm-diameter electrode dot⁴³ (A ≈ 0.0013 μm²). Notably, the estimated 0.5 fJ is about 5 orders of magnitude smaller than that in a spin-transfer-torque-mediated current-controlled skyrmion switching (see Supplemental Fig. S10-11 and Note S2).

In summary, we have computationally demonstrated a repeatable switching (creation and deletion) of an isolated Néel skyrmion purely driven by voltage-induced strains transmitted from a juxtaposed piezoelectric. An ultralow-energy consumption of ~0.5 fJ per switching is envisaged. Unlike existing reports of voltage^21,22 or stress^25,30 controlled skyrmion switching in magnetic bulk crystals or thin films, the present scheme demonstrated in a 3D geometrically confined nanomagnet obviates the need of using a magnetic field. Although a magnetic ultrathin nanodisk with interfacial DMI is used for demonstration, the computational model established through this work can be adapted to model strain-mediated skyrmion switching in magnetic bulk crystals/thin-films/nanostructures that exhibit bulk-type DMI. Our findings are expected to stimulate experimental efforts into strain-mediated voltage control of skyrmions and other chiral spin structures for ultralow-energy spintronic devices.

Methods

In our phase-field model, the spin structure is described by the spatial distributions of local M = M_s(m_x, m_y, m_z), where m_i(i = x, y, z) the normalized local magnetization along a Cartesian axis. The total magnetic free energy F_tot(m) of a magnetic ultrathin nanostructure with DMI can be expressed as,

$$F_{{\mathrm{tot}}} = {\int} {(f_{{\mathrm{anis}}} + f_{{\mathrm{exch}}} + f_{{\mathrm{DMI}}} + f_{{\mathrm{stray}}} + f_{{\mathrm{elast}}})} dV,$$

(2)

where the terms in the integrand denote the volumetric densities (J/m³) of perpendicular magnetic anisotropy (arising from the interface), Heisenberg-type symmetric exchange energy, Dyzaloshinskii-Moriya (DM)-type antisymmetric exchange energy, stray field energy, and elastic energy, respectively. The average intrinsic energy density f_intrin is defined as the sum of the volume average of the f_anis, f_exch,f_DMI, and f_stray.

The expression of f_anis has the typical form of uniaxial magnetic anisotropy along the z axis,

$$f_{{\mathrm{anis}}} = K_1\left( {1 - m_{\mathrm{z}}^2} \right) + K_2\left( {1 - m_{\mathrm{z}}^2} \right)^2,$$

(3)

where K₁ and K₂ are coefficients of perpendicular magnetic anisotropy, and m_z is the normalized magnetization along the z axis. Here the perpendicular magnetic anisotropy mainly arise from the magnetic interface anisotropy⁴⁴ $f_{{\mathrm{inter}}} = - \left( {K_{{\mathrm{inter}}}/d} \right)m_z^2$, where K_inter ≈ K₁d ≈ 1.08 mJ/m². The Heisenberg-type symmetric exchange energy density is given by f_exch = A_ex(∇m).²

In an ultrathin magnet where the DMI arises from the interface with its adjacent heavy metals, the interfacial DMI free energy f_DMI is given as,⁴⁵

$$f_{{\mathrm{DMI}}} = D\left( {m_z\frac{{\partial m_x}}{{\partial x}} - m_x\frac{{\partial m_z}}{{\partial x}} + m_z\frac{{\partial m_y}}{{\partial y}} - m_y\frac{{\partial m_z}}{{\partial y}}} \right).$$

(4)

When D > 0, minimizing $f_{{\mathrm{DMI}}}^{\mathrm{i}}$ yields a positive $\frac{{\partial m_z}}{{\partial x}}$ or $\frac{{\partial m_z}}{{\partial y}}$ in the propagating direction of the cycloidal spin spiral (see Fig. 1c). Note that D is proportional to $\frac{{\left| {{\mathbf{D}}_{12}} \right|}}{{ad}}$,⁶ where D₁₂ describes the atomistic DMI (denoted as H_DM) between two neighboring atomic spins S₁ and S₂ through H_DM = −D₁₂(S₁ × S₂), a is the lattice parameter of the ultrathin magnet. For an amorphous or polycrystalline magnetic disk with ∞m symmetry, D₁₂ is always parallel to the magnet/heavy-metal interface (see Fig. 1a). Note that D₁₂ may change once the applied strain modifies the lattice parameter a. Due to a lack of available data of strain-modulated D in magnetic ultrathin nanostructures, we discussed the influence of D on the thermodynamic stability of a skyrmion (Fig. 2) and the critical strains for skyrmion creation/deletion (Fig. 5a).

In a confined magnetic system with interfacical DMI, using variational calculation,⁴⁶ the variations of the exchange energy and interfacial DMI energy are written as

$${\mathrm{\delta }}\left( {{\int} {f_{{\mathrm{exch}}}} dV} \right) = 2A_{{\mathrm{ex}}}\mathop {\int}\limits_{\partial V} {\frac{{\partial {\mathbf{m}}}}{{\partial {\mathbf{n}}}}} \cdot {\mathrm{\delta }}{\mathbf{m}}dS - 2A_{{\mathrm{ex}}}{\int} {\left( {\nabla ^2{\mathbf{m}}} \right)} \cdot {\mathrm{\delta }}{\mathbf{m}}dV$$

(5)

$${\mathrm{\delta }}(\smallint f_{{\mathrm{DMI}}}dV) = - D{\int}_{\partial V} {(({\mathbf{n}} \times z) \times {\mathbf{m}})} \cdot {\mathrm{\delta }}{\mathbf{m}}dS + 2D\smallint ((\nabla \cdot {\mathbf{m}})z - \nabla m_z) \cdot {\mathrm{\delta }}{\mathbf{m}}dV$$

(6)

where ∂V denotes the surface of the magnet, n is the outward-pointing unit normal of the surface, and dS is the surface element. The variations of the free energies contain the surface terms and the volume terms (the second integrals on the right). Minimizing the combined surface terms of the variations of exchange energy and the interfacial DMI energy (i.e., the first integrals on the right of Eqs. 5–6), i.e., ${\mathrm{\delta }}F_{{\mathrm{Surface}}} = 2A_{{\mathrm{ex}}}\mathop {\int}\limits_{\partial V} {\left( {\frac{{\partial {\mathbf{m}}}}{{\partial {\mathbf{n}}}} - \frac{D}{{2A_{{\mathrm{ex}}}}}\left( {{\mathbf{n}} \times z} \right) \times {\mathbf{m}}} \right)} \cdot {\mathrm{\delta }}{\mathbf{m}}dS = 0$, yields the boundary condition,

$$\frac{{d{\mathbf{m}}}}{{d{\mathbf{n}}}} = \frac{D}{{2A_{{\mathrm{ex}}}}}\left( {{\mathbf{n}} \times z} \right) \times {\mathbf{m}}.$$

(7)

The stray field energy density $f_{{\mathrm{stray}}} = - 0.5\mu _0M_s{\mathbf{H}}_{\mathrm{d}} \cdot {\mathbf{m}}$, where the stray field H_d is obtained by solving the magnetostatic equilibrium equation $\nabla \cdot \mu _0\left( {{\mathbf{H}}_{\mathrm{d}} + M_s{\mathbf{m}}} \right) = 0$ under a finite-size boundary condition based on the convolution theorem evaluated using the Fast Fourier Transform.⁴⁷

The elastic energy density $f_{{\mathrm{elast}}} = 0.5\left( {{\mathbf{\varepsilon }}^{{\mathrm{tot}}} - {\mathbf{\varepsilon }}^0} \right) \cdot {\mathbf{c}} \cdot \left( {{\mathbf{\varepsilon }}^{{\mathrm{tot}}} - {\mathbf{\varepsilon }}^0} \right)$, where c denotes the elastic stiffness tensor. The stress-free strain $\varepsilon _{ii}^0 = \frac{3}{2}\lambda _{100}\left( {m_i^2 - \frac{1}{3}} \right)$ and $\varepsilon _{ik}^0 = \frac{3}{2}\lambda _{111}m_im_k$ for i, k = x, y, z. The total strain ${\mathbf{\varepsilon }}^{{\mathrm{tot}}} = {\bar{\mathbf \varepsilon }} + {\mathbf{\varepsilon }}^{{\mathrm{het}}}$. The first term $\overline {\mathbf{\varepsilon }}$ is the average strain over the three-phase simulation system (including the nanodisk, piezoelectric, and vacuum, see Supplemental Fig. S12), which equals the homogeneous strain on the bottom plane of the piezoelectric layer. The second term ε^het describes the local variations of strains that are related to both the size/geometry of the magnetic nanostructure and the spatially varying magnetizations, and is obtained by solving the elastic equilibrium equation $\nabla \cdot \left( {{\mathbf{c}}\left( {{\mathbf{\varepsilon }}^{{\mathrm{tot}}} - {\mathbf{\varepsilon }}^0} \right)} \right) = 0$ using the Fourier-spectral iteration method.⁴⁸ Since ε⁰ depends on the local magnetization m, a two-way coupling between the m and the ε^het is established. Similar approach has been adopted by other phase-field models⁴⁹ or finite-element models⁵⁰ in order to achieve such full coupling between local magnetization dynamics and elasticity. A fixed displacement boundary condition (corresponding to the applied biaxial in-plane strain ε_app) is applied on the bottom plane of the piezoelectric in the simulation system (see Fig. S12), while a stress-free boundary condition at the top surface of the magnetic disk; see details in ref. ⁵¹ The stress-free boundary conditions at the lateral surfaces of the island are automatically considered by setting the elastic stiffness tensor of the surrounding vacuum as zero.

It is worth pointing out that the equilibrium average strain in the nanodisk is slightly smaller than the applied strain ε_app due to strain relaxation near the lateral surfaces of the nanodisk. For example, under a biaxial in-plane isotropic ε_app of 0.4%, the average strain in a 220-nm-diameter nanodisk is 0.381%. The equilibrium strain distribution simulated using our in-house elastic solver described above is well consistent with that obtained from finite-element analysis in COMSOL Multiphysics^® (see Supplemental Fig. S13).

The variational derivative of the F_tot with respect to the local magnetization yields the expression of effective magnetic field, i.e., ${\mathbf{H}}_{{\mathrm{eff}}} = - \frac{1}{{\mu _0M_{\mathrm{s}}}}\frac{{{\mathrm{\delta }}F_{{\mathrm{tot}}}}}{{{\mathrm{\delta }}{\mathbf{m}}}}$, which is the driving force for the evolution of local magnetization m in the framework of Landau-Lifshitz-Gilbert (LLG) type dynamics. The classical LLG equation reads as,

$$\frac{{\partial {\mathbf{m}}}}{{\partial t}} = - \frac{{\gamma _0}}{{1 + \alpha ^2}}\left[ {\left( {{\mathbf{m}} \times {\mathbf{H}}_{{\mathrm{eff}}}} \right) + \alpha {\mathbf{m}} \times \left( {{\mathbf{m}} \times {\mathbf{H}}_{{\mathrm{eff}}}} \right)} \right],$$

(8)

where γ₀ is the gyromagnetic ratio and α the Gilbert damping coefficient. Eq. (8) was solved using the classical Runge–Kutta method with a dimensionless discretized time step ${\mathrm{\Delta }}t^ \ast = \frac{{\gamma _0M_{\mathrm{s}}}}{{1 + \alpha ^2}}{\mathrm{\Delta }}t = 0.01$. Our testing shows that the use of a smaller reduced time step of 0.005 yields almost the same result. The equilibrium state (e.g., t = t_eq, see Fig. 3) is considered to be reached when $\left| {{\mathrm{\Delta }}\langle m_z\rangle /{\mathrm{\Delta }}t^ \ast } \right| < 10^{ - 4}$, where ${\mathrm{\Delta }}\langle m_z\rangle$ denotes the change in the volume average of normalized perpendicular magnetization m_z per time step Δt^*. The simulations were performed in three-dimensional discretized cells of $n_x{\mathrm{\Delta }}x \times n_y{\mathrm{\Delta }}y \times n_z{\mathrm{\Delta }}z$, where n_i and Δi (i = x, y, z) indicate the number of cells and corresponding cell size along a Cartesian axis. Specifically, we use a constant n_z = 17 where the bottom 11 layers of grids describe the elastically stiff piezoelectric layer (meaning that the piezoelectric has a large Young’s modulus), the middle 2 layers describes the magnetic ultrathin nanostructure including its lateral surrounding vacuum space, and the top 4 layers describes the space on top of the magnet. Δz is set as 0.55 nm to describe a 1.1-nm-thick magnetic disk. Various disk diameters were described by varying n_x and n_y under a constant in-plane cell size ${\mathrm{\Delta }}x = {\mathrm{\Delta }}y = 1\,{\mathrm{nm}}$. In most cases, using a smaller in-plane cell of 0.5 nm yields almost the same results. However, when either the interfacial DMI strength D or the disk diameter is relatively small (e.g, see blue circles in Fig. 2b,c where the skyrmion has a notably higher energy than the other spin structures), only the use of smaller in-plane cells (e.g., 0.5 nm) allows us to access these highly metastable skyrmions. A similar case has been reported in previous micromagnetic simulations.⁶

The materials parameters for ultrathin Co₂₀Fe₆₀B₂₀ used in simulations are listed as follows: K₁ = 0.978 mJ/m³, K₂ = 11.08 kJ/m³, M_s = 1.25 MA/m, α = 0.04, λ₁₀₀ = λ₁₁₁ = λ_s = 3.7 × 10⁻⁵ (ref. ⁵²); γ₀ = 2.2 × 10⁵ m A⁻¹·s⁻¹ (ref. ⁵³); A_ex = 1.9 × 10⁻¹¹ J/m for Co₂₀Fe₆₀B₂₀ (CoFeB) nanoislands with a thickness range of 0.9–1.3 nm (ref. ⁵⁴); c₁₁ = 218.1 GPa, c₁₂ = 93.46 GPa, which were calculated based on a Young’s modulus of 162 GPa (ref. ⁵⁵) and a Poisson’s ratio of 0.3 (ref. ⁵⁶); In the present simulations, the elastic stiffness tensor of the piezoelectric is set as the same as that of the magnetic island, i.e.,c_p = c_island for simplicity. Nevertheless, our tests show that the equilibrium strain state in the magnetic nanodisk would not have an appreciable difference if the piezoelectric layer has a relatively high Young’s modulus (see Supplemental Table S1 and a brief discussion therein).