Abstract
Many functional materials can be characterized by a specific pattern in their electronic band structure, for example, Dirac materials, characterized by a linear crossing of bands; topological insulators, characterized by a “Mexican hat” pattern or an effectively free electron gas, characterized by a parabolic dispersion. To find material realizations of these features, manual inspection of electronic band structures represents a relatively easy task for a small number of materials. However, the growing amount of data contained within modern electronic band structure databases makes this approach impracticable. To address this problem, we present an automatic graphical pattern search tool implemented for the electronic band structures contained within the Organic Materials Database. The tool is capable of finding user-specified graphical patterns in the collection of thousands of band structures from high-throughput calculations in the online regime. Using this tool, it only takes a few seconds to find an arbitrary graphical pattern within the ten electronic bands near the Fermi level for 26,739 organic crystals. The source code of the developed tool is freely available and can be adapted to any other electronic band structure database.
Similar content being viewed by others
Introduction
Recent developments in materials informatics1,2 combined with ever-growing computational power have opened the way towards performing high-throughput calculations based on first-principles (ab initio) methods.3 This approach significantly facilitates the accelerated discovery of various materials with special functional properties.4,5,6,7,8,9 As a result, we witness an exponentially increasing amount of data usually organized in the form of databases like the Materials Project,10 the Computational 2D Materials Database11 or the Organic Materials Database (OMDB),12 to name but a few. To keep pace with the amount of data generated, there has to be a commensurate development of data mining and information retrieval tools capable of answering non-trivial questions about the data. Here, we present the online graphical pattern search tool which is capable of finding user-specified graphical patterns in a collection of thousands of electronic band structures (EBS).
Recently, we witness an ongoing interest in extending the theory of electronic bands. This effort is mainly motivated by two ideas: the search for semimetals with low-energy excitations behaving as exotic quasi-particles13 and the recent developments in the topological band theory.8,9,14,15,16,17 Realizations of non-trivial EBS features comprise the massless Dirac-fermions which were experimentally verified in graphene18 as well as the Weyl-fermions, which were found for instance in TaAs crystals.19 With the introduction of the so-called Weyl type-II semimetals20—Weyl semimetals with heavily tilted energy-momentum cones—it is claimed that elementary excitations of the crystal can even mimic the physics of electrons close to the event horizon of black holes.21 This interpretation suddenly opens the path to verify theoretical statements of black hole physics within relatively easily approachable measurements on single crystals. More exotic quasiparticles, which were discussed in a similar manner, are, for example, the double Dirac semimetal,22 the node-line semimetals,23 the hourglass fermions24 or the triple-fermion materials.25
To find material realizations of these topological band features, manual inspection of EBSs represents a relatively easy task for a small number of materials. However, this approach becomes impracticable for thousands of band structures contained in modern EBS databases. Despite providing basic search functionality, most of the online databases lack non-trivial online search tools for EBS data querying and analysis. Our tool’s software implementation based on the approximate nearest neighbor search algorithm is designed to match the constraints of web applications in terms of fast execution time and low memory usage. The tool is accessible within the web interface of the OMDB hosting thousands of EBSs for previously synthesized organic crystals at https://omdb.diracmaterials.org/search/pattern. The source code of the developed tool is freely available at https://github.com/OrganicMaterialsDatabase/EBS-search and can be adapted to any other EBS database.
The rest of the paper is organized as follows. In Results, we describe the pattern search tool interface and its implementation. In Discussion, application examples for the discovery of novel functional materials are shown. Finally, technical details related to the OMBD data and pattern-matching algorithms are provided in Methods.
Results
Pattern search algorithm
For a three-dimensional crystalline solid, the EBS is a four-dimensional object representing energy levels of electrons dependent on a three-dimensional momentum vector. With the aim to capture its most distinctive features in such cases, the EBS is usually calculated along specific paths within the Brillouin zone, for example, depending on the crystalline symmetry.26 Hence, properties of the EBS can be effectively characterized by one-dimensional patterns involving one or multiple bands.
To locate query patterns in the EBS data from the ab initio calculations stored in the OMDB, we employ a moving window approach. Each continuous path in the Brillouin zone is scanned with a moving window of width w in the momentum space with the stride s, specifying the number of data points the window jumps at each scanning step. Since the EBS is calculated numerically along a discrete mesh with different spacing for different paths within the Brillouin zone, linear interpolation is used to approximate energy values between the mesh points. For each moving window, we uniformly select d energy values from each band and form a vector to be compared with a query pattern, being also represented as a vector in the same way (Fig. 1a). Thus, in the case of a query pattern consisting of n bands, the resulting vector dimensionality is d × n (Fig. 1c). It is important to note that the present pattern search algorithm does not take into account the distance between bands (for instance, the distance between the maximum value of the lower band and the minimum value of the upper band in the n = 2 case), which needs to be specified explicitly by the user.
A short summary of the pattern search algorithm. For each moving window of size w, d points are selected from each band for the analysis. Although the dimension of an electronic band along some high-symmetry path in the Brillouin zone is one, the dimension of the corresponding feature space, being represented in a vector form, is defined by the number of points in it. For instance, for a moving window comprising 2 bands with 3 points each a, the dimensionality of the corresponding feature space is 3 for each band b and 6 for the final concatenated vector c. In the last step, the distance between the normalized concatenated vector and query pattern vector is calculated
To measure the similarity between a vector obtained from the moving window and the query vector, the cosine distance \(\sqrt {2 - 2{\kern 1pt} {\mathrm{cos}}{\kern 1pt} \theta }\) is used, where θ is the angle between the normalized vectors. The normalization makes the cosine distance equivalent to the Euclidean (L2) distance. It also makes the distance insensitive to energy scaling. As θ ranges from 0 (two vectors are the same) to π (two vectors are opposite), the distance ranges from 0.0 to 2.0, respectively. Finally, K nearest vectors to the query vector are retrieved.
Unfortunately, finding the nearest vectors becomes computationally demanding with respect to memory and CPU usage, especially if it comes to online applications. A straightforward exhaustive search algorithm, which goes through every vector, requires the number of comparisons equal to the total number of vectors to be queried. For example, applying the moving window approach with the realistic parameters w = 0.4, d = 16 and s = 2 for 10 bands near the Fermi surface for 26,739 materials in the OMDB produces over 1.6 × 107 vectors to query. As performance is crucial for online implementation, the exhaustive solution becomes impractical.
The exhaustive search can be accelerated with a computation-memory trade-off using a precalculated index structure based on search space partitioning. We implemented fast data access using the open-source ANNOY library,27 which uses the approximate nearest neighbor search algorithm. During the indexing step, it creates multiple binary tree structures, where each intermediate node represents a split and each leaf node represents an area in the search space (Fig. 2). This precalculated index helps to significantly reduce the search time. More details about the approximate nearest neighbor algorithm can be found in Methods.
An example of the ANNOY algorithm for 100 points in a 2D space. a First, the space is split into two subspaces. The split occurs as the equidistant hyperplane between two randomly selected points indicated by the dashed line. For each subspace, this step is repeated recursively, until the number of points is below a certain threshold. b Using the constructed binary tree, the nearest neighbors can be found in logarithmic time. The algorithm generalizes to higher dimensional spaces. For instance, for a pattern consisting of 2 bands with 3 points each, the dimensionality of the corresponding search space is 6
Since the bands near the Fermi level are usually of physical interest, we have indexed the 9 closest pairs of bands (5 bands above and 5 below the Fermi level). Thus, at the current stage, only these bands are available for the online search. We started with the implementation for the patterns consisting of two bands. However, the approach can be extended in a similar manner to patterns involving an arbitrary number of bands.
The tool’s interface
The developed pattern search tool is available online at https://omdb.diracmaterials.org/search/pattern. The tool’s web interface is shown in Fig. 3. A user can either select one of the predefined query patterns (two crossing straight lines or two parabolas) or use the free drawing input interface to search for an arbitrary pattern. Also, a user can specify the band indices with respect to the Fermi level where the search is performed, the moving window size in the momentum space, the maximum/minimum distance between the bands, if zero density of states between the bands is required, and other basic filtering options, such as space group number or chemical composition of the materials of interest.
The web interface of the pattern search tool. A user can either select a predefined pattern or use the free drawing input interface to search for an arbitrary pattern (a sketch of “Mexican hat” is shown). Also, a user can specify bands of interest, moving window size, distance and density of states between the bands in the pattern, along with other basic filtering options like space group number or chemical composition of the materials of interest
Performance tests and calibration
To test and calibrate our tool, we use the EBS data contained in the OMDB. We also provide additional synthetic data tests together with the source code at https://github.com/OrganicMaterialsDatabase/EBS-search.
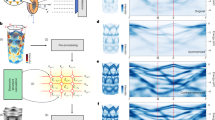
The first parameters to be defined are the moving window size w and the stride s. With this aim, we test the sensitivity of the cosine distance to the various distortions of the search pattern. The results are shown in Fig. 4. As can be verified, the distance between the query pattern and the example increases introducing shifts, obliques, skews, or other nonlinear distortions. While s should be small with respect to w not to miss any possible search results (we use s = 2 DFT mesh points), the moving window size w is more task-specific. It should correspond to the expected characteristic momentum scale of the pattern of interest. For example, Fig. 5a suggests that the top search results for a linear crossing pattern show a much better agreement for a window size of w = 0.4 than for w = 0.8. At the same time, a similar test for two gapped parabolas gives qualitatively acceptable results for both moving window sizes (Fig. 5b). As w is pattern-dependent, its value should be specified by the user. Furthermore, it is worth noting that for smaller values of w, we are restricted by the mesh resolution in the momentum space stemming from the ab initio calculations. For example, for the EBSs contained in the OMDB, the moving window for w = 0.4 contains only 14.4 mesh points per band on average (minimum 9 and maximum 33).
Sensitivity of the cosine (L2) distance (solid blue line) and the scaled Manhattan (L1) distance (dashed gray line) to various distortions of the Dirac crossing pattern: a shift, b oblique, c skew and d nonlinear distortion/change of the characteristic scale. The distorted patterns are shown for the red dots. High-frequency noise and outliers are not included because band structures are usually smooth objects with low variance over a characteristic scale
Comparison of the top 6 search results for linear crossings a and two gapped parabolas (the gap is not shown) b for two different moving window sizes: 0.4 (first row) and 0.8 (second row). The top search results for the linear crossings have much better quality for w = 0.4 than for w = 0.8, while the search for two gapped parabolas gives qualitatively acceptable results for both moving window sizes. The titles above the graphs indicate the OMDB-ID. The values for E and k match the values on the website
It is also important to check a maximum value of the distance for a search result to be of acceptable quality. Since similarity to a pattern is an essentially subjective quality specific to the task in hand, we resort to visual inspection of the search results. Figure 6 shows that this value can vary from 0.8 for a linear crossing (Fig. 6a) to 0.5 for two gapped parabolas (Fig. 6b). On the website, we show the top search results ranked by their distance to the query pattern and use this threshold value in a warning message only.
Pattern search results for a linear crossing in the two highest valence bands a and two parabolas in the highest valence and lowest conduction bands b. Each row shows the nearest vectors (best search results) starting from a distance threshold, for threshold values 0.0, 0.5, 0.8, 0.9, 1.0 and 1.5, respectively, for the moving window size of 0.4. The distance between upper and lower bands was set to be less than 0.0001 eV for a and was not restricted for b. The titles above the graphs indicate the OMDB-ID. The values for E and k match the values on the website
As mentioned before, the exact nearest neighbor search algorithm is not applicable in the context of a web application due to the high computational demand. To tackle this issue, we choose the approximate nearest neighbor algorithm implemented in the ANNOY library, which has two parameters to tune: the number of search trees, N, and the number of points to examine, K. Increasing both parameters gives more precise search results at the expense of computational resources. Namely, N affects the memory usage and K affects the search time.
To tune these parameters, we compare the performance of the top 100 search results of the approximate nearest neighbor search algorithm for different values of N and K to those of the exact algorithm. As a ground truth, we use the top 100 exhaustive search results with w = 0.4 for the linear crossing pattern in the two bands below the Fermi level. As can be seen in Fig. 7, the performance of the approximate nearest neighbor search is close to the exact solution but the search time is significantly reduced. For example, using the values N = 20 and K = 1500, the approximate search is more than two orders of magnitude faster in comparison to the exact algorithm by obtaining comparable search results. The level of approximation can be always adjusted to the computational resources available.
The quality of the top 100 search results obtained using the ANNOY library grows with the number of trees N for fixed K = 1500 a and the number of leaf nodes K for fixed N = 20 b. As a ground truth, we used the top 100 search results from the exact algorithm for the linear crossing pattern with a moving window size of w = 0.4 in the two highest valence bands. The precision is calculated as the fraction of coinciding search results and micro-averaged over 10 different ANNOY indices
Discussion
It has been shown by several research groups that the data mining approach has been successful, for example, for the search of stable nitride perovskites,28 thermoelectric materials,4 electrocatalytic materials for hydrogen evolution,5 or lithium-ion battery cathodes.6 Using a pattern search analysis of the data within the Electronic Structure Project,29 Klintenberg et al. identified 17 candidates for strong topological insulators by mining for materials exhibiting the specific “Mexican hat” shaped dispersion relation.7 Similarly, by searching for linear crossings in band structures, novel Dirac materials can be identified as recently shown using the data in the OMDB8,9 and the Materials Project database.30 Alternatively, new functional materials can be predicted by comparison of specific features in the EBSs of known prototype materials to the EBSs in electronic structure databases, as shown for example in the case of potential high-temperature superconductors.31,32 Similar statistical methods can be also used to identify systematic trends in strongly correlated f-electron materials.33
Here, we present a new approach to search for novel functional materials characterized by a specific pattern in their electronic structure, such as Dirac materials, topological insulators, and novel semimetals with low-energy excitations behaving as exotic quasi-particles.
A data-mining approach by means of the described pattern-matching algorithm can be a powerful tool. As the first example, we consider the linear crossing of two bands indicating Dirac materials. This class of materials has been extensively studied due to the exceptional transport and optical properties.34,35 To achieve an isolated crossing in the energy space, the additional constraint of having vanishing density of states at the crossing point was applied. Since the majority of organic crystals are insulating,12 we searched for the pattern in the first and second highest valence bands. The maximum band distance was set to 0.01 eV and the moving window size was restricted to 0.4. Using this conditions, the algorithm found 51 matching results, where the best one has the match error of 0.075 and band distance of 0 eV. The corresponding band structure is plotted in Fig. 8a, which belongs to the material C9H5ClN2O2 (OMDB-ID 4381, COD-ID 7155013), crystallizing in a triclinic crystal. It is also worth mentioning that, using an offline version of the presented tool, several novel organic Dirac materials have been already predicted.8,9
Examples of search results for the patterns which might be interesting from a physical point of view: Dirac crossing, OMDB-ID 4381 a; two touching parabolas, OMDB-ID 4492 b; Mexican hat, OMDB-ID 2308 c. Plotted using Highcharts library55
Whereas a linear crossing of bands corresponds to a nearly free electron gas of massless Dirac fermions, two touching parabolas mimic the behavior of massive free electrons corresponding to the Schrödinger equation. However, the search for two touching parabolas did not retrieve any materials with vanishing density of states at the touching point. Having weakened this criterion, the search for two touching parabolas in the second and third valence bands retrieved 1443 materials with the matching error for the top result of 0.224. The corresponding band structure is illustrated in Fig. 8b, which belongs to C20H20BrN3O3 (OMDB-ID 4492, COD-ID 7153203), having a monoclinic crystal structure.
Next to semimetals, materials possessing a gap can also show specific patterns. The most relevant examples are the topological insulators,36 where an overlap of two bands combined with a forbidden crossing leads to the specific Mexican hat shape of bands. This phenomenon is also referred to as band inversion. While the bulk of a topological insulator is insulating, metallic states on the surface can be found as a consequence of the topological gap. Well-known examples comprise the materials PbxSn1−xTe37,38,39 or Bi2Se3.40 The theory of topological gaps is clearly not restricted to a band gap at the Fermi level but can be generalized to any occurring spectral gap in the band structure. By searching for the Mexican hat shape in the third and fourth bands below the Fermi level, we found 290 materials using a moving window size of 0.8. The band distance was allowed to be in the range of 0.05–9 eV and the density of states was forced to be zero between the bands. As an example, the material C11H17ClO2 (OMDB-ID 2308, COD-ID 4030217) was found with the match error of 0.59 (Fig. 8c).
Methods
Organic materials database (OMDB)
The Organic Materials Database (OMDB)12 is an online database available at https://omdb.diracmaterials.org containing the output of ab initio calculations based on density functional theory (DFT)41,42 for 26,739 (at the moment of writing) previously synthesized three-dimensional organic crystal structures taken from the Crystallography Open Database (COD).43 The DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP).44 The OMDB contains EBSs calculated along high symmetry \(\vec k\)-paths in the Brillouin zone which were automatically generated by the Pymatgen package.45 Electronic bands for each path were calculated on a discrete mesh consisting of 20 points independently of its length in the momentum space. For the pattern search, we use continuous paths suggested by Pymatgen. However, we plan to extend the search to cover all possible combinations of calculated paths sharing the same high-symmetry point. Although the calculations were performed spin-polarized, we do not distinguish between spin-up and spin-down bands for the pattern search task. More details about the DFT calculations can be found in ref. 12.
Problem overview
The problem of locating patterns similar to a target (query) pattern in a sequence of data points has a long interdisciplinary history. Related approaches are typically based on scanning the sequence with a moving window followed by the comparison of these shorter subsequences with the query.46 This approach has several dimensions to explore. The first one is related to the data representation. As an alternative to the raw data points, a fitted model or a transformation, such as Fourier,47 wavelet48 or dimensionality reduction,49 can be employed. Second, a similarity measure between the subsequences and the query need to be defined. Most of them are based on the Lp-norms, however, more advanced probability measures50 have also been discussed. Finally, for practical applications, an efficient search algorithm is necessary. Usually, it involves indexing the subsequences obtained by a moving window with a tree-like partition structure. The presented solution in this paper uses a cosine similarity (equivalent to the L2 distance for normalized vectors) and binary search trees as implemented in the open-source ANNOY library.27 No advanced data transformations are used.
Nearest neighbor search algorithm
The main idea of the nearest neighbor search51 is to find the nearest vectors to a query vector, given some distance measure. The most straightforward (exact) nearest neighbor algorithm iterates through each vector and calculates the distance to the query. This linear complexity algorithm can be accelerated with a computation-memory trade-off using a pre-calculated index structure based on search space partitioning. However, the related algorithms are not exact anymore, because they can miss some search results. Nevertheless, due to the high computational demand of the exact search, it becomes necessary to use an approach which returns “close enough” neighbors in order to obtain a good speed improvement. In many cases, approximate methods perform comparably to the exact one.52 Many open-source libraries are available where various indexing strategies and approximation methods have been implemented, for example, “FAISS” released by Facebook AI Research,53 “ANNOY” by Spotify,27 and Non-Metric Space Library (NMSLIB).54
The back-end of the graphical pattern search tool is implemented using the open-source ANNOY library27 which is based on the approximate nearest neighbor search. During the indexing step, it creates a binary tree structure for the data vectors where each intermediate node represents a split and each leaf node represents an area in the search space. It keeps splitting the space randomly using equidistant hyperplanes between two randomly selected vectors in each node until the number of vectors in each subspace is below a certain threshold. It can also use multiple trees N (n_trees in the ANNOY documentation) in order to improve the quality of search results at the expense of memory usage. When a user tries to find closest neighbors of a query vector, the library first finds the leaf node that the query vector would belong to and collects K vectors to test (search_k in the ANNOY documentation) from that node as well as nearby leaf nodes for each tree. Then, it eliminates the duplicates which come from different trees and calculates the distance between each selected vector and the query. Here, N and K can be tuned to find a trade-off between the algorithm’s precision and performance.
Data availability
The online graphical pattern search tool for electronic band structure data contained in the Organic Materials Database is available at https://omdb.diracmaterials.org/search/pattern. The source code of the developed tool is available at https://github.com/OrganicMaterialsDatabase/EBS-search. The electronic band structure data that support the findings of this study are available from the Organic Materials Database https://omdb.diracmaterials.org.
References
Rodgers, J. R. & Cebon, D. Materials informatics. Mrs. Bull. 31, 975–980 (2006).
Ferris, K. F., Peurrung, L. M. & Marder, J. M. Materials informatics: fast track to new materials. Adv. Mater. Process. 165, 50–51 (2007).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Wang, S., Wang, Z., Setyawan, W., Mingo, N. & Curtarolo, S. Assessing the thermoelectric properties of sintered compounds via high-throughput ab-initio calculations. Phys. Rev. X 1, 021012 (2011).
Greeley, J., Jaramillo, T. F., Bonde, J., Chorkendorff, I. & Norskov, J. K. Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat. Mater. 5, 909–913 (2006).
Hautier, G. et al. Phosphates as lithium-ion battery cathodes: an evaluation based on high-throughput ab initio calculations. Chem. Mater. 23, 3495–3508 (2011).
Klintenberg, M., Haraldsen, J. T. & Balatsky, A. V. Computational search for strong topological insulators: an exercise in data mining and electronic structure. Appl. Phys. Res. 6, 31 (2014).
Geilhufe, R. M., Borysov, S. S., Bouhon, A. & Balatsky, A. V. Data mining for three-dimensional organic Dirac materials: focus on space group 19. Sci. Rep. 7, 7298 (2017).
Geilhufe, R. M., Bouhon, A., Borysov, S. S. & Balatsky, A. V. Three-dimensional organic Dirac-line materials due to nonsymmorphic symmetry: a data mining approach. Phys. Rev. B 95, 041103 (2017).
Rasmussen, F. A. & Thygesen, K. S. Computational 2D materials database: electronic structure of transition-metal dichalcogenides and oxides. J. Phys. Chem. C. 119, 13169–13183 (2015).
Jain, A. et al. The materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Borysov, S. S., Geilhufe, R. M. & Balatsky, A. V. Organic materials database: an open-access online database for data mining. PLoS ONE 12, e0171501 (2017).
Bradlyn, B. et al. Beyond Dirac and Weyl fermions: unconventional quasiparticles in conventional crystals. Science 353, aaf5037 (2016).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
Wieder, B. J. & Kane, C. L. Spin-orbit semimetals in the layer groups. Phys. Rev. B 94, 155108 (2016).
Bouhon, A. & Black-Schaffer, A. M. Global band topology of simple and double Dirac-point semimetals. Phys. Rev. B 95, 241101 (2017).
Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M. & Soluyanov, A. A. Nodal-chain metals. Nature 538, 75 (2016).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Volovik, G. E. & Zhang, K. Lifshitz transitions, type-II Dirac and Weyl fermions, event horizon and all that. J. Low. Temp. Phys. 189, 276–299 (2017).
Wieder, B. J., Kim, Y., Rappe, A. M. & Kane, C. L. Double Dirac semimetals in three dimensions. Phys. Rev. Lett. 116, 186402 (2016).
Yu, R., Weng, H., Fang, Z., Dai, X. & Hu, X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu 3 PdN. Phys. Rev. Lett. 115, 036807 (2015).
Wang, Z., Alexandradinata, Aris., Cava, R. J. & Bernevig, B. A. Hourglass fermions. Nature 532, 189–194 (2016).
Lv, B. et al. Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature 546, 627–631 (2017).
Setyawan, W. & Curtarolo, S. High-throughput electronic band structure calculations: challenges and tools. Comput. Mater. Sci. 49, 299–312 (2010).
ANNOY library. https://github.com/spotify/annoy, accessed 01 Aug 2017.
Sarmiento-Perez, R., Cerqueira, T. F. T., Körbel, S., Botti, S. & Marques, M. A. L. Prediction of stable nitride perovskites. Chem. Mater. 27, 5957–5963 (2015).
Ortiz, C., Eriksson, O. & Klintenberg, M. Data mining and accelerated electronic structure theory as a tool in the search for new functional materials. Comput. Mater. Sci. 44, 1042–1049 (2009).
Yan, Q., Chen, R. & Neaton, J. Data-driven discovery of new Dirac semimetal materials. Bull. Am. Phys. Soc. 62 (2017). BAPS.2017.MAR.H1.5, http://meetings.aps.org/link/BAPS.2017.MAR.H1.5.
Klintenberg, M. & Eriksson, O. Possible high-temperature superconductors predicted from electronic structure and data-filtering algorithms. Comput. Mater. Sci. 67, 282–286 (2013).
Geilhufe, R. M., Borysov, S. S., Kalpakchi, D., & Balatsky, A. V. Towards novel organic high-Tc superconductors: data mining using density of states similarity search. Phys. Rev. Mater. 2, 024802 (2018).
Herper, H. C. et al. Combining electronic structure and many-body theory with large databases: a method for predicting the nature of 4f states in Ce compounds. Phys. Rev. Mater. 1, 033802 (2017).
Sarma, S. D., Adam, S., Hwang, E. H. & Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 83, 407–470 (2011).
Abergel, D. S. L., Apalkov, V., Berashevich, J., Ziegler, K. & Chakraborty, T. Properties of graphene: a theoretical perspective. Adv. Phys. 59, 261–482 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 8, 800–803 (2012).
Geilhufe, M. et al. Effect of hydrostatic pressure and uniaxial strain on the electronic structure of Pb1−xSnxTe. Phys. Rev. B 92, 235203 (2015).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Gražulis, S. et al. Crystallography open database—an open-access collection of crystal structures. J. Appl. Crystallogr. 42, 726–729 (2009).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Ong, S. P. et al. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Agrawal, R, Lin, K.-I, Sawhney, H. S., & Shim, K. Fast similarity search in the presence of noise, scaling, and translation in time-series databases. (eds Dayal, U., Gray, P. M. D. & N., Shojiro) In Proceedings of the 21st International Conference on Very Large Data Bases, VLDB ’95, 490–501 (Morgan Kaufmann Publishers Inc, San Francisco, CA, USA, 1995).
Agrawal, R., Faloutsos, C. & Swami, A. Efficient similarity search in sequence databases. In Foundations of Data Organization and Algorithms (ed Lomet, D. B.) 69–84 (Springer, Berlin, Heidelberg, 1993).
Chan, K.-P. & Fu, A. W.-C. Efficient time series matching by wavelets. In Proceedings of the15th International Conference on Data Engineering (Cat. no.99CB36337) 126–133 (eds Kitsuregawa, M., Maciaszek, L., Papazoglou, M. & Pu C., IEEE Computer Society Press, Los Alamitos, CA, USA, 1999).
Keogh, E., Chakrabarti, K., Pazzani, M. & Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 3, 263–286 (2001).
Keogh, E. & Smyth, P. A probabilistic approach to fast pattern matching in time series databases. In Proceedings of the Third International Conference on Knowledge Discovery and Data Mining, KDD’97 (eds Heckerman, D., Mannila, H., Pregibon, D., Uthurusamy, R.), 24–30 (AAAI Press, Menlo Park, CA, USA, 1997).
Yianilos, P. Nin Data structures and algorithms for nearest neighbor search in general metric spaces. (ed Ramachandran, V.) In Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA’93, 311–321 (Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 1993).
Andoni, A. & Indyk, P. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. In 2006 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06) (ed Arora, S.), 459–468 (IEEE Computer Society Press, Los Alamitos, CA, USA, 2006).
Johnson, J., Douze, M. & Jégou, H. Billion-scale similarity search with GPUs. arXiv preprint arXiv:1702.08734 (2017).
Boytsov, L. & Naidan, B. Engineering efficient and effective non-metric space library. In Similarity Search and Applications - 6th International Conference, SISAP 2013, A Coruña, Spain, October 2–4, 2013, Proceedings, 280–293 (eds Brisaboa, N., Pedreira, O., Zezula, P., Springer, Heidelberg, 2013).
Highsoft AS. http://highcharts.com, accessed 22 June 2018.
Acknowledgements
We are grateful for the support from the Villum Foundation, Swedish Research Council Grant no. 638-2013-9243, the Knut and Alice Wallenberg Foundation and the European Research Council under the European Union’s Seventh Framework Program (FP/2207-2013)/ERC Grant agreement no. DM-321031. The authors acknowledge computational resources from the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre at Linköping University as well as the High Performance Computing Center North.
Author information
Authors and Affiliations
Contributions
A.V.B. and S.S.B. designed the study. S.S.B., B.O., and M.B.G. developed the search tool. R.M.G. performed the DFT calculations and the search for functional materials. All authors tested the search tool, analyzed the results, wrote, and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borysov, S.S., Olsthoorn, B., Gedik, M.B. et al. Online search tool for graphical patterns in electronic band structures. npj Comput Mater 4, 46 (2018). https://doi.org/10.1038/s41524-018-0104-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0104-9
This article is cited by
-
Deep learning approach to genome of two-dimensional materials with flat electronic bands
npj Computational Materials (2023)
-
Machine learning of phase transitions in nonlinear polariton lattices
Communications Physics (2022)
-
Shifting computational boundaries for complex organic materials
Nature Physics (2021)