Phase-field model of pitting corrosion kinetics in metallic materials

Abstract

Pitting corrosion is one of the most destructive forms of corrosion that can lead to catastrophic failure of structures. This study presents a thermodynamically consistent phase field model for the quantitative prediction of the pitting corrosion kinetics in metallic materials. An order parameter is introduced to represent the local physical state of the metal within a metal-electrolyte system. The free energy of the system is described in terms of its metal ion concentration and the order parameter. Both the ion transport in the electrolyte and the electrochemical reactions at the electrolyte/metal interface are explicitly taken into consideration. The temporal evolution of ion concentration profile and the order parameter field is driven by the reduction in the total free energy of the system and is obtained by numerically solving the governing equations. A calibration study is performed to couple the kinetic interface parameter with the corrosion current density to obtain a direct relationship between overpotential and the kinetic interface parameter. The phase field model is validated against the experimental results, and several examples are presented for applications of the phase-field model to understand the corrosion behavior of closely located pits, stressed material, ceramic particles-reinforced steel, and their crystallographic orientation dependence.

Introduction

Corrosion is the gradual destruction of materials (usually metallic materials) via chemical and/or electrochemical reaction with their environment. It costs about 3.1% of the gross domestic product (GDP) in the United States, which is much more than the cost of all natural disasters combined. Localized corrosion, such as pitting corrosion, is one of the most destructive forms of corrosion; it leads to the catastrophic failure of structures and raises both human safety and financial concerns.^1,2,3 Pitting corrosion of stainless steel usually occurs in two different stages: (1) pit initiation from passive film breakage^4,5,6 and (2) pit growth.^{2,3,7,8,9,10,11,12} In this study, we focused on the development of a phase-field modeling capability to study pit growth by considering both anodic and cathodic reactions.

In the past few decades, great efforts have been made to develop numerical models for pitting corrosion. The moving interface and the electrical double layer at the metal/electrolyte interface are the two challenging problems faced by most of these numerical models. These numerical models can be divided according to the method in which a moving interface is incorporated in their models. Several steady state^{9,10,13,14,15,16,17,18} and transient state^{19,20,21,22,23,24,25,26,27,28} models have been developed over the years that did not allow for changes in the shape and dimensions of the pits/crevices as corrosion proceeds.

Recent advances in numerical techniques, such as the finite element method, the finite volume method, the arbitrary Lagrangian–Eulerian method, the mesh-free method, and the level set method have encouraged researchers to model the evolving morphology of the pits with a moving interface. Most of these modeling efforts have used a sharp interface to represent the corroding surface, which requires the matching mesh at each time step,^11,29 thus increasing the errors associated with the violation of mass conservation laws and increasing the computation cost. The finite volume method models overcome this problem by creating a matching mesh as a function of the concentration of ions, but they are still unable to model complex microstructures.^12,30,31 A mesh-free method, the peridynamic model, has been implemented to model pitting corrosion, but it only considered electrochemical reactions without considering the ionic transport in the electrolyte.⁷

Over the past three decades, the phase field (PF) method has emerged as a powerful simulation tool for modeling of microstructure evolution. PF models study the phase transformation by defining the system’s free energy, and the system’s microstructure evolution is predicted by free energy minimization. The PF approach has been extensively applied to many materials processes, such as solidification, dendrite growth, solute diffusion and segregation, phase transformation, electrochemical deposition, dislocation dynamics, crack propagation, void formation and migration, gas bubble evolution, and electrochemical processes.³²

PF models assume a diffusive interface at the phase boundaries rather than a sharp one, which makes the mathematical functions continuous at the interface. A few recent attempts have been made to use the PF method to model pitting corrosion and stress corrosion cracking without the consideration of cathodic reactions, ionic transport and in particular the dependence of overpotential on metal ion concentration in the electrolyte.^33,34 In reality, the transport of ionic species in the electrolyte often plays a very important role in diffusion controlled corrosion processes, and the effects of these ionic species must be incorporated to model the process adequately. In this study, a PF method is used to model pitting corrosion by considering both anodic and cathodic reactions, transport of ionic species and the dependence of overpotential on metal ion concentration in the electrolyte.

This paper is organized as follows. Firstly, we describe the system and the electrochemical reactions considered in this work followed by the construction of PF model. The total free energy of this PF model consists of three parts: bulk free energy, gradient energy and electrostatic energy. We used the KKS model³⁵ to construct the bulk free energy and the interfacial energy. Secondly, we developed the governing equations which comprise of mass diffusion, electromigration, and chemical reaction terms, whereas the interface conditions are incorporated by introducing an order parameter that defines the system’s physical state at each material point. Thirdly, a study is included to couple the kinetic interface parameter and the system’s total overpotential. Fourthly, the PF model is validated against the experimental results and previous numerical models. Lastly, several case studies are presented to demonstrate the strength of this proposed PF model.

Results and discussion

The system and electrochemical reactions considered

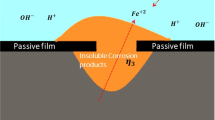
The system studied consists of stainless steel 304 (SS304) in dilute salt water (Fig. 1). It is assumed that new passive film will not form in this system. We will consider the effects of passive film formation in a future study. In this model, the following electrochemical reactions and kinetics are considered.

Fig. 1

Schematic of the chemical reactions that occur during the pitting corrosion process

For the oxidation of main metal alloy elements in SS304,

$$Fe\,\rightarrow\,Fe^{+ 2} + 2e^-$$

$$Ni\,\rightarrow\,Ni^{ + 2} + 2e^ -$$

$$Cr\,\rightarrow\,Cr^{ + 3} + 3e^ -$$

In the following, M_e is used to represent the effective metal in SS304 with an average charge number of z₁. The material properties of SS304 such as molar concentration in solid phase (c_solid = 143 mol/L),¹² saturation concentration in the electrolyte (c_sat = 5.1 mol/L),¹² effective diffusion coefficient (D₁ = 8.5 × 10⁻¹⁰ m²/s),¹² and the average charge number (z₁ = 2.19) based on Fe, Ni, Cr, and their mole fractions within the alloy (taken from Ref. ¹²). The above reactions can then be simplified to

$$M_e\,\rightarrow\,M_e^{z_1} + z_1e^ -$$

(1)

The anodic dissolution of the metal is assumed to follow Butler–Volmer equation,

$$i_a = i_0\left[ {\exp \left( {\frac{{\alpha _az_1F\varphi _{s,o}}}{{R_gT}}} \right) - \exp \left( { - \frac{{\alpha _cz_1F\varphi _{s,o}}}{{R_gT}}} \right)} \right]$$

(2)

where F is the Faraday constant, R_g is the gas constant, T is the temperature, φ_s,o is the polarization overpotential, i_o is the exchange current density, α_a is the anodic charge transfer coefficient, α_c is the cathodic charge coefficient (α_c = 1 − α_a). The values of the above mentioned parameters are reported in Table 1s (supplementary material).

For the hydrogen discharge reaction in Eq. (3), the corresponding rate is given in Eq. (4)

$$H^ + + e^ - \to \frac{1}{2}H_2$$

(3)

$$J_5 = J_{50}\left[ {H^ + } \right]exp\left( {\frac{{\alpha _5F}}{{R_gT}}\varphi _{s,o}} \right)$$

(4)

For reduction of water (Eq. (5)), the corresponding rate is given in Eq. (6)

$$H_2O + e^ - \to H + OH^ -$$

(5)

$$J_6 = J_{60}exp\left( {\frac{{\alpha _6F}}{{R_gT}}\varphi _{s,o}} \right)$$

(6)

Experimental values of i₀, J₅₀, J₆₀, α_a, α₅, and α₆ are given in Table 1s.

In this work, the following two reactions in the electrolyte are considered

$$M_e^{z_1} + H_2O\rightleftharpoons\,M_eOH^{z_1 - 1} + H^ +$$

(7)

$$H_2O\rightleftharpoons\,OH^ - + H^ +$$

(8)

The equilibrium constants of reactions in Eqs. (7) and (8) are defined as K₁ and K₂, respectively.

$$K_1 = \frac{{k_{1f}}}{{k_{1b}}},\,K_2 = \frac{{k_{2f}}}{{k_{2b}}}$$

where k_1f, k_1b, k_2f, and k_2b are the forward and backward reaction rates. Therefore, a total of six ion species are considered in this model,

$$M_e^{z_1} = c_1;M_eOH^{z_2} = c_2;Cl^{z_3} = c_3;Na^{z_4} = c_4;H^{z_5} = c_5;OH^{z_6} = c_6$$

where z_i (i = 1, 2, ……6) are the charge numbers of the respective species (their values are given in Table 2s), and c_i (i = 1, 2, ……6) are the normalized concentrations of the respective species. The normalized concentration c_i is determined by C_i = C_i/C_solid for i = 1,2,…,6, where C_i represents the molar concentration of ionic species. The constants K₁ and K₂ can also be expressed as a function of C_i.

$$K_1 = C_2C_5/C_1,\,K_2 = C_5C_6$$

The phase field model for corrosion

The surface of the metal is normally covered with the passive film; however, a partial breakdown in the film can occur, which may initiate pits like the one illustrated in Fig. 1. The model consists of two phases: the solid phase M_e (i.e., the metal part) and the liquid phase (i.e., the electrolyte part). The driving force for metal corrosion and microstructure evolution is from the minimization of the system’s total free energy, which usually consists of bulk free energy E_b, interface energy E_i, and long-range interaction energies such as elastic strain energy E_s and electrostatic energy E_e.^36,37 The system’s total energy can be expressed as

$$E = E_b + E_i + E_s + E_e$$

(9)

The inclusion of elastic and/or plastic deformation in the model is completely feasible because it has been done in other systems.^38,39,40 It can be even necessary to include the strain energy term if a volumetric non-compatible passive film develops during corrosion. Because the formation of a passive film will not be considered in the first stage of this work, for simplicity, the elastic strain energy is not considered here. In a later section, the effect of applied or residual stress on pitting will be studied using the concept of overpotential rather than strain energy. Now we have,

$$E = E_b + E_i + E_e$$

(10)

$$E = {\int} {\left[ {f_b\left( {c_1,\eta } \right) + \frac{{\alpha _u}}{2}\left( {\nabla \eta } \right)^2 + z_1FC_1\varphi } \right]} dV$$

(11)

where f_b(c₁, η), derived in the next section, is the local bulk free energy density, which is a function of the normalized concentration of the ionic species c₁ and order parameter η; the second term in Eq. (11) represents the gradient energy density that contributes to the interfacial energy, in which α_u is the gradient energy coefficient, which is related to physical parameters in a later section; and the third term in Eq. (11) represents the electrostatic energy density where C₁ is the molar concentration of metal ion and φ is the electrostatic potential.

Bulk free energy density

To determine the bulk free energy density f_b(c₁, η), we use the model proposed by Kim et al. for binary alloys.³⁵ We chose KKS model because the model has less limitations on the interface thickness as compared to some other models such as model presented by the model by Wheeler et al.⁴¹ The detailed derivations of all functions in the KKS model were skipped here and readers are referred to the original paper.³⁵ In KKS model, the model parameters can be analytically determined by material properties and experimental conditions for the concerned system. In KKS model, at each point, the material is regarded as a mixture of two coexisting phases, and a local equilibrium between the two phases is always assumed:

$$c_1 = h\left( \eta \right)c_s + \left[ {1 - h\left( \eta \right)} \right]c_l$$

(12)

$$\partial f_s\left( {c_s} \right)/\partial c_s = \partial f_l\left( {c_l} \right)/\partial c_l$$

(13)

where c_s and c_l represent the normalized concentrations of the solid and liquid phases, respectively; h(η) is a monotonously varying function from h(0) = 0 to h(1) = 1. In this study, it is assumed that h(η) = η²(−2η + 3). In Eq. (13), the free energy densities of the solid and liquid phases are expressed as f_s(c_s) and f_l(c_l), respectively. Because the concentration is considered to be a mixture of solid and liquid phases at each point, by following the same argument, the bulk free energy density of the solid and liquid phases are expressed in a similar manner,

$$f_b(c_1,\eta ) = h\left( \eta \right)f_s(c_s) + \left[ {1 - h\left( \eta \right)} \right]f_l(c_l) + wg(\eta )$$

(14)

This is a double well potential in the energy space. The height of the double well potential is w, and g(η) = η²(1 − η)². This expression has two minima at η = 0 and η = 1, which represent the electrolyte phase and the solid phase, respectively.

For this system, f_s(c_s) and f_l(c_l) can reasonably be considered as parabolic functions.⁴²

$$f_s\left( {c_s} \right) = A(c_s - c_{eq,s})^2$$

(15)

$$f_l\left( {c_l} \right) = A\left( {c_l - c_{eq,l}} \right)^2$$

(16)

where c_eq,s = 1 and c_eq,l = C_sat/C_solid are the normalized equilibrium concentrations of the solid and liquid phases, respectively. The temperature-dependent free energy density proportionality constant A is considered to be equal for both the liquid and solid phases. Its value is calculated in such a manner that the driving force for the metal corrosion in the approximated resulting system is quite close to that of the original thermodynamic system.⁴²

The evolution of phase order parameter η and metal ion concentration c₁ in time and space are assumed to obey the Ginzburg–Landau (also known as Allen–Cahn)⁴³ and Cahn–Hilliard⁴⁴ equations, respectively.

$$\frac{{\partial \eta }}{{\partial t}} = - L\frac{{\delta E}}{{\delta \eta }} = L\left[ {\nabla \alpha _u\nabla \eta + h\prime \left( \eta \right)\left\{ {f_l\left( {c_l} \right) - f_s\left( {c_s} \right) - \left( {c_l - c_s} \right)\frac{{\partial f_l\left( {c_l} \right)}}{{\partial c_l}}} \right\} - wg\prime \left( \eta \right)} \right]$$

(17)

$$\begin{array}{*{20}{l}} {\frac{{\partial {\mathrm{c}}_1}}{{\partial {\mathrm{t}}}}} \hfill & = \hfill & {\nabla M\nabla \frac{{\delta E}}{{\delta c_1}} + R_1} \hfill \cr {} \hfill & = \hfill & {\nabla \left[ {D_1\left( \eta \right)\nabla c_1} \right] + \nabla \left[ {D_1\left( \eta \right)h\prime \left( \eta \right)\left( {c_l - c_s} \right)\nabla \eta } \right]} \hfill \cr {} \hfill & {} \hfill & {+ \nabla \left[ {\frac{{z_1Fc_1D_1\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right) + R_1} \hfill \end{array}$$

(18)

where L is the kinetic parameter that represents the solid–liquid interface mobility, and M is the mobility of metal ions and expressed as $M = D_1(\eta )/(\partial ^2f_b/\partial c_1^2)$. In Eq. (18), R₁ is the source and/or sink term for metal ions due to reaction (Eq. (7)), and it takes the form of (−k_1fc₁ + k_1bc₂c₅)y₁(u). The function y₁(η) defined below is to ensure that reaction (Eq. (7)) occurs only in the electrolyte phase.

$${\mathrm{y}}_1\left( \eta \right) = \left\{ {\begin{array}{*{20}{l}} {1;} \hfill & {\eta \le 0} \hfill \cr {} \hfill & {0 < \eta < 0.1} \hfill \cr {0;} \hfill & {\eta \ge 0.1} \hfill \end{array}} \right.\left( {{\mathrm{linearly}}\,{\mathrm{change}}\,{\mathrm{from}}1\,{\mathrm{to}}\,0} \right)$$

(19)

Conservation of charge

In this study, we follow Dassault’s work rather than following Guyer’s model^45,46 which simplifies the model by removing the need to discretize the double layer at the metal–electrolyte interface. It allows our PF model to simulate the corrosion process from meso- to macro-length scales, as compared to Guyer’s model, which was limited to nanoscale. It is also possible to incorporate the effect of the laminar/turbulent flow of the electrolyte on the metal–electrolyte interface in case of moving electrolyte.⁴⁷ Here, the conservation of charge can be expressed as

$$\frac{{\partial \rho _e}}{{\partial t}} = \nabla \left\{ {\sigma _e\left[ {1 - y_1\left( \eta \right)} \right]\nabla \varphi } \right\} + y_1\left( \eta \right)FC_{solid}{\sum} {z_i} \frac{{\partial c_i}}{{\partial t}}$$

(20)

where ρ_e is the charge density and σ_e is the electrical conductivity of the metal in the solid phase. The function [1 − y₁(η)] interpolates the electrical conductivity, σ_e in the solid phase to zero in the electrolyte phase, where y₁(η) is defined in Eq. (19). The time needed for charge accumulation across the interface due to the diffusion of ionic species is much longer than that required to achieve steady-state charge accumulation across the interface, so the conservation of charge in the above system can be considered at a steady state. The relation given in Eq. (20) is reduced to

$$0 = \nabla \left\{ {\sigma _e\left[ {1 - y_1\left( \eta \right)} \right]\nabla \varphi } \right\} + y_1(\eta )FC_{solid}{\sum} {z_i} \frac{{\partial c_i}}{{\partial t}}$$

(21)

Gradient energy coefficient

The height of the double well potential w and the gradient energy coefficient α_u can be related to the interface energy ϱ and the interface thickness l³³

$${\it{\varrho }} = 4\sqrt {w\alpha _u}$$

(22)

$$l = \sqrt 2 \alpha \prime \sqrt {\frac{{\alpha _u}}{w}}$$

(23)

where α′ is a constant value determined by the order parameter u. If the interface region is defined as 0.05 < η < 0.95; the value of α′ is 2.94.³⁵

Transport equations for other ionic species in the electrolyte

The governing equations of the other five ionic species are the Nernst–Planck equations with chemical reaction terms. They are expressed as

$$\frac{{\partial {\mathrm{c}}_2\left( {{\boldsymbol{x}},t} \right)}}{{\partial {\mathrm{t}}}} = \nabla \left[ {D_2\left( \eta \right)\nabla c_2} \right] + \nabla \left[ {\frac{{z_2Fc_2D_2\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right) + R_2$$

(24)

$$\frac{{\partial {\mathrm{c}}_3\left( {{\boldsymbol{x}},t} \right)}}{{\partial {\mathrm{t}}}} = \nabla \left[ {D_3\left( \eta \right)\nabla c_3} \right] + \nabla \left[ {\frac{{z_3Fc_3D_3\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right)$$

(25)

$$\frac{{\partial {\mathrm{c}}_4\left( {{\boldsymbol{x}},t} \right)}}{{\partial {\mathrm{t}}}} = \nabla \left[ {D_4\left( \eta \right)\nabla c_4} \right] + \nabla \left[ {\frac{{z_4Fc_4D_4\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right)$$

(26)

$$\frac{{\partial {\mathrm{c}}_5\left( {{\boldsymbol{x}},t} \right)}}{{\partial {\mathrm{t}}}} = \nabla \left[ {D_5\left( \eta \right)\nabla c_5} \right] + \nabla \left[ {\frac{{z_5Fc_5D_5\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right) + R_5$$

(27)

$$\frac{{\partial {\mathrm{c}}_6\left( {{\boldsymbol{x}},t} \right)}}{{\partial {\mathrm{t}}}} = \nabla \left[ {D_6\left( \eta \right)\nabla c_6} \right] + \nabla \left[ {\frac{{z_6Fc_6D_6\left( \eta \right)}}{{R_gT}}\nabla \varphi } \right]y_1\left( \eta \right) + R_6$$

(28)

where R₂ is the source/sink term originated from the electrochemical reaction in Eq. (7) which takes the form as [k_1fc₁ − k_1bc₂c₅]y₁(η). The rates of forward and backward reaction are expressed by k_1f and k_1b respectively. It is assumed that no electrochemical reaction occurs inside the metal part. This is ensured by y₁(η) defined in Eq. (19). R₅ and R₆ are the source/sink terms originated from electrochemical reactions in Eqs. (7) and (8) and take the form as $\left[ {k_{1f}c_1 - k_{1b}c_2c_5 + k_{2f} - k_{2b}c_5c_6} \right]y_1\left( \eta \right) - \left( {\frac{{J_5}}{{z_5FC_{solid}}}} \right)y_2\left( \eta \right)$ and $\left[ {k_{2f} - k_{2b}c_5c_6} \right]y_1\left( \eta \right) - \left( {\frac{{J_6}}{{z_6FC_{solid}}}} \right)y_2\left( \eta \right)$ respectively. The rates of forward and backward reactions for the hydrolysis of water are represented by k_2f and k_2b, respectively. It should be noted that R₅ and R₆ have an additional term near the metal–electrolyte interface due to the cathodic reactions considered in Eqs. (3) and (5) where J₅ and J₆ are defined in Eqs. (4) and (6) respectively. These reaction terms are multiplied by a step function y₂(η) to ensure that these reactions only happen in a small region near the metal surface.

$${\mathrm{y}}_2\left( \eta \right) = \left\{ {\begin{array}{*{20}{l}} {1;} \hfill & {0.01 \le \eta < 0.05} \hfill \cr {0;} \hfill & {\eta \ge 0.05} \hfill \cr {0;} \hfill & {\eta < 0.01} \hfill \end{array}} \right.$$

(29)

It should also be noted that, in Eqs. (25) and (26) there are no source/sink terms because it was assumed that c₃ (Cl⁻) and c₄ (Na⁺) does not take part in any reactions. This is not true if a salt film can be formed. The effect of salt film formation will be studied in a future study.

The electrostatic potential, φ, is governed by Eq. (21) coupled with the governing Eqs. (18) and (24–28). The diffusivity D_i is a function of the order parameter η. As it is known, the diffusivity of ionic species differs in the metal and electrolyte phase. The diffusivities of all the ions were defined using a step function of the order parameter η. For metal ion c₁, a step function as expressed in Eq. (30) is used in which the diffusivity value in metal is assumed to be γ times less than that in electrolyte. A step function as expressed in Eq. (31) is used for all other ionic species (c₂, c₃, c₄, c₅, and c₆).

$${\mathrm{D}}_1\left( \eta \right) = \left\{ {\begin{array}{*{20}{l}} {D_1;} \hfill & {\eta < 0.90} \hfill \cr {} \hfill & {0.90 \le \eta \le 0.95} \hfill \cr {D_1/\gamma ;} \hfill & {\eta > 0.95} \hfill \end{array}} \right.\,\left( {{\mathrm{linearly}}\,{\mathrm{change}}\,{\mathrm{from}}\,D_1{\mathrm{to}}\,D_1/\gamma } \right)$$

(30)

$${\mathrm{D}}_{\mathrm{i}}\left( {\mathrm{\eta}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\mathrm{D}}_{\mathrm{i}};} \hfill & {\eta < 0.90} \hfill \cr {} \hfill & {0.90 \le \eta \le 0.95} \hfill \cr {0;} \hfill & {\eta > 0.95} \hfill \end{array}} \right.\,\left( {{\mathrm{linearly}}\,{\mathrm{change}}\,{\mathrm{from}}\,D_i\,{\mathrm{to}}\,0} \right)$$

(31)

for i = 2,3,….,6.

Overpotential

The overpotential is expressed as

$$\varphi _{s,o} = \varphi _m - \varphi _{m,se} - \varphi _c - \varphi _l$$

(32)

where φ_m is the potential in the metal phase also known as applied potential; φ_m,se is the standard electrode potential in the metal; and φ_c is the concentration overpotential expressed in (33).

$$\varphi _c = \frac{{R_gT}}{{Fz_1}}\ln\frac{{c_{1b}}}{{c_{eq,l}}}$$

(33)

The concentration of $M_e^{z_1}$ near the interface is,

$$c_{1b} = \left\{ {\begin{array}{*{20}{l}} {c_1;} \hfill & {\left( {\eta = 0.05} \right)} \hfill \cr {0;} \hfill & {\left( {\eta < 0.05} \right)} \hfill \cr {0;} \hfill & {\left( {\eta > 0.05} \right)} \hfill \end{array}} \right.$$

(34)

The electrostatic potential near the interface is,

$$\varphi _l = \left\{ {\begin{array}{*{20}{l}} {\varphi ;} \hfill & {\left( {\eta = 0.05} \right)} \hfill \cr {0;} \hfill & {\left( {\eta < 0.05} \right)} \hfill \cr {0;} \hfill & {\left( {\eta > 0.05} \right)} \hfill \end{array}} \right.$$

(35)

Kinetic interface parameter and overpotential relation

In this model, the metal corrosion is described by the order parameter η. The corrosion rate is controlled by the kinetic interface parameter L. The shift in the corrosion mode from activation-controlled to diffusion-controlled can be modeled by continuous variation of the kinetic interface parameter L. The relationship between the kinetic interface parameter L and the corrosion rate is linear in the activation-controlled mode.³³ From the Butler–Volmer equation, as expressed in (2), the kinetic interface parameter has an effect on overpotential similar to that of the current density, as expressed below in (36). A similar technique is also implemented in a peridynamic model, in which the interface diffusivity is directly related to the current density for Tafel relation.⁷

$$L = L_o\left[ {\exp \left( {\frac{{\alpha _az_1F\varphi _{s,o}}}{{R_gT}}} \right) - \exp \left( { - \frac{{\alpha _cz_1F\varphi _{s,o}}}{{R_gT}}} \right)} \right]$$

(36)

Following the method developed in Refs ⁷ and³³ and using the experimental values for SS304 (reported in Table 1s), i₀ = 1.0 × 10⁻⁶A/cm² and α_a = 0.26, we calculated L₀ = 1.94 × 10⁻¹³ m³/(Js).

1D PF model

We implemented the PF model to simulate the corrosion evolution in 1D. The simulations are executed at T = 293.15 K (20 °C) with metal potential of 844 mV SHE (standard hydrogen electrode) (i.e., 600 mV SCE [saturated calomel electrode]) in a 1 M NaCl solution. The temperature dependence of the diffusion coefficient is governed by the Einstein relation.¹² The PF simulation results for the corrosion length are then compared with the 1D pencil electrode of experimental findings.³ The simulations are performed for 400 s, and the results of the corroded length are plotted against the square root of time $\left( {\sqrt t } \right)$. The simulation results agree well with the experimental results, as illustrated in Fig. 2. The 1D PF model and the 1D pencil electrode experimental results show similar slopes.

Fig. 2

Comparison of corrosion kinetics of 1D PF model with 1D pencil electrode (1D growth in an artificial pit) in 1 M NaCl at 20 °C and 600 mV (SCE).³

A qualitative study on the concentration distribution of ionic species inside the electrolyte is performed as done in many classical numerical models for crevice and pitting corrosion.^9,10,48 It is difficult to quantitatively measure the molar concentration distribution of ionic species in the electrolyte experimentally. Because such experimental data is lacking, we have discussed these concentration variations theoretically. Figure 1s (supplementary material) shows the concentration in mol/L on a logarithmic scale. The higher value of metal ions near the interface results in a slight increase in the [H⁺] ion concentration (i.e., a decrease in the pH value) due to strong coupling between C₁, C₂, and C₅. The value of [H⁺] increases as the overpotential increases because it results in a higher production rate of metal ions and hydrolysis of metal ions. Although, this study was performed on a lower overpotential, but a small increase in C₅ can still be seen in Fig. 1s (supplementary material). This increase in positive charge is neutralized by the migration of chloride ions towards the interface, as shown in Fig. 1s (supplementary material).

To investigate the effects of metal potential, several simulations were performed to show the behavior of corrosion under different metal potentials. Figure 2s (supplementary material) shows that the corrosion rate obtained for these metal potentials are of the same order of the magnitude as the experimental results.⁴⁹ The experimental results plotted in Fig. 2s (supplementary material) give the maximum corrosion rates that can be achieved at the corresponding metal potential. A calibration study was also performed to achieve a corrosion rate for PF 1D model simulation close to experimental ones by varying exchange current density (i₀). It was found that if the value of i₀ is chosen equal to twice the reported value (i₀ = 1 × 10⁻⁶ A/cm²) in Table 1s (supplementary material), then the corrosion rate agree well with the experimental values.⁴⁹ For the sake of consistency, all the presented modeling results are simulated by using the same of value of i₀ as reported in Table 1s (supplementary material). The overpotential for the corresponding corrosion rates are shown in Fig. 3s (supplementary material).

PF simulations for 2D model

The 2D simulations are performed with a metal potential of 600 mV SCE (844 mV SHE). The boundary conditions and initial values are the same as described in Fig. 7s (supplementary material). To compare the 2D PF model results with the experimental ones, a 300 μm by 240 μm rectangular geometry is considered in which the metal and electrolyte parts are equally divided, as shown in Fig. 4s (supplementary material). A 60 μm wide and 20 μm deep semi-elliptical pit is assumed. The remaining surface, as shown in Fig. 4s, is considered to have a passive oxide film. Figure 4s (supplementary material) shows the concentration distribution inside the electrolyte at various time intervals. In Fig. 3, the 2D PF model results are compared with the 2D foil experiment results reported in the literature.³ The evolution of pitting depth over the time shows a trend similar to that found in the experimental results³ but with deeper pitting depths than the experimantal data. As mentioned earlier, the regrowth of passive film may be an important factor. We will include the formation of passive film in a future study. The contours of the electrostatic potential distribution for the simulations with the above conditions are shown in Fig. 5s (supplementary material).

Fig. 3

Comparison of 2D PF model with 2D foil experiment at 600 mV (SCE) at 20 °C.³

Case studies

Case study 1: Interaction of closely located pits

In reality, multiple pits can nucleate due to changes in chemistry on the metal surface, whereas most numerical models consider only the nucleation or growth of a single pit. A few efforts have been made to understand both experimentally and numerically the interaction of multiple pits.^50,51 Because we have not considered pit initiation in our PF model, we apply our PF model to two narrow initial openings of 5 μm each at distances of (a) 12 μm and (b) 5 μm at an applied metal potential of 200 mV SHE. The boundary conditions and initial values are the same as those given in Fig. 7s (supplementary material). Figure 4 shows the changes in the morphology of pits with and without interaction in (b) and (a), respectively. It can be seen that without their interaction, these pits corrode at a rate similar to that at which they grow individually. After the pits interact, the chemical compositions of the ionic species change in the vicinities of the pits in the electrolyte. The interaction between the two pits can have either a positive or negative effect on pit growth.⁵² In this study the interaction of the two closely located pits had a positive effect which can be seen in Fig. 4 (b) at t = 6 s. The corroded material in both cases was estimated which suggested that the corrosion rate was increased in case (b). Two pits finally coalesce to form a wider pit, similar to the pits formed in real-life metallic structures (i.e., multiple pits nucleate on the corroding surface and interact with each other), which are wider.

Fig. 4

Multiple-pit morphology changes over time and changes in corrosion rate after the interaction of two pits

Case study 2: Pitting corrosion in a stressed material

Like other alloys, stainless steel can have stressed zones (tensile and compressive). It is believed that overpotential is not uniform in the case of stressed zones, which results in different corrosion rates in different material locations and directions. The experimental findings⁵³ show that most pits grow in locations near the scratched lines on the surface that result from mechanical polishing. These scratched lines could result in strain hardening, as revealed by electrochemical analysis.⁵³ The experimental findings also illustrate that overpotential is not uniform in the presence of residual stresses. Gutman explained the same phenomenon with his theoretical model in which the compressive stress zone has less overpotential than the unstressed zone and the tensile stress zone.⁵⁴ The overpotential is directly related to the corrosion current density. The relationship between the overpotential of the compressive stress zone (φ_comp,s), the unstressed zone (φ_s,o), and the tensile stress zone (φ_tens,s) is φ_comp,s < φ_s,o < φ_tens,s. It should be noted that corrosion rate in plastically deformed zones is greater than that of elastically deformed zones, due to the presence of high density dislocations in plastically deformed zones. In this study, we applied the overpotential dependence on applied/residual stress proposed by Gutman.⁵⁴ According to Gutman’s model,⁵⁴ residual stress of 600MPa corresponds to a change in overpotential of about 20mV in our system. Here, we model a material with both tensile and compressive stress zones, which have an overpotential difference of φ_comp,s = φ_s,o − 20 mV and φ_tens,s = φ_s,o + 20 mV, whereas φ_s,o is calculated from (32). A small opening of 6 μm is considered at the material’s surface. The boundary conditions and initial values are the same as those given in Fig. 7s (supplementary material). Figure 5 shows that areas under tensile stress corrode at a faster rate than areas in the compressive stress zone. The pit morphology is closer to that of pits formed during a natural corrosion process because, in most natural scenarios, the corrosion process begins when the passive film is damaged by strain hardening of the surface. In fact, in most of these cases, multiple pits coalesce and grow faster along width than depth. This process is already illustrated in the previous case in which two closely located pits interact.

Fig. 5

Pit growth at φ_m = −400 mV (SHE) for a material with tensile and compressive residual stresses

Case Study 3: Crystallographic plane-dependent pitting corrosion

Several studies suggested that crystallographic orientations greatly affect the propagation rates and morphology of the corroding pits.^55,56,57 This dependence is usually attributed to factors such as close packing of crystal planes, reaction rate variation along different plane orientations and density of crystalline defects on micro scale. Here, we demonstrate that this PF model can be a good tool to study this phenomenon in detail. The crystal orientations affect the rate of corrosion because planes with lower atomic densities usually corrode at faster rates than planes with higher atomic densities.⁵⁷ It has been reported that the corrosion rate tends to increase in the order of {111} < {110} ≤ {100}. The corrosion rate in the crystallographic plane {111} is one third of {100}.⁵⁷ The scenario in which planes {110} and {100} corrode at the same rate is considered because no exact value is available for their ratio. We implemented our PF model to study the effects of the crystallographic plane orientation on pit growth. The domain geometry considered is 30 μm × 27 μm, as shown in Fig. 6. The PF simulations are performed at a lower metal potential of −400 mV SHE because it is believed that the crystallographic orientation dependence is limited to lower overpotentials when the corrosion process is activation controlled.^33,58 A small opening of 6 μm is considered at the surface of the material. The initial values and boundary conditions are the same as described in Fig. 7s (supplementary material). Crystallographic planes {111}, {110}, and {100} are represented by blue, brown, and magenta, respectively, in Fig. 6, which shows that the pit shape is no longer uniform because {111} corrodes at one third the rate of the other two planes. This pit morphology illustrates the strength of our PF model under complex microstructures, with which most sharp interface models fail to cope.

Fig. 6

Pit morphology evolution over time under crystalline dependent corrosion

Case Study 4: Pitting corrosion in ceramic particle–reinforced steel

Ceramic particles such as TiB₂ and/or TiC are often embedded into steel to improve its stiffness, strength,⁵⁹ and wear resistance.⁶⁰ Although the addition of these ceramic particles improves some of the material’s mechanical properties, it has very little effect on corrosion resistance.⁶¹ In fact, these reinforcements may enhance stress corrosion cracking (SCC) because they can change the stress distribution near the pits. In case of SCC, a higher stress concentration can be resulted at the tip of a growing pit when the pit reaches a ceramic particle. Metal corrodes faster at the high tensile stress region in the vicinity of a ceramic particle. As we are not studying SCC in this study, the effect of stress concentration will not be considered here. Because the ceramic particles are far less reactive than steel, we assume that they are non-corrodible in salt solution. To ensure that the ceramic particles do not corrode in the salt solution, we considered L to be equal to zero for the ceramic particles. A small opening of 6 μm is assumed at the surface of the material. The boundary conditions and initial values are the same as those described in Fig. 7s (supplementary material). Figure 7 shows that the pit morphology changes with the presence of ceramic materials. This example elaborates the ability of this PF model to handle complex structures.

Fig. 7

Pit growth in ceramic particle–reinforced steel at φ_m = 200 mV (SHE)

In this study, we have developed a PF model for metal corrosion with ion transport in the electrolyte and this model is used to study pitting corrosion of SS304 in salt water. It is shown that once the kinetic interface parameter is calibrated with the material’s exchange current density, the model has the potential to predict corrosion behavior over the whole range of reaction and diffusion-controlled processes. The simulation results showed that the PF model predictions agree well with the experimental results and that the model has the ability to handle complex microstructures, such as the interaction of closely located pits, the effects of stress on pitting, the effects of ceramic particles, and crystallographic plane orientation on corrosion.

Method

Finite element method, Galerkin method,⁶² is used for space discretization while Backwards differentiation formula (BDF) method⁶³ is used for the time integration of the governing partial differential Eqs (17, 18, 21, 24–28). Triangular Lagrangian mesh elements were chosen to discretize the space. It was ensured that we have at least 12 mesh elements inside the diffuse interface to accurately approximate η (order parameter) and the piecewise functions based on η.

Data availability

The data and codes supporting the findings of this study are available from the corresponding author on reasonable request.