Introduction

Interactions between dislocations gliding in intersecting slip planes play fundamental roles in the strain hardening during plastic deformation of crystalline materials.1,2,3,4 Dislocation intersections lead to the formation of dislocation junctions in minimum energy configurations. In face-centered cubic (FCC) crystals, the sessile junction known as Lomer–Cottrell lock5,6 is assumed to be the most stable barrier to further dislocation motion in the traditional view.1,3 However, Madec and co-workers7 reported that the interaction between two intersecting dislocations with collinear Burgers vectors is the strongest of all dislocation reactions. Previous modeling and simulations7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24 on investigating the dislocation intersections emphasized the importance of the interaction details between individual dislocations, including not only the long-range elastic interactions but also the short-range core reactions. Most of these researches suggested that the dislocation interactions can be studied by multiscale approaches, where the discrete dislocation dynamics (DDD) based on continuum elasticity theory deals with the long-range elastic attraction or repulsion, and atomistic simulations the short-range reaction rules.9 Different from the DDD techniques that require priori rules as inputs,10 another simulation method also based on continuum elastic theory called phase field model (PFM)25,26,27,28,29,30 can straightforwardly account for the effects of short-range core reactions by incorporating the generalized stacking fault energy (γ-surface)11 from atomistic or first principle calculations, such as dislocation dissociation.31,32,33,34,35 With this advantage, the PFM model of dislocation shows great potential in modeling dislocation intersections.

The evolution of dislocations is determined by minimizing the total system energy in the PFM. The total energy terms include the elastic energy, the crystalline energy and gradient energy. The elastic energy accounts for the long-range elastic interactions among dislocations coupled with applied stress, and it is given by the Khachaturyan–Shatalov linear elasticity theory36,37,38 combined with the exact 3-D Green function. The crystalline energy and gradient energy induced by the local disregistry of atomic positions describe the short-range core–core reactions. In the original PFM,25 the simplest approximation of the crystalline energy can describe the states of dislocation gliding individually in the different slip planes, but it does not account for dislocation reaction within the same slip plane. Shen and Wang have extended the approximation of this energy by coupling different slip modes within one slip plane to describe coplanar dislocation reactions and dislocation network formation.39 However, for different slip planes, previous PFM of dislocation formulated the crystalline energy by simple linear superposition of the interplanar potential of each individual slip plane. Thus, the core interactions between dislocations gliding in intersecting slip planes are not completely considered in this particular form of the crystalline energy although the long-range elastic interactions among multiple slip modes on different slip planes are already taken into account. For example, Ruffini et al.40 adopted this crystalline energy formulation to simulate the collinear annihilation of two dislocation loops with opposite Burgers vector gliding in the intersecting slip planes, but the results showed that the two loops cannot be annihilated physically at their intersection.

In this paper, we refine the formulation of the crystalline energy in the previous PFM by coupling the potential of two intersecting planes to update PFM for the dislocation intersections, and then as a proof of concept, we simultaneously utilize the previous and the improved PFMs to study the collinear reaction of intersecting perfect dislocations in FCC or simple cubic (SC) crystals. This paper is organized as follows: in “Results and discussion” section, the previous PFM is briefly reviewed and the updated PFM with the improvement of the crystalline energy formulation is introduced. In “Methods” section, both the PFMs with or without updating the crystalline energy are applied to simulate interaction between the two intersecting dislocation loops with opposite Burgers vector in FCC crystals. The calculated result for the collinear interaction in FCC crystals is also compared with the previous simulation result using discrete dislocation dynamics to show the distinct difference between the two PFMs. And then the differences of the dislocation structures and mechanical responses between the two PFMs are discussed during the collinear junction formations and the glide dislocations interacting with forest dislocations in a SC crystal for simplicity, one by one. On the basis of these results, the main conclusion is summarized.

Results and discussion

Model

In PFM of dislocation, a set of non-conserved phase field variables η(α, m α , r) is introduced to represent the amount of relative slips in the slip plane α and the slip direction m α in units of the Burgers vector b(α, m α ). The regions with η(α, m α , r) ≠ 0 and η(α, m α , r) = 0 describe the slipped and unslipped parts in a crystal, respectively. The dislocation lines are viewed as the boundaries between the slipped and unslipped regions. The eigenstrain \(\varepsilon _{ij}^0\left( {\bf{r}} \right)\) induced by the inelastic slips can be expressed as25

$$\varepsilon _{ij}^0\left( {\bf{r}} \right) = \mathop {\sum}\limits_{\alpha ,m_\alpha } {\frac{{b_i\left( {\alpha ,m_\alpha } \right)n_j\left( \alpha \right) + b_j\left( {\alpha ,m_\alpha } \right)n_i\left( \alpha \right)}}{{2d}}\eta \left( {\alpha ,m_\alpha ,r} \right)},$$
(1)

where n j (α) is the component of the unit normal vector of the slip plane α and d is the inter-planar distance between slip planes.

The evolution of η(α, m α , r) characterizing the dislocation assembly is governed by minimizing the total system free energy. In the original formulations, the total system free energy includes the elastic energy, the crystalline energy and gradient energy. According to the careful discussions on the similarities and differences between the PFM and Peierls-Nabarro (PN) model41,42 in ref. 29, the PFM is allowed to fully converge to the PN model through some amendments. Therefore, in this study, we remove the gradient term and strictly confine Burgers vector distribution within the slip planes by using \(\eta _m^\alpha\) (α, m α , r) = \(\eta _m^\alpha\) (α, m α , r α )δ(r − r α ) in the PFM for keeping in line with the PN model, where r α is the position vector on the slip plane α and δ defined as a Dirac function is equal to one on the slip plane α. In this situation, the equilibrium dislocation core width is determined by balancing the elastic energy and the crystalline energy. Thus the total energy is expressed as

$$E^{\mathrm{tot}} = E_{\mathrm{ela}} + E_{\mathrm{cry}}.$$
(2)

The Khachaturyan-Shatalov theory provides the exact solution of the elastic energy Eela as a function of the eigenstrain and the external applied stress \(\sigma _{ij}^{{\mathrm{ext}}}\):

$$\begin{array}{*{20}{l}} {E_{ela}} \hfill & = \hfill & {\frac{1}{2}\mathop {\int}\limits_{\left| {\bf{\xi }} \right| \ne 0} {\left[ {C_{ijkl}\tilde \varepsilon _{ij}^0\left( {\bf{\xi }} \right)\tilde \varepsilon _{kl}^0\left( {\bf{\xi }} \right)^ \ast } \right.} } \hfill \\ {} \hfill & {} \hfill & {\left. { - e_i\tilde \sigma _{ij}^0\left( {\bf{\xi }} \right)\Omega _{jk}\left( {\bf{e}} \right)\tilde \sigma _{kl}^0\left( {\bf{\xi }} \right)^ \ast e_l} \right]\frac{{{\mathrm{d}}^3\xi }}{{\left( {2\pi } \right)^3}}} \hfill \\ {} \hfill & \hfill & - {{\int} {\sigma _{ij}^{{\mathrm{ext}}}} \varepsilon _{ij}^0\left( {\bf{r}} \right){\mathrm{d}}^3r - \frac{V}{2}C_{ijkl}^{ - 1}\sigma _{ij}^{{\mathrm{ext}}}\sigma _{kl}^{{\mathrm{ext}}},} \hfill \end{array}$$
(3)

where C ijkl is the elastic moduli tensor, ξ is the vector in the Fourier space, and \({\bf{e}} = {\bf{\xi }}{\mathrm{/}}\left| {\bf{\xi }} \right|\) is the unit vector along ξ. \(\tilde \varepsilon _{ij}^0\left( {\bf{\xi }} \right)\) is the Fourier transformation of \(\varepsilon _{ij}^0\left( {\bf{r}} \right)\) given by the equation \(\tilde \varepsilon _{ij}^0\left( {\bf{\xi }} \right) = {\int} {\varepsilon _{ij}^0\left( {{\bf{r}},t} \right)e^{-i{\bf{\xi }} \cdot {\bf{r}}}d^3r}\). \(\tilde \sigma _{ij}^0\left( {\bf{\xi }} \right) = C_{ijkl}\tilde \varepsilon _{kl}^0\left( {\bf{\xi }} \right)\). \({\mathrm{\Omega }}\left( e \right)_{jk} = \left( {C_{jlpk}e_le_p} \right)^{ - 1}\) is the elastic Green function, and the symbol * denotes the complex conjugation. The integral \(\smallint _{\left| {\bf{\xi }} \right| \ne 0}\) is in the Fourier space excluding the points at \(\left| {\bf{\xi }} \right| = 0\) and V is the total volume of the system. The average strain is derived as \(\bar \varepsilon _{ij} = C_{ijkl}^{ - 1}\sigma _{kl}^{\mathrm{ext}} + \bar \varepsilon _{ij}^0\) for stress-controlled condition and \(\bar \varepsilon _{ij} = \varepsilon _{ij}^{\mathrm{ext}}\) for strain-controlled condition. After substitution of Eq. (1) into Eq. (3), the elastic energy is an explicit functional of the phase field variables in the Fourier space.

The crystalline energy is given by the integral of the periodical potential f cry describing the atomic misfit energy in the dislocation core:

$$E_{\mathrm{cry}} = {\int} {f_{\mathrm{cry}}} d^3r.$$
(4)

The general expression of the periodical function fcry can be proposed as a Fourier expansion series:43

$$f_{\mathrm{cry}} = \mathop {\sum}\limits_{\bf{H}} {A\left( {\bf{H}} \right)} \left\{ {1 - {\mathrm{exp}}\left[ {i2\pi {\bf{H}} \cdot {\bf{b}}\left( {\bf{r}} \right)} \right]} \right\},$$
(5)

where b(r) = \(\mathop {\sum}\limits_{\alpha ,m_\alpha } {{\bf{b}}\left( {\alpha ,m_\alpha } \right)}\) \(\eta \left( {\alpha ,m_\alpha ,{\bf{r}}} \right)\) is the total Burgers vector, H are the reciprocal lattice vectors of the host lattice and A(H) are positive Fourier coefficients reflecting the symmetry of the crystal lattice. In the original PFM,25 the simplified approximation of fcry is formulated by imitating the periodic Peierls potential:

$$f_{\mathrm{cry}} = \mathop {\sum}\limits_{\alpha ,m_\alpha } {A{\kern 1pt} {\mathrm{sin}}^2\pi } \eta \left( {\alpha ,m_\alpha ,{\bf{r}}} \right),$$
(6)

where A = μb2/(2π2d2), μ is the shear modulus and b is the magnitude of the Burgers vector for the corresponding slip system. In this expression of fcry given by Eq. (6), there is no coupling among the different phase field variables, therefore the core reactions among dislocations are not considered. Shen and Wang have demonstrated the limitation of the crystalline energy derived from Eq. (6) in details and introduced the new expressions of this energy to account for the dislocation core-core reactions in ref. 39.

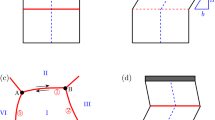
FCC {111} slip planes are chosen for discussion by Shen and Wang.39 As shown in Fig. 1, the total Burgers vector caused by glide of the three perfect dislocations on the single (111) α plane is given:

$${\bf{b}}^\alpha \left( {\bf{r}} \right) = \eta _1^\alpha \left( {\bf{r}} \right){\bf{b}}_1^\alpha + \eta _2^\alpha \left( {\bf{r}} \right){\bf{b}}_2^\alpha + \eta _3^\alpha \left( {\bf{r}} \right){\bf{b}}_3^\alpha ,$$
(7)

where \({\bf{b}}_{\mathrm{1}}^\alpha\) = a/2(i − k), \({\bf{b}}_{\mathrm{2}}^\alpha\) = a/2(j − i), \({\bf{b}}_{\mathrm{3}}^\alpha\) = a/2(k − j), a is the lattice parameter, i, j, k are unit vectors of the coordinate system. The total Burgers vector on the (111) plane bα(r) is expressed by the field variables:

$${\bf{b}}^\alpha \left( {\bf{r}} \right) = \frac{a}{2}\left[ {\left( {\eta _{\mathrm{1}}^\alpha - \eta _{\mathrm{2}}^\alpha } \right){\bf{i}} + \left( {\eta _{\mathrm{2}}^\alpha - \eta _{\mathrm{3}}^\alpha } \right){\bf{j}} + \left( {\eta _{\mathrm{3}}^\alpha - \eta _{\mathrm{1}}^\alpha } \right){\bf{k}}} \right].$$
(8)

A periodical potential that reflects the symmetry in FCC crystal is employed in ref. 39, and it is dependent on the Burgers vector \({\bf{b}} = \left( {b_i,b_j,b_k} \right)\):

$$f\left( {\bf{b}} \right) = A\left( {1 - {\mathrm{cos}}{\kern 1pt} 2\pi \frac{{b_i}}{a}{\mathrm{cos}}{\kern 1pt} 2\pi \frac{{b_j}}{a}{\mathrm{cos}}{\kern 1pt} 2\pi \frac{{b_k}}{a}} \right).$$
(9)

Substituting Eq. (8) into Eq. (9), the periodical potential is

$$f_{\mathrm{cry}}^\alpha = A\left[ {1 - {\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _2^\alpha - \eta _3^\alpha } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _3^\alpha - \eta _1^\alpha } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _1^\alpha - \eta _2^\alpha } \right)} \right].$$
(10)
Fig. 1
figure 1

Schematic of two intersecting slip planes (111) and \(\left( {\bar 1\bar 11} \right)\) in a FCC crystal. The Burgers vectors of six types of perfect dislocations in the two planes are shown

Full size image

Therefore, the crystalline energy derived from Eq. (10) is easily proved to be able to describe the core reactions among dislocations gliding in single (111) α plane such as \({\bf{b}}_1^\alpha + {\bf{b}}_2^\alpha = - {\bf{b}}_3^\alpha\). To derive a more general expression of the crystalline energy including different slip planes, however, Shen and Wang adopt the simple linear superposition of the potential given by Eq. (10). According to this simplest approximation, the expression of the integrand of the crystal energy for two intersecting slip planes (111) α and \(\left( {\bar 1\bar 11} \right)\) β in FCC crystal as shown in Fig. 1 is given here for simplicity:

$$\begin{array}{c}f_{\mathrm{cry}} = A\left[ {2 - {\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _2^\alpha - \eta _3^\alpha } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _3^\alpha - \eta _1^\alpha } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _1^\alpha - \eta _2^\alpha } \right)} \right.\\ \left. { - {\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _2^\beta - \eta _3^\beta } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _3^\beta - \eta _1^\beta } \right){\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _1^\beta - \eta _2^\beta } \right)} \right].\end{array}$$
(11)

In this formulation, there is coupling among the phase field variables in single slip planes but no coupling among the phase field variables in different slip planes. Thus the crystalline energy given by Eq. (11) does not take into account the core reactions between dislocations gliding in intersecting slip planes in ref. 39. For examples, we consider the collinear reaction between two dislocations with Burgers vector \({\bf{b}}_2^\alpha = a\left[ {\bar 110} \right]{\mathrm{/}}2\) gliding on the (111) plane and \({\bf{b}}_2^\beta = a\left[ {1\bar 10} \right]{\mathrm{/}}2\) gliding on the \(\left( {\bar 1\bar 11} \right)\) plane as shown in Fig. 1, respectively. When the two dislocations collide, they can annihilate completely, leaving no product. However, according to Eq. (11), the integrand of the crystalline energy at the intersection of these two planes is fcry = A\(\left( {{\mathrm{sin}}^2{\kern 1pt} \pi \eta _2^\alpha + {\mathrm{sin}}^2{\kern 1pt} \pi \eta _2^\beta } \right)\), which is twice of that of either unreacted dislocation as shown in Eq. (6) rather than zero.

To describe the core reactions among the dislocations gliding in the intersecting slip planes, the expressions of the crystalline energy need to be improved. To proceed, we consider two intersecting slip planes (111) and \(\left( {\bar 1\bar 11} \right)\) in FCC crystal as shown in Fig. 1. Since the dislocation reactions at the intersection may be influenced by the dislocations on both slip planes, the total Burgers vector is expressed by the combination of all phase field variables on the two planes:

$$\begin{array}{*{20}{l}} {{\bf{b}}\left( {\bf{r}} \right)} \hfill & = \hfill & {\eta _1^\alpha \left( {\bf{r}} \right){\bf{b}}_1^\alpha + \eta _2^\alpha \left( {\bf{r}} \right){\bf{b}}_2^\alpha } \hfill \\ {} \hfill & {} \hfill & { \hskip-9pt + \eta _3^\alpha \left( {\bf{r}} \right){\bf{b}}_3^\alpha + \eta _1^\beta \left( {\bf{r}} \right){\bf{b}}_1^\beta } \hfill \\ {} \hfill & {} \hfill & { \hskip-9pt + \eta _2^\beta \left( {\bf{r}} \right){\bf{b}}_2^\beta + \eta _3^\beta \left( {\bf{r}} \right){\bf{b}}_3^\beta } \hfill \\ {} \hfill & {\mathrm{ = }} \hfill & {b_i{\bf{i}} + b_j{\bf{j}} + b_k{\bf{k}},} \hfill \end{array}$$
(12)

where b i  = \(\frac{a}{2}\left( {\eta _1^\alpha - \eta _2^\alpha - \eta _1^\beta + \eta _2^\beta } \right)\), b j  = \(\frac{a}{2}\left( {\eta _2^\alpha - \eta _3^\alpha - \eta _2^\beta + \eta _3^\beta } \right)\), b k  = \(\frac{a}{2}\left( {\eta _3^\alpha - \eta _1^\alpha + \eta _3^\beta - \eta _1^\beta } \right)\). Substituting Eq. (12) into Eq. (9), the integrand of the crystalline energy is

$$\begin{array}{*{20}{l}} {f_{\mathrm{cry}}} \hfill & = \hfill & {A\left[ {1 - {\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _2^\alpha - \eta _3^\alpha - \eta _2^\beta + \eta _3^\beta } \right)} \right.} \hfill \\ {} \hfill & {} \hfill & {{\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _3^\alpha - \eta _1^\alpha + \eta _3^\beta - \eta _1^\beta } \right)} \hfill \\ {} \hfill & {} \hfill & {\left. {{\mathrm{cos}}{\kern 1pt} \pi \left( {\eta _1^\alpha - \eta _2^\alpha - \eta _1^\beta + \eta _2^\beta } \right)} \right].} \hfill \end{array}$$
(13)

We now use this improved expression of the integrand of the crystalline energy to account for the collinear interaction. Equation 13 is a generalization of Eq. (11). On the individual slip plane, Eq. (13) is the same as Eq. (11), while at the intersection on both slip planes, Eq. (13) has the coupling term with respect to the Burgers vectors on both slip planes and Eq. (11) does not. For example, according to Eqs. (11), (12), and (13), when two dislocations with Burgers vector \({\bf{b}}_2^\alpha\) gliding on the (111) plane and \({\bf{b}}_2^\beta\) gliding on the \(\left( {\bar 1\bar 11} \right)\) plane meet each other, the integrand of the crystalline energy at the intersection is \(f_{\mathrm{cry}} = A{\kern 1pt} {\mathrm{sin}}^2\pi\) \(\left( {\eta _2^\alpha - \eta _2^\beta } \right)\), which is exactly equal to zero if \(\eta _2^\alpha = \eta _2^\beta\). Therefore the core annihilation in the collinear interaction is correctly represented by the improved form of the crystalline energy.

For the description of the core reactions in dislocation intersections, we have briefly discussed the limitations of the crystalline energy given by Eq. (11) in the previous PFM and introduced the new expressions of this energy term given by Eq. (13) in the improved model. It should be noted that both Eq. (11) in the previous PFM and Eq. (13) in the improved model are special forms of the general expressions of Eq. (5), however Eq. (13) appears as a better approximation describing collinear interactions among dislocations from intersecting glide planes. Since the integrands of the crystalline energy expressed by Eqs. (5) and (13) are solely dependent on the total Burgers vector, they do not provide any barriers in the crystalline energy for cross-slip of a perfect dislocation according to the discussions in ref.39.

Besides the collinear interaction, other binary junctions formed by the perfect dislocation intersections in FCC crystals are the Hirth lock, the glissile junction and the Lomer lock. We carefully check the changes in the PFM with the crystalline energy of Eq. (11) and the PFM with Eq. (13) in describing the core energy for all the four kinds of junctions in FCC crystals, and the evaluation results are shown in Table 1. In this evaluation, we assume that the two dislocations before reaction and the product junction after the reaction have equivalent slip characterized by the field variable η. From Table 1, it is easily found that the crystalline energy after the reaction derived from Eq. (11) in the PFM model is twice as that of either unreacted dislocation for all the four junction types because of the simple linear superposition. On the other hand, the crystalline energy derived by Eq. (13) in the improved PFM model correctly describes the core energy of the product junction for all the four types of reactions, since Eq. (13) is a function of solely the total Burgers vector. Comparing the two energy terms derived from Eqs. (11) and (13), only the Hirth lock can be described by the PFM with the crystalline energy of Eq. (11).

Table 1 Four kinds of binary junctions in FCC crystals
Full size table

It is worth noting that the GSFE similar to γ surface is not incorporated into the crystalline energy yet. Describing the intersections of partial dislocations requires more accurate 3D periodical potential associated the γ surface as the integrand of the crystalline energy, and this will be addressed in the future study.

For the slip systems with two slip planes as shown in Fig. 1, the evolution processes of the six phase field variables are governed by the time-dependent Ginzburg-Landau kinetic equations:25

$$\frac{{\partial \eta _n^m\left( {{\bf{r}},t} \right)}}{{\partial t}} = - L\frac{{\delta E^{tot}}}{{\delta \eta _n^m\left( {{\bf{r}},t} \right)}},$$
(14)

where m = α, β, n = 1, 2, 3, t is the time, L is the positive kinetic coefficients related to dislocation mobility. The equilibrium configuration corresponds to \(\delta E^{tot}{\mathrm{/}}\delta \eta _n^m = 0\).

The collinear interaction is the strongest of all the reactions and can provide considerable contribution to strain hardening.7 Thus we focus our discussions on the collinear interactions between perfect dislocations lying in the intersecting slip planes.

Intersecting of two dislocation loops with the opposite Burgers vector

The interaction between two dislocation loops with collinear Burgers vector gliding in two intersecting slip planes in an FCC crystal is considered here. A dislocation loop with Burgers vector \({\bf{b}}_2^\alpha\) on the (111) plane and another dislocation loop with Burgers vector \({\bf{b}}_2^\beta\) on the \(\left( {\bar 1\bar 11} \right)\) plane are initially located in their own planes, as shown in Fig. 2a. The computational cell is 128a × 128a × 128a and remote periodic boundary conditions are used. The two dislocation loops can expand under an applied stress σ11 = −0.05μ, and interact with each other when they reach the intersecting line of the two slip planes. Physically, the two loops will be annihilated at their intersection because of \({\bf{b}}_2^\alpha + {\bf{b}}_2^\beta = 0\). The simulation results of the dislocation intersection by the PFMs with the crystalline energy of Eqs. (11) or (13) are shown in Fig. 2b, c respectively, and the dislocation line is represented by the non-zero crystalline energy distribution fcry. In Fig. 2b, as the same as the simulation results of Ruffini et al.40 a dislocation segment with non-zero crystalline energy along the intersection line still forms during the reactions of the two loops. It is not surprising because the previous PFM employs the crystalline energy of Eq. (11) formulated by a linear superposition which is not equal to zero in this situation. Contrary to the result of the PFM with the crystalline energy of Eq. (11), simulation by the improved PFM employing the crystalline energy formulation of Eq. (13) displays that the two loops are annihilated when they meet each other as shown in Fig. 2c, because the Eq. (13) is formulated by a coupling form and the integrand is always zero while two dislocation segments are fully encountered. These results indicate that the PFM with the crystalline energy of Eq. (13) can correctly capture the collinear annihilation between the intersecting dislocations with opposite Burgers vector.

Fig. 2
figure 2

Collinear reaction between two dislocation loops with Burgers vector \({\bf{b}}_2^\alpha = a\left[ {\bar 110} \right]{\mathrm{/}}2\) and \({\bf{b}}_2^\beta = a\left[ {1\bar 10} \right]{\mathrm{/}}2\) in the slip planes (111) and \(\left( {\bar 1\bar 11} \right)\) respectively under an applied stress σ11 = −0.05μ in a FCC crystal with the size of (128a)3. a Initial configuration. b Results of the PFM with the crystalline energy of Eq. (11). c Results of the PFM with the crystalline energy of Eq. (13)

Full size image

Formations of the collinear junctions

A multiscale approach was employed to investigate the dependence of the collinear annihilation on the orientation of the dislocation lines in an FCC crystal by Madec et al. in ref.7. In this subsection, we also study the same problem to check the capability of the previous and improved PFMs. Figure 3a shows the initial configuration of two intersecting dislocation in a FCC crystal. Dislocation segment with Burgers vector \({\bf{b}}_2^\alpha = a\left[ {\bar 110} \right]{\mathrm{/}}2\) on the (111) plane and another dislocation segment with Burgers vector \({\bf{b}}_2^\beta = a\left[ {1\bar 10} \right]{\mathrm{/}}2\) on the \(\left( {\bar 1\bar 11} \right)\) plane are intersected at their midpoint. Initially, the two segments are straight and make angles of ϕα and ϕβ with the intersection \(\left[ {1\bar 10} \right]\) of the two slip planes respectively. In the absence of applied stress, when the two dislocation segments are pinned at their ends, they are allowed to relax driven by their interaction forces until they reach a stable configuration. Three states appear in the final configuration:7 The two intersecting dislocations can zip a junction when collinear annihilation is energetically favorable, or mutually pin each other at their intersection point at a crossed state, or move apart from each other under their repulsive forces. In the PFMs with the crystalline energy of Eqs. (11) or (13), such structures and formation processes of the dislocation configurations are captured by numerically solving Eq. (14) in the periodic computational domain (128a)3. Figure 3b,c show the simulated final equilibrium structures of the two intersection dislocations under ϕα = ϕβ = 45° without applied stress by using the PFMs with the crystalline energy of Eqs. (11) or (13), respectively. The simulated results in Fig. 3b show that the two dislocations move apart from each other. However, in Fig. 3c, partial annihilation of the two dislocation lines produces a junction with zero Burgers vector, which is the same as the simulation results by DDD for ϕα = ϕβ = 45° in ref. 7. As shown in Fig. 2b, c, the junction formed by collinear annihilation in the PFM with the crystalline energy of Eq. (13) leads to a perfect crystal without generating any kind of energy, but residual crystalline energy still exists for the collinear junction in the PFM model with the crystalline energy of Eq. (11). Therefore, for the two intersecting dislocations shown in Fig. 3a, junction formation is energetically favorable in the improved PFM. Obviously, the two dislocations repel each other in the initial state as shown in Fig. 3a, but they still zip a junction simulated by the improved PFM in Fig. 3c. Madec et al. in ref. 7 have also given the reason: the dislocation lines with flexibility can annihilate each other through bending and twisting, although they are elastically repulsive.

Fig. 3
figure 3

Collinear junction formed by the two dislocation segments with Burgers vectors \({\bf{b}}_2^\alpha = a\left[ {\bar 110} \right]{\mathrm{/}}2\) and \({\bf{b}}_2^\beta = a\left[ {1\bar 10} \right]{\mathrm{/}}2\) in the slip planes (111) and \(\left( {\bar 1\bar 11} \right)\) making angles of ϕα and ϕβ with the \(\left[ {\bar 1{\mathrm{1}}0} \right]\) intersection of the two slip planes respectively in a FCC crystal with the size of (128a)3. a Initial configuration. b, c The equilibrium configurations simulated by b the previous and c the improved PFMs for ϕα = ϕβ = 45°. d–f Mapping of the collinear interaction with respect to ϕα and ϕβ from d the previous PFM, e the improved PFM and f the DDD model in ref. 7, the symbols indicate the equilibrium configuration: squares indicate collinear annihilation, circles indicate repulsive interaction and crosses indicate crossed state

Full size image

We continue to investigate the equilibrium configurations of the collinear junctions with varying ϕα and ϕβ ranging from −180° to 180° by the PFMs with the crystalline energy of Eqs. (11) or (13). By using squares to indicate junction formation, circles to indicate repulsive interaction and crosses to indicate crossed state, the final state of the two intersecting dislocation simulated by the PFMs with the crystalline energy of Eq. (11) or (13) are mapped with respect to ϕα and ϕβ in Fig. 3d, e, respectively. For direct comparisons with the DDD simulation results, Fig. 3f shows the mapping of the collinear interaction obtained from ref. 7. The results simulated by the improved PFM in Fig. 3e are in good agreement with the DDD’s results in Fig. 3f. In the improved PFM and the DDD model, the collinear annihilations appear in a vast majority in the relaxed configurations, although half of the initial configurations correspond to segments that are elastically repulsive. On the other hand, in the PFM with the crystalline energy of Eq. (11), the probability of occurrence of collinear junctions is relatively low, which is against the theory that the high strength of the collinear reaction is due to intrinsic stability and high probability of occurrence.7

Glide dislocations interacting with forest dislocations

In this subsection, the effects of the collinear annihilation emerging only in the improved PFM on the stress-strain curves of the crystalline solids are investigated. For simplicity, we consider a simple cubic (SC) crystal with the size of (128a)3 and only two slip systems are activated here. The glide dislocations are located in the parallel (001) planes and the forest dislocations are lying in the (010) planes. External pure shear strain ε13 is applied to drive the glide dislocations to move and interact with the forest dislocations, and we simultaneously calculate the corresponding shear stress σ13 to obtain the stress-strain curve. The initial dislocation density of this system is ρ = 5 × 1016/m2.

Figure 4a shows the strain-controlled stress-strain curves of glide dislocations interacting with forest dislocations obtained from the simulation results of the PFMs with the crystalline energy of Eqs. (11) or (13) under the quasi-static conditions. The results obviously show that both the yield stress and the flow stress in the improved PFM with the crystalline energy of Eq. (13) are higher than the ones in the PFM with the crystalline energy of Eq. (11) because of low energy state of large dislocation junctions formed by collinear annihilations. It is important to note that the yield stress and elastic strain limit predicted by the PFMs here and elsewhere33 are much higher than the ones obtained by the DDD models,7 since limited activated slip systems are considered in single crystals within small computational domain. In this limited computational system, the strain-controlled stress–strain curves here exhibiting features of work softening is very different from the stress-controlled curves exhibiting features of work hardening. The unzipping of the junction and further slip of the glide dislocation leads to an abrupt stress drop after yielding in the strain-controlled case but causes a strain burst in the stress-controlled case,33 and the collecting behaviors of many unzipping events result in the whole stress-strain curves. In addition, dislocation annihilations reduce the dislocation density, and dislocation multiplication such as Frank-Read source is limited in the small computational domain. This is possibly why no work hardening is observed.

Fig. 4
figure 4

Glide dislocations interact with forest dislocations in a FCC crystal with the size of (128a)3. a Simulated results of the stress-strain curves by the PFMs. b, c Simulated dislocation structures at ε13 = 8% corresponding to (a) by (b) the PFM with the crystalline energy of Eq. (11) and c the PFM with the crystalline energy of Eq. (13), the segments colored in purple are glide dislocations and in orange are the forest dislocations

Full size image

For direct view of the dislocation evolution, we capture the dislocation structures of the crystal at ε13 = 8% in the PFMs with the crystalline energy of Eqs. (11) or (13) as shown in Fig. 4b, c, respectively. It is found that the dislocation density in the improved PFM is much lower, because the dislocation annihilations occur only in this model. Thus, the inability of simulating the collinear annihilation in the PFM with the crystalline energy of Eq. (11) can significantly affect the plastic flow in multislip systems. We should note the reason for choosing SC crystals here. In the SC crystals the activated planes are parallel to the coordinate planes, thus there are relatively low “image” stresses, which have little effects on the forest dislocations under the applied pure shear strain. However for the activated intersecting {111} planes in FCC crystals, the relatively large “image” forces are generated when the periodic boundary conditions are used. The forest dislocations in FCC crystals in the small computational domain are unstable and always slip away before reacting with the glide dislocations. One has to increase the size of the computational domain to capture glide dislocations interacting with forest dislocations in FCC crystals by using the improved PFM.

To further explain the effects of the dislocation annihilations on the mechanical response in details, we study the interaction between a single glide dislocation and a single forest dislocation by the PFMs with the crystalline energy of Eqs. (11) or (13) in a SC crystal with the size of (128a)3. A screw dislocation segment with Burgers vector \({\bf{b}}_0^\alpha = a\left[ {\bar 100} \right]\) on the (001) plane tends to transmit across an intersecting forest edge dislocation with Burgers vector \({\bf{b}}_0^\beta = a\left[ {100} \right]\) on the (010) plane under an external applied stress τ13 as shown in Fig. 5a. Initially, the two dislocation segments are pinned at their ends. The transmission processes under τ13 = 0.05μ simulated by the PFMs with the crystalline energy of Eqs. (11) or (13) are shown in Fig. 5b, c, respectively. In the PFM with the crystalline energy of Eq. (11) as shown in Fig. 5b, the screw dislocation easily transmits across the edge dislocation and continues to glide in the slip plane, indicating that 0.05μ is sufficient to overcome the barrier of the edge dislocation. However, in the PFM with the crystalline energy of Eq. (13) as shown in Fig. 5c, the glide dislocation is blocked by the forest dislocation through collinear annihilation, higher applied stress (nearly 0.09μ) is required to unzip the collinear junction and drive the glide dislocation to move. Full annihilation of the interacting dislocation segments occurring only in the improved PFM make the collinear junction much stronger due to its zero energy state, thus the glide dislocation needs higher applied stress to unzip the junction and transmit across the forest dislocation as compared with the PFM with the crystalline energy of Eq. (11). This required higher unzipping and transmission stress also can give the reason of the higher yield stress and the higher flow stress in the stress-strain curve simulated by the improved PFM as shown in Fig. 4a.

Fig. 5
figure 5

A glide screw dislocation segment with Burgers vector \({\bf{b}}_0^\alpha = a\left[ {\bar 100} \right]\) on the (001) plane transmits across a forest edge dislocation with Burgers vector \({\bf{b}}_0^\beta = a\left[ {100} \right]\) on the (010) plane under an external applied stress τ13 = 0.05μ in a SC crystal with the size of (128a)3. a Initial configuration. b Results of the PFM with the crystalline energy of Eq. (11). c Results of the PFM with the crystalline energy of Eq. (13)

Full size image

In summary, we have improved expressions of the crystalline energy in previous PF models to describe the core interactions between the perfect dislocations gliding on the intersecting planes in FCC or SC crystalline materials. The improved formulation of this energy is fully dependent on the total Burgers vector of all the slip planes at the intersection line of these slip planes and automatically accounts for the reactions during dislocation intersections such as collinear annihilation, Lomer lock and so on. The improved and previous PFMs have been applied to study the collinear interactions, and the collinear annihilation appears only in the results simulated by the improved PFM. The collinear annihilation absence in the previous PFM strongly affects the formation of collinear junction and stress-strain response of the crystals. These applications of the improved and previous PFMs indicate that the improvement is absolutely necessary for PFM of dislocation intersections. Additionally, the improved model may be extended with the help of 3D potentials associated γ surface to quantify the cross-slip and core dissociation processes within multiple slip planes in future.

Methods

By substituting Eqs. (1), (3), (4), and (11) into Eq. (2) in the previous PFM or by substituting Eqs. (1), (3), (4), and (13) into Eq. (2) in the improved PFM, the total system energy Etot becomes functional of the six phase field variables. By using a finite difference method combined with FFT algorithm, Eq. (14) can be numerically solved in its reduced form with all physical lengths measured in unit a, all the stresses in unit μ (the shear modulus) and the time in unit t(t = 1/Lμ). The dimensionless coefficient in the crystalline energy is A* = 1/2π2. All the simulations are performed in the computational cell 128 × 128 × 128 with periodic boundary conditions.

Data availability

The data and codes supporting the findings of this study are available from the corresponding author on reasonable request.