Abstract
A passivation layer called the solid electrolyte interphase (SEI) is formed on electrode surfaces from decomposition products of electrolytes. The SEI allows Li+ transport and blocks electrons in order to prevent further electrolyte decomposition and ensure continued electrochemical reactions. The formation and growth mechanism of the nanometer thick SEI films are yet to be completely understood owing to their complex structure and lack of reliable in situ experimental techniques. Significant advances in computational methods have made it possible to predictively model the fundamentals of SEI. This review aims to give an overview of state-of-the-art modeling progress in the investigation of SEI films on the anodes, ranging from electronic structure calculations to mesoscale modeling, covering the thermodynamics and kinetics of electrolyte reduction reactions, SEI formation, modification through electrolyte design, correlation of SEI properties with battery performance, and the artificial SEI design. Multi-scale simulations have been summarized and compared with each other as well as with experiments. Computational details of the fundamental properties of SEI, such as electron tunneling, Li-ion transport, chemical/mechanical stability of the bulk SEI and electrode/(SEI/) electrolyte interfaces have been discussed. This review shows the potential of computational approaches in the deconvolution of SEI properties and design of artificial SEI. We believe that computational modeling can be integrated with experiments to complement each other and lead to a better understanding of the complex SEI for the development of a highly efficient battery in the future.
Similar content being viewed by others
Introduction
Solid electrolyte interphase (SEI) in Li-ion batteries
Rechargeable lithium-based batteries1,2,3 have enabled a revolution from tiny electronics to aerospace, gradually replacing the conventional batteries like alkaline, Ni-Cd, and lead-acid batteries due to their higher energy density. It has been more than two decades since the first Li-ion battery (LIB) was commercialized by SONY in 1991.1,3 The energy density has been increased stepwise by approximately 5 Wh kg−1 every year, for the past several decades, and is approximately 160 Wh kg−1 now. However, the current energy density still does not meet the needs of vehicle electrification (500–700 Wh kg−1).2
One of the main obstacles restraining the improvement of lithium-based battery performance is the electrode/electrolyte interface, which is the key to understand battery electrochemistry, as it is where the electron and Li-ion combine and then get stored in the electrode, via intercalation, alloying, or simply as Li metal.4,5,6,7,8,9 This interface is usually further complicated by a passivation layer on the electrode. The understanding of this passivation layer on negative electrodes started from its observation on lithium metal soaked in non-aqueous electrolyte by Dey.4 Peled5 introduced the concept of solid electrolyte interphase in 1979 as an electronically insulating and ionically conducting passivation layer, formed between the electrode and electrolyte, acting as a solid electrolyte; and thus, it is named as the SEI. This model was further enriched with the inclusion of compositional information observed over two decades and summarized by Peled et al.6 in 1997 and by Aurbach et al.7 in 1999. On one hand, a dense and intact SEI can restrict the electron tunneling and thus prohibit further reduction of the electrolyte, which is vital for the chemical and electrochemical stability of a battery. On the other hand, SEI formation and growth consume active lithium and electrolyte materials, leading to capacity fading, increasing battery resistance, and poor power density. Until today, SEI is still regarded as “the most important but least understood (component) in rechargeable Li-ion batteries” which can be attributed to the complexity of the chemical and electrochemical reactions to form it and insufficient direct measurement of its physical properties.8,9
The formation of SEI layer occurs when the redox potential of the electrodes used in a battery lies outside the electrochemical window of the electrolyte, which was schematically shown by Goodenough and Kim10 (Fig. 1a). When the lowest unoccupied molecular orbital (LUMO) of the electrolyte is higher than the Fermi energy of anode, the electrolyte is stable in the battery; otherwise, the electrolyte can be reduced. Likewise, the electrolyte is expected to be stable if the highest occupied molecular orbital (HOMO) of the electrolyte is lower than the cathode Fermi energy level. The density functional theory (DFT) computed electrochemical windows of the common electrolyte components11,12,13,14,15 have been summarized in the past.16 However, Fig. 1a is oversimplified for the electrolyte, which typically contains salts dissolved in solvents and mixed with various additives. These details can shift the reduction potentials dramatically, as demonstrated in Fig. 1b.17 Specifically, F-transfer reactions during reduction reaction occur for many anions at potentials, where LUMO calculations would indicate they should be stable. Similarly, H-transfer reactions are often coupled with electrolyte oxidation, so the oxidation potential is lower than the calculated HOMO.18,19,20 Nevertheless, the LUMO of most electrolyte components are higher than the lithiated graphite (~0.1 eV) and lithium metal (0 eV) voltage, and hence reduction of electrolyte on the anode is expected. In comparison to the SEI on the cathode, the SEI on the anode is more unstable due to the evident reduction reactions and the larger volume expansion of anode materials.21 Due to its importance to battery performance and durability, extensive investigations have been conducted on anode SEI films. The failure mechanisms for SEI on different anodes vary dramatically due to their unique lithiation/delithiation characteristics. Therefore, this review will focus on SEI formed on the anode materials. While many review articles exist in the literature,7,8,9,22,23,24,25 this one will focus on computational studies related to SEI formation, growth, properties, functionalities, as well as electrolyte and artificial SEI design.
a Schematic open-circuit energy diagram of an electrolyte. ΦA and ΦC are the anode and cathode work functions. Eg is the electrolyte’s electrochemical stability window. μA and μC are the redox potential of the anode and cathode, respectively10 (Copyright: American Chemical Society). b Computed reduction potential for several common solvents, additives, and desolated ions. Data compiled from Delp et al.17
The anode SEI usually consists of reduction products of electrolytes formed through the reactions between electrode and electrolytes due to the electron leakage from the anode.7,8,9 Research over the past four decades has contributed to an extensive understanding of the SEI formation and composition26,27,28,29 and this understanding has been summarized in other reviews.22,23,24 Briefly, the SEI is a thin film with a complex and heterogeneous sub-structure. The SEI film can be viewed as a multi-layered structure—an inorganic inner layer near the electrode/SEI interface (Li2CO3, LiF, and Li2O), that allows Li+ transport; and an organic (dilithium ethylene glycol dicarbonate (Li2EDC) and ROLi, where R depends on the solvent) outer layer, which is heterogeneous, porous, and permeable to both Li+ and electrolyte solvent molecules, near the SEI/electrolyte interface.6,7,8,22,23,24,30,31 The in-plane structural and compositional heterogeneity of SEI was resolved recently. Formation of the SEI structure was observed by in situ electrochemical atomic force microscopy (AFM) on a graphite electrode.32 The three-dimensional multi-layer SEI structure and its mechanical properties were measured by scanning force spectroscopy for a Si electrode.33 In a more comprehensive view, SEI is a multi-layered film, wherein each layer of the SEI has a mosaic structure whose composition, structure, and properties evolve with time. Different components in the SEI, as well as their properties, influence the performance of SEI in coordinated complex ways.8,25,34 The progressive understanding of SEI over the past 50 years has been summarized in Fig. 2.
A brief history of SEI on negative electrodes, from its discovery, understanding, to design, was summarized from experiments and calculations in the past four decades. a: Early in 1970, Dey4 first observed the passivation layer on lithium metal. b The effective SEI layer on graphite was confirmed in 1990.42 c In 1979, Peled5 introduced the concept of SEI (Copyright: The Electrochemical Society). Various experimental works started to report the chemistry of SEI and subsequently proposed the formation mechanisms of the SEI. Among them, d Nazri and Muller26 and Aurbach et al.27 identified Li2CO3 as one of the main components in SEI in 1985 and 1987, respectively. Combined with this chemical information, e Peled6 pictured SEI as a mosaic structure and translated it into an equivalent circuit model in 1997 (Copyright: The Electrochemical Society). f Aurbach et al.7 illustrated the formation process of SEI starting from electrolyte reduction on electrode surface (Copyright: Elsevier). g Direct observation of the time evolution of the multi-component and multi-layer SEI formation was observed by Cresce et al.32 in 2014 using in situ electrochemical AFM (Copyright: American Chemical Society). h In 2000–2001, quantum chemical calculations were employed to simulate electrolyte reduction and oxidation reaction pathways that contribute to SEI formation12,14,15 (Copyright: Elsevier). i In 2004, physics-based continuum models were developed to simulate SEI growth, assuming SEI is mainly Li2CO3.203 However, many properties were still missing. j In 2010, Xu et al.172 measured the Li-ion transport energy barrier from experiment (Copyright: American Chemical Society). k Assuming the inorganic layer of SEI is Li2CO3, Shi et al.31 calculated the Li-ion diffusion in Li2CO3 via a “knock-off’” mechanism and, together with the porous organic layer, they proposed the two-layer/two-mechanism model (Copyright: American Chemical Society). g The mechanical property, namely, the Young’s Modulus of SEI on a silicon anode, was measured by Zheng et al.33 and they revealed modulus map along with the SEI structure map (Copyright: Royal Society of Chemistry). l The fundamental understanding of SEI lead to artificial SEI design. Using atomic layer deposition, Jung et al.220 deposited nm thick Al2O3 coatings on an assembled graphite anode and demonstrated improved durability (Copyright: John Wiley & Sons). m Kozen et al.221 used ALD coating to protect a Li metal electrode in 2015 (Copyright: American Chemical Society), 45 years after SEI was observed on Li metal in the non-aqueous electrolyte
The challenges of designing SEI for Li-ion batteries
Two major unknowns have been hindering the “design” of SEI films for current lithium-based battery. Firstly, the electrolyte reduction reactions near the electrode surface leading to this complicated structure are unclear. Secondly, for such a complicated structure, the structure–property relationships are largely unknown. Because of these two unknowns, the design of SEI has always been a trial-and-error process. Due to the importance of SEI, the battery field has been constantly seeking new ways to modify the SEI formed inside of Li-ion battery cells during cycling (referred as “in vivo” design to make an analogy with living cells) or by depositing an artificial SEI coating on the electrode before cell-assembly (referred as “in vitro” design). The ultimate goal is to achieve less irreversible capacity loss and to reduce interface resistance for improved battery performance. The in vivo SEI is usually obtained via different additives. In contrast, the in vitro SEI design is expected to be more controllable compared to the in vivo modification due to the complex parasitic reactions at the anode/electrolyte interface.
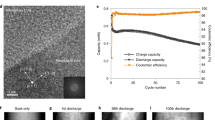
Although the SEI was first observed on lithium electrode in non-aqueous electrolytes, the metallic lithium anode was replaced by graphite anode due to safety reasons.35 To achieve high energy density in LIBs, high-capacity electrodes such as Si, Sn, Sb, and their alloys were introduced3,36 and lithium metal gained renewed interest owing to its high specific capacity, low density, and lowest redox potential.37,38,39,40,41 The SEI on graphite can provide acceptable life in commercial Li-ion batteries, even though more than 50% capacity loss in a well-engineered LIB can be attributed to the SEI growth.42,43,44 In contrast, SEI design faces more challenges for the development of high-capacity anode materials. For example, the SEI is unstable for an anode material like Si after repeated cycling due to the large volume change accompanying its high capacity.36 The large volume change induces SEI damage, leading to low Coulombic efficiency (as shown in Fig. 3). Nano-structured Si can avoid Si fracture, but because of the high surface area, it must be optimized along with a chemically and mechanically stable SEI in order to avoid SEI mechanical–electrochemical degradation and to achieve high Coulombic efficiency.45 In terms of lithium metal anode, dendrites, which can lead to short circuits and electronically disconnected lithium, is still an unresolved issue.37,39,40,41 The origin of the issue is the extremely active Li metal surface, as SEI has to form on Li surfaces. As the Li metal surface becomes rough, mossy, and dendritic, continuous parasitic SEI growth occurs, leading to a low Coulombic efficiency. Thus, an ideal SEI film should restrain dendrite growth, surface roughening, and reduce the unexpected side reactions at the SEI/electrolyte interface.23,40 These new SEI design challenges require coupled and systematic design approaches.37
SEI failure mechanisms for different anode materials. a The SEI is relatively stable on graphite electrode but still can crack due to the volume expansion and contraction during cycling; b more SEI mechanical failure is expected on Li storage metals, such as Si or Sn, due to larger volume change; and c the surface morphology change of metallic lithium is accompanied by new SEI formation in each cycle233 (Copyright: The Electrochemical Society)
Scope of this review: modeling of SEI on negative electrode surface
It is still difficult for current experimental methods to characterize the SEI properties (beyond chemical composition), especially the thermodynamic and kinetic properties. Fortunately, predictive modeling can compensate for the limitations of experimental research and play an important role in understanding battery science with the length scales ranging from electrons to the full battery system.38,46,47,48,49,50,51,52,53
This review will focus on modeling efforts in the investigation of SEI films on the anode. We not only provide comments on the existing state-of-the-art research but also dedicate efforts to reveal the future research needs on this topic. We will first discuss the modeling of SEI formation, especially the initial reduction mechanisms of the electrolyte in the section “Modeling of electrolyte reduction mechanisms”. How these insights lead to the computational design of electrolyte additives will be discussed in the section “In vivo modification and design of the SEI”. In the section “Correlation of SEI properties with battery performance, starting from known components”, we review computational studies that predict the ion/electron transport and mechanical properties based on known SEI components, and (briefly) on correlating these SEI properties with battery performance, degradation, and aging. Then, the opportunities for the design of an artificial SEI will be reviewed in the section “In vitro design of the SEI”.
Modeling of electrolyte reduction mechanisms
The reduction of an electrolyte on an anode surface can be viewed as the initial formation process of an SEI film, which plays an important role in the SEI composition.54,55 Many mechanisms such as one- and two-electron reduction of electrolytes have been proposed27 based on SEI composition analysis. However, it is challenging to directly capture the reactions at the electrode/electrolyte interface experimentally, as some of the reactions could occur at the picosecond (ps) timescale. Thus, quantum chemistry (QC) and molecular dynamics (MD) simulations have been extensively employed to unravel the initial electrolyte reduction and decomposition mechanisms.
Although Fig. 1a illustrates the fundamentals of SEI formation from electrolyte reduction on the anode surfaces, the electrolyte for LIB is a much more complicated solution. It typically contains LiPF6 salt dissolved in a mixture of organic solvents, which contains the high dielectric ingredients, such as ethylene carbonate (EC), and low viscosity ingredients, such as dimethyl carbonate (DMC), diethyl carbonate (DEC), and ethylmethyl carbonate (EMC). Salt dissolves in the non-aqueous solution via strong ion–solvent interactions. Therefore, the reduction voltage of the electrolyte is not only determined by the gas phase LUMO10 of an individual component (which can be easily computed) but is also related to the concentration, solvent polarity, and ion–solvent coordination.56,57 Here, we will review the computational work on reduction of pure EC, electrolyte mixtures of EC and propylene carbonate (PC), and with dissolved LiPF6 as examples to systematically introduce the application of computational methods to model electrolyte reduction reactions. Figure 1 is limited on the thermodynamics of electrolyte reduction voltage, while the SEI formation reactions are also governed by kinetics, as many metastable species are found in the SEI. Therefore, simulations on reduction thermodynamics and kinetics will also be reviewed.
Furthermore, the electrolyte reduction mechanisms on a (bare) electrode surface might only play a role in the initial formation process of SEI. As the reduction products accumulate on the electrode surface, the reduction mechanism can be different as the surface becomes more electronically insulating. This process can be considered as a part of the SEI evolution process. The simulation of this process, however, has not yet reached a point wherein it can be validated by experiments.
EC solvent decomposition mechanism
Predicting the reduction voltage of EC
EC, with high polarity and dielectric constant, is one of the most important ingredients in the electrolyte. In 1995, Blint58 calculated the binding energy of Li+ with EC and showed that it is higher than water and several other ether and carbonyl oxygen containing species. In 2000, Li and Balbuena14 first applied QC to investigate the experimentally proposed EC reduction mechanism proposed by Aurbach et al.59 This is a significant step, as the majority of SEI reaction mechanisms in the literature were deduced from experimentally observed products, and QC can confirm these mechanisms by calculating the energies of the intermediate structures along the proposed reaction pathways. Jointly, they reinforce each other to reveal the SEI formation mechanisms. In 2001, Wang et al.15 and Zhang et al.12 investigated the possible reduction and oxidation pathways for EC, respectively. Following these initial QC calculations, the reduction pathways for EC have been modeled extensively.15,60,61,62,63,64,65,66,67,68,69 Typically Li-ion will be surrounded by 4–5 EC in the first solvation shell in the solution. To capture the solvent effect, Wang et al.15 explicitly calculated the possible reduction processes of super-molecules of Li+(EC) n (n = 1–5) using high-level DFT method in Gaussian 98. They treated the bulk solvent as a macroscopic and continuum medium using the polarized continuum models. This detailed reaction pathway study gave many important insights. First, the solvent plays an important role. They found that isolated EC is unlikely to be reduced because of its negative adiabatic electron affinity. In fact, EC− anion has been observed experimentally.70 The difference between LUMO/HOMO orbitals of EC− in gas and solution phases was shown in a later study by Yu et al.60 Under the effect of a continuum solvent model, EC can be reduced via one-electron and possibly two-electron reactions in the solution. By computing the EC reduction pathways with Li+ and increasing numbers of EC in Li+(EC) n , Wang et al.15 confirmed the currently generally accepted two-step reduction pathways on the surface that Li+(EC) n is initially reduced to an ion-pair intermediate undergoing homolytic C–O bond cleavage, giving a radical anion coordinated with Li+. They also revealed, for the first time, all the possible products could be generated from EC decomposition, such as dilithium butylene dicarbonate (Li2BDC), Li2EDC, LiO(CH2)2CO2(CH2)2OCO2Li, Li(CH2)2OCO2Li, and Li2CO3, some of which are just now being detected experimentally71 due to the difficulty in characterizing such a complex system. The formation of Li2BDC is the most thermodynamically favored, but it has high solubility. Therefore, the compounds with low solubility in the electrolyte, such as Li2EDC, become dominant components in SEI. Li2CO3 indeed can form, but may only form at a lower EC concentration. The experimentally proposed reduction reaction to form C2H4 gas was also validated.
With the development of supercomputers, ab initio MD (AIMD) became feasible for larger systems.60,62,65 Using AIMD, Leung and Budzien62 tracked the initial decomposition process of liquid EC on graphite surfaces with different edge terminations. They confirmed the two EC decomposition pathways. Depending on which C–O bond is cleaved, CO or C2H4 gas can be generated, as shown in Table 1. For the first time, CO evolution, observed in experiments,72 was predicted in AIMD with explicit solvents. The one-electron reaction pathway was further elucidated in later works.60,65 This was also confirmed by electron paramagnetic resonance spectroscopy measurement.73
Due to the limited size in DFT-based calculations, atomistic force fields were developed and parameterized for Li-ion battery electrolyte systems to enable classical MD simulations with a longer time scale and larger system size. Classical force field, such as COMPASS (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) with fixed charge, can reproduce the energetics of Li+ interactions with organic reduction products, such as Li2EDC and dilithium 1,2-propylene dicarbonate (Li2PDC).74 Borodin and Smith75 developed a many-body polarizable force field, APPLE&P (Atomistic Polarizable Potential for Liquids, Electrolytes, and Polymers), which allows the charged ion, such as Li+, to polarize the neighboring solvent molecules and anions by introducing atomic dipoles or by shifting charges in response to the electric field. They parameterized APPLE&P with QC calculations of EC and DMC complexes with Li+ and LiPF6.75 These classical force fields cannot describe breaking of covalent bonds, and hence they are mainly used to capture the solution structures and transport properties of electrolyte (for example, 1 M LiPF6 salt dissolved in EC or DMC solvent)19,74,75,76,77 and some key liquid properties (such as density, cohesive energy, solubility in the solvent) of SEI components, which will be discussed in the section “Correlation of SEI properties with battery performance, starting from known components“.
In order to capture the electrolyte decomposition, the ReaxFF reactive force field, which employs a bond-order term and a variable charge based on the electronegativity-equalization method (EEM) to describe the covalent and ionic bond-forming-breaking, was developed for the Li–C–H–O system.63,69,78 It was used to simulate EC and DMC solvent decomposition when exposed to Li metal.78 Although it has been observed that solvent decomposition reactions led to a nanometer-thick SEI film formation, these reactions were mainly chemical reaction of EC (or DMC) with Li metal or Li atom, rather than electrochemical reactions. The newly developed method, eReaxFF, with an extended EEM method or more precisely the atom-condensed Kohn−Sham DFT approximated to second-order (ACKS2) method, can treat electrons explicitly in a pseudo-classical manner, allowing redox reaction simulations. With the eReaxFF, EC reduction pathway in a system including 60 EC molecules and 40 lithium atoms was revisited by MD simulations (Fig. 4b).69 The results show similar phenomena to those observed in AIMD,60 such as electron transfer, ring opening of EC, and radical termination. Thus, eReaxFF method is a big step forward in the MD application in SEI investigation, which can be further extended to larger systems. However, the parameterization of ReaxFF and eReaxFF for such a complex system is non-trivial, and the accuracy, compatibility, and transferability of force field parameters require constant improvement.
Electron transfer from a AIMD and b MD with eReaxFF simulations. (a) Adapted from Yu’s Snapshots at 0 fs, and 55 fs after a second excess electron is added to EC liquid. Color scheme: C gray, H white, O red, Li/Li+ blue. The EC with two excess electrons is shown as a ball-and-stick figure, whereas all other intact ECs are stick figures60 (Copyright: The Electrochemical Society). b Snapshots of liquid EC with excess electrons. Color scheme: C cyan, H white, O red, Li+ purple, electron large blue sphere69 (Copyright: American Chemical Society)
Quantifying the onset voltage for EC reduction reaction is still challenging for computation at both quantum and molecular levels.66,68 The equilibrium voltage can be computed via a thermodynamic chemical cycle for lithium electrode reaction, as shown in Fig. 5a.15 ∆G sol is the solvation free energy of Li+, ΦM is the work function of the inert metal electrodes, ∆G e is the ionization free energy, and ∆G vap is the vaporization free energy. In this method, the difference of the lithium electrode potential in aqueous and organic electrolytes depends only on the variation of free energy of Li+ in solution. Wang et al.15 used this method and found the reduction potential of Li+(EC)4 is about −2.2 V on the physical scale, which is comparable to the experimentally observed reduction potential of EC at 0.8 V versus Li/Li+ (corresponding to the physical scale of −2.36 V).43,44 Recently, Leung and Tenney66 created a half-cell with the model system of a LiC6/liquid-EC interface. They computed the free energy change of Li+ transfer from EC solvent to LiC6 as ΔG t , and defined it as experimentally known, 0.1 V vs. Li/Li+. Applying a surface electron density (σ) on LiC6 will mimic an experimentally well-calibrated applied voltage (shifting the fermi level of the electrode), which can lead to EC decomposition.66 The calculation showed that the zero charge surface is corresponding to a potential of 1.24 V vs. Li/Li+ metal (Fig. 5b).66 Thus, the surface is negatively charged at zero volt vs. Li/Li+, and the excess electron density on the anode surface favors electrolyte decomposition.
Methods to compute the reduction voltage. a The electrochemical cycle of lithium electrode reaction. Species in the gas phase, solid phase, and solution phase are denoted as ‘(g)’, ‘(s)’, and ‘(sol.)’, respectively. The vaporization and solvation processes are denoted as subscripts, ‘vap’ and ‘sol’, respectively. Adapted from15 (Copyright: American Chemical Society). b AIMD simulations of the predicted potential (−ΔGt/|e|) calibrated with free energy for Li+ transfer from the LiC6 phase to the middle of the liquid EC region as the surface charge (σ) varies. Crosses denote the three data points computed, with 0, 1, and 2 mobile Li+, respectively66 (Copyright: American Chemical Society)
Predicting the reduction kinetics of EC
The two-step reduction reactions may not occur at the same time, and thus the reaction products and therefore SEI compositions will be time dependent. Li and Balbuena14 first clarified that, for EC reduction reaction, the one-electron transfer is the rate-determining step, while the two-electron transfer reaction is 10 times faster. Additional simulations have revealed that the reduction voltage of the one-electron and two-electron reduction reactions of EC are not exactly the same. Borodin et al.79,80 screened about ~100 carbonate molecules and 300 phosphate molecules and found that the second electron reduction potential is higher than the first reduction potential for the majority of them, indicating that if these singly reduced species stick near the negative electrode long enough, they are likely to undergo the second reduction reaction.
The electrolyte composition can change the reaction pathway and kinetics, resulting in different reduction products, which were observed in both experiments44,81 and calculations.14,15,62 For example, it is believed that, for EC reduction, Li2CO3 is likely to form at a low EC concentration, while Li2EDC is likely to form at a high EC concentration.14,15,59,82 In other words, the reaction products are not only determined by the thermodynamics (the energy landscape) but also critically dependent on the kinetic barriers for these reactions.65,83 The calculated reaction rate depends on computational methods, and as Perdew–Burke–Ernzerhof hybrid (PBE0) functional finds much slower ring-opening dynamics, while Perdew–Burke–Ernzerhof (PBE) functional is more suited to two-electron reactions.60,65 Leung65 computed the energy barriers, took the kinetics into account, and proposed the EC reduction products map. The charge transfer kinetics was evaluated based on the Markus theory. The results revealed that CO formation is more kinetically favorable while C2H4 formation is more thermodynamically favorable, as shown in Fig. 6.65 As the SEI grows thicker, the availability of electrons decreases. Therefore, the EC may first reduce following the two-electron reduction process, but later on it may follow the one-electron reduction mechanism. As the SEI grows thicker, the kinetics of these reduction reactions may play an even more important role in determining the SEI formation and growth than the thermodynamics reduction potential.82
Different SEI formation regimes with steady-state reactions and a homogeneous reaction zone assumed. The axes are the one-electron and two-electron tunneling rates, Green and violet dashed lines represent applied potentials of 0.0 and 0.53 V versus Li/Li+. OC2H4O2− is not the final product. Oligomers are not explicitly considered but are secondary products in the OC2H4O2− region and may be present at low k e rate in the “BDC” region. In the presence of electrode surfaces, CO32− formation rate can be much faster and the CO32− regime expands65 (Copyright: Elsevier)
Towards a realistic electrolyte: the impact of other solvent and salt species
Many of the electrolyte reduction studies discussed above were based on the pure EC solvent. However, the real electrolyte is usually comprised of more than one solvent and suitable additives. Taking the electrolyte mixture into account is a necessary step towards fully comprehending the reactions at the anode/electrolyte interface.
Reduction potential of each solvent component
First, every solvent and salt species will decompose at its unique voltage. Tasaki74 found that the order for the solvent molecule to undergo the first electron reduction is EC > PC > VC > DMC > EMC > DEC, with EC being the most likely to be reduced. VC, on the other hand, is most likely to undergo the second electron reduction, followed by EC and PC, as VC > EC > PC.74 The reduction voltage is sensitive to the nearby Li+. When the Li+-solvent complexes in implicit solvent are considered, the first electron reduction order changed to VC > PC ~ EC ~ DMC (cis–trans) > DMC (cis–cis).17 Overall, the trend is consistent with the conclusion of Wang and Balbuena84 that the electron affinity of cyclic carbonates (EC) is higher than linear carbonates (DMC, DEC, EMC), which leads to the favorable reduction of EC in the cyclic–linear mixed electrolytes.
Effects of the Li-salt anion
Ideally, LiPF6 salt is dissolved as Li+ and PF6− by the solvent for most of the time. However, the poor chemical stability of dry LiPF6 raises many concerns about its thermal decomposition (reaction 1) and reaction with trace water (reaction 2)
The product HF is considered as a major degradation cause for the electrolyte in LIB. The decomposed compounds, such as PF5 and POF3, can also trigger cascade reactions with solvents.
Some of these hypothetical electrolyte degradation mechanisms were investigated by Tasaki85 using DFT calculations. He examined the reaction of PF5 with various solvents and found negative reaction free energy, suggesting the formation of the PF5-solvent adduct in solution for EC, DEC, DMC, and γ-butyrolactone. The decomposition of LiPF6 is advocated in a more polar solvent.85 Okamoto67 investigated the reaction of LiPF6 with water and the subsequent reaction of POF3 with EC (reaction 3)
He found that the EC ring opening reaction is not favored unless Li+ and PF6− ions are included in the model.67 These modeling results generally agree qualitatively with experimental observations.81
The anion in the salt can participate in electrolyte reduction reactions and impact the SEI formation. A recent DFT study17 showed that anion PF6− reduction in the presence of LiF, formed due to anion defluorination, occurs at much higher potentials than the reduction of EC, DMC, and PC. Interestingly, LiBF4 reduction occurs at much lower potentials than EC, DMC, and PC. This is supported by the experimentally measured reduction potential, which is 1.7 V and 0.8 V for LiPF6- and LiBF4-based electrolytes (EC/EMC mixture), respectively.17 Therefore, LiPF6 influences the passivation layer formation more significantly than LiFB4. In this example, the DFT calculations provided important insight into the reasons behind different SEI composition in LiPF6- and LiBF4-based electrolytes.17
Highly concentrated protic and aprotic electrolyte can increase the defluorination reduction potential to >2.4 V due to the multiple Li+ coordination to the anions, compared with ion pairs and isolated anions.86,87 Recently, a stable protective SEI in the aqueous electrolyte was also confirmed in an experiment–simulation joint work.88
Effect of solvation structure
The SEI chemistry is also dictated by Li+-solvation sheath, which was recently characterized by Cresce et al.89 The solvent–solvent and salt–solvent local structures can dramatically change the reduction voltage and kinetics, resulting in many electrolyte concentration-dependent phenomena. The concentration of the electrolyte mixture (solvent, salt, and additives) and the applied voltage can also affect the solvation structure near the surface and, subsequently, impact the electrolyte reduction.75,89,90,91,92,93,94 Computationally, Borodin et al.79 cautioned that the solvation sheath structure geometry optimization is more important for accurately predicting the reduction potential than the oxidation potential.
Since most solvents have multiple components, it is important to know how solvation sheath changes from a pure to mixed solvent.75 MD simulations with a polarizable force field can describe both the dynamic and static properties of a mixed electrolyte. Although DMC has a lower dielectric constant, Borodin and colleagues75,89 found that it participated in the Li+-solvation sheath in mixed EC/DMC electrolyte. This observation is confirmed by QC calculations of small solvation clusters. In addition to this, the MD predicted Li diffusion, which is strongly related to the solvation structures and EC/DMC motions, also agrees with experiments.75 When EC is mixed with PC, Li+ prefers to bond with PC than EC, which has been observed by modeling and experiments.89 The consequence of this effect will be further discussed in the section “EC vs. PC and VC on graphite electrodes”.
The solvation sheath fluctuates near the electrode surface under the bias of electric field.90,91,92 Vatamanu et al.91 simulated the electrolyte structure change under an applied field with MD simulations and demonstrated that the interfacial composition of electrolytes near the graphite anode depends on the applied potential. The composition and structure of the SEI layer evolve as a function of the applied potential in a working lithium half-cell.91 Boyer et al.93 performed MD simulations with a classical force field and demonstrated the different rearrangements of EC and DMC on a graphite edge surface under the applied electric field. Thus, the electrolyte structure rearrangement near the electrode surface will certainly impact the onset of the reduction reactions and the Li+ de-solvation process. Vatamanu et al.95 recently summarized the MD techniques to simulate the electrode/electrolyte interface structure under an applied field. They also modified the original constant electrode potential method using Gaussian distributed charges by adding an energy term, which is capable of mimicking the dynamical charge fluctuation on the anode surface.95 Although MD simulations cannot predict the decomposition voltage, the local structures can serve as an important input to a higher level of QC simulations.
Effect of the anode surface state
The anode surface also plays an important role in determining the decomposition thermodynamics. Leung and Budzien compared EC decomposition on the basal plane of lithiated graphite (LiC6), terminated with =O, –OH and –H and found that C = O edges provide a larger driving force for EC reduction62 The observation that EC is more inclined to decompose in the presence of oxygen/hydroxyl termination is consistent with other simulation results.96 Besides graphite, EC decomposition was simulated on Li,57,60,97 Si,45,64,98 and Sn99 electrodes as well.
Due to the lower potential of Li metal than graphite, the decomposition of EC on Li metal is spontaneous and much faster than that on LiC6 surfaces.60 Ebadi et al.97 performed AIMD and showed that EC reduction pathway to form CO is energetically more favorable on the Li metal surface, different from that on graphite surface.60,65 Therefore, solvents with lower reduction voltages, such as dioxolane (DOL) and dimethoxyethane (DME), are often used for Li metal anode. Camacho-Forero et al.100 have shown that both DOL and DME are stable on Li metal surface during the AIMD simulations, in contrast with the spontaneous decomposition of EC on Li metal. They also simulated the decomposition process of lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) and lithium bis(fluorosulfonyl)imide (LiFSI) at 1 and 4 M concentrations in DME on Li metal surface and found that LiFSI shows a complete decomposition in terms of forming LiF as one of the main SEI products.57 One of the specific application of Li metal anode is for Li–S batteries, where the precipitation of Li2S on the anode from the shuttling of soluble polysulfide (PS) needs to be avoided. DFT and AIMD simulations have revealed that PS decomposes, before any of the electrolyte component does, forming Li2S.100 The crystalline Li2S precipitation on Li metal surface is also thermodynamically stable.101 Thus, the component, structure and property of the SEI layer in Li–S battery is rather different from that of the traditional LIBs. A recent work combined in situ X-ray photoelectron spectroscopy with AIMD study and revealed the evolution of SEI with three stages, giving a molecular-level insight for the formation of SEI in Li–S batteries.102
Electrolyte decomposition is a function of the electrode surface potential. When Si becomes lithiated, its voltage drops, and therefore the lithium concentration in silicon greatly influences the electrolyte reduction reactions.53,64,98,99 Martinez de la Hoz et al.64 found that EC can be reduced by two different two-electron mechanisms (one simultaneous and one sequential) on intermediately lithiated silicon surfaces (LiSi). A later work done by Ma and Balbuena98 provided a more detailed reduction mechanism of EC under the low lithiated state of silicon anode. They argued that both one-electron and two-electron reduction processes are possible, depending on the local density of EC and Li-ions. The one-electron reduction is favored at a high EC concentration, while the two-electron reduction is favorable at a high Li-ion concentration. Recently, an AIMD work showed that both the salt-LiPF6 and solvent-EC participate in SEI formation on Si anode,103 consistent with the reduction voltage calculated by Delp et al.17 Additionally, the EC decomposition on un-lithiated, Li-covered, and fully lithiated Sn surfaces, as well as on a pure Li surface, was studied by Moradabadi et al.99 They showed that the decomposition is preferred on Li/β–Sn (100) and Li17Sn4 (001) surfaces rather than on Li (100) in spite of its lower potential, suggesting that decomposition of EC molecules not only depends on the surface potential but also akin to the surface chemical compositions and kinetics.
Buildup of the nanometer-thick SEI layer
The above-mentioned investigations of reduction reactions on a bare electrode surface are more related to the initial stage of SEI formation. Leung and Leenheer showed104 that the solvent molecules absorbed on the surface can greatly reduce the surface voltage and impact the electrolyte double layer structure under the applied electric field. This means that as the SEI gradually covers the conductive electrode surface, further electrolyte reduction will be different from the mechanism on a bare-conducting electrode surface. Kinetic Monte Carlo was used to simulate the early stage formation of SEI with regards to the lithium-ion intercalation on a graphite anode.55,105 However, the buildup of a nanometer-thick passivating SEI layer due to these formation processes is still not fully captured by modeling, due to the lack of multi-scale simulation methods.
Firstly, the formation of SEI is not only confined to the reduction process, since many decomposed species can be dissolved into the electrolyte, but only those with low solubility might deposit on the anode surface. For example, the less soluble Li2CO3 and Li2EDC15,106 were found in SEI instead of the soluble thermodynamically more stable products. Ushirogata et al.107 did two-step calculations. First, they performed AIMD to allow the electrolyte to decompose, then extracted the stable SEI film components and examined their solubility in the EC solvent and their adhesion to a graphite electrode surface. They proposed a “near-shore aggregation” SEI formation mechanism as shown in Fig. 7.107 The decomposed electrolyte components will desorb into the electrolyte near the surface and form aggregates, which then coalesce and adsorb on the anode surface. This “solution-mediated” mechanism rather than the “surface-mediated” mechanism would allow the formation of several tens of nanometer-thick SEI film.
Ushirogata et al.107 proposed that the SEI film formation process follows b a near-shore aggregation mechanism instead of a a surface growth mechanism, meaning the reduced electrolyte compounds with limited solubility in the electrolyte can desorb into the electrolyte near the electrode surface, form aggregates, then deposit on the electrode surface to complete the SEI formation (Copyright: The Electrochemical Society)
Secondly, as the electrolyte is reduced, some decomposed compounds will deposit on the anode surface and gradually form the growing SEI layer.108 Thus, the surface chemistry, surface potential, and the availability of electrons or solvents will gradually change, and hence the electrolyte reduction products and therefore the SEI components will change accordingly. However, this process spans multiple time and length scales. Takenaka et al.108 developed a hybrid method with MD (using classical force field) in combination with MC (fed by reaction energetics computed with DFT) to overcome the time and length scales of SEI formation. A nanometer-thick SEI film with a two-layer structure was observed in their simulation. A qualitatively reasonable SEI formation picture emerged (Fig. 8). Although the formalism is rigorous, all the reaction rates were set to be equal in the current model, limiting its predicting power. With correct reaction rates, diffusion rates, electron tunneling and transfer rates, and the reorganization energy of the electrolyte molecules, it can be extended to a multi-scale SEI formation model.109
Snapshots of the SEI films and electrolytes. Color scheme: SEI film green, Li+ blue, PF3 (C2H4, or C3H6) gray, EC (PC) purple, PF6− orange. The left panels show the side views while the middle and right ones show the front views of the interface structures in the SEI films (visualized in the depth 0 ≤ z ≤ 20 Å of the view from the side of bulk electrolyte)108 (Copyright: American Chemical Society)
In vivo modification and design of the SEI
With the understanding of electrolyte reduction mechanisms and the methods developed to simulate EC reduction reactions, many additives were investigated by computational methods in order to achieve a common goal of modifying and designing the SEI inside of LIBs during cycling (in vivo design). Simulations were performed to identify the mechanism as to how each electrolyte additive impacts the SEI formation and functionality. One example is designing the sacrificial additives, which will be reduced before the solvent (EC for example) to help form a robust SEI layer that inhibits further solvent reductions. Therefore, the reduction voltage has been computed as the main descriptor for many electrolyte species, which are summarized in Table 2. With the recognized mechanisms and descriptors, high-throughput computational screening can be performed to explore new additives. This section will review the efforts in these two thrusts.
Understanding the role of electrolyte additives
Modeling is being integrated with experiments to rationalize some key SEI questions, such as why PC cannot form a stable SEI layer67 whereas VC is helpful to form a stable one. Here, “stable” is a loosely defined term, as we do not know the specific SEI properties responsible for the lifetime of a battery yet. Therefore, whether an electrolyte additive or a specific SEI component is “beneficial” to the cell performance is generally based on experimental conclusions. In this section, we will focus on three key questions of electrolyte additives: (a) understanding the effect of VC on SEI formation in comparison with PC; (b) understanding the effect of FEC on SEI formation, especially on Si and Sn electrodes which experience large volume expansion; and (c) the role of ES to avoid PC co-intercalation.
EC vs. PC and VC on graphite electrodes
Through comparative studies, one would like to shed some light on why some additives lead to SEI with “better” performance than others. Many modeling studies have been performed to rationalize why PC cannot form a “better” performing SEI but VC can.22,110 PC and EC have similar structural and dielectric properties. PC could arguably show an advantage due to its lower melting temperature and lower viscosity than EC. However, PC-based electrolytes cause exfoliation of graphite electrode, preventing the formation of a stable SEI.42
The exfoliation mechanism was explained by various models. Wang et al. compared Li+(PC) n and Li+(VC) n clusters,111 following their calculation of Li+(EC) n clusters.15 They found that PC solvates Li+ more strongly than EC or VC. This is consistent with the recent experimental and simulation work by Cresce et al.89 Therefore, it becomes more difficult for Li-ion to desolvate from PC, and co-intercalation of PC with Li-ion into graphite may occur, causing graphite exfoliation. The co-intercalation-induced stress has been measured by Mukhopadhyay et al.112 The co-intercalation process has also been modeled by DFT113,114 and MD simulations with a classical force field.115 Lee and Carignano115 found that PC intercalates into graphite ∼200 times faster than EC, just due to the size difference of the two. The co-intercalation can be mitigated by covering the graphite edge, for example, by covalently linking polyethylene oxide (PEO) to graphite, as demonstrated through MD simulations conducted by Guk et al.116 with ReaxFF. The stability of graphite-intercalation-compounds was computed by DFT methods with van der Waals corrections. It was found that the solvent cluster, Li+-solvated by dimethyl sulfone Li(DMSO)4 and salt anions, ClO4− and PF6−, can all intercalate into graphite, but the larger cluster, Li+-solvated by dibuthoxy ethane (LiDBE2), cannot, agreeing with other modeling and experimental results.117
In terms of reduction potential, PC is more difficult to be reduced than EC and VC,15,111 and more specifically, follows the order of VC > EC > PC for the second electron reduction.74,118 The ring-opening reaction of VC occurs via a homolytic C (carbonyl carbon)-O rupture first in the solvated complex111 and is more likely to undergo the second electron reduction than EC or PC.74 Ushirogata et al.119 considered the effect of VC from both thermodynamic and kinetic point of view via AIMD simulations. They found that by adding VC to the electrolyte, the normal two-electron reduction of EC can be suppressed.119 They argued that the VC additive protects the anode by reacting with the EC anion radical to suppress the two-electron reduction of EC rather than only being sacrificed to form the SEI components.119
Tasaki74 further argued that the reduced product Li2EDC of EC has higher density, stronger cohesive energy, and less solubility in the solvent than that of PC. Takenaka et al.108 demonstrated that SEI formed from PC-based electrolyte is sparser than that formed by EC, as shown in Fig. 8. Since the SEI layer formed by the reduced PC products is easier for electrolyte migration, it is not an effective passivation layer.
FEC and its decomposition product: LiF
Fluoroethylene carbonate (FEC) gained renewed interests,56,64,98,120,121 as it shows promise as an electrolyte additive for improved SEI passivation on Si- and Sn-based anode.122,123 It is insightful to compare how EC, VC, and FEC reduce differently on these electrode surfaces. In order to simulate the reduction reaction of electrolytes, Si was lithiated. The lithium concentration in Si is correlated to the anode potential, and AIMD simulations were used to investigate its effect on the reduction pathways for EC and VC.56,64,98,121 For example, on less lithiated Si anodes (LiSi2 and LiSi), VC may be reduced via a two-electron mechanism, yielding an opened VC2− anion. In the case of Li13Si4, such a species receives two extra electrons from the anode surface producing an adsorbed CO2− anion and a radical anion -OC2H2O2−.64 The EC and VC reduction can also be changed by the nearby salt and a new CO2 formation pathway for VC was reported.56 FEC, on the other hand, shows less dependence on the lithium content in Si. Overall, the two-electron transfer process is thermodynamically and kinetically favorable for FEC reduction.98,120 The F− can detach after the reduction of FEC, and combine with Li+ to form LiF.120 LiF is an important reduction product of FEC observed in the SEI with FEC additives. LiF formation, in turn, increases the reduction potential of FEC from ~0.8 eV (without LiF) to 1.5–2 V (with nearby LiF),17,79,86 consistent with a reduction peak of around 1.7 V measured for electrolytes with FEC as an additive.17,123 Such a mechanism can also lead to concentration-dependent SEI products. Another AIMD work recently done by Martinez de la Hoz et al.56 ascribed the concentration dependence to the chances of radicals getting closer to the reactive sites on the surface. FEC also exhibits more variations of reaction pathways and more adsorption modes than EC. These reduction products may oligomerize and yield a more stable and denser SEI film.
ES to avoid PC co-intercalation into graphite
Since PC can cause exfoliation and degradation of graphite anode surface, it is believed that if one can design an additive, that can reduce before PC has a chance to co-intercalate into and reduce on graphite, an effective SEI may form. Motivated by this mechanism and a simple descriptor (reduction voltage), various experimental and modeling efforts have been pursued. The early theoretical investigation of ES was performed in the gas phase.124 The reduction potential of ES is calculated to be in the range of 1.90–1.93 V,125 in accordance with the experimental values (1.8–2.0 V).126 The reduction potential of ES is a little higher than PC and hence ES will reduce prior to PC. One- and two-electron reduction reactions are possible for ES to generate the main products, such as Li2SO3, (CH2OSO2Li)2, CH3CH(OSO2Li)CH2OCO2Li, and ROSO2Li.127 The sulfite additives were demonstrated to be more efficient than carbonate additives in PC-based electrolytes.118 Similarly, other sulfites118 including vinyl ethylene sulfite (VES), butylene sulfite (BS),128,129,130 sulfuric esters (SE), sultone (PS and PES), fluorinated sultone (FPS), and 1, 3-benzodioxol-2-one (BO) were reported to show higher reduction voltages in calculations and improved capacity retention in experiments (suggesting better SEI) for PC-based electrolytes.124,125,126,127,128,129,130,131,132,133,134,135 However, none of these studies went on to further comment if the additives lead to any changes in the chemistry, morphology, and properties of the SEI, such as the density, cohesive energy, solubility, and porosity, which were associated with SEI performance as argued by Tasaki74 and Takenaka et al.108 More additive examples with relatively larger molecular formula were also investigated and are summarized in Table 2. Commonly, these additives possess lower LUMO energy levels than the main electrolyte solvents and can be reduced before the main electrolyte solvents.136,137,138,139,140,141
With the insights and success of electrolyte additive design, more candidates were explored, especially when new battery systems are explored, such as Li–S and Li–air (O2) batteries. New computational electrolyte (in terms of additives, salt, and solvents) design tends to go in parallel with experiments. These examples include designing Boron-based anion receptors to be used in lithium-ion and metal-air batteries;49 pursuing ionic liquid for its wider stability window;19,76,77 ranking thermal stability of salt, as LiClO4 > LiCF3SO3 > LiTFSI > TEABF4 > LiBF4 > LiPF6, via modeling and experiments;142 enhancing thermal stability,61 re-ranking and optimizing the current electrolyte components compatible to Si and Li electrodes.143 It is worth to point out there are limitations of using this oversimplified model to connect the reduction and oxidation process of solutions with molecular orbital theory, as Ue et al.144 have illustrated, using the oxidation voltage as an example, that the experimentally measured oxidation potential also varies with scan rate.
High-throughput calculations to search for new electrolyte additives
The quest for new additives can be dramatically accelerated by computation. In 2009, Han et al.145 calculated the ionization potential and oxidation potential for 108 organic molecules to search for electrolytes with high oxidation voltage. For the reduction reaction, 7381 EC-based structures have been screened by Halls and Tasaki146 in 2010. Based on the comparison of the fundamental electrochemical properties of a reductive additive required for efficient SEI formation, many descriptors can be used, such as HOMO, LUMO, electron affinity (EA), relative dipole moment, and chemical hardness (η). Two screening criteria for suitable SEI formation additives were suggested by Halls and Tasaki:146 low LUMO energy (high EA) and small η. They used an automated approach to generate an additive library based on fluoro- and alkyl-derivatized EC (shown in Fig. 9a), then analyzed and screened the derivatives for suitable additives using high-throughput QC solutions. The elementary workflow is illustrated in Fig. 9b.146 One of the promising fluoro-derivatized EC is displayed in Fig. 9c. Previously mentioned additives, which have shown improved SEI performance, such as FEC and BS, satisfied the descriptors proposed in this work. Note that FEC is automatically generated in the library. In addition to reduction potentials, Park et al.147 further proposed that a low Li+ binding energy is another descriptor for additive screening, as less binding energy of Li+-additive corresponds to easier de-solvation. Recently, Delp et al.17 emphasized the importance of Li-solvent binding energy in determining the first solvation shell structure. They used the relative Li+-solvent binding energies from the cluster—continuum calculations in conjunction with the reduction potentials in order to estimate the probability of the solvent/additive to be in the Li+ coordination shell and undergoing reduction. Jankowski et al.148 and Borodin79 examined the accuracy of common quantum methods in predicting these key properties. By combining QC calculations for assessing both the thermodynamic and kinetic effects, Husch and Korth149 provided a set of descriptors for screening new electrolytes by considering the anode SEI formation and graphite exfoliation, which is named as “redox fingerprint analysis” (RFPA). The success of computational electrolyte screening relies on these key descriptors. However, these descriptors mainly focused on the initial SEI formation and thermodynamics. As we discussed in the section “Buildup of the nanometer thick SEI layer”, the fundamental understanding and the computational methods that can describe the formation of the tens of nanometer-thick SEI from the electrolyte reduction have not been fully developed. Therefore, it is yet to be established how these initial reduction processes control the composition and morphology and, more importantly, the properties of SEI films. For this purpose, the development of multi-scale high-throughput computational methods is required.150,151
a EC core structure (left panel) and R-group structures (right panel) used to enumerate the structure library, with Z denoting the connection point; b screening workflow; c a typical efficient additive screened out, the color scheme is the same with Table 1, F atom is denoted as light-blue146 (Copyright: Elsevier B. V.)
Nevertheless, high-throughput quantum chemical analysis and virtual screening are revolutionizing materials discovery for integrated design of devices, such as Li-ion batteries. Additionally, in order to satisfy advanced batteries with high potential electrode materials, new electrolytes with a wider electrochemical window are being explored computationally.152 At the same time, electrode materials are being computationally screened according to their energy density and safety descriptors.153 The SEI layer, sandwiched between the electrolyte and electrode, controlling the performance and degradation of LIBs, should be designed along with the electrolyte and electrode materials. However, what is the ideal property of the SEI?
Correlation of SEI properties with battery performance, starting from known components
An efficient SEI film can be responsible for the better performance and longer life of a battery. Generally, the functionalities of SEI can be concluded as follows. First, it should be able to block the interaction between electrons (from the electrode) and the electrolyte to avoid further electrolyte reduction reactions. This can be achieved by either blocking the electron transport (via tunneling or other electron leakage mechanisms) or by blocking the electrolyte diffusion through the SEI. Second, the SEI should not impede Li-ion transport from the electrolyte to the electrode. This process includes Li-ions de-solvating from the electrolyte at the SEI/electrolyte interface, diffusing through the SEI layer, and combining with the electrons at the electrode/SEI interface. Third, the SEI should be chemically stable, i.e., not reacting with or dissolving into the electrolyte. Fourth, the SEI should be mechanically stable, meaning it should not crack or delaminate while the electrode experiences volume expansion and contraction during charge–discharge cycles. Thus, its mechanical properties, such as modulus, fracture toughness, and adhesion on the electrode surface, should be considered as well. It is unlikely that one SEI component can satisfy all these criteria simultaneously. Thus, the unique multi-component and multi-layer nature of the naturally (in vivo) formed SEI might be desired. However, how can one quantify these properties, so as to design an artificial SEI (in vitro) with well-controlled chemistry, structure, and thickness? Additionally, how can one further design the SEI layer on the anode materials that experience dramatic deformation, such as Sn, Si, and Li?
Therefore, it is required to fully characterize and quantify the chemistry–structure vs. property relationship for the SEI film. However, due to its thinness and insufficient characterization tools to directly probe its physical properties, its structure–property relationship has been largely unknown until recent years. Additionally, not every component detected on the anode surface functions as the SEI layer. Therefore, it is important to know the structure–property relationship of each component and their correlations in the SEI layer. In order to take advantage of predictive modeling, starting from the ab initio level, a new strategy to deconvolute the structure–property relationships of the SEI layer has been identified. The new strategy is to computationally interrogate the properties of the idealized SEI components, such as Li2CO3, LiF, Li2O, Li2EDC, Li2BDC … and their mixtures, and then correlate these properties with both in vivo and in vitro SEI design. Table 3 summarizes the key SEI components and their computed key properties. These new modeling efforts are joined by precise surface coating technology development, such as atomic layer deposition (ALD) and molecular layer deposition (MLD) methods, which can deposit conformal thin insulating coating at atomic scale on an electrode surface.154,155 In this section, we will first review the modeling insights on SEI properties and the connection of SEI properties to the battery degradation mechanisms, including the chemical and mechanical instability of the electrode/SEI/electrolyte interfaces.9
Electron Insulating Properties of the Inorganic Components in SEI
It is well-accepted that the natural formation and growth of SEI can be attributed to the electron flow via tunneling from the bare surface of negative electrodes during the initial battery charge, while continuous SEI growth can also be induced by the porous SEI or radical electron transfer, which has been discussed in section "Buildup of the Nano-meter Thick SEI Layer". In order for the passivation layer to protect the electrolyte from further reduction, it was suggested by Peled that the electron tunneling should be blocked.5,156,157,158 Leung et al.157 simulated the EC reduction kinetics on Li and LiC6 electrodes covered by a 0.7–1 nm thick artificial oxide SEI layer (Ai2O3 and LiAlO2 to illustrate the effect of ALD oxide layer) using AIMD and constrained DFT (cDFT) (Fig. 10).157 They demonstrated that, on a bare Li metal electrode surface, EC immediately accepts electrons and decomposes, and the process is adiabatic. In contrast, the reduction of EC on a sub-nanometer insulating layer covered electrode surface falls within the non-adiabatic regime. Therefore, the molecular reorganization energy, estimated using the cDFT approach and the Marcus theory harmonic construction, plays a key role in slowing down electron transfer to the electrolyte. This translates into electrolyte reduction rate in the range of 10−4–10−5 s, compared to 10−12 s on a bare Li electrode. At this stage, SEI should continue to grow until electron tunneling diminishes. However, increasing the SEI layer thickness in AIMD simulation of a full electrode/SEI/electrolyte model is limited by the computational cost.
a AIMD simulations show that on bare Li metal electrode surfaces, EC accepts electrons and decomposes within picoseconds, and b the oxide coating (LiAlO2 on lithiated graphite) effectively slows down the electron transfer to the adsorbed EC, and this slow charge transfer reaction occurs within the nonadiabatic regime, which can be calculated by constrained DFT (cDFT)157 (Copyright: American Chemical Society)
A simplified model system developed by Lin et al.156 treated the SEI layer as a crystalline thin film, consisting of Li2CO3 or LiF (commonly observed inorganic components in the inner layer of SEI). They computed the electron tunneling barrier from DFT calculations and estimated the critical thickness d* that can limit the electron tunneling probability (e−40 to be extremely low) using one-dimensional WKB (Wentzel-Kramers-Brillouin) tunneling modeling. They found that the tunneling barrier is 3.98 (6.26 HSE) eV and 1.78 (4.10 HSE) eV for LiF and Li2CO3, respectively, using GGA/PBE (HSE) functionals. Therefore, a 2 nm thick crystalline LiF and a 3 nm thick Li2CO3 should be enough to block the electron tunneling. The observation that LiF has better electron insulating property than Li2CO3 is consistent with another interface model evaluating the electron potential drop at LiF/Li and Li2CO3/Li interfaces.159 Leung and Jungjohann160 also reported that LiF with more negative electron affinity is more effective for electron blocking than Li2O on Li electrode surface. Through a novel DFT/Green’s function method, Benitez et al.162,162 computed the electron transfer resistance (dV/dI) in a nano-device model consisting of an electrode and a molecule representing SEI components, such as Li2CO3, LiF, Li2O, or lithiated SiO2. They found that Li2CO3 is more electrically insulating than LiF and Li2O,162 which contradicts the prediction of Lin et al.156 The contradiction might be attributed to the different calculation methods and the use of molecular vs. crystalline materials. Both structures are relevant, as molecular/amorphous structures may be more representative at the initial stages of SEI formation, and crystalline structure may present later during SEI formation.
To further correlate the SEI formation with the observed capacity loss, Li et al.163 correlated the capacity loss with the electron tunneling property of the SEI in an analytical model, and Lin et al.156 developed a simple analytical model to estimate the irreversible capacity loss due to the Li-ions consumed in the formation of these SEI layers on the (graphite) anode surface, as the following:
where M h is the molar mass of the host material, N h is the number of Li-ions stored per host atom, A h is the Brunauere–Emmette–Teller (BET)-specific surface area (area/weight) of the host material, and N a is the Avogadro constant. Taking the DFT-predicted tunneling barrier into account, this simple analytical model gives results consistent with experiments by Joho et al.164 This surprising agreement suggests that the initial irreversible capacity loss is indeed due to the self-limiting electron tunneling property of the SEI. Therefore, aligning the band gap of insulating coating with electrode materials165 can be an efficient method to screen insulating coating materials. For nanomaterials, much larger first cycle irreversible capacity loss than graphite is always expected due to the large surface area. Furthermore, surface defects can also capture Li+, causing the first cycle irreversible capacity loss, as demonstrated by DFT calculations and experiments for single-walled carbon nanotube bundles anode.166
However, typically an ~50 nm instead of 2–3 nm thick SEI is deposited on graphite electrode after cycling with LiPF6/EC and LiPF6/EMC electrolytes.167 Thus, the self-limiting tunneling model is only responsible for the initial SEI formation, but other electron transport mechanisms must be responsible for electron leakage through thicker SEI components on the order of 10–100 nm. Therefore, the electron transfer mechanism for SEI with a thickness beyond the electron tunneling distance needs to be investigated. This may be related to the defects in the SEI film, such as polarons,168 interstitials,169 and radicals.158 One possible electron leakage mechanism in Li2CO3 is the existence of a neutral Li0 interstitial point defect.169 Shi et al.169 illustrated that a Li atom, which can be viewed as a Li-ion interstitial and a polaron on the nearby carbon atoms, can diffuse with a small ~0.3 eV energy barrier in Li2CO3. The inner inorganic SEI layer is more likely to be a polycrystalline or an amorphous structure, rather than a crystal. Recently, Leung and Jungjohann160 demonstrated that the grain boundaries in the SEI film, such as Li2O and LiF, are convenient for neutral Li0 to reside and the Li0 can act as a mediator for electron leakage from the electrode, causing further growth of lithium dendrite. Soto et al.158 demonstrated that the electrons can transfer via small radicals to continue electrolyte reduction reactions. The polymer species may not survive the radical attack,170 and cause continuous SEI growth, which will be future explained in the section “Chemical stability of the SEI components”. The SEI deformation due to electrode volume change can also change its electron insulating properties. DFT calculations have shown that the electron tunneling barrier in LiF decreases under tension,156 suggesting mechanical–electrochemical coupling. Deformation also leads to SEI fracture causing electron leakage. However, incorporating grain boundaries and fractures in SEI is challenging for DFT level of calculations due to the simulation size.
Li-ion diffusion through the SEI layer: two layers, two mechanisms
Based on the definition of “SEI”, it must allow Li-ion to pass. Yamada et al.171 measured the kinetics of Li-ion transfer from the electrolyte to the graphite (highly oriented pyrolytic graphite (HOPG)) anode via impedance spectroscopy, observed an energy barrier of 58 kJ mol−1 (~0.6 eV) for the overall interfacial Li+ transfer, and further showed its dependence on the SEI components and the de-solvation ability of Li-ion from the electrolyte. Xu et al.172 experimentally measured that the activation energy of the Li-ion interfacial transport on a Li4Ti5O12 (LTO) anode (without SEI) is ~52 kJ mol−1, while it becomes ~60–70 kJ mol−1 (~0.6–0.7 eV) on a SEI-covered graphite anode. However, it is still hard to clearly determine the activation energy for each step, as de-solvation and Li-ion transport in SEI are two intertwined processes. How Li-ion passes through the SEI layer was revealed by the time-of-flight secondary-ion-mass spectrometer (TOF-SIMS) measurements combined with the isotope exchange experiment performed by Lu and Harris.30 They showed that the anion and possibly electrolyte only penetrates the outer ~5 nm of the SEI layer, but the Li-ion has penetrated through the ~20 nm thick SEI layer. This is coherent with the two-layer structure model of the SEI, a porous (organic) outer layer permeable to Li+, salt anions (dissolved in the electrolyte), and even solvent molecules, and a dense (inorganic) inner layer facilitating only Li-ion transport. These experiments motivated many modeling efforts to explicitly predict the Li transport at the complex electrode/SEI/electrolyte interface. It is still challenging to properly model the electrochemical charge transfer process, which requires a quantum level of accuracy and a structure of electrode/SEI/electrolyte interface with a size beyond QC calculations. Therefore, DFT, density functional-based tight binding (DFTB), MD, and multi-scale modeling need to complement each other in order to accurately model this process.
Ionic conductivity of the SEI components
Since Li2CO3 is a main component of SEI, as was demonstrated in the experiments of Lu and Harris,30 we shall first review the modeling of its diffusion mechanism. Li+ diffusion is carried by point defects, such as vacancies or interstitials. The migration barrier of Li vacancy and Li interstitial in crystalline Li2CO3 have been computed by Chen et al.173 and Iddir and Curtiss,174 respectively. The ionic conductivity depends on the migration energy and the defect concentration, which is related to the defect formation energy. The formation energy relies on the chemical potential of Li. Since the SEI is covering the electrode, it is reasonable to assume, at equilibrium, the chemical potential of Li should be
where the Li chemical potential of the electrode, \(\mu _{Li\_electrode}\), can be translated to the open circuit voltage (OCV) of the lithiated electrode materials. Therefore, Shi and Qi31 derived the voltage-dependent defects formation energy, ranked all possible defects in Li2CO3, and determined that Li-ion interstitial is the dominant diffusion carrier in Li2CO3 on anode materials. Furthermore, Shi et al.31 found that the Li-ion interstitial diffuses through Li2CO3 via a knock-off mechanism, meaning that the Li-ion replaces another Li-ion in the lattice position rather than moving itself via a direct hopping mechanism, as illustrated in Fig. 11a. Based on this new mechanism, a multi-scale modeling was then developed by formulating the mesoscale transport equations for a new two-layer/two-mechanism model, where Li-ion diffuses in the pore of the outer layer of SEI and diffuses through the inner layer via the knock-off mechanism. This diffusion model predicted the TOF-SIMS measured unusual isotope 6Li+/7Li+ ratio profile,30 which increases from the SEI/electrolyte interface and peaks at a depth of 5 nm, and then gradually decreases within the dense layer. With no fitting parameters, the multi-scale modeling approach is applicable to model the ionic conductivity in complex SEI films on the surface of electrodes.
a Energy profile, transition-state structure (upper left inset), and schematic diagram of diffusion pathway (upper right inset) of the Lii+ diffusion from site Ai along [010] direction via the “knock-off“ mechanism31 (Copyright: American Chemical Society). b Displacements of the Li+ over 50 ns for ordered Li2EDC at 393K176 (Copyright: American Chemical Society)
Borodin et al.175,176 investigated the Li-ion conductivity in Li2EDC and Li2BDC177 with a many-body polarizable force field (APPLE&P). They estimated that both the ordered and disordered Li2EDC phases show similar Li+ migration energy barrier of 0.64 eV when fitted to Arrhenius relationship below 500 K.178 The Li+ conductivity is slightly faster in Li2BDC. In both cases, the ordered Li2EDC and Li2BDC have faster Li+ transport than the amorphous structures, due to the more concentrated Li+ layer. Chain-like and loop-like Li-ion transport mechanisms are revealed from the simulations, as shown in Fig. 11b, which are similar to the knock-off mechanism in Li2CO3, as shown in Fig. 11a.31
LiF and Li2O are the other two dominant inorganic components in the inner SEI layer. Pan et al.179 showed that the ionic diffusion in LiF is carried by Li-ion vacancy hopping, using DFT calculations. Vacancy-mediated diffusion mechanisms (knock-off, direct exchange, and hopping) were reported in classical MD simulations of Li2CO3, LiF, and Li2O.180 Pan et al.179 predicted the ionic conductivity of LiF is at least three orders of magnitude lower than that in Li2CO3 and Li2O, and similar conclusions were drawn by Yildirim et al.181 An interesting study by Soto et al.182 showed that the SEI based on Na+ is easier for Li+ transport, and thus switching the cation Li+ vs. Na+ in a premade SEI can enhance the Li+ conductivity. In addition to that, the low adsorption energy of Li adsorbates on LiF leads to low in-plane diffusion barrier of Li ad-atoms,183 which was considered to be beneficial for restraining the Li dendrite growth.
An effective method to increase the charge carrier concentration is doping, since the defect formation energy of these inorganic materials (Li2CO3, LiF, Li2O) is much higher than the migration energy barrier, the ionic conductivity is limited by the carriers’ concentration. Thus, the computational efforts in determining the dominating diffusion carrier lead to a very useful solution. Note the ionic conductivity and the dominating diffusion carriers’ dependence on voltage.169,179 Shi et al.169 found that the diffusion carrier in Li2CO3 is Li-ion interstitial under 0.98 V. Therefore, using BO33− to replace CO32− in Li2CO3 can create more Li-ion interstitials, leading to higher ionic conductivity.169 Doping LiF on the anode with Ca2+, Mg2+, Al3+, or La3+ can increase the concentration of Li+ vacancies, thereby resulting in a higher ionic conductivity.38,169,179
Another method to increase the diffusion carrier concentration is taking advantage of the space charge layer effect184 created by heterogeneous structures and grain boundaries.34,185 Given the difference of the Li diffusion carriers in Li2CO3 and LiF, Pan et al.185 combined the DFT predicted interfacial defect reaction energetics and the continuum Poisson–Boltzmann relationship to understand the effect of mixing LiF and Li2CO3 on Li-ion conductivity. They found that a space charge layer is formed via the defect reaction across the Li2CO3 and LiF interface, which results in the dramatically increased Li-ion interstitial concentration in Li2CO3 and an increased Li vacancy concentration in LiF, as illustrated in Fig. 12. The high conductivity of such a design was also simultaneously demonstrated by an experiment.34 It would be ideal if the Li2CO3/LiF interface is perpendicular to the anode surface and the size and distribution of LiF can be controlled experimentally as the model had suggested.185 This is an important step to describe the mosaic nature of the SEI film.
DFT predicted defect concentrations in typical SEI components, a Li2CO3, and c LiF as a function of the open circuit potential of the electrode it covers. For an SEI with a mixture of Li2CO3 and LiF, b there is a chemical driving force for Li+ to move from LiF to Li2CO3, causing a space charging layer to enhance the Li+ transport near the LiF|Li2CO3 interface38 (Copyright: American Chemical Society)
Li-ion de-solvation at the SEI/electrolyte interface
The Li+ de-solvation at the SEI/electrolyte interface also requires an activation energy. To model an electrode/SEI/electrolyte structure, atomistic MD was often used. Jorn et al.92 compared the electrolyte structure with or without an SEI covering the graphite edge surface and showed that Li-ions migrate closer to the SEI/electrolyte interface under an applied electric field with increasing LiF content and SEI thickness, as shown in Fig. 13a. A later MD simulation by Borodin and Bedrov predicted that the activation energy for Li+ de-solvation at the SEI/electrolyte interface is 0.42 (~42 kJ mol−1) and 0.46 eV (~47 kJ mol−1) for the Li2EDC/electrolyte and Li2BDC/electrolyte interfaces, respectively.186 Boyer et al.93 performed MD simulations of this process and showed an accumulation of Li+ on graphite surface under different charge densities. These large-scale MD simulations described the electrolyte structural changes under the applied electric field, but have not been able to predict the energetics of electrolyte reduction reactions or the charge transfer reaction, due to the force field limitation.
DFTB offers a fast and efficient quantum mechanical simulation by means of a second-order expansion of the Kohn–Sham total energy in DFT with respect to charge density fluctuations. It was used to calculate the Li-ion transfer energetics through the electrode/SEI/electrolyte interface (with ~1000 atoms), as shown in Fig. 13b.38 It showed that the de-solvation energy is much lower than the solvation energy since only two out of five EC molecules need to be stripped from the first solvation sheath when Li+ is observed on the Li2CO3 surface. It also showed that a slightly negatively charged Li metal surface is not enough to plate Li+ onto the electrode since Li+ solvation in the EC electrolyte is much more energetically favored. The energy landscape of Li transport at this interface structure also suggests that diffusion through the SEI can be the rate-limiting step if no defect is considered in Li2CO3.
Mechanical properties (modulus and adhesion) of the SEI components
The mechanical stability of an efficient SEI means that it should remain intact when the electrode expands/contracts during lithiation/delithiation. Elastic deformation of SEI is more preferred than permanent (irreversible) plastic deformation. Since the deformation of SEI is inevitable, fracture and delamination of SEI should be avoided, and therefore its toughness and adhesion to the electrode are the two key descriptors.
The elasticity of the SEI depends on its components and structure. Shang et al.187 computed the elastic properties of Li2CO3 with DFT. With the integration of experimental and computational studies, Shin et al.188 gave the stiffness of dominant constituents in SEI in the order of LiF > Li2CO3 > Li2EDC > LiMC > PEO. The stiffness decreases roughly from the inorganic components to the organic and then to the polymeric parts.188 According to the recent simulations with the APPLE&P force field, Li2BDC is less stiff than Li2EDC.177
In addition to the bulk modulus, the work of adhesion is equally important for the SEI. Adhesion of Li2CO3 on bare and lithiated graphite has been modeled using DFT and only the (001) surface of Li2CO3 tightly bonds with graphite with a work of adhesion of 1.86 J m−2.189 DFT calculations showed that the Li2CO3/Li interface bears higher interfacial mechanical stability than LiF/Li interface.159 However, even the maximum work of adhesion at the Li(001)/Li2CO3(001) interface is only 0.17 J m−2, which is relatively low for typical metal/ceramics interfaces. With classical Monte Carlo (MC) and DFT-based methods, Soto and Balbuena190 found that the oligomers attach/adhere firmly to the Li13Si4 (010) surface with calculated adsorption energies in a range of 3–4 eV and if the coverage oligomer on the surface reaches approximately 1 oligomer per nm2, the surface–oligomer interaction will dominate the stabilization of the interface system.
Verbrugge et al.191 constructed a core–shell model and derived the lithiation-induced-stress model to evaluate the stress in the SEI layer due to the volume change of the electrode. Taking the input from DFT-computed chemical and mechanical properties, they showed that the SEI layer can sustain the deformation of a conventional graphite electrode but not a silicon electrode. Therefore, artificial coatings need to be designed along with the structure of Si electrode. This will be discussed in the section “Explore the surface chemistry and treatment: unlimited choices”.
Chemical stability of the SEI components
Solubility and reactivity (chemical and electrochemical) are signified as two descriptors for the chemical stability of the SEI components. These processes continue to consume active Li-ions and result in further irreversible capacity loss.
Some of the inorganic and organic compounds can be dissolved in the non-aqueous solvents. Tasaki and Harris192 performed MD simulations with the COMPASS force field to calculate the solubility of the main SEI components in organic electrolyte and found the following order: Li2EDC > LiOCO2CH3 > LiOH > LiOCO2C2H5 > LiOCH3 > LiF > [LiCO2]2 > Li2CO3 > Li2O. These semi-organic components can be thermodynamically unstable against the highly reactive anode. As shown by Leung et al.,193 components such as Li2CO3 and Li2EDC are thermodynamically unstable near the equilibrium Li/Li+ potential, and readily decompose to more stable species, such as Li2O.
Since the electrolyte reduction reactions are multi-step reactions, products from one-electron reduction reaction can be reduced further. This especially contributes to the electrochemical instability of the outer organic SEI components, such as Li2EDC and other radicals.158,167,194 According to the first-principles calculation, Soto et al.158 argued that additives like VC and FEC are welcome due to their fast polymerization, forming a more stable SEI, leading to the controlled SEI growth as shown in Fig. 14.158 They first proposed that the electrochemical stability of the reduction products is more crucial than the stability of electrolyte components. If the deposited products on anode are electrochemically unstable, they are prone to be attacked by radicals, which carry electrons, and become reduced, causing SEI growth and capacity loss. The inorganic LiF aggregates generated from the decomposition of FEC additive can stabilize the SEI film by adsorbing the organic SEI film components through the strong F-Li binding.195,196 The organic components in the outer layer can also chemically react with moisture or acid, causing more SEI degradation.194
One principle for SEI growth points to the chemical stability of the reduced species, based on the insights obtained from comparative AIMD calculations. EC solvents form unstable SEI species (such as Li2EDC and oligomers), which are prone to radical attack, causing continuous SEI growth, while successful additives, such as VC or FEC, lead to more stable polymer species, and thus more compact SEI outer layer and controlled SEI growth158 (Copyright: American Chemical Society)
Reductive cation can also lead to SEI growth. A well-known degradation mechanism is called “Mn poisoning of SEI”. The Mn2+ ions can dissolute from the LiMn2O4 cathode, migrate to the anode surface, and cause SEI growth. However, the reason for this mechanism has been highly debated. A recent DFT-based simulation revealed that the Mn2+ lands between the inorganic Li2CO3 and organic Li2EDC in the SEI layer of graphite anode and facilitates the further electrochemical reduction and decomposition of Li2EDC.197
SEI growth and battery aging: mechanisms and multi-scale modeling
Though the initially formed SEI might be simple,167 the SEI on the anode is subject to change during the electrochemical cycling process.198,199 Its evolution, due to the above-mentioned mechanical and chemical failure mechanisms, can lead to various aging processes in LIBs (capacity fading, self-discharge, impedance rise).21 Since Newman and Tobias200 established the battery simulation model for a porous electrode in the 1960s,200 continuum level of modeling that describes SEI growth and battery degradation has been developed long before the recent advancements in atomistic modeling. However, continuum modeling often suffers from the lack of directly measured physical parameters or mechanistic relationships, as reviewed by Newman et al.201 in 2003. With the development of predictive modeling, the gap between these two levels can start to be bridged.
The SEI growth can be limited by the electron leakage through the dense layer of SEI. In 1979, Peled5 derived a parabolic growth model of SEI based on the assumption that the electron leakage through the SEI layer is the rate-limiting process for SEI growth. By adopting the model of Peled, Broussely et al.202 derived that the capacity loss increases with the square root of time, assuming that the parasitic reaction was governed by the electronic conductivity of the SEI. Christensen and Newman203 developed a physics-based continuum model to simulate both Li+ and electron transport through the SEI in order to estimate the film growth rate, film resistance, and the irreversible capacity loss. They have used available parameters of Li2CO3 at that time (2004) in the model, while assumptions still had to be made due to the lack of some directly measured parameters (for example, Li interstitial concentration, conductivity). Since these parameters can be predicted from DFT, multi-scale modeling with atomistic-scale mechanisms and parameters input into the continuum model can be a powerful combination. A framework that takes into account the atomistic kinetic information is the SEI growth model given by Colclasure et al.,204 who incorporated the detailed chemical kinetics as well as multicomponent transport properties into the SEI growth model throughout charge and discharge cycles. Another bottom-up approach was developed by Hao et al.,109 wherein they verified the square root relationship between SEI film thickness and time, and found that the Li-ion content fluctuates due to the heterogeneous structure of SEI.
The SEI growth can also be limited by the electrolyte diffusion through the porous SEI layer. For example, Ploehn et al.205 presented a solvent diffusion-limited model on a planar graphite surface as functions of temperature and concentrations within the surrounding electrolyte solution. This model also gave the square root relationship between the capacity loss and time. The thermal effect was further coupled with the electrochemical model by Liu et al.206 Pinson and Bazant207 started with a simple single-particle model that can accurately explain the experimentally observed capacity fade in commercial cells with graphite anodes. They then extended the theory to porous graphite electrodes and rapidly degrading nanostructured silicon electrodes, where the large surface area changes during cycling promote capacity loss and SEI growth.207
Taking the two-layer SEI model into consideration, Tang et al.208 developed a series of different theoretical predictions based on different growth mechanisms and tried to use them to interpret the electrochemical measurements. Such a comparison led to the new insight that a gradual densification of SEI was the best model to explain the experiments.208 The multi-layer-mosaic growth model of SEI developed by Guan et al.209 with the phase-field method fits the experimental work done by Tang et al.208 well.
New insights for atomistic modeling have been incorporated into continuum models as well. In contrast to the homogenous SEI morphology and single transport mechanism modeling, Single et al.210,211 used the two-layer/two-mechanism model30,31 to describe the SEI morphology with a continuum model. Both electron conduction and solvent diffusion are modeled as rate-determining transport mechanisms. The square root dependence with time is also attained in accordance with previous studies.202
In vitro design of the SEI
Explore the surface chemistry and treatment: unlimited choices
Many attempts have been dedicated towards designing a surface coating layer to achieve the multi-functionality of the SEI, which is considered as “in vitro” design of the SEI. The in vitro design of the SEI provides unlimited material choices for SEI chemistry and processing methods. High-throughput calculations and computational screening are therefore needed to guide the discovery of the most promising candidates.212,213,214
Reactive gas treatment (N2, O2, CO2, F2, and SO2) on lithium metal can create a passivation layer with controlled structural, electronic, and elastic properties of the electrode surface.215 Among the gases investigated by DFT and MD calculations, Koch et al.215 revealed that N2-treated adlayer is the most elastic compliant passivation layer for the interface between lithium and adsorbate, minimizing the possibility of crack formation and lithium dendrite growth. Recently, DFT-based high-throughput calculations indicated that the nitride compounds display extremely high stability against lithium metal, due to the relatively low cathodic limit vs. Li/Li+.216 Considering the high ionic conductivity in Li3N,217 the nitration process can form an effective coating layer on lithium anode.
ALD155,157,218 and MLD219 coating on the electrodes are two prevailing methods to protect the electrodes from direct contact with the electrolyte and to hinder solvent decomposition on anode surfaces. They offer more varieties than reactive gas treatment. These methods can form conformal artificial SEI with precisely controlled distribution and thickness and have shown great promise.220,221,222
Al2O3 is one of the first ALD coatings applied to the lithium-based battery. It is electron insulating with a bandgap of 9.9 eV.223 The slow electron transfer rate mitigates the solvent decomposition and active lithium consumption to some extent, as confirmed by simulations and experiments.157,165 Therefore, the capacity loss of ALD-coated electrode is dramatically reduced due to less SEI formation, effectively increasing the Coulombic efficiency and high-rate cycling stability.165 Aluminum alkoxide (alucone) is one of the organic MLD coatings that showed improved performance for Li and Si electrodes.219,224
Different SEI components and artificial SEI coating materials can be categorized into fully lithiated and non-fully lithiated materials. Li2O, Li2CO3, LiF, Li2EDC, LiPON are fully lithiated and they will not be lithiated during battery operation. However, many oxide coatings can be lithiated, as Li can replace the M in MO to form Li2O+M, and M can also be continually lithiated. Note that the Li or Si electrode surfaces are always covered by a thin layer of oxides (Li2O and SiO2, respectively) after being exposed to air. Using DFT-computed OCV, Kim and Qi225 showed that SiO2 and Al2O3 start to be lithiated before Si (lithiated at ~0.4 eV), at around 0.68 and 0.9 eV, respectively. With ReaxFF MD simulations of a Si-core-oxide-shell structure, Kim et al.226 further demonstrated that when the Si core is fully lithiated, the composition of SiO2 and the Al2O3 shells will be highly lithiated.
Therefore, once in operation, these oxide coatings are inevitably lithiated along with the electrode until a chemical potential equilibrium, as shown in Eq. 5, is reached. Besides oxides, carbon-based and alucone coatings can all be lithiated.227 Upon lithiation, the electronic, ionic transport and mechanical properties of these coating materials may change accordingly.225,227 Therefore, the design of SEI chemical compositions should consider its properties after lithiation.
Design of the coating geometry: considering the evolving properties
Verbrugge et al.191 pointed out that artificial coatings need to be designed along with the structure of Si and Li electrodes, as the naturally formed SEI components cannot accommodate the large electrode deformation. ALD and MLD provide coating materials with various mechanical properties, such as being more elastic and/or having larger elongation till fracture.
Due to the precise control of the coating thickness offered by ALD and MLD techniques, the artificial SEI chemistry and geometry can be co-designed with the nanostructured Si, in order to achieve an overall high Coulombic efficiency. Zhang et al.228 have shown the relationship of a coating fracture criterion with its thickness for SnO2 nanowire lithiated axially. More complex structures, such as a coated hollow Si core, can be designed to avoid failure by relying on the coating to impose mechanical constraints in order to force the deformation of Si inward. Zhao et al.229 have developed an analytical mechanics model to predict the size of Si and the thickness of the coating that can achieve a mechanically stable coated hollow Si system during lithiation. Stournara et al.230 predicted the coating fracture energy, modulus, and the Si–C interface fracture energy at both non-lithiated and fully lithiated levels by DFT calculations and input into the Zhao229 model. It then predicted that if the Si-core radius is less than 200 nm and C-shell thickness is about 10 nm, the coating will not fracture or delaminate up to 80% of SOC.
As we discussed in the previous sections, many coatings can be lithiated, and the mechanical properties of these coatings can be lithiation dependent,225 just like some electrode materials.231 Lithiation softens Al2O3 whereas it stiffens SiO2. The lithiation of SiO2 was reported to be favorable by breaking the Si–O bond.232 Using ReaxFF and MD simulations, Kim et al.226 simulated the lithiation process of SiO2- and Al2O3-coated Si-nanowires, as shown in Fig. 15. They proposed that a coating with elastic modulus gradient, softer outside, harder inside, is beneficial to avoid cracking of the coating layer during Si expansion. The self-accelerating lithiation process and the lithiation induced softening in Al2O3 coating naturally provide such a modulus gradient, and therefore it did not crack compared to the SiO2 coating at the same thickness without this property.225 This example gave a relationship between the film thickness and Si core size to avoid coating cracking,
where h is the coating thickness, R is the radius of the Si wire, σ f is the coating fracture stress, ΔG is the chemical potential for lithiation, and Ω is the atomic volume of lithium. As long as the coating property values after lithiation have been used, the size ratio agrees well with the MD case study.226 These multi-scale modeling examples show feasibility of the virtual design of SEI in vitro at both material and geometry levels.
Illustration of the reactive MD simulation of the lithiation process of oxide (shell) covered Si nanowires (core) (Si yellow, O red, Li: cyan)226 (Copyright: Royal Society of Chemistry)
Outlook
Current modeling efforts based on the known SEI components and structures are reviewed from predictive modeling perspectives. The ideal SEI layer should possess two features: electronically insulating and Li-ion conducting. Since the in vivo SEI is usually formed due to electrolyte reduction, electron transfer and Li-ion diffusion mechanisms are important to understand the SEI formation and evolution. Modeling these mechanisms is non-trivial, as they occur at different lengths and time scales and face different modeling challenges and limitations. This overview summarizes the modeling efforts on SEI formation, growth, and properties and reminds us to envision and comprehend SEI as a multi-layered, mosaic, and evolving structure.
Modeling methods, ranging from electronic to atomic scale models and phenomenological models, are equally important and should be coordinated with each other in order to make qualitative and quantitative predictions. For example, the relatively accurate basic physical/chemical/electrochemical properties (such as electron tunneling, thickness, voltage calculation, ionic conductivity, interfacial properties, etc.) predicted from electronic/atomic models can be parameterized and incorporated in large-scale models to provide a more predictive macroscopic picture of SEI and its impact on Li-ion battery performance.
Obstacles lie ahead, in order for us to understand the real status of SEI inside the battery cell. It is challenging to comprehensively establish the structure–property relationship of SEI owing to its multi-component/multi-structure characteristics. Additionally, the computational simulations are all conducted with an idealized model instead of including all the complexities of a real system, and this can be a limitation or an advantage for modeling. Last but not the least, the approaches applied in understanding the SEI in aprotic batteries can be extended to the solid-state battery, wherein the SEI can also form in vivo, resulting from chemical or electrochemical reactions. With an extensive understanding of the existing SEI films, both in vivo and in vitro designs are possible to optimize the battery performance.
References
Tarascon, J. M. & Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 414, 359–367 (2001).
Zu, C.-X. & Li, H. Thermodynamic analysis on energy densities of batteries. Energy Environ. Sci. 4, 2614–2624 (2011).
Goodenough, J. B. & Park, K.-S. The Li-ion rechargeable battery: a perspective. J. Am. Chem. Soc. 135, 1167–1176 (2013).
Dey, A. N. Film formation on lithium anode in propylene carbonate. J. Electrochem. Soc. 117, C248 (1970).
Peled, E. The electrochemical behavior of alkali and alkaline earth metals in nonaqueous battery systems—the solid electrolyte interphase model. J. Electrochem. Soc. 126, 2047–2051 (1979).
Peled, E., Golodnitsky, D. & Ardel, G. Advanced model for solid electrolyte interphase electrodes in liquid and polymer electrolytes. J. Electrochem. Soc. 144, L208–L210 (1997).
Aurbach, D. et al. New insights into the interactions between electrode materials and electrolyte solutions for advanced nonaqueous batteries. J. Power Sources 81, 95–111 (1999).
Winter, M. The solid electrolyte interphase—the most important and the least understood solid electrolyte in rechargeable Li batteries. Z. Fur Phys. Chem. 223, 1395–1406 (2009).
Verma, P., Maire, P. & Novak, P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries. Electrochim. Acta 55, 6332–6341 (2010).
Goodenough, J. B. & Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 22, 587–603 (2010).
Xing, L., Borodin, O., Smith, G. D. & Li, W. Density functional theory study of the role of anions on the oxidative decomposition reaction of propylene carbonate. J. Phys. Chem. A. 115, 13896–13905 (2011).
Zhang, X. R., Pugh, J. K. & Ross, P. N. Computation of thermodynamic oxidation potentials of organic solvents using density functional theory. J. Electrochem. Soc. 148, E183–E188 (2001).
Borodin, O. & Jow, T. R. in Non-Aqueous Electrolytes for Lithium Batteries. Vol. 33 ECS Transactions (eds B. Lucht, W. A. Henderson, T. R. Jow, & M. Ue) 77–84 (The electrochemical Society, NJ, 2011).
Li, T. & Balbuena, P. B. Theoretical studies of the reduction of ethylene carbonate. Chem. Phys. Lett. 317, 421–429 (2000).
Wang, Y. X., Nakamura, S., Ue, M. & Balbuena, P. B. Theoretical studies to understand surface chemistry on carbon anodes for lithium-ion batteries: reduction mechanisms of ethylene carbonate. J. Am. Chem. Soc. 123, 11708–11718 (2001).
Gauthier, M. et al. Electrode–electrolyte interface in Li-ion batteries: current understanding and new insights. J. Phys. Chem. Lett. 6, 4653–4672 (2015).
Delp, S. A. et al. Importance of reduction and oxidation stability of high voltage electrolytes and additives. Electrochim. Acta 209, 498–510 (2016).
Wu, F., Borodin, O. & Yushin, G. In situ surface protection for enhancing stability and performance of conversion-type cathodes. MRS Energ. Sustain. 4, E9 (2017).
Seo, D. M., Borodin, O., Han, S.-D., Boyle, P. D. & Henderson, W. A. Electrolyte solvation and ionic association II. Acetonitrile-lithium salt mixtures: highly dissociated salts. J. Electrochem. Soc. 159, A1489–A1500 (2012).
Borodin, O. et al. Modeling insight into battery electrolyte electrochemical stability and interfacial structure. Acc. Chem. Res. 50, 2886–2894 (2017).
Vetter, J. et al. Ageing mechanisms in lithium-ion batteries. J. Power Sources 147, 269–281 (2005).
Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 104, 4303–4417 (2004).
Xu, K. Electrolytes and interphases in Li-ion batteries and beyond. Chem. Rev. 114, 11503–11618 (2014).
Agubra, V. A. & Fergus, J. W. The formation and stability of the solid electrolyte interface on the graphite anode. J. Power Sources 268, 153–162 (2014).
An, S. J. et al. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon N.Y. 105, 52–76 (2016).
Nazri, G. & Muller, R. H. Composition of surface layers on Li electrodes in PC, LiClO4 of very low water content. J. Electrochem. Soc. 132, 2050–2054 (1985).
Aurbach, D., Daroux, M. L., Faguy, P. W. & Yeager, E. Identification of surface films formed on lithium in propylene carbonate solutions. J. Electrochem. Soc. 134, 1611–1620 (1987).
Kanamura, K., Tamura, H. & Takehara, Z.-I. XPS analysis of a lithium surface immersed in propylene carbonate solution containing various salts. J. Electroanal. Chem. 333, 127–142 (1992).
Kanamura, K., Tamura, H., Shiraishi, S. & Takehara, Zi XPS analysis of lithium surfaces following immersion in various solvents containing LiBF4. J. Electrochem. Soc. 142, 340–347 (1995).
Lu, P. & Harris, S. J. Lithium transport within the solid electrolyte interphase. Electrochem. Commun. 13, 1035–1037 (2011).
Shi, S. Q. et al. Direct calculation of Li-ion transport in the solid electrolyte interphase. J. Am. Chem. Soc. 134, 15476–15487 (2012).
v. Cresce, A., Russell, S. M., Baker, D. R., Gaskell, K. J. & Xu, K. In situ and quantitative characterization of solid electrolyte interphases. Nano. Lett. 14, 1405–1412 (2014).
Zheng, J. et al. 3D visualization of inhomogeneous multi-layered structure and Young’s modulus of the solid electrolyte interphase (SEI) on silicon anodes for lithium ion batteries. Phys. Chem. Chem. Phys. 16, 13229–13238 (2014).
Zhang, Q. L. et al. Synergetic Effects of inorganic components in solid electrolyte interphase on high cycle efficiency of lithium ion batteries. Nano Lett. 16, 2011–2016 (2016).
Slane, S. M. & Foster, D. L. Lithium ion rechargeable intercalation cell. US1076-H; CA2053746-A (1992).
Zhang, W.-J. A review of the electrochemical performance of alloy anodes for lithium-ion batteries. J. Power Sources 196, 13–24 (2011).
Xu, W. et al. Lithium metal anodes for rechargeable batteries. Energy Environ. Sci. 7, 513–537 (2014).
Li, Y., Leung, K. & Qi, Y. Computational exploration of the Li-electrode/electrolyte interface in the presence of a nanometer thick solid-electrolyte interphase layer. Acc. Chem. Res. 49, 2363–2370 (2016).
Zhang, K., Lee, G.-H., Park, M., Li, W. & Kang, Y.-M. Recent Developments of the Lithium Metal Anode for Rechargeable Non-AqueousBatteries. Adv. Energy Mater. 6, 1600811 (2016).
Cheng, X. B. et al. A review of solid electrolyte interphases on lithium metal anode. Adv. Sci. 3, 1500213 (2016).
Lin, D., Liu, Y. & Cui, Y. Reviving the lithium metal anode for high-energy batteries. Nat. Nanotech. 12, 194–206 (2017).
Fong, R., Von Sacken, U. & Dahn, J. R. Studies of lithium intercalation into carbons using nonaqueous electrochemical cells. J. Electrochem. Soc. 137, 2009–2013 (1990).
Naji, A., Ghanbaja, J., Humbert, B., Willmann, P. & Billaud, D. Electroreduction of graphite in LiClO4-ethylene carbonate electrolyte. characterization of the passivating layer by transmission electron microscopy and fourier-transform infrared spectroscopy. J. Power Sources 63, 33–39 (1996).
Novak, P., Joho, F., Imhof, R., Panitz, J. C. & Haas, O. In situ investigation of the interaction between graphite and electrolyte solutions. J. Power Sources 81, 212–216 (1999).
Soto, F. A., Martinez de la Hoz, J. M., Seminario, J. M. & Balbuena, P. B. Modeling solid-electrolyte interfacial phenomena in silicon anodes. Curr. Opin. Chem. Eng. 13, 179–185 (2016).
Meng, Y. S. & Arroyo-de Dompablo, M. E. First principles computational materials design for energy storage materials in lithium ion batteries. Energy Environ. Sci. 2, 589–609 (2009).
Ouyang, C. & Chen, L. Physics towards next generation Li secondary batteries materials: a short review from computational materials design perspective. Sci. China Phys. Mech. 56, 2278–2292 (2013).
Franco, A. A. Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: concepts, methods and challenges. RSC Adv. 3, 13027–13058 (2013).
Reddy, V. P., Blanco, M. & Bugga, R. Boron-based anion receptors in lithium-ion and metal-air batteries. J. Power Sources 247, 813–820 (2014).
Shi, S. et al. Multi-scale computation methods: their applications in lithium-ion battery research and development. Chin. Phys. B 25, 018212 (2016).
Grazioli, D., Magri, M. & Salvadori, A. Computational modeling of Li-ion batteries. Comput. Mech. 58, 889–909 (2016).
Urban, A., Seo, D. H. & Ceder, G. Computational understanding of Li-ion batteries. NPJ Comput. Mater. 2, 16002 (2016).
Galvez-Aranda, D. E., Ponce, V. & Seminario, J. M. Molecular dynamics simulations of the first charge of a Li-ion—Si-anode nanobattery. J. Mol. Model. 23, 120 (2017).
Balbuena, P. B. in Review on Electrochemical Storage Materials and Technology. Vol. 1597, AIP Conference Proceedings (eds D. C. Meyer & T. Leisegang) 82–97 (American Institute of Physics, New York, 2014).
Ramos-Sanchez, G. et al. Computational studies of interfacial reactions at anode materials: initial stages of the solid-electrolyte-interphase layer formation. J. Electrochem. En. Conv. Stor. 13, 031002 (2016).
Martinez de la Hoz, J. M., Soto, F. A. & Balbuena, P. B. Effect of the electrolyte composition on SEI reactions at Si anodes of Li-ion batteries. J. Phys. Chem. C 119, 7060–7068 (2015).
Camacho-Forero, L. E., Smith, T. W. & Balbuena, P. B. Effects of high and low salt concentration in electrolytes at lithium-metal anode surfaces. J. Phys. Chem. C 121, 182–194 (2017).
Blint, R. J. Binding of ether and carbonyl oxygens to lithium ion. J. Electrochem. Soc. 142, 696–702 (1995).
Aurbach, D., Levi, M. D., Levi, E. & Schechter, A. Failure and stabilization mechanisms of graphite electrodes. J. Phys. Chem. B 101, 2195–2206 (1997).
Yu, J., Balbuena, P. B., Budzien, J. & Leung, K. Hybrid DFT functional-based static and molecular dynamics studies of excess electron in liquid ethylene carbonate. J. Electrochem. Soc. 158, A400–A410 (2011).
Xu, M. et al. Investigation and application of lithium difluoro(oxalate)borate (LiDFOB) as additive to improve the thermal stability of electrolyte for lithium-ion batteries. J. Power Sources 196, 6794–6801 (2011).
Leung, K. & Budzien, J. L. Ab initio molecular dynamics simulations of the initial stages of solid-electrolyte interphase formation on lithium ion battery graphitic anodes. Phys. Chem. Chem. Phys. 12, 6583–6586 (2010).
Bedrov, D., Smith, G. D. & van Duin, A. C. T. Reactions of singly-reduced ethylene carbonate in lithium battery electrolytes: a molecular dynamics simulation study using the ReaxFF. J. Phys. Chem. A. 116, 2978–2985 (2012).
Martinez de la Hoz, J. M., Leung, K. & Balbuena, P. B. Reduction mechanisms of ethylene carbonate on Si anodes of lithium-ion batteries: effects of degree of lithiation and nature of exposed surface. ACS Appl. Mater. Interfaces 5, 13457–13465 (2013).
Leung, K. Two-electron reduction of ethylene carbonate: a quantum chemistry re-examination of mechanisms. Chem. Phys. Lett. 568-569, 1–8 (2013).
Leung, K. & Tenney, C. M. Toward first principles prediction of voltage dependences of electrolyte/electrolyte interfacial processes in lithium ion batteries. J. Phys. Chem. C. 117, 24224–24235 (2013).
Okamoto, Y. Ab initio calculations of thermal decomposition mechanism of LiPF6-based electrolytes for lithium-ion batteries. J. Electrochem. Soc. 160, A404–A409 (2013).
Leung, K. Predicting the voltage dependence of interfacial electrochemical processes at lithium-intercalated graphite edge planes. Phys. Chem. Chem. Phys. 17, 1637–1643 (2015).
Islam, M. M. & van Duin, A. C. T. Reductive decomposition reactions of ethylene carbonate by explicit electron transfer from lithium: an eReaxFF molecular dynamics study. J. Phys. Chem. C. 120, 27128–27134 (2016).
Hammer, N. I. et al. Dipole-bound anions of highly polar molecules: ethylene carbonate and vinylene carbonate. J. Chem. Phys. 120, 685–690 (2004).
Jin, Y. et al. Identifying the structural basis for the increased stability of the solid electrolyte interphase formed on silicon with the additive fluoroethylene carbonate. J. Am. Chem. Soc. 139, 14992–15004 (2017).
Onuki, M. et al. Identification of the source of evolved gas in Li-ion batteries using (13)C-labeled solvents. J. Electrochem. Soc. 155, A794–A797 (2008).
Shkrob, I. A., Zhu, Y., Marin, T. W. & Abraham, D. Reduction of carbonate electrolytes and the formation of solid-electrolyte interface (SEI) in lithium-ion batteries. 1. Spectroscopic observations of radical intermediates generated in one-electron reduction of carbonates. J. Phys. Chem. C 117, 19255–19269 (2013).
Tasaki, K. Solvent decompositions and physical properties of decomposition compounds in Li-ion battery electrolytes studied by DFT calculations and molecular dynamics simulations. J. Phys. Chem. B 109, 2920–2933 (2005).
Borodin, O. & Smith, G. D. Quantum chemistry and molecular dynamics simulation study of dimethyl carbonate: ethylene carbonate electrolytes doped with LiPF6. J. Phys. Chem. B. 113, 1763–1776 (2009).
Borodin, O. Polarizable force field development and molecular dynamics simulations of ionic liquids. J. Phys. Chem. B. 113, 11463–11478 (2009).
Seo, D. M. et al. Electrolyte solvation and ionic association I. Acetonitrile-lithium salt mixtures: intermediate and highly associated salts. J. Electrochem. Soc. 159, A553–A565 (2012).
Kim, S. P., van Duin, A. C. T. & Shenoy, V. B. Effect of electrolytes on the structure and evolution of the solid electrolyte interphase (SEI) in Li-ion batteries: a molecular dynamics study. J. Power Sources 196, 8590–8597 (2011).
Borodin, O., Olguin, M., Spear, C. E., Leiter, K. W. & Knap, J. Towards high throughput screening of electrochemical stability of battery electrolytes. Nanotechnology 26, 354003 (2015).
Borodin, O. et al. Challenges with quantum chemistry-based screening of electrochemical stability of lithium battery electrolytes. ECS Trans. 69, 113–123 (2015).
Campion, C. L., Li, W. T. & Lucht, B. L. Thermal decomposition of LiPF6-based electrolytes for lithium-ion batteries. J. Electrochem. Soc. 152, A2327–A2334 (2005).
Aurbach, D., Moshkovich, M., Cohen, Y. & Schechter, A. The study of surface film formation on noble-metal electrodes in alkyl carbonates/Li salt solutions, using simultaneous in situ AFM, EQCM, FTIR, and EIS. Langmuir 15, 2947–2960 (1999).
Leung, K. Electronic structure modeling of electrochemical reactions at electrode/electrolyte interfaces in lithium ion batteries. J. Phys. Chem. C 117, 1539–1547 (2013).
Wang, Y. X. & Balbuena, P. B. Theoretical studies on cosolvation of Li ion and solvent reductive decomposition in binary mixtures of aliphatic carbonates. Int. J. Quantum Chem. 102, 724–733 (2005).
Tasaki, K., Kanda, K., Nakamura, S. & Ue, M. Decomposition of LiPF6 and stability of PF5 in Li-ion battery electrolytes—density functional theory and molecular dynamics studies. J. Electrochem. Soc. 150, A1628–A1636 (2003).
Kim, H. et al. In situ formation of protective coatings on sulfur cathodes in lithium batteries with LiFSI-based organic electrolytes. Adv. Energy Mater. 5, 1401792 (2015).
Suo, L. et al. Advanced high-voltage aqueous lithium-ion battery enabled by “water-in-bisalt” electrolyte. Angew. Chem. Int. Ed. 55, 7136–7141 (2016).
Suo, L. et al. How solid-electrolyte interphase forms in aqueous electrolytes. J. Am. Chem. Soc. 139, 18670–18680 (2017).
Cresce, A. V. W., Borodin, O. & Xu, K. Correlating Li+ solvation sheath structure with interphasial chemistry on graphite. J. Phys. Chem. C 116, 26111–26117 (2012).
Owejan, J. E., Owejan, J. P., DeCaluwe, S. C. & Dura, J. A. Solid electrolyte interphase in Li-ion batteries: evolving structures measured in situ by neutron reflectometry. Chem. Mater. 24, 2133–2140 (2012).
Vatamanu, J., Borodin, O. & Smith, G. D. Molecular dynamics simulation studies of the structure of a mixed carbonate/LiPF6 Electrolyte near graphite surface as a function of electrode potential. J. Phys. Chem. C 116, 1114–1121 (2012).
Jorn, R., Kumar, R., Abraham, D. P. & Voth, G. A. Atomistic modeling of the electrode-electrolyte interface in Li-ion energy storage systems: electrolyte structuring. J. Phys. Chem. C 117, 3747–3761 (2013).
Boyer, M. J., Vilciauskas, L. & Hwang, G. S. Structure and Li+ ion transport in a mixed carbonate/LiPF6 electrolyte near graphite electrode surfaces: a molecular dynamics study. Phys. Chem. Chem. Phys. 18, 27868–27876 (2016).
Ponce, V., Galvez-Aranda, D. E. & Seminario, J. M. Analysis of a Li-Ion Nanobattery with Graphite Anode Using Molecular Dynamics Simulations. J. Phys. Chem. C. 121, 12959–12971 (2017).
Vatamanu, J., Bedrov, D. & Borodin, O. On the application of constant electrode potential simulation techniques in atomistic modelling of electric double layers. Mol. Simula. 43, 838–849 (2017).
Ganesh, P., Kent, P. R. C. & Jiang, D.-E. Solid-electrolyte interphase formation and electrolyte reduction at Li-ion battery graphite anodes: insights from first-principles molecular dynamics. J. Phys. Chem. C. 116, 24476–24481 (2012).
Ebadi, M., Brandell, D. & Araujo, C. M. Electrolyte decomposition on Li-metal surfaces from first-principles theory. J. Chem. Phys. 145, 204701 (2016).
Ma, Y. & Balbuena, P. B. DFT study of reduction mechanisms of ethylene carbonate and fluoroethylene carbonate on Li+-adsorbed Si clusters. J. Electrochem. Soc. 161, E3097–E3109 (2014).
Moradabadi, A., Bakhtiari, M. & Kaghazchi, P. Effect of anode composition on solid electrolyte interphase formation. Electrochim. Acta 213, 8–13 (2016).
Camacho-Forero, L. E., Smith, T. W., Bertolini, S. & Balbuena, P. B. Reactivity at the lithium–metal anode surface of lithium–sulfur batteries. J. Phys. Chem. C 119, 26828–26839 (2015).
Liu, Z., Bertolini, S., Balbuena, P. B. & Mukherjee, P. P. Li2S film formation on lithium anode surface of Li–S batteries. ACS Appl. Mater. Interfaces 8, 4700–4708 (2016).
Nandasiri, M. I. et al. In situ chemical imaging of solid-electrolyte interphase layer evolution in Li–S batteries. Chem. Mater. 29, 4728–4737 (2017).
Hankins, K., Soto, F. A. & Balbuena, P. B. Insights into the Li Intercalation and SEI Formation on LiSi Nanoclusters. J. Electrochem. Soc. 164, E3457–E3464 (2017).
Leung, K. & Leenheer, A. How voltage drops are manifested by lithium ion configurations at interfaces and in thin films on battery electrodes. J. Phys. Chem. C 119, 10234–10246 (2015).
Methekar, R. N., Northrop, P. W. C., Chen, K., Braatz, R. D. & Subramanian, V. R. Kinetic Monte Carlo simulation of surface heterogeneity in graphite anodes for lithium-ion batteries: passive layer formation. J. Electrochem. Soc. 158, A363–A370 (2011).
Wang, Y. X. & Balbuena, P. B. Associations of lithium alkyl dicarbonates through O···Li···O interactions. J. Phys. Chem. A 106, 9582–9594 (2002).
Ushirogata, K., Sodeyama, K., Futera, Z., Tateyama, Y. & Okuno, Y. Near-shore aggregation mechanism of electrolyte decomposition products to explain solid electrolyte interphase formation. J. Electrochem. Soc. 162, A2670–A2678 (2015).
Takenaka, N., Suzuki, Y., Sakai, H. & Nagaoka, M. On electrolyte-dependent formation of solid electrolyte interphase film in lithium-ion batteries: strong sensitivity to small structural difference of electrolyte molecules. J. Phys. Chem. C 118, 10874–10882 (2014).
Hao, F., Liu, Z., Balbuena, P. B. & Mukherjee, P. P. Mesoscale elucidation of solid electrolyte interphase layer formation in Li-ion battery anode. J. Phys. Chem. C 121, 26233–26240 (2017).
Balbuena, P. B. & Wang, Y. Lithium-ion batteries: solid-electrolyte interphase. (World Scientific, Singapore, 2004).
Wang, Y. X. & Balbuena, P. B. Theoretical insights into the reductive decompositions of propylene carbonate and vinylene carbonate: density functional theory studies. J. Phys. Chem. B 106, 4486–4495 (2002).
Mukhopadhyay, A., Tokranov, A., Xiao, X. & Sheldon, B. W. Stress development due to surface processes in graphite electrodes for Li-ion batteries: a first report. Electrochim. Acta 66, 28–37 (2012).
Tasaki, K., Goldberg, A. & Winter, M. On the difference in cycling behaviors of lithium-ion battery cell between the ethylene carbonate- and propylene carbonate-based electrolytes. Electrochim. Acta 56, 10424–10435 (2011).
Tasaki, K., Goldberg, A., Liang, J.-J. & Winter, M. in Non-Aqueous Electrolytes for Lithium Batteries. Vol. 33, ECS Transactions (eds B. Lucht, W. A. Henderson, T. R. Jow, & M. Ue) 59–69 (The electrochemical Society, New Jersey, 2011).
Lee, O. S. & Carignano, M. A. Exfoliation of electrolyte-intercalated graphene: molecular dynamics simulation study. J. Phys. Chem. C 119, 19415–19422 (2015).
Guk, H., Kim, D., Choi, S.-H., Chung, D. H. & Han, S. S. Thermostable artificial solid-electrolyte interface layer covalently linked to graphite for lithium ion battery: molecular dynamics simulations. J. Electrochem. Soc. 163, A917–A922 (2016).
Tasaki, K. Density functional theory study on structural and energetic characteristics of graphite intercalation compounds. J. Phys. Chem. C 118, 1443–1450 (2014).
Bhatt, M. D. & O’Dwyer, C. The role of carbonate and sulfite additives in propylene carbonate-based electrolytes on the formation of SEI layers at graphitic Li-ion battery anodes. J. Electrochem. Soc. 161, A1415–A1421 (2014).
Ushirogata, K., Sodeyama, K., Okuno, Y. & Tateyama, Y. Additive effect on reductive decomposition and binding of carbonate-based solvent toward solid electrolyte interphase formation in lithium-ion battery. J. Am. Chem. Soc. 135, 11967–11974 (2013).
Leung, K. et al. Modeling electrochemical decomposition of fluoroethylene carbonate on silicon anode surfaces in lithium ion batteries. J. Electrochem. Soc. 161, A213–A221 (2014).
Martinez de la Hoz, J. M. & Balbuena, P. B. Reduction mechanisms of additives on Si anodes of Li-ion batteries. Phys. Chem. Chem. Phys. 16, 17091–17098 (2014).
McArthur, M. A., Trussler, S. & Dahn, J. R. In situ investigations of SEI layer growth on electrode materials for lithium-ion batteries using spectroscopic ellipsometry. J. Electrochem. Soc. 159, A198–A207 (2012).
Yang, Z., Gewirth, A. A. & Trahey, L. Investigation of fluoroethylene carbonate effects on Tin-based lithium-ion battery electrodes. ACS Appl. Mater. Interfaces 7, (6557–6566 (2015).
Xing, L., Li, W., Xu, M., Li, T. & Zhou, L. The reductive mechanism of ethylene sulfite as solid electrolyte interphase film-forming additive for lithium ion battery. J. Power Sources 196, 7044–7047 (2011).
Sun, Y. & Wang, Y. New insights into the electroreduction of ethylene sulfite as an electrolyte additive for facilitating solid electrolyte interphase formation in lithium ion batteries. Phys. Chem. Chem. Phys. 19, 6861–6870 (2017).
Wrodnigg, G. H., Besenhard, J. O. & Winter, M. Ethylene sulfite as electrolyte additive for lithium-ion cells with graphitic anodes. J. Electrochem. Soc. 146, 470–472 (1999).
Leggesse, E. G. & Jiang, J.-C. Theoretical study of the reductive decomposition of ethylene sulfite: a film-forming electrolyte additive in lithium ion batteries. J. Phys. Chem. A. 116, 11025–11033 (2012).
Xu, M. Q. et al. Effect of butyl sultone on the Li-ion battery performance and interface of graphite electrode. Acta Phys. Chim. Sin. 22, 335–340 (2006).
Chen, R. et al. Butylene sulfite as a film-forming additive to propylene carbonate-based electrolytes for lithium ion batteries. J. Power Sources 172, 395–403 (2007).
Xu, M. Q., Li, W. S., Zuo, X. X., Liu, J. S. & Xu, X. Performance improvement of lithium ion battery using PC as a solvent component and BS as an SEI forming additive. J. Power Sources 174, 705–710 (2007).
Xing, L. D., Wang, C. Y., Xu, M. Q., Li, W. S. & Cai, Z. P. Theoretical study on reduction mechanism of 1,3-benzodioxol-2-one for the formation of solid electrolyte interface on anode of lithium ion battery. J. Power Sources 189, 689–692 (2009).
Self, J., Hall, D. S., Madec, L. & Dahn, J. R. The role of prop-1-ene-1,3-sultone as an additive in lithium-ion cells. J. Power Sources 298, 369–378 (2015).
Leggesse, E. G. & Jiang, J.-C. Theoretical study of the reductive decomposition of 1,3-propane sultone: SEI forming additive in lithium-ion batteries. RSC Adv. 2, 5439–5446 (2012).
Jung, H. M. et al. Fluoropropane sultone as an SEI-forming additive that outperforms vinylene carbonate. J. Mater. Chem. A 1, 11975–11981 (2013).
Ding, Z., Li, X., Wei, T., Yin, Z. & Li, X. Improved compatibility of graphite anode for lithium ion battery using sulfuric esters. Electrochim. Acta 196, 622–628 (2016).
Wang, B. et al. Effects of 3,5-bis(trifluoromethyl)benzeneboronic acid as an additive on electrochemical performance of propylene carbonate-based electrolytes for lithium ion batteries. Electrochim. Acta 54, 816–820 (2008).
Xu, M., Zhou, L., Xing, L., Li, W. & Lucht, B. L. Experimental and theoretical investigations on 4,5-dimethyl- 1,3 dioxol-2-one as solid electrolyte interface forming additive for lithium-ion batteries. Electrochim. Acta 55, 6743–6748 (2010).
Xu, M. et al. Experimental and theoretical investigations of dimethylacetamide (DMAc) as electrolyte stabilizing additive for lithium ion batteries. J. Phys. Chem. C 115, 6085–6094 (2011).
Hall, D. S. et al. Surface-electrolyte interphase formation in lithium-ion cells containing pyridine adduct additives. J. Electrochem. Soc. 163, A773–A780 (2016).
Forestier, C. et al. Facile reduction of pseudo-carbonates: promoting solid electrolyte interphases with dicyanoketene alkylene acetals in lithium-ion batteries. J. Power Sources 303, 1–9 (2016).
Forestier, C. et al. Comparative investigation of solid electrolyte interphases created by the electrolyte additives vinyl ethylene carbonate and dicyano ketene vinyl ethylene acetal. J. Power Sources 345, 212–220 (2017).
Lu, Z., Yang, L. & Guo, Y. Thermal behavior and decomposition kinetics of six electrolyte salts by thermal analysis. J. Power Sources 156, 555–559 (2006).
Tasaki, K., Kanda, K., Kobayashi, T., Nakamura, S. & Ue, M. Theoretical studies on the reductive decompositions of solvents and additives for lithium-ion batteries near lithium anodes. J. Electrochem. Soc. 153, A2192–A2197 (2006).
Ue, M., Murakami, A. & Nakamura, S. Anodic stability of several anions examined by ab initio molecular orbital and density functional theories. J. Electrochem. Soc. 149, A1572–A1577 (2002).
Han, Y.-K., Jung, J., Yu, S. & Lee, H. Understanding the characteristics of high-voltage additives in Li-ion batteries: Solvent effects. J. Power Sources 187, 581–585 (2009).
Halls, M. D. & Tasaki, K. High-throughput quantum chemistry and virtual screening for lithium ion battery electrolyte additives. J. Power Sources 195, 1472–1478 (2010).
Park, M. H., Lee, Y. S., Lee, H. & Han, Y.-K. Low Li+ binding affinity: an important characteristic for additives to form solid electrolyte interphases in Li-ion batteries. J. Power Sources 196, 5109–5114 (2011).
Jankowski, P., Wieczorek, W. & Johansson, P. SEI-forming electrolyte additives for lithium-ion batteries: development and benchmarking of computational approaches. J. Mol. Model. 23, 6–6 (2017).
Husch, T. & Korth, M. How to estimate solid-electrolyte-interphase features when screening electrolyte materials. Phys. Chem. Chem. Phys. 17, 22799–22808 (2015).
Knap, J., Spear, C., Leiter, K., Becker, R. & Powell, D. A computational framework for scale‐bridging in multi‐scale simulations. Int. J. Numer. Meth. Eng. 108, 1649–1666 (2016).
Jorn, R. & Kumar, R. Breaking the scales: electrolyte modeling in metal-ion batteries. Electrochem. Soc. Interface 26, 55–59 (2017).
Qu, X. H. et al. The electrolyte genome project: a big data approach in battery materials discovery. Comput. Mater. Sci. 103, 56–67 (2015).
Wang, Y., Zhang, W., Chen, L., Shi, S. & Liu, J. Quantitative description on structure-property relationships of Li-ion battery materials for high-throughput computations. Sci. Technol. Adv. Mat. 18, 134–146 (2017).
George, S. M. Atomic layer deposition: an overview. Chem. Rev. 110, 111–131 (2010).
Riley, L. A., Cavanagh, A. S., George, S. M., Lee, S.-H. & Dillon, A. C. Improved mechanical integrity of ALD-coated composite electrodes for Li-ion batteries. Electrochem. Solid State Lett. 14, A29–A31 (2011).
Lin, Y.-X. et al. Connecting the irreversible capacity loss in Li-ion batteries with the electronic insulating properties of solid electrolyte interphase (SEI) components. J. Power Sources 309, 221–230 (2016).
Leung, K. et al. Using atomic layer deposition to hinder solvent decomposition in lithium ion batteries: first-principles modeling and experimental studies. J. Am. Chem. Soc. 133, 14741–14754 (2011).
Soto, F. A., Ma, Y., Martinez de la Hoz, J. M., Seminario, J. M. & Balbuena, P. B. Formation and growth mechanisms of solid-electrolyte interphase layers in rechargeable batteries. Chem. Mater. 27, 7990–8000 (2015).
Liu, Z. et al. Interfacial study on solid electrolyte interphase at Li metal anode: implication for Li dendrite growth. J. Electrochem. Soc. 163, A592–A598 (2016).
Leung, K. & Jungjohann, K. L. Spatial heterogeneities and onset of passivation breakdown at lithium anode interfaces. J. Phys. Chem. C 121, 20188–20196 (2017).
Benitez, L., Cristancho, D., Seminario, J. M., Martinez de la Hoz, J. M. & Balbuena, P. B. Electron transfer through solid-electrolyte-interphase layers formed on Si anodes of Li-ion batteries. Electrochim. Acta 140, 250–257 (2014).
Benitez, L. & Seminario, J. M. Electron transport and electrolyte reduction in the solid-electrolyte interphase of rechargeable lithium ion batteries with silicon anodes. J. Phys. Chem. C 120, 17978–17988 (2016).
Li, D. et al. Modeling the SEI-formation on graphite electrodes in LiFePO4 batteries. J. Electrochem. Soc. 162, A858–A869 (2015).
Joho, F. et al. Relation between surface properties, pore structure and first-cycle charge loss of graphite as negative electrode in lithium-ion batteries. J. Power Sources 97, 78–82 (2001).
Feng, T. et al. Low-cost Al2O3 coating layer as a preformed SEI on natural graphite powder to improve coulombic efficiency and high-rate cycling stability of lithium-ion batteries. ACS Appl. Mater. Interfaces 8, 6512–6519 (2016).
Ramos-Sanchez, G., Chen, G., Harutyunyan, A. R. & Balbuena, P. B. Theoretical and experimental investigations of the Li storage capacity in single-walled carbon nanotube bundles. RSC Adv. 6, 27260–27266 (2016).
Nie, M. et al. Lithium ion battery graphite solid electrolyte interphase revealed by microscopy and spectroscopy. J. Phys. Chem. C. 117, 1257–1267 (2013).
Garcia-Lastra, J. M., Myrdal, J. S. G., Christensen, R., Thygesen, K. S. & Vegge, T. DFT plus U study of polaronic conduction in Li2O2 and Li2CO3: implications for Li-Air batteries. J. Phys. Chem. C. 117, 5568–5577 (2013).
Shi, S., Qi, Y., Li, H. & Hector, L. G. Jr. Defect thermodynamics and diffusion mechanisms in Li2CO3 and implications for the solid electrolyte interphase in Li-Ion batteries. J. Phys. Chem. C. 117, 8579–8593 (2013).
Bumm, L. A., Arnold, J. J., Dunbar, T. D., Allara, D. L. & Weiss, P. S. Electron transfer through organic molecules. J. Phys. Chem. B 103, 8122–8127 (1999).
Yamada, Y., Iriyama, Y., Abe, T. & Ogumi, Z. Kinetics of lithium ion transfer at the interface between graphite and liquid electrolytes: effects of solvent and surface film. Langmuir 25, 12766–12770 (2009).
Xu, K., von Cresce, A. & Lee, U. Differentiating contributions to “ion transfer” barrier from interphasial resistance and Li+ desolvation at electrolyte/graphite interface. Langmuir 26, 11538–11543 (2010).
Chen, Y. C., Ouyang, C. Y., Song, L. J. & Sun, Z. L. Electrical and lithium ion dynamics in three main components of solid electrolyte interphase from density functional theory study. J. Phys. Chem. C 115, 7044–7049 (2011).
Iddir, H. & Curtiss, L. A. Li ion diffusion mechanisms in bulk monoclinic Li2CO3 crystals from density functional studies. J. Phys. Chem. C 114, 20903–20906 (2010).
Borodin, O., Smith, G. D. & Fan, P. Molecular dynamics simulations of lithium alkyl carbonates. J. Phys. Chem. B 110, 22773–22779 (2006).
Borodin, O., Zhuang, G. R. V., Ross, P. N. & Xu, K. Molecular dynamics simulations and experimental study of lithium ion transport in dilithium ethylene dicarbonate. J. Phys. Chem. C. 117, 7433–7444 (2013).
Bedrov, D., Borodin, O. & Hooper, J. B. Li+ transport and mechanical properties of model solid electrolyte interphases (SEI): insight from atomistic molecular dynamics simulations. J. Phys. Chem. C. 121, 16098–16109 (2017).
Borodin, O. in Electrolytes for Lithium and Lithium-Ion Batteries (eds T. R. Jow, K. Xu, O. Borodin, & M. Ue) 371-401 (Springer, New York, 2014).
Pan, J., Cheng, Y.-T. & Qi, Y. General method to predict voltage-dependent ionic conduction in a solid electrolyte coating on electrodes. Phys. Rev. B 91, 134116 (2015).
Benitez, L. & Seminario, J. M. Ion diffusivity through the solid electrolyte interphase in lithium-ion batteries. J. Electrochem. Soc. 164, E3159–E3170 (2017).
Yildirim, H., Kinaci, A., Chan, M. K. Y. & Greeley, J. P. First-principles analysis of defect thermodynamics and ion transport in inorganic SEI compounds: LiF and NaF. ACS Appl. Mater. Interfaces 7, 18985–18996 (2015).
Soto, F. A. et al. Tuning the Solid Electrolyte Interphase for Selective Li- and Na-Ion Storage in Hard Carbon. Adv. Mater. 29, 1606860 (2017).
Fan, L., Zhuang, H. L., Gao, L., Lu, Y. & Archer, L. A. Regulating Li deposition at artificial solid electrolyte interphases. J. Mater. Chem. A 5, 3483–3492 (2017).
Liang, C. C. Conduction characteristics of the lithium iodide-aluminum oxide solid electrolytes. J. Electrochem. Soc. 120, 1289–1292 (1973).
Pan, J., Zhang, Q., Xiao, X., Cheng, Y.-T. & Qi, Y. Design of nanostructured heterogeneous solid ionic coatings through a multiscale defect model. ACS Appl. Mater. Interfaces 8, 5687–5693 (2016).
Borodin, O. & Bedrov, D. Interfacial structure and dynamics of the lithium alkyl dicarbonate SEI components in contact with the lithium battery electrolyte. J. Phys. Chem. C 118, 18362–18371 (2014).
Shang, S.-L. et al. Lattice dynamics, thermodynamics and elastic properties of monoclinic Li2CO3 from density functional theory. Acta Mater. 60, 5204–5216 (2012).
Shin, H., Park, J., Han, S., Sastry, A. M. & Lu, W. Component-/structure-dependent elasticity of solid electrolyte interphase layer in Li-ion batteries: experimental and computational studies. J. Power Sources 277, 169–179 (2015).
Zvereva, E., Caliste, D. & Pochet, P. Interface identification of the solid electrolyte interphase on graphite. Carbon N.Y. 111, 789–795 (2017).
Soto, F. A. & Balbuena, P. B. Elucidating oligomer-surface and oligomer-oligomer interactions at a lithiated silicon surface. Electrochim. Acta 220, 312–321 (2016).
Verbrugge, M. W., Qi, Y., Baker, D. R. & Cheng, Y.-T. Diffusion-Induced Stress within Core–Shell Structures and Implications for Robust Electrode Design and Materials Selection (Wiley-VCH Verlag, Weinheim, 2015).
Tasaki, K. & Harris, S. J. Computational study on the solubility of lithium salts formed on lithium ion battery negative electrode in organic solvents. J. Phys. Chem. C. 114, 8076–8083 (2010).
Leung, K., Soto, F., Hankins, K., Balbuena, P. B. & Harrison, K. L. Stability of solid electrolyte interphase components on lithium metal and reactive anode material surfaces. J. Phys. Chem. C 120, 6302–6313 (2016).
Xu, K. et al. Syntheses and characterization of lithium alkyl mono- and dicarbonates as components of surface films in Li-lon batteries. J. Phys. Chem. B 110, 7708–7719 (2006).
Okuno, Y., Ushirogata, K., Sodeyama, K. & Tateyama, Y. Decomposition of the fluoroethylene carbonate additive and the glue effect of lithium fluoride products for the solid electrolyte interphase: an ab initio study. Phys. Chem. Chem. Phys. 18, 8643–8653 (2016).
Zhang, Q. & Kaghazchi, P. Dependence of ion transport on the electronegativity of the constituting atoms in ionic crystals. Chemphyschem 18, 965–969 (2017).
Leung, K. First-principles modeling of Mn(II) migration above and dissolution from LixMn2O4 (001) surfaces. Chem. Mater. 29, 2550–2562 (2017).
Aurbach, D., Ein‐Ely, Y. & Zaban, A. The surface chemistry of lithium electrodes in alkyl carbonate solutions. J. Electrochem. Soc. 141, L1–L3 (1994).
Herstedt, M., Abraham, D. P., Kerr, J. B. & Edström, K. X-ray photoelectron spectroscopy of negative electrodes from high-power lithium-ion cells showing various levels of power fade. Electrochim. Acta 49, 5097–5110 (2004).
Newman, J. S. & Tobias, C. W. Theoretical analysis of current distribution in porous electrodes. J. Electrochem. Soc. 109, 1183–1191 (1962).
Newman, J., Thomas, K. E., Hafezi, H. & Wheeler, D. R. Modeling of lithium-ion batteries. J. Power Sources 119, 838–843 (2003).
Broussely, M. et al. Aging mechanism in Li ion cells and calendar life predictions. J. Power Sources 97-98, 13–21 (2001).
Christensen, J. & Newman, J. A mathematical model for the lithium-ion negative electrode solid electrolyte interphase. J. Electrochem. Soc. 151, A1977–A1988 (2004).
Colclasure, A. M., Smith, K. A. & Kee, R. J. Modeling detailed chemistry and transport for solid-electrolyte-interface (SEI) films in Li-ion batteries. Electrochim. Acta 58, 33–43 (2011).
Ploehn, H. J., Ramadass, P. & White, R. E. Solvent diffusion model for aging of lithium-ion battery cells. J. Electrochem. Soc. 151, A456–A462 (2004).
Liu, L., Park, J., Lin, X., Sastry, A. M. & Lu, W. A thermal-electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. J. Power Sources 268, 482–490 (2014).
Pinson, M. B. & Bazant, M. Z. Theory of SEI formation in rechargeable batteries: capacity fade, accelerated aging and lifetime prediction. J. Electrochem. Soc. 160, A243–A250 (2013).
Tang, M., Lu, S. & Newman, J. Experimental and theoretical investigation of solid-electrolyte-interphase formation mechanisms on glassy carbon. J. Electrochem. Soc. 159, A1775–A1785 (2012).
Guan, P., Liu, L. & Lin, X. Simulation and experiment on solid electrolyte interphase (SEI) morphology evolution and lithium-ion diffusion. J. Electrochem. Soc. 162, A1798–A1808 (2015).
Single, F., Horstmann, B. & Latz, A. Dynamics and morphology of solid electrolyte interphase (SEI). Phys. Chem. Chem. Phys. 18, 17810–17814 (2016).
Single, F., Horstmann, B. & Latz, A. Revealing SEI morphology: in-depth analysis of a modeling approach. J. Electrochem. Soc. 164, E3132–E3145 (2017).
Thackeray, M. M., Wolverton, C. & Isaacs, E. D. Electrical energy storage for transportation-approaching the limits of, and going beyond, lithium-ion batteries. Energy Environ. Sci. 5, 7854–7863 (2012).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 65, 1501–1509 (2013).
Aykol, M. et al. High-throughput computational design of cathode coatings for Li-ion batteries. Nat. Commun. 7, 13779 (2016).
Koch, S. L., Morgan, B. J., Passerini, S. & Teobaldi, G. Density functional theory screening of gas-treatment strategies for stabilization of high energy-density lithium metal anodes. J. Power Sources 296, 150–161 (2015).
Y, Z., X, H. & Y, M. Strategies based on nitride materials chemistry to stabilize Li metal anode. Adv. Sci. 4, 1600517 (2017).
Boukamp, B. A. & Huggins, R. A. Fast ionic conductivity in lithium nitride. Mater. Res. Bull. 13, 23–32 (1978).
Shi, L., Xu, A. & Zhao, T. First-principles investigations of the working mechanism of 2D h-BN as an Interfacial layer for the anode of lithium metal batteries. ACS Appl. Mater. Interfaces 9, (1987–1994 (2017).
Ma, Y. et al. Structure and reactivity of alucone-coated films on Si and LixSiy surfaces. ACS Appl. Mater. Interfaces 7, 11948–11955 (2015).
Jung, Y. S. et al. Ultrathin direct atomic layer deposition on composite electrodes for highly durable and safe Li-ion batteries. Adv. Mater. 22, 2172–2176 (2010).
Kozen, A. C. et al. Next-generation lithium metal anode engineering via atomic layer deposition. Acs Nano 9, 5884–5892 (2015).
Xiao, X. C., Lu, P. & Ahn, D. Ultrathin multifunctional oxide coatings for lithium ion batteries. Adv. Mater. 23, 3911–3915 (2011).
Katiyar, P., Jin, C. & Narayan, R. J. Electrical properties of amorphous aluminum oxide thin films. Acta Mater. 53, 2617–2622 (2005).
Piper, D. M. et al. Reversible high-capacity Si nanocomposite anodes for lithium-ion batteries enabled by molecular layer deposition. Adv. Mater. 26, 1596–1601 (2014).
Kim, S.-Y. & Qi, Y. Property evolution of Al2O3 coated and uncoated Si electrodes: a first principles investigation. J. Electrochem. Soc. 161, F3137–F3143 (2014).
Kim, S.-Y. et al. Self-generated concentration and modulus gradient coating design to protect Si nano-wire electrodes during lithiation. Phys. Chem. Chem. Phys. 18, 3706–3715 (2016).
Gomez-Ballesteros, J. L. & Balbuena, P. B. Reduction of electrolyte components on a coated Si anode of lithium-ion batteries. J. Phys. Chem. Lett. 8, 3404–3408 (2017).
Zhang, L. Q. et al. Controlling the lithiation-induced strain and charging rate in nanowire electrodes by coating. ACS Nano 5, 4800–4809 (2011).
Zhao, K., Pharr, M., Hartle, L., Vlassak, J. J. & Suo, Z. Fracture and debonding in lithium-ion batteries with electrodes of hollow core–shell nanostructures. J. Power Sources 218, 6–14 (2012).
Stournara, M. E., Qi, Y. & Shenoy, V. B. From ab initio calculations to multiscale design of Si/C core–shell particles for Li-ion anodes. Nano. Lett. 14, 2140–2149 (2014).
Qi, Y., Hector, L. G. Jr., James, C. & Kim, K. J. Lithium concentration dependent elastic properties of battery electrode materials from first principles calculations. J. Electrochem. Soc. 161, F3010–F3018 (2014).
Perez-Beltran, S., Ramirez-Caballero, G. E. & Balbuena, P. B. First-principles calculations of lithiation of a hydroxylated surface of amorphous silicon dioxide. J. Phys. Chem. C 119, 16424–16431 (2015).
Heine, J. et al. Fluoroethylene carbonate as electrolyte additive in tetraethylene glycol dimethyl ether based electrolytes for application in lithium ion and lithium metal batteries. J. Electrochem. Soc. 162, A1094–A1101 (2015).
Huang, J., Fan, L.-Z., Yu, B., Xing, T. & Qiu, W. Density functional theory studies on the B-containing lithium salts. Ionics 16, 509–513 (2010).
Zhang, X. R., Kostecki, R., Richardson, T. J., Pugh, J. K. & Ross, P. N. Electrochemical and infrared studies of the reduction of organic carbonates. J. Electrochem. Soc. 148, A1341–A1345 (2001).
Wang, Y. X., Nakamura, S., Tasaki, K. & Balbuena, P. B. Theoretical studies to understand surface chemistry on carbon anodes for lithium-ion batteries: how does vinylene carbonate play its role as an electrolyte additive? J. Am. Chem. Soc. 124, 4408–4421 (2002).
Bhatt, M. D. & O’Dwyer, C. Solid electrolyte interphases at Li-ion battery graphitic anodes in propylene carbonate (PC)-based electrolytes containing FEC, LiBOB, and LiDFOB as additives. Chem. Phys. Lett. 618, 208–213 (2015).
Profatilova, I. A., Kim, S.-S. & Choi, N.-S. Enhanced thermal properties of the solid electrolyte interphase formed on graphite in an electrolyte with fluoroethylene carbonate. Electrochim. Acta 54, 4445–4450 (2009).
Vollmer, J. M., Curtiss, L. A., Vissers, D. R. & Amine, K. Reduction mechanisms of ethylene, propylene, and vinylethylene carbonates—a quantum chemical study. J. Electrochem. Soc. 151, A178–A183 (2004).
Yu, T. et al. Effect of sulfolane on the morphology and chemical composition of the solid electrolyte interphase layer in lithium bis(oxalato) borate-based electrolyte. Surf. Interface Anal. 46, 48–55 (2014).
Nie, M., Xia, J. & Dahn, J. R. Development of pyridine-boron trifluoride electrolyte additives for lithium-ion batteries. J. Electrochem. Soc. 162, A1186–A1195 (2015).
Kaymaksiz, S. et al. Electrochemical stability of lithium salicylato-borates as electrolyte additives in Li-ion batteries. J. Power Sources 239, 659–669 (2013).
Panitz, J.-C., Wietelmann, U., Wachtler, M., Ströbele, S. & Wohlfahrt-Mehrens, M. Film formation in LiBOB-containing electrolytes. J. Power Sources 153, 396–401 (2006).
Zhang, L. et al. Molecular engineering toward stabilized interface: an electrolyte additive for high-performance Li-ion battery. J. Electrochem. Soc. 161, A2262–A2267 (2014).
Acknowledgements
A.W. and S.S. acknowledge the support from the National Key Research and Development Program of China (No. 2017YFB0701600), the National Natural Science Foundation of China (Nos. 51372228, 51622207 and U1630134). S.K. and Y.Q. acknowledge the support from the Department of Energy, Office of Energy Efficiency and Renewable Energy (EERE), under the Awards #DE-EE0007787 and #DE-EE0007803.
Author information
Authors and Affiliations
Contributions
All authors contributed to collecting the references and outlining the review paper. A.W., S.S., and Y.Q. drafted the review. Y.Q. led the writing of the review. All authors participated in revising the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, A., Kadam, S., Li, H. et al. Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries. npj Comput Mater 4, 15 (2018). https://doi.org/10.1038/s41524-018-0064-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-018-0064-0
This article is cited by
-
Materials descriptors of machine learning to boost development of lithium-ion batteries
Nano Convergence (2024)
-
Standardized cycle life assessment of batteries using extremely lean electrolytic testing conditions
Communications Materials (2024)
-
Enhancing ReaxFF for molecular dynamics simulations of lithium-ion batteries: an interactive reparameterization protocol
Scientific Reports (2024)
-
Quinoxaline derivatives as cathode for aqueous zinc battery
Journal of Solid State Electrochemistry (2024)
-
Forming a stable SEI layer by the synergy effect of methyl p-toluenesulfonate electrolyte additive in Li-ion batteries
Ionics (2024)