First-principles prediction of high-entropy-alloy stability

Abstract

High entropy alloys (HEAs) are multicomponent compounds whose high configurational entropy allows them to solidify into a single phase, with a simple crystal lattice structure. Some HEAs exhibit desirable properties, such as high specific strength, ductility, and corrosion resistance, while challenging the scientist to make confident predictions in the face of multiple competing phases. We demonstrate phase stability in the multicomponent alloy system of Cr–Mo–Nb–V, for which some of its binary subsystems are subject to phase separation and complex intermetallic-phase formation. Our first-principles calculation of free energy predicts that the configurational entropy stabilizes a single body-centered cubic (BCC) phase from T = 1700 K up to melting, while precipitation of a complex intermetallic is favored at lower temperatures. We form the compound experimentally and confirm that it develops as a single BCC phase from the melt, but that it transforms reversibly at lower temperatures.

Introduction

Exploring new materials with outstanding properties is an eternal pursuit of scientists and engineers. High entropy alloys (HEAs) constitute a newly-emerging class of materials that offer enhanced mechanical and corrosion properties for practical applications, while presenting challenges to the scientist making predictions in the face of compositional complexity.^{1,2,3,4,5,6,7,8,9,10,11,12,13} Alloys of two or three species often phase-separate, and when they form a compound, it is often a complex ordered structure with multiple Wyckoff positions. Thus, HEAs are remarkable for forming single phases that are, moreover, simple lattice structures in which all atomic positions are equivalent. Trial-and-error experimental approaches to test the phase stability of HEAs are costly and time-consuming, while previously-reported phase-formation rules are empirical and susceptible to the alloy, systems^14,15 motivating a first-principles theoretical approach to accelerate the design of HEAs through the prediction of phase stability and microstructure.

Here we illustrate these ideas by demonstrating phase stability in the quaternary Cr–Mo–Nb–V alloy system. Some of its binary and ternary subsystems are subject to phase separation and complex intermetallic phase formation. Utilizing fully first-principles calculations of the free energies of the full quaternary and its competing binary and ternary phases, we predict that the configurational entropy stabilizes a single body-centered cubic (BCC) solid solution at high temperatures, but that it will precipitate a complex intermetallic Laves phase at lower temperatures. Experimentally, we verify the formation of the single-phase BCC solid solution from the melt, confirm the precipitation of the Laves phase at low temperatures, and observe that it reverts to a single BCC phase upon annealing at high temperatures, thus illustrating the entropic stabilization principle of HEAs.

Results

Quaternary alloy system

Consider the four-component alloy system of Cr–Mo–Nb–V. All four elements take body-centered-cubic (BCC, Pearson type cI2, Strukturbericht A2) structures. Taking elements pairwise, we note that mixing enthalpies for the BCC solid solution are positive for Cr–Mo, Cr–Nb, and Nb–V (see Fig. 1), indicating low-temperature phase separation, while the remaining cases, Cr–V, Mo–Nb, and Mo–V, have negative enthalpies,^16,17 indicating stability down to low temperatures. Experimentally, Cr–Nb has a complete miscibility gap at all temperatures below melting, while phase separation has not been seen experimentally in the case of Cr–Mo¹⁸ and Nb–V,¹⁹ though it is predicted.^20,21 Cr–Nb and Nb–V are predicted²² to form Laves phases of types cF24 (Strukturbericht C15) and hP12 (Strukturbericht C14). Both Laves phases are observed experimentally in Cr–Nb,²³ while neither has yet been reported in Nb–V. Experimental investigations of the ternaries show that Cr–Mo–Nb phase-separates²⁴ and Cr–Nb–V forms a C15-Laves phase,²⁵ while Cr–Mo–V and Mo–Nb–V become complete solid solutions.¹⁸ No quaternary phases have been reported experimentally.

Fig. 1

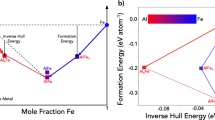
Formation enthalpies calculated from density functional theory (DFT) (magenta diamonds) and cluster expansions^22,30 (green plus signs) for a Cr–Mo, b Cr–Nb, and c Nb–V. Violet square and blue star are Laves Phases of Pearson types cF24 (Strukturbericht C15) and hP12 (C14), respectively. Solid black lines are convex hulls

Inspection of Fig. 1 offers a clue to why experiments on Cr–Mo and Nb–V fail to observe the predicted miscibility gaps, while separation is seen in Cr–Nb. The mixing enthalpies are relatively low in Cr–Mo and Nb–V, compared with Cr–Nb, so their estimated critical temperatures for phase separation are low (1213 and 653 K, respectively^20,21). Meanwhile, the melting temperatures of Cr–Mo and Nb–V are relatively high (2093 and 2133 K, respectively). Since atomic diffusion far below the melting temperature can be slow, phase separation will be difficult to observe on experimental time scales. The problem is even more severe for complex structures, potentially explaining the failure so far to observe the predicted NbV₂ C14-Laves phase. In contrast, the high mixing enthalpies that destabilize the Cr–Nb solid solution, together with the relatively-low melting temperature of 1893 K that enhances diffusion, make it possible to observe both the phase separation and the Laves-phase formation experimentally.

Turning to the full quaternary, we will test its stability at high temperatures by calculating its free energy relative to the most-likely competing phases, namely, the coexistence of a Mo-rich BCC medium entropy alloy with a CrNbV-rich Laves phase. A working hypothesis is that the single phase is stabilized by a large configurational entropy of mixing, and that the entropy is maximized for the simple BCC lattice structure in which all sites are equivalent. However, we expect the lower enthalpy of the competing phases to predominate at lower temperatures where the entropy is less relevant, leading to the precipitation of a ternary CrNbV Laves phase as temperature drops. At very low temperatures, we anticipate complete phase separation into four coexisting phases.

Free energy calculation

For each phase, we calculate the Helmholtz free energy as a sum of discrete configurational, vibrational, and electronic contributions,^22,26 F(x,T,V) = F ^c + F ^v + F ^e. The composition variable, x, is expressed as a four-component vector in our composition space. Because metallurgical experiments are generally carried out at low pressure (P ≈ 0), the Gibbs free energy, $G\left( {x,T} \right) = {\rm {min}}_{V} \left( {F + PV} \right)$, of each phase is simply the Helmholtz free energy, F, evaluated at its minimizing volume. If we have a mixture of phases, i, each having a mole fraction γ _i , the total free energy is G = ∑ _i γ _i G _i (x _i ,T).

Consider the phase separation of a CrNbV Laves phase from a CrMoNbV BCC solid solution, expressed as

$${\rm{CrMoNbV}} \to {\rm{C}}{\rm r_{1 - \gamma }}{\rm{M}}{{\rm{o}}_1}{\rm{N}}{{\rm{b}}_{1 - \gamma }}{{\rm{V}}_{1 - \gamma }} + {\rm{C}}{{\rm{r}}_\gamma }{\rm{N}}{{\rm{b}}_\gamma }{{\rm{V}}_\gamma },$$

(1)

where γ ∈ (0,1) represents the progress of the reaction. The fraction of the Laves phase is 3γ/4, leaving a fraction 1 − 3γ/4 of the BCC phase. The BCC phase becomes increasingly Mo-rich, with the composition of x _Mo = 1/(4 − 3γ), while the remaining elements have the composition x _α  = (1 − γ)/(4 − 3γ) for α = Cr, Nb, or V. Thus, the total free energy for a two-phase mixture of Laves with a partially-transformed BCC structure is

$${G_{{\rm{Tot}}}}\left( {{x_{{\rm{Mo}}}}} \right) = \left( {1 - 3\gamma /4} \right){G_{{\rm{BCC}}}} + \left( {3\gamma /4} \right){G_{{\rm{Laves}}}}\\ = {G_{{\rm{Laves}}}} + \left( {{G_{{\rm{BCC}}}} - {G_{{\rm{Laves}}}}} \right)/4{x_{{\rm{Mo}}}},$$

(2)

and G _BCC depends on x _Mo. Equation (2) holds for the total Gibbs free energy and also for the separate configurational, vibrational, and electronic components.

To calculate the configurational free energy, G _c (x,T), we apply our hybrid Monte Carlo/molecular dynamics method (MCMD²⁷) to anneal the short-range chemical order. Over the temperature range of interest (T = 1000 K through melting around 2133 K), the chemical order was found to be moderate and nearly temperature independent. In particular, the configurational entropy, remained within 2% of the ideal value.²⁸ Thus, we take the mixing entropy of the BCC solid solution as ideal, S ^c = k _B ∑ _α x _α log x _α . We calculate the configurational enthalpy of formation, relative to pure elements, ΔH _c , by quenching our simulated structures to T = 0 K through the relaxation of atomic coordinates and lattice parameters. The resulting enthalpies (see Fig. S1a in the Supplementary Information) are nearly independent of the annealing temperature but exhibit a strong variation with respect to composition.

Applying MCMD to the C15-Laves phase of CrNbV reveals that Cr and V readily substitute on the 16d Wyckoff sites but they do not mix to any appreciable degree with Nb, which remains on the 8a sites. Hence, we take the entropy of CrNbV as S ^c = (2/3) k _B log2. The total Gibbs configurational free energy of formation is the sum of the BCC and Laves terms weighted by their respective fractions, as in Eq. (2).

The vibrational free energy is calculated in the harmonic approximation from the vibrational density of states (DOS), g(ν), via the single vibrational mode free energy

$$\begin{array}{l}\\ {f^v}\left( \nu \right) = {k_B}Tlog\left[ {2sinh\left( {h\nu /2{k_B}T} \right)} \right],\quad {F^v} = {\int} g\left( \nu \right){f^v}\left( \nu \right){\rm{d}}\nu ,\\ \\ \end{array}$$

(3)

where g(ν) is obtained by the direct method²⁹ by means of force constants that we determine using density functional perturbation theory at T = 0 K. Figure 2a compares vibrational densities of states for the equiatomic BCC phase and the Laves phase. The Laves phase has some high-frequency phonons that are absent in the BCC phase, while the BCC phase has a small but persistent excess of low-frequency phonons, lowering $F_{{\rm{BCC}}}^v$ relative to $F_{{\rm{Laves}}}^v$ (Fig. 2b and d). These differences reflect the tetrahedral close-packed structure of the Laves phase, compared with the relatively-open BCC structure. To model phase separation, we require the composition dependence of ΔF ^v. We find that the differences in the BCC vibrational free energy with respect to composition, x _Mo, are small, compared with the difference between the BCC and Laves phases (see Fig. S2 in the Supplementary Information), and hence may be treated as composition-independent.

Fig. 2

Contributions to free energies, comparing BCC and Laves phases. The BCC composition is CrMoNbV, while the Laves phase is CrNbV. a Vibrational density of states (modes/THz/atom) showing small excess high frequency modes of the Laves phase; b Vibrational free energies (eV/atom) showing near equality, with the BCC phase very slightly lower; c Electronic density of states (states/eV/atom) showing the BCC phase higher at E _F ; d Configurational, vibrational, and electronic free energy differences, F _BCC − F _Laves, all favor the BCC phase

The electronic free energy is calculated from the single electron DOS, D(E), predicted at T = 0 K by density functional theory (DFT), and the Fermi occupation function, f _T (E) = 1/(exp((E − E _F )/k _B T)+1) (here E _F is the Fermi energy), and associated entropy, s _T (E), for individual states of energy E,

$$\begin{array}{ccccc}\\ {s_T}\left( E \right) = {f_T}\left( E \right)log{f_T}\left( E \right) + \left( {1 - {f_T}\left( E \right)} \right)log\left( {1 - {f_T}\left( E \right)} \right).\\ \\ \end{array}$$

(4)

We determine the electronic free energy, F ^e = E ^e − TS ^e, where

$$\begin{array}{l}\\ {E^e} = {\int} {\rm{d}}E D\left( E \right)\left( {{f_T}(E) - {f_0}(E)} \right)\left( {E - {E_F}} \right),\quad {S^e} = - {k_B}{\int} {\rm{d}}ED\left( E \right){s_T}\left( E \right).\\ \end{array}$$

(5)

Figure 2c shows that the electronic densities of states near ${E_F}$ differ significantly between BCC and Laves phases. This difference has a significant composition dependence, as can be seen within a rigid band model from the irregular shape of $D(E)$ near ${E_F}$ (increasing ${x_{{\rm{Mo}}}}$ increases ${E_F}$).

Because we utilize the harmonic approximation, thermal expansion is neglected, and the vibrational Helmholtz free energies, F ^v and F ^e, can be added directly to the configurational Gibbs free energy, G ^c. Thus, combining the above results, we have obtained the free energy, G, expressed as a function of transformation, γ, or composition, x _Mo, and temperature, T. Figure 3 graphs this function, revealing minima with γ 0 for T < 1700 K, implying phase separation. From T = 1700 K up to melting above T = 2100 K, however, the minima occur at the boundary, γ = 0 (i.e., x _Mo = 1/4), indicating that a single BCC phase is stable.

Fig. 3

a Free energy, G ₂(γ,T), for a two-phase BCC + Laves mixture with compositions given by Eq. (1), relative to G ₁, the free energy of the equiatomic BCC HEA. b Minimizing values of x _Mo, γ, and BCC and Laves-phase fractions as functions of temperature

Experimental results

In order to validate the predicted high-temperature stability and low-temperature transformation, we synthesized a sample by arc melting and casting. The as-cast sample was found to be a single BCC phase, with the characteristic of dendrites and interdendrites (Fig. 4a, d). The single phase remained intact under 21 days annealing at temperatures up to 1273 K, but exhibited the precipitation of a C15-Laves phase under annealing of 3 days at 1473 K (Fig. 4b, d). The C15 phase disappeared when the 1473 K-annealed sample was annealed at 1673 K for 12 h (Fig. 4c, d). Meanwhile, equiaxed grains appeared instead of the original dendrites and interdendrites, indicating that the pristine BCC phase was restored at 1673 K. This reversible transformation (BCC + Laves phases at low temperatures, and full BCC phase at high temperatures) is consistent with our theoretical prediction. Further annealing at 1873 K revealed additional impurity-stabilized phases (see Fig. S3b in the Supplementary Information), including a novel CCr₃Nb₃ carbide of Pearson type cF112.

Fig. 4

Electron micrographs of the a as-cast Cr–Mo–Nb–V sample (scale bar 100 μm), b following the T = 1473 K anneal (scale bar 10 μm), and c following the T = 1673 K anneal (scale bar 10 μm). d Synchrotron x-ray patterns

Table 1 reports the compositions of the C15 and BCC phases in the 1473 K-annealed state. Figure S4 in the Supplementary Information shows the distribution of constitutive elements after annealing the 1473 K-annealed sample at 1673 K for 12 h. No obvious segregation was observed within the BCC phase in the 1673 K-annealed state. Figure S3 presents the microstructures after annealing the alloy at 1273 and 1873 K. It can be seen that the alloy still keeps the characteristic of dendrites and interdendrites under the 21 days annealing at 1273 K (Fig. S3a). After annealing at 1873 K, multiple phases appeared in the alloy, including BCC, CCr₃Nb₃, and an unidentified needle-like phase (Fig. S3b).

Table 1 Chemical composition (atom %) of the as-cast sample and the observed phases in the T = 1473 K annealed state

The chemical distribution of the CCr₃Nb₃ phase in the 1873 K-annealed state was further detected by energy-dispersive X-ray spectroscopy (EDS), as shown in Fig. S5 in the Supplementary Information. An Fd$\bar 3$m symmetry was identified by transmission electron microscopy (TEM) selected area diffraction (SAED) (Fig. 5), suggesting a phase of the structure type of NiTi₂ with a lattice parameter a = 11.7 Å. As demonstrated below, this phase is stabilized by carbon impurities and can incorporate silicon substitution in place of Cr. These impurities likely enter from our furnace environment and the softened quartz tube.

Fig. 5

a Bright-field (BF) image of the CCr₃Nb₃ phase in the T = 1873 K-annealed state. b–d Selected area electron diffraction (SAED) patterns at zone axes 100, 110, and 123. Scale bars indicate 200 nm⁻¹ in part a and 5 nm⁻¹ in parts (b–d)

Discussion

So far we focused on the primary competitor to the HEA, namely, the separation into a Laves phase plus a BCC medium entropy alloy (MEA). In principle, according to the Gibbs phase rule, the system could contain up to four independent phases at low temperatures. We employed the Alloy Theoretic Automatic Toolkit cluster expansion³⁰ to generate a variety of candidate low-temperature binary, ternary, and quaternary configurations based on decorations of the BCC lattice. Based on enthalpies, we predict that the equiatomic CrMoNbV decomposes at low temperatures²² into four competing phases, Cr₂V.tI6, CrNbV.cF24, MoNb.oC12, and Mo₄V₃.hR7 subject to the stoichiometric relationship

$$\begin{array}{ccccc}\\ 10\,{\hbox{CrMoNbV}}\, \to \, 3\,{\rm{C}}{{\rm{r}}_2}{\rm{V}}\, + \,6\,{\rm{MoNb}}\, + \,4\,{\rm{CrNbV}}\, + \,1\,{\rm{M}}{{\rm{o}}_4}{{\rm{V}}_3}.\\ \\ \end{array}$$

(6)

Relaxed lattice parameters and Wyckoff coordinates of these structures are given in Table S1 in the Supplementary Information.

Assuming that all four phases are stoichiometric, we neglect the configurational entropy and set G ^c = ΔH ^c. Combining G ^c with F ^v and F ^e, and weighting the contributions according to Eq. (6), we obtain the function displayed in Fig. S6 labeled as G ₄. Notice that G ₄ crosses the single-phase equiatomic HEA free energy, G ₁, around T = 800 K, indicating a transition from the HEA to the 4-phase mixture at low temperatures. On the same figure, we plot the free energy, G ₂, of the 2-phase mixture, and this value lies below G ₁ and G ₄ over the range of T = 500– 1700 K. Accordingly, the HEA does not transform directly to the 4-phase mixture upon cooling, but instead exhibits a 2-phase region in between. The upper transition at T = 1700 K is continuous, with G ₂ joining G ₁ tangentially. This trend is reflected in the continuity of composition variables, as illustrated in Fig. 3b of the main text. The lower transition is discontinuous within the present model, with G ₄ crossing G ₂ transversally at 500 K. However, because it corresponds to chemical ordering on the BCC lattice, the actual behavior may be more complicated with multiple intervening phases and possibly continuous transitions. These transitions occur at low temperatures, making it doubtful that they can be observed experimentally.

What is the impact of assumptions and approximations we have made? Because Cr₂Nb exhibits a high-temperature C14-Laves phase (Pearson type hP12), and the structure is predicted to be stable at low temperatures in NbV₂, we checked the free energy of CrNbV as a C14-Laves phase. At this equiatomic composition, the free energy of C15 remains below the free energy of C14, for all temperatures below melting, justifying our neglect of the C14 phase. By taking the ideal entropy of mixing in the BCC phase, we overestimate the mixing entropy by about 2%, which amounts to an error of 3 meV/atom at 1700 K. Repeating our phase-transition prediction, we find that this error is equivalent to underestimating the transition temperature by approximately 25 K. In contrast, our neglect of the BCC vibrational free energy composition dependence has no effect on the transition temperature, because the mole-fraction of Laves phase vanishes at the transition. The underlying DFT energetics likely provides the largest, and most poorly-controlled approximation, whose impact cannot be readily predicted, motivating the need for experimental validation.

As mentioned above, TEM identified a Cr–Nb-rich impurity phase of space group $Fd\bar 3m$ (group #227), and proposed the structure type of NiTi₂ (Pearson type cF96). This structure proved energetically unfavorable as a Cr–Nb binary. However, carbon impurities at octahedral interstitial sites stabilize the phase in compositions CCr₃Nb₃ and CCr₂Nb₄ (both Pearson type cF112). Thus, we predict the existence of a previously-unknown stable carbide in the C–Cr–Nb alloy system. Table S2 in the Supplementary Information gives crystallographic details of the CCr₃Nb₃.cF112 phase, which we predict to be stable against all known binary and ternary competing phases, with the formation enthalpy of ΔH = −220 meV/atom, relative to pure elements. Substituting a single Si atom at a Cr2 site results in a quaternary that is stable against all known competing phases, with the formation enthalpy of ΔH = −275/meV/atom. CCr₂Nb₄ is similar to CCr₃Nb₃, but with Nb occupying the 16c site.

In summary, we have predicted the existence of a single-phase refractory HEA. This phase is stabilized at high temperatures primarily by the configurational entropy of mixing despite the immiscibility of constituent elements and a competing complex intermetallic phase, which leads to phase separation at low temperatures. A reversible phase transformation restores the entropically-stabilized BCC phase at high temperatures, illustrating one of the foundational principles of HEAs. Our theoretical methods, combining the quantum-mechanical total-energy calculation with statistical mechanics to predict free energies, can be applied to many problems in alloy design.

Methods

Enthalpy of formation

First-principles calculations are performed using projector augmented wave potentials^31,32 in the generalized gradient approximation,³³ as implemented in the Vienna Ab-initio Simulation Package (VASP³⁴). Structures were fully relaxed in lattice parameters and internal coordinates at T = 0 K using the energy cutoff of 400 eV and k-point densities sufficient to achieve convergence of 1 meV/atom or better. Hybrid MCMD²⁷ generated BCC solid-solution configurations over a series of Mo-rich compositions with an appropriate short-range order. These calculations used default energy cutoffs and a single k-point in systems of size N = 128 atoms. Figure S1a shows the resulting enthalpies of formation, relative to pure elements, which we find fit well to a quadratic polynomial.

Electronic free energy

We utilize the same series of Mo-rich configurations to evaluate electronic densities of states and electronic free energies. The integral in Eq. (5) can be expanded in power series in temperature.²² Expressing D(E) = D(E _F ) + D′(E _F )(E − E _F ) + D′′(E _F )(E − E _F )² + $\cdots$, we find

$${F^e} = - D\left( {{E_F}} \right){\pi ^2}{T^2}/6 - 7D''\left( {{E_F}} \right){\pi ^4}{T^4}/180 - \cdots .$$

(7)

Odd powers drop out, and truncating at T ⁴ is sufficient even at quite high T. Here we fit coefficients, a and b, to F ^e(T) = a(T/1000)² + b(T/1000)⁴ over the range of T = 0–2000 K. The composition dependence of F ^e is irregular, as can be inferred from the double minima in D(E) (see Fig. S1). Hence, we model F ^e by fitting a and b to 6th-order polynomials of x _Mo, as illustrated in Fig. S1c.

Vibrational free energy

The vibrational free energy is calculated in the harmonic approximation from the vibrational DOS, g(ν). This value is obtained from the force-constant matrix, Φ _ij  = ∂² U/∂R _i ∂R _j , which VASP determines using density functional perturbation theory at T = 0 K. Our calculations utilize a plane-wave basis with the energy cutoff of 400 eV, “accurate” precision to avoid wrap-around errors, and an additional support grid for augmentation charges.

The dynamical matrix at the wavevector q is^26,29

$${{\rm{D}}_{ij}}({\it{q}}) = \frac{1}{{\sqrt {{m_i}{m_j}} }} {e^{2\pi i{{q}} \cdot {{\rm{R}}_{ij}}}}{{{\Phi }}_{ij}}.$$

(8)

We diagonalize D _ij (q) to obtain vibrational frequencies, ν(q), and sample the full Brillouin zone to obtain the DOS, g(ν). Representative densities of states, calculated in 27-atom cells for various compositions, are shown in Fig. S2. Notice that g(ν) is relatively insensitive to the composition, but that the BCC DOS differs significantly from the C15-Laves phase.

Because we utilize the harmonic approximation, thermal expansion is neglected, and the vibrational Helmholtz free energy, F ^v, can be added directly to the configurational Gibbs free energy, G ^c. In the high-temperature range of interest, the free energy varies classically, with quantum effects relevant only for establishing offsets in the energy and entropy. Thus, we can fit F ^v(T) with high precision using only a single parameter, an effective Debye temperature, Θ _D , chosen to match the quantum-based free energy in the classical regime. We set

$$\begin{array}{ccccc}\\ {F^v}\left( T \right) = & \frac{9}{8}{k_B}{{{\Theta }}_D} - {k_B}T\left[ {{D_3}({{{\Theta }}_D}/T) - log\left( {1 - {e^{ - {{{\Theta }}_D}/T}}} \right)} \right]\\ \\ \end{array}$$

(9)

with ${D_3}(z) = 1 - 3z/8 + {z^2}/20 + \cdots$ the third order Debye function.³⁵ We set Θ _D  = 393 K for the BCC HEAs, and Θ _D  = 420 K for the Laves phase, as appropriate values to reproduce the high temperature free energy.

Sample preparation

The CrMoNbV alloy was fabricated by arc-melting the constituent elements (purity 99.9 weight percent), then drop casting into a water-cooled copper hearth. To achieve a homogeneous distribution of elements in the alloy, the melting and solidification processes were repeated five times. The composition of the sample was measured by the low-magnification EDS method. The measurements were repeated twice at different regions (see Table 1). Annealed samples of the CrMoNbV alloy were encapsulated in quartz tubes, filling with high-purity argon after vacuuming several times. The samples were heat treated at 1273 K for 21 days and 1473 K for 3 days, respectively, and then water quenched to validate the stability of the BCC phase. After obtaining the 1473 K-annealed samples, another annealing treatment at 1673 K for 12 h was performed using a 1473 K-annealed sample to verify the stability of the C15-Laves phase. Further annealing at 1863 K revealed a novel carbide stabilized by impurities.

Microscopy

A LEO Gemini 1525 field emission scanning electron microscopy (SEM) coupled with EDS was utilized to characterize the microstructure and composition of this alloy. Transmission-electron microscopy (TEM) was conducted to identify the new phase in the 1863 K-annealed state, using ZEISS LIBRA 200 HT FE MC coupled with EDS. The SEM specimens were initially polished with 1200-grit SiC paper and, subsequently, vibrationally polished using 0.05 μm SiC liquid for the final surface clarification. Focused ion beam (FIB) milling was used for the preparation of TEM specimens, targeting the specific phase. The average compositions of each phase were measured at five different locations to ensure compositional accuracy.

X-ray diffraction

Synchrotron X-ray diffraction experiments were carried out at the Argonne National Laboratory, Advanced Photon Source, using the beamline 11-ID-C. The bulk specimens (~1 mm thick) after the SEM characterization were measured by a beam energy of 111 keV (0.11798 Å) with a beam size of 0.5 × 0.5 mm.

Data Availability

The authors declare that all data supporting the findings of this study are available within the paper and its supplementary information files.